question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
binary-prefix-divisible-by-5 | c++ solution with explaination of modulo | c-solution-with-explaination-of-modulo-b-xtqr | Let say we have "011111". It produces 0, 1, 3, 7, 15, 31 . If we track modulo instead, we will have 0, 1, 3, 2, 0, 1 so the result is the same. we are interest | Astrophile_M | NORMAL | 2021-05-29T14:37:35.203688+00:00 | 2021-05-29T14:37:35.203723+00:00 | 82 | false | Let say we have "011111". It produces 0, 1, 3, 7, 15, 31 . If we track modulo instead, we will have 0, 1, 3, 2, 0, 1 so the result is the same. we are interested if our number is divisible by 5 or not. So to stop the overflow, modulo will make the number smaller and answer remain same. \n```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n vector<bool> v;\n int x = nums[0];\n if(x==0) v.push_back(1);\n else v.push_back(0); \n for(int i=1;i<nums.size();i++)\n {\n x = 2*x + nums[i];\n if(x%5==0)\n {\n v.push_back(1);\n }\n else\n {\n v.push_back(0);\n }\n x=x%5; \n }\n return v;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
binary-prefix-divisible-by-5 | Fast and Simple C++ | fast-and-simple-c-by-arpit_sat-279e | \nvector<bool> prefixesDivBy5(vector<int>& A) {\n\tint val=0;\n\tvector<bool> res(A.size());\n\tfor(int i=0;i<A.size();i++)\n\t{\n\t\tval=val*2+A[i];\n\t\tif(va | Arpit_Sat | NORMAL | 2021-04-04T17:41:49.206153+00:00 | 2021-04-04T17:41:49.206193+00:00 | 117 | false | ```\nvector<bool> prefixesDivBy5(vector<int>& A) {\n\tint val=0;\n\tvector<bool> res(A.size());\n\tfor(int i=0;i<A.size();i++)\n\t{\n\t\tval=val*2+A[i];\n\t\tif(val%5==0)\n\t\t\tres[i]=true;\n\t\tval=val%5;\n\t}\n\treturn res;\n}\n``` | 1 | 0 | [] | 0 |
binary-prefix-divisible-by-5 | Easy python3 implementation | easy-python3-implementation-by-zwerhu-yqd0 | isDivisible = [False for i in range(len(A))]\n result = A[0]\n isDivisible[0] = True if result % 5 == 0 else False \n for i in range(1, len | zwerhu | NORMAL | 2021-04-03T22:49:18.106431+00:00 | 2021-04-03T22:49:18.106477+00:00 | 78 | false | isDivisible = [False for i in range(len(A))]\n result = A[0]\n isDivisible[0] = True if result % 5 == 0 else False \n for i in range(1, len(A)):\n result = 2 * result + A[i]\n isDivisible[i] = True if result % 5 == 0 else False \n \n return isDivisible\n | 1 | 0 | [] | 0 |
binary-prefix-divisible-by-5 | c++(4ms 99,80%) bit manipulation (with comments) | c4ms-9980-bit-manipulation-with-comments-8asm | Runtime: 4 ms, faster than 99.80% of C++ online submissions for Binary Prefix Divisible By 5.\nMemory Usage: 13.9 MB, less than 62.92% of C++ online submissions | zx007pi | NORMAL | 2021-03-21T20:27:59.555780+00:00 | 2021-03-21T20:27:59.555815+00:00 | 152 | false | Runtime: 4 ms, faster than 99.80% of C++ online submissions for Binary Prefix Divisible By 5.\nMemory Usage: 13.9 MB, less than 62.92% of C++ online submissions for Binary Prefix Divisible By 5.\n```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& A) {\n vector<bool> ans;\n unsigned long rep = 0; //binary representation\n for(int i = 0; i < A.size(); i++){\n int limit = i + 60; //fetch 60 numbers\n \n for(int j = i; j != A.size() && j != limit; j++){ \n rep = (rep<<1) | A[j] ; //add bit\n if(rep%5) ans.push_back(false); //if not divisible 5\n else ans.push_back(true); //if yes\n }\n \n rep %= 5; //take remainder \n i = limit - 1; \n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C', 'C++'] | 1 |
binary-prefix-divisible-by-5 | Time O(n) Space O(1) Python3 solution | time-on-space-o1-python3-solution-by-mhv-h5d8 | \n\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n # time O(n)\n # space O(1)\n output = []\n last_bit | mhviraf | NORMAL | 2021-02-11T03:21:52.064771+00:00 | 2021-02-11T03:22:07.865139+00:00 | 136 | false | \n```\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n # time O(n)\n # space O(1)\n output = []\n last_bit = 0\n for i in range(len(A)):\n new_bit = last_bit*2 + A[i]\n output.append(new_bit % 5 == 0)\n last_bit = new_bit\n return output\n``` | 1 | 0 | ['Python', 'Python3'] | 0 |
binary-prefix-divisible-by-5 | Easy C++ Binary Prefix Divisible By 5 | easy-c-binary-prefix-divisible-by-5-by-r-g390 | Naive Solution\nRefrence - https://leetcode.com/problems/binary-prefix-divisible-by-5/discuss/265601/Detailed-Explanation-using-Modular-Arithmetic-O(n)\n\n\ncla | rajawatbanna | NORMAL | 2021-01-22T06:27:03.298766+00:00 | 2021-01-22T06:27:03.298810+00:00 | 147 | false | # Naive Solution\nRefrence - https://leetcode.com/problems/binary-prefix-divisible-by-5/discuss/265601/Detailed-Explanation-using-Modular-Arithmetic-O(n)\n\n```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& A) {\n vector<bool> lks;\n int n=0;\n for(auto x:A){\n n=(n*2+x)%5;\n lks.push_back(n==0);\n }\n return lks;\n }\n};\n```\n\n# Bitwise Solution\n```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& A) {\n vector<bool> lks;\n int n=0;\n for(auto x:A){\n n=(n<<1 | x)%5;\n lks.push_back(n==0);\n }\n return lks;\n }\n};\n```\n# TOC Solution\nRefrence - https://leetcode.com/problems/binary-prefix-divisible-by-5/discuss/800137/C%2B%2B-simple-Transition-graph-99-fast\n\n```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& A) {\n int q = 0; \n vector<bool> lks(A.size());\n \n for(int i=0; i<A.size(); i++){\n int n = A[i];\n if(q == 0) q = n; \n else if(q == 1) q = 2 + n; \n else if(q == 2) q = n == 1 ? 0 : 4; \n else if(q == 3) q = q - (2-n); \n else if(q == 4) q = q - (1-n); \n lks[i] = q == 0; \n }\n return lks;\n }\n};\n``` | 1 | 0 | ['C'] | 0 |
binary-prefix-divisible-by-5 | Java Solution | java-solution-by-suruchigarg12-a1cd | \nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n int n = 0;\n List<Boolean> ans = new ArrayList<>();\n \n fo | suruchigarg12 | NORMAL | 2020-12-07T04:02:40.528957+00:00 | 2020-12-07T04:02:40.529001+00:00 | 173 | false | ```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n int n = 0;\n List<Boolean> ans = new ArrayList<>();\n \n for(int num : A){\n n += num;\n ans.add(n%5 == 0);\n n = n*2;\n n = n%5;\n }\n \n return ans;\n \n }\n}\n``` | 1 | 0 | [] | 0 |
binary-prefix-divisible-by-5 | c++ solution easy | c-solution-easy-by-dilipsuthar60-9glw | \nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& A) \n {\n vector<bool>v;\n int n=A.size();\n int num=A[0];\n | dilipsuthar17 | NORMAL | 2020-11-24T08:42:41.114845+00:00 | 2020-11-24T08:42:41.114873+00:00 | 197 | false | ```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& A) \n {\n vector<bool>v;\n int n=A.size();\n int num=A[0];\n if(num%5==0)\n {\n v.push_back(true);\n }\n else\n {\n v.push_back(false);\n }\n for(int i=1;i<n;i++)\n {\n num=(num<<1|A[i]);\n if(num%5==0)\n {\n num=num%5;\n v.push_back(true);\n }\n else\n {\n num=num%5;\n v.push_back(false);\n }\n }\n return v;\n }\n};\n``` | 1 | 0 | [] | 0 |
binary-prefix-divisible-by-5 | Java | Modular Arithmetic | java-modular-arithmetic-by-rajarshi-sark-6h0s | \nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n int n = 0;\n List<Boolean> answer = new ArrayList<>();\n \n | rajarshi-sarkar | NORMAL | 2020-11-19T16:28:41.060804+00:00 | 2020-11-19T16:28:41.060850+00:00 | 156 | false | ```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n int n = 0;\n List<Boolean> answer = new ArrayList<>();\n \n for(int num : A) {\n n += num;\n answer.add(n % 5 == 0);\n n *= 2;\n n = n % 5;\n }\n \n return answer;\n }\n}\n``` | 1 | 0 | [] | 0 |
binary-prefix-divisible-by-5 | Python, mod | python-mod-by-blue_sky5-030m | \nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]: \n num = 0\n for i in range(len(A)):\n num = 2*num | blue_sky5 | NORMAL | 2020-11-11T02:55:37.539112+00:00 | 2020-11-11T02:55:37.539159+00:00 | 148 | false | ```\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]: \n num = 0\n for i in range(len(A)):\n num = 2*num + A[i]\n A[i] = True if num % 5 == 0 else False\n \n return A\n``` | 1 | 0 | ['Python3'] | 0 |
binary-prefix-divisible-by-5 | Simple & Easy Solution by Python 3 | simple-easy-solution-by-python-3-by-jame-jd1p | \nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n for i in range(1, len(A)):\n A[i] += A[i - 1] * 2\n retu | jamesujeon | NORMAL | 2020-10-31T14:26:34.813183+00:00 | 2020-10-31T14:26:34.813208+00:00 | 134 | false | ```\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n for i in range(1, len(A)):\n A[i] += A[i - 1] * 2\n return [n % 5 == 0 for n in A]\n``` | 1 | 0 | ['Python3'] | 0 |
binary-prefix-divisible-by-5 | Faster then 100% JAVA C++ | faster-then-100-java-c-by-akshatkamboj37-yb51 | UPVOTE IF YOU LIKE\n\n\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& A) {\n int n = A.size();\n vector<bool> res(n,fals | Akshatkamboj37 | NORMAL | 2020-10-12T06:17:09.457765+00:00 | 2020-10-12T06:17:09.457805+00:00 | 119 | false | # UPVOTE IF YOU LIKE\n```\n\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& A) {\n int n = A.size();\n vector<bool> res(n,false);\n int val = 0 ;\n for(int i=0;i<n;i++){\n if(!((val = val*2 + A[i])%=5)) \n res[i]=true;\n }\n return res;\n }\n};\n``` | 1 | 1 | [] | 0 |
binary-prefix-divisible-by-5 | Python simple solution | python-simple-solution-by-shubham_1611-b234 | \nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n n=len(A)\n ans=[]\n sub=""\n \n for i in range | shubham_1611 | NORMAL | 2020-09-28T00:50:54.269155+00:00 | 2020-09-28T00:50:54.269184+00:00 | 139 | false | ```\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n n=len(A)\n ans=[]\n sub=""\n \n for i in range(n):\n sub=sub+str(A[i])\n num=int(sub,2)\n \n if num % 5==0:\n ans.append(True)\n else:\n ans.append(False)\n \n \n return ans \n``` | 1 | 0 | ['Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | [C++, Java, Python] 🏓 Ping Pong Dijkstra | c-java-python-ping-pong-dijkstra-by-toju-4yvg | \n# Intuition\nWe want to find minimum time to reach bottom right cell. We\'ll have to traverse the matrix as the time in each cell allows. We can use a priorit | tojuna | NORMAL | 2023-02-26T04:01:22.713529+00:00 | 2023-02-26T05:23:22.040025+00:00 | 12,367 | false | \n# Intuition\nWe want to find minimum time to reach bottom right cell. We\'ll have to traverse the matrix as the time in each cell allows. We can use a priority queue to keep track of time.\nSome things to keep in mind:\n1. If we can not move to the neighboring cells from starting position we can not move anywhere in the matrix hence answer is -1. \n2. But if we can move to the neighboring cells from starting position, we can move anywhere in the matrix. We can wait by playing "ping pong" between previous cell and current cell till a neighboring cell opens up.\n\n\n# Approach\n* If `grid[0][1] > 1 and grid[1][0] > 1` we can not move anywhere from cell `grid[0][0]` hence answer is `-1`\n* Use priority queue to find next cell with minimum time to move to it\n* If time for a neighbor (target) cell is > 1 + time for current cell. We can not directly move to target cell. We will have to "ping pong" between previous cell and current cell. When playing ping pong between previous and current cell there can be two cases. \n * Let\'s say time for target cell is 4 and current time is 2, difference = 2 (even).\n * Move to prev cell, time = 3\n * Move to curr cell, time = 4\n * Move to target cell, time = 5. \n * Hence we reach target cell with time: **target cell time + 1** when difference between target cell time and curr cell time is even.\n * Let\'s say time for target cell is 5 and current time is 2, difference = 3 (odd).\n * Move to prev cell, time = 3\n * Move to curr cell, time = 4\n * Move to target cell, time = 5. \n * Hence we reach target cell with time: target cell time when difference between target cell time and curr cell time is odd.\n * This "ping pong" is captured in the `wait` variable in the code\n\n\n# Complexity\n- Time complexity: `O(mnlog(mn))`\n\n- Space complexity: `O(mn)`\n\n# Code\n**Python3**:\n```\ndef minimumTime(self, grid: List[List[int]]) -> int:\n if grid[0][1] > 1 and grid[1][0] > 1: return -1\n m, n = len(grid), len(grid[0])\n visited = set()\n pq = [(grid[0][0], 0, 0)]\n \n while pq:\n time, row, col = heappop(pq)\n if row == m-1 and col == n-1: return time\n if (row, col) in visited: continue\n visited.add((row, col))\n for dr, dc in [(0, 1), (0, -1), (1, 0), (-1, 0)]:\n r, c = row + dr, col + dc\n if 0 <= r < m and 0 <= c < n and (r, c) not in visited:\n wait = 1 if ((grid[r][c] - time) % 2 == 0) else 0\n heappush(pq, (max(time + 1, grid[r][c] + wait), r, c))\n```\n\n**C++**\n```\nint minimumTime(vector<vector<int>>& grid) {\n // Check if the starting points are blocked\n if (grid[0][1] > 1 && grid[1][0] > 1) return -1;\n \n int m = grid.size(), n = grid[0].size();\n vector<vector<int>> dirs{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n vector<vector<bool>> visited(m, vector<bool>(n, false));\n priority_queue<vector<int>, vector<vector<int>>, greater<>> pq;\n \n pq.push({grid[0][0], 0, 0}); // Start at top-left corner\n while (!pq.empty()) {\n // Get the current time, row, and column\n int time = pq.top()[0], row = pq.top()[1], col = pq.top()[2];\n pq.pop();\n \n // Check if we\'ve reached the bottom-right corner\n if (row == m - 1 && col == n - 1) return time;\n \n // Mark the current cell as visited\n if (visited[row][col]) continue;\n visited[row][col] = true;\n \n // Explore the neighboring cells\n for (auto dr: dirs) {\n int r = row + dr[0], c = col + dr[1];\n if (r < 0 || r >= m || c < 0 || c >= n || visited[r][c]) continue;\n \n // Calculate the time required to reach the neighboring cell\n int wait = (grid[r][c] - time) % 2 == 0;\n pq.push({max(grid[r][c] + wait, time + 1), r, c});\n }\n }\n return -1; // We couldn\'t reach the bottom-right corner. \n // We will never actually encounter this in practice.\n}\n```\n\n**Java**:\n```\npublic int minimumTime(int[][] grid) {\n if (grid[0][1] > 1 && grid[1][0] > 1) return -1;\n \n int m = grid.length, n = grid[0].length;\n int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n boolean[][] visited = new boolean[m][n];\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));\n pq.offer(new int[]{grid[0][0], 0, 0});\n \n while (!pq.isEmpty()) {\n int[] curr = pq.poll();\n int time = curr[0], row = curr[1], col = curr[2];\n \n if (row == m - 1 && col == n - 1) return time;\n if (visited[row][col]) continue;\n visited[row][col] = true;\n \n for (int[] dir : dirs) {\n int r = row + dir[0], c = col + dir[1];\n if (r < 0 || r >= m || c < 0 || c >= n || visited[r][c]) continue;\n int wait = ((grid[r][c] - time) % 2 == 0) ? 1 : 0;\n pq.offer(new int[]{Math.max(grid[r][c] + wait, time + 1), r, c});\n }\n }\n return -1;\n}\n``` | 213 | 0 | ['C++', 'Java', 'Python3'] | 26 |
minimum-time-to-visit-a-cell-in-a-grid | ✅ Video | Beats 100% | Dijkstra's Algorithm | video-beats-100-dijkstras-algorithm-by-p-98q3 | \n\nhttps://youtu.be/Kj98r8IgJOQ?si=t5CGvV0eYvsxm6dX\n\n# #1 Mod Dijkstra\'s Algorithm (Beats 95-100%)\npython3 []\nclass Solution:\n def minimumTime(self, g | Piotr_Maminski | NORMAL | 2024-11-25T23:51:36.918129+00:00 | 2024-11-29T03:31:44.379105+00:00 | 10,347 | false | \n\nhttps://youtu.be/Kj98r8IgJOQ?si=t5CGvV0eYvsxm6dX\n\n# #1 Mod Dijkstra\'s Algorithm (Beats 95-100%)\n```python3 []\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n MOVES = ((-1, 0), (0, 1), (1, 0), (0, -1))\n \n if grid[0][1] > 1 and grid[1][0] > 1:\n return -1\n \n rows, cols = len(grid), len(grid[0])\n pq = [(0, 0, 0)] # time, row(x), col(y)\n seen = [[False] * cols for _ in range(rows)]\n seen[0][0] = True\n \n while pq:\n time, row, col = heappop(pq)\n \n for dr, dc in MOVES:\n newRow, newCol = row + dr, col + dc\n \n if (newRow < 0 or newRow >= rows or \n newCol < 0 or newCol >= cols or \n seen[newRow][newCol]):\n continue\n \n newTime = time + 1\n if grid[newRow][newCol] > newTime:\n newTime += (grid[newRow][newCol] - time) // 2 * 2\n \n if newRow == rows - 1 and newCol == cols - 1:\n return newTime\n \n seen[newRow][newCol] = True\n heappush(pq, (newTime, newRow, newCol))\n \n return -1\n```\n```cpp []\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n if (grid[0][1] > 1 && grid[1][0] > 1) return -1;\n \n int rows = grid.size();\n int cols = grid[0].size();\n \n priority_queue<pair<int, pair<int, int>>, \n vector<pair<int, pair<int, int>>>, \n greater<pair<int, pair<int, int>>>> minHeap;\n \n minHeap.push({0, {0, 0}}); // time, row(x), col(y)\n \n vector<vector<int>> seen(rows, vector<int>(cols, 0));\n seen[0][0] = 1;\n \n vector<pair<int, int>> moves = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\n \n while (!minHeap.empty()) {\n auto curr = minHeap.top();\n int currTime = curr.first;\n int currRow = curr.second.first;\n int currCol = curr.second.second;\n \n minHeap.pop();\n \n if (currRow == rows - 1 && currCol == cols - 1) \n return currTime;\n \n for (auto move : moves) {\n int nextRow = move.first + currRow;\n int nextCol = move.second + currCol;\n \n if (nextRow >= 0 && nextCol >= 0 && \n nextRow < rows && nextCol < cols && \n !seen[nextRow][nextCol]) {\n \n int waitTime = ((grid[nextRow][nextCol] - currTime) % 2 == 0) ? 1 : 0;\n int nextTime = max(currTime + 1, grid[nextRow][nextCol] + waitTime);\n \n minHeap.push({nextTime, {nextRow, nextCol}});\n seen[nextRow][nextCol] = 1;\n }\n }\n }\n return -1;\n }\n};\n```\n```cpp [C++ v2]\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n if (grid[0][1] > 1 && grid[1][0] > 1) return -1;\n \n int rows = grid.size();\n int cols = grid[0].size();\n int maxPos = rows * cols;\n \n priority_queue<pair<int, int>, \n vector<pair<int, int>>, \n greater<pair<int, int>>> minHeap;\n \n minHeap.push({0, 0}); // time, encoded position\n \n vector<bool> seen(maxPos, false); \n seen[0] = true;\n \n const int moves[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\n \n while (!minHeap.empty()) {\n auto [currTime, pos] = minHeap.top();\n int currRow = pos / cols;\n int currCol = pos % cols;\n \n minHeap.pop();\n \n if (currRow == rows - 1 && currCol == cols - 1) \n return currTime;\n \n for (const auto& move : moves) {\n int nextRow = move[0] + currRow;\n int nextCol = move[1] + currCol;\n int nextPos = nextRow * cols + nextCol;\n \n if (nextRow >= 0 && nextCol >= 0 && \n nextRow < rows && nextCol < cols && \n !seen[nextPos]) {\n \n int waitTime = ((grid[nextRow][nextCol] - currTime) % 2 == 0) ? 1 : 0;\n int nextTime = max(currTime + 1, grid[nextRow][nextCol] + waitTime);\n \n minHeap.push({nextTime, nextPos});\n seen[nextPos] = true;\n }\n }\n }\n return -1;\n }\n};\n```\n```java []\nclass Solution {\n private static final int[][] MOVES = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};\n \n public int minimumTime(int[][] grid) {\n int rows = grid.length;\n int cols = grid[0].length;\n \n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n \n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]); \n boolean[][] seen = new boolean[rows][cols];\n \n pq.offer(new int[]{0, 0, 0}); // time, row, col\n seen[0][0] = true;\n \n while (!pq.isEmpty()) {\n int[] curr = pq.poll();\n int time = curr[0];\n int row = curr[1];\n int col = curr[2];\n \n for (int[] dir : MOVES) {\n int newRow = row + dir[0];\n int newCol = col + dir[1];\n \n if (newRow < 0 || newRow >= rows || \n newCol < 0 || newCol >= cols || \n seen[newRow][newCol]) {\n continue;\n }\n \n int newTime = time + 1;\n if (grid[newRow][newCol] > newTime) {\n int wait = ((grid[newRow][newCol] - newTime + 1) / 2) * 2;\n newTime += wait;\n }\n \n if (newRow == rows - 1 && newCol == cols - 1) {\n return newTime;\n }\n \n seen[newRow][newCol] = true;\n pq.offer(new int[]{newTime, newRow, newCol});\n }\n }\n \n return -1;\n }\n}\n```\n```csharp []\npublic class Solution {\n private static readonly (int dr, int dc)[] MOVES = { (-1, 0), (0, 1), (1, 0), (0, -1) };\n \n public int MinimumTime(int[][] grid) {\n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n \n int rows = grid.Length;\n int cols = grid[0].Length;\n var pq = new PriorityQueue<(int time, int row, int col), int>();\n pq.Enqueue((0, 0, 0), 0); // time, row, col, queue\n \n bool[][] seen = new bool[rows][];\n for (int i = 0; i < rows; i++) {\n seen[i] = new bool[cols];\n }\n seen[0][0] = true;\n \n while (pq.Count > 0) {\n var (time, row, col) = pq.Dequeue();\n \n foreach (var (dr, dc) in MOVES) {\n int newRow = row + dr;\n int newCol = col + dc;\n \n if (newRow < 0 || newRow >= rows || \n newCol < 0 || newCol >= cols || \n seen[newRow][newCol]) {\n continue;\n }\n \n int newTime = time + 1;\n if (grid[newRow][newCol] > newTime) {\n newTime += ((grid[newRow][newCol] - time) / 2) * 2;\n }\n \n if (newRow == rows - 1 && newCol == cols - 1) {\n return newTime;\n }\n \n seen[newRow][newCol] = true;\n pq.Enqueue((newTime, newRow, newCol), newTime);\n }\n }\n \n return -1;\n }\n}\n```\n```golang []\ntype Cell struct {\n time, row, col int\n}\n\ntype PriorityQueue []Cell\n\nfunc (pq PriorityQueue) Len() int { return len(pq) }\nfunc (pq PriorityQueue) Less(i, j int) bool { return pq[i].time < pq[j].time }\nfunc (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }\nfunc (pq *PriorityQueue) Push(x interface{}) { *pq = append(*pq, x.(Cell)) }\nfunc (pq *PriorityQueue) Pop() interface{} {\n old := *pq\n n := len(old)\n item := old[n-1]\n *pq = old[0 : n-1]\n return item\n}\n\nfunc minimumTime(grid [][]int) int {\n if grid[0][1] > 1 && grid[1][0] > 1 {\n return -1\n }\n \n rows, cols := len(grid), len(grid[0])\n minHeap := &PriorityQueue{}\n heap.Init(minHeap)\n heap.Push(minHeap, Cell{0, 0, 0}) // time, row, col\n \n seen := make([][]int, rows)\n for i := range seen {\n seen[i] = make([]int, cols)\n }\n seen[0][0] = 1\n \n moves := [][2]int{{0, 1}, {0, -1}, {1, 0}, {-1, 0}}\n \n for minHeap.Len() > 0 {\n curr := heap.Pop(minHeap).(Cell)\n currTime := curr.time\n currRow := curr.row\n currCol := curr.col\n \n if currRow == rows-1 && currCol == cols-1 {\n return currTime\n }\n \n for _, move := range moves {\n nextRow := move[0] + currRow\n nextCol := move[1] + currCol\n \n if nextRow >= 0 && nextCol >= 0 && \n nextRow < rows && nextCol < cols && \n seen[nextRow][nextCol] == 0 {\n \n waitTime := 0\n if (grid[nextRow][nextCol]-currTime)%2 == 0 {\n waitTime = 1\n }\n nextTime := max(currTime+1, grid[nextRow][nextCol]+waitTime)\n \n heap.Push(minHeap, Cell{nextTime, nextRow, nextCol})\n seen[nextRow][nextCol] = 1\n }\n }\n }\n return -1\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n```javascript [JS]\n// JavaScript\n\nvar minimumTime = function(grid) {\n const MOVES = [[-1, 0], [0, 1], [1, 0], [0, -1]];\n \n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n \n const rows = grid.length;\n const cols = grid[0].length;\n const seen = Array(rows).fill().map(() => Array(cols).fill(false));\n seen[0][0] = true;\n \n const pq = new MinPriorityQueue({\n priority: x => x[0]\n });\n pq.enqueue([0, 0, 0]); // time, row, col\n \n while (!pq.isEmpty()) {\n const [time, row, col] = pq.dequeue().element;\n \n for (const [dr, dc] of MOVES) {\n const newRow = row + dr;\n const newCol = col + dc;\n \n if (newRow < 0 || newRow >= rows || \n newCol < 0 || newCol >= cols || \n seen[newRow][newCol]) {\n continue;\n }\n \n let newTime = time + 1;\n if (grid[newRow][newCol] > newTime) {\n newTime += Math.floor((grid[newRow][newCol] - time) / 2) * 2;\n }\n \n if (newRow === rows - 1 && newCol === cols - 1) {\n return newTime;\n }\n \n seen[newRow][newCol] = true;\n pq.enqueue([newTime, newRow, newCol]);\n }\n }\n \n return -1;\n};\n```\n```rust []\nuse std::collections::BinaryHeap;\nuse std::cmp::Reverse;\n\nimpl Solution {\n pub fn minimum_time(grid: Vec<Vec<i32>>) -> i32 {\n let moves = [(-1, 0), (0, 1), (1, 0), (0, -1)];\n \n if grid[0][1] > 1 && grid[1][0] > 1 {\n return -1;\n }\n \n let (rows, cols) = (grid.len(), grid[0].len());\n let mut pq = BinaryHeap::new();\n let mut seen = vec![vec![false; cols]; rows];\n \n pq.push(Reverse((0, 0, 0))); // (time, row, col)\n seen[0][0] = true;\n \n while let Some(Reverse((time, row, col))) = pq.pop() {\n for &(dr, dc) in &moves {\n let new_row = row as i32 + dr;\n let new_col = col as i32 + dc;\n \n if new_row < 0 || new_row >= rows as i32 || \n new_col < 0 || new_col >= cols as i32 ||\n seen[new_row as usize][new_col as usize] {\n continue;\n }\n \n let mut new_time = time + 1;\n let cell_value = grid[new_row as usize][new_col as usize];\n \n if cell_value > new_time {\n new_time += ((cell_value - time) / 2) * 2;\n }\n \n if new_row as usize == rows - 1 && new_col as usize == cols - 1 {\n return new_time;\n }\n \n seen[new_row as usize][new_col as usize] = true;\n pq.push(Reverse((new_time, new_row as usize, new_col as usize)));\n }\n }\n \n -1\n }\n}\n```\n```ruby []\ndef minimum_time(grid)\n moves = [[-1, 0], [0, 1], [1, 0], [0, -1]]\n \n return -1 if grid[0][1] > 1 && grid[1][0] > 1\n \n rows, cols = grid.length, grid[0].length\n pq = [[0, 0, 0]] # time, row(x), col(y)\n seen = Array.new(rows) { Array.new(cols, false) }\n seen[0][0] = true\n \n while !pq.empty?\n time, row, col = pq.shift\n \n moves.each do |dr, dc|\n new_row, new_col = row + dr, col + dc\n \n next if new_row < 0 || new_row >= rows ||\n new_col < 0 || new_col >= cols ||\n seen[new_row][new_col]\n \n new_time = time + 1\n if grid[new_row][new_col] > new_time\n new_time += ((grid[new_row][new_col] - time) / 2) * 2\n end\n \n return new_time if new_row == rows - 1 && new_col == cols - 1\n \n seen[new_row][new_col] = true\n \n insert_idx = pq.bsearch_index { |x| x[0] > new_time } || pq.length\n pq.insert(insert_idx, [new_time, new_row, new_col])\n end\n end\n \n -1\nend\n```\n\n- Complexity: Time O(RC * log(RC)) & Space O(RC) [R- rows, C - columns ]\n\n# #2 Mod Dijkstra\'s Algorithm (from video)\n\n\n```python3 []\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n if min(grid[0][1], grid[1][0]) > 1:\n return -1\n\n min_heap = [(0, 0, 0)] # (time, r, c)\n ROWS, COLS = len(grid), len(grid[0])\n visit = set()\n\n while min_heap:\n t, r, c = heapq.heappop(min_heap)\n if (r, c) == (ROWS - 1, COLS - 1):\n return t\n\n nei = [(r + 1, c), (r - 1, c), (r, c + 1), (r, c - 1)]\n for nr, nc in nei:\n if nr < 0 or nc < 0 or nr == ROWS or nc == COLS or (nr, nc) in visit:\n continue\n\n wait = 0\n if abs(grid[nr][nc] - t) % 2 == 0:\n wait = 1\n n_time = max(grid[nr][nc] + wait, t + 1)\n heapq.heappush(min_heap, (n_time, nr, nc))\n visit.add((nr, nc))\n```\n```cpp []\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n if (min(grid[0][1], grid[1][0]) > 1) {\n return -1;\n }\n \n int ROWS = grid.size(), COLS = grid[0].size();\n priority_queue<vector<int>, vector<vector<int>>, greater<>> minHeap;\n minHeap.push({0, 0, 0}); // {time, r, c}\n set<pair<int, int>> visit;\n \n while (!minHeap.empty()) {\n auto curr = minHeap.top();\n minHeap.pop();\n int t = curr[0], r = curr[1], c = curr[2];\n \n if (r == ROWS - 1 && c == COLS - 1) {\n return t;\n }\n \n vector<pair<int, int>> dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n for (auto [dr, dc] : dirs) {\n int nr = r + dr, nc = c + dc;\n if (nr < 0 || nc < 0 || nr == ROWS || nc == COLS || \n visit.count({nr, nc})) {\n continue;\n }\n \n int wait = (abs(grid[nr][nc] - t) % 2 == 0) ? 1 : 0;\n int nTime = max(grid[nr][nc] + wait, t + 1);\n minHeap.push({nTime, nr, nc});\n visit.insert({nr, nc});\n }\n }\n return -1;\n }\n};\n```\n```java []\nclass Solution {\n public int minimumTime(int[][] grid) {\n if (Math.min(grid[0][1], grid[1][0]) > 1) {\n return -1;\n }\n \n int ROWS = grid.length, COLS = grid[0].length;\n PriorityQueue<int[]> minHeap = new PriorityQueue<>((a, b) -> a[0] - b[0]);\n minHeap.offer(new int[]{0, 0, 0}); // {time, r, c}\n Set<String> visit = new HashSet<>();\n \n while (!minHeap.isEmpty()) {\n int[] curr = minHeap.poll();\n int t = curr[0], r = curr[1], c = curr[2];\n \n if (r == ROWS - 1 && c == COLS - 1) {\n return t;\n }\n \n int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n for (int[] dir : dirs) {\n int nr = r + dir[0], nc = c + dir[1];\n String key = nr + "," + nc;\n \n if (nr < 0 || nc < 0 || nr == ROWS || nc == COLS || \n visit.contains(key)) {\n continue;\n }\n \n int wait = (Math.abs(grid[nr][nc] - t) % 2 == 0) ? 1 : 0;\n int nTime = Math.max(grid[nr][nc] + wait, t + 1);\n minHeap.offer(new int[]{nTime, nr, nc});\n visit.add(key);\n }\n }\n return -1;\n }\n}\n```\n```csharp []\npublic class Solution {\n public int MinimumTime(int[][] grid) {\n if (Math.Min(grid[0][1], grid[1][0]) > 1) {\n return -1;\n }\n \n int ROWS = grid.Length, COLS = grid[0].Length;\n var minHeap = new PriorityQueue<(int t, int r, int c), int>();\n minHeap.Enqueue((0, 0, 0), 0); // (time, r, c)\n var visit = new HashSet<string>();\n \n while (minHeap.Count > 0) {\n var (t, r, c) = minHeap.Dequeue();\n \n if (r == ROWS - 1 && c == COLS - 1) {\n return t;\n }\n \n var dirs = new[] { (1, 0), (-1, 0), (0, 1), (0, -1) };\n foreach (var (dr, dc) in dirs) {\n int nr = r + dr, nc = c + dc;\n string key = $"{nr},{nc}";\n \n if (nr < 0 || nc < 0 || nr == ROWS || nc == COLS || \n visit.Contains(key)) {\n continue;\n }\n \n int wait = (Math.Abs(grid[nr][nc] - t) % 2 == 0) ? 1 : 0;\n int nTime = Math.Max(grid[nr][nc] + wait, t + 1);\n minHeap.Enqueue((nTime, nr, nc), nTime);\n visit.Add(key);\n }\n }\n return -1;\n }\n}\n```\n```golang []\npackage main\n\nimport (\n "container/heap"\n "fmt"\n)\n\ntype MinHeap [][]int\n\nfunc (h MinHeap) Len() int { return len(h) }\nfunc (h MinHeap) Less(i, j int) bool { return h[i][0] < h[j][0] }\nfunc (h MinHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\n\nfunc (h *MinHeap) Push(x interface{}) {\n *h = append(*h, x.([]int))\n}\n\nfunc (h *MinHeap) Pop() interface{} {\n old := *h\n n := len(old)\n x := old[n-1]\n *h = old[0 : n-1]\n return x\n}\n\nfunc abs(x int) int {\n if x < 0 {\n return -x\n }\n return x\n}\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n return b\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n\nfunc minimumTime(grid [][]int) int {\n if min(grid[0][1], grid[1][0]) > 1 {\n return -1\n }\n \n rows, cols := len(grid), len(grid[0])\n minHeap := &MinHeap{}\n heap.Init(minHeap)\n heap.Push(minHeap, []int{0, 0, 0}) // time, r, c\n visited := make(map[string]bool)\n \n dirs := [][]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}\n \n for minHeap.Len() > 0 {\n curr := heap.Pop(minHeap).([]int)\n t, r, c := curr[0], curr[1], curr[2]\n \n if r == rows-1 && c == cols-1 {\n return t\n }\n \n for _, dir := range dirs {\n nr, nc := r+dir[0], c+dir[1]\n key := fmt.Sprintf("%d,%d", nr, nc)\n \n if nr < 0 || nc < 0 || nr == rows || nc == cols || visited[key] {\n continue\n }\n \n wait := 0\n if abs(grid[nr][nc]-t)%2 == 0 {\n wait = 1\n }\n nTime := max(grid[nr][nc]+wait, t+1)\n heap.Push(minHeap, []int{nTime, nr, nc})\n visited[key] = true\n }\n }\n return -1\n}\n```\n```javascript [JS]\n// JavaScript\n\nvar minimumTime = function(grid) {\n if (Math.min(grid[0][1], grid[1][0]) > 1) {\n return -1;\n }\n \n const ROWS = grid.length;\n const COLS = grid[0].length;\n const minHeap = new MinPriorityQueue({ priority: x => x[0] });\n minHeap.enqueue([0, 0, 0]); // [time, r, c]\n const visited = new Set();\n \n const dirs = [[1, 0], [-1, 0], [0, 1], [0, -1]];\n \n while (!minHeap.isEmpty()) {\n const [t, r, c] = minHeap.dequeue().element;\n \n if (r === ROWS - 1 && c === COLS - 1) {\n return t;\n }\n \n for (const [dr, dc] of dirs) {\n const nr = r + dr;\n const nc = c + dc;\n const key = `${nr},${nc}`;\n \n if (nr < 0 || nc < 0 || nr === ROWS || nc === COLS || visited.has(key)) {\n continue;\n }\n \n const wait = Math.abs(grid[nr][nc] - t) % 2 === 0 ? 1 : 0;\n const nTime = Math.max(grid[nr][nc] + wait, t + 1);\n minHeap.enqueue([nTime, nr, nc], nTime);\n visited.add(key);\n }\n }\n return -1;\n};\n```\n```typescript [TS]\n// TypeScript\n\nfunction minimumTime(grid: number[][]): number {\n if (Math.min(grid[0][1], grid[1][0]) > 1) {\n return -1;\n }\n \n const ROWS = grid.length;\n const COLS = grid[0].length;\n const minHeap = new MinPriorityQueue({ priority: x => x[0] });\n minHeap.enqueue([0, 0, 0]); // [time, r, c]\n const visited = new Set<string>();\n \n const dirs = [[1, 0], [-1, 0], [0, 1], [0, -1]];\n \n while (!minHeap.isEmpty()) {\n const [t, r, c] = minHeap.dequeue().element;\n \n if (r === ROWS - 1 && c === COLS - 1) {\n return t;\n }\n \n for (const [dr, dc] of dirs) {\n const nr = r + dr;\n const nc = c + dc;\n const key = `${nr},${nc}`;\n \n if (nr < 0 || nc < 0 || nr === ROWS || nc === COLS || visited.has(key)) {\n continue;\n }\n \n const wait = Math.abs(grid[nr][nc] - t) % 2 === 0 ? 1 : 0;\n const nTime = Math.max(grid[nr][nc] + wait, t + 1);\n minHeap.enqueue([nTime, nr, nc]);\n visited.add(key);\n }\n }\n return -1;\n}\n```\n\n- Complexity: Time O(RC * log(RC)) & Space O(RC) [R- rows, C - columns ]\n\n\n\n\n# Explanation\n\n\n---\n\n## Intuition\n\n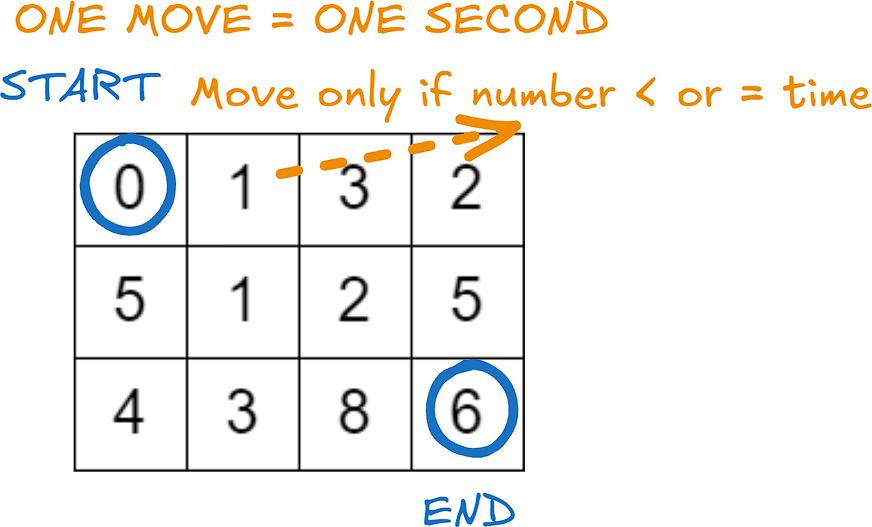\n\n\n\n\n\n\n\n\n\n\n## Graph Theory\n\n- (IMO) the best explaining Video on graph from Google engineer.\nhttps://youtu.be/09_LlHjoEiY?si=EKU-b9pAafWX1Wea\n\n#### [Interview Questions and Answers Repository](https://github.com/RooTinfinite/Interview-questions-and-answers)\n\n | 47 | 3 | ['C++', 'Java', 'Go', 'TypeScript', 'Python3', 'Rust', 'Ruby', 'JavaScript', 'C#'] | 5 |
minimum-time-to-visit-a-cell-in-a-grid | [Python/C++] clean Dijkstra's algorithm solution with explanation | pythonc-clean-dijkstras-algorithm-soluti-dxdg | Explaination\n\nThis problem can be solved using the Dijkstra\'s algorithm with a small variation.\n\nFirstly, note that we can always reach the bottom-right ce | alanlzl | NORMAL | 2023-02-26T04:01:00.289722+00:00 | 2023-02-26T04:23:49.647453+00:00 | 6,639 | false | **Explaination**\n\nThis problem can be solved using the Dijkstra\'s algorithm with a small variation.\n\nFirstly, note that we can always reach the bottom-right cell of the matrix if we can move to at least one adjacent cell (i.e. `grid[0][1]` or `grid[1][0]`). After that, we can simply move back and forth to spend time as needed.\n\nIt\'s also worth noting that we may not always be able to move to an adjacent cell immediately. For example, in Example 1, we have to step back to cell (1,1) before moving to cell (1,3) because we must move every second.\n\nSince it takes an even number of seconds to "stand still" when moving back and forth, we need to wait for an extra second if we want to move after an odd number of seconds\n\nAfter accounting for these factors, we can use the standard Dijkstra\'s algorithm to find the answer.\n\n<br/>\n\n**Complexity**\n\nTime complexity: `O(MNlog(MN))`\nSpace complexity: `O(MN)`\n\n<br/>\n\n**Python**\n```Python\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n if grid[0][1] > 1 and grid[1][0] > 1:\n return -1\n visited = [[False] * n for _ in range(m)]\n heap = [(0, 0, 0)] # (t, r, c)\n while heap:\n t, r, c = heapq.heappop(heap)\n if r == m - 1 and c == n - 1:\n return t\n if visited[r][c]:\n continue\n visited[r][c] = True\n for dr, dc in ((0, 1), (0, -1), (1, 0), (-1, 0)):\n nr, nc = r + dr, c + dc\n if nr < 0 or nr >= m or nc < 0 or nc >= n or visited[nr][nc]:\n continue\n wait = (grid[nr][nc] - t) % 2 == 0\n nt = max(grid[nr][nc] + wait, t + 1)\n heapq.heappush(heap, (nt, nr, nc))\n return -1\n```\n\n<br/>\n\n**C++**\n```cpp\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size();\n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n vector<vector<int>> directions{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n vector<vector<bool>> visited(m, vector<bool>(n, false));\n priority_queue<vector<int>, vector<vector<int>>, greater<>> pq;\n pq.push({0, 0, 0}); // (t, r, c)\n while (!pq.empty()) {\n auto cur = pq.top();\n int t = cur[0], r = cur[1], c = cur[2];\n pq.pop();\n if (r == m - 1 && c == n - 1) {\n return t;\n }\n if (visited[r][c]) {\n continue;\n }\n visited[r][c] = true;\n for (const auto& dir : directions) {\n int nr = r + dir[0], nc = c + dir[1];\n if (nr < 0 || nr >= m || nc < 0 || nc >= n || visited[nr][nc]) {\n continue;\n }\n bool wait = (grid[nr][nc] - t) % 2 == 0;\n int nt = max(grid[nr][nc] + wait, t + 1);\n pq.push({nt, nr, nc});\n }\n }\n return -1;\n }\n};\n``` | 45 | 0 | ['C++', 'Python3'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | Easy Dijkstra | Video solution | Intuition explained | easy-dijkstra-video-solution-intuition-e-c1nd | Intuition\nDoes the solution always exist? \n\n# Approach\nQ. Is there any case where we can not reach the end? \nans: Yes!\n\nQ. That\'s the example test case | i_pranav | NORMAL | 2023-02-26T06:25:34.014322+00:00 | 2023-02-26T07:04:59.309617+00:00 | 2,477 | false | # Intuition\nDoes the solution always exist? \n\n# Approach\nQ. Is there any case where we can not reach the end? \nans: Yes!\n\nQ. That\'s the example test case that has already been provided to us. The exact specifics are that if I can not go to (1,0) and even (0,1) from (0,0) then my answer doesn\'t exist! \nNow in what case it isn\'t possible for me to go to these 2 indices? \nans: Since grid[0][0]=0 hence when the value at (1,0) or (0,1) is greater than 1 itself then I would be blocked. \n\nQ. Is it possible for me to always reach the end otherwise? \nans: yes, let me prove this. Say we are at some node X it\'s parent node is P (all nodes except for (0,0) have a parent node). and from X we want to go to Y. Now 2 cases would arise \ncase1. currentTime(at which I am on X)+1>=VAL[Y], in this case the time I can simply go to Y. \ncase2. I\'ll go back and forth between X and P. 1 unit of time would be spent going from X to P and another to go from P to X. so a round trip would cost us 2 time units. Since we can perform any roundtrips this way hence we add 2*N time where N is the number of roundtrips! \nafter performing some number of roundtrips our time+1 would become greater than VAL[Y] and now I can go to Y! The only point to be noted is that when you peform these roundtrips then it\'s possible that you reach a valud of time t which is 1 more than the optimum value. let\'s say currTime=6, Val[Y]=8 so now you go from X to P and P to X and your time increases by 2 units. so you are at X now with currTime =6+2=8, you need 1 more unit of time to go to Y so you reach there at time 8+1=9 whereas the optimum time would\'ve been 8 units.\n\nVideo solution: https://youtu.be/FEl1u9FvHLE\n\n\n\nPS- code is not mine, I modified the code of some other contributer. \n# Complexity\n- Time complexity:\n- O(m*n*log(mn))\n- Space complexity:\n- O(mn)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n# Code\n```\nclass Solution {\npublic:\nint minimumTime(vector<vector<int>>& grid) {\n // Check if the starting points are blocked\n if (grid[0][1] > 1 && grid[1][0] > 1) return -1;\n \n int n = grid.size(), m = grid[0].size();\n int dirs[]={1,0,-1,0,1};\n int visited[n][m];\n memset(visited,0,sizeof visited);\n priority_queue<vector<int>, vector<vector<int>>, greater<>> pq;\n \n pq.push({grid[0][0], 0, 0}); // Start at top-left corner\n while (!pq.empty()) {\n // Get the current time, row, and column\n int time = pq.top()[0], row = pq.top()[1], col = pq.top()[2];\n pq.pop();\n \n if (row == n - 1 && col == m - 1) return time;\n \n if (visited[row][col]) continue;\n visited[row][col] = true;\n for (int i=0;i<4;i++) {\n int r = row + dirs[i], c = col + dirs[i+1];\n if (r < 0 || r >= n || c < 0 || c >= m || visited[r][c]) continue;\n int wait = (grid[r][c] - time) % 2 == 0?1:0; // we would have to wait 1 more extra unit of time if the difference was already odd. \n pq.push({max(grid[r][c] + wait, time + 1), r, c});\n }\n }\n return -1; \n}\n};\n``` | 33 | 0 | ['C++'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | Dijkstra's Algorithm||87ms Beats 100% | dijkstras-algorithm87ms-beats-100-by-anw-h5yj | Intuition\n Describe your first thoughts on how to solve this problem. \nIt\'s again a question on shortest path.\nSo, Dijkstra\'s Algorithm is applied again.\n | anwendeng | NORMAL | 2024-11-29T00:21:35.270519+00:00 | 2024-12-01T23:37:32.047464+00:00 | 14,149 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt\'s again a question on shortest path.\nSo, Dijkstra\'s Algorithm is applied again.\nThe solution is almost the same in solving [3341. Find Minimum Time to Reach Last Room I](https://leetcode.com/problems/find-minimum-time-to-reach-last-room-i/solutions/6000622/dijkstra-shortest-path18ms-beats-100/). Instead of waiting til the time comes, just make a back and forth movement when necessary, the number of such steps can be any multiple of 2.\n\nPython code is made.\nA* search solution is added.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. The only edge case is when `grid[1][0]>1 && grid[0][1]>1`, just return -1.\n2. Use matrix convention $n \\times m$ matrix `grid`\n3. Set min heap `pq` to hold the info tuple `(time, i, j)`; this part can be slightly modified for the speed.\n4. The distance matrix is 2d array `time`; this part can be modified.\n4. Push info tuple at (0, 0) with time=0 to pq; set `time[0][0]=0`\n5. As long as `pq` is not empty, proceed the BFS over `pq`\n6. Get the info tuple from the top, say `[t, i, j] = pq.top()` then pop\n7. If reaching the destination return `t`\n8. Traverse all four directions, check the adjacent cell `isOutside(r, s, n, m)`, if yes skip it\n9. Compute minimum time to reach (r, s)\n```\nint w=((grid[r][s]-t)&1)?0:1;\nint nextTime = max(t+1, grid[r][s]+w);// backward if neccessary\n```\n11. update if this path having quicker time\n```\nif (nextTime < time[r][s]) {\n time[r][s] = nextTime;\n pq.emplace(nextTime, r, s);\n}\n```\n12. End of the loop, put `return -1;` that will never reach.\n13. Version 2 & Version 3 are so made that 2D arrays are converted into 1D ones, & possibly use C-arrays. \n14. The 3rd C++ version `pq` holds the 64-bit int `((uint64_t)time<<32)+idx(i, j))` which is a C-array.\n15. The pop, push in 1st version is replaced by `pop_heap, push_heap` in the 3rd version.\n# Why no visited array?\nDijkstra\'s Algorithm is in fact a Greedy Algorithm finding the shortest path with ****non-negative weights****. In the codes `if (nextTime < time[r][s]){...}` eliminates the possiblity for revisiting the cell `(r,s)`. By several times of praticing Dijsktra\'s Algorithm, it makes me to figure out this fact.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nm \\log(nm))$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(nm)$$\n# Code||C++ v1 131ms Beats 96.32%||C++ v3 87ms Beats 100%\n\n```cpp [C++ v1]\nusing info = tuple<int, short, short>; // (time, i, j)\nconst static int d[5] = {0, 1, 0, -1, 0};\nclass Solution {\npublic:\n inline static bool isOutside(short i, short j, short n, short m) {\n return i < 0 || i >= n || j < 0 || j >= m;\n }\n\n int minimumTime(vector<vector<int>>& grid) {\n if (grid[1][0]>1 && grid[0][1]>1) return -1;// edge case\n \n short n = grid.size(), m = grid[0].size();\n vector<vector<int>> time(n, vector<int>(m, INT_MAX));\n priority_queue<info, vector<info>, greater<info>> pq;\n\n // Start at (0, 0) with time=0 \n pq.emplace(0, 0, 0);\n time[0][0] = 0;\n while (!pq.empty()) {\n auto [t, i, j] = pq.top();\n pq.pop();\n // cout<<" t="<<int(t)<<" i="<<int(i)<<" j="<<int(j)<<endl;\n // reach the destination\n if (i == n - 1 && j == m - 1)\n return t;\n\n // Traverse all four directions\n for (int a = 0; a < 4; a++) {\n int r = i + d[a], s = j + d[a + 1];\n if (isOutside(r, s, n, m)) continue;\n\n // minimum time to reach (r, s)\n int w=((grid[r][s]-t)&1)?0:1;\n int nextTime = max(t+1, grid[r][s]+w); // backward if neccessary\n\n // update if this path having quicker time\n if (nextTime < time[r][s]) {\n time[r][s] = nextTime;\n pq.emplace(nextTime, r, s);\n }\n }\n }\n\n return -1; // never reach\n }\n};\n\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n```cpp [C++ v3]\nusing info = pair<int, int>; // (time, i*m+j)\nconst static int d[5] = {0, 1, 0, -1, 0};\nclass Solution {\npublic:\n inline static bool isOutside(int i, int j, int n, int m) {\n return i < 0 || i >= n || j < 0 || j >= m;\n }\n inline static int idx(int i, int j, int m) { return i * m + j; }\n\n int minimumTime(vector<vector<int>>& grid) {\n if (grid[1][0] > 1 && grid[0][1] > 1)\n return -1; // edge case\n\n const int n = grid.size(), m = grid[0].size(), N = 100000;\n int time[N];\n fill(time, time + n * m, INT_MAX);\n uint64_t pq[N];\n int back = 0;\n\n // Start at (0, 0) with time=0\n pq[back++] = 0;\n time[0] = 0;\n while (back > 0) {\n pop_heap(pq, pq + back, greater<>{});\n auto tij = pq[--back];\n int t = tij >> 32, ij = tij & ((1 << 30) - 1), i = ij / m,\n j = ij - i * m;\n\n // cout<<" t="<<int(t)<<" i="<<int(i)<<" j="<<int(j)<<endl;\n // reach the destination\n if (i == n - 1 && j == m - 1)\n return t;\n\n // Traverse all four directions\n for (int a = 0; a < 4; a++) {\n int r = i + d[a], s = j + d[a + 1];\n if (isOutside(r, s, n, m))\n continue;\n\n // minimum time to reach (r, s)\n int w = ((grid[r][s] - t) & 1) ? 0 : 1;\n int nextTime =\n max(t + 1, grid[r][s] + w); // backward if neccessary\n\n // update if this path having quicker time\n int rs=idx(r, s, m);\n if (nextTime < time[rs]) {\n time[rs] = nextTime;\n pq[back++] = ((uint64_t)nextTime << 32) + rs;\n push_heap(pq, pq + back, greater<>{});\n }\n }\n }\n\n return -1; // never reach\n }\n};\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# Dijkstra\'s algorithm is suitible to find the shortest path in a weighted Graph\n[Please turn on English subtitles if necessary. 1631 Path With Minimum Effort]\n[https://youtu.be/IkpRzCICL_g?si=joY6antLDgu2RHpB](https://youtu.be/IkpRzCICL_g?si=joY6antLDgu2RHpB)\nMany questions can be solved by using variants of Dijkstra\'s algorithm.\n[1631. Path With Minimum Effort](https://leetcode.com/problems/path-with-minimum-effort/solutions/4049711/c-dijkstra-s-algorithm-vs-dfs-binary-search-vs-union-find-pseudo-metric-91-ms-beats-98-93/)\n[2699. Modify Graph Edge Weights](https://leetcode.com/problems/modify-graph-edge-weights/solutions/5709135/dijkstras-algo-finds-min-distance-by-adding-wildcard-edges477ms-beats-9485/)\n[2290. Minimum Obstacle Removal to Reach Corner](https://leetcode.com/problems/minimum-obstacle-removal-to-reach-corner/solutions/6090250/dijkstra-algorithm-with-weights-same-as-grid-vs-bfs-over-circular-deque-beats-100/)\n[3341. Find Minimum Time to Reach Last Room I](https://leetcode.com/problems/find-minimum-time-to-reach-last-room-i/solutions/6000622/dijkstra-shortest-path18ms-beats-100/)\n[2699. Modify Graph Edge Weights](https://leetcode.com/problems/modify-graph-edge-weights/solutions/5709135/dijkstras-algo-finds-min-distance-by-adding-wildcard-edges477ms-beats-9485/)<--Hardest one ever solved\n# Python code\n```\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n if grid[1][0] > 1 and grid[0][1] > 1:\n return -1\n R, C = len(grid), len(grid[0])\n\n def isOutside(i, j):\n return i < 0 or i >= R or j < 0 or j >= C\n\n def idx(i, j):\n return i * C + j\n\n N = R * C\n time = [2**31] * N\n pq = [0]\n\n time[0] = 0\n while len(pq):\n tij = heappop(pq)\n t, ij = tij >> 32, tij & ((1 << 30) - 1)\n i, j = divmod(ij, C)\n if i == R - 1 and j == C - 1:\n return t\n\n for di, dj in [(0, 1), (1, 0), (0, -1), (-1, 0)]:\n r, s = i + di, j + dj\n if isOutside(r, s):\n continue\n\n w = 0 if (grid[r][s] - t) & 1 else 1\n nextTime = max(t + 1, grid[r][s] + w)\n\n rs = idx(r, s)\n if nextTime < time[rs]:\n time[rs] = nextTime\n heappush(pq, (nextTime << 32) + rs)\n return -1\n\n```\n# A* search \n```\nconst static int d[5] = {0, 1, 0, -1, 0};\nclass Solution {\npublic:\n inline static bool isOutside(int i, int j, int n, int m) {\n return i < 0 || i >= n || j < 0 || j >= m;\n }\n inline static int idx(int i, int j, int m) { return i * m + j; }\n // Use Manhattan distance as heuristic function\n inline static int64_t h(int i, int j, int n, int m) {\n return n + m - 2 - i - j;\n }\n\n int minimumTime(vector<vector<int>>& grid) {\n if (grid[1][0] > 1 && grid[0][1] > 1)\n return -1; // edge case\n\n const int n = grid.size(), m = grid[0].size(), N = 100000;\n int time[N];\n fill(time, time + n * m, INT_MAX);\n uint64_t pq[N];\n int back = 0;\n\n // Start at (0, 0) with f=0+h, note f<<32\n pq[back++] = h(0, 0, n, m)<<32;\n time[0] = 0;\n while (back > 0) {\n pop_heap(pq, pq + back, greater<>{});\n auto fij = pq[--back];\n int f = fij >> 32, ij = fij & ((1 << 30) - 1), i = ij / m,\n j = ij - i * m;\n int heur=h(i, j, n, m), t=f-heur;\n // cout<<" t="<<int(t)<<" i="<<int(i)<<" j="<<int(j)<<endl;\n // reach the destination\n if (heur==0)\n return t;\n\n // Traverse all four directions\n for (int a = 0; a < 4; a++) {\n int r = i + d[a], s = j + d[a + 1];\n if (isOutside(r, s, n, m) || time[idx(r, s, m)] != INT_MAX)\n continue;\n\n // minimum time to reach (r, s)\n int w = ((grid[r][s] - t) & 1) ? 0 : 1;\n int nextTime =\n max(t + 1, grid[r][s] + w); // backward if neccessary\n\n // update if this path having quicker time\n int rs = idx(r, s, m);\n if (nextTime < time[rs]) {\n time[rs] = nextTime;\n pq[back++] = ((h(r, s, n, m) + nextTime) << 32) + rs;\n push_heap(pq, pq + back, greater<>{});\n }\n }\n }\n\n return -1; // never reach\n }\n};\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n | 28 | 0 | ['Array', 'Bit Manipulation', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'C++', 'Python3'] | 4 |
minimum-time-to-visit-a-cell-in-a-grid | Djackstra Solution Visualisation, Commented solution | djackstra-solution-visualisation-comment-veju | \n# Intuition\n Describe your first thoughts on how to solve this problem. \n\nIf you find this useful please give it an upvote!\nSince we have to find the mini | Priyanshu_Chaudhary_ | NORMAL | 2023-02-26T04:03:55.934788+00:00 | 2023-02-26T05:34:00.732928+00:00 | 2,571 | false | \n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n**If you find this useful please give it an upvote!**\nSince we have to find the minimum time and we have to search it. This boils down to **BFS**. However, we have to approach it greedily so we should use **djackstra\'s algorithm which uses minimum Priority_queue\ninstead of queue in bfs**.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe start from `{0,0}`;\nThere are 4 cases that are possible:\n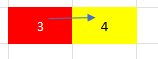\n* If we are at red block at `time=3 sec`, we can move to yellow block at `time=4 sec`. \n \n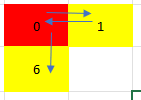\n* If we are at red block at t=1 sec and want to move to block 5\nwe can keep on moving `1->0->1->0->1->1` until we move back to 1 at 5 sec and in that case we move to block 5 at t=7 sec.grid[X][Y]+1\n(if difference is **even**, we reach at `grid[X][Y]+1`)\n\n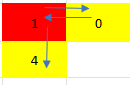\n* To reach from 0 to 4 we keep on moving `0->1->0->1` until at red block and reach it at t=4sec. \n(if difference is **odd**, we reach at `grid[X][Y]`)\n\n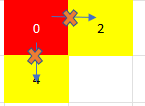\n* If we are at `{0,0}` and we have these two cases above we cannot move to any and in this case we will `return -1`;(edge case).\n\n\n* **Visited array** keeps into account **minimum time instant at which we reach that position X,Y**. If it is smaller than current instant `par[0]+1>=visited[X][Y]` we dont add it in our priority_queue.\n# Complexity\n- Time complexity: O(m*n log(m*n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m*n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution {\npublic:\n int dir[5]={1,0,-1,0,1};\n int visited[1001][1001]; //keeps the minimum instant we reached a point X,Y.\n int minimumTime(vector<vector<int>>& grid) \n {\n \n int m=grid.size(),n=grid[0].size(); \n if(grid[0][1]>1 and grid[1][0]>1) //edgecase: \n return -1; \n for(int i=0;i<m;i++)\n for(int j=0;j<n;j++)\n visited[i][j]=INT_MAX;#initialise visted to INT_MAX. \n priority_queue<pair<int,pair<int,int>>,vector<pair<int,pair<int,int>>>,greater<pair<int,pair<int,int>>>>pq; \n#initialise min priority queue for djackstra traversal\n pq.push({0,{0,0}});\n visited[0][0]=0; #starting position\n while(!pq.empty())\n {\n auto temp=pq.top();\n int par[3]={temp.first,temp.second.first,temp.second.second}; // par[0]->time,par[1]-> i, par[2]-> j\n if(par[1]==m-1 and par[2]==n-1)\n return par[0];\n pq.pop();\n for(int k=0;k<4;k++)\n {\n int X=par[1]+dir[k];\n int Y=par[2]+dir[k+1];\n if(X<0||Y<0||X==m||Y==n||par[0]+1>=visited[X][Y])\n continue; //do not visit is we go out of boundary, or reach node if we have only reached there at smaller time\n int time=0;\n if(par[0]+1>grid[X][Y]) time=par[0]+1; //if we reach at time instant greater\n#than grid[X][Y] time will be par[0]+1; \n else if((grid[X][Y]-par[0])%2) time=grid[X][Y]; //if diff between the two times is odd we will reach that node in time =grid[X][Y];\n else time=grid[X][Y]+1; //if diff between the two times is even we will reach that node in time =grid[X][Y]+1;\n pq.push({time,{X,Y}});\n visited[X][Y]=time; #update time\n }\n }\n return -1;\n }\n};\n``` | 19 | 0 | ['Shortest Path', 'C++'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | Java PriorityQueue with Comments | java-priorityqueue-with-comments-by-zade-m1d1 | \nclass Solution {\n private static final int[][] DIRS = new int[][] { { 1, 0 }, { -1, 0}, { 0, 1 }, { 0, -1 } };\n public int minimumTime(int[][] grid) { | zadeluca | NORMAL | 2023-02-26T04:00:57.675835+00:00 | 2023-02-26T04:01:42.681008+00:00 | 1,766 | false | ```\nclass Solution {\n private static final int[][] DIRS = new int[][] { { 1, 0 }, { -1, 0}, { 0, 1 }, { 0, -1 } };\n public int minimumTime(int[][] grid) {\n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n \n int m = grid.length;\n int n = grid[0].length;\n \n PriorityQueue<int[]> heap = new PriorityQueue<>((a, b) -> a[2] - b[2]);\n heap.offer(new int[] { 0, 0, 0 }); // row, col, time\n \n boolean[][] visited = new boolean[m][n];\n \n while (!heap.isEmpty()) {\n int[] entry = heap.poll();\n int row = entry[0];\n int col = entry[1];\n int time = entry[2];\n if (row == m - 1 && col == n - 1) {\n return time;\n }\n if (visited[row][col]) {\n continue;\n }\n visited[row][col] = true;\n \n for (int[] dir : DIRS) {\n int r = row + dir[0];\n int c = col + dir[1];\n if (r < 0 || r == m || c < 0 || c == n || visited[r][c]) {\n continue;\n }\n \n if (grid[r][c] <= time + 1) {\n // if it is possible to move to neighbor, do it\n heap.offer(new int[] { r, c, time + 1 });\n } else {\n // If we cant move to neighbor yet, we can hop to the previous cell\n // and back to current cell as many times as we need to until\n // sufficient time has passed.\n // The trick here is that if the difference between the current time\n // and the time we need is even, we will arrive back at the current cell\n // 1 second "late" and so we will move to the neighbor 1 second after\n // the minimum neighbor time.\n int diff = grid[r][c] - time;\n if (diff % 2 == 1) {\n heap.offer(new int[] { r, c, grid[r][c] });\n } else {\n heap.offer(new int[] { r, c, grid[r][c] + 1 });\n }\n }\n }\n }\n return -1; // will never reach here\n }\n}\n``` | 17 | 0 | ['Heap (Priority Queue)', 'Java'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | Python | Greedy pattern & Shortest Path (Dijkstra) | python-greedy-pattern-shortest-path-dijk-0oe0 | see the Successfully Accepted Submission\n\n# Code\npython3 []\nimport heapq\nfrom typing import List\n\nclass Solution:\n def minimumTime(self, grid: List[L | Khosiyat | NORMAL | 2024-11-29T00:51:58.339997+00:00 | 2024-11-29T00:51:58.340019+00:00 | 3,085 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/minimum-time-to-visit-a-cell-in-a-grid/submissions/1465412021/?envType=daily-question&envId=2024-11-29)\n\n# Code\n```python3 []\nimport heapq\nfrom typing import List\n\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n directions = [(1, 0), (-1, 0), (0, 1), (0, -1)] # Down, Up, Right, Left\n \n # If the starting point is blocked, return -1\n if grid[0][1] > 1 and grid[1][0] > 1:\n return -1\n \n m, n = len(grid), len(grid[0])\n heap = [(0, 0, 0)] # (time, row, col)\n visited = [[False] * n for _ in range(m)] # To track visited cells\n \n while heap:\n time, row, col = heapq.heappop(heap)\n \n # If we reach the bottom-right corner, return the time\n if row == m - 1 and col == n - 1:\n return time\n \n # Skip if already visited\n if visited[row][col]:\n continue\n visited[row][col] = True\n \n # Explore all directions\n for dr, dc in directions:\n r, c = row + dr, col + dc\n \n # Check bounds and if already visited\n if 0 <= r < m and 0 <= c < n and not visited[r][c]:\n if grid[r][c] <= time + 1:\n heapq.heappush(heap, (time + 1, r, c))\n else:\n diff = grid[r][c] - time\n if diff % 2 == 1:\n heapq.heappush(heap, (grid[r][c], r, c))\n else:\n heapq.heappush(heap, (grid[r][c] + 1, r, c))\n \n # If no valid path is found, return -1\n return -1\n\n```\n\n\n## Steps of the Algorithm\n\n1. **Input Check**:\n - If both adjacent cells to the start point `(0, 0)` are inaccessible, return `-1`.\n\n2. **Initialization**:\n - Define the directions for movement: Down, Up, Right, and Left.\n - Initialize a min-heap with the starting point `(time=0, row=0, col=0)`.\n - Create a `visited` matrix to keep track of already processed cells.\n\n3. **Dijkstra-like Exploration**:\n - While the heap is not empty:\n 1. Pop the smallest element from the heap (the current cell with the smallest "time cost").\n 2. If this cell is the target (bottom-right corner), return the time.\n 3. Mark the cell as visited and explore its neighbors.\n 4. For each valid neighbor:\n - If the cell can be reached at the current time or the next step, calculate the time to reach and push it into the heap.\n - If the cell\'s value enforces waiting, compute the next valid time and push it into the heap, adjusting for parity (even/odd time constraints).\n\n4. **No Path Found**:\n - If the loop ends without reaching the target, return `-1`.\n\n---\n\n## Algorithm Complexity\n\n### Time Complexity\n- **Heap Operations**: Each cell can be pushed into the heap at most once, and each operation is \\(O(\\log(mn))\\), where \\(m \\times n\\) is the grid size.\n- **Neighbor Exploration**: Each cell checks at most 4 neighbors.\n- **Overall**: \\(O((m \\times n) \\log(m \\times n))\\), where \\(m\\) is the number of rows and \\(n\\) is the number of columns.\n\n### Space Complexity\n- **Heap**: Stores up to \\(O(m \\times n)\\) entries for the grid cells.\n- **Visited Matrix**: Requires \\(O(m \\times n)\\) space.\n- **Overall**: \\(O(m \\times n)\\).\n\n---\n\n## Explanation of Key Details\n\n- **Grid Constraints**: The value of `grid[r][c]` indicates the earliest time the cell can be accessed.\n- **Time Adjustment**: If the current time doesn\u2019t align with the cell\u2019s availability due to even/odd parity, the algorithm calculates the next valid time.\n- **Dijkstra-Like Strategy**: Ensures that paths are explored in increasing order of their cumulative time, guaranteeing the minimum time solution.\n\n\n---\n\n## Algorithm Pattern\n\nThis algorithm follows the **Greedy** pattern with **Shortest Path (Dijkstra)** principles:\n1. A **min-heap** is used to always expand the node with the current minimum "time cost."\n2. Cells are visited in increasing order of their minimum reachable time, ensuring the shortest possible path to any cell.\n\n\n | 16 | 1 | ['Python3'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | Back 'n' Forth Dijkstra | back-n-forth-dijkstra-by-votrubac-oeav | Good ol\' Dijkstra once you work out the details.\n\nFirst of all, if the required time for both g[0][1] and g[1][0] is greater than one, we cannot move (return | votrubac | NORMAL | 2023-02-26T06:11:53.598361+00:00 | 2023-02-26T06:52:34.299913+00:00 | 1,462 | false | Good ol\' Dijkstra once you work out the details.\n\nFirst of all, if the required time for both `g[0][1]` and `g[1][0]` is greater than one, we cannot move (return `-1`).\n\nOtherwise, we can always reach the bottom-right cell. If the current time (plus 1) is less than required, we can "wait" till the required time.\n\n> We do not wait, of course - instead, we put the required time into the priority queue. \n\nNote that we may need to add `1` to the required time, as we advance the current time in the increments of `2` seconds (by going back and forth). \n\n> For example, if the current time is `3`, and the required time is 9, we can get back to the current cell at `5`, `7`, and `9` seconds, so arrive at the adjacent cell at tenth second.\n\nFinally, we need to use "visited" matrix (`vis`) to track the shortest time to arrive at each cell.\n\n**C++**\n```cpp\nint dir[5] = {0, 1, 0, -1, 0};\nint minimumTime(vector<vector<int>>& g) {\n int m = g.size(), n = g[0].size();\n if (min(g[0][1], g[1][0]) > 1)\n return -1;\n vector<vector<int>> vis(m, vector<int>(n, INT_MAX));\n priority_queue<array<int, 3>> pq;\n pq.push({0, 0, 0});\n while(!pq.empty()) {\n auto [neg_sec, i, j] = pq.top(); pq.pop();\n if (i == m - 1 && j == n - 1)\n break;\n for (int d = 0; d < 4; ++d) {\n int x = i + dir[d], y = j + dir[d + 1];\n if (min(x, y) >= 0 && x < m && y < n) {\n int sec = -neg_sec + 1;\n if (sec < g[x][y])\n sec = g[x][y] + (g[x][y] - sec) % 2;\n if (sec < vis[x][y]) {\n vis[x][y] = sec;\n pq.push({-sec, x, y});\n }\n }\n }\n }\n return vis.back().back();\n}\n``` | 13 | 0 | ['C'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | Graph + Matrix solution [EXPLAINED] | graph-matrix-solution-explained-by-r9n-79bn | IntuitionFind the shortest time to reach the bottom-right corner of the grid, considering the conditions of when I need to wait based on the values in each cell | r9n | NORMAL | 2025-01-06T02:43:06.107763+00:00 | 2025-01-06T02:43:06.107763+00:00 | 22 | false | # Intuition
Find the shortest time to reach the bottom-right corner of the grid, considering the conditions of when I need to wait based on the values in each cell. The challenge is to account for both the time spent moving and waiting, ensuring that I can find the most efficient path.
# Approach
I’ll use a priority queue to always process the cell with the smallest time first, moving in all four directions (up, right, down, left), updating the time as I go. I’ll also mark visited cells to avoid reprocessing and account for waiting times when necessary by adjusting the time if the current cell requires more time to proceed.
# Complexity
- Time complexity:
𝑂((𝑁 × 𝑀) log (𝑁 × 𝑀)), where 𝑁 is the number of rows and 𝑀 is the number of columns. This is because we use a priority queue, and each cell can be pushed and popped from the queue once.
- Space complexity:
O(N×M), which is used to store the seen array and the priority queue, both of which store up to N × M elements in the worst case.
# Code
```rust []
use std::cmp::Reverse;
use std::collections::BinaryHeap;
const MOVES: [[i32; 2]; 4] = [[-1, 0], [0, 1], [1, 0], [0, -1]]; // Possible moves (up, right, down, left)
impl Solution {
pub fn minimum_time(grid: Vec<Vec<i32>>) -> i32 {
let rows = grid.len(); // Get the number of rows in the grid
let cols = grid[0].len(); // Get the number of columns in the grid
// If the top-right or bottom-left corners have a non-zero value greater than 1, it's impossible to proceed
if grid[0][1] > 1 && grid[1][0] > 1 {
return -1;
}
let mut pq = BinaryHeap::new(); // BinaryHeap is a max-heap, so we reverse values to simulate a min-heap
let mut seen = vec![vec![false; cols]; rows]; // 2D array to track visited cells
// Start from the top-left corner (0, 0) with a time of 0
pq.push(Reverse((0, 0, 0))); // (time, row, col)
seen[0][0] = true; // Mark the starting cell as visited
// Start processing the cells in the priority queue
while let Some(Reverse(curr)) = pq.pop() {
let (time, row, col) = curr; // Get the current time, row, and column from the queue
// Try moving in all four directions
for dir in MOVES.iter() {
let new_row = row as i32 + dir[0]; // Calculate the new row position
let new_col = col as i32 + dir[1]; // Calculate the new column position
// Skip if out of bounds or already visited
if new_row < 0 || new_row >= rows as i32 || new_col < 0 || new_col >= cols as i32 || seen[new_row as usize][new_col as usize] {
continue;
}
// Calculate the new time (move to the next cell)
let mut new_time = time + 1;
// If the cell requires waiting, calculate how long to wait
if grid[new_row as usize][new_col as usize] > new_time {
let wait = ((grid[new_row as usize][new_col as usize] - new_time + 1) / 2) * 2; // Wait for the right time
new_time += wait; // Increment the time by the wait time
}
// If we reached the bottom-right corner, return the time
if new_row == (rows - 1) as i32 && new_col == (cols - 1) as i32 {
return new_time;
}
// Mark the new cell as visited
seen[new_row as usize][new_col as usize] = true;
// Push the new time and position to the priority queue
pq.push(Reverse((new_time, new_row as usize, new_col as usize)));
}
}
// If no valid path to the bottom-right corner, return -1
-1
}
}
``` | 11 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'Rust'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | [Python3] Modified Dijkstra. Detailed Solution. | python3-modified-dijkstra-detailed-solut-850m | Intuition\nDijkstra algorithm should always be considered first in shortest time/path questions.\n\n# Approach\nFirst observation:\nIf grid[0][1] <= 1 or grid[1 | qinzhe | NORMAL | 2023-02-26T04:12:26.227709+00:00 | 2023-02-26T07:09:51.141706+00:00 | 1,050 | false | # Intuition\nDijkstra algorithm should always be considered first in shortest time/path questions.\n\n# Approach\nFirst observation:\nIf ```grid[0][1] <= 1``` or ```grid[1][0] <= 1```, then you can always reach the bottom right position because you can jump back and forth between the starting point ```(0, 0)``` and its neighbour.\n\nSecond observation:\nFor each position ```(r, c)```, you can visit it either at odd time or at even time, you won\'t be able to visit ```(r, c)``` at both an odd time and an even time. This is because if you jump out and jump in, it will take `2` seconds, so the time you can visit a cell should be `t`, `t + 2`, `t + 4`, ..., where all of them are all even or all odd, depends on whether `t` is even or not.\n\nFinally:\nIt\'s just the standard Dijkstra\'s algorithm, when you are about to visit a new cell `(r + dr, c + dc)`, assume the current time is `t`\n- if `t + 1` and `grid[r + dr][c + dc]` are of the same parity (e.g. both odd or both even), then earliest time you can visit `(r + dr, c + dc)` is either `t + 1` or `grid[r][c]`. \n- if `t + 1` and `grid[r + dr][c + dc]` are of different parity, then earliest time you can visit `(r + dr, c + dc)` is either `t + 1` or `grid[r][c] + 1`. Notice that we have `+1` here so that after that, `t + 1` and `grid[r][c] + 1` will have the same parity. \n\n# Complexity\n- Time complexity:\n$$O(mn log(mn))$$. Recall that for a standard Dijkstra algorithm, the time complexity is $$O((|V| + |E|) log V)$$, in our case, both $|V|$ and $|E|$ are $$O(mn)$$.\n\n- Space complexity:\n$$O(mn)$$. Recall that for a standard Dijkstra algorithm, the space complexity is $$O(|V| + |E|)$$, in our case, both $|V|$ and $|E|$ are $$O(mn)$$.\n\n# Code\n```\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n if grid[0][1] > 1 and grid[1][0] > 1:\n return -1\n\n m, n = len(grid), len(grid[0])\n heap = [(0, 0, 0)]\n min_time = [[inf] * n for _ in range(m)]\n min_time[0][0] = 0\n \n while heap:\n curr_time, r, c = heappop(heap)\n for dr, dc in [[-1, 0], [1, 0], [0, -1], [0, 1]]:\n if 0 <= r + dr < m and 0 <= c + dc < n:\n if curr_time + 1 >= min_time[r + dr][c + dc]:\n continue\n else:\n if (curr_time + 1 - grid[r + dr][c + dc]) % 2 == 0:\n min_time[r + dr][c + dc] = max(curr_time + 1, grid[r + dr][c + dc])\n else:\n min_time[r + dr][c + dc] = max(curr_time + 1, grid[r + dr][c + dc] + 1)\n heappush(heap, (min_time[r + dr][c + dc], r + dr, c + dc))\n return min_time[-1][-1]\n``` | 10 | 0 | ['Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Dijkstra’s Magic | Find the Fastest Path | C++ | Java | Python | JavaScript 🚀 | dijkstras-magic-find-the-fastest-path-c-u13ie | \n# \u2B06\uFE0FUpvote if it helps \u2B06\uFE0F \n\n---\n\n## Connect with me on Linkedin Bijoy Sing.\n\n---\n\n\n###### Solution in C++, Python, Java, and Jav | BijoySingh7 | NORMAL | 2024-11-29T06:04:24.000827+00:00 | 2024-11-29T06:04:24.000862+00:00 | 2,496 | false | \n# \u2B06\uFE0FUpvote if it helps \u2B06\uFE0F \n\n---\n\n## Connect with me on Linkedin [Bijoy Sing](https://www.linkedin.com/in/bijoy-sing-236a5a1b2/).\n\n---\n\n\n###### *Solution in C++, Python, Java, and JavaScript*\n\n```cpp []\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n int m = grid.size();\n int n = grid[0].size();\n\n // Check if it\'s impossible to reach the destination from the start\n if (grid[0][1] > 1 && grid[1][0] > 1) return -1;\n\n vector<vector<int>> time(m + 1, vector<int>(n + 1, INT_MAX));\n vector<vector<int>> vis(m + 1, vector<int>(n + 1, 0));\n\n priority_queue<pair<int, pair<int, int>>, \n vector<pair<int, pair<int, int>>>, \n greater<pair<int, pair<int, int>>>> pq;\n pq.push({0, {0, 0}}); // Start from the top-left corner\n\n int x[] = {0, 0, 1, -1};\n int y[] = {1, -1, 0, 0};\n\n while (!pq.empty()) {\n auto p = pq.top();\n pq.pop();\n\n int t = p.first;\n int curx = p.second.first;\n int cury = p.second.second;\n\n // Return time if we reach the bottom-right corner\n if (curx == m - 1 && cury == n - 1) {\n return t;\n }\n\n if (vis[curx][cury]) continue;\n vis[curx][cury] = 1;\n\n for (int i = 0; i < 4; i++) {\n int newx = curx + x[i];\n int newy = cury + y[i];\n\n if (newx >= 0 && newx < m && newy >= 0 && newy < n) {\n int needtime = t + 1;\n\n // Adjust time based on grid values\n if (grid[newx][newy] > t + 1) {\n int diff = grid[newx][newy] - t;\n needtime = (diff % 2) ? grid[newx][newy] : grid[newx][newy] + 1;\n }\n\n if (needtime < time[newx][newy]) {\n time[newx][newy] = needtime;\n pq.push({needtime, {newx, newy}});\n }\n }\n }\n }\n\n return -1;\n }\n};\n```\n\n```python []\nclass Solution:\n def minimumTime(self, grid):\n m = len(grid)\n n = len(grid[0])\n\n # Check if it\'s impossible to reach the destination from the start\n if grid[0][1] > 1 and grid[1][0] > 1:\n return -1\n\n time = [[float(\'inf\')] * (n + 1) for _ in range(m + 1)]\n vis = [[0] * (n + 1) for _ in range(m + 1)]\n\n pq = []\n heapq.heappush(pq, (0, (0, 0))) # Start from the top-left corner\n\n x = [0, 0, 1, -1]\n y = [1, -1, 0, 0]\n\n while pq:\n t, (curx, cury) = heapq.heappop(pq)\n\n # Return time if we reach the bottom-right corner\n if curx == m - 1 and cury == n - 1:\n return t\n\n if vis[curx][cury]:\n continue\n vis[curx][cury] = 1\n\n for i in range(4):\n newx = curx + x[i]\n newy = cury + y[i]\n\n if 0 <= newx < m and 0 <= newy < n:\n needtime = t + 1\n\n # Adjust time based on grid values\n if grid[newx][newy] > t + 1:\n diff = grid[newx][newy] - t\n needtime = grid[newx][newy] if diff % 2 else grid[newx][newy] + 1\n\n if needtime < time[newx][newy]:\n time[newx][newy] = needtime\n heapq.heappush(pq, (needtime, (newx, newy)))\n\n return -1\n```\n\n```java []\nclass Solution {\n public int minimumTime(int[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n\n // Check if it\'s impossible to reach the destination from the start\n if (grid[0][1] > 1 && grid[1][0] > 1)\n return -1;\n\n int[][] time = new int[m + 1][n + 1];\n int[][] vis = new int[m + 1][n + 1];\n\n for (int i = 0; i <= m; i++) {\n for (int j = 0; j <= n; j++) {\n vis[i][j] = 0;\n time[i][j] = Integer.MAX_VALUE;\n }\n }\n\n PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));\n pq.add(new int[]{0, 0, 0}); // Start from the top-left corner\n\n int[] x = {0, 0, 1, -1};\n int[] y = {1, -1, 0, 0};\n\n while (!pq.isEmpty()) {\n int[] p = pq.poll();\n int t = p[0];\n int curx = p[1];\n int cury = p[2];\n\n // Return time if we reach the bottom-right corner\n if (curx == m - 1 && cury == n - 1) {\n return t;\n }\n\n if (vis[curx][cury] == 1) continue;\n vis[curx][cury] = 1;\n\n for (int i = 0; i < 4; i++) {\n int newx = curx + x[i];\n int newy = cury + y[i];\n\n if (newx >= 0 && newx < m && newy >= 0 && newy < n) {\n int needtime = t + 1;\n\n // Adjust time based on grid values\n if (grid[newx][newy] > t + 1) {\n int diff = grid[newx][newy] - t;\n if (diff % 2 == 1)\n needtime = grid[newx][newy];\n else\n needtime = grid[newx][newy] + 1;\n }\n\n if (needtime < time[newx][newy]) {\n time[newx][newy] = needtime;\n pq.add(new int[]{needtime, newx, newy});\n }\n }\n }\n }\n\n return -1;\n }\n}\n```\n\n```javascript []\nclass Solution {\n minimumTime(grid) {\n const m = grid.length;\n const n = grid[0].length;\n\n // Check if it\'s impossible to reach the destination from the start\n if (grid[0][1] > 1 && grid[1][0] > 1) return -1;\n\n const time = Array.from({ length: m + 1 }, () => Array(n + 1).fill(Infinity));\n const vis = Array.from({ length: m + 1 }, () => Array(n + 1).fill(0));\n\n const pq = [];\n pq.push([0, 0, 0]); // Start from the top-left corner\n\n const x = [0, 0, 1, -1];\n const y = [1, -1, 0, 0];\n\n while (pq.length) {\n pq.sort((a, b) => a[0] - b[0]);\n const [t, curx, cury] = pq.shift();\n\n // Return time if we reach the bottom-right corner\n if (curx === m - 1 && cury === n - 1) {\n return t;\n }\n\n if (vis[curx][cury]) continue;\n vis[curx][cury] = 1;\n\n for (let i = 0; i < 4; i++) {\n const newx = curx + x[i];\n const newy = cury + y[i];\n\n if (newx >= 0 && newx < m && newy >= 0 && newy < n) {\n let needtime = t + 1;\n\n // Adjust time based on grid values\n if (grid[newx][newy] > t + 1) {\n const diff = grid[newx][newy] - t;\n needtime = diff % 2 ? grid[newx][newy] : grid[newx][newy] + 1;\n }\n\n if (needtime < time[newx][newy]) {\n time[newx][newy] = needtime;\n pq.push([\n\nneedtime, newx, newy]);\n }\n }\n }\n }\n\n return -1;\n }\n}\n```\n\n\n---\n\n# Intuition\nThe problem is about finding the minimum time required to travel from the top-left corner to the bottom-right corner of a grid, where each cell has a time delay that varies based on the previous time spent. The goal is to determine the shortest time by navigating through the grid while respecting these delays.\n\nWe can treat this problem as a shortest path problem on a weighted graph. Each grid cell is a node, and the edges between nodes are the possible movements between adjacent cells, with edge weights determined by the time constraints of the grid.\n\n# Approach\nWe will use **Dijkstra\'s algorithm**, a well-known algorithm for finding the shortest path in a graph with non-negative edge weights. The key idea is:\n1. Initialize a priority queue to store the current minimum time to reach each cell.\n2. Start from the top-left corner (0,0) and initialize the time taken to reach it as 0.\n3. For each cell, explore its neighboring cells (up, down, left, right) and update their minimum travel time.\n4. If a cell\'s new computed time is less than its previously computed time, update it and push the new time into the priority queue.\n5. Stop when we reach the bottom-right corner, at which point the accumulated time will be the minimum time.\n\n# Complexity\n- **Time complexity**: $$O(E \\log V)$$ \n Where \\(E\\) is the number of edges (which is approximately \\(4 \\times m \\times n\\)) and \\(V\\) is the number of vertices (which is \\(m \\times n\\)). The log factor arises from the priority queue operations.\n\n- **Space complexity**: $$O(m \\times n)$$ \n We use two \\(m \\times n\\) matrices: one for the `time` array (storing the shortest times to reach each cell) and one for the `visited` array.\n\n---\n# Feel free to comment! \uD83D\uDE0A\n### *If you have any questions or need further clarification, feel free to drop a comment below! I\'m happy to help!* | 9 | 0 | ['Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | C++ || Modified Dijkstra's Algorithm || Explained Approach || Commented code | c-modified-dijkstras-algorithm-explained-84t5 | Intuition\n Describe your first thoughts on how to solve this problem. \nSome sort of modified dijkstra\'s algorth will be used.\n# Approach\n Describe your app | batman14 | NORMAL | 2023-02-26T23:16:48.794749+00:00 | 2023-02-26T23:16:48.794785+00:00 | 624 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSome sort of modified dijkstra\'s algorth will be used.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMODIFICATION of DIJKSTRA\'S ALGO :-\n\nWe will mainatain a time visited 2d array for keeping the track of minimum time to reach the node.\nDifferent cases will occur :\n1. the grid node is not yet visited && current time >= grid node time : simply upgarde the time array and push values in minheap.\n2. the grid node is not yet visited && current time < grid node time : check the difference btw current time and grid node time ; it its even -> use grid node time in time array and push values in minheap , and if odd -> use grid node time + 1 in time array and push values in minheap.\n3. the grid node is visited before && current time < time matrix value : here arise two subcases :-\n3.a. if grid node value <= current time : simply upgarde the time array and push values in minheap.\n3.b. if grid node value > current time : arise two sub-subcases : check the difference btw current time and grid node time :-\n3.b.1. if it its even -> use grid node time in time array and push values in minheap .\n3.b.2. if its odd -> use grid node time + 1 in time array and push values in minheap. \n\n\n\n\n\n \n# Complexity\n- Time complexity : O(mn * (mn)log(mn))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(n*m) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n typedef pair<int,pair<int,int>> p;\n \n int minimumTime(vector<vector<int>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n \n //case when no moves can be made [can\'t reach the destination]\n if(grid[0][1]>1 && grid[1][0]>1) return -1;\n \n //helping matrices\n vector<vector<int>> time(n, vector<int> (m,INT_MAX));\n vector<int> drow {0,-1,0,1};\n vector<int> dcol {-1,0,1,0};\n \n //minHeap for dijkstra\'s\n priority_queue<p,vector<p>,greater<p>> q;\n //pushing initial values of source\n q.push({0,{0,0}});\n time[0][0] = 0;\n int res = INT_MAX;\n \n while(!q.empty()) {\n auto it = q.top();\n q.pop();\n int r = it.second.first;\n int c = it.second.second;\n int t = it.first;\n \n //case when destination is reached (possible answer)\n if(r==n-1 && c==m-1) \n res = min(res,t);\n \n //incrementing time for the next new moves\n t++;\n \n //checking all four directions\n for(int i=0; i<4; i++) {\n int dr = r+drow[i];\n int dc = c+dcol[i];\n \n if(dr>=0&&dr<n&&dc>=0&&dc<m) {\n if(time[dr][dc]==INT_MAX) {\n //case 1\n if(grid[dr][dc]<=t) {\n time[dr][dc] = t;\n q.push({t,{dr,dc}});\n }\n //case 2\n else {\n int dif = grid[dr][dc]-t;\n if(dif%2==0) {\n time[dr][dc] = grid[dr][dc];\n q.push({grid[dr][dc],{dr,dc}});\n }\n else {\n time[dr][dc] = grid[dr][dc]+1;\n q.push({grid[dr][dc]+1,{dr,dc}});\n }\n }\n }\n else {\n if(time[dr][dc]>t) {\n //case 3.a\n if(grid[dr][dc]<=t) {\n time[dr][dc] = t;\n q.push({t,{dr,dc}}); \n }\n //case 3.b\n else {\n int dif = grid[dr][dc]-t;\n if(dif%2==0) {\n time[dr][dc] = grid[dr][dc];\n q.push({grid[dr][dc],{dr,dc}});\n }\n else {\n time[dr][dc] = grid[dr][dc]+1;\n q.push({grid[dr][dc]+1,{dr,dc}});\n }\n }\n }\n }\n }\n }\n }\n \n if(res==INT_MAX)\n return -1;\n return res;\n }\n};\n```\n\n\n\n\n | 9 | 0 | ['Breadth-First Search', 'Matrix', 'Shortest Path', 'C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | [C++] Dijkstra only code | c-dijkstra-only-code-by-dbestvarun-2hl5 | {:style="width:440px"}\n\n---\ncpp [easyAF\uD83D\uDE3C.cpp]\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n\n int m = grid | dbestvarun | NORMAL | 2024-11-29T11:55:31.102023+00:00 | 2024-11-29T11:55:31.102049+00:00 | 711 | false | {:style="width:440px"}\n\n---\n```cpp [easyAF\uD83D\uDE3C.cpp]\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n\n int m = grid.size(), n = grid[0].size();\n if (grid[0][1] > 1 && grid[1][0] > 1)\n return -1;\n\n vector<vector<int>> ans(m, vector<int>(n, INT_MAX));\n vector<pair<int, int>> direc = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};\n\n priority_queue<pair<int, pair<int, int>>> pq; // max heap in c++\n // storing time in negative values to make it act like a min heap for\n // time.\n pq.push({0, {0, 0}});\n while (pq.size()) {\n\n auto it = pq.top();\n pq.pop();\n\n for (auto e : direc) {\n\n int x = it.second.first + e.first,\n y = it.second.second + e.second;\n\n if (x < 0 || y < 0 || x >= m || y >= n)\n continue;\n\n int time = -it.first + 1;\n\n if (time < grid[x][y])\n time = grid[x][y] + ((grid[x][y] - time) & 1); // waiting takes 2 secons (back n forth)\n\n if (time < ans[x][y]) {\n ans[x][y] = time;\n pq.push({-time, {x, y}});\n }\n }\n }\n\n return ans[m - 1][n - 1];\n }\n};\n``` | 7 | 0 | ['Breadth-First Search', 'Heap (Priority Queue)', 'C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Video Explanation (With Intuition) | video-explanation-with-intuition-by-codi-awh1 | Explanation\n\nhttps://youtu.be/GAj_Q78lYP4\n\nClick here if the preview above doesn\'t works\n\nNote - Video will be public at 12:15PM IST.\n\n# Code\n\n#defin | codingmohan | NORMAL | 2023-02-26T06:19:00.349785+00:00 | 2023-02-26T06:19:00.349831+00:00 | 314 | false | # Explanation\n\nhttps://youtu.be/GAj_Q78lYP4\n\n[Click here if the preview above doesn\'t works](https://youtu.be/GAj_Q78lYP4)\n\nNote - Video will be public at 12:15PM IST.\n\n# Code\n```\n#define F first\n#define S second\n\nconst vector<vector<int>> neighbours = {\n {0, 1},\n {1, 0},\n {0, -1},\n {-1, 0}\n};\n\nstruct Node {\n int time;\n int row, col;\n \n Node (int _time, int _row, int _col) : time(_time), row(_row), col(_col) {}\n \n bool operator < (const Node& rhs) const {\n if (time != rhs.time) return time < rhs.time;\n if (row != rhs.row) return row < rhs.row;\n return col < rhs.col;\n }\n};\n\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n int rows = grid.size();\n int cols = grid[0].size(); \n \n if (grid[0][1] > 1 && grid[1][0] > 1) return -1;\n \n vector<vector<int>> time_to_reach(rows, vector<int>(cols, 1e9));\n time_to_reach[0][0] = 0;\n \n set<Node> q;\n for (int r = 0; r < rows; r ++) {\n for (int c = 0; c < cols; c ++) {\n q.insert(Node(time_to_reach[r][c], r, c));\n }\n }\n \n while (!q.empty()) {\n Node cur = *q.begin();\n q.erase (q.begin());\n \n for (auto i : neighbours) {\n int r = cur.row + i[0], c = cur.col + i[1];\n if (r < 0 || r >= rows || c < 0 || c >= cols) continue;\n \n int wait_time = max(0, grid[r][c] - cur.time - 1);\n if (wait_time % 2 != 0) wait_time ++;\n \n int new_time = cur.time + wait_time + 1;\n if (time_to_reach[r][c] > new_time) {\n q.erase (Node(time_to_reach[r][c], r, c));\n time_to_reach[r][c] = new_time;\n q.insert (Node(time_to_reach[r][c], r, c));\n }\n }\n }\n \n return time_to_reach[rows-1][cols-1];\n }\n};\n``` | 7 | 0 | ['C++'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | Python | Dijkstra | Simple Solution | python-dijkstra-simple-solution-by-aryon-kj7g | Code\n\nfrom heapq import heappush, heappop\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n | aryonbe | NORMAL | 2023-02-26T04:02:13.414082+00:00 | 2023-02-26T04:02:13.414125+00:00 | 523 | false | # Code\n```\nfrom heapq import heappush, heappop\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n if grid[0][1] > 1 and grid[1][0] > 1: \n return -1\n heap = [(0,0,0)]\n visited = set()\n while heap:\n d, i, j = heappop(heap)\n if (i, j) in visited: continue\n visited.add((i,j))\n if (i, j) == (m-1, n-1): return d\n for di, dj in [[-1,0], [1,0], [0,-1], [0,1]]:\n if 0 <= i + di < m and 0 <= j + dj < n and (i + di, j + dj) not in visited:\n t = grid[i+di][j+dj]\n gap = max(t-(d+1), 0)\n heappush(heap, (d + 1 + gap + (gap%2), i + di, j + dj))\n``` | 7 | 0 | ['Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | BFS + PriorityQueue | bfs-priorityqueue-by-svolkovichs-yogd | Intuition\nOn every step we will go to cell we can visit at minimum time.\n\n# Approach\nWe will use BFS + priority queue. Among all possible cells we select on | svolkovichs | NORMAL | 2023-02-26T17:43:13.461454+00:00 | 2023-02-26T17:43:13.461494+00:00 | 892 | false | # Intuition\nOn every step we will go to cell we can visit at minimum time.\n\n# Approach\nWe will use BFS + priority queue. Among all possible cells we select one we can reach at minimum time. How can we calculate minimum time we can reach particular cell. Let consider following example:\n\nFrom [0,0] we can move to [0,1] at minute 1. At minute 2 we can move to [1,1] at minute 2. At minute 3 we can move to [1,2]. Let calculate at what minute we can move to cell [1,3]. We can not move to it instantly but we can move back and forward untill we can. So we move back to [1,1] at minute 4, move to [1,2] at minute 5 and move to [1,3] at minute 6. We seond 2 seconds to do step back/forward. So if at time N we considering move to grid[i][j] = M we can calculate minimum time to reach it as following:\n```javascript\nif N + 1 >= M\n time = N + 1\nelse\n diff = M - N -1 // seconds we need to wait untill we can move to this cell\n time = diff MOD 2 == 0 ? M : M + 1 // We spend 2 seconds to do step back/forward so if difference is even we can move at M if not at M + 1\n```\n**No Path**\nThere is only one case when there is now path when both first possible steps [0,1] and [1,0] greater than 1. In this case we can not move. In all other cases we can do step back/forward in any particular cell untill next cell is avalalbe to move in.\n\n# Complexity\n- Time complexity:\nO(N*Log(N))\n\n- Space complexity:\nO(N)\n\n# Code\n```\n/**\n * @param {number[][]} grid\n * @return {number}\n */\nlet visited = new Set()\nconst moves = [[0, -1], [0, 1], [1, 0], [-1, 0]]\nvar minimumTime = function(grid) {\n visited = new Set();\n // Check if there is no path\n if(grid[0][1] > 1 && grid[1][0] > 1){\n return -1\n }\n \n return solve(grid)\n};\n\nfunction solve(grid){\n const heap = new MinPriorityQueue()\n heap.enqueue([0, 0, 0], 0)\n while(heap.size() > 0){\n let c = heap.dequeue().element\n let i = c[0]\n let j = c[1]\n let key = `${i}_${j}`\n visited.add(key)\n let time = c[2]\n if(i == grid.length -1 && j == grid[0].length-1) {\n return time\n }\n const nm = moves.map(m => [i + m[0], j + m[1]]).filter(m => m[0] >= 0 && m[1] >= 0 && m[0] < grid.length && m[1] < grid[0].length).filter(m => !visited.has(`${m[0]}_${m[1]}`))\n \n for(let m of nm) {\n let nt = time+1\n if(time + 1 < grid[m[0]][m[1]]) {\n let diff = grid[m[0]][m[1]] - time-1\n nt = diff % 2 == 0 ? \n grid[m[0]][m[1]] : grid[m[0]][m[1]] + 1\n \n }\n visited.add(`${m[0]}_${m[1]}`)\n heap.enqueue([...m, nt], nt)\n }\n }\n return -1;\n}\n\n\n``` | 6 | 0 | ['JavaScript'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | pure bfs, no heap, max(grid[i][j])+mn | pure-bfs-no-heap-maxgridijmn-by-jimhorng-6ye9 | Approach\n1) as regular BFS, move 1 level at a time and record adjacent cells as new level\n2) the difference is, if adjacent cell\'s required time > current ti | jimhorng | NORMAL | 2023-02-26T15:19:21.099142+00:00 | 2023-03-05T02:09:16.182723+00:00 | 829 | false | # Approach\n1) as regular BFS, move 1 level at a time and record adjacent cells as new level\n2) the difference is, if `adjacent cell\'s required time > current time + 1`, meaning we need to move back-and-forth to reach this cell, so put them in future level to be processed\n3) for 2), one caveat is that when steps between adjacent cell\'s time and current time is odd, it can move back-and-forth till exact adjacent cell time to reach it,\nbut when it is even, it need 1 extra move to reach the adjacent cell\n\ne.g. \n```\nt=0 t[5] = (1,0)\n 0 1 2 3\n0[0*,1a,3 ,2 ]\n1[5f,1 ,2 ,5 ]\n2[4 ,3 ,8 ,6 ]\n\nt=1 t[4] = (2,2)\n 0 1 2 3 t[5] = (1,0)\n0[0-,1*,3f,2 ]\n1[5f,1a,2 ,5 ]\n2[4 ,3 ,8 ,6 ]\n\nt=2 t[4] = (2,2)\n 0 1 2 3 t[5] = (1,0)\n0[0-,1-,3f,2 ]\n1[5f,1*,2a,5 ]\n2[4 ,3a,8 ,6 ]\n\nt=3 t[4] = (2,2)\n 0 1 2 3 t[5] = (1,0)\n0[0-,1-,3f,2 ] t[6] = (1,3)\n1[5f,1-,2*,5f] t[8] = (2,2)\n2[4a,3*,8f,6 ]\n\nt=4 t[5] = (1,0)\n 0 1 2 3 t[6] = (1,3)\n0[0-,1-,3*,2a] t[8] = (2,2)\n1[5f,1-,2-,5f]\n2[4*,3-,8f,6 ]\n\nt=5 \n 0 1 2 3 t[6] = (1,3)\n0[0-,1-,3-,2*] t[8] = (2,2)\n1[5*,1-,2-,5f]\n2[4-,3-,8f,6 ]\n\nt=6 \n 0 1 2 3 \n0[0-,1-,3-,2-] t[8] = (2,2)\n1[5-,1-,2-,5*]\n2[4-,3-,8f,6a]\n\nt=7 \n 0 1 2 3 \n0[0-,1-,3-,2-] t[8] = (2,2)\n1[5-,1-,2-,5-]\n2[4-,3-,8f,6*]\n```\n\n# Complexity\n- Time complexity: O(max(grid[i][j])+mn)\n- Space complexity: O(m*n)\n\n\n# Code\n```python\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n R, C = 0, 1\n nr, nc = len(grid), len(grid[0])\n\n def get_nx(r, c):\n for r_nx, c_nx in ((r+1,c),(r-1,c),(r,c+1),(r,c-1)):\n if 0 <= r_nx <= nr-1 and 0 <= c_nx <= nc-1:\n yield r_nx, c_nx\n\n # main\n if grid[0][1] > 1 and grid[1][0] > 1:\n return -1\n start, end = (0, 0), (nr-1, nc-1)\n t_to_cells = defaultdict(set)\n t = 0\n t_to_cells[t].add(start)\n visited = {start}\n while True:\n for r, c in t_to_cells[t]:\n for r_nx, c_nx in get_nx(r, c):\n if (r_nx, c_nx) in visited:\n continue\n if grid[r_nx][c_nx] > t+1:\n t_diff = grid[r_nx][c_nx] - t\n t_nx = t + t_diff if t_diff % 2 == 1 else t + t_diff + 1\n else:\n t_nx = t+1\n if (r_nx, c_nx) == end:\n return t_nx\n t_to_cells[t_nx].add((r_nx, c_nx))\n visited.add((r_nx, c_nx))\n t += 1\n\n``` | 6 | 0 | ['Breadth-First Search', 'Python3'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | Not so efficient yet coded by my own dijkstra based solution | not-so-efficient-yet-coded-by-my-own-dij-j2tu | IntuitionThe problem requires finding the minimum time to travel from the top-left corner to the bottom-right corner of a grid while following specific movement | udit_s05 | NORMAL | 2025-02-03T22:37:47.689304+00:00 | 2025-02-03T22:37:47.689304+00:00 | 55 | false | # Intuition
The problem requires finding the minimum time to travel from the top-left corner to the bottom-right corner of a grid while following specific movement constraints. Since the grid contains values that determine the waiting time at each cell, we need to decide the best route efficiently. This is a shortest-path problem in a weighted grid, and we use Dijkstra’s algorithm with a priority queue (min-heap) to always expand the least time-consuming path first.
# Approach
Edge Case Check:
If both grid[0][1] > 1 and grid[1][0] > 1, it is impossible to move from the starting position, so return -1.
Initialization
Create a minTime matrix initialized to INT_MAX to store the minimum time to reach each cell.
Create a visited matrix to track visited cells.
Define movement directions (up, down, left, right).
Use a min-heap (priority queue) that stores {current_time, row, col} to explore cells in increasing order of time.
Dijkstra’s Algorithm using Priority Queue
Start with {0, 0, 0} (time at the starting cell is 0).
While the queue is not empty:
Extract the cell with the minimum time.
If we reach (m-1, n-1), return the time.
If the cell is already visited, continue.
Mark the cell as visited.
Explore all four possible directions.
For each neighbor (Nrow, Ncol):
If out of bounds or already visited, skip.
If the next cell’s value ≤ currTime + 1, move immediately (currTime + 1).
If grid[Nrow][Ncol] > currTime + 1:
If the difference is even, wait 1 extra unit (grid[Nrow][Ncol] + 1).
If the difference is odd, move at exactly grid[Nrow][Ncol].
Return -1
If we never reach the destination, return -1.
# Complexity
- Time complexity:𝑂(𝑚×𝑛log(𝑚×𝑛))O(m×nlog(m×n))
- Space complexity: O(mxn)
# Code
```cpp []
class Solution {
public:
int minimumTime(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
if (grid[0][1] > 1 && grid[1][0] > 1)
return -1;
vector<vector<int>> minTime(m, vector<int>(n, INT_MAX));
vector<vector<bool>> visited(m, vector<bool>(n, false));
vector<vector<int>> directions = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
priority_queue<vector<int>, vector<vector<int>>, greater<>> pq;
pq.push({grid[0][0], 0, 0});
minTime[0][0] = 0;
while (!pq.empty()) {
auto curr = pq.top();
pq.pop();
int currTime = curr[0], row = curr[1], col = curr[2];
if (row == m - 1 && col == n - 1) return currTime;
if(visited[row][col]) continue;
visited[row][col] = true;
for (auto& dir : directions) {
int Nrow = row + dir[0];
int Ncol = col + dir[1];
if(Nrow<0 || Nrow>=m || Ncol<0 || Ncol>=n || visited[Nrow][Ncol]) continue;
if(grid[Nrow][Ncol] <= currTime+1){
pq.push({currTime+1, Nrow, Ncol});
minTime[Nrow][Ncol] = currTime+1;
} else if((grid[Nrow][Ncol]-currTime)%2 == 0){
pq.push({grid[Nrow][Ncol]+1, Nrow, Ncol});
minTime[Nrow][Ncol] = grid[Nrow][Ncol] + 1;
}else{
pq.push({grid[Nrow][Ncol], Nrow, Ncol});
minTime[Nrow][Ncol] = grid[Nrow][Ncol];
}
}
}
return -1;
}
};
``` | 5 | 0 | ['Shortest Path', 'C++'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | BFS | Solution for LeetCode#2577 | bfs-solution-for-leetcode2577-by-samir02-2jqv | \n\n# Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires finding the minimum time to reach the bottom-right cell of a | samir023041 | NORMAL | 2024-11-29T03:35:30.921876+00:00 | 2024-11-29T03:35:30.921914+00:00 | 2,100 | false | \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires finding the minimum time to reach the bottom-right cell of a grid, where each cell contains a time value. The intuition is to use a priority queue (min-heap) to always process the cell with the minimum time first, similar to Dijkstra\'s algorithm.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Use a priority queue to store cells to visit, ordered by time.\n2. Start from the top-left cell (0,0) with time 0.\n3. For each cell, check its neighbors:\n\t- If the neighbor\'s time is less than or equal to current time + 1, we can move there immediately.\n\t- If not, we need to wait. The waiting time is calculated to be the minimum even number of steps required.\n4. Keep track of visited cells to avoid revisiting.\n5. Continue until we reach the bottom-right cell or exhaust all possibilities.\n\n# Complexity\n- Time complexity: O(mn log(mn))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(mn)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minimumTime(int[][] grid) {\n int m=grid.length;\n int n=grid[0].length;\n PriorityQueue<int[]> pq=new PriorityQueue<>((a,b)->a[2]-b[2]); // Array: row, col, value\n boolean[][] visited=new boolean[m][n];\n \n\n if (grid[0][1] > 1 && grid[1][0] > 1){ \n return -1;\n }\n\n int[][] moves={ {0,-1},{0,1},{-1,0},{1,0}};\n\n pq.add(new int[]{0,0,0});\n while(!pq.isEmpty()){\n int[] arr=pq.poll();\n int row=arr[0];\n int col=arr[1];\n int time=arr[2];\n \n if(row==m-1 && col==n-1){\n return time;\n } \n\n if(visited[row][col]) continue;\n visited[row][col]=true;\n\n\n for(int[] move:moves){\n int nrow=row+move[0];\n int ncol=col+move[1];\n\n if(nrow>=0 && nrow<m && ncol>=0 && ncol<n && !visited[nrow][ncol]){\n int newtime=0; \n \n // if(time+1>=grid[nrow][ncol]) newtime=time+1;\n // else if((grid[nrow][ncol]-time)%2==0) newtime=grid[nrow][ncol]+1; //even\n // else newtime=grid[nrow][ncol]; //odd\n\n int diff=grid[nrow][ncol]-time; \n if(diff<=1) newtime=time+1; \n else newtime=time+1+(diff/2)*2;\n\n pq.add(new int[]{nrow,ncol,newtime});\n \n }\n }\n\n\n }\n\n return -1;\n }\n}\n``` | 5 | 0 | ['Java'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | Easy C++ Dijkstra with conditions | easy-c-dijkstra-with-conditions-by-maybe-1t62 | Intuition\n Describe your first thoughts on how to solve this problem. \nIt seemed like a straightforward shortest path problem with some modification due to th | maybeat12 | NORMAL | 2023-02-26T04:06:04.815237+00:00 | 2023-02-26T10:27:05.510584+00:00 | 1,282 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt seemed like a straightforward shortest path problem with some modification due to the given condition: \n\n> You can visit the cell `(row, col)` only when the time you visit it is **greater than or equal** to `grid[row][col]`.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nA simple dijkstra where the following conditions are kept in mind:\n\n> If the `value` of adjacent element is less than the distance required to reach it, then the distance will be exactly `distance[x][y] + 1`\n\n> Otherwise two cases:\n1. **The parity is same:** the distance will be exactly `grid[x][y] + 1` because you can visit the previous cell and come back but then the distance would be \n`(dis[x][y] + 1) + 1`\n\n2. **The parity is different:** the distance will be exactly `grid[x][y]` because you can just visit the previous cell and come back and then the distance would be \n`(dis[x][y] + 1)`\n\n# Complexity\n- Time complexity: $$O((M * N) * log(M * N) + (M * N))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(M*N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n// please upvote if you find it useful :)\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n \n // -1 condition\n \n if(grid[0][1] > 1 and grid[1][0] > 1){\n return -1;\n }\n \n // main code\n vector<vector<int>> dis(n + 1, vector<int> (m + 1, 1e6));\n \n priority_queue<pair<int,pair<int,int>>, vector<pair<int,pair<int,int>>>, greater<>> q;\n \n q.push({0,{0,0}}); // dist, src_x, src_y\n \n dis[0][0] = 0;\n \n while(!q.empty()){\n int d = q.top().first;\n int x = q.top().second.first;\n int y = q.top().second.second;\n q.pop();\n if (d > dis[x][y]) continue; // Skip if `d` is not updated to latest version!\n \n // move down\n if(x + 1 < n){\n if(dis[x + 1][y] > d + 1){\n \n if(grid[x + 1][y] <= d + 1){\n dis[x + 1][y] = d + 1;\n }\n else{\n dis[x + 1][y] = ((grid[x + 1][y] % 2) == (d % 2) ? (grid[x + 1][y] + 1) : grid[x + 1][y]);\n }\n q.push({dis[x + 1][y],{x + 1, y}});\n \n }\n \n }\n \n // move up\n if(x - 1 >= 0){\n if(dis[x - 1][y] > d + 1){\n \n if(grid[x - 1][y] <= d + 1){\n dis[x - 1][y] = d + 1;\n }\n else dis[x - 1][y] = ((grid[x - 1][y] % 2) == (d % 2) ? (grid[x - 1][y] + 1) : grid[x - 1][y]);\n q.push({dis[x - 1][y], {x - 1, y}});\n }\n \n }\n \n // move right\n if(y + 1 < m){\n if(dis[x][y + 1] > d + 1){\n \n if(grid[x][y + 1] <= d + 1){\n dis[x][y + 1] = d + 1;\n }\n else dis[x][y + 1] = (dis[x][y + 1], (grid[x][y + 1] % 2) == (d % 2) ? (grid[x][y + 1] + 1) : grid[x][y + 1]);\n q.push({dis[x][y + 1], {x, y + 1}});\n }\n \n }\n \n // move left\n if(y - 1 >= 0){\n if(dis[x][y - 1] > d + 1){\n \n if(grid[x][y - 1] <= d + 1){\n dis[x][y - 1] = d + 1;\n }\n else dis[x][y - 1] = ((grid[x][y - 1] % 2) == (d % 2) ? (grid[x][y - 1] + 1) : grid[x][y - 1]);\n q.push({dis[x][y - 1],{x, y - 1}});\n }\n \n }\n \n \n }\n \n return dis[n - 1][m - 1];\n }\n};\n```\n# Questions Asked:\n1. How does this work `if (d > dis[x][y]) continue;`?\n- Firstly it wasn\'t necessary here because any cell can be visited at most 4 times so the current cell `{x, y}` would have been pushed to the minHeap that many times. In the worst case, the cell will pop and process for its adjacent cells that can be atmost 4, each time it takes time to visit adjacent cells, there is up to 4 cells like current cell.\n\n- What if it was a graph question where a node may be connected to V other nodes, so in that case this line can be useful in avoiding visiting all V nodes as explained above. | 5 | 0 | ['Shortest Path', 'C++'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | Easiest Sol Java || Beats 100% ✅ || Simple Dijkstra's Algorithm | easiest-sol-java-beats-100-simple-dijkst-6pc8 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves navigating a grid where each cell has a time constraint representi | user6791FW | NORMAL | 2024-11-29T16:08:20.042022+00:00 | 2024-11-29T16:08:20.042057+00:00 | 56 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves navigating a grid where each cell has a **time constraint** representing the earliest time you can enter it. The goal is to find the **minimum time** to reach the bottom-right corner while respecting these constraints.\n\nThe challenge comes from needing to **wait** when trying to enter a cell too early and ensuring the path is the fastest possible. The intuition is similar to **Dijkstra\'s algorithm** for finding the shortest path in a weighted graph, where:\n1. The grid cells are the nodes.\n2. Moving between adjacent cells is equivalent to edges with weights of 1 (plus any waiting time).\n3. The priority queue processes nodes (cells) in increasing order of their entry time.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Grid Initialization**:\n - Treat the grid as a graph where each cell is a node.\n - Use a **priority queue** (min-heap) to always process the next cell with the smallest entry time.\n\n2. **Handling Time Constraints**:\n - For each neighboring cell, calculate the time it will take to reach it.\n - If the cell\'s constraint (`grid[row][col]`) requires waiting, calculate the **additional time needed** to align with its accessibility.\n\n3. **Breadth-First Search with Priority Queue**:\n - Start from `(0, 0)` at time `0`.\n - Process neighboring cells, updating the minimum time to reach them and adding them to the priority queue.\n - Stop processing when you reach the destination `(rows-1, cols-1)`.\n\n4. **Edge Cases**:\n - If the starting cell\'s neighbors are inaccessible early on, return `-1`.\n - If no valid path exists (queue is exhausted without reaching the destination), return `-1`.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1. **Grid Traversal**:\n - Each cell is processed at most once, and every move explores up to 4 neighbors. This results in \\(O(R \\times C \\times 4)\\), where \\(R\\) and \\(C\\) are the number of rows and columns.\n\n2. **Priority Queue Operations**:\n - Inserting and removing an element in the priority queue takes \\(O(\\log(R \\times C))\\), and there are at most \\(R \\times C\\) cells to process.\n - Total complexity for priority queue operations is \\(O((R \\times C) \\log(R \\times C))\\).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n1. **Priority Queue**:\n - Stores at most \\(R \\times C\\) cells.\n - Space complexity: \\(O(R \\times C)\\).\n\n2. **Visited Array**:\n - A 2D array `seen` of size \\(R \\times C\\) is used to track visited cells.\n - Space complexity: \\(O(R \\times C)\\).\n\n# Code\n```java []\nclass Solution {\n private static final int[][] MOVES = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};\n \n public int minimumTime(int[][] grid) {\n int rows = grid.length;\n int cols = grid[0].length;\n \n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n \n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]); \n boolean[][] seen = new boolean[rows][cols];\n \n pq.offer(new int[]{0, 0, 0}); // time, row, col\n seen[0][0] = true;\n \n while (!pq.isEmpty()) {\n int[] curr = pq.poll();\n int time = curr[0];\n int row = curr[1];\n int col = curr[2];\n \n for (int[] dir : MOVES) {\n int newRow = row + dir[0];\n int newCol = col + dir[1];\n \n if (newRow < 0 || newRow >= rows || \n newCol < 0 || newCol >= cols || \n seen[newRow][newCol]) {\n continue;\n }\n \n int newTime = time + 1;\n if (grid[newRow][newCol] > newTime) {\n int wait = ((grid[newRow][newCol] - newTime + 1) / 2) * 2;\n newTime += wait;\n }\n \n if (newRow == rows - 1 && newCol == cols - 1) {\n return newTime;\n }\n \n seen[newRow][newCol] = true;\n pq.offer(new int[]{newTime, newRow, newCol});\n }\n }\n \n return -1;\n }\n}\n``` | 4 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'Java'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | 🔥Beats 100 % 🔥 | ✔️ Optimized Dijkstra's Algorithm ✔️ | O(m * nlog(m * n)) | beats-100-optimized-dijkstras-algorithm-zkqyv | Intuition\nThis solution uses a priority queue min-heap to efficiently explore the grid in increasing order of time, ensuring the optimal path is chosen to reac | ntrcxst | NORMAL | 2024-11-29T03:01:39.825210+00:00 | 2024-11-29T03:01:39.825239+00:00 | 303 | false | # Intuition\nThis solution uses a **priority queue** `min-heap` to efficiently explore the `grid` in increasing order of time, ensuring the **optimal path** is chosen to reach the target cell at the **bottom-right corner** `rows - 1` `cols - 1`.\n\n# Approach\n`Step 1` **Early Exit Condition**\n- If both possible moves from the starting position `(0, 0)` **either down or right** require more than **1 second** `grid[0][1] > 1 && grid[1][0] > 1` then the traversal is impossible from the start. The function `returns -1` immediately.\n\n`Step 2` **Initialization**\n- **Directions Array (MOVES) :** Specifies the four possible movement directions: up `({-1, 0})`, right `({0, 1})`, down `({1, 0})`, and left `({0, -1})`. This is used for exploring neighboring cells.\n- **Priority Queue :** The **priority queue** stores cells with the format `{time, row, col}`, where time is the current time to reach a given cell. \n- **Seen Array :** Tracks whether a cell has been visited to avoid **reprocessing** and **infinite loops**.\n\n`Step 3` **Start BFS-like Search**\n- **Add the starting Cell :** `0, 0` to the **priority queue** with the time set to 0: `pq.offer(new int[]{0, 0, 0})`. \n- **Mark it as visited :** `seen[0][0] = true`.\n\n`Step 4` **Explore Cells**\n- **Pop the Cell with Minimum Time :** Main loop continues as long as the priority queue is not empty. It processes the cell with the smallest time.\n- **For Each Direction :** For each direction in the `MOVES` array `(up, right, down, left)`, compute the `newRow` and `newCol` by applying the direction to the current cell\'s coordinates.\n- **Boundary Check :** Skip cells that are out of bounds or already visited.\n\n`Step 5` **Calculate New Time for Neighbors**\n- **Compute New Time :** Start with the `newTime = time + 1` \n- **Check Wait Time :** If moving to the next cell requires more time `grid[newRow][newCol] > newTime`. \n - **Calculate the wait time :** This ensures that the wait time is adjusted based on the current time and the constraints in the grid.\n - `wait = ((grid[newRow][newCol] - newTime + 1) / 2) * 2`. \n \n- **Update Time :** Add wait time to the new time, so `newTime += wait`.\n\n`Step 6` **Reaching the Target**\n- If the current cell is the **bottom-right corner** `rows - 1, cols - 1`, return the `newTime` as the answer since we\'ve reached the destination.\n\n`Step 7` **Push the Neighbor to the Priority Queue**\n- If neighbor is valid and hasn\'t been visited yet, mark visited and push updated time and coordinates to the `priority queue`.\n\n`Step 8` **Termination**\n- If the priority queue is exhausted and the target cell hasn\'t been reached `return -1`, indicating that it\'s impossible to reach the **bottom-right corner.**\n\n# Complexity\n- Time complexity: $$O(M * Nlog(M * N))$$\n- Space complexity : $$O(M * N)$$\n\n# Code\n```java []\nclass Solution\n{\n private static final int[][] MOVES = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}}; // Directions for movement (up, right, down, left)\n \n public int minimumTime(int[][] grid)\n {\n int rows = grid.length;\n int cols = grid[0].length;\n\n // Step 1: If both initial moves are blocked, return -1\n if (grid[0][1] > 1 && grid[1][0] > 1)\n {\n return -1; // Both right and down from (0, 0) are not possible\n }\n\n // Step 2: Initialize the priority queue and the visited array\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]); // Min-heap based on time\n boolean[][] seen = new boolean[rows][cols];\n\n pq.offer(new int[]{0, 0, 0}); // Start with (0, 0) at time 0\n seen[0][0] = true;\n\n // Step 3: BFS-like traversal using priority queue\n while (!pq.isEmpty())\n {\n int[] curr = pq.poll(); // Get the current cell with the smallest time\n int time = curr[0];\n int row = curr[1];\n int col = curr[2];\n\n // Step 4: Explore all four directions\n for (int[] dir : MOVES)\n {\n int newRow = row + dir[0];\n int newCol = col + dir[1];\n\n // Step 5: Skip invalid cells (out of bounds or already visited)\n if (newRow < 0 || newRow >= rows || newCol < 0 || newCol >= cols || seen[newRow][newCol])\n {\n continue;\n }\n\n // Step 6: Calculate the time to move to the next cell\n int newTime = time + 1;\n if (grid[newRow][newCol] > newTime)\n {\n int wait = ((grid[newRow][newCol] - newTime + 1) / 2) * 2; // Wait if necessary\n newTime += wait;\n }\n\n // Step 7: If we reached the target cell, return the current time\n if (newRow == rows - 1 && newCol == cols - 1)\n {\n return newTime;\n }\n\n // Step 8: Mark the cell as visited and add it to the priority queue\n seen[newRow][newCol] = true;\n pq.offer(new int[]{newTime, newRow, newCol});\n }\n }\n\n // Step 9: If no path is found, return -1\n return -1;\n }\n}\n``` | 4 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'Queue', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'Java'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | ✅ Dijkstra's Algorithm | Easy to Understand | Detailed Video Explanation 🔥 | dijkstras-algorithm-easy-to-understand-d-o6mv | Intuition\nThe problem requires finding the minimum time to traverse from the top-left to the bottom-right of a grid while adhering to specific constraints on c | sahilpcs | NORMAL | 2024-11-29T02:52:52.221325+00:00 | 2024-11-29T02:52:52.221365+00:00 | 604 | false | # Intuition\nThe problem requires finding the minimum time to traverse from the top-left to the bottom-right of a grid while adhering to specific constraints on cell accessibility. Since the grid has a time constraint for visiting each cell, the goal is to explore paths efficiently and prioritize reaching cells sooner. This suggests using a shortest-path algorithm like Dijkstra\'s, which ensures that we always explore the least-time-consuming paths first.\n\n# Approach\n1. **Initialization**:\n - Start from the top-left cell at time 0.\n - Use a priority queue (min-heap) to prioritize cells based on the time required to reach them.\n\n2. **Traversal**:\n - Use a Dijkstra-like approach, where at each step, the cell with the smallest time value is processed.\n - For each cell, attempt to move to its neighbors (up, down, left, right).\n - For each neighbor, calculate the earliest possible time it can be visited. If the difference between the current time and the cell\'s minimum required time is odd, adjust the time to satisfy the constraints.\n\n3. **Conditions**:\n - If the neighbor cell is out of bounds or already visited, skip it.\n - If the bottom-right cell is reached, return the time taken.\n\n4. **Termination**:\n - If the queue is empty and the bottom-right cell has not been reached, return -1.\n\n# Complexity\n- **Time complexity**: \n $$O(m \\cdot n \\cdot \\log(m \\cdot n))$$ \n - The grid has \\(m \\cdot n\\) cells. \n - Each cell is processed once, and adding/removing from the priority queue takes \\(O(\\log(m \\cdot n))\\). \n\n- **Space complexity**: \n $$O(m \\cdot n)$$ \n - Space is required for the `visited` array and the priority queue, both of size \\(m \\cdot n\\).\n\n# Code\n```java []\nclass Solution {\n // Direction vectors for moving in four directions: right, left, down, up\n int[][] dir = { {0, 1}, {0, -1}, {1, 0}, {-1, 0} };\n int m, n;\n boolean[][] visited;\n\n public int minimumTime(int[][] grid) {\n // Base case: If both adjacent cells from the start are inaccessible, return -1\n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n\n // Initialize dimensions of the grid\n m = grid.length;\n n = grid[0].length;\n\n // Priority queue to implement Dijkstra\'s algorithm (min-heap based on time)\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[2] - b[2]);\n visited = new boolean[m][n];\n\n // Add the starting cell to the priority queue: {row, col, time}\n pq.offer(new int[]{0, 0, 0});\n\n // Process the priority queue until empty\n while (!pq.isEmpty()) {\n int[] curr = pq.poll();\n int row = curr[0], col = curr[1], time = curr[2];\n\n // If the bottom-right cell is reached, return the time taken\n if (row == m - 1 && col == n - 1) return time;\n\n // Skip if the current cell is already visited\n if (visited[row][col]) continue;\n\n // Mark the current cell as visited\n visited[row][col] = true;\n\n // Explore all four possible directions\n for (int[] d : dir) {\n int r = row + d[0], c = col + d[1];\n\n // Check if the neighboring cell is valid (within bounds and not visited)\n if (!valid(r, c)) continue;\n\n // Calculate the earliest time to reach the neighboring cell\n // Adjust time based on parity to match the cell\'s constraint\n int f = (grid[r][c] - time) % 2 == 0 ? 1 : 0;\n int t = Math.max(time + 1, grid[r][c] + f);\n\n // Add the neighboring cell to the priority queue\n pq.offer(new int[]{r, c, t});\n }\n }\n // If the bottom-right cell is unreachable, return -1\n return -1;\n }\n\n // Helper method to check if a cell is within bounds and not visited\n private boolean valid(int i, int j) {\n return i >= 0 && j >= 0 && i < m && j < n && !visited[i][j];\n }\n}\n```\n\n\nLeetCode 2577 Minimum Time to Visit a Cell In a Grid | Graph | Hard | Dijkstra\'s algo | Google\nhttps://youtu.be/u72HaTxPg0Q | 4 | 0 | ['Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'Java'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | [Python3] Simple Dijkstra with modification | python3-simple-dijkstra-with-modificatio-6rea | Intuition\nA small change to Dijkstra\'s algorithm is that we move back and forth until a new cell unlocks after some time. We calculate when the neighbor cell | khadyothan | NORMAL | 2024-11-29T01:15:08.425811+00:00 | 2024-11-29T01:15:08.425850+00:00 | 218 | false | # Intuition\nA small change to Dijkstra\'s algorithm is that we move back and forth until a new cell unlocks after some time. We calculate when the neighbor cell becomes available and push it into the heap with that time.\n\n# Code\n```python3 []\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n ROWS, COLS = len(grid), len(grid[0])\n directions = [[1, 0], [-1, 0], [0, 1], [0, -1]]\n heap = [(grid[0][0], 0, 0)]\n visit = set()\n visit.add((0, 0))\n\n if grid[0][1] > 1 and grid[1][0] > 1:\n return -1\n\n while heap:\n time, r, c = heapq.heappop(heap)\n\n if r == ROWS - 1 and c == COLS - 1:\n return time\n\n for dr, dc in directions:\n nr, nc = r + dr, c + dc\n if 0 <= nr < ROWS and 0 <= nc < COLS and (nr, nc) not in visit:\n visit.add((nr, nc))\n if grid[nr][nc] <= time + 1:\n heapq.heappush(heap, [time + 1, nr, nc])\n else:\n if (grid[nr][nc] - time) % 2 == 0:\n heapq.heappush(heap, [grid[nr][nc] + 1, nr, nc])\n else:\n heapq.heappush(heap, [grid[nr][nc], nr, nc])\n \n return -1\n\n\n``` | 4 | 0 | ['Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Shortest Path', 'Python3'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | Modified Dijkstra || Edge Cases || graph || C++ | modified-dijkstra-edge-cases-graph-c-by-enc00 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | oreocraz_273 | NORMAL | 2024-08-02T06:40:54.738546+00:00 | 2024-08-02T06:40:54.738582+00:00 | 374 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& a) {\n \n int m=a.size();\n int n=a[0].size();\n if(a[0][1]>1 && a[1][0]>1)\n return -1;\n //bool vis[m+1][n+1];\n // memset(vis,false,sizeof(vis));\n set<vector<int>> q;\n q.insert({0,0,0});\n vector<vector<int>> dp(m,vector<int>(n,INT_MAX));\n dp[0][0]=0;\n vector<int> dir{0,1,0,-1,0};\n\n while(!q.empty())\n {\n vector<int> c=*(q.begin());\n q.erase(q.begin());\n int x=c[1],y=c[2];\n int time=c[0];\n if(x==(m-1) && y==(n-1))\n return time;\n for(int i=0;i<4;i++)\n {\n int nx=x+dir[i];\n int ny=y+dir[i+1];\n if(min(nx,ny)>=0 && nx<m && ny<n)\n {\n int d=a[nx][ny]-time;\n if(time+1>=a[nx][ny] && time+1<dp[nx][ny])\n {\n q.erase({dp[nx][ny],nx,ny});\n dp[nx][ny]=time+1;\n q.insert({dp[nx][ny],nx,ny});\n }\n else if(time+1<a[nx][ny])\n {\n int d=a[nx][ny]-time;\n if(d%2)\n {\n if(a[nx][ny]<dp[nx][ny])\n {\n q.erase({dp[nx][ny],nx,ny});\n dp[nx][ny]=a[nx][ny];\n q.insert({dp[nx][ny],nx,ny});\n }\n }\n else\n {\n if(a[nx][ny]+1<dp[nx][ny])\n {\n q.erase({dp[nx][ny],nx,ny});\n dp[nx][ny]=a[nx][ny]+1;\n q.insert({dp[nx][ny],nx,ny});\n }\n }\n }\n }\n }\n }\n\n return -1;\n \n }\n};\n``` | 4 | 0 | ['Graph', 'Ordered Set', 'C++'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | Python || Dijkstra Variant || Explained | python-dijkstra-variant-explained-by-in_-b18i | There is only one case where we can\'t reach last cell , i.e. when all cells adjacent to (0,0) are greater than 1.\nOtherwise we can always keep switching betwe | iN_siDious | NORMAL | 2023-04-18T06:04:15.187905+00:00 | 2023-04-18T06:20:39.180964+00:00 | 361 | false | There is only one case where we can\'t reach last cell , i.e. when all cells adjacent to (0,0) are greater than 1.\nOtherwise we can always keep switching between current cell and the last visited cell to pass the time.\nNow when we are moving from one cell to its adjacent cell -\n1) if the difference between grid value of new cell and current cost is odd and grid value is greater than cost then we can move to new cell with it\'s required grid value.\n2) otherwise if difference is even and new cell grid value is greater than cost then we can only reach it by grid value+1 (since we will need 1 extra move while swtiching between current and previously visited cell).\n3) If grid value of new cell is less than or equal to current cost then we can always move to new cell with new_cost=cost+1 (This is normal bfs move) .\n\nTime Complexity - O(m* n * log (m* n))\n\nCode : \n```\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n m,n=len(grid),len(grid[0])\n directions=((0,1),(1,0),(-1,0),(0,-1))\n i,j,flag=0,0,0\n for di,dj in directions:\n ni,nj=i+di,j+dj\n if 0<=ni<m and 0<=nj<n and grid[ni][nj]<=1: flag=1;break;\n if not flag: return -1\n heap=[]\n heappush(heap,(0,0,0))\n dist=[[sys.maxsize]*n for _ in range(m)]\n while heap:\n cost,i,j=heappop(heap)\n if i==m-1 and j==n-1: return cost\n for di,dj in directions:\n ni,nj=i+di,j+dj\n if 0<=ni<m and 0<=nj<n:\n new_cost=cost+1\n if grid[ni][nj]>cost:\n if abs(cost-grid[ni][nj])%2==0:\n new_cost=grid[ni][nj]+1\n else:\n new_cost=grid[ni][nj]\n if new_cost<dist[ni][nj]:\n dist[ni][nj]=new_cost\n heappush(heap,(new_cost,ni,nj))\n \n \n``` | 4 | 0 | ['Breadth-First Search', 'Heap (Priority Queue)', 'Python', 'Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | [Python] BFS with priority queue; Explained | python-bfs-with-priority-queue-explained-8wcn | The BFS can be used to solve the minimum time or minimum length problem.\n\n(1) In this problem, we must move to a different cell every second. Thus, the only c | wangw1025 | NORMAL | 2023-02-27T06:36:09.613092+00:00 | 2023-02-27T06:38:25.005858+00:00 | 215 | false | The BFS can be used to solve the minimum time or minimum length problem.\n\n(1) In this problem, we must move to a different cell every second. Thus, the only case that we cannot reach the bottom right cell is that all the cells next to (0, 0) has required visit time larger than 1. If we have more than 2 visited cells, we can move back and forth so that the required visit time can meet.\n\n(2) Since we are moving back and forth, the minimum increment of time is 2. If the difference between the required visit time of next cell and the current time is multiple of 2, we need add one more second before we can reach the next cell.\n\n(3) Sort all the cells in a priority queue based on the next visit time, so that we can always visit the cell using the minimum time.\n\nWhenever, we reach the bottom right cell, we can return the visiting time.\n\n```\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n nrow = len(grid)\n ncol = len(grid[0])\n \n visited = set()\n visit_queue = [(0, 0, 0)]\n visited.add((0, 0))\n \n ans = -1\n while visit_queue:\n visit_time, r, c = heapq.heappop(visit_queue)\n if r == nrow - 1 and c == ncol - 1:\n ans = visit_time\n break\n \n for ncell in {(0, 1), (1, 0), (0, -1), (-1, 0)}:\n nr = r + ncell[0]\n nc = c + ncell[1]\n if nr >= 0 and nr < nrow and nc >= 0 and nc < ncol and (nr, nc) not in visited:\n if grid[nr][nc] <= visit_time + 1:\n heapq.heappush(visit_queue, (visit_time + 1, nr, nc))\n visited.add((nr, nc))\n elif len(visited) >= 2:\n if (grid[nr][nc] - visit_time - 1) % 2:\n heapq.heappush(visit_queue, (grid[nr][nc] + 1, nr, nc))\n else:\n heapq.heappush(visit_queue, (grid[nr][nc], nr, nc))\n visited.add((nr, nc))\n \n return ans\n``` | 4 | 0 | ['Python3'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | Java🍵✅ | java-by-mani-26-fd1z | Complexity\n- Time complexity: O(n\xD7m\xD7log(n\xD7m))\n\n- Space complexity: O(n\xD7m)\n\n# Code\njava []\nclass Solution {\n public int minimumTime(int[][ | mani-26 | NORMAL | 2024-11-30T02:10:18.960671+00:00 | 2024-11-30T02:10:18.960717+00:00 | 17 | false | # Complexity\n- Time complexity: **O(n\xD7m\xD7log(n\xD7m))**\n\n- Space complexity: **O(n\xD7m)**\n\n# Code\n```java []\nclass Solution {\n public int minimumTime(int[][] grid) {\n if (grid[0][1] > 1 && grid[1][0] > 1)\n return -1;\n int n = grid.length;\n int m = grid[0].length;\n boolean[][] visited = new boolean[n][m];\n final int[][] DIRECTIONS = { { 1, 0 }, { -1, 0 }, { 0, 1 }, { 0, -1 } };\n\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));\n pq.add(new int[] { 0, 0, 0 }); // {time, row, col}\n\n while (!pq.isEmpty()) {\n int[] curr = pq.poll();\n int time = curr[0];\n int row = curr[1];\n int col = curr[2];\n\n if (row == n - 1 && col == m - 1) {\n return time;\n }\n\n if (visited[row][col]) continue;\n visited[row][col] = true;\n\n for (int[] direction : DIRECTIONS) {\n int newRow = row + direction[0];\n int newCol = col + direction[1];\n\n if (newRow >= 0 && newCol >= 0 && newRow < n && newCol < m && !visited[newRow][newCol]) {\n int waitTime = ((grid[newRow][newCol] - time) % 2 == 0) ? 1 : 0;\n int newTime = Math.max(grid[newRow][newCol] + waitTime, time + 1);\n pq.add(new int[] { newTime, newRow, newCol });\n }\n }\n \n }\n return -1;\n }\n}\n\n``` | 3 | 0 | ['Breadth-First Search', 'Heap (Priority Queue)', 'Java'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | 97% in time, 70 in space using djikistra | 97-in-time-70-in-space-using-djikistra-b-cslf | \n\n# Approach\nIf you are able to move once, you can reach any cell because you can just oscillate between 2 cells. If you are at i,j at an odd time let\'s say | yellowfence | NORMAL | 2024-11-29T16:44:00.329988+00:00 | 2024-11-29T16:44:00.330041+00:00 | 120 | false | \n\n# Approach\nIf you are able to move once, you can reach any cell because you can just oscillate between 2 cells. If you are at i,j at an odd time let\'s say 5 and you want to go to i+1, j and grid[i+1][j] = 9 then you can\'t reach grid[i+1][j] at 9 time because oscillation takes 2 seconds. Hence, you will reach grid[i+1][j] at 10th second. \n\n\nUse standard djikistra algorithm and the above mentioned formula to get to the last position. \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(m*n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m*n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n priority_queue<pair<int, pair<int,int>>, vector<pair<int, pair<int,int>>>, greater<>> pq;\n pq.emplace(0, make_pair(0,0));\n int m = grid.size();\n int n = grid[0].size();\n vector<vector<int>> visited(m, vector<int>(n, -1));\n visited[0][0] = 0;\n vector<pair<int,int>> dir = {{1,0}, {0,1}, {-1, 0}, {0,-1}};\n if(grid[1][0] > 1 && grid[0][1] > 1) {\n return -1;\n }\n while(!pq.empty()) {\n auto [time, p] = pq.top();\n pq.pop();\n if(p.first == m-1 && p.second == n-1) {\n return time;\n }\n int i = p.first;\n int j = p.second;\n for(int ptr = 0;ptr<4;ptr++) {\n int resi = i + dir[ptr].first;\n int resj = j + dir[ptr].second;\n if(resi>=0 && resj>=0 && resi < m && resj<n) {\n int timet = max(time+1, grid[resi][resj] + ((time%2 == grid[resi][resj]%2) ? 1 : 0));\n if((visited[resi][resj] == -1 || visited[resi][resj] > timet)) {\n visited[resi][resj] = timet;\n pq.emplace(timet, make_pair(resi, resj));\n }\n }\n }\n }\n return -1;\n }\n};\n``` | 3 | 0 | ['C++'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | C# 62ms Runtime Dijkstra with array instead of priority queue | c-62ms-runtime-dijkstra-with-array-inste-lt49 | Approach\n\nUsing List<(int, int)>[200_000] in place of PriorityQueue<(int, int, int), int> sped up the Dijkstra implementation x5.\n\nThe constant 200_000 must | ConnectedPuddle | NORMAL | 2024-11-29T01:20:13.352103+00:00 | 2024-11-29T01:20:13.352132+00:00 | 34 | false | # Approach\n\nUsing `List<(int, int)>[200_000]` in place of `PriorityQueue<(int, int, int), int>` sped up the Dijkstra implementation `x5`.\n\nThe constant `200_000` must be greater than `m * n + Max(grid[i][j])`\n\n\n\n\n\n# Code\n```csharp []\npublic class Solution {\n private int[] directions = [0, 1, 0, -1, 0];\n public int MinimumTime(int[][] grid) {\n if (grid[1][0] > 1 && grid[0][1] > 1)\n {\n return -1;\n }\n int m = grid.Length;\n int n = grid[0].Length;\n bool[,] visited = new bool[m, n];\n visited[0, 0] = true;\n List<(int, int)>[] queue = new List<(int, int)>[200_000];\n queue[0] = [(0, 0)];\n for (int time = 0; time < 200_000; time++)\n {\n if (queue[time] is null)\n {\n continue;\n }\n while (queue[time].Count > 0)\n {\n (int x, int y) = queue[time][^1];\n queue[time].RemoveAt(queue[time].Count-1);\n for (int i = 0; i < 4; i++)\n {\n int a = x + directions[i];\n int b = y + directions[i+1];\n if (a < 0 || a >= m || b < 0 || b >= n || visited[a, b])\n {\n continue;\n }\n int newTime = Math.Max(\n time + 1,\n grid[a][b] + (grid[a][b] + a + b) % 2\n );\n if (a == m-1 && b == n-1)\n {\n return newTime;\n }\n visited[a, b] = true;\n if (queue[newTime] is null)\n {\n queue[newTime] = [(a, b)];\n }\n else\n {\n queue[newTime].Add((a, b));\n }\n }\n }\n }\n throw new Exception();\n }\n}\n``` | 3 | 0 | ['C#'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Easy C++ Code || Runtime beats - 99.89% , Memory beats - 88.68% | easy-c-code-runtime-beats-9989-memory-be-zn8j | Intuition\n Describe your first thoughts on how to solve this problem. \n\n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Tim | Edwards310 | NORMAL | 2024-11-29T01:07:23.300338+00:00 | 2024-11-29T01:09:11.168532+00:00 | 608 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n\n int m = grid.size();\n int n = grid[0].size();\n\n vector<int> visited(m * n, -1);\n\n priority_queue<pair<int, int>, vector<pair<int, int>>,\n greater<pair<int, int>>>\n q;\n\n q.push({0, 0});\n visited[0] = 0;\n vector<int> dir = {0, -1, 0, 1, 0};\n\n if (grid[1][0] > 1 && grid[0][1] > 1)\n return -1;\n\n while (q.size() > 0) {\n\n auto node = q.top();\n q.pop();\n\n int row = node.second / n;\n int col = node.second % n;\n\n int val = node.second;\n\n int t = node.first;\n\n if (row == m - 1 && col == n - 1) {\n return t;\n }\n for (int j = 0; j < 4; j++) {\n\n int new_row = row + dir[j];\n int new_col = col + dir[j + 1];\n\n if (new_row < 0 || new_row >= m || new_col < 0 || new_col >= n)\n continue;\n\n int val = new_row * n + new_col;\n if (visited[val] != -1)\n continue;\n\n if (grid[new_row][new_col] <= t + 1)\n visited[val] = t + 1;\n else if ((t + 1) % 2 != grid[new_row][new_col] % 2)\n visited[val] = grid[new_row][new_col] + 1;\n else\n visited[val] = grid[new_row][new_col];\n q.push({visited[val], val});\n }\n }\n\n return -1;\n }\n};\n``` | 3 | 2 | ['Array', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'Python', 'C++', 'Java', 'C#'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | C++ solution using priority queue | c-solution-using-priority-queue-by-sachi-gcbm | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Sachin_Kumar_Sharma | NORMAL | 2024-03-29T06:43:21.299915+00:00 | 2024-03-29T06:43:21.299947+00:00 | 14 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(M*N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(M*N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n int m=grid.size(),n=grid[0].size();\n\n if(grid[0][1]>1 && grid[1][0]>1) return -1;\nint dir[]={1,0,-1,0,1};\n vector<vector<bool>> vis(m,vector<bool>(n,false));\n \n priority_queue<vector<int>,vector<vector<int>>,greater<vector<int>>> pq;\n\n pq.push({grid[0][0],0,0});\n\n while(!pq.empty()){\n int time=pq.top()[0],r=pq.top()[1],c=pq.top()[2];\n pq.pop();\n\n if(r==m-1 && c==n-1) return time;\n\n if(vis[r][c]) continue;\n vis[r][c]=true;\n\n for(int i=0;i<4;i++){\n int nr=r+dir[i],nc=c+dir[i+1];\n\n if(nr<0 || nc<0 || nr>=m || nc>=n || vis[nr][nc]) continue;\n\n int wait=(grid[nr][nc]-time)%2==0?1:0;\n\n pq.push({max(grid[nr][nc]+wait,time+1),nr,nc});\n }\n\n }\n\n return -1;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | C++ | Dijkstra + flip-flopping | Simple Logic | c-dijkstra-flip-flopping-simple-logic-by-lrq5 | ```\nclass Solution {\npublic:\n // To check whether the node is in range or not...\n bool isValid(int row, int col, vector>& grid){\n return row > | SourabCodes | NORMAL | 2023-03-01T20:41:25.945277+00:00 | 2023-03-01T20:41:25.945340+00:00 | 198 | false | ```\nclass Solution {\npublic:\n // To check whether the node is in range or not...\n bool isValid(int row, int col, vector<vector<int>>& grid){\n return row >= 0 && col >= 0 && row < grid.size() && col < grid[0].size();\n }\n \n int minimumTime(vector<vector<int>>& grid) {\n \n // min heap...\n priority_queue<pair<int,pair<int,int>>, vector<pair<int,pair<int,int>>>, greater<pair<int,pair<int,int>>>> pq;\n \n \n int n = grid.size();\n int m = grid[0].size();\n \n // Base cases...\n if(n > 1 && m > 1){\n if(grid[0][1] > grid[0][0] + 1 && grid[1][0] > grid[0][0] + 1){\n return -1;\n }\n }\n \n if(n > 1 && m == 0){\n if(grid[1][0] > grid[0][0] + 1){\n return -1;\n }\n }\n \n if(n == 0 && m > 1){\n if(grid[0][1] > grid[0][0] + 1){\n return -1;\n }\n }\n \n // Initializing distance array...\n vector<vector<int>> dists(n,vector<int>(m,INT_MAX));\n \n \n int dr[] = {0,1,0,-1};\n int dc[] = {-1,0,1,0};\n \n pq.push({0,{0,0}});\n \n dists[0][0] = 0;\n \n // Dijkstra\n \n while(!pq.empty()){\n auto tops = pq.top();\n pq.pop();\n \n int dist = tops.first;\n \n int row = tops.second.first;\n int col = tops.second.second;\n \n if(row == grid.size() - 1 && col == grid[0].size() - 1){\n return dist;\n \n }\n \n for(int i = 0 ; i < 4; i++){\n \n int newrow = row + dr[i];\n int newcol = col + dc[i];\n \n // Simple as explained in the question conditions are applied...\n \n if(isValid(newrow,newcol,grid) && grid[newrow][newcol] <= dist + 1){\n \n if(dists[newrow][newcol] > dist + 1){\n pq.push({dist + 1, {newrow,newcol}});\n dists[newrow][newcol] = dist + 1;\n \n }\n \n }\n \n // If the conditions are not matched then there must be a cell smaller than grid[row][col] that is the cell from which iterator reached on grid[row][col]. It can go back and forth in those two cells increasing the time and making the iterator able to reach new cell... \n \n // Number of times the back and forth process occured will be grid[newrow][newcol] - (dist) - 1...\n \n // If this number is odd then to make the iterator reach again at grid[row][col] we add 1 in it...\n \n else if(isValid(newrow,newcol,grid) && grid[newrow][newcol] > dist + 1){\n \n int diff = grid[newrow][newcol] - (dist);\n diff--;\n \n if((diff&1)){\n diff++;\n }\n \n if(dists[newrow][newcol] > dist + diff + 1){\n pq.push({dist + diff + 1, {newrow,newcol}});\n dists[newrow][newcol] = dist + diff + 1;\n }\n }\n \n }\n \n }\n \n return -1;\n \n }\n}; | 3 | 0 | ['Math', 'Breadth-First Search', 'Graph'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | [Python3] Dijkstra's algo | python3-dijkstras-algo-by-ye15-ajnw | \n\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n if grid[0][1] <= 1 or grid[1][0] <= 1: \n m, n = len(grid), le | ye15 | NORMAL | 2023-02-26T04:06:50.748655+00:00 | 2023-02-26T04:06:50.748687+00:00 | 432 | false | \n```\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n if grid[0][1] <= 1 or grid[1][0] <= 1: \n m, n = len(grid), len(grid[0])\n pq = [(0, 0, 0)]\n dist = defaultdict(lambda : inf, {(0, 0) : 0})\n while pq: \n x, i, j = heappop(pq)\n if (i, j) == (m-1, n-1): return x \n for ii, jj in (i-1, j), (i, j-1), (i, j+1), (i+1, j): \n if 0 <= ii < m and 0 <= jj < n: \n xx = x + 1 + max(0, (grid[ii][jj] - x)//2*2) \n if dist[ii, jj] > xx: \n heappush(pq, (xx, ii, jj))\n dist[ii, jj] = xx \n return -1 \n``` | 3 | 0 | ['Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | ✅ [Python & JavaScript] - Easiest Solutions ✅ | python-javascript-easiest-solutions-by-d-9ktn | Code\npython3 []\nfrom heapq import heappush, heappop\n\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n m, n = len(grid), le | DanielOL | NORMAL | 2024-11-29T18:52:24.287152+00:00 | 2024-11-29T18:52:24.287192+00:00 | 43 | false | # Code\n```python3 []\nfrom heapq import heappush, heappop\n\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n counter = [[float(\'inf\')] * n for _ in range(m)]\n\n def is_valid(i, j):\n return 0 <= i < m and 0 <= j < n\n\n moves = [(-1, 0), (1, 0), (0, 1), (0, -1)]\n\n heap = []\n heappush(heap, (0, 0, 0))\n counter[0][0] = 0\n\n if grid[0][1] > 1 and grid[1][0] > 1:\n return -1\n\n while heap:\n current, a, b = heappop(heap)\n\n if (a, b) == (m - 1, n - 1):\n return current\n\n for ip, jp in moves:\n ni, nj = ip + a, jp + b\n if is_valid(ni, nj):\n aux = 0\n if current + 1 < grid[ni][nj]:\n aux = grid[ni][nj]\n if (grid[ni][nj] - current - 1) % 2 != 0:\n aux += 1\n else:\n aux = current + 1\n\n if aux < counter[ni][nj]:\n heappush(heap, (aux, ni, nj))\n counter[ni][nj] = aux\n\n return -1 if counter[m - 1][n - 1] == float(\'inf\') else counter[m - 1][n - 1]\n```\n``` javascript []\n/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar minimumTime = function(grid) {\n const m = grid.length;\n const n = grid[0].length;\n const counter = Array.from({ length: m }, () => Array(n).fill(Infinity));\n\n const isValid = (i, j) => i >= 0 && i < m && j >= 0 && j < n;\n\n const moves = [\n [-1, 0], [1, 0], [0, 1], [0, -1]\n ];\n\n const heap = [];\n heap.push([0, 0, 0]); // [time, row, col]\n counter[0][0] = 0;\n\n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n\n while (heap.length > 0) {\n // Min-heap pop: remove the smallest element\n heap.sort((a, b) => a[0] - b[0]);\n const [current, a, b] = heap.shift();\n\n if (a === m - 1 && b === n - 1) {\n return current;\n }\n\n for (const [ip, jp] of moves) {\n const ni = a + ip;\n const nj = b + jp;\n\n if (isValid(ni, nj)) {\n let aux = 0;\n if (current + 1 < grid[ni][nj]) {\n aux = grid[ni][nj];\n if ((grid[ni][nj] - current - 1) % 2 !== 0) {\n aux += 1;\n }\n } else {\n aux = current + 1;\n }\n\n if (aux < counter[ni][nj]) {\n heap.push([aux, ni, nj]);\n counter[ni][nj] = aux;\n }\n }\n }\n }\n\n return counter[m - 1][n - 1] === Infinity ? -1 : counter[m - 1][n - 1];\n};\n```\n---\n#### Also check out [@GloriousEvolution](https://leetcode.com/u/albrtt/) \'s useful solution.\n---\n | 2 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'Python3', 'JavaScript'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | Simple Dijkstra's Algorithm solution with Exp | C++ | Beats 100% | Most optimized | simple-dijkstras-algorithm-solution-with-zx8f | Complexity\n- Time complexity:\nO( M x N log (M x N) )\n- Space complexity:\nO( M x N )\n\n# Code\ncpp []\nclass Solution {\npublic:\n int minimumTime(vector | ujjwal141 | NORMAL | 2024-11-29T17:29:21.035444+00:00 | 2024-11-29T17:29:21.035470+00:00 | 65 | false | # Complexity\n- Time complexity:\nO( M x N log (M x N) )\n- Space complexity:\nO( M x N )\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n\n if(grid[0][1] > 1 && grid[1][0] > 1)\n return -1;\n\n int n = grid.size(), m = grid[0].size();\n\n int X[4] = {0, 0, -1, 1};\n int Y[4] = {-1, 1, 0, 0};\n\n priority_queue< pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, greater<pair<int, pair<int, int>>> > pq;\n\n pq.push({0, {0, 0}}); // time, x, y .. using Min Heap with respect to time go get minimum time to reach destination .\n\n vector<vector<int>> visited(n, vector<int> (m , 0)); // to check this element is previously visited or not .\n\n visited[0][0] = 1; \n\n while(!pq.empty()){\n int time = pq.top().first;\n int currX = pq.top().second.first;\n int currY = pq.top().second.second;\n pq.pop();\n \n if(currX == n-1 && currY == m-1)\n return time;\n\n for(int i=0 ;i<4 ;i++){\n int newX = currX + X[i];\n int newY = currY + Y[i];\n\n if(newX >= 0 && newX < n && newY >= 0 && newY < m && visited[newX][newY] == 0 ){\n if(grid[newX][newY] <= time + 1) \n pq.push({time+1, {newX, newY}});\n else{\n int diff = grid[newX][newY] - time;\n \n if(diff % 2)\n pq.push({time + diff, {newX, newY}});\n else\n pq.push({time + diff + 1 , {newX, newY}});\n } \n visited[newX][newY] = 1; \n }\n }\n } \n\n return -1;\n }\n};\n``` | 2 | 0 | ['Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Easy beat 100% runtime and memory at the same time with C++ | easy-beat-100-runtime-and-memory-at-the-25u8b | Intuition\nWe can transfer the question to an easy shortest path problem.\nEasy point minimum time required will be min(adjacent time, grid.time+1/0).\n\n# Appr | william6715 | NORMAL | 2024-11-29T11:32:17.426339+00:00 | 2024-11-29T12:37:21.548903+00:00 | 243 | false | # Intuition\nWe can transfer the question to an easy shortest path problem.\nEasy point minimum time required will be **min(adjacent time, grid.time+1/0)**.\n\n# Approach\nEarly return when grid[0][1] and grid[1][0] bigger than 1 at the same time. It is the only situation with no solution.\nFirst, put the top-left cell into the priority_queue.\nEach time pick the cell with minimum cost (cost_i) in priority_queue with move one distance.\nTwo situations after one moving:\n1. If the adjacent cell required time smaller than cost_i + 1, new cost will be cost_i + 1;\n2. If the required time bigger than cost_i + 1, the new cost will be grid[new x][new y] + 1/0. \nBecause we can keep going back and forth between two points until required time is reached. \n(Eg. cost_i +1 +2 +2.... until >= grid[new x][new y])\n\n**Based on the pq priority and the same edge cost, We can guarantee when we first time touch the cell, it gets mimimum cost**. \nFinally, we can get the minimum required time when we touch the cell[m-1][n-1].\n\n# Complexity\n- Time complexity:\nO(MN*log(MN)) \n\n- Space complexity:\nO(MN) \n\nhttps://leetcode.com/problems/minimum-time-to-visit-a-cell-in-a-grid/submissions/1465730112/?envType=daily-question&envId=2024-11-29\n\n# Code\n```cpp []\nclass Solution {\n int factor = 1024;\n vector<int> dir = {-1,0,1,0,-1};\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n if(grid[0][1] > 1 && grid[1][0] > 1) return -1;\n int m = grid.size();\n int n = grid[0].size();\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;\n pq.push({0,0});\n grid[0][0] = -1;\n while(!pq.empty()){\n auto [cost, pos] = pq.top();\n pq.pop();\n int x = pos / factor;\n int y = pos % factor;\n if(x == m-1 && y == n-1)\n return cost;\n for(int i=0; i<4; ++i){\n int newx = x + dir[i];\n int newy = y + dir[i+1];\n if(newx>=0 && newx<m && newy>=0 && newy<n && grid[newx][newy] != -1){\n int newcost = cost + 1;\n if(newcost < grid[newx][newy]){\n if((grid[newx][newy] - newcost) % 2 == 1)\n newcost = grid[newx][newy] + 1;\n else\n newcost = grid[newx][newy];\n }\n pq.push({newcost, (newx * factor + newy)});\n grid[newx][newy] = -1;\n }\n }\n }\n return -1000; // will no go to here\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | Beat 95% users || C++ || Easy to understand || Detailed Solution | beat-95-users-c-easy-to-understand-detai-2pzl | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves traversing a grid, starting from the top-left corner to the bottom | Abhishekjha6908 | NORMAL | 2024-11-29T10:58:36.844276+00:00 | 2024-11-29T10:58:36.844303+00:00 | 126 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves traversing a grid, starting from the top-left corner to the bottom-right corner, with each cell having a time value. The movement from one cell to another can only happen under certain conditions based on the time, and some cells may require a wait to become accessible. The goal is to find the minimum time required to reach the destination, considering these constraints\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can approach this problem using a modified Dijkstra\u2019s algorithm with a priority queue. Each state will store the current time and position in the grid. At each step, we explore the neighboring cells, calculate the required time to move to that cell, and push the new state into the priority queue. The **wait** condition determines whether we need to delay moving to a cell. If a cell is visited for the first time, we proceed to explore its neighbors. The algorithm will stop once we reach the destination.\n\n**Steps:**\n1. Start from the top-left cell with time 0.\n2. Use a priority queue to always process the cell with the least time.\n3. For each cell, check its four neighbors. For each valid neighbor, calculate the time to move to it (considering the wait time).\n4. Push the new state (time and position) into the priority queue.\n5. Stop when the bottom-right cell is reached or if no valid path exists.\n# Complexity\n- Time complexity: $$O(m*n*log(m*n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nWe process each cell at most once, and for each cell, we perform a constant amount of work to check its neighbors and update the priority queue.\n- Space complexity: $$O(m*n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nWe store the visited cells and the priority queue, both of which have a size proportional to the number of cells in the grid.\n# Code\n```cpp []\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n if(min(grid[0][1],grid[1][0])>1) return -1;\n priority_queue<pair<int,pair<int,int>>,vector<pair<int,pair<int,int>>>, greater<pair<int,pair<int,int>>>> pq;\n pq.push({0,{0,0}}); //time,row,column\n int m = grid.size();\n int n = grid[0].size();\n vector<vector<int>> visit(m,vector<int>(n,0));\n while(!pq.empty()){\n auto it = pq.top();\n pq.pop();\n int t = it.first;\n int r = it.second.first;\n int c = it.second.second;\n if(r==m-1 && c==n-1) return t;\n int row[] = {0,-1,0,1};\n int col[] = {-1,0,1,0};\n for(int i=0;i<4;i++){\n int nr = r+row[i];\n int nc = c+col[i];\n if(nr<0 || nc<0 || nr==m || nc==n || visit[nr][nc]==1){\n continue;\n }\n int wait = 0;\n if(abs(grid[nr][nc]-t)%2==0){\n wait = 1;\n }\n int newtime = max(grid[nr][nc]+wait,t+1);\n pq.push({newtime,{nr,nc}});\n visit[nr][nc] = 1;\n }\n }\n return 0;\n }\n \n};\n``` | 2 | 0 | ['Breadth-First Search', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Easy to understand || Beat 98%✅ | easy-to-understand-beat-98-by-yash9325-mqed | Intuition\nThe problem is about finding the shortest time to reach the bottom-right cell of a grid while respecting the constraints on the earliest time each ce | yash9325 | NORMAL | 2024-11-29T08:19:43.817393+00:00 | 2024-11-29T08:19:43.817420+00:00 | 16 | false | # **Intuition**\nThe problem is about finding the shortest time to reach the bottom-right cell of a grid while respecting the constraints on the earliest time each cell can be visited. This can be solved using a **Dijkstra-like approach**, as it involves minimizing a cost (time) to reach the destination.\n\n---\n\n# **Approach**\n1. **Initial Check**: If the first move from `(0,0)` is blocked (`grid[0][1] > 1` and `grid[1][0] > 1`), return `-1`.\n2. **Priority Queue**:\n - Use a priority queue to process cells in the order of increasing time.\n - Each entry is `{row, col, time}`.\n3. **Time Calculation**:\n - If the current time meets the cell\u2019s time constraint, move immediately.\n - If not, wait until the earliest valid time, adjusting for parity:\n - If the time difference is odd, add an extra second.\n4. **Termination**:\n - Return the time when the bottom-right cell is reached.\n - If no path exists, return `-1`.\n---\n\n# **Complexity**\n- **Time**: O(N\u2217M\u2217Log(N\u2217M))\n- **Space**: O(N\u2217M)\n\n\n# Code\n```java []\nclass Solution {\n // directions {right ,top,down,left}\n private final static int[][] directions = { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };\n\n public int minimumTime(int[][] grid) {\n if (grid[0][1] > 1 && grid[1][0] > 1) // initially no move possible\n return -1;\n PriorityQueue<int[]> queue = new PriorityQueue<>((a, b) -> a[2] - b[2]); // queue{row,col,time}\n queue.offer(new int[] { 0, 0, 0 });\n boolean[][] visited = new boolean[grid.length][grid[0].length];\n visited[0][0] = true;\n while (!queue.isEmpty()) {\n int[] cell = queue.poll();\n for (int[] direction : directions) {\n int nx = cell[0] + direction[0];\n int ny = cell[1] + direction[1];\n int currentTime = cell[2];\n if (nx >= 0 && nx < grid.length && ny >= 0 && ny < grid[0].length && !visited[nx][ny]) {\n int time = grid[nx][ny] - currentTime; // time difference b/w curr time and grid time to move\n if (time == 1) {\n time = grid[nx][ny];\n } else if (time <= 0) {\n time = currentTime + 1;\n } else {\n time = Math.max(grid[nx][ny], currentTime) + (time % 2 == 0 ? 1 : 0);\n }\n if (nx == grid.length - 1 && ny == grid[0].length - 1)\n return time;\n queue.offer(new int[] { nx, ny, time });\n visited[nx][ny] = true;\n }\n }\n }\n return -1;\n }\n```\n```c++ []\nusing namespace std;\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n int n = grid.size(), m = grid[0].size();\n // Directions for moving in 4 directions: right, down, left, up\n vector<array<int, 2>> directions = { {0, 1}, {1, 0}, {0, -1}, {-1, 0} };\n // If the first move is blocked, return -1\n if (grid[0][1] > 1 && grid[1][0] > 1) \n return -1;\n // Priority queue for Dijkstra-like traversal (min-heap): {time, row, col}\n priority_queue<array<int, 3>, vector<array<int, 3>>, greater<>> pq;\n pq.push({0, 0, 0}); // Start from the top-left corner at time 0\n // Visited array to avoid revisiting cells\n vector<vector<bool>> visited(n, vector<bool>(m, false));\n visited[0][0] = true;\n while (!pq.empty()) {\n auto [currentTime, x, y] = pq.top();\n pq.pop();\n // Explore all neighbors\n for (auto [dx, dy] : directions) {\n int nx = x + dx, ny = y + dy;\n // Check if the neighbor is within bounds and not visited\n if (nx >= 0 && nx < n && ny >= 0 && ny < m && !visited[nx][ny]) {\n int time = grid[nx][ny] - currentTime; // Time difference to satisfy the grid condition\n if (time == 1) {\n time = grid[nx][ny];\n } else if (time <= 0) {\n time = currentTime + 1;\n } else {\n time = max(grid[nx][ny], currentTime) + (time % 2 == 0 ? 1 : 0);\n }\n // If we reach the bottom-right cell, return the time\n if (nx == n - 1 && ny == m - 1)\n return time;\n // Mark the neighbor as visited and add it to the priority queue\n pq.push({time, nx, ny});\n visited[nx][ny] = true;\n }\n }\n }\n // If the bottom-right cell is not reachable, return -1\n return -1;\n }\n};\n```\n | 2 | 0 | ['Java'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Beats 100% ✅|| Waiting Time Approach || Simple Dijkstra's Algorithm || C++ || Java || Python3 | beats-100-waiting-time-approach-simple-d-pvtl | Initial Check:\n\n If it\'s impossible to leave the top-left cell because the required time for the first move (grid[0][1] or grid[1][0]) is greater than 1, ret | Sparsh_786 | NORMAL | 2024-11-29T05:50:27.863594+00:00 | 2024-11-29T05:51:10.250455+00:00 | 371 | false | **Initial Check:**\n\n* If it\'s impossible to leave the top-left cell because the required time for the first move (grid[0][1] or grid[1][0]) is greater than 1, return -1.\n\n**Priority Queue Setup:**\n\n* Use a priority queue (min-heap) to always explore the next cell with the smallest possible arrival time.\n* Push the starting cell (0, 0) with time 0 into the queue.\n\n**Traversal Logic:**\n\nWhile the queue is not empty:\n* Pop the cell with the minimum time from the queue.\n* Check if this cell is the bottom-right cell; if so, return the current time.\n* Mark the cell as visited to prevent revisiting.\n\n**Neighbor Exploration:**\n\nFor each adjacent cell (up, down, left, right):\n* Check if it is within bounds and not visited.\n* Calculate the minimum time to enter this cell:\n* Ensure the time is at least the required time for the cell (grid[newX][newY]).\n* Adjust the waiting time if the parity (odd/even) of the current time and the required time doesn\'t align.\n\n**Update Priority Queue:**\n\n* Push the newly calculated time and coordinates of the adjacent cell into the priority queue.\n\n**Final Case:**\n\n* If the queue is empty and the bottom-right cell hasn\'t been reached, return -1.\n\n\n\n**C++ Code**\n\n```\ntypedef pair<int, pair<int,int>> par;\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n int row = grid.size();\n int col = grid[0].size();\n if(min(grid[0][1], grid[1][0])>1)\n return -1;\n vector<vector<bool>> visited(row, vector<bool>(col));\n queue<par> q1;\n q1.push({0,{0,0}});\n visited[0][0] = true;\n vector<pair<int,int>> dirs{{0,1}, {1,0}, {0,-1}, {-1,0}};\n while(!q1.empty()) {\n auto curr = q1.top();\n q1.pop();\n int x = curr.second.first;\n int y = curr.second.second;\n int time = curr.first;\n \n if(x==row-1 && y==col-1)\n return time;\n \n for(int i=0;i<4;i++) {\n int newX = dirs[i].first + x;\n int newY = dirs[i].second + y;\n if(newX>=0 && newX<row && newY>=0 && !visited[newX][newY] && newY<col) {\n int waitingTime = 0;\n int diff = abs(grid[newX][newY]-time);\n if(!(diff&1))\n waitingTime = 1;\n int newTime = max(grid[newX][newY] + waitingTime, time+1);\n q1.push({newTime, {newX, newY}});\n visited[newX][newY] = true;\n }\n }\n }\n return -1;\n }\n};\n```\n\n**Java Code**\n\n```\nimport java.util.*;\n\nclass Solution {\n public int minimumTime(int[][] grid) {\n int row = grid.length;\n int col = grid[0].length;\n\n if (Math.min(grid[0][1], grid[1][0]) > 1) \n return -1;\n\n PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));\n pq.add(new int[]{0, 0, 0});\n\n boolean[][] visited = new boolean[row][col];\n visited[0][0] = true;\n\n int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};\n\n while (!pq.isEmpty()) {\n int[] current = pq.poll();\n int time = current[0];\n int x = current[1];\n int y = current[2];\n\n if (x == row - 1 && y == col - 1) \n return time;\n\n for (int[] dir : directions) {\n int newX = x + dir[0];\n int newY = y + dir[1];\n\n if (newX >= 0 && newX < row && newY >= 0 && newY < col && !visited[newX][newY]) {\n int waitingTime = 0;\n int diff = Math.abs(grid[newX][newY] - time);\n\n if ((diff & 1) == 0) \n waitingTime = 1;\n\n int newTime = Math.max(grid[newX][newY] + waitingTime, time + 1);\n pq.add(new int[]{newTime, newX, newY});\n visited[newX][newY] = true;\n }\n }\n }\n\n return -1;\n }\n}\n```\n\n**Python3 Code**\n\n```\nfrom heapq import heappush, heappop\nfrom typing import List\n\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n row, col = len(grid), len(grid[0])\n\n if min(grid[0][1], grid[1][0]) > 1:\n return -1\n\n pq = []\n heappush(pq, (0, 0, 0))\n\n visited = [[False] * col for _ in range(row)]\n visited[0][0] = True\n\n directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]\n\n while pq:\n time, x, y = heappop(pq)\n\n if x == row - 1 and y == col - 1:\n return time\n\n for dx, dy in directions:\n newX, newY = x + dx, y + dy\n\n if 0 <= newX < row and 0 <= newY < col and not visited[newX][newY]:\n diff = abs(grid[newX][newY] - time)\n waitingTime = 1 if diff % 2 == 0 else 0\n newTime = max(grid[newX][newY] + waitingTime, time + 1)\n heappush(pq, (newTime, newX, newY))\n visited[newX][newY] = True\n\n return -1\n``` | 2 | 0 | ['Breadth-First Search', 'Graph', 'C', 'Heap (Priority Queue)', 'Python', 'Java', 'Python3'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | C# Solution for Minimum Time to Visit a Cell In a Grid Problem | c-solution-for-minimum-time-to-visit-a-c-9cem | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem can be thought of as finding the shortest path in a grid, where each cell h | Aman_Raj_Sinha | NORMAL | 2024-11-29T04:17:53.978303+00:00 | 2024-11-29T04:17:53.978342+00:00 | 76 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem can be thought of as finding the shortest path in a grid, where each cell has a \u201Cgate\u201D that only opens at a specific time (grid[row][col]). You start at the top-left cell at time 0 and must reach the bottom-right cell while navigating through cells in four directions (up, down, left, right). Moving takes exactly 1 second, and you may have to wait at certain cells if the required time (grid[row][col]) is not met. The challenge is to minimize the total time taken.\n\nThis is akin to a shortest-path problem in a weighted graph, where the edge weights are dynamic and depend on the time synchronization needed to move to the next cell.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tDijkstra-like Algorithm:\n\t\u2022\tUse a priority queue (min-heap) to always explore the cell that can be reached in the shortest time.\n\t\u2022\tEach entry in the queue represents (time, row, col) where time is the earliest time you can reach that cell.\n2.\tPriority Queue Setup:\n\t\u2022\tStart from (0, 0) with time = 0.\n\t\u2022\tPush the starting cell into the priority queue with an initial time of 0.\n3.\tMovement Logic:\n\t\u2022\tAt each step, dequeue the cell (time, row, col) with the smallest time.\n\t\u2022\tTry to move in all four possible directions (up, down, left, right).\n\t\u2022\tCalculate the nextTime as time + 1.\n\t\u2022\tIf nextTime < grid[newRow][newCol], check whether the difference between grid[newRow][newCol] and nextTime is even or odd:\n\t\u2022\tIf even, move at exactly grid[newRow][newCol].\n\t\u2022\tIf odd, wait an extra second to synchronize, and move at grid[newRow][newCol] + 1.\n4.\tVisited Array:\n\t\u2022\tUse a visited 2D array to track cells that have already been processed to avoid redundant calculations.\n5.\tTermination:\n\t\u2022\tIf the bottom-right cell (m-1, n-1) is reached, return the time.\n\t\u2022\tIf all possible cells have been processed and (m-1, n-1) has not been reached, return -1.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1.\tPriority Queue Operations:\n\t\u2022\tThe priority queue holds up to m x n elements at any time.\n\t\u2022\tEach insertion or removal from the queue takes O(log(m x n)) time.\n2.\tProcessing Each Cell:\n\t\u2022\tEach cell is processed once, and each can be pushed into the priority queue once.\n\t\u2022\tHence, total insertions and deletions are O(m x n).\n\nThus, the total time complexity is O(m x n log(m x n)).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n1.\tPriority Queue:\n\t\u2022\tThe queue stores up to m x n cells.\n2.\tVisited Array:\n\t\u2022\tThe visited array is of size m x n.\n\nThus, the total space complexity is O(m x n).\n\n# Code\n```csharp []\npublic class Solution {\n public int MinimumTime(int[][] grid) {\n int m = grid.Length;\n int n = grid[0].Length;\n\n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n\n var pq = new PriorityQueue<(int time, int row, int col), int>();\n pq.Enqueue((0, 0, 0), 0);\n\n bool[,] visited = new bool[m, n];\n int[][] directions = new int[][] {\n new int[] {0, 1}, \n new int[] {1, 0}, \n new int[] {0, -1}, \n new int[] {-1, 0} \n };\n\n while (pq.Count > 0) {\n var (time, row, col) = pq.Dequeue();\n\n if (row == m - 1 && col == n - 1) {\n return time; \n }\n\n if (visited[row, col]) continue;\n visited[row, col] = true;\n\n foreach (var dir in directions) {\n int newRow = row + dir[0];\n int newCol = col + dir[1];\n\n if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n) {\n int nextTime = time + 1;\n int requiredTime = grid[newRow][newCol];\n\n if (nextTime < requiredTime) {\n int wait = (requiredTime - nextTime) % 2 == 0 ? 0 : 1;\n nextTime = requiredTime + wait;\n }\n\n if (!visited[newRow, newCol]) {\n pq.Enqueue((nextTime, newRow, newCol), nextTime);\n }\n }\n }\n }\n\n return -1;\n }\n}\n``` | 2 | 0 | ['C#'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | ✅ Simple Java Solution | simple-java-solution-by-harsh__005-52lq | CODE\nJava []\nfinal int[][] dirs = {{-1,0}, {1,0}, {0,-1}, {0,1}};\npublic int minimumTime(int[][] grid) {\n\tint r = grid.length, c = grid[0].length;\n\tif(gr | Harsh__005 | NORMAL | 2024-11-29T03:26:38.218640+00:00 | 2024-11-29T03:26:38.218661+00:00 | 288 | false | ## **CODE**\n```Java []\nfinal int[][] dirs = {{-1,0}, {1,0}, {0,-1}, {0,1}};\npublic int minimumTime(int[][] grid) {\n\tint r = grid.length, c = grid[0].length;\n\tif(grid[0][1] > 1 && grid[1][0] > 1) return -1;\n\n\tint[][] dp = new int[r][c];\n\tfor(int[] arr: dp) Arrays.fill(arr, -1);\n\tdp[0][0] = 0;\n\n\tQueue<int[]> bfs = new LinkedList<>();\n\tbfs.add(new int[]{0,0});\n\twhile(!bfs.isEmpty()) {\n\t\tint top[] = bfs.remove();\n\t\tfor(int dir[] : dirs) {\n\t\t\tint nr = top[0]+dir[0], nc = top[1]+dir[1];\n\t\t\tif(nr<0 || nc<0 || nr==r || nc==c) continue;\n\t\t\tint next = dp[top[0]][top[1]]+1;\n\t\t\tif(next < grid[nr][nc]) {\n\t\t\t\tint diff = grid[nr][nc]-next;\n\t\t\t\tif(diff%2 != 0) diff++;\n\t\t\t\tnext += diff;\n\t\t\t}\n\n\t\t\tif(next >= grid[nr][nc] && (dp[nr][nc] == -1 || next < dp[nr][nc])) {\n\t\t\t\tdp[nr][nc] = next;\n\t\t\t\tbfs.add(new int[]{nr,nc});\n\t\t\t}\n\t\t}\n\t}\n\treturn dp[r-1][c-1];\n}\n``` | 2 | 0 | ['Java'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | JS 🎊🎊🎉 | js-by-csathnere-wz5z | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | csathnere | NORMAL | 2024-11-29T02:43:00.250660+00:00 | 2024-11-29T02:43:00.250685+00:00 | 233 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar minimumTime = function(grid) {\n if(grid[0][1] > 1 && grid[1][0] > 1) return -1\n\n const m = grid.length\n const n = grid[0].length\n const dirs = [[0,1],[1,0],[0,-1],[-1,0]]\n const visited = Array.from({length: m}, ()=>Array(n).fill(false))\n visited[0][0] = true\n\n const pq = new MinPriorityQueue({priority: x => x[0]})\n pq.enqueue([0,0,0])\n\n while(!pq.isEmpty()){\n let [t,i,j] = pq.dequeue().element\n\n for(let [dx, dy] of dirs){\n let x = i+dx\n let y = j+dy\n if(x < 0 || x >= m) continue\n if(y < 0 || y >= n) continue\n if(visited[x][y] === true) continue\n\n let newTime = t+1\n if(grid[x][y] > newTime){\n newTime += Math.floor((grid[x][y] - t) / 2) * 2\n }\n\n if(x === m-1 && y === n-1){\n return newTime\n }\n \n visited[x][y] = true\n pq.enqueue([newTime, x, y])\n }\n }\n\n\n return -1\n};\n``` | 2 | 0 | ['JavaScript'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | 100% Beats Baby Solution | 100-beats-baby-solution-by-sumeet_sharma-5oze | Intuition\nThe problem involves finding the minimum time required to traverse a grid with specific constraints. The intuition is to treat this as a pathfinding | Sumeet_Sharma-1 | NORMAL | 2024-11-29T02:26:03.169399+00:00 | 2024-11-29T02:26:03.169433+00:00 | 400 | false | # Intuition\nThe problem involves finding the minimum time required to traverse a grid with specific constraints. The intuition is to treat this as a pathfinding problem where each cell has a cost, influenced by its value and traversal rules. Using Dijkstra\'s algorithm or a priority queue allows us to efficiently explore the grid and minimize the traversal cost.\n#\n-----\n\n\n\n# Approach\n1. **Edge Case Handling**: Check if the grid\'s first step is infeasible (`grid[0][1] > 1` and `grid[1][0] > 1`), as no valid path can exist in such cases.\n2. **Initialization**:\n - Use a priority queue to always process the smallest cost first.\n - Maintain a `distance` matrix initialized to `INT_MAX` to track the minimum cost to reach each cell.\n3. **Traversal**:\n - Start at the top-left corner with cost `0`.\n - Explore all four possible directions (up, down, left, right).\n - Calculate the additional time cost required to reach the next cell based on its value and the current time (`v`).\n - Push the new state into the priority queue if a better time is found.\n4. **Termination**: The process terminates when the bottom-right cell is dequeued from the priority queue, yielding the minimum cost. If unreachable, return `-1`.\n\n# Complexity\n- **Time Complexity**: \n $$O(m \\cdot n \\cdot \\log(m \\cdot n))$$ \n where \\(m\\) and \\(n\\) are the grid\'s dimensions. Each cell is processed once, and each operation in the priority queue takes \\(O(\\log(m \\cdot n))\\).\n\n- **Space Complexity**: \n $$O(m \\cdot n)$$ \n for the `distance` matrix and priority queue.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n if (grid[0][1] > 1 && grid[1][0] > 1)\n return -1; // edge case\n int m = grid.size(), n = grid[0].size();\n priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>,\n greater<>>\n pq;\n vector<vector<int>> d(m, vector<int>(n, INT_MAX));\n pq.push({0, 0, 0});\n d[0][0] = 0;\n while (!pq.empty()) {\n auto [v, i, j] = pq.top();\n pq.pop();\n if (i == m - 1 && j == n - 1)\n return v;\n int dir[5] = {-1, 0, 1, 0, -1};\n for (int k = 0; k < 4; ++k) {\n int ii = i + dir[k], jj = j + dir[k + 1];\n if (ii >= 0 && ii < m && jj >= 0 && jj < n) {\n int diff = grid[ii][jj] - v;\n if (diff < 0)\n diff = 0;\n else if (diff & 1)\n diff = diff / 2 * 2;\n int vv = v + 1 + diff;\n if (d[ii][jj] > vv) {\n d[ii][jj] = vv;\n pq.push({vv, ii, jj});\n }\n }\n }\n }\n return -1;\n }\n};\nvoid FastIO() {\n ios_base::sync_with_stdio(0);\n cin.tie(0);\n // cout.tie(0);\n}\n``` | 2 | 0 | ['C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Minimum Time to visit a cell in a grid - Easy Explanation -🌟 Beats 100% 🌟 | minimum-time-to-visit-a-cell-in-a-grid-e-4bn4 | Intuition\n \nPriority Queue can be used with the custom comparator that the first element of the prioirity Queue array that is time is arranged in ascending or | RAJESWARI_P | NORMAL | 2024-11-29T01:47:32.404358+00:00 | 2024-11-29T01:47:32.404381+00:00 | 106 | false | # Intuition\n \nPriority Queue can be used with the custom comparator that the first element of the prioirity Queue array that is time is arranged in ascending order in the priorityQueue.\n\nTo check if the cell is already visited or not, seen boolean array is used for the size of the grid.\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n**Static variable**:\n\nInitialize static array MOVES , all four directions that are possible from one grid position.\n\n private static final int[][] MOVES={{-1,0},{0,1},{1,0},{0,-1}};\n\n**Initialization**:\n\nInitialize rows to be the number of rows in the grid(grid.length) and cols to be the number of column in the grid(grid[0].length).\n\n int rows=grid.length;\n int cols=grid[0].length;\n\n**Base Condition**:\n\nIf the element in the next time of the grid may in 0,1 or 1,0 cell -> if both are greater than time 1, We cannot move further , then we return -1.\n\n if(grid[0][1]>1 && grid[1][0]>1)\n {\n return -1;\n }\n\n**Initialization for processing of the grid**:\n\nDeclare priority Queue with the element as integer array and with custom comparator as a[0] < b[0] in the ascending order of time.\n\n PriorityQueue<int[]> pq=new PriorityQueue<>((a,b)->a[0]-b[0]);\n\nDeclare boolean array seen with the size of the grid.\n\n boolean[][] seen=new boolean[rows][cols];\n\nInitialize priorityQueue with first element as {0,0,0} because at the grid position (0,0) -> the time is also 0.\n\n pq.offer(new int[]{0,0,0});\n\nInitialize the first position (0,0) to be true because it is now reached and it could not be visited again.\n\n seen[0][0]=true;\n\n**Finding Minimum Time to visit**:\n\nIterate through the priority Queue until it is empty.\n\n while(!pq.isEmpty()){\n\nFrom the priorityQueue , poll the element which is the integer array with time(curr[0]) , row(curr[1]) and col(curr[2]).\n\n int[] curr=pq.poll();\n int time=curr[0];\n int row=curr[1];\n int col=curr[2];\n\nIterate through all the direction that is possible.\n\n \n for(int[] dir:MOVES){\n\nFind newRow(row+dir[0]) and column(col+dir[1]) by adding with the original row and column and check if it is within 0 to number of rows or cols.Otherwise , continue with next iteration.\n\n int newRow=row+dir[0];\n int newCol=col+dir[1];\n\n if(newRow<0 || newRow>=rows || newCol<0 || newCol>=cols || seen[newRow][newCol])\n {\n continue;\n }\n\nAnd newTime is equal to the available time plus 1.\n\n int newTime=time+1;\n\nCheck if the grid element is greater than time.If so we have to calculate the wait by ((grid[newRow][newCol] - newTime + 1) / 2 )*2.\n\nIncrement the newTime with the wait.\n\n if(grid[newRow][newCol]>newTime)\n {\n int wait=((grid[newRow][newCol] - newTime + 1) / 2 )*2;\n newTime+=wait;\n }\n\nIf we reach the bottom right, then newRow is equal to rows -1 and newCol is equal to cols-1, so return the newTime calculated so far.\n\n if(newRow==rows-1 && newCol==cols-1)\n {\n return newTime;\n }\n\nUpdate seen of the newRow and newCol to be true and insert the processed element\'s newTime, newRow and newCol to the priorityQueue.\n\n seen[newRow][newCol]=true;\n pq.offer(new int[]{newTime,newRow,newCol});\n\n**Returning the value**:\n\nReturn the newTime which is calculated if we reach the bottom right of the grid.Otherwise , return -1. \n\n return -1;\n\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- ***Time complexity***: **O((rowsxcols).log(rowsxcols))**.\n rows -> number of rows in the grid.\n cols -> number of cols in the grid.\n\nEach cell is processed once and operation on priority Queue takes \n**O((rowsxcols).log(rowsxcols))**.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- ***Space complexity***: **O(rowsxcols)**.\n rows -> number of rows in the grid.\n cols -> number of cols in the grid.\n\nSpace is used for priority Queue and the seen array which is almost\n \n PriorityQueue = O(rowsxcols).\n seen array = O(rowsxcols).\n\n Hence the total space is **O(rowsxcols) + O(rowsxcols) = O(rowsxcols)**.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n private static final int[][] MOVES={{-1,0},{0,1},{1,0},{0,-1}};\n public int minimumTime(int[][] grid) {\n int rows=grid.length;\n int cols=grid[0].length;\n\n if(grid[0][1]>1 && grid[1][0]>1)\n {\n return -1;\n }\n\n PriorityQueue<int[]> pq=new PriorityQueue<>((a,b)->a[0]-b[0]);\n boolean[][] seen=new boolean[rows][cols];\n\n pq.offer(new int[]{0,0,0});\n seen[0][0]=true;\n\n while(!pq.isEmpty())\n {\n int[] curr=pq.poll();\n int time=curr[0];\n int row=curr[1];\n int col=curr[2];\n\n for(int[] dir:MOVES)\n {\n int newRow=row+dir[0];\n int newCol=col+dir[1];\n\n if(newRow<0 || newRow>=rows || newCol<0 || newCol>=cols || seen[newRow][newCol])\n {\n continue;\n }\n int newTime=time+1;\n\n if(grid[newRow][newCol]>newTime)\n {\n int wait=((grid[newRow][newCol] - newTime + 1) / 2 )*2;\n newTime+=wait;\n }\n\n if(newRow==rows-1 && newCol==cols-1)\n {\n return newTime;\n }\n seen[newRow][newCol]=true;\n pq.offer(new int[]{newTime,newRow,newCol});\n }\n }\n return -1;\n }\n}\n``` | 2 | 0 | ['Array', 'Heap (Priority Queue)', 'Matrix', 'Java'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Beats 100% ✅✅|Dijkstra's Algorithm|Kotlin | beats-100-dijkstras-algorithmkotlin-by-c-8sl5 | Intuition\nIn this problem, we\'re looking for the minimum time to reach the bottom-right cell, where each cell has a minimum time requirement. This creates a w | thearchetypee | NORMAL | 2024-11-29T01:14:50.126043+00:00 | 2024-11-29T02:20:02.329761+00:00 | 54 | false | # Intuition\nIn this problem, we\'re looking for the minimum time to reach the bottom-right cell, where each cell has a minimum time requirement. This creates a weighted graph problem, where the weights are the time we need to wait at each cell.\n\n# Approach\n\nLet\'s break down the solution:\n\n1. Initial Setup:\n The solution starts by creating a grid called `times` where each cell is initialized to infinity (Int.MAX_VALUE). This grid keeps track of the minimum time needed to reach each cell. We set times[0][0] = 0 since we start at the top-left.\n\n2. Priority Queue:\n We use a priority queue (PriorityQueue in Kotlin) that orders cells by their time. Each element in the queue contains (row, col, time). The priority queue ensures we always process the cell with the minimum time first.\n\n3. Main Algorithm Loop:\n ```kotlin\n while (pq.isNotEmpty()) {\n val (row, col, time) = pq.poll()\n \n if (time > times[row][col]) continue // Skip if we found a better time\n if (row == m - 1 && col == n - 1) return time // Reached destination\n ```\n We keep processing cells until we either reach the destination or run out of cells to process.\n\n4. Time Calculation: For each neighboring cell, we calculate two times:\n ```kotlin\n val newTime = time + 1 // Basic time to move to next cell\n val waitTime = if (grid[newRow][newCol] > newTime) {\n grid[newRow][newCol] + (grid[newRow][newCol] - newTime) % 2\n } else newTime\n ```\n This is where the problem gets interesting. If we can\'t enter the cell immediately (grid[newRow][newCol] > newTime), we need to wait. The waiting calculation ensures we wait long enough to satisfy the cell\'s minimum time requirement.\n\nLet\'s see an example with the input grid:\n```\n[[0,1,3,2],\n [5,1,2,5],\n [4,3,8,6]]\n```\n\nStarting at (0,0):\n1. Initial state: times[0][0] = 0\n2. From (0,0), we can move to (0,1) or (1,0):\n - For (0,1): grid[0][1] = 1, we can move there at time 1\n - For (1,0): grid[1][0] = 5, we need to wait until time 5\n\n3. The priority queue will process (0,1) first since it has lower time\n4. From (0,1), we explore (0,2) and (1,1)\n And so on...\n\nThe algorithm continues this way, always choosing the path with minimum time, until we reach the bottom-right cell or determine it\'s impossible.\n\n# Complexity\n\n- Time complexity: O(MN log(MN))\n - Priority queue operations take O(log(MN)) time\n - Each cell can be visited multiple times but bounded by maximum time\n - Total operations = O(MN) vertices \xD7 O(log(MN)) for priority queue\n\n- Space complexity: O(MN)\n - times[][] array: O(MN)\n - Priority queue: O(MN) worst case\n - Additional space (directions array, temp variables): O(1)\n\n# Code\n```kotlin []\nclass Solution {\n fun minimumTime(grid: Array<IntArray>): Int {\n if (grid[0][1] > 1 && grid[1][0] > 1) return -1\n \n val m = grid.size\n val n = grid[0].size\n val directions = arrayOf(intArrayOf(1, 0), intArrayOf(-1, 0), intArrayOf(0, 1), intArrayOf(0, -1))\n val times = Array(m) { Array(n) { Int.MAX_VALUE } }\n times[0][0] = 0\n \n val pq = PriorityQueue<IntArray>(compareBy { it[2] })\n pq.offer(intArrayOf(0, 0, 0))\n \n while (pq.isNotEmpty()) {\n val (row, col, time) = pq.poll()\n \n if (time > times[row][col]) continue\n if (row == m - 1 && col == n - 1) return time\n \n for ((dr, dc) in directions) {\n val newRow = row + dr\n val newCol = col + dc\n \n if (newRow in 0 until m && newCol in 0 until n) {\n val newTime = time + 1\n val waitTime = if (grid[newRow][newCol] > newTime) {\n grid[newRow][newCol] + (grid[newRow][newCol] - newTime) % 2\n } else newTime\n \n if (waitTime < times[newRow][newCol]) {\n times[newRow][newCol] = waitTime\n pq.offer(intArrayOf(newRow, newCol, waitTime))\n }\n }\n }\n }\n return -1\n }\n}\n```\n\n## [Updated] How are we calculating waitTime?\nLet me break down the waitTime calculation and explain the intuition behind it. This is one of the trickier parts of the solution.\n\nFirst, let\'s understand what we\'re trying to solve:\n```kotlin\nval newTime = time + 1 // Time after moving to the new cell\nval waitTime = if (grid[newRow][newCol] > newTime) {\n grid[newRow][newCol] + (grid[newRow][newCol] - newTime) % 2\n} else newTime\n```\n\nLet\'s say we\'re at time 3 and want to move to a cell that requires minimum time 7 (grid[newRow][newCol] = 7). What should we do?\n\nCase 1: When grid[newRow][newCol] <= newTime\n- If we can enter the cell immediately (the cell\'s required time is less than or equal to our arrival time)\n- We just use newTime (time + 1)\n- Example: We arrive at time 8, cell requires time 7 \u2192 we can enter immediately at time 8\n\nCase 2: When grid[newRow][newCol] > newTime\nThis is where it gets interesting. Let\'s work through an example:\n- We arrive at time 4 (newTime)\n- Cell requires time 7 (grid[newRow][newCol])\n- We can\'t enter immediately, so we need to wait\n- But here\'s the key insight: We can\'t just wait until time 7!\n\nWhy? Because of an important constraint in the problem: we must keep moving every second. We can\'t stay in the same place. So if we need to wait, we need to move back and forth between adjacent cells until we reach the required time.\n\nThe formula `grid[newRow][newCol] + (grid[newRow][newCol] - newTime) % 2` handles this:\n1. First part `grid[newRow][newCol]`: We need at least this much time\n2. Second part `(grid[newRow][newCol] - newTime) % 2`: This accounts for the back-and-forth movement\n\nLet\'s see a concrete example:\n```\nCurrent time: 4\nCell requires: 7\ngap = 7 - 4 = 3\n\nWe need to:\nt=4: Try to enter but can\'t\nt=5: Move back\nt=6: Move forward\nt=7: Finally enter\n\nThe formula gives us:\n7 + (7-4)%2 = 7 + 3%2 = 7 + 1 = 8\n```\n\nThe %2 part is crucial because:\n- If the gap is even, we\'ll end up back at the cell at exactly the required time\n- If the gap is odd, we\'ll need one extra move to get back to the cell | 2 | 0 | ['Heap (Priority Queue)', 'Kotlin'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Beats 61% Python dijkstra, edge cases explained with examples SUPER CLEAR! | beats-61-python-dijkstra-edge-cases-expl-9vxp | Intuition\n Describe your first thoughts on how to solve this problem. \nDijkstra in 2d matrix with edge cases, do this problem first.\nhttps://leetcode.com/pro | ix221 | NORMAL | 2024-11-17T03:55:39.814060+00:00 | 2024-11-17T03:55:39.814086+00:00 | 153 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDijkstra in 2d matrix with edge cases, do this problem first.\nhttps://leetcode.com/problems/swim-in-rising-water/\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThere are 2 cases:\nThe current time allows us to visit the neighboring cell, then we simply increment time by 1 and visit that cell if it is a minimum according to dijkstra algorithm.\n\nThe other case is if the current time + 1 does not hit the allowed time.\nThen, the difference matters. To stall the time, we can move from the cell we are at to the cell to the left or up or down (doesn\'t really matter in principle) back and forth. \n\nIf the difference between the next cell and current time is even, we have to add an extra one. \nFor example, if current time is t=1 and we are trying to go to 5, \nwe go left (t = 2), right (t=3), left(t=4), right(t=5) (but we are still at the original cell), so we add 1 more to move to the next cell.\n\nif current time is t=1 and we are trying to go to 4, \nwe go left (t = 2), right (t=3), and then we can directly go right again to 4. \n\nThus \n```\ndiff = grid[newx][newy] - currTime \nif diff%2 == 0:\n newTime = grid[newx][newy] + 1\nelse:\n newTime = grid[newx][newy]\n```\nhandles this edge case.\n# Complexity\n- Time complexity:\n$$O(M*Nlog(M*N))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(M*N)$$\n# Code\n```python3 []\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n #dijkstra\n if grid[0][1] > 1 and grid[1][0] > 1: #cant move from start \n return -1\n\n directions = [(1,0), (0, 1), (-1,0), (0, -1)]\n minheap = [(0, 0, 0)]\n m = len(grid)\n n = len(grid[0])\n minTime = [[float(\'inf\') for _ in range(n)] for _ in range(m)]\n\n while minheap:\n currTime, x, y = heappop(minheap)\n if x == m-1 and y == n-1: #reached end\n return currTime\n\n for dx, dy in directions:\n newx = x+dx\n newy = y+dy\n\n if 0<=newx<m and 0<=newy<n:\n if grid[newx][newy] <= currTime+1 and currTime+1 < minTime[newx][newy]:\n minTime[newx][newy] = currTime+1\n heappush(minheap, (currTime+1, newx, newy))\n \n diff = grid[newx][newy] - currTime \n if diff%2 == 0:\n newTime = grid[newx][newy] + 1\n else:\n newTime = grid[newx][newy]\n\n if grid[newx][newy] > currTime+1 and newTime < minTime[newx][newy]:\n minTime[newx][newy] = newTime\n heappush(minheap, (newTime, newx, newy))\n return -1 #cant reach end\n``` | 2 | 0 | ['Python3'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | 12 lines scala bfs recursion | 12-lines-scala-bfs-recursion-by-vititov-7oy1 | \nobject Solution {\n import collection.immutable.{TreeMap,TreeSet}\n def minimumTime(grid: Array[Array[Int]]): Int = {\n def f(q:Set[(Int,(Int,Int))], v:M | vititov | NORMAL | 2024-04-14T18:13:13.976311+00:00 | 2024-04-14T18:13:13.976344+00:00 | 13 | false | ```\nobject Solution {\n import collection.immutable.{TreeMap,TreeSet}\n def minimumTime(grid: Array[Array[Int]]): Int = {\n def f(q:Set[(Int,(Int,Int))], v:Map[(Int,Int),Int]): Int = {\n lazy val ((t0:Int,(x0:Int,y0:Int)),t) = (q.head, q.tail)\n lazy val aa = List((x0-1)->y0, x0->(y0+1), x0->(y0-1), (x0+1)->y0)\n .collect{case (x:Int,y:Int) if x>=0 && y>=0 && x < grid.size && y < grid.head.size =>\n lazy val tm = grid(x)(y)\n lazy val inc = 1 - (tm-t0)%2\n ((t0+1) max (tm+inc)) -> (x,y) \n }.filterNot{case (tm,xy) => v.contains(xy) && v(xy) <= tm }\n if(q.isEmpty) v((grid.size-1),(grid.head.size-1))\n else f(t ++ aa, v ++ (aa.map{case (tm,xy) => xy -> tm }))\n }\n if((grid(1)(0) min grid(0)(1)) > 1 ) -1 else f(TreeSet(grid(0)(0) -> (0,0)), Map((0,0) -> grid(0)(0)))\n }\n}\n\n``` | 2 | 0 | ['Scala'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | C++ Modified Dijkstra | Detailed Explanation | c-modified-dijkstra-detailed-explanation-dvgc | Intuition\n Describe your first thoughts on how to solve this problem. \nWe are asked to move in adjacent cell every second.\nBut what if the unvisited cell\'s | YashGadia36 | NORMAL | 2023-08-18T15:59:14.547514+00:00 | 2023-08-18T15:59:14.547540+00:00 | 183 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe are asked to move in adjacent cell every second.\nBut what if the unvisited cell\'s time is much more greater than current time passed?\nHere, we will need to iterate on the peviously visited cells so that the time is passed. But doing this will lead to TLE.\nSo, we need to keep a track of at what minimum time the cell can be visited after re-iterating on the visited cells.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- If`grid[0][1]`and`grid[1][0]`are greater than 1, then we cannot move anywhere from the first cell. So answer will be`-1`.\n- If`time passed + 1 sec`is greater than or equal to`grid[i][j]`, then the cell will unlock at the same instance.\n- Else, we will need to waste some time visiting the already visited cells so that the time is passed and the cell will unlock.\nIf we are standing at a cell and no matter whichever path is chosed to visit the already visited cells, it will always take`even`amount of time to go and come back to the current cell.\nSo, if the time passed is even,\n - If`grid[i][j]`is odd, then cell`{i, j}`will unlock at`grid[i][j]`time because revisiting the visited cells and coming back will take even amount of time no matter whichever path is traversed and then +1 second to go to locked cell.\n - If`grid[i][j]`is even, then cell`{i, j}`will unlock at`grid[i][j] + 1`time.\n- If time passed is odd,\n - If`grid[i][j]`is even, then cell`{i, j}`will unlock at`grid[i][j]`time because revisiting the visited cells and coming back will take even amount of time no matter whichever path is traversed and then +1 second to go to locked cell. \n - If`grid[i][j]`is odd, then cell`{i, j}`will unlock at`grid[i][j] + 1`time.\n\n# Complexity\n- Time complexity: O(n * m * log(n * m)).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n * m).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\nprivate:\n vector<int> dr = {0, +1, 0, -1};\n vector<int> dc = {+1, 0, -1, 0};\n\npublic:\n bool isValid(int row, int col, int n, int m) {\n return (row >= 0 && row < n && col >= 0 && col < m);\n }\n\n int minimumTime(vector<vector<int>>& grid) {\n int n = grid.size(), m = grid[0].size();\n\n // We can\'t iterate anywhere except the first cell.\n if(grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n\n vector<vector<int>> vis(n, vector<int>(m, -1));\n set<pair<int, pair<int, int>>> st;\n // {time, {row, col}}.\n st.insert({0, {0, 0}});\n vis[0][0] = 0;\n\n while(st.size() != 0) {\n auto it = *(st.begin());\n int time = it.first;\n int x = it.second.first;\n int y = it.second.second;\n st.erase(it);\n\n for(int i = 0; i < 4; ++i) {\n int newX = x + dr[i];\n int newY = y + dc[i];\n if(isValid(newX, newY, n, m) && vis[newX][newY] == -1) {\n // No need to waste time as cell is already unlocked.\n if(time + 1 >= grid[newX][newY]) {\n vis[newX][newY] = time + 1;\n st.insert({time + 1, {newX, newY}});\n }\n // Need to waste time.\n else {\n if(time % 2 == 0) {\n if(grid[newX][newY] % 2 == 1) {\n vis[newX][newY] = grid[newX][newY];\n st.insert({grid[newX][newY], {newX, newY}});\n } \n else {\n vis[newX][newY] = grid[newX][newY] + 1;\n st.insert({grid[newX][newY] + 1, {newX, newY}});\n }\n }\n else {\n if(grid[newX][newY] % 2 == 0) {\n vis[newX][newY] = grid[newX][newY];\n st.insert({grid[newX][newY], {newX, newY}});\n } \n else {\n vis[newX][newY] = grid[newX][newY] + 1;\n st.insert({grid[newX][newY] + 1, {newX, newY}});\n }\n }\n }\n }\n }\n }\n\n return vis[n - 1][m - 1];\n }\n};\n``` | 2 | 0 | ['Graph', 'Matrix', 'Ordered Set', 'Shortest Path'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Video Explanation (Hindi) || Dijkstra Algorithm || Edge Case || C++ | video-explanation-hindi-dijkstra-algorit-nz6s | Intuition\n Describe your first thoughts on how to solve this problem. \nhttps://youtu.be/lZM00M5oljY\n\n# Approach\n Describe your approach to solving the prob | pkpawan | NORMAL | 2023-02-26T11:58:52.488080+00:00 | 2023-02-26T12:00:01.054950+00:00 | 621 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nhttps://youtu.be/lZM00M5oljY\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe first check cell(0,1) and (1,0) if they both have value>1 we cannot find solution as we will not be able to move forwards.\n\nWe will use dijkstra algorithms to get smallest cost cell first while doing bfs to reduce time cost.\n\nThere is one edge case , if we want to move from cell(i,j) to neighbour cell and we need additional \'x\' time and \'x\' is **even** then we need \'x+1\' time .\n\nLike we are at (1,1) with time = 2, and want to go to (1,2) with time 4 we need additional 2 sec time but we will have to give (3) sec time to get there. As 2 sec will be exhausted going to cell(1,0)and coming back to (1,1) , and we need additonal \'1\' to reach (1,2)\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(m*n log (m *n))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m*n)\n# Code\n```\n\nclass Solution {\npublic:\n \n \n \n int minimumTime(vector<vector<int>>& grid) {\n\n //if cell 0,1 and cell 1,0 have >1 values then we cannot move ahed \n //from 0,0 so no sollution\n if(grid[0][1]>1 && grid[1][0]>1)return -1;\n\n int n = grid.size();\n int m = grid[0].size();\n \n //visited array we will process each cell atmax once\n vector<vector<int>>vis(n,vector<int>(m));\n \n //using priroirty queue to give us minimum cost cell first\n priority_queue<pair<int,pair<int,int>>>bfs;\n bfs.push({0,{0,0}});\n \n \n while(!bfs.empty()){\n pair<int,pair<int,int>>temp = bfs.top();\n bfs.pop();\n\n //here x,y are coordinates of current cell\n //tm is the total time to reach till this cell\n int x = temp.second.first;\n int y = temp.second.second;\n int tm = abs(temp.first);\n \n //the first time we get to the last cell we return the time taken\n //we are using Dijkstra algorithm so it will most optimal answer\n //in first go\n if(x == n-1 && y == m-1)return tm;\n \n //we dont process already visited/processed cell\n if(vis[x][y])continue;\n\n //marking the cell visited/processed\n vis[x][y] = 1;\n \n //now we will try to go to all valid neighbours \n\n //move up\n if((x-1)>=0){\n int req = grid[x-1][y] - tm;\n //finding the required time\n\n if(req<=1)req = max(req,1);\n else {\n //if time is even we need one extra time \n if(req%2==0)req ++;\n }\n //if condition is satisfied to move to the grid cell\n if((tm+req)>= grid[x-1][y] && vis[x-1][y] == 0){\n \n bfs.push({-(tm+req),{x-1,y}});\n }\n \n }\n \n //move down\n if((x+1)<n){\n int req = grid[x+1][y] - tm;\n \n\n if(req<=1)req = max(req,1);\n else {\n if(req%2==0)req ++;\n }\n \n if((tm+req)>= grid[x+1][y] && vis[x+1][y] == 0){\n \n bfs.push({-(tm+req),{x+1,y}});\n } \n }\n \n //move up\n if((y-1)>=0){\n int req = grid[x][y-1] - tm;\n \n if(req<=1)req = max(req,1);\n else {\n if(req%2==0)req ++;\n }\n \n if((tm+req)>= grid[x][y-1] && vis[x][y-1] == 0){\n \n bfs.push({-(tm+req),{x,y-1}});\n }\n }\n \n //move down\n if((y+1)<m){\n int req = grid[x][y+1] - tm;\n \n if(req<=1)req = max(req,1);\n else {\n if(req%2==0)req ++;\n }\n \n if((tm+req)>= grid[x][y+1] && vis[x][y+1] == 0){\n \n bfs.push({-(tm+req),{x,y+1}});\n }\n }\n \n \n }\n \n return -1;\n \n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Shortest Path - BFS | shortest-path-bfs-by-ajay_jeena_leetcode-iwcf | Approach - We will use a priority queue to store the cells visited and also the minimum time required to get to the cell and mark the cell visited and from each | ajay_jeena_leetcode | NORMAL | 2023-02-26T10:39:58.701519+00:00 | 2023-02-26T11:54:19.673824+00:00 | 936 | false | Approach - We will use a priority queue to store the cells visited and also the minimum time required to get to the cell and mark the cell visited and from each cell we will try to move in all the four directions whenever possible.\nPoints to note - \n\t1- We will use min priority queue with time as the criteria to keep our cells in increasing order.\n\t2-At any cell if we cannot make move due to the higher value of time required to get to that cell then there will be a cell from where we reach to current cell with which we can make some to and fro motions to satisfy the given condition.\n```\nclass Solution {\npublic:\n \n int minimumTime(vector<vector<int>>& grid) {\n int m=grid.size(), n=grid[0].size();\n if(grid[0][1]!=1 && grid[1][0]!=1 && grid[0][1]!=0 && grid[1][0]!=0) return -1;\n vector<vector<int>> vis(1002,vector<int>(1001,0));\n priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq;\n vector<int> dx={1,0,-1,0};\n vector<int> dy={0,1,0,-1};\n \n pq.push({0,0,0});\n while(pq.size()>0){\n \n auto curr=pq.top();\n pq.pop();\n int x=curr[1], y=curr[2], cost=curr[0];\n cout<<cost<<" ";\n if(x==m-1 && y==n-1) return cost;\n for(int i=0;i<4;i++){\n if(x+dx[i]<m && y+dy[i]<n && x+dx[i]>=0 && y+dy[i]>=0 && (vis[x+dx[i]][y+dy[i]]==0)){\n vis[x+dx[i]][y+dy[i]]=1;\n int val=0;\n if(grid[x+dx[i]][y+dy[i]]<=cost){\n val=cost;\n }\n else{\n int z=(grid[x+dx[i]][y+dy[i]]-cost)/2;\n val=cost+2*abs(z);\n }\n pq.push({val+1, x+dx[i], y+dy[i]});\n }\n }\n }\n return -2;\n }\n};\n``` | 2 | 0 | ['Breadth-First Search', 'C'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | DFS Approach - Stuck (C++) | dfs-approach-stuck-c-by-jaimit25-i8a6 | Not able to clear all test cases, what am i doing wrong?\n\nvector<int> row = {-1, 0, 1, 0};\nvector<int> col = {0, 1, 0, -1};\n\nbool isVisited(int r, int c, v | jaimit25 | NORMAL | 2023-02-26T04:36:15.228503+00:00 | 2023-02-26T04:57:07.717880+00:00 | 1,440 | false | Not able to clear all test cases, what am i doing wrong?\n```\nvector<int> row = {-1, 0, 1, 0};\nvector<int> col = {0, 1, 0, -1};\n\nbool isVisited(int r, int c, vector<vector<int>> &visited) {\n if (visited[r][c] == 1)\n return true;\n return false;\n}\nint tm = 0 ;\nvoid help(vector<vector<int>> &grid, int i, int j, vector<vector<int>> &visited,\n bool &flag, int &time) {\n\n // cout<<i<<" "<<j<<endl;\n visited[i][j] = 1;\n if(time < grid[i][j]){\n return;\n }\n\n // cout << grid[i][j] << endl;\n int n = grid.size();\n int m = grid[0].size();\n\n if (i == n - 1 && j == m - 1) {\n // cout<< " base case"<<endl;\n flag = true;\n tm = max(tm,time);\n return;\n }\n\n\n for (int k = 0; k < 4; k++) {\n int r = i + row[k];\n int c = j + col[k];\n \n if (r >= 0 && r < n && c >= 0 && c < m ) {\n \n if (!isVisited(r, c, visited)) {\n time ++;\n // cout<<"Time : "<<time<<endl;\n help(grid,r,c,visited,flag,time);\n visited[r][c] = 0;\n time--;\n }\n } \n }\n}\n```\n\nThank you! | 2 | 0 | ['Depth-First Search', 'Recursion', 'C'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | JAVA solution | PriorityQueue | java-solution-priorityqueue-by-gunner77-ad3s | \n\nclass Solution {\n \n\tpublic int minimumTime(int[][] grid) {\n \n \n int n = grid.length, m = grid[0].length;\n if(grid[0][0 | gunner77 | NORMAL | 2023-02-26T04:08:01.932553+00:00 | 2023-02-26T04:25:48.142336+00:00 | 256 | false | \n\nclass Solution {\n \n\tpublic int minimumTime(int[][] grid) {\n \n \n int n = grid.length, m = grid[0].length;\n if(grid[0][0] > t) return -1;\n if(grid[0][1] > 1 && grid[1][0] > 1) return -1;\n \n int[][] dir = {{-1,0}, {1,0}, {0,-1}, {0,1}};\n \n PriorityQueue<int[]> q = new PriorityQueue<>( (a, b)->(a[2]-b[2]) );\n boolean[][] vis = new boolean[n][m];\n q.offer(new int[]{0, 0, 0});\n \n while(!q.isEmpty()){\n int[] e = q.remove();\n \n vis[e[0]][e[1]] = true;\n \n if(e[0] == n-1 && e[1] == m-1) return e[2];\n \n for(int[] d: dir){\n int new_x = e[0]+d[0], new_y = e[1]+d[1];\n \n if(new_x < 0 || new_y < 0 || new_x >= n || new_y >= m || vis[new_x][new_y]) continue;\n vis[new_x][new_y] = true;\n int diff = grid[new_x][new_y]-e[2];\n \n if(diff <= 1){\n q.offer(new int[]{new_x, new_y, e[2]+1});\n }else{\n if(diff%2 == 0){\n q.offer(new int[]{new_x, new_y, e[2]+diff+1});\n }else{\n q.offer(new int[]{new_x, new_y, e[2]+diff});\n }\n }\n \n }\n \n }\n return -1;\n }\n} | 2 | 0 | [] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | C++ BFS/PQ Code with explanation | c-bfspq-code-with-explanation-by-jinyeli-suwy | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach : bfs with priority queue\n Describe your approach to solving the problem. | jinyeli1996 | NORMAL | 2023-02-26T04:02:17.040543+00:00 | 2023-03-08T05:21:08.534535+00:00 | 1,375 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach : bfs with priority queue\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: (m*n)log(m*n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n int row=grid.size(), col=grid[0].size(), ans=INT_MAX;\n vector<vector<int>> direction{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n vector<vector<bool>> visited(row, vector<bool>(col, false));\n \n priority_queue<vector<int>, vector<vector<int>>, greater<>> pq;\n \n visited[0][0]=true;\n \n pq.push({0, 0, 0});\n // do initial explore\n if(grid[1][0]<=1){\n pq.push({1, 1, 0});\n visited[1][0]=true;\n }\n if(grid[0][1]<=1){\n pq.push({1, 0, 1});\n visited[0][1]=true;\n }\n \n // if no initial round return 0\n if(pq.size()==1){\n return -1;\n }\n \n while(pq.size()){\n auto curr = pq.top();\n pq.pop();\n int time=curr[0];\n int r=curr[1], c=curr[2];\n \n if(r==row-1 && c==col-1){\n ans=min(ans, time);\n }\n \n for(auto& i:direction){\n int newR=r+i[0];\n int newC=c+i[1];\n if(newR>=0 && newR<row && newC>=0 && newC<col && visited[newR][newC]==false){\n if(time+1>=grid[newR][newC]){\n pq.push({time+1, newR, newC});\n // if difference between two cell is more than 1\n }else{\n int diff=grid[newR][newC]-time;\n // steps to get two next cell\n if(diff%2==0){\n pq.push({grid[newR][newC]+1, newR, newC});\n }else{\n pq.push({grid[newR][newC], newR, newC});\n }\n }\n visited[newR][newC]=true;\n }\n }\n }\n \n \n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 4 |
minimum-time-to-visit-a-cell-in-a-grid | Dijkstra's | dijkstras-by-akshaypatidar33-1bp2 | Code | akshaypatidar33 | NORMAL | 2025-02-06T09:42:40.235577+00:00 | 2025-02-06T09:42:40.235577+00:00 | 14 | false |
# Code
```cpp []
class Solution {
public:
int minimumTime(vector<vector<int>>& grid) {
if(grid[0][0]>0 || (grid[0][1]>1 && grid[1][0]>1)) return -1;
int n = grid.size(), m = grid[0].size();
vector<vector<int>> dist(n,vector<int>(m,INT_MAX));
priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, greater<pair<int, pair<int, int>>>> pq;
pq.push({0,{0,0}});
int dir[] = {0,1,0,-1,0};
dist[0][0]=0;
while(!pq.empty()){
auto[time, xy] = pq.top();
auto[x, y]=xy;
pq.pop();
for(int i=0; i<4; i++){
int nx = x+dir[i], ny = y+dir[i+1];
if(nx>=0 && ny>=0 && nx<n && ny<m){
int diff = abs(grid[nx][ny]-time);
int newtime = diff%2==0? grid[nx][ny]+1:grid[nx][ny];
if(time+1>=grid[nx][ny] && dist[nx][ny]>time+1){
dist[nx][ny]=time+1;
pq.push({dist[nx][ny], {nx, ny}});
}else if(time+1<grid[nx][ny] && dist[nx][ny]>newtime){
dist[nx][ny]=newtime;
pq.push({dist[nx][ny], {nx, ny}});
}
}
}
}
return dist.back().back();
}
};
``` | 1 | 0 | ['Breadth-First Search', 'Heap (Priority Queue)', 'Matrix', 'C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Still a variation of Djikstra. The hardness is the identify the wandering? | still-a-variation-of-djikstra-the-hardne-ltup | Intuition\n Describe your first thoughts on how to solve this problem. \nOkay, where did I stuck? I understand the trick of wandering around, but i cannot think | minhtud04 | NORMAL | 2024-11-30T20:53:31.211411+00:00 | 2024-11-30T20:53:31.211432+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOkay, where did I stuck? I understand the trick of wandering around, but i cannot think of using it as the optimal route to reach grid[i][j]. I mean the problem becomes simple when you have the min-Time to reach each grid[i][j] ? The hardness comes from think about using this wandering odd/even to achieve this min-time \n\n(IDK, I keep questioning how could they know which one to continue, but this is djisktra, and I should focus on how to achieve djisktra, which is to find min-time to get to each grid[i][j])\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n\n\n\n #Why disktra? Keep a current time + keep the min possible next move?\n\n # THe only case that I cant move is when surrounded at first step?\n\n if grid[0][1] > 1 and grid[1][0] > 1:\n return -1\n \n\n #It\'s still Djisktra, but the twist lied in identify the minimum time to reach that grid[i][j] if we need to wandering around\n dirs = [(1,0), (0,1), (-1,0), (0,-1)]\n ROW, COL = len(grid), len(grid[0])\n\n visited = [[0 for i in range(COL)] for j in range(ROW)]\n visited[0][0] = 1\n \n ans = -1\n heap = [(0,0,0)]\n\n while heap:\n time, curR, curC = heapq.heappop(heap)\n if (curR, curC) == (ROW-1, COL - 1):\n ans = time\n break\n for dr, dc in dirs:\n newR, newC = curR + dr, curC + dc\n if newR >= 0 and newR < ROW and newC >= 0 and newC < COL and visited[newR][newC] == 0:\n \n needTime = grid[newR][newC]\n if needTime < time:\n needTime = time+1\n elif (needTime - time) % 2 == 0:\n needTime += 1\n heapq.heappush(heap, (needTime, newR, newC))\n visited[newR][newC] = 1\n \n return ans\n \n\n\n \n\n\n\n``` | 1 | 0 | ['Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Swift💯 | swift-by-upvotethispls-qo7n | Modified Dijkstra (accepted answer)\nWe cannot "idle" on a node waiting for access to a neighbor, instead we must hop back and forth with a previous node. This | UpvoteThisPls | NORMAL | 2024-11-29T18:41:16.964647+00:00 | 2024-11-29T21:20:36.733413+00:00 | 11 | false | **Modified Dijkstra (accepted answer)**\nWe cannot "idle" on a node waiting for access to a neighbor, instead we must hop back and forth with a previous node. This is calculated, not simulated, so to do that, we must factor in the parity of the difference of time `t` arriving at node `P` and `t+Q.minT` of node `Q`. This is calculated as `((Q.minT - t) & 1 + 1)&1`, or more simply, `((Q.minT-t)&1^1)`\n```\nimport Algorithms\nimport Collections\nclass Solution {\n struct HeapItem: Comparable {\n var t,x,y:Int\n var tuple: (Int,Int,Int) {(t,x,y)}\n public static func <(a:Self, b:Self)->Bool {a.t<b.t}\n }\n\n func minimumTime(_ grid: [[Int]]) -> Int {\n guard min(grid[1][0], grid[0][1]) < 2 else { return -1 }\n let deltas = [0,1,0,-1,0].adjacentPairs()\n let (rows, cols) = (grid.count, grid[0].count)\n var visited = Array(repeating: Array(repeating: false, count: cols), count: rows)\n var heap = Heap([HeapItem(t:grid[0][0],x:0,y:0)])\n \n while let (time, c, r) = heap.popMin()?.tuple {\n guard !visited[r][c] else { continue }\n guard (r,c) != (rows-1, cols-1) else { return time }\n for (x,y) in deltas.lazy.map{dx,dy in (c+dx, r+dy)}\n where 0..<cols ~= x && 0..<rows ~= y && !visited[y][x] {\n let t = max(grid[y][x] + ((grid[y][x]-time)&1^1), time+1)\n heap.insert(HeapItem(t:t,x:x,y:y))\n }\n visited[r][c] = true\n }\n return -1\n }\n}\n``` | 1 | 0 | ['Swift'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | 29-11-2024 | 29-11-2024-by-normalizer-wnm0 | \n\n# Code\ncpp []\nusing info = tuple<int, short, short>; // (time, i, j)\nconst static int d[5] = {0, 1, 0, -1, 0};\nclass Solution {\npublic:\n inline sta | Normalizer | NORMAL | 2024-11-29T15:17:38.579978+00:00 | 2024-11-29T15:17:38.580011+00:00 | 9 | false | \n\n# Code\n```cpp []\nusing info = tuple<int, short, short>; // (time, i, j)\nconst static int d[5] = {0, 1, 0, -1, 0};\nclass Solution {\npublic:\n inline static bool isOutside(short i, short j, short n, short m) {\n return i < 0 || i >= n || j < 0 || j >= m;\n }\n\n int minimumTime(vector<vector<int>>& grid) {\n if (grid[1][0]>1 && grid[0][1]>1) return -1;// edge case\n \n short n = grid.size(), m = grid[0].size();\n vector<vector<int>> time(n, vector<int>(m, INT_MAX));\n priority_queue<info, vector<info>, greater<info>> pq;\n\n // Start at (0, 0) with time=0 \n pq.emplace(0, 0, 0);\n time[0][0] = 0;\n while (!pq.empty()) {\n auto [t, i, j] = pq.top();\n pq.pop();\n // cout<<" t="<<int(t)<<" i="<<int(i)<<" j="<<int(j)<<endl;\n // reach the destination\n if (i == n - 1 && j == m - 1)\n return t;\n\n // Traverse all four directions\n for (int a = 0; a < 4; a++) {\n int r = i + d[a], s = j + d[a + 1];\n if (isOutside(r, s, n, m)) continue;\n\n // minimum time to reach (r, s)\n int w=((grid[r][s]-t)&1)?0:1;\n int nextTime = max(t+1, grid[r][s]+w); // backward if neccessary\n\n // update if this path having quicker time\n if (nextTime < time[r][s]) {\n time[r][s] = nextTime;\n pq.emplace(nextTime, r, s);\n }\n }\n }\n\n return -1; // never reach\n }\n};\n\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n``` | 1 | 0 | ['C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Swift | Dijkstra | swift-dijkstra-by-pagafan7as-76pu | Code\nswift []\nimport Collections\n\nstruct Node: Comparable {\n var row: Int\n var col: Int\n var time: Int\n\n static func < (lhs: Node, rhs: Nod | pagafan7as | NORMAL | 2024-11-29T12:03:18.394201+00:00 | 2024-11-29T12:05:49.794817+00:00 | 30 | false | # Code\n```swift []\nimport Collections\n\nstruct Node: Comparable {\n var row: Int\n var col: Int\n var time: Int\n\n static func < (lhs: Node, rhs: Node) -> Bool {\n lhs.time < rhs.time\n }\n}\n\nclass Solution {\n func minimumTime(_ grid: [[Int]]) -> Int {\n guard grid[0][1] <= 1 || grid[1][0] <= 1 else { return -1 }\n\n let (m, n) = (grid.count, grid.first?.count ?? 0)\n var visited = Array(repeating: Array(repeating: false, count: n), count: m)\n var heap = Heap([Node(row: 0, col: 0, time: 0)])\n\n while let currentNode = heap.popMin() {\n if (currentNode.row, currentNode.col) == (m - 1, n - 1) { return currentNode.time }\n if visited[currentNode.row][currentNode.col] { continue }\n\n for (dr, dc) in [(1, 0), (-1, 0), (0, 1), (0, -1)] {\n let (nextRow, nextCol) = (currentNode.row + dr, currentNode.col + dc)\n if !(0..<m).contains(nextRow) || !(0..<n).contains(nextCol) { continue }\n let waitTime = (grid[nextRow][nextCol] - currentNode.time) % 2 == 0 ? 1 : 0\n let nextTime = max(grid[nextRow][nextCol] + waitTime, currentNode.time + 1)\n heap.insert(Node(row: nextRow, col: nextCol, time: nextTime))\n }\n\n visited[currentNode.row][currentNode.col] = true\n }\n return -1\n }\n}\n``` | 1 | 0 | ['Swift'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | C++ Solution || 95% Beat Time || Shortest path | c-solution-95-beat-time-shortest-path-by-w1bk | Intuition\n Describe your first thoughts on how to solve this problem. \nA Slight variation of shortest path.\n\n# Approach\n Describe your approach to solving | vishalmaurya59 | NORMAL | 2024-11-29T11:08:55.394690+00:00 | 2024-11-29T11:08:55.394722+00:00 | 13 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nA Slight variation of shortest path.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity: $$O(n*mlog(n*m))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n*m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\n#define piii pair<int,pair<int,int>>\n\nclass Solution {\npublic:\n bool check(int i,int j,int n, int m){\n return i>=0 && j>=0 && i<n && j<m;\n }\n\n int minimumTime(vector<vector<int>>& grid) {\n int n=grid.size(), m=grid[0].size();\n if(grid[1][0]>1 && grid[0][1]>1) return -1;\n\n vector<vector<bool>> visited(n,vector<bool>(m,0));\n priority_queue<piii,vector<piii>,greater<piii>> pq;\n\n pq.push({0,{0,0}});\n int row,col,val;\n int r[4]={-1,1,0,0};\n int c[4]={0,0,-1,1};\n\n while(!pq.empty()){\n val=pq.top().first;\n row=pq.top().second.first;\n col=pq.top().second.second;\n pq.pop();\n\n if(row==n-1 && col==m-1) break;\n\n for(int i=0;i<4;i++){\n int x=row+r[i], y=col+c[i];\n if(check(x,y,n,m) && !visited[x][y]){\n visited[x][y]=1;\n if(grid[x][y]<=val) pq.push({val+1,{x,y}});\n else{\n if((grid[x][y]-val)%2==0) \n pq.push({grid[x][y]+1,{x,y}});\n else pq.push({grid[x][y],{x,y}});\n }\n }\n }\n }\n return val;\n\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | This is so stupid its funny | this-is-so-stupid-its-funny-by-3nd3r1-58vv | Code\ngolang []\ntype Item struct {\n\ti int\n j int\n\tpriority int\n\tindex int\n}\n\ntype PriorityQueue []*Item\n\nfunc (pq PriorityQueue) Len() int { ret | 3nd3r1 | NORMAL | 2024-11-29T09:23:29.396469+00:00 | 2024-11-29T09:23:29.396505+00:00 | 48 | false | # Code\n```golang []\ntype Item struct {\n\ti int\n j int\n\tpriority int\n\tindex int\n}\n\ntype PriorityQueue []*Item\n\nfunc (pq PriorityQueue) Len() int { return len(pq) }\n\nfunc (pq PriorityQueue) Less(i, j int) bool {\n\treturn pq[i].priority < pq[j].priority\n}\n\nfunc (pq PriorityQueue) Swap(i, j int) {\n\tpq[i], pq[j] = pq[j], pq[i]\n\tpq[i].index = i\n\tpq[j].index = j\n}\n\nfunc (pq *PriorityQueue) Push(x any) {\n\tn := len(*pq)\n\titem := x.(*Item)\n\titem.index = n\n\t*pq = append(*pq, item)\n}\n\nfunc (pq *PriorityQueue) Pop() any {\n\told := *pq\n\tn := len(old)\n\titem := old[n-1]\n\told[n-1] = nil // avoid memory leak\n\titem.index = -1 // for safety\n\t*pq = old[0 : n-1]\n\treturn item\n}\n\nfunc offset(a int, b int) int {\n if a%2 != b%2 {\n return 1\n }\n return 0\n}\n\nfunc minimumTime(grid [][]int) int {\n vis := make([][]bool, len(grid))\n for i:=0; i<len(vis); i++ {\n vis[i] = make([]bool, len(grid[0]))\n }\n\n pq := make(PriorityQueue, 0)\n heap.Init(&pq)\n heap.Push(&pq, &Item{i: 0, j: 0, priority: 0})\n\n for len(pq) > 0 {\n s := heap.Pop(&pq).(*Item)\n i := s.i\n j := s.j\n if vis[i][j] {\n continue\n }\n vis[i][j] = true\n\n if i == len(grid)-1 && j == len(grid[0])-1 {\n return s.priority\n }\n\n if (i-1>=0 && s.priority + 1 >= grid[i-1][j]) || (i+1<len(grid) && s.priority + 1 >= grid[i+1][j]) || (j-1>=0 && s.priority + 1 >= grid[i][j-1]) || (j+1<len(grid[0]) && s.priority + 1 >= grid[i][j+1]) {\n if i-1>=0 {\n heap.Push(&pq, &Item{i: i-1, j: j, priority: max(s.priority+1, grid[i-1][j]+offset(grid[i-1][j], s.priority+1))})\n }\n if i+1 < len(grid) {\n heap.Push(&pq, &Item{i: i+1, j: j, priority: max(s.priority+1, grid[i+1][j]+offset(grid[i+1][j], s.priority+1))})\n }\n if j-1>=0 {\n heap.Push(&pq, &Item{i: i, j: j-1, priority: max(s.priority+1, grid[i][j-1]+offset(grid[i][j-1], s.priority+1))})\n }\n if j+1 < len(grid[0]) {\n heap.Push(&pq, &Item{i: i, j: j+1, priority: max(s.priority+1, grid[i][j+1]+offset(grid[i][j+1], s.priority+1))})\n }\n }\n\n }\n\n return -1\n}\n``` | 1 | 0 | ['Go'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | BFS Solution with Great Observations! Easy to Understand! | bfs-solution-with-great-observations-eas-3b1s | Intuition\nThe problem involves finding the minimum time to traverse a grid while respecting cell-specific time constraints. My first thought was to leverage br | rohitaas_beri | NORMAL | 2024-11-29T08:27:07.457289+00:00 | 2024-11-29T08:27:07.457359+00:00 | 80 | false | # Intuition\nThe problem involves finding the minimum time to traverse a grid while respecting cell-specific time constraints. My first thought was to leverage breadth-first search (BFS) for exploring paths in a grid, as it is well-suited for shortest path problems. However, the constraints on traversal time make this problem unique. Oscillating at the starting point (0,0) until the grid becomes traversable is a clever way to handle time alignment issues, ensuring feasibility without overcomplicating the logic.\n\nBinary search on time is a natural optimization since the solution space (time) is large, and feasibility checks for each time can be efficiently performed using BFS.\n\n\n# Approach\nPre-check for Feasibility:\n\nIf there are no neighbors of (0,0) with a time constraint \u2264 1, it is impossible to start, so return -1.\nBinary Search on Time:\n\nUse binary search to minimize the time required to traverse the grid.\nFor each midpoint (mid) in the search, compute the actual time as actualMid = 2 * mid + (n + m) % 2 to handle grid parity.\nBFS for Feasibility Check:\n\nPerform BFS starting from the target cell (n-1, m-1) to check if it\'s possible to reach (0,0) with the given time.\nTrack the remaining time at each cell using a canDo array initialized to -1.\nFor each cell, traverse its neighbors if the neighbor\'s grid time is \u2264 the current cell\'s remaining time - 1.\nOscillation to Align Time:\n\nIf (0,0) is reachable before the required time, oscillate between (0,0) and its neighbors until it is feasible to proceed toward (n-1, m-1).\nResult:\n\nThe binary search returns the smallest mid where BFS confirms feasibility.\n\n\n# Complexity\n- Time complexity:\n$$O(n*m * log(1e5))$$\n\n- Space complexity:\n$$O(n*m)$$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n int n = grid.size(), m = grid[0].size();\n\n // Step 1: Check if it\'s even possible to start\n // If (0,0)\'s neighbors are not accessible with time <= 1, return -1\n bool canStart = false;\n for (int i = -1; i <= 1; i++) {\n for (int j = -1; j <= 1; j++) {\n if (abs(i) != abs(j)) { // Only consider valid neighbors (not diagonals)\n int nx = i, ny = j;\n if (nx >= 0 && nx < n && ny >= 0 && ny < m) {\n if (grid[nx][ny] <= 1) {\n canStart = true;\n }\n }\n }\n }\n }\n if (!canStart) {\n return -1; // Early exit if no valid start path exists\n }\n\n // Step 2: Binary search on time\n // We are looking for the minimum `mid` such that we can traverse the grid\n int low = 0, high = 1e5, ans = -1;\n while (low <= high) {\n int mid = (low + high) >> 1;\n\n // Convert mid to the actual time required (consider parity of grid dimensions)\n int actualMid = 2 * mid + (n + m) % 2;\n\n // Step 3: Feasibility test using BFS\n if (isFeasible(grid, n, m, actualMid)) {\n ans = actualMid; // Store the result if feasible\n high = mid - 1; // Search for a smaller time\n } else {\n low = mid + 1; // Search for a larger time\n }\n }\n return ans;\n }\n\nprivate:\n // Helper function to check if it\'s feasible to traverse the grid with given `time`\n bool isFeasible(const vector<vector<int>>& grid, int n, int m, int time) {\n if (time < grid[n - 1][m - 1]) return false; // Impossible if time < destination\'s requirement\n\n // Initialize a 2D array to track the maximum allowable time at each cell\n vector<vector<int>> canDo(n, vector<int>(m, -1));\n canDo[n - 1][m - 1] = time;\n\n // BFS initialization\n queue<pair<int, int>> q;\n q.push({n - 1, m - 1});\n\n while (!q.empty()) {\n auto [x, y] = q.front();\n q.pop();\n\n int pathTime = canDo[x][y]; // Current time remaining to traverse\n\n // Explore neighbors\n for (int i = -1; i <= 1; i++) {\n for (int j = -1; j <= 1; j++) {\n if (abs(i) != abs(j)) { // Only consider valid neighbors (no diagonals)\n int nx = x + i, ny = y + j;\n\n // Check bounds and if the neighbor hasn\'t been visited\n if (nx >= 0 && nx < n && ny >= 0 && ny < m && canDo[nx][ny] == -1) {\n // If the neighbor\'s grid time is within the remaining time\n if (grid[nx][ny] <= pathTime - 1) {\n canDo[nx][ny] = pathTime - 1; // Update allowable time for this cell\n q.push({nx, ny}); // Push neighbor into the queue\n }\n }\n }\n }\n }\n }\n\n // Check if we reached the start cell (0,0)\n return canDo[0][0] != -1;\n }\n};\n\n``` | 1 | 0 | ['Binary Search', 'Breadth-First Search', 'C++'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | [C++] || Exact Dijkstra Algo || Priority Queue | c-exact-dijkstra-algo-priority-queue-by-qj8o4 | \nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) \n {\n int n = grid.size(), m = grid[0].size();\n \n if(grid | RIOLOG | NORMAL | 2024-11-29T07:01:02.283771+00:00 | 2024-11-29T07:01:02.283808+00:00 | 20 | false | ```\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) \n {\n int n = grid.size(), m = grid[0].size();\n \n if(grid[0][1] > grid[0][0] + 1 and grid[1][0] > grid[0][0] + 1) return -1;\n \n priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, greater<pair<int, pair<int, int>>>> pq;\n vector<vector<bool>>vis(n, vector<bool>(m, false));\n \n vis[0][0] = true;\n pq.push({0, {0, 0}});\n \n int dx[] = {-1, 0, 1, 0};\n int dy[] = {0, 1, 0, -1};\n \n while(!pq.empty())\n {\n int count = pq.top().first;\n int row = pq.top().second.first;\n int col = pq.top().second.second;\n pq.pop();\n \n if (row == n - 1 and col == m - 1) return count;\n \n for (int i=0;i<4;i++)\n {\n int newRow = row + dx[i];\n int newCol = col + dy[i];\n \n if (newRow >= 0 and newRow < n and newCol >= 0 and newCol < m)\n {\n if (vis[newRow][newCol]) continue;\n \n if (grid[newRow][newCol] <= count + 1) \n {\n pq.push({count+1, {newRow, newCol}});\n }\n else\n {\n int timeTaken = grid[newRow][newCol] - count ;\n if (timeTaken % 2 == 0) timeTaken = grid[newRow][newCol] + 1;\n else timeTaken = grid[newRow][newCol];\n \n pq.push({timeTaken, {newRow, newCol}});\n }\n \n vis[newRow][newCol] = true;\n }\n }\n }\n \n return -1;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | [C++] Easy hard | c-easy-hard-by-bora_marian-00ks | Notice that you can move back and forth multiple times to reach a single cell, meaning you can use a previous cell to go back and return to the current cell as | bora_marian | NORMAL | 2024-11-29T06:23:47.863843+00:00 | 2024-11-29T14:23:34.331520+00:00 | 105 | false | Notice that you can move back and forth multiple times to reach a single cell, meaning you can use a previous cell to go back and return to the current cell as many times as necessary to accumulate the required time. The only situation where moving back and forth is not possible is at the very first move, `-1` will be returned when `grid[0][1] > 1 && grid[1][0] > 1`.\n\nI keep a two-dimensional array t, where `t[i][j]` represents the minimum time to arrive cell `(i,j)`.\nTo move from cell `(i,j)` to an adjacent cell `(ii, jj)` we handle the following cases:\n - `grid[ii][jj] <= top[0] + 1`, we can directly move to the cell without any delay.\n - `grid[ii][jj] > top[0] + 1`, we need to move back and forth to a previous cell.Let `diff = grid[ii][jj] - t[i][j]`, then:\n - When diff is even the minimum time will `grid[ii][jj] + 1`\n - othewise `grid[ii][jj]`.\n# Code\n```cpp []\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n if (grid[0][1] > 1 && grid[1][0] > 1)\n return -1;\n vector<int> di = {0, 0, -1, 1};\n vector<int> dj = {-1, 1, 0, 0};\n int n = grid.size(), m = grid[0].size();\n vector<vector<int>>t(n, vector<int>(m, INT_MAX));\n set<vector<int>>ms;\n ms.insert({0, 0, 0});\n while(!ms.empty()) {\n auto top = *ms.begin();\n ms.erase(ms.begin());\n for (int k = 0; k < 4; k++) {\n int ii = top[1] + di[k];\n int jj = top[2] + dj[k];\n if (!(ii >= 0 && ii < n && jj >= 0 && jj < m))\n continue;\n if (grid[ii][jj] <= top[0] + 1) {\n if(t[ii][jj] > top[0] + 1) {\n t[ii][jj] = top[0] + 1;\n ms.insert({t[ii][jj], ii, jj});\n }\n continue;\n }\n int diff = grid[ii][jj] - top[0];\n int min_ii_jj = diff % 2 == 0 ? grid[ii][jj] + 1 : grid[ii][jj];\n if (t[ii][jj] > min_ii_jj) {\n t[ii][jj] = min_ii_jj;\n ms.insert({min_ii_jj, ii, jj});\n }\n }\n }\n return t[n-1][m-1];\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Easy Solution in C++ | easy-solution-in-c-by-dhanu07-tyma | Intuition\n Describe your first thoughts on how to solve this problem. \nTo solve the problem of finding the minimum time to traverse a grid while waiting for c | Dhanu07 | NORMAL | 2024-11-29T05:51:12.578254+00:00 | 2024-11-29T05:51:12.578276+00:00 | 28 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve the problem of finding the minimum time to traverse a grid while waiting for certain cells to become accessible, we can think of this as a pathfinding problem on a weighted graph. Each cell in the grid can be viewed as a node, and the edges between nodes correspond to possible movements (up, down, left, right). The challenge arises from the fact that some cells can only be accessed at specific times, which adds a layer of complexity to the traversal\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGrid Representation: The grid is represented as a 2D vector where each cell contains the time at which it becomes accessible.\n\nPriority Queue: We will use a min-heap (priority queue) to always expand the least time-consuming path first. This allows us to implement a modified version of Dijkstra\'s algorithm.\n\nInitialization: Start from the top-left corner of the grid (0, 0) with an initial time of 0. Push this position onto the priority queue.\n\nTraversal: While the priority queue is not empty:\n\nExtract the cell with the minimum time.\nIf this cell is the bottom-right corner of the grid, return the current time as the minimum time to reach the destination.\nFor each possible move (up, down, left, right), calculate the next cell\'s time:\nIf the current time is less than the time required to enter the next cell, calculate the waiting time.\nPush the new position and the calculated time into the priority queue if it hasn\'t been visited yet.\nVisited Tracking: Use a 2D vector to keep track of visited cells to prevent processing the same cell multiple times.\n\nEdge Case Handling: If both the right and down cells from the starting position are blocked initially (i.e., they require a time greater than 1), return -1 immediately since it\'s impossible to move.\n# Complexity\nTime complexity: The time complexity of this approach is (O(V \\log V)), where (V) is the number of cells in the grid (i.e., (rows \\times cols)). Each cell can be added to the priority queue once, and extracting the minimum from the priority queue takes logarithmic time.\n\nSpace complexity: The space complexity is (O(V)) due to the storage required for the priority queue and the visited array, where (V) is the number of cells in the grid.\n# Code\n```cpp []\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n if (grid[0][1] > 1 && grid[1][0] > 1) return -1;\n \n int rows = grid.size();\n int cols = grid[0].size();\n \n priority_queue<pair<int, pair<int, int>>, \n vector<pair<int, pair<int, int>>>, \n greater<pair<int, pair<int, int>>>> minHeap;\n \n minHeap.push({0, {0, 0}});\n \n vector<vector<int>> seen(rows, vector<int>(cols, 0));\n seen[0][0] = 1;\n \n vector<pair<int, int>> moves = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\n \n while (!minHeap.empty()) {\n auto curr = minHeap.top();\n int currTime = curr.first;\n int currRow = curr.second.first;\n int currCol = curr.second.second;\n \n minHeap.pop();\n \n if (currRow == rows - 1 && currCol == cols - 1) \n return currTime;\n \n for (auto move : moves) {\n int nextRow = move.first + currRow;\n int nextCol = move.second + currCol;\n \n if (nextRow >= 0 && nextCol >= 0 && \n nextRow < rows && nextCol < cols && \n !seen[nextRow][nextCol]) {\n \n int waitTime = ((grid[nextRow][nextCol] - currTime) % 2 == 0) ? 1 : 0;\n int nextTime = max(currTime + 1, grid[nextRow][nextCol] + waitTime);\n \n minHeap.push({nextTime, {nextRow, nextCol}});\n seen[nextRow][nextCol] = 1;\n }\n }\n }\n return -1;\n }\n};\n``` | 1 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Simple JAVA Solution | Greedy | Dijkstras Algorithm | Graph | simple-java-solution-greedy-dijkstras-al-6ymt | \n# Complexity\n- Time complexity: O(nm log(nm))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n*m)\n Add your space complexity here, e.g | Sivaganesh-B | NORMAL | 2024-11-29T05:29:39.389425+00:00 | 2024-11-29T05:29:39.389460+00:00 | 86 | false | \n# Complexity\n- Time complexity: O(n*m log(n*m))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n*m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minimumTime(int[][] grid) {\n \n if(grid[0][1]>=2 && grid[1][0]>=2) return -1;\n int[][] dir = new int[][]{{0,1},{1,0},{-1,0},{0,-1}};\n int n = grid.length,m=grid[0].length;\n boolean vis[][] = new boolean[n][m];\n PriorityQueue<int[]> q = new PriorityQueue<>((a,b)-> a[0]-b[0]);\n q.add(new int[]{0,0,0});\n while(!q.isEmpty())\n {\n int[] cur = q.poll();\n int t = cur[0],r = cur[1],c = cur[2];\n if(r==n-1 && c==m-1) return t;\n if(vis[r][c]) continue;\n vis[r][c]=true;\n\n for(int[] i:dir)\n {\n int nr = r + i[0],nc = c + i[1];\n if(nr<0 || nr>=n || nc<0 || nc >=m || vis[nr][nc]) continue;\n int cycle = ((grid[nr][nc] - t) % 2 ==0) ? 1 : 0;\n q.add(new int[]{Math.max(grid[nr][nc]+cycle,t+1),nr,nc});\n }\n }\n return -1;\n }\n}\n``` | 1 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'Java'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Python Dijkstra, Code w/ Notes | python-dijkstra-code-w-notes-by-2pillows-yiq5 | Code\npython3 []\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n # if no cells to move at start, then invalid\n if gr | 2pillows | NORMAL | 2024-11-29T05:25:58.164457+00:00 | 2024-11-29T05:25:58.164498+00:00 | 9 | false | # Code\n```python3 []\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n # if no cells to move at start, then invalid\n if grid[0][1] > 1 and grid[1][0] > 1:\n return -1\n\n m, n = len(grid), len(grid[0]) # row and cols\n \n directions = [(0, 1), (1, 0), (0, -1), (-1, 0)] # up, down, left right\n \n heap = [(0, 0, 0)] # starting time, x, y\n\n visited = [[False] * n for _ in range(m)] # set all cells to not visited except start\n visited[0][0] = True\n \n while heap:\n time, x, y = heapq.heappop(heap) # get cell w/ lowest time\n \n # if current cell is bottom right, then return time\n if x == m - 1 and y == n - 1:\n return time\n \n # explore all directions of current cell\n for dx, dy in directions:\n nx, ny = x + dx, y + dy\n \n if 0 <= nx < m and 0 <= ny < n and not visited[nx][ny]:\n visited[nx][ny] = True \n\n # can immediately visit if cell time <= current time + 1\n if grid[nx][ny] <= time + 1:\n heapq.heappush(heap, (time + 1, nx, ny))\n\n # can\'t visit right now, add w/ time for when visit possible\n else:\n diff = grid[nx][ny] - time # wait time before can visit\n\n if diff % 2 == 1: # wait time is odd, cell time = time + 1\n heapq.heappush(heap, (grid[nx][ny], nx, ny))\n\n # ex. dif = 3, path = 0 -> 1 -> 2 -> 1 -> 4, time = 4\n # 0 - -\n # 1 4 -\n # 2 - -\n \n else: # wait time is even, cell time = time + 1 + 1\n heapq.heappush(heap, (grid[nx][ny] + 1, nx, ny))\n\n # ex. dif = 2, path = 0 -> 1 -> 2 -> 1 -> 3, time = 4\n # 0 - -\n # 1 3 -\n # 2 - -\n \n # invalid path\n return -1\n\n``` | 1 | 0 | ['Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | JAVA SOLUTION | java-solution-by-ritikk876-np7e | Intuition\n\nThe solution uses a priority queue (min-heap) to handle the time constraints for each cell. Each cell in the grid has a minimum time it becomes acc | Ritikk876 | NORMAL | 2024-11-29T05:17:56.440508+00:00 | 2024-11-29T05:17:56.440540+00:00 | 42 | false | # Intuition\n\nThe solution uses a priority queue (min-heap) to handle the time constraints for each cell. Each cell in the grid has a minimum time it becomes accessible, and if you arrive before that time, you must wait. The priority queue ensures that we always process the cell with the least time first, exploring paths efficiently. For each cell, we check its neighbors and update their times, considering the waiting time if necessary. By using BFS with the priority queue and a visited array, the algorithm ensures we find the minimum time to reach the bottom-right cell.\n\n# Approach\n\nThe approach uses a modified Dijkstra\'s algorithm with a priority queue to handle the time constraints for each cell in the grid:\n\nPriority Queue: We use a priority queue (min-heap) to always process the cell with the smallest time first, ensuring an optimal traversal of the grid.\n\nTime Calculation: Each cell in the grid has a minimum required time for access. As we move to neighboring cells, we ensure that the time we arrive at a cell is greater than or equal to the cell\'s required time. If not, we wait until it\'s accessible.\n\nBFS-like Traversal: Starting from the top-left corner, we explore the grid in four directions (up, down, left, right). For each neighboring cell, we calculate the earliest possible time we can visit it (considering both the time spent moving and any waiting time if necessary).\n\nVisited Array: We use a visited array to track the minimum time we\'ve reached each cell to avoid revisiting with a worse time.\n\nTermination: The process continues until we reach the bottom-right cell, and the time at that point is the minimum time required. If we can\'t reach the bottom-right cell, we return -1.\n\nThis approach ensures that we efficiently calculate the minimum time while respecting the waiting constraints at each cell.\n\n# Complexity\n- Time complexity:O((n\xD7m)\u22C5log(n\xD7m))\n\n\n- Space complexity:O(n\xD7m)\n\n\n# Code\n```java []\nclass Pair {\n int row, col, time;\n Pair(int row, int col, int time) {\n this.row = row;\n this.col = col;\n this.time = time;\n }\n}\n\nclass Solution {\n public int minimumTime(int[][] grid) {\n if(grid[0][1] > 1 && grid[1][0] > 1) return -1;\n\n int n = grid.length;\n int m = grid[0].length;\n int[][] dirs = new int[][]{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n\n boolean[][] visited = new boolean[n][m];\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));\n pq.offer(new int[]{grid[0][0], 0, 0});\n\n while (!pq.isEmpty()) {\n int[] curr = pq.poll();\n int time = curr[0];\n int row = curr[1];\n int col = curr[2];\n\n if (row == n - 1 && col == m - 1) {\n return time;\n }\n if (visited[row][col]) continue;\n visited[row][col] = true;\n\n for (int[] dir : dirs) {\n int r = row + dir[0];\n int c = col + dir[1];\n if (r < 0 || r >= n || c < 0 || c >= m || visited[r][c]) continue;\n int wait = (grid[r][c] - time) % 2 == 0 ? 1 : 0;\n pq.offer(new int[]{Math.max(grid[r][c] + wait, time + 1), r, c});\n }\n }\n return -1;\n }\n}\n\n\n``` | 1 | 0 | ['Array', 'Breadth-First Search', 'Heap (Priority Queue)', 'Matrix', 'Java'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Simple BFS Java Solution | simple-bfs-java-solution-by-aryan0703-9jqv | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Aryan0703 | NORMAL | 2024-11-29T04:16:52.078522+00:00 | 2024-11-29T04:16:52.078559+00:00 | 75 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n final int[][] dirs = {{-1,0}, {1,0}, {0,-1}, {0,1}};\npublic int minimumTime(int[][] grid) {\n\tint r = grid.length, c = grid[0].length;\n\tif(grid[0][1] > 1 && grid[1][0] > 1) return -1;\n\n\tint[][] dp = new int[r][c];\n\tfor(int[] arr: dp) Arrays.fill(arr, -1);\n\tdp[0][0] = 0;\n\n\tQueue<int[]> bfs = new LinkedList<>();\n\tbfs.add(new int[]{0,0});\n\twhile(!bfs.isEmpty()) {\n\t\tint top[] = bfs.remove();\n\t\tfor(int dir[] : dirs) {\n\t\t\tint nr = top[0]+dir[0], nc = top[1]+dir[1];\n\t\t\tif(nr<0 || nc<0 || nr==r || nc==c) continue;\n\t\t\tint next = dp[top[0]][top[1]]+1;\n\t\t\tif(next < grid[nr][nc]) {\n\t\t\t\tint diff = grid[nr][nc]-next;\n\t\t\t\tif(diff%2 != 0) diff++;\n\t\t\t\tnext += diff;\n\t\t\t}\n\n\t\t\tif(next >= grid[nr][nc] && (dp[nr][nc] == -1 || next < dp[nr][nc])) {\n\t\t\t\tdp[nr][nc] = next;\n\t\t\t\tbfs.add(new int[]{nr,nc});\n\t\t\t}\n\t\t}\n\t}\n\treturn dp[r-1][c-1];\n}\n}\n``` | 1 | 0 | ['Java'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Java Solution for Minimum Time to Visit a Cell In a Grid Problem | java-solution-for-minimum-time-to-visit-1nbxb | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem can be visualized as navigating through a grid where each cell represents a | Aman_Raj_Sinha | NORMAL | 2024-11-29T04:13:28.985492+00:00 | 2024-11-29T04:13:28.985521+00:00 | 43 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem can be visualized as navigating through a grid where each cell represents a \u201Cgate\u201D that opens only at or after a specific time (grid[row][col]). The goal is to reach the bottom-right corner (m-1, n-1) from the top-left (0, 0) in the minimum possible time. Each move (up, down, left, right) takes exactly 1 second, but sometimes you must \u201Cwait\u201D for the gate (cell) to open. The task is similar to finding the shortest path in a weighted graph, where the weight is dynamic based on time.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tDijkstra-like Algorithm:\n\t\u2022\tUse a priority queue (min-heap) to explore the grid in order of the earliest possible time to reach each cell.\n\t\u2022\tEach entry in the queue is a triplet {row, col, time}, representing the cell and the time it took to reach it.\n2.\tInitialization:\n\t\u2022\tStart from (0, 0) at time 0 and push this into the priority queue.\n\t\u2022\tIf the only adjacent cells (0, 1) or (1, 0) require a time greater than 1, return -1 immediately since you can\u2019t move.\n3.\tTime Calculation for Moves:\n\t\u2022\tFor each move to a neighboring cell (newRow, newCol), the time increases by 1.\n\t\u2022\tIf the nextTime (current time + 1) is less than the cell\u2019s required time (grid[newRow][newCol]), calculate how much longer you must wait:\n\t\u2022\tIf the difference is even, move at grid[newRow][newCol].\n\t\u2022\tIf the difference is odd, wait an extra second to synchronize and move at grid[newRow][newCol] + 1.\n4.\tVisited Array:\n\t\u2022\tTrack visited cells using a boolean[][] visited array to avoid redundant processing.\n5.\tTermination:\n\t\u2022\tIf you reach the bottom-right cell (m-1, n-1), return the current time.\n\t\u2022\tIf the queue is empty and the bottom-right has not been reached, return -1\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime Complexity: O(m x n log(m x n))\n\n\u2022\tThe grid contains m x n cells.\n\u2022\tEach cell can be added to the priority queue at most once, so there are O(m x n) insertions.\n\u2022\tEach insertion and extraction from the priority queue takes O(log(m x n)).\n\u2022\tThus, the total complexity is O(m x n log(m x n)).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSpace Complexity: O(m x n)\n\n\u2022\tPriority Queue: Stores up to O(m x n) cells at any time.\n\u2022\tVisited Array: An array of size m x n to track visited cells.\n\u2022\tAuxiliary Data: Small constant space for temporary variables and directions array.\n\n# Code\n```java []\nclass Solution {\n public int minimumTime(int[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n\n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(a[2], b[2]));\n pq.offer(new int[]{0, 0, 0}); \n\n boolean[][] visited = new boolean[m][n];\n int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};\n\n while (!pq.isEmpty()) {\n int[] current = pq.poll();\n int row = current[0], col = current[1], time = current[2];\n\n if (row == m - 1 && col == n - 1) {\n return time;\n }\n\n if (visited[row][col]) continue;\n visited[row][col] = true;\n\n for (int[] dir : directions) {\n int newRow = row + dir[0];\n int newCol = col + dir[1];\n\n if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n) {\n int nextTime = time + 1;\n int requiredTime = grid[newRow][newCol];\n\n \n if (nextTime < requiredTime) {\n int wait = (requiredTime - nextTime) % 2 == 0 ? 0 : 1;\n nextTime = requiredTime + wait;\n }\n\n if (!visited[newRow][newCol]) {\n pq.offer(new int[]{newRow, newCol, nextTime});\n }\n }\n }\n }\n\n return -1;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Rust | rust-by-nuclearoreo-v63q | Code\nrust []\nuse std::collections::{HashSet, BinaryHeap};\nuse std::cmp::Reverse;\n\nimpl Solution {\n pub fn minimum_time(grid: Vec<Vec<i32>>) -> i32 {\n | nuclearoreo | NORMAL | 2024-11-29T03:47:11.730243+00:00 | 2024-11-29T03:47:11.730276+00:00 | 27 | false | # Code\n```rust []\nuse std::collections::{HashSet, BinaryHeap};\nuse std::cmp::Reverse;\n\nimpl Solution {\n pub fn minimum_time(grid: Vec<Vec<i32>>) -> i32 {\n if grid[0][1] > 1 && grid[1][0] > 1 {\n return -1;\n }\n\n let (m, n) = (grid.len(), grid[0].len());\n let mut q = BinaryHeap::from([Reverse((grid[0][0], 0, 0))]);\n let mut visited = HashSet::from([(0, 0)]);\n let mut res = -1;\n\n while let Some(Reverse((time, x, y))) = q.pop() {\n if x == m - 1 && y == n - 1 {\n res = time;\n break;\n }\n\n for (dx, dy) in [(0, 1), (1, 0), (0, -1), (-1, 0)] {\n let (nx, ny) = ((x as i32 + dx) as usize, (y as i32 + dy) as usize);\n if nx < m && ny < n && !visited.contains(&(nx, ny)) {\n visited.insert((nx, ny));\n let move_time = if (grid[nx][ny] - time) % 2 == 0 { 1 } else { 0 };\n q.push(Reverse(((time + 1).max(grid[nx][ny] + move_time), nx, ny)));\n }\n }\n }\n\n res\n }\n}\n``` | 1 | 0 | ['Rust'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | [dart] PriorityQueue, Go and Back step solution | dart-priorityqueue-go-and-back-step-solu-lkmh | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | hyungzin | NORMAL | 2024-11-29T02:49:31.061558+00:00 | 2024-11-29T02:49:31.061581+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```dart []\nclass Solution {\n int minimumTime(List<List<int>> grid) {\n final dir = [(0, -1), (0, 1), (-1, 0), (1, 0)];\n final n = grid.length, m = grid[0].length;\n final dp = List.generate(n, (_) => List.filled(m, 10000000001));\n final pq = PriorityQueue<(int, int, int)>((a, b) => a.$3.compareTo(b.$3));\n pq.add((0,0,0));\n while (!pq.isEmpty){\n final (y, x, t) = pq.remove();\n // The count of next cells that we can reach from current cell.\n final canReach = dir.map((a) => (a.$1 + y, a.$2 + x))\n .where((a) => !(a.$1 < 0 || a.$1 >= n || a.$2 < 0 || a.$2 >= m))\n .where((a) => grid[a.$1][a.$2] <= t + 1)\n .length;\n for (final (dy, dx) in dir){\n int ny = y + dy, nx = x + dx, nt = t + 1;\n if (ny < 0 || ny >= n || nx < 0 || nx >= m) continue;\n if (nt < grid[ny][nx]){\n if (canReach == 0) continue;\n // if cells we can reach > 0\n // we can increase time by go and back step\n // +2 time each go and back\n int diff = grid[ny][nx] - nt;\n if (diff % 2 == 1) diff++;\n nt += diff;\n }\n if (dp[ny][nx] <= nt) continue;\n dp[ny][nx] = nt;\n pq.add((ny, nx, nt));\n }\n }\n final res = dp.last.last;\n if (res == 10000000001) return -1;\n return res;\n }\n}\n\n\nclass PriorityQueue<T> { \n\tList<T> _elements = []; \n\tComparator<T> _comparator; \n\tPriorityQueue(this._comparator); \n\t\n\tvoid add(T element) { \n\t\t_elements.add(element); \n\t\t_bubbleUp(_elements.length - 1); \n\t} \n\t\n\tT remove() { \n\t\tif (isEmpty) throw StateError("Cannot remove from empty priority queue."); \n\t\tT result = _elements.first; \n\t\tif (_elements.length == 1) { \n\t\t\t_elements.removeLast(); \n\t\t} else { \n\t\t\t_elements[0] = _elements.removeLast(); \n\t\t\t_bubbleDown(0); \n\t\t} return result; \n\t} \n\t\t\n\tT get first { \n\t\tif (isEmpty) throw StateError(\'empty\'); \n\t\treturn _elements.first; \n\t} \n\tbool get isNotEmpty => !_elements.isEmpty; \n\tbool get isEmpty => _elements.isEmpty; \n\t\n\tint get length => _elements.length; \n\t\n\tvoid _bubbleUp(int index) { \n\t\twhile (index > 0) { \n\t\t\tint parent = (index - 1) >> 1; \n\t\t\tif (_comparator(_elements[index], _elements[parent]) >= 0) break; \n\t\t\t_swap(index, parent); index = parent; \n\t\t} \n\t} \n\t\n\tvoid _bubbleDown(int index) { \n\t\tint leftChild; \n\t\tint rightChild; \n\t\tint minChild; \n\t\twhile (true) { \n\t\t\tleftChild = (index << 1) + 1; \n\t\t\trightChild = leftChild + 1; \n\t\t\tminChild = index; \n\t\t\tif (leftChild < _elements.length && _comparator(_elements[leftChild], _elements[minChild]) < 0) { \n\t\t\t\tminChild = leftChild; \n\t\t\t} \n\t\t\tif (rightChild < _elements.length && _comparator(_elements[rightChild], _elements[minChild]) < 0) { \n\t\t\t\tminChild = rightChild; \n\t\t\t} \n\t\t\tif (minChild == index) break; \n\t\t\t_swap(index, minChild); index = minChild; \n\t\t}\n\t} \n\t\n\tvoid _swap(int i, int j) { \n\t\tT temp = _elements[i]; \n\t\t_elements[i] = _elements[j]; \n\t\t_elements[j] = temp; \n\t} \n}\n``` | 1 | 0 | ['Dart'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Java with Dijkstra's Algorithm Approach | java-with-dijkstras-algorithm-approach-b-bjhw | Intuition\nThe problem is essentially about finding the shortest path from the top-left corner to the bottom-right corner of a grid. The challenge lies in the f | ThomasLuuu | NORMAL | 2024-11-29T02:20:42.377038+00:00 | 2024-11-29T02:20:42.377059+00:00 | 43 | false | # Intuition\nThe problem is essentially about finding the shortest path from the top-left corner to the bottom-right corner of a grid. The challenge lies in the fact that the grid values impose constraints on when each cell can be accessed. This hints at a Dijkstra-like approach where we prioritize the earliest possible time to reach each cell.\n\n# Approach\n1. **Initial Feasibility Check**: If the immediate neighbors of the starting cell are inaccessible, it\'s impossible to proceed, so return `-1`.\n2. **Dijkstra\'s Algorithm**: Use a priority queue to explore cells in increasing order of the time required to reach them.\n3. **Transition Rules**:\n - For each neighboring cell, calculate the earliest possible time it can be reached, accounting for the parity (even/odd nature of time relative to the grid value).\n - Update the minimum time to reach the neighbor if this new time is better.\n4. **Termination**: If the bottom-right corner is reached, return the time. If the queue is exhausted and the target hasn\'t been reached, return `-1`.\n\n# Complexity\n- **Time Complexity**: \n $$O(m \\cdot n \\cdot \\log(m \\cdot n))$$, where \\(m\\) and \\(n\\) are the dimensions of the grid. Each cell is processed once, and operations on the priority queue are logarithmic in the number of elements.\n- **Space Complexity**:\n $$O(m \\cdot n)$$ for the `minTimeToReach` array and the priority queue.\n\n# Code\n```java\nclass Solution {\n public int minimumTime(int[][] grid) {\n int rows = grid.length, cols = grid[0].length;\n\n if (Math.min(grid[0][1], grid[1][0]) > 1) {\n return -1;\n }\n\n int[][] minTimeToReach = new int[rows][cols];\n for (int i = 0; i < rows; i++) {\n for (int j = 0; j < cols; j++) {\n minTimeToReach[i][j] = Integer.MAX_VALUE;\n }\n }\n minTimeToReach[0][0] = 0;\n\n PriorityQueue<int[]> priorityQueue = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));\n priorityQueue.offer(new int[]{0, 0, 0});\n\n int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};\n\n while (!priorityQueue.isEmpty()) {\n int[] current = priorityQueue.poll();\n int currentTime = current[0], currentRow = current[1], currentCol = current[2];\n\n if (currentRow == rows - 1 && currentCol == cols - 1) {\n return currentTime;\n }\n\n if (currentTime != minTimeToReach[currentRow][currentCol]) {\n continue;\n }\n\n for (int[] direction : directions) {\n int newRow = currentRow + direction[0], newCol = currentCol + direction[1];\n if (newRow < 0 || newRow >= rows || newCol < 0 || newCol >= cols) {\n continue;\n }\n\n int newTime = Math.max(currentTime + 1, grid[newRow][newCol] + 1 - (grid[newRow][newCol] - currentTime) % 2);\n if (newTime >= minTimeToReach[newRow][newCol]) {\n continue;\n }\n\n minTimeToReach[newRow][newCol] = newTime;\n priorityQueue.offer(new int[]{newTime, newRow, newCol});\n }\n }\n\n return -1;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | [Go] Simple Heap Queue Solution | go-simple-heap-queue-solution-by-hiro111-kigo | Code\ngolang []\nimport (\n "container/heap"\n)\n\nfunc minimumTime(grid [][]int) int {\n // Edge case\n if grid[0][1] > 1 && grid[1][0] > 1 {\n | Hiro111 | NORMAL | 2024-11-29T02:18:11.351381+00:00 | 2024-11-29T02:18:11.351410+00:00 | 8 | false | # Code\n```golang []\nimport (\n "container/heap"\n)\n\nfunc minimumTime(grid [][]int) int {\n // Edge case\n if grid[0][1] > 1 && grid[1][0] > 1 {\n return -1\n }\n m, n := len(grid), len(grid[0])\n h := &Heap{[3]int{0, 0, 0}}\n grid[0][0] = -1\n for {\n v := heap.Pop(h).([3]int)\n for _, d := range directions {\n r, c := v[1] + d[0], v[2] + d[1]\n if r < 0 || r >= m || c < 0 || c >= n || grid[r][c] == -1 {\n // out of boundary, or already visted\n continue\n }\n // maintain t (time to visit {r, c})\n t := v[0] + 1\n if grid[r][c] > t {\n t = grid[r][c]\n if (r + c) % 2 != t % 2 {\n t++\n }\n }\n if r == m - 1 && c == n - 1 {\n // Found the goal\n return t\n }\n grid[r][c] = -1 // Mark the position as visited\n heap.Push(h, [3]int{t, r, c})\n }\n }\n}\n\nvar directions = [4][2]int{\n {0, 1},\n {1, 0},\n {0, -1},\n {-1, 0},\n}\n\ntype Heap [][3]int\nfunc (h Heap) Len() int { return len(h) }\nfunc (h Heap) Less(i, j int) bool { return h[i][0] < h[j][0] }\nfunc (h Heap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\nfunc (h *Heap) Push(v any) { *h = append(*h, v.([3]int)) }\nfunc (h *Heap) Pop() any {\n n := len(*h) - 1\n old := *h\n v := old[n]\n *h = old[:n]\n return v\n}\n``` | 1 | 0 | ['Go'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | Golang solution with the explanation | golang-solution-with-the-explanation-by-uz438 | Intuition\nThe problem requires finding the minimum time to travel from the top-left to the bottom-right of the grid while adhering to the constraints of cell a | alekseiapa | NORMAL | 2024-11-29T00:30:49.803121+00:00 | 2024-11-29T00:30:49.803160+00:00 | 45 | false | # Intuition\nThe problem requires finding the minimum time to travel from the top-left to the bottom-right of the grid while adhering to the constraints of cell availability. A shortest-path algorithm, similar to Dijkstra\'s, is well-suited for this problem because we are minimizing the time to reach each cell.\n\nKey insights:\n1. Use a priority queue to always process the cell with the smallest time first.\n2. Handle cell availability by calculating the required wait time if the current time does not satisfy the cell\'s constraints.\n\n# Approach\n1. **Priority Queue**:\n - Use a priority queue (min-heap) to process cells in increasing order of time.\n - Each entry in the queue contains the current time, row, and column of a cell.\n\n2. **Edge Case Handling**:\n - If the initial neighbors of the starting cell are blocked (i.e., `grid[1][0] > 1` and `grid[0][1] > 1`), return `-1` as the destination is unreachable.\n\n3. **Time Matrix**:\n - Maintain a 2D matrix `time` to store the minimum time to reach each cell. Initialize all cells with infinity (`INT_MAX`) except the starting cell, which is `0`.\n\n4. **Neighbor Traversal**:\n - For each cell, check its four neighbors (up, down, left, right).\n - Compute the earliest possible time to move to the neighbor based on the constraints:\n - If the current time plus 1 is less than the neighbor\'s grid constraint, calculate the wait time required to synchronize the timing (adjust for even/odd constraints).\n - If the new time to reach the neighbor is smaller than its recorded time, update it and push it into the priority queue.\n\n5. **Termination**:\n - If the bottom-right cell is reached, return the time. If the queue is empty and the destination is not reached, return `-1`.\n\n# Complexity\n- **Time Complexity**: \n \\(O(n \\cdot m \\cdot \\log(n \\cdot m))\\), where \\(n\\) and \\(m\\) are the number of rows and columns in the grid. \n - Each cell can be pushed into the priority queue at most once.\n - Priority queue operations (push and pop) take \\(O(\\log(n \\cdot m))\\).\n\n- **Space Complexity**: \n \\(O(n \\cdot m)\\), for the `time` matrix and priority queue storage.\n\n# Code\n```golang []\ntype Info struct {\n\ttime, row, col int\n}\n\ntype MinHeap []Info\n\nfunc (h MinHeap) Len() int { return len(h) }\nfunc (h MinHeap) Less(i, j int) bool { return h[i].time < h[j].time }\nfunc (h MinHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\nfunc (h *MinHeap) Push(x interface{}) { *h = append(*h, x.(Info)) }\nfunc (h *MinHeap) Pop() interface{} {\n\told := *h\n\tn := len(old)\n\titem := old[n-1]\n\t*h = old[:n-1]\n\treturn item\n}\n\nvar directions = [5]int{0, 1, 0, -1, 0}\n\nfunc isOutside(row, col, rows, cols int) bool {\n\treturn row < 0 || row >= rows || col < 0 || col >= cols\n}\n\nfunc minimumTime(grid [][]int) int {\n\trows := len(grid)\n\tcols := len(grid[0])\n\n\t// Edge case: if the immediate neighbors are blocked\n\tif grid[1][0] > 1 && grid[0][1] > 1 {\n\t\treturn -1\n\t}\n\n\ttime := make([][]int, rows)\n\tfor i := range time {\n\t\ttime[i] = make([]int, cols)\n\t\tfor j := range time[i] {\n\t\t\ttime[i][j] = math.MaxInt32\n\t\t}\n\t}\n\n\tpq := &MinHeap{}\n\theap.Push(pq, Info{time: 0, row: 0, col: 0})\n\ttime[0][0] = 0\n\n\tfor pq.Len() > 0 {\n\t\tcurr := heap.Pop(pq).(Info)\n\t\tcurrTime, currRow, currCol := curr.time, curr.row, curr.col\n\n\t\t// If we reached the bottom-right cell\n\t\tif currRow == rows-1 && currCol == cols-1 {\n\t\t\treturn currTime\n\t\t}\n\n\t\t// Explore neighbors\n\t\tfor d := 0; d < 4; d++ {\n\t\t\tnextRow := currRow + directions[d]\n\t\t\tnextCol := currCol + directions[d+1]\n\n\t\t\tif isOutside(nextRow, nextCol, rows, cols) {\n\t\t\t\tcontinue\n\t\t\t}\n\n\t\t\t// Calculate next time\n\t\t\twait := 0\n\t\t\tif (grid[nextRow][nextCol]-currTime)&1 == 0 {\n\t\t\t\twait = 1\n\t\t\t}\n\t\t\tnextTime := max(currTime+1, grid[nextRow][nextCol]+wait)\n\n\t\t\t// Update if the path is quicker\n\t\t\tif nextTime < time[nextRow][nextCol] {\n\t\t\t\ttime[nextRow][nextCol] = nextTime\n\t\t\t\theap.Push(pq, Info{time: nextTime, row: nextRow, col: nextCol})\n\t\t\t}\n\t\t}\n\t}\n\n\treturn -1\n}\n\nfunc max(a, b int) int {\n\tif a > b {\n\t\treturn a\n\t}\n\treturn b\n}\n``` | 1 | 0 | ['Go'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | BFS with Min Heap (Optimized) | bfs-with-min-heap-optimized-by-stalebii-fzpe | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | stalebii | NORMAL | 2024-08-23T14:27:43.811318+00:00 | 2024-08-23T14:27:43.811355+00:00 | 56 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(m * n * log (m * n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m * n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n # base\n if grid[0][1] > 1 and grid[1][0] > 1:\n return -1\n\n dirs = [(0, 1), (1, 0), (0, -1), (-1, 0)]\n m, n = len(grid), len(grid[0])\n\n minhpq = [(0, 0, 0)] # stores (time, i, j) increasngly\n visited = {(0, 0)} # trace back visited cell\n\n while minhpq:\n time, i, j = heappop(minhpq)\n\n # stop; found a solution\n if i == m - 1 and j == n - 1:\n return time\n\n for di, dj in dirs:\n di, dj = i + di, j + dj\n \n # pass; infeasible or seen before\n if di < 0 or di >= m or dj < 0 or dj >= n or (di, dj) in visited:\n continue\n\n # wait is at max 1 to move from (i, j) to (di, dj)\n wait = 1 if (grid[di][dj] - time) % 2 == 0 else 0\n\n # take the max for the next possible valid time\n next_time = max(time + 1, grid[di][dj] + wait)\n\n # push the new cell into min heap\n heappush(minhpq, (next_time, di, dj))\n visited.add((di, dj))\n\n return -1\n``` | 1 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Python | Dijkstra’s Algorithm | python-dijkstras-algorithm-by-manojkumar-45t0 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | manojkumar-g | NORMAL | 2024-04-23T06:44:36.571993+00:00 | 2024-04-23T06:44:36.572020+00:00 | 12 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom heapq import heappush,heappop\nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n R = len(grid)\n C = len(grid[0])\n # Check if there is a path exist\n has_path = False\n for r,c in ((0,1),(1,0)):\n if 0<=r<R and 0<=c<C:\n if grid[r][c] <= 1 :\n has_path = True\n if not has_path : return -1\n heap = [(0,0,0)]\n dist = {}\n dist[(0,0)] = 0\n visited = set()\n while heap:\n _,r,c = heappop(heap)\n if (r,c) in visited: continue\n if r == R-1 and c == C-1:\n break\n visited.add((r,c))\n cur_time = dist[(r,c)]\n for nr,nc in ((r+1,c),(r-1,c),(r,c+1),(r,c-1)):\n if (nr,nc) in visited : continue\n if 0<=nr<R and 0<=nc<C:\n cost = None\n if grid[nr][nc] <= cur_time + 1:\n cost = 1\n else:\n cost = grid[nr][nc] - cur_time\n if cost%2 == 0 :\n cost += 1\n if cost:\n if cur_time + cost < dist.get((nr,nc),float(\'inf\')):\n dist[(nr,nc)] = cur_time + cost\n heappush(heap,(dist[(nr,nc)],nr,nc))\n return dist[(R-1,C-1)]\n \n``` | 1 | 0 | ['Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | easy c++ solution | easy-c-solution-by-ar_it_is-hs8g | Intuition\nwe will not reach the destination only when grid[0][1]and grid[1][0] both of them are greater than one otherwise we can go to the grid which is reach | ar_it_is | NORMAL | 2023-05-02T07:55:33.682105+00:00 | 2023-05-02T07:55:33.682154+00:00 | 188 | false | # Intuition\nwe will not reach the destination only when grid[0][1]and grid[1][0] both of them are greater than one otherwise we can go to the grid which is reachable and can increse time by oscillating between the places .For even we will see in howmany minimum time it is possible and we will do the same for odd. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n int n =grid.size();\n int m =grid[0].size();\n vector<pair<int,int>>direc={{0,1},{0,-1},{1,0},{-1,0}};\n vector<vector<long long>>mov(n,vector<long long>(m,1e10));\n set<pair<long long,pair<int,int>>>st;\n mov[0][0]=0;\n st.insert({0,{0,0}});\n if(grid[0][1]>1&&grid[1][0]>1){\n return -1;\n }\n while(!st.empty()){\n auto it =*st.begin();\n long long dis =it.first;\n int row = it.second.first;\n int col = it.second.second;\n st.erase(st.begin());\n if(dis>mov[row][col])continue;\n for(auto p:direc){\n int nr =row+p.first;\n int nc= col+p.second;\n if(nr>=0&&nr<n&&nc>=0&&nc<m){\n long long add=1;\n if(dis+1>=grid[nr][nc]){\n add=1;\n }\n else{\n if((grid[nr][nc]-dis)%2==0){\n add=grid[nr][nc]-dis+1;\n }\n else{\n add=grid[nr][nc]-dis;\n }\n }\n if(mov[row][col]+add<mov[nr][nc]){\n mov[nr][nc]=dis+add;\n st.insert({mov[nr][nc],{nr,nc}});\n }\n \n }\n }\n }\n return mov[n-1][m-1];\n \n \n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | [c++] || Dijkstra || One of the most Understable & Simple solution | c-dijkstra-one-of-the-most-understable-s-4m07 | \nclass Solution {\n vector<pair<int,int>> moves={{1,0},{0,1},{-1,0},{0,-1}};\n vector<vector<int>> dp;\n bool check(int x,int y,int n,int m){\n | thinker37 | NORMAL | 2023-03-11T17:05:47.609541+00:00 | 2023-03-11T17:05:47.609577+00:00 | 81 | false | ```\nclass Solution {\n vector<pair<int,int>> moves={{1,0},{0,1},{-1,0},{0,-1}};\n vector<vector<int>> dp;\n bool check(int x,int y,int n,int m){\n if(x>=0 && x<n && y>=0 && y<m)return true;\n return false;\n }\n \npublic:\n int minimumTime(vector<vector<int>>& grid) {\n int n=grid.size();\n int m=grid[0].size();\n dp.assign(n+1,vector<int>(m+1,INT_MAX));\n \n set<pair<int,pair<int,int>>> st;\n st.insert({0,{0,0}});\n \n if(grid[1][0]>1 && grid[0][1]>1)return -1;\n while(!st.empty()){\n auto it=*st.begin();\n int px=it.second.first;\n int py=it.second.second;\n int d=it.first;\n st.erase(it);\n for(int i=0;i<4;i++){\n int x=px+moves[i].first;\n int y=py+moves[i].second;\n if(!check(x,y,n,m))continue;\n if(d+1>=grid[x][y]){\n if(dp[x][y]>d+1){ st.insert({d+1,{x,y}}); dp[x][y]=d+1; }\n }\n else{\n if(d%2==(grid[x][y])%2){\n if(dp[x][y]>grid[x][y]+1){ st.insert({grid[x][y]+1,{x,y}}); dp[x][y]=grid[x][y]+1;}\n \n }\n else if(d%2!=(grid[x][y])%2){\n if(dp[x][y]>grid[x][y]){ st.insert({grid[x][y],{x,y}});dp[x][y]=grid[x][y]; }\n }\n }\n }\n }\n \n if(dp[n-1][m-1]==INT_MAX){\n return -1;\n }\n else return dp[n-1][m-1];\n \n }\n};\n``` | 1 | 0 | ['Graph'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | Dijkstra | BFS + PriorityQueue | dijkstra-bfs-priorityqueue-by-panevskii-i82p | Code\n\nconst moves = [[0, -1], [0, 1], [1, 0], [-1, 0]]\n\nfunction minimumTime(grid: number[][]): number {\n const N = grid.length;\n const M = grid[0]. | panevskii | NORMAL | 2023-02-26T18:38:17.447553+00:00 | 2023-02-26T18:38:39.357270+00:00 | 68 | false | # Code\n```\nconst moves = [[0, -1], [0, 1], [1, 0], [-1, 0]]\n\nfunction minimumTime(grid: number[][]): number {\n const N = grid.length;\n const M = grid[0].length;\n\n const check = (x: number, y: number) => x >= 0 && y >= 0 && x < N && y < M;\n\n let visited: boolean[][] = [...new Array(N)].map(_ => new Array(M).fill(false));\n\n if(grid[0][1] > 1 && grid[1][0] > 1){\n return -1\n }\n \n const heap = new MinPriorityQueue()\n heap.enqueue([0, 0, 0], 0);\n\n while (heap.size()) {\n let [i, j, time] = heap.dequeue().element;\n \n visited[i][j] = true;\n\n if (i == N -1 && j == M - 1) {\n return time\n }\n\n for (const [diffX, diffY] of moves) {\n const newX = i + diffX, newY = j + diffY;\n if (!check(newX, newY)) {\n continue;\n }\n\n if (visited[newX][newY]) {\n continue;\n }\n\n let newTime = time + 1\n if (time + 1 < grid[newX][newY]) {\n let diff = grid[newX][newY] - time-1\n newTime = diff % 2 == 0 ? \n grid[newX][newY] : grid[newX][newY] + 1\n \n }\n\n visited[newX][newY] = true;\n heap.enqueue([newX, newY, newTime], newTime)\n }\n }\n\n return -1;\n};\n\n``` | 1 | 0 | ['TypeScript'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Graph traversal using a priority queue (Golang) | graph-traversal-using-a-priority-queue-g-mdht | Intuition\nGraph traversal using a priority queue.\n\nIf the time difference with the neighboring cell is even, then we can go back and forth (for example, to t | mastedm | NORMAL | 2023-02-26T12:50:03.165930+00:00 | 2023-02-26T12:50:03.165969+00:00 | 35 | false | # Intuition\nGraph traversal using a priority queue.\n\nIf the time difference with the neighboring cell is even, then we can go back and forth (for example, to the previous cell), thus "wait"\n\n# Code\n```\ntype Cell struct {\n\ttime int\n\trow int\n\tcol int\n}\n\ntype PriorityQueue []*Cell\n\nfunc (pq PriorityQueue) Len() int { return len(pq) }\n\nfunc (pq PriorityQueue) Less(i, j int) bool {\n\treturn pq[i].time < pq[j].time\n}\n\nfunc (pq PriorityQueue) Swap(i, j int) {\n\tpq[i], pq[j] = pq[j], pq[i]\n}\n\nfunc (pq *PriorityQueue) Push(x interface{}) {\n\t*pq = append(*pq, x.(*Cell))\n}\n\nfunc (pq *PriorityQueue) Pop() interface{} {\n\told := *pq\n\tn := len(old)\n\titem := old[n-1]\n\told[n-1] = nil\n\t*pq = old[0 : n-1]\n\treturn item\n}\n\nfunc minimumTime(grid [][]int) int {\n\tif grid[0][1] > 1 && grid[1][0] > 1 {\n\t\treturn -1\n\t}\n\n\tvar row, col, extra int\n\n\tm, n := len(grid), len(grid[0])\n\n\tvisited := make([]int, 1001*1001+1, 1001*1001+1)\n\n\tds := [][]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}\n\n\tpq := make(PriorityQueue, 0)\n\theap.Push(&pq, &Cell{grid[0][0], 0, 0})\n\n\tfor len(pq) > 0 {\n\t\tcell := heap.Pop(&pq).(*Cell)\n\n\t\tif cell.row == m-1 && cell.col == n-1 {\n\t\t\treturn cell.time\n\t\t}\n\n\t\tif visited[cell.row*1001+cell.col] == 1 {\n\t\t\tcontinue\n\t\t}\n\t\tvisited[cell.row*1001+cell.col] = 1\n\n\t\tfor _, d := range ds {\n\t\t\trow, col = cell.row+d[0], cell.col+d[1]\n\t\t\tif 0 <= row && row < m && 0 <= col && col < n && visited[row*1001+col] == 0 {\n\t\t\t\textra = 0\n\t\t\t\tif (grid[row][col]-cell.time)%2 == 0 {\n\t\t\t\t\textra = 1\n\t\t\t\t}\n\n\t\t\t\theap.Push(&pq, &Cell{max(cell.time+1, grid[row][col]+extra), row, col})\n\t\t\t}\n\t\t}\n\t}\n\n\treturn -1\n}\n\nfunc max(a, b int) int {\n\tif a > b {\n\t\treturn a\n\t}\n\treturn b\n}\n\n\n``` | 1 | 0 | ['Go'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | C++ Clean Code|| Dijkstra’s Algorithm || Self Explanatory | c-clean-code-dijkstras-algorithm-self-ex-2vpx | Intuition\nJust Simple Dijkstra\u2019s implementation we try to go to all nodes possible from current code and if we can\'t reach there at given time than we as | Meet_Sinojia | NORMAL | 2023-02-26T11:16:00.364981+00:00 | 2023-02-26T11:16:00.365014+00:00 | 1,036 | false | # Intuition\nJust Simple Dijkstra\u2019s implementation we try to go to all nodes possible from current code and if we can\'t reach there at given time than we assume that travel back and forth and increase time, and if value of new time for that node is less than the current value in resultant vector than update and add that in priority queue.\n\n# Complexity\n- Time complexity:\nO( E log(V) ) { for Dijkstra\u2019s Algorithm }\n\n- Space complexity:\nO( |E| + |V| ) { for priority queue and dist array } + O( |V| ) { for storing the final path }\n\nWhere E = Number of edges and V = Number of Nodes.\n\n# Code\n```\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) \n {\n int n = grid.size();\n int m = grid[0].size();\n vector<vector<int>> res(n,vector<int>(m,1e9));\n \n if(grid[0][1]>grid[0][0]+1 && grid[1][0]>grid[0][0]+1)\n {\n return -1;\n }\n \n priority_queue<pair<int,pair<int,int>>,vector<pair<int,pair<int,int>>>,greater<pair<int,pair<int,int>>>> pq;\n \n pq.push({0,{0,0}});\n \n int nr[] = {-1,0,1,0};\n int nc[] = {0,1,0,-1};\n \n while(!pq.empty())\n {\n auto it = pq.top();\n pq.pop();\n int time = it.first;\n int r = it.second.first;\n int c = it.second.second;\n \n for(int i=0;i<4;i++)\n {\n int x = r + nr[i];\n int y = c + nc[i];\n \n if(x>=0 && x<n && y>=0 && y<m)\n {\n int ntime;\n \n if(time + 1 < grid[x][y])\n {\n ntime = grid[x][y];\n \n if(((time+1)+ntime)%2)\n {\n ntime++;\n }\n }\n \n else\n {\n ntime = time+1;\n }\n \n // We will go back and forth with prev. node till time will be \n // greater or equal\n if(ntime < res[x][y])\n {\n res[x][y]=ntime;\n pq.push({ntime,{x,y}});\n }\n }\n }\n }\n \n if(res[n-1][m-1]==INT_MAX)\n {\n res[n-1][m-1]=-1;\n }\n return res[n-1][m-1];\n }\n};\n``` | 1 | 0 | ['C++'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | Modified Dijkstra Solution || C++ | modified-dijkstra-solution-c-by-shreyd01-whql | We will be using dijkstra algorithm to find minimum time to reach bottom right from top left.\n\n\n\n\n\n\n\ntypedef pair<int,int> pi;\nclass Solution {\npublic | shreyd01 | NORMAL | 2023-02-26T04:31:44.934105+00:00 | 2023-02-26T04:31:44.934145+00:00 | 121 | false | We will be using dijkstra algorithm to find minimum time to reach bottom right from top left.\n\n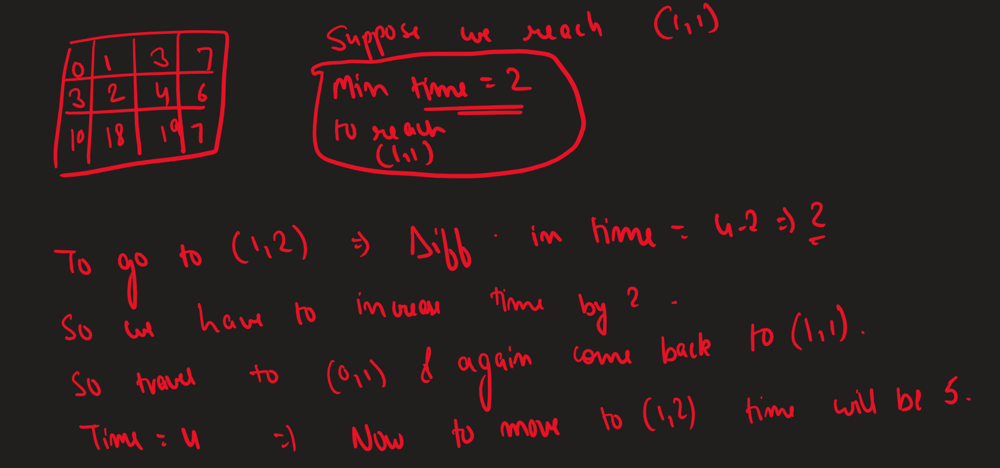\n\n\n\n\n```\ntypedef pair<int,int> pi;\nclass Solution {\npublic:\n \n int isSafe(int x, int y, int m, int n){\n \n\t\t//returns whether a point lies within the grid or not\n if(x<0 or y<0 or x==m or y==n)\n return 0;\n \n return 1;\n \n }\n int minimumTime(vector<vector<int>>& grid) {\n\t\t\t\n\t\t// If the neighbouring cells of grid[0][0] is not 1, we will be not able to travel forward so just return -1\t\n if(grid[1][0]>1 and grid[0][1]>1)\n return -1;\n \n\t\t// priority queue\n\t\t// 1st value in pair - Time required to reach that point\n\t\t// 2nd pair - Coordinates (x,y)\n\n priority_queue<pair<int,pi>,vector<pair<int,pi>>,greater<pair<int,pi>>> pq;\n pq.push({0,{0,0}});\n int m = grid.size();\n int n = grid[0].size();\n \n\t\t// Dist vector of vector to store min time required to reach a point\n vector<vector<int>> dist(m,vector<int> (n,INT_MAX));\n\t\t\n\t\t// Defining available moves\n vector<vector<int>> moves = {{1,0},{-1,0},{0,1},{0,-1}};\n \n while(!pq.empty()){\n \n auto tmp = pq.top();\n pq.pop();\n \n int val = tmp.first;\n int x = tmp.second.first;\n int y = tmp.second.second;\n \n\t\t\t//If we have reached the right bottom return the min time\n if(x == m-1 and y == n-1)\n return val;\n \n for(int i=0;i<4;i++){\n \n int nx = x+moves[i][0];\n int ny = y+moves[i][1];\n \n if(!isSafe(nx,ny,m,n))\n continue;\n \n\t\t\t\t// Finding the difference between time of the cells\n int currDist = grid[nx][ny] - val;\n \n currDist = max(currDist,0);\n \n\t\t\t\t//If the distance between the times of 2 cell is even then we have to increment required time\n if(currDist%2 == 0)\n currDist++;\n \n if(dist[nx][ny]>val+currDist)\n {\n dist[nx][ny] = val+currDist;\n pq.push({dist[nx][ny],{nx,ny}});\n }\n \n }\n \n }\n return -1;\n \n \n }\n};\n\n``` | 1 | 0 | ['Heap (Priority Queue)'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | [Java] Simple Priority Queue | Speed 98.31% | java-simple-priority-queue-speed-9831-by-cxl3 | \n\n# Code\n\n public int minimumTime(int[][] grid) {\n if(grid[0][1] > 1 && grid[1][0] > 1) return -1;\n int m = grid.length, n = grid[0].leng | ken0207 | NORMAL | 2023-02-26T04:01:39.300130+00:00 | 2023-03-10T02:52:04.192253+00:00 | 573 | false | \n\n# Code\n```\n public int minimumTime(int[][] grid) {\n if(grid[0][1] > 1 && grid[1][0] > 1) return -1;\n int m = grid.length, n = grid[0].length;\n int[][] directions = new int[][]{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n PriorityQueue<int[]> pq = new PriorityQueue<int[]>((a, b) -> a[0] - b[0]); \n pq.add(new int[]{0, 0, 0});//int[step, i, j]\n boolean[][] visited = new boolean[m][n];\n visited[0][0] = true;\n while(!pq.isEmpty()){\n int[] cur = pq.poll(); //current smallest step\n for(int[] direction : directions){\n int i = cur[1] + direction[0];\n int j = cur[2] + direction[1];\n if(i < 0 || i == m || j < 0 || j == n || visited[i][j]) continue;\n visited[i][j] = true;\n int step = cur[0] + 1;\n if(grid[i][j] > step) step = (grid[i][j] - step) % 2 + grid[i][j];\n if(i == m - 1 && j == n - 1) return step;\n pq.add(new int[]{step , i, j});\n } \n }\n return -1;\n }\n``` | 1 | 0 | ['Java'] | 2 |
minimum-time-to-visit-a-cell-in-a-grid | Dijkstra | dijkstra-by-filinovsky-qhdj | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Filinovsky | NORMAL | 2025-02-25T18:07:59.717026+00:00 | 2025-02-25T18:07:59.717026+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def setval(self):
return 10**9
def dijkstra(self, i, j, grid):
from collections import defaultdict
import heapq
n, m = len(grid), len(grid[0])
queue = [(0, i, j)]
dist = defaultdict(self.setval)
dist[(i, j)] = 0
while queue:
d, i, j = heapq.heappop(queue)
pairs = [(i, min(j + 1, m - 1)), (i, max(j - 1, 0)), (min(i + 1, n - 1), j), (max(i - 1, 0), j)]
for x, y in pairs:
val = grid[x][y]
k = 0 if (val - d) % 2 else 1
num = 1 if d + 1 >= val else val + k - d
if d + num < dist[(x, y)]:
dist[(x, y)] = d + num
heapq.heappush(queue, (dist[(x, y)], x, y))
return dist[(n - 1, m - 1)]
def minimumTime(self, grid: list[list[int]]) -> int:
n, m = len(grid), len(grid[0])
if grid[min(1, n - 1)][0] > 1 and grid[0][min(1, m - 1)] > 1:
return -1
return self.dijkstra(0, 0, grid)
``` | 0 | 0 | ['Graph', 'Heap (Priority Queue)', 'Shortest Path', 'Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | dijkstra | dijkstra-by-saikumarkundlapelli-ppjp | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | saikumarkundlapelli | NORMAL | 2025-02-21T18:07:03.114539+00:00 | 2025-02-21T18:07:03.114539+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<pair<int, int>> directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int minimumTime(vector<vector<int>>& grid) {
int m=grid.size();
int n=grid[0].size();
if(grid[1][0]>grid[0][0]+1 and grid[0][1]>grid[0][0]+1){
return -1;
}
vector<vector<int>> distance(m, vector<int>(n, INT_MAX));
priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, greater<pair<int, pair<int, int>>>> pq;
pq.push({0, {0, 0}});
distance[0][0]=0;
while(pq.size()>0){
int time = pq.top().first;
int i = pq.top().second.first;
int j = pq.top().second.second;
pq.pop();
for(auto dir : directions){
int new_i = i+dir.first;
int new_j = j+dir.second;
if(new_i>=0 and new_i<m and new_j>=0 and new_j<n){
int n_time=0;
if(time+1<grid[new_i][new_j]){
n_time=grid[new_i][new_j];
int diff=grid[new_i][new_j]-time-1;
n_time = diff%2==0?n_time:n_time+1;
}
else{
n_time=time+1;
}
if(n_time<distance[new_i][new_j]){
distance[new_i][new_j]=n_time;
pq.push({n_time, {new_i, new_j}});
}
}
}
}
return distance[m-1][n-1]==INT_MIN?-1:distance[m-1][n-1];
}
};
``` | 0 | 0 | ['Heap (Priority Queue)', 'C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.