question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-time-to-visit-a-cell-in-a-grid | CPP | BFS - shortest path + greedy | cpp-bfs-shortest-path-greedy-by-kena7-gbow | Code | kenA7 | NORMAL | 2025-02-09T09:09:58.820171+00:00 | 2025-02-09T09:09:58.820171+00:00 | 5 | false |
# Code
```cpp []
class Solution {
public:
#define vt vector<int>
int dx[4]={1,0,-1,0};
int dy[4]={0,1,0,-1};
bool valid(int i,int j, int m,int n)
{
if(i>=0 && j>=0 && i<m && j<n)
return true;
return false;
}
bool possible(int i,int j, int t, vector<vector<int>>& grid)
{
int m=grid.size(), n=grid[0].size();
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(valid(x,y,m,n) && grid[x][y]<=t+1)
return true;
}
return false;
}
int minimumTime(vector<vector<int>>& grid)
{
int m=grid.size(), n=grid[0].size();
priority_queue<vt,vector<vt>,greater<vt>>pq;
pq.push({0,0,0});
vector<vector<bool>>vis(m,vector<bool>(n,false));
vis[0][0]=true;
while(!pq.empty())
{
int t=pq.top()[0],i=pq.top()[1],j=pq.top()[2];
pq.pop();
if(i==m-1 && j==n-1)
return t;
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(valid(x,y,m,n) && !vis[x][y])
{
if(grid[x][y]<=t+1)
{
pq.push({t+1,x,y});
vis[x][y]=true;
}
else if(possible(i,j,t,grid))
{
int diff=(grid[x][y]-t);
int td=diff+((diff+1)%2);
pq.push({t+td,x,y});
vis[x][y]=true;
}
}
}
}
return -1;
}
};
``` | 0 | 0 | ['C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Dijkstra's | dijkstras-by-akshaypatidar33-8onk | Code | akshaypatidar33 | NORMAL | 2025-02-06T09:42:37.759079+00:00 | 2025-02-06T09:42:37.759079+00:00 | 2 | false |
# Code
```cpp []
class Solution {
public:
int minimumTime(vector<vector<int>>& grid) {
if(grid[0][0]>0 || (grid[0][1]>1 && grid[1][0]>1)) return -1;
int n = grid.size(), m = grid[0].size();
vector<vector<int>> dist(n,vector<int>(m,INT_MAX));
priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, greater<pair<int, pair<int, int>>>> pq;
pq.push({0,{0,0}});
int dir[] = {0,1,0,-1,0};
dist[0][0]=0;
while(!pq.empty()){
auto[time, xy] = pq.top();
auto[x, y]=xy;
pq.pop();
for(int i=0; i<4; i++){
int nx = x+dir[i], ny = y+dir[i+1];
if(nx>=0 && ny>=0 && nx<n && ny<m){
int diff = abs(grid[nx][ny]-time);
int newtime = diff%2==0? grid[nx][ny]+1:grid[nx][ny];
if(time+1>=grid[nx][ny] && dist[nx][ny]>time+1){
dist[nx][ny]=time+1;
pq.push({dist[nx][ny], {nx, ny}});
}else if(time+1<grid[nx][ny] && dist[nx][ny]>newtime){
dist[nx][ny]=newtime;
pq.push({dist[nx][ny], {nx, ny}});
}
}
}
}
return dist.back().back();
}
};
``` | 0 | 0 | ['Breadth-First Search', 'Heap (Priority Queue)', 'Matrix', 'C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Dijkstra’s Algorithm | dijkstras-algorithm-by-zozo_tm-zaaw | Code | zozo_tm | NORMAL | 2025-01-25T02:17:51.924465+00:00 | 2025-01-25T02:17:51.924465+00:00 | 2 | false |
# Code
```python3 []
class Solution:
def minimumTime(self, grid: List[List[int]]) -> int:
# edge case
if grid[0][1] > 1 and grid[1][0] > 1:
return -1
# initialize
m, n = len(grid), len(grid[0])
trans = [(0,1),(0,-1),(1,0),(-1,0)]
INF = float('inf')
time_cost = [[INF] * n for _ in range(m)]
# Queue
minheap = []
heapq.heappush(minheap,(0,0,0)) # t, i, j
time_cost[0][0] = 0
# main loop
while minheap:
time, x, y = heapq.heappop(minheap)
if x == m-1 and y == n-1:
return time
if time > time_cost[x][y]:
continue
arrival = time + 1
for transx, transy in trans:
nx, ny = transx + x, transy + y
if 0 <= nx < m and 0 <= ny < n:
# no need to wait
if arrival >= grid[nx][ny]:
newtime = arrival
# need to wait
else:
newtime = grid[nx][ny] + (1 if (grid[nx][ny] - arrival) % 2 == 1 else 0)
# update cost array
if time_cost[nx][ny] > newtime:
time_cost[nx][ny] = newtime
heapq.heappush(minheap,(time_cost[nx][ny], nx, ny))
return -1
``` | 0 | 0 | ['Array', 'Heap (Priority Queue)', 'Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | 2577. Minimum Time to Visit a Cell In a Grid | 2577-minimum-time-to-visit-a-cell-in-a-g-v1rl | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-19T03:51:53.829087+00:00 | 2025-01-19T03:51:53.829087+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
import heapq
from typing import List
class Solution:
def minimumTime(self, grid: List[List[int]]) -> int:
if grid[0][1] > 1 and grid[1][0] > 1:
return -1
num_rows, num_cols = len(grid), len(grid[0])
possible_moves = [(1, 0), (-1, 0), (0, 1), (0, -1)]
explored = set()
priority_queue = [(grid[0][0], 0, 0)]
while priority_queue:
current_time, current_x, current_y = heapq.heappop(priority_queue)
if (current_x, current_y) == (num_rows - 1, num_cols - 1):
return current_time
if (current_x, current_y) in explored:
continue
explored.add((current_x, current_y))
for move_x, move_y in possible_moves:
next_x, next_y = current_x + move_x, current_y + move_y
if not self._is_valid_position(explored, next_x, next_y, num_rows, num_cols):
continue
waiting_time = 1 if (grid[next_x][next_y] - current_time) % 2 == 0 else 0
new_time = max(grid[next_x][next_y] + waiting_time, current_time + 1)
heapq.heappush(priority_queue, (new_time, next_x, next_y))
return -1
def _is_valid_position(self, explored, next_x, next_y, num_rows, num_cols):
return 0 <= next_x < num_rows and 0 <= next_y < num_cols and (next_x, next_y) not in explored
``` | 0 | 0 | ['Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Python (Simple Dijkstra's algorithm) | python-simple-dijkstras-algorithm-by-rno-o5ko | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | rnotappl | NORMAL | 2025-01-07T18:24:13.956911+00:00 | 2025-01-07T18:24:13.956911+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def minimumTime(self, grid):
m, n = len(grid), len(grid[0])
if grid[0][1] > 1 and grid[1][0] > 1:
return -1
stack, dict1 = [(0,0,0)], {}
for i in range(m):
for j in range(n):
dict1[(i,j)] = float("inf")
dict1[(0,0)] = 0
while stack:
time,x,y = heapq.heappop(stack)
if x == m-1 and y == n-1:
return time
for (nx,ny) in [(x+1,y),(x-1,y),(x,y+1),(x,y-1)]:
if 0 <= nx < m and 0 <= ny < n:
if time+1 >= grid[nx][ny]:
new_time = time+1
else:
if (grid[nx][ny]-time)%2 == 0:
new_time = grid[nx][ny]+1
else:
new_time = grid[nx][ny]
if dict1[(nx,ny)] > new_time:
dict1[(nx,ny)] = new_time
heapq.heappush(stack,(dict1[(nx,ny)],nx,ny))
return -1
``` | 0 | 0 | ['Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | I hope you like it | i-hope-you-like-it-by-sajedkarimy-q9li | Let's say, I am just proud of myself 😅.First, note that if we can take the first move, we can reach the last cell too, as we can move back and fourth between th | sajedkarimy | NORMAL | 2025-01-06T08:35:37.370863+00:00 | 2025-01-06T08:35:37.370863+00:00 | 5 | false |
Let's say, I am just proud of myself 😅.
First, note that if we can take the first move, we can reach the last cell too, as we can move back and fourth between the first two cells till all the cells are open to enter.
Moreover, assuming a cell is reachable via a path of valid cells (including the target as well), we can be at that cell only if `(time + row + col) % 2 == 0`, where row and cell denote the location of cell. By this, I mean for any `cell = (row, col)`, if `(row + col) % 2 == 0`, then we can be there only if `time % 2 == 0`.
In the following code, we iterate over the time, and keep track of all the cells that are adjecent to the cells we have visited so far. At each time, if the timer is even, this means that we can be visiting a new valid even cell which was adjecent to our visited cells, and move to an odd cell. So we pop from even current adjecnt cells, and push new odd adjacents to the odd heap.
# Complexity
- Time complexity:
Note that it is possible to push all the cells in the heap, and pop all of them. This task is equivalent to sorting, which takes $n\log n$, where $n$ is the number of elements. So, the time complexity of this algorithm is:
$O(mn\log(mn))$
- Space complexity:
$O(mn)$
# Code
```python3 []
import heapq
class Solution:
def minimumTime(self, grid: List[List[int]]) -> int:
if grid[0][1] > 1 and grid[1][0] > 1:
return -1
m = len(grid)
n = len(grid[0])
even = [(0,0,0)]
odd = []
visited = [[False] * n for _ in range(m)]
visited[0][0] = True
timer = 0
for i in range(10 ** 6):
pop_heap, push_heap = (even, odd) if timer % 2 == 0 else (odd, even)
processing_cells = []
while pop_heap and pop_heap[0][0] <= timer:
processing_cells.append(heapq.heappop(pop_heap))
for cell in processing_cells:
if (cell[1] == m - 1) and (cell[2] == n - 1):
return timer
for direction in {(0,1), (0,-1), (1,0), (-1,0)}:
row = cell[1] + direction[0]
col = cell[2] + direction[1]
if (0 <= row) and (row < m) and (0 <= col) and (col < n):
if not visited[row][col]:
visited[row][col] = True
heapq.heappush(push_heap, (grid[row][col], row, col))
timer += 1
if (not even) and (not odd):
break
return -1
``` | 0 | 0 | ['Python3'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | easiest bfs & dijkstra soln, java code. | easiest-bfs-dijkstra-soln-java-code-by-p-s5hb | Intuition & Approachcase1: when on start cell, we have two options to explore with, right or down, and time taken to reach them is 1s, but if their minTime > 1, | piyush_mehta22 | NORMAL | 2024-12-26T05:37:12.310608+00:00 | 2024-12-26T05:37:12.310608+00:00 | 6 | false | # Intuition & Approach
<!-- Describe your first thoughts on how to solve this problem. -->
case1: when on start cell, we have two options to explore with, right or down, and time taken to reach them is 1s, but if their minTime > 1, we can't go anywhere, we stuck, we return -1
case2: when we stuck on some other cell, where its new neighbors have minTime > currTime(whatever time we have) we may have to revisit on old path to pass out time until we can explore new neighbor, point is once we are out of first cell, we can always reach endpoint, now its about reaching in minimum time as possible, so for that use pq
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
bfs: O(mn)
pq: one cell may add new 4 cells, (if all 4 are still unvisited), over all all cells will be added once at max, so worst case TC = O(mn log(mn))
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
vis array: O(mn)
pq: O(mn)
# Code
```java []
class Solution {
public int minimumTime(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int time = 0;
if(grid[0][1] > 1 && grid[1][0] > 1) return -1;
boolean[][] vis = new boolean[m][n];
PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[2] - b[2]);
vis[0][0] = true;
q.add(new int[]{0, 0, time});
int[] delrow = {-1, 0, 1, 0};
int[] delcol = {0, 1, 0, -1};
while(!q.isEmpty()) {
int[] top = q.poll();
int currRow = top[0];
int currCol = top[1];
int currTime = top[2];
if(currRow == m-1 && currCol == n-1) return currTime;
for(int i=0;i<4;i++) {
int nrow = currRow + delrow[i];
int ncol = currCol + delcol[i];
if(nrow >= 0 && nrow < m && ncol >= 0 && ncol < n && !vis[nrow][ncol]) {
if(currTime + 1 >= grid[nrow][ncol]) {
q.add(new int[]{nrow, ncol, currTime+1});
} else {
int diff = grid[nrow][ncol];
if(((diff - currTime) & 1) == 1)
q.add(new int[]{nrow, ncol, diff});
else q.add(new int[]{nrow, ncol, diff+1});
}
vis[nrow][ncol] = true;
}
}
}
return -1;
}
}
``` | 0 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'Java'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | C++ solution | c-solution-by-csld-cjw2 | 2577. Minimum Time to Visit a Cell In a GridSolutionGood day, let’s tease our brain.Understanding the problemThe problem asks us to find the minimum time requir | csld | NORMAL | 2024-12-20T16:03:05.736330+00:00 | 2024-12-20T16:03:05.736330+00:00 | 7 | false | # 2577. Minimum Time to Visit a Cell In a Grid
## Solution
Good day, let’s tease our brain.
### Understanding the problem
The problem asks us to find the minimum time required traversing from the top-left to the bottom-right, this implicitly implies the fact that we maybe using Dijkstra’s algorithm to solve this.
Different from a normal Dijkstra problem where the graph is pre-defined, that is, the weight between two connected node is a constant and would not be further modified. In this problem, there is no `fixed` distance between two node, the distance is dynamic, which is defined by the current value and the value that is to-be-traversed.
### Understanding ‘cost’ in this problem
In Dijkstra, the reason that ‘cost’ is so important because it directly affects our dicision, whether to pick this node as the next traversing node or not, whether push it or not…etc.
Well, similarly in this problem, we also wish to obtain this kind of information. But the key factor is the situation expand the possiblities of the cost required.
If the difference between `grid[r][c]` and `curr_time`
- if difference is odd, `new_time` = `grid[r][c]`
- else `new_time` = `grid[r][c]` + 1
The value that we store in the distance vector, and the given grid defines the cost of our traversing operation mutually.
### Start traversing
Note that since we are given a grid, there is no need to consturct a adjacent list or adjacent matrix, since a grid itself suffice the attrbute of a normal and viable graph.
Initially, we assume the cost requried from source to every other node is `INT_MAX`. Then, for each possible traversing option, we traverse to that node.
### Observation
there are two different sceraio: smaller or bigger. To find the required time:
case 1: `curr_time` >= `grid[r][c]`
- then `new_time` = `curr_time` + 1
case 2: `curr_time` < `grid[r][c]`
- then find difference between `grid[r][c]` and `curr_time`
- if difference is odd, `new_time` = `grid[r][c]`
- else `new_time` = `grid[r][c]` + 1
We implement this logic as follows:
```cpp
int nt = time + 1;
if (nt < grid[ni][nj]) {
nt = grid[ni][nj];
if ((nt - time) % 2 == 0) {
nt++;
}
}
```
Now, the new time variable stands for the time required if we travserse from source node to our current location, and then do further traverse to the next. If there exist an alternative distance value in distance array which represnets other value traversing from another path, which is smaller than the value that we currnetly holds, we just ignore our calculated value, since it is useless.
Conversely, if the value we possess is smaller than the value that is currently presnet in the distance array, we update the value, and further push the new node to the pq since we found another better path, it is worth explore.
Dijkstra aims to find the shortest path from the source node to the dest node, that means for each excellent path we discovered, we need to explore the possiblity of this new discovery.
### Note
Notice that once we are at the end of the grid, that means we are certainly able to return the value because the node storing in the pq is: the time required starting from top-left, i, and j. just rememeber to halt the program once this occured.
If pq is empty, that means we never reached the desired cell in the given graph, we reutrn -1.
## Code
```cpp
#define maxN 100005
using pii = pair<int, int>;
using piii = tuple<int, int, int>;
class Solution {
public:
int di[4] = {0, -1, 0, 1};
int dj[4] = {-1, 0, 1, 0};
int minimumTime(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
if (grid[0][1] > 1 && grid[1][0] > 1) return -1;
vector<vector<int>> distance(n, vector<int>(m, INT_MAX));
distance[0][0] = 0;
priority_queue<piii, vector<piii>, greater<>> pq;
pq.push({0, 0, 0});
while (!pq.empty()) {
auto [time, i, j] = pq.top();
pq.pop();
if (i == n - 1 && j == m - 1) {
return time;
}
for (int k = 0; k < 4; k++) {
int ni = i + di[k];
int nj = j + dj[k];
if (ni < 0 || ni >= n || nj < 0 || nj >= m) {
continue;
}
int nt = time + 1;
if (nt < grid[ni][nj]) {
nt = grid[ni][nj];
if ((nt - time) % 2 == 0) {
nt++;
}
}
if (nt < distance[ni][nj]) {
distance[ni][nj] = nt;
pq.push({nt, ni, nj});
}
}
}
return -1;
}
};
```
| 0 | 0 | ['C++'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | Dijkstra question in Google interview | dijkstra-question-in-google-interview-by-i27j | null | guohaoyu110 | NORMAL | 2024-12-11T06:58:13.442919+00:00 | 2024-12-11T06:58:13.442919+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\u8FD9\u4E2A\u89E3\u6CD5\u5E76\u6CA1\u6709\u771F\u7684\u201C\u9000\u56DE\u53BB\u201D\uFF0C\u800C\u662F\u901A\u8FC7\u539F\u5730\u7B49\u5F85\u6765\u6EE1\u8DB3\u65F6\u95F4\u7EA6\u675F\u3002 \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\u4E3A\u4EC0\u4E48\u4E0D\u9700\u8981\u56DE\u9000\n1. \u52A8\u6001\u89C4\u5212\u601D\u8DEF\uFF1A\n\n\u6BCF\u6B21\u90FD\u4ECE\u5806\u4E2D\u53D6\u51FA\u5F53\u524D\u65F6\u95F4\u6700\u77ED\u7684\u8DEF\u5F84\uFF0C\u8FD9\u79CD\u8D2A\u5FC3\u7B56\u7565\u4FDD\u8BC1\u4E86\u8DEF\u5F84\u7684\u6700\u4F18\u6027\u3002\n\u539F\u5730\u7B49\u5F85\u5DF2\u7ECF\u53EF\u4EE5\u8C03\u6574\u65F6\u95F4\u5230\u7B26\u5408\u8981\u6C42\u7684\u72B6\u6001\uFF0C\u65E0\u9700\u591A\u4F59\u7684\u56DE\u9000\u64CD\u4F5C\u3002\n2. \u6027\u80FD\u4F18\u5316\uFF1A\n\n\u5982\u679C\u5B9E\u73B0\u56DE\u9000\uFF0C\u4F1A\u5F15\u5165\u989D\u5916\u7684\u8DEF\u5F84\u8BB0\u5F55\u548C\u590D\u6742\u7684\u903B\u8F91\u5224\u65AD\uFF0C\u589E\u52A0\u7B97\u6CD5\u590D\u6742\u5EA6\u548C\u8FD0\u884C\u65F6\u95F4\u3002\n\u539F\u5730\u7B49\u5F85\u7684\u5B9E\u73B0\u66F4\u76F4\u63A5\uFF0C\u4E5F\u7B26\u5408\u5B9E\u9645\u95EE\u9898\u7684\u9700\u6C42\u3002\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO((m\xD7n)\u22C5log(m\xD7n))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m\xD7n)\n# Code\n```python3 []\nimport heapq \nclass Solution:\n def minimumTime(self, grid: List[List[int]]) -> int:\n if not grid:\n return -1\n if grid[0][1] > 1 and grid[1][0] > 1:\n return -1\n ROWS, COLS = len(grid), len(grid[0])\n directions = [(-1,0), (1,0), (0,1), (0,-1)]\n minHeap = [(0, 0, 0)] # current_time, row, col \n visited = set()\n visited.add((0,0)) # row and col \n while minHeap:\n current_time, row, col = heapq.heappop(minHeap)\n if row == ROWS - 1 and col == COLS - 1:\n return current_time \n for dr, dc in directions:\n nr, nc = dr + row, dc + col \n if 0 <= nr < ROWS and 0 <= nc < COLS and (nr, nc) not in visited:\n # \u904D\u5386\u56DB\u4E2A\u65B9\u5411 (dr, dc), \u8BA1\u7B97\u90BB\u5C45\u5355\u5143\u683C (nr, nc) \n waitTime = max(0, grid[nr][nc] - (current_time + 1)) \n if waitTime % 2 == 1:\n waitTime += 1\n new_time = waitTime + current_time + 1\n visited.add((nr,nc)) \n heapq.heappush(minHeap, (new_time, nr, nc)) \n return -1\n\n\n\n``` | 0 | 0 | ['Python3'] | 1 |
minimum-time-to-visit-a-cell-in-a-grid | Java solution. | java-solution-by-neelarunabh-najx | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | neelarunabh | NORMAL | 2024-12-08T00:54:14.696005+00:00 | 2024-12-08T00:54:14.696030+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(m * n log(m * n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minimumTime(int[][] grid) {\n // If both initial moves require more than 1 second, impossible to proceed\n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n\n int rows = grid.length, cols = grid[0].length;\n // Possible movements: down, up, right, left\n int[][] directions = { { 1, 0 }, { -1, 0 }, { 0, 1 }, { 0, -1 } };\n boolean[][] visited = new boolean[rows][cols];\n\n // Priority queue stores {time, row, col}\n // Ordered by minimum time to reach each cell\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) ->\n Integer.compare(a[0], b[0])\n );\n pq.add(new int[] { grid[0][0], 0, 0 });\n\n int minTime = -1;\n while (!pq.isEmpty()) {\n int[] curr = pq.poll();\n int time = curr[0], row = curr[1], col = curr[2];\n\n // Check if reached target\n if (row == rows - 1 && col == cols - 1) {\n minTime = time;\n break;\n }\n\n // Skip if cell already visited\n if (visited[row][col]) {\n continue;\n }\n visited[row][col] = true;\n\n // Try all four directions\n for (int[] d : directions) {\n int nextRow = row + d[0], nextCol = col + d[1];\n if (!isValid(visited, nextRow, nextCol)) {\n continue;\n }\n\n // Calculate the wait time needed to move to next cell\n int waitTime = ((grid[nextRow][nextCol] - time) % 2 == 0)\n ? 1\n : 0;\n int nextTime = Math.max(\n grid[nextRow][nextCol] + waitTime,\n time + 1\n );\n pq.add(new int[] { nextTime, nextRow, nextCol });\n }\n }\n return minTime;\n }\n\n // Checks if given cell coordinates are valid and unvisited\n private boolean isValid(boolean[][] visited, int row, int col) {\n return (\n row >= 0 &&\n col >= 0 &&\n row < visited.length &&\n col < visited[0].length &&\n !visited[row][col]\n );\n }\n}\n``` | 0 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'Java'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | C solution. | c-solution-by-neelarunabh-sr1z | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | neelarunabh | NORMAL | 2024-12-08T00:50:57.422405+00:00 | 2024-12-08T00:50:57.422433+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(m * n log(m * n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m * n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c []\nstruct Node {\n int time;\n int row;\n int col;\n};\n\nstruct MinHeap {\n struct Node* array;\n int size;\n int capacity;\n};\n\n// Function to swap two nodes\nvoid swap(struct Node* a, struct Node* b) {\n struct Node temp = *a;\n *a = *b;\n *b = temp;\n}\n\n// Function to create a MinHeap\nstruct MinHeap* createMinHeap(int capacity) {\n struct MinHeap* minHeap = (struct MinHeap*)malloc(sizeof(struct MinHeap));\n minHeap->size = 0;\n minHeap->capacity = capacity;\n minHeap->array = (struct Node*)malloc(capacity * sizeof(struct Node));\n return minHeap;\n}\n\n// Function to resize the heap when it\'s full\nvoid resizeMinHeap(struct MinHeap* minHeap) {\n minHeap->capacity *= 2;\n minHeap->array = (struct Node*)realloc(minHeap->array, minHeap->capacity * sizeof(struct Node));\n}\n\n// Function to heapify up\nvoid heapifyUp(struct MinHeap* minHeap, int idx) {\n int parent = (idx - 1) / 2;\n if (idx > 0 && minHeap->array[parent].time > minHeap->array[idx].time) {\n swap(&minHeap->array[parent], &minHeap->array[idx]);\n heapifyUp(minHeap, parent);\n }\n}\n\n// Function to insert a new node into MinHeap\nvoid insertMinHeap(struct MinHeap* minHeap, struct Node node) {\n // Resize the heap if it\'s full\n if (minHeap->size == minHeap->capacity) {\n resizeMinHeap(minHeap);\n }\n\n minHeap->array[minHeap->size] = node;\n heapifyUp(minHeap, minHeap->size);\n minHeap->size++;\n}\n\n// Function to heapify down\nvoid heapifyDown(struct MinHeap* minHeap, int idx) {\n int smallest = idx;\n int left = 2 * idx + 1;\n int right = 2 * idx + 2;\n\n if (left < minHeap->size && minHeap->array[left].time < minHeap->array[smallest].time) {\n smallest = left;\n }\n if (right < minHeap->size && minHeap->array[right].time < minHeap->array[smallest].time) {\n smallest = right;\n }\n\n if (smallest != idx) {\n swap(&minHeap->array[smallest], &minHeap->array[idx]);\n heapifyDown(minHeap, smallest);\n }\n}\n\n// Function to extract the minimum node from MinHeap\nstruct Node extractMin(struct MinHeap* minHeap) {\n struct Node minNode = minHeap->array[0];\n minHeap->array[0] = minHeap->array[minHeap->size - 1];\n minHeap->size--;\n heapifyDown(minHeap, 0);\n return minNode;\n}\n\n// Checks if given cell coordinates are valid and unvisited\nbool isValid(int row, int col, int gridSize, int gridColSize) {\n return row >= 0 && col >= 0 && row < gridSize && col < gridColSize;\n}\n\nint minimumTime(int** grid, int gridSize, int* gridColSize) {\n // If both initial moves require more than 1 second, impossible to proceed\n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n\n // Possible movements: down, up, right, left\n int directions[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n bool** visited = (bool**)malloc(gridSize * sizeof(bool*));\n for (int i = 0; i < gridSize; i++) {\n visited[i] = (bool*)malloc((*gridColSize) * sizeof(bool));\n for (int j = 0; j < (*gridColSize); j++) {\n visited[i][j] = false;\n }\n }\n\n struct MinHeap* pq = createMinHeap(gridSize * (*gridColSize));\n struct Node startNode = {0, 0, 0};\n insertMinHeap(pq, startNode);\n \n int minTime = -1;\n while (pq->size > 0) {\n struct Node curr = extractMin(pq);\n int time = curr.time, row = curr.row, col = curr.col;\n\n // Check if reached the target\n if (row == gridSize - 1 && col == (*gridColSize) - 1) {\n minTime = time;\n break;\n }\n\n // Skip if cell is already visited\n if (visited[row][col]) {\n continue;\n }\n visited[row][col] = true;\n\n // Try all four directions\n for (int i = 0; i < 4; i++) {\n int nextRow = row + directions[i][0], nextCol = col + directions[i][1];\n if (!isValid(nextRow, nextCol, gridSize, *gridColSize)) {\n continue;\n }\n\n // Calculate the wait time needed to move to next cell\n int nextTime = time + 1;\n if (grid[nextRow][nextCol] > nextTime) {\n // We have to wait for grid[nextRow][nextCol] to become reachable\n int waitTime = (grid[nextRow][nextCol] - nextTime) % 2 == 0 ? 0 : 1;\n nextTime = grid[nextRow][nextCol] + waitTime;\n }\n\n struct Node nextNode = {nextTime, nextRow, nextCol};\n insertMinHeap(pq, nextNode);\n }\n }\n\n free(pq->array);\n free(pq);\n for (int i = 0; i < gridSize; i++) {\n free(visited[i]);\n }\n free(visited);\n \n return minTime;\n}\n``` | 0 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'C', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path'] | 0 |
minimum-time-to-visit-a-cell-in-a-grid | C++ solution. | c-solution-by-neelarunabh-tvfc | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | neelarunabh | NORMAL | 2024-12-08T00:37:26.400832+00:00 | 2024-12-08T00:37:26.400855+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(m * n log(m * n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m * n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minimumTime(vector<vector<int>>& grid) {\n // If both initial moves require more than 1 second, impossible to\n // proceed\n if (grid[0][1] > 1 && grid[1][0] > 1) {\n return -1;\n }\n\n int rows = grid.size(), cols = grid[0].size();\n // Possible movements: down, up, right, left\n vector<vector<int>> directions = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n vector<vector<bool>> visited(rows, vector<bool>(cols, false));\n\n // Priority queue stores {time, row, col}\n // Ordered by minimum time to reach each cell\n priority_queue<vector<int>, vector<vector<int>>, greater<>> pq;\n pq.push({grid[0][0], 0, 0});\n\n int minTime = -1;\n while (!pq.empty()) {\n auto curr = pq.top();\n pq.pop();\n int time = curr[0], row = curr[1], col = curr[2];\n\n // Check if reached target\n if (row == rows - 1 && col == cols - 1) {\n minTime = time;\n break;\n }\n\n // Skip if cell already visited\n if (visited[row][col]) {\n continue;\n }\n visited[row][col] = true;\n\n // Try all four directions\n for (auto& d : directions) {\n int nextRow = row + d[0], nextCol = col + d[1];\n if (!isValid(visited, nextRow, nextCol)) {\n continue;\n }\n\n // Calculate the wait time needed to move to next cell\n int waitTime =\n ((grid[nextRow][nextCol] - time) % 2 == 0) ? 1 : 0;\n int nextTime = max(grid[nextRow][nextCol] + waitTime, time + 1);\n pq.push({nextTime, nextRow, nextCol});\n }\n }\n return minTime;\n }\n\nprivate:\n // Checks if given cell coordinates are valid and unvisited\n bool isValid(vector<vector<bool>>& visited, int row, int col) {\n return row >= 0 && col >= 0 && row < visited.size() &&\n col < visited[0].size() && !visited[row][col];\n }\n};\n``` | 0 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'C++'] | 0 |
two-best-non-overlapping-events | Very Simple sort + greedy: No DP, no Binary Search, no Heap/PQ/BST | very-simple-sort-greedy-no-dp-no-binary-2erca | Split events into separate start & end, keep track of best event that has ended so far.\n\n\n# super clean, no need for DP or BST.\nclass Solution:\n def max | elimsamazak1 | NORMAL | 2021-11-01T08:57:38.687898+00:00 | 2021-11-01T09:11:54.284740+00:00 | 7,688 | false | Split events into separate start & end, keep track of best event that has ended so far.\n\n```\n# super clean, no need for DP or BST.\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n proc = []\n ans = m = 0 # m represents max value of finished event so far\n for s,e,v in events:\n proc.append( (s, True, v) ) # time, is_start, val\n proc.append( (e+1, False, v) ) # use e+1 (inclusive)\n proc.sort() # sort by time\n \n for time, is_start, val in proc:\n if is_start:\n ans = max(ans, m+val)\n else:\n m = max(m, val)\n return ans\n\n``` | 123 | 0 | [] | 20 |
two-best-non-overlapping-events | 100% Beats Simple Binary Search | 100-beats-simple-binary-search-by-sumeet-ez91 | Solution Explanation: Maximizing the Sum of Two Non-overlapping Events \uD83C\uDF1F\n\n## Intuition \uD83D\uDCA1\nThe problem asks us to select at most two non- | Sumeet_Sharma-1 | NORMAL | 2024-12-08T02:00:49.279663+00:00 | 2024-12-08T11:42:28.257163+00:00 | 25,252 | false | # Solution Explanation: Maximizing the Sum of Two Non-overlapping Events \uD83C\uDF1F\n\n## Intuition \uD83D\uDCA1\nThe problem asks us to select at most two non-overlapping events such that the sum of their values is maximized. The key challenge is ensuring that the two selected events do not overlap. We need an approach that allows us to efficiently find the best combination of two events.\n\n### Thought Process \uD83E\uDDE0:\n1. **Event Structure**: Each event is represented by three values: the **start time**, the **end time**, and the **value**. The goal is to choose two events where one starts strictly after the other ends. The more valuable the event, the better, so we want to maximize the sum of their values.\n \n2. **Sorting by Start Time** \uD83D\uDCC5: One of the first things we can do to organize the events is to sort them by their start time. This makes it easier to look ahead at events that may be a valid candidate for pairing.\n\n3. **Avoid Redundancy with a Suffix Array** \uD83D\uDD04: Instead of searching for the best second event for every single event, we can create a **suffix array** that stores the maximum possible value for non-overlapping events that occur after a given event. This allows us to quickly get the best possible event for pairing, saving us from redundant checks.\n\n4. **Efficient Searching with Binary Search** \uD83D\uDD0D: After sorting the events, we can use **binary search** to find the next valid event that starts after the current event ends. This ensures that we can efficiently check for valid pairs without having to iterate over all subsequent events.\n\n---\n\n## Approach \uD83D\uDD27\n\n### 1. Sort Events by Start Time \uD83D\uDCCA\nThe first step is to sort the events based on their **start time**. This way, we process each event in chronological order, making it easy to find the subsequent event that starts after the current event ends. Sorting ensures that we can quickly identify events that may or may not overlap with the current one.\n\n### 2. Create a Suffix Array \uD83D\uDDC2\nWe create a **suffix array** to keep track of the maximum possible value of non-overlapping events from the current event to the last event. The idea behind the suffix array is simple:\n- Start by initializing the last event\u2019s value as the maximum value.\n- Then, working backwards through the list of events, update the suffix array with the highest event value encountered so far.\n- This array allows us to quickly access the best possible future event without needing to repeatedly check all future events.\n\n### 3. Binary Search for Non-overlapping Events \uD83D\uDD0D\nFor each event, we need to find the first event that starts after the current event ends. Since the events are sorted by start time, we can use **binary search** to efficiently find this next valid event. If no such event exists, we just move on to the next one. If a valid event is found, we can easily retrieve its value from the suffix array and calculate the total value.\n\n### 4. Maximize the Total Value \uD83D\uDCB8\nFor each event:\n- First, we check if attending only this event yields a higher value than the current maximum sum.\n- Then, if a valid second event is found (using the binary search), we calculate the sum of the current event\u2019s value and the best possible future event value (from the suffix array).\n- We update the maximum sum accordingly, ensuring that we track the best combination of non-overlapping events.\n\n---\n\n## Complexity \uD83D\uDCC8\n\n- **Time Complexity** \u23F1\uFE0F:\n - **Sorting** the events by their start time takes \\(O(n \\log n)\\).\n - For each event, **binary search** is used to find the next event that starts after the current event ends, which takes \\(O(\\log n)\\).\n - Therefore, the overall time complexity is \\(O(n \\log n)\\), where \\(n\\) is the number of events.\n\n- **Space Complexity** \uD83D\uDCE6:\n - We use an array of size \\(n\\) to store the **suffix maximum values**. This space is necessary to store the maximum values of non-overlapping events starting from each index.\n - Therefore, the space complexity is \\(O(n)\\).\n\n\n\n---\n\n## Key Insights \u2728\n\n### Sorting by Start Time \uD83D\uDDD3\uFE0F\nBy sorting the events by their start time, we ensure that we can efficiently look ahead for the next valid event. This helps us structure the problem in a way that allows for efficient searching and avoids unnecessary checks.\n\n### Binary Search for Next Event \uD83D\uDD0D\nBinary search helps us find the first event that starts after the current event ends in **logarithmic time**. This ensures that we are not wasting time checking each event one by one.\n\n### Suffix Array for Max Values \uD83D\uDC8E\nThe suffix array provides a quick way to access the best possible non-overlapping event from the current event onward. It allows us to avoid recalculating the maximum for every event, which saves time and makes the solution efficient.\n\n### Efficient Pairing of Events \uD83D\uDD17\nThe combination of sorting, binary search, and the suffix array makes the solution very efficient in finding the best pair of non-overlapping events. It allows us to maximize the sum of the values in \\(O(n \\log n)\\) time, which is optimal for this problem.\n\n---\n\nThis approach efficiently solves the problem while ensuring that we minimize unnecessary computations. The use of sorting, binary search, and the suffix array ensures that the solution is both time-efficient and easy to understand. \uD83C\uDF89\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n int n = events.size();\n \n sort(events.begin(), events.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[0] < b[0];\n });\n \n vector<int> suffixMax(n);\n suffixMax[n - 1] = events[n - 1][2];\n \n for (int i = n - 2; i >= 0; --i) {\n suffixMax[i] = max(events[i][2], suffixMax[i + 1]);\n }\n \n int maxSum = 0;\n \n for (int i = 0; i < n; ++i) {\n int left = i + 1, right = n - 1;\n int nextEventIndex = -1;\n \n while (left <= right) {\n int mid = left + (right - left) / 2;\n if (events[mid][0] > events[i][1]) {\n nextEventIndex = mid;\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n \n if (nextEventIndex != -1) {\n maxSum = max(maxSum, events[i][2] + suffixMax[nextEventIndex]);\n }\n \n maxSum = max(maxSum, events[i][2]);\n }\n \n return maxSum;\n }\n};\n\n```\n```Python3 []\nfrom typing import List\n\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n n = len(events)\n \n # Step 1: Sort the events by their start time\n events.sort(key=lambda x: x[0])\n \n # Step 2: Create the suffix array for the maximum event value from each event onward\n suffixMax = [0] * n\n suffixMax[n - 1] = events[n - 1][2] # Initialize the last event\'s value\n \n # Populate the suffixMax array\n for i in range(n - 2, -1, -1):\n suffixMax[i] = max(events[i][2], suffixMax[i + 1])\n \n # Step 3: For each event, find the next event that starts after it ends\n maxSum = 0\n \n for i in range(n):\n left, right = i + 1, n - 1\n nextEventIndex = -1\n \n # Perform binary search to find the next non-overlapping event\n while left <= right:\n mid = left + (right - left) // 2\n if events[mid][0] > events[i][1]:\n nextEventIndex = mid\n right = mid - 1\n else:\n left = mid + 1\n \n # If a valid next event is found, update the max sum\n if nextEventIndex != -1:\n maxSum = max(maxSum, events[i][2] + suffixMax[nextEventIndex])\n \n # Also consider the case where we take only the current event\n maxSum = max(maxSum, events[i][2])\n \n return maxSum\n\n```\n```Java []\nimport java.util.*;\n\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n int n = events.length;\n \n // Step 1: Sort the events by their start time\n Arrays.sort(events, (a, b) -> a[0] - b[0]);\n \n // Step 2: Create the suffix array for the maximum event value from each event onward\n int[] suffixMax = new int[n];\n suffixMax[n - 1] = events[n - 1][2]; // Initialize the last event\'s value\n \n // Populate the suffixMax array\n for (int i = n - 2; i >= 0; --i) {\n suffixMax[i] = Math.max(events[i][2], suffixMax[i + 1]);\n }\n \n // Step 3: For each event, find the next event that starts after it ends\n int maxSum = 0;\n \n for (int i = 0; i < n; ++i) {\n int left = i + 1, right = n - 1;\n int nextEventIndex = -1;\n \n // Perform binary search to find the next non-overlapping event\n while (left <= right) {\n int mid = left + (right - left) / 2;\n if (events[mid][0] > events[i][1]) {\n nextEventIndex = mid;\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n \n // If a valid next event is found, update the max sum\n if (nextEventIndex != -1) {\n maxSum = Math.max(maxSum, events[i][2] + suffixMax[nextEventIndex]);\n }\n \n // Also consider the case where we take only the current event\n maxSum = Math.max(maxSum, events[i][2]);\n }\n \n return maxSum;\n }\n}\n\n```\n```C# []\npublic class Solution {\n public int MaxTwoEvents(int[][] events) {\n int n = events.Length;\n \n // Step 1: Sort the events by their start time\n Array.Sort(events, (a, b) => a[0].CompareTo(b[0]));\n \n // Step 2: Create the suffix array for the maximum event value from each event onward\n int[] suffixMax = new int[n];\n suffixMax[n - 1] = events[n - 1][2]; // Initialize the last event\'s value\n \n // Populate the suffixMax array\n for (int i = n - 2; i >= 0; i--) {\n suffixMax[i] = Math.Max(events[i][2], suffixMax[i + 1]);\n }\n \n // Step 3: For each event, find the next event that starts after it ends\n int maxSum = 0;\n \n for (int i = 0; i < n; i++) {\n int left = i + 1, right = n - 1;\n int nextEventIndex = -1;\n \n // Perform binary search to find the next non-overlapping event\n while (left <= right) {\n int mid = left + (right - left) / 2;\n if (events[mid][0] > events[i][1]) {\n nextEventIndex = mid;\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n \n // If a valid next event is found, update the max sum\n if (nextEventIndex != -1) {\n maxSum = Math.Max(maxSum, events[i][2] + suffixMax[nextEventIndex]);\n }\n \n // Also consider the case where we take only the current event\n maxSum = Math.Max(maxSum, events[i][2]);\n }\n \n return maxSum;\n }\n}\n\n```\n```Ruby []\n# @param {Integer[][]} events\n# @return {Integer}\ndef max_two_events(events)\n # Step 1: Sort the events by their start time\n events.sort_by! { |event| event[0] }\n\n # Step 2: Create the suffix array for the maximum event value from each event onward\n n = events.length\n suffix_max = Array.new(n)\n suffix_max[n - 1] = events[n - 1][2] # Initialize the last event\'s value\n\n # Populate the suffix_max array\n (n - 2).downto(0) do |i|\n suffix_max[i] = [events[i][2], suffix_max[i + 1]].max\n end\n\n # Step 3: For each event, find the next event that starts after it ends\n max_sum = 0\n\n (0...n).each do |i|\n left, right = i + 1, n - 1\n next_event_index = -1\n\n # Perform binary search to find the next non-overlapping event\n while left <= right\n mid = left + (right - left) / 2\n if events[mid][0] > events[i][1]\n next_event_index = mid\n right = mid - 1\n else\n left = mid + 1\n end\n end\n\n # If a valid next event is found, update max_sum\n if next_event_index != -1\n max_sum = [max_sum, events[i][2] + suffix_max[next_event_index]].max\n end\n\n # Also consider the case where we take only the current event\n max_sum = [max_sum, events[i][2]].max\n end\n\n max_sum\nend\n```\n```javascript []\n/**\n * @param {number[][]} events\n * @return {number}\n */\nvar maxTwoEvents = function(events) {\n const n = events.length;\n \n // Step 1: Sort the events by their start time\n events.sort((a, b) => a[0] - b[0]);\n \n // Step 2: Create the suffix array for the maximum event value from each event onward\n let suffixMax = new Array(n);\n suffixMax[n - 1] = events[n - 1][2]; // Initialize the last event\'s value\n \n // Populate the suffixMax array\n for (let i = n - 2; i >= 0; i--) {\n suffixMax[i] = Math.max(events[i][2], suffixMax[i + 1]);\n }\n \n // Step 3: For each event, find the next event that starts after it ends\n let maxSum = 0;\n \n for (let i = 0; i < n; i++) {\n let left = i + 1, right = n - 1;\n let nextEventIndex = -1;\n \n // Perform binary search to find the next non-overlapping event\n while (left <= right) {\n let mid = Math.floor((left + right) / 2);\n if (events[mid][0] > events[i][1]) {\n nextEventIndex = mid;\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n \n // If a valid next event is found, update the max sum\n if (nextEventIndex !== -1) {\n maxSum = Math.max(maxSum, events[i][2] + suffixMax[nextEventIndex]);\n }\n \n // Also consider the case where we take only the current event\n maxSum = Math.max(maxSum, events[i][2]);\n }\n \n return maxSum;\n};\n```\n```Rust []\nimpl Solution {\n pub fn max_two_events(events: Vec<Vec<i32>>) -> i32 {\n let n = events.len();\n\n // Step 1: Sort the events by their start time\n let mut events = events;\n events.sort_by(|a, b| a[0].cmp(&b[0]));\n\n // Step 2: Create the suffix array for the maximum event value from each event onward\n let mut suffix_max = vec![0; n];\n suffix_max[n - 1] = events[n - 1][2]; // Initialize the last event\'s value\n \n // Populate the suffix_max array\n for i in (0..n - 1).rev() {\n suffix_max[i] = suffix_max[i + 1].max(events[i][2]);\n }\n\n // Step 3: For each event, find the next event that starts after it ends\n let mut max_sum = 0;\n\n for i in 0..n {\n let mut left = i + 1;\n let mut right = n - 1;\n let mut next_event_index = -1;\n\n // Perform binary search to find the next non-overlapping event\n while left <= right {\n let mid = left + (right - left) / 2;\n if events[mid][0] > events[i][1] {\n next_event_index = mid as i32;\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n\n // If a valid next event is found, update max_sum\n if next_event_index != -1 {\n let next_event_index = next_event_index as usize;\n max_sum = max_sum.max(events[i][2] + suffix_max[next_event_index]);\n }\n\n // Also consider the case where we take only the current event\n max_sum = max_sum.max(events[i][2]);\n }\n\n max_sum\n }\n}\n\n``` | 117 | 0 | ['Binary Search', 'C', 'Sorting', 'C++', 'Java', 'Python3', 'Rust', 'Ruby', 'JavaScript', 'C#'] | 22 |
two-best-non-overlapping-events | C++ || Recursion + Memoization || Easy Understanding | c-recursion-memoization-easy-understandi-sugz | \n// Basically my intuition is sort of similar like Knapsack picking.\n// We have two options : Pick Event or Don\'t Pick an event.\n// If we "Pick event", we\' | simp_coder | NORMAL | 2021-10-30T18:16:12.372473+00:00 | 2021-10-30T18:25:21.555093+00:00 | 5,612 | false | ```\n// Basically my intuition is sort of similar like Knapsack picking.\n// We have two options : Pick Event or Don\'t Pick an event.\n// If we "Pick event", we\'ll just add to our sum, then we\'ll find out an event whose starting time > ending time of the event that we picked and \n// we\'ll keep progressing like this until we hit 2. (as we can only pick at most two events)\n// If we "Don\'t Pick the event" we\'ll move on\n// And basically our maxvalue would be max outcome of ("Pick Event", "Don\'t Pick Event")\n\nclass Solution {\npublic:\n \n //Main Function\n int maxTwoEvents(vector<vector<int>>& events) {\n int n=events.size();\n vector<vector<int>>dp(n,vector<int>(2,-1));\n \n //Sorting because since we need to find an event that has starting time > ending time \n //of previous event selected, so applying binary search would help there.\n sort(events.begin(),events.end());\n \n return solve(events,0,0,dp);\n }\n \n //Helper function\n int solve(vector<vector<int>>&nums,int idx,int k,vector<vector<int>>&dp)\n {\n // Base case\n if(k==2)\n {\n return 0;\n }\n if(idx>=nums.size())\n {\n return 0;\n }\n \n // Memoization check\n if(dp[idx][k]!=-1)\n {\n return dp[idx][k];\n }\n \n //Basically ending times of the events\n vector<int>ans={nums[idx][1],INT_MAX,INT_MAX};\n \n //Searching the event whose starting time > ending time of previous event selected\n int nextindex=upper_bound(begin(nums),end(nums),ans)-begin(nums);\n \n //Pick event\n int include=nums[idx][2]+solve(nums,nextindex,k+1,dp);\n \n //Don\'t Pick event\n int exclude=solve(nums,idx+1,k,dp);\n \n return dp[idx][k]=max(include,exclude); //Max of(Pick, Not Pick)\n }\n};\n``` | 88 | 4 | ['Memoization', 'C', 'Binary Tree'] | 15 |
two-best-non-overlapping-events | C++ | with explanation | Concise | DP | c-with-explanation-concise-dp-by-aman282-tk2v | Idea:-\n1. Sort the events according to startTime and iterate from last.\n2. maxi will store maximum value from events whose startTime>= current event\'s startT | aman282571 | NORMAL | 2021-10-30T16:00:44.789961+00:00 | 2021-10-31T02:23:42.062437+00:00 | 8,730 | false | **Idea:-**\n1. Sort the events according to ```startTime``` and iterate from last.\n2. ```maxi``` will store maximum value from events whose ```startTime>= current event\'s startTime```.\n3. So when we are iterating over events we check the map to find an event whose ```startTime``` is greater than current event\'s endTime.\n4. Update the ```maxi and ans``` accordingly.\n\n**Similar problem:-** [Maximum Profit in Job Scheduling](https://leetcode.com/problems/maximum-profit-in-job-scheduling/)\n**Time Complexity :-** O(nlog(n)).\n```\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& e) {\n int size=e.size(),ans=0,maxi=0;\n sort(e.begin(),e.end());\n map<int,int>mp;\n while(size--){\n auto it=mp.upper_bound(e[size][1]);\n maxi=max(maxi,e[size][2]);\n mp[e[size][0]]=maxi;\n if(it==mp.end())\n ans=max(ans,maxi);\n else\n ans=max(ans,e[size][2]+it->second);\n }\n return ans;\n }\n};\n```\nDo **UPVOTE** if it helps :) | 81 | 3 | ['Dynamic Programming', 'C'] | 10 |
two-best-non-overlapping-events | Sort + Min Heap | sort-min-heap-by-votrubac-rilf | We sort events by the start date, and then go left to right. We also track end times and values in a min heap.\n\nWhen we process an event, we remove past event | votrubac | NORMAL | 2021-10-30T17:46:06.317240+00:00 | 2021-10-30T17:56:13.588938+00:00 | 6,609 | false | We sort events by the start date, and then go left to right. We also track end times and values in a min heap.\n\nWhen we process an event, we remove past events from the min heap, and track the `max_val` so far.\n\n**C++**\nPriority queue is a max heap by default; we can just store end times as negative instead of providing a custom comparator.\n\n```cpp\nint maxTwoEvents(vector<vector<int>>& events) {\n int res = 0, max_val = 0;\n priority_queue<pair<int, int>> pq;\n sort(begin(events), end(events));\n for (auto &e : events) {\n for(; !pq.empty() && -pq.top().first < e[0]; pq.pop())\n max_val = max(max_val, pq.top().second);\n res = max(res, max_val + e[2]);\n pq.push({-e[1], e[2]});\n }\n return res;\n}\n``` | 73 | 0 | ['C'] | 11 |
two-best-non-overlapping-events | Python: Actually simple with heap | python-actually-simple-with-heap-by-berg-50l0 | So, notice that if we sort events, then we always have the left bound increasing. Therefore, we can keep a heap of (right_bound, value) tuples from events that | bergjak | NORMAL | 2021-10-30T16:26:51.906560+00:00 | 2021-10-30T16:39:38.683659+00:00 | 2,285 | false | So, notice that if we sort events, then we always have the left bound increasing. Therefore, we can keep a heap of (right_bound, value) tuples from events that we have seen so far. Whenever the current left bound becomes larger than the right_bound on the stack, that means we can start poppping from the heap to look for the next possible interval pairing. We simply record the best value seen so far, and since every next event has a larger left, we can always pair with the values that have popped off the heap.\n\nPlease upvote if helpful!\n```\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n events.sort()\n res = 0\n best_value_to_the_left_of_all_intervals = 0\n intervals_seen_so_far = []\n for left, r, v in events:\n heappush(intervals_seen_so_far, (r, v))\n while intervals_seen_so_far and intervals_seen_so_far[0][0] < left:\n R, V = heappop(intervals_seen_so_far)\n best_value_to_the_left_of_all_intervals = max(best_value_to_the_left_of_all_intervals, V)\n res = max(res, best_value_to_the_left_of_all_intervals + v)\n return res | 38 | 1 | [] | 4 |
two-best-non-overlapping-events | Simple Java solution with explanation - Sort + Heap | simple-java-solution-with-explanation-so-19gr | This problem can be solved with the help of heap.\n\n- First sort all events by start time. If start time of two events are equal, sort them by end time.\n- The | divyagarg2601 | NORMAL | 2021-10-30T16:00:46.800283+00:00 | 2021-10-31T01:10:57.144542+00:00 | 2,499 | false | This problem can be solved with the help of `heap`.\n\n- First sort all events by start time. If start time of two events are equal, sort them by end time.\n- Then take a priority queue that takes an array containing `[endtime, value]`. Priority queue will sort elements on the basis of `end time`.\n- Iterate through events, for each event `e`, calculate maximum value from all events that ends before `e[0]` (i.e. start time). Let\'s store this value in `maxVal` variable.\n- Now answer will be `ans = max(ans, e[2] + maxVal)`.\n\n```java\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n int n = events.length;\n Arrays.sort(events, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);\n PriorityQueue<int[]> queue = new PriorityQueue<int[]>((a, b) -> a[0] - b[0]);\n \n int maxVal = 0, ans = 0;\n for(int[] e : events){ \n int start = e[0];\n while(!queue.isEmpty()){\n if(queue.peek()[0] >= start)\n break;\n int[] eve = queue.remove();\n maxVal = Math.max(maxVal, eve[1]);\n }\n ans = Math.max(ans, e[2] + maxVal);\n queue.add(new int[]{e[1], e[2]});\n }\n \n return ans;\n }\n}\n```\n\n**Note: If you have any doubt, please ask question, I\'ll be happpy to answer.\nIf you like solution, please upvote** | 37 | 0 | [] | 9 |
two-best-non-overlapping-events | Sort+ Greedy vs DP+binary Search||22ms beats 100% | sort-greedy-vs-dpbinary-search22ms-beats-hzql | Intuition\n Describe your first thoughts on how to solve this problem. \nThe events[i] has the info (start[i], end[i], value[i]). How to distinguish between sta | anwendeng | NORMAL | 2024-12-08T00:50:03.165912+00:00 | 2024-12-08T02:45:16.928130+00:00 | 6,378 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe events[i] has the info (start[i], end[i], value[i]). How to distinguish between `start` and `end` & to find a way keeping correct time ordering?\n\nConsider the info tuple `(time, isEnd, value)`; there are 2 tuples for 1 event. So build an array over the info tuples. Sort it then use Greedy.\n\nFor speed-up, the info tuple can packed into a 64-bit unsigned which is really fast, run in 22 ms beating 100%.\n\nA DP+binary search solution is also made using take or skip argument also applied for solving the hard question [1235. Maximum Profit in Job Scheduling](https://leetcode.com/problems/maximum-profit-in-job-scheduling/solutions/4514682/c-binary-search-dp-99-ms-beats-99-29/)\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Build up an array `time` of size `2*n`\n2. Use a loop to proceed from `i=1` to `n-1`: `s=events[i][0], e=events[i][1], v=events[i][2]`. let `time[2*i]={s, 0, v};\n time[2*i+1]={e, 1, v}`\n3. sort `time`\n4. Transverse the sorted `time`\n5. For each iteration, say `[t, isEnd, v]`, if `isEnd` which means it can take `v` for consideration & update `maxV=max(maxV, v)` otherwise update `ans=max(ans, maxV+v)`\n6. 2nd C++ is just packing of info tuple `(time, isEnd, value)` into an `uint64_t` which speeds up probably twice of the speed.\n7. A recursive DP(memo) with binary search is done which is slow as expected.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n\\log n)$$ \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ \n# Sort+Greedy Code using info tuple||49ms beats 91.89%\n```cpp []\nclass Solution {\npublic:\n using info=tuple<int, bool, int>;\n static int maxTwoEvents(vector<vector<int>>& events) {\n const int n=events.size();\n vector<info> time(n*2);\n for(int i=0; i<n; i++){\n int s=events[i][0], e=events[i][1], v=events[i][2];\n time[2*i]={s, 0, v};\n time[2*i+1]={e, 1, v};\n }\n sort(time.begin(), time.end());\n int ans=0, maxV=0, n2=n*2;\n for(auto& [t, isEnd, v]: time){\n if (isEnd) maxV=max(maxV, v);\n else ans=max(ans, maxV+v);\n }\n return ans; \n }\n};\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```\n# 2nd C++ using Packing info||22ms beats 100%\n```\nclass Solution {\npublic:\n// using info=tuple<int, bool, int>;\n static int maxTwoEvents(vector<vector<int>>& events) {\n const int n=events.size();\n vector<uint64_t> time(n*2);\n for(int i=0; i<n; i++){\n int s=events[i][0], e=events[i][1], v=events[i][2];\n time[2*i]=((uint64_t)s<<21)+v; // packing\n time[2*i+1]=((uint64_t)e<<21)+(1<<20)+v;//packing\n }\n sort(time.begin(), time.end());\n int ans=0, maxV=0, n2=n*2;\n for(auto info: time){\n bool isEnd=(info>>20)&1; //extract isEnd from info\n int v=info&((1<<20)-1); //extract v from info\n if (isEnd) maxV=max(maxV, v);\n else ans=max(ans, maxV+v);\n }\n return ans; \n }\n};\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```\n# Similar to 1235. Maximum Profit in Job Scheduling\nIn that hard question, DP+binary search is applied [ref](https://leetcode.com/problems/maximum-profit-in-job-scheduling/solutions/4514682/c-binary-search-dp-99-ms-beats-99-29/), a similar method is also doable for this medium question, but not fast.\n# C++ using sort+binary Search+DP||135ms Beats 43.24%\n```\nclass Solution {\npublic:\n int n;\n int dp[2][100000];// (i, j=index)\n vector<int> next;\n int f(int i, int j, vector<vector<int>>& events){\n if (i>=2 || j>=n) return 0;\n if (dp[i][j]!=-1) return dp[i][j];\n int v=events[j][2];\n int take=v+f(i+1, next[j], events);\n int skip=f(i, j+1, events);\n return dp[i][j]=max(take, skip);\n }\n int maxTwoEvents(vector<vector<int>>& events) {\n n=events.size();\n sort(events.begin(), events.end());\n next.resize(n);\n for(int j=0; j<n; j++)\n next[j]=upper_bound(events.begin()+j, events.end(), vector<int>{events[j][1], INT_MAX, INT_MAX})-events.begin();\n\n memset(dp, -1, sizeof(dp));\n return f(0, 0, events);\n }\n};\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n``` | 33 | 0 | ['Binary Search', 'Dynamic Programming', 'Greedy', 'Bit Manipulation', 'Sorting', 'C++'] | 13 |
two-best-non-overlapping-events | C++ | Sorting + Priority Queue | DP+ Binary Search | c-sorting-priority-queue-dp-binary-searc-r47t | Solution 1: Sorting + Priority Queue\n\nSteps:\n1. First sort the events on basis of their starting time .\n2. We will use priority queue to store events that h | priyal04 | NORMAL | 2021-11-30T08:30:06.916848+00:00 | 2021-11-30T10:53:27.615697+00:00 | 2,320 | false | ### Solution 1: Sorting + Priority Queue\n\n**Steps:**\n1. First sort the events on basis of their starting time .\n2. We will use priority queue to store events that have started before the current event.\n3. Elements in priority queue are of type vector {minus of endTime , startTime , value} (ordered by endTime i.e element that finishes first is at top).\n4. Instead of using min heap, I have stored minus of endTime.\n5. We will use a variable maxVal to store maximum value so far.\n\n```\nint maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(),events.end());\n int maxVal = 0;\n \n priority_queue<vector<int>> pq;\n int ans = 0;\n \n for(auto e : events){\n while(!pq.empty() and ((-pq.top()[0]) < e[0])){\n maxVal = max(maxVal , pq.top()[2]);\n pq.pop();\n }\n ans = max(ans , e[2]+maxVal);\n pq.push({(-e[1]) , e[0] , e[2]});\n }\n return ans;\n }\n```\n\nTime Complexity : O(nlogn), as each element will be pushed and poped only once in priority queue.\nSpace Complexity: O(n)\n\n### Solution 2: Recursion + Binary Search\nWe have 2 choices : Either attend a particular event or don\'t attend.\n```\nclass Solution {\n int func(int ind , int eventsAttended , vector<vector<int>>& events){\n //base case\n if(ind == events.size() || eventsAttended == 2){\n return 0;\n }\n \n //Choice 1 : attend this event\n vector<int> tempVec = {events[ind][1] , INT_MAX , INT_MAX};\n int nextInd = upper_bound(events.begin() , events.end() , tempVec) - events.begin(); //find index of next event whose start time is greater than ending time of current event\n int val1 = events[ind][2] + func(nextInd , eventsAttended+1 , events);\n \n //Choice 2: don\'t attend\n int val2 = func(ind+1 , eventsAttended , events);\n \n return max(val1 , val2);\n }\n \npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin() , events.end());\n \n return func(0,0,events);\n }\n};\n```\n\nThis solution will lead to TLE.\n\n### Solution 3: Recursion + Memoization\n\n```\nclass Solution {\n int func(int ind , int eventsAttended , vector<vector<int>>& events , vector<vector<int>>& dp){\n //base case\n if(ind == events.size() || eventsAttended == 2){\n return 0;\n }\n \n if(dp[ind][eventsAttended] != -1)\n return dp[ind][eventsAttended];\n \n //Choice 1 : attend this event\n vector<int> tempVec = {events[ind][1] , INT_MAX , INT_MAX};\n int nextInd = upper_bound(events.begin() , events.end() , tempVec) - events.begin();\n int val1 = events[ind][2] + func(nextInd , eventsAttended+1 , events,dp);\n \n //Choice 2: don\'t attend\n int val2 = func(ind+1 , eventsAttended , events,dp);\n \n return dp[ind][eventsAttended] = max(val1 , val2);\n }\n \npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin() , events.end());\n int n = events.size();\n \n vector<vector<int>> dp(n , vector<int>(2 , -1));\n return func(0,0,events,dp);\n }\n};\n```\n\n***Do Upvote if you find the solution helpful!*** | 27 | 3 | ['Dynamic Programming', 'C', 'Sorting', 'Heap (Priority Queue)', 'Binary Tree'] | 4 |
two-best-non-overlapping-events | Java Sorting (10 liner) | java-sorting-10-liner-by-vikrant_pc-6xz5 | \npublic int maxTwoEvents(int[][] events) {\n\tint result = 0, maxOfCompletedEvents = 0;\n\tArrays.sort(events, (x,y)->x[0]-y[0]); // Sort by Start time\n\tPr | vikrant_pc | NORMAL | 2021-10-30T16:00:47.604661+00:00 | 2021-10-30T17:48:10.820709+00:00 | 1,734 | false | ```\npublic int maxTwoEvents(int[][] events) {\n\tint result = 0, maxOfCompletedEvents = 0;\n\tArrays.sort(events, (x,y)->x[0]-y[0]); // Sort by Start time\n\tPriorityQueue<int[]> inProgressQueue = new PriorityQueue<>((x,y)->x[1]-y[1]); // sorted by end time\n\tfor(int[] currentEvent : events) {\n\t\twhile(!inProgressQueue.isEmpty() && inProgressQueue.peek()[1] < currentEvent[0])\n\t\t\tmaxOfCompletedEvents = Math.max(maxOfCompletedEvents, inProgressQueue.poll()[2]);\n\t\tresult = Math.max(result, maxOfCompletedEvents + currentEvent[2]);\n\t\tinProgressQueue.offer(currentEvent);\n\t}\n\treturn result;\n}\n``` | 21 | 3 | [] | 4 |
two-best-non-overlapping-events | Simple Solution with Priority Queue | ✅Beats 100% | C++ | Java | Python | JavaScript | simple-solution-with-priority-queue-beat-a2b9 | \n\n# \u2B06\uFE0FUpvote if it helps \u2B06\uFE0F \n\n---\n\n## Connect with me on Linkedin Bijoy Sing. \n\n---\n\n\n## Follow me also on Codeforces: Bijoy Si | BijoySingh7 | NORMAL | 2024-12-08T05:28:07.941455+00:00 | 2024-12-08T17:39:47.146358+00:00 | 4,173 | false | \n\n# \u2B06\uFE0FUpvote if it helps \u2B06\uFE0F \n\n---\n\n## Connect with me on Linkedin [Bijoy Sing](https://www.linkedin.com/in/bijoy-sing-236a5a1b2/). \n\n---\n\n\n## Follow me also on Codeforces: [Bijoy Sing](https://codeforces.com/profile/BijoySingh7) \n\n---\n\n\n###### *Solution in C++, Python, Java, and JavaScript* \n\n```cpp []\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(), events.end());\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;\n int maxVal = 0, ans = 0;\n\n for (const auto& event : events) {\n int start = event[0], end = event[1], value = event[2];\n\n while (!pq.empty() && pq.top().first < start) {\n maxVal = max(maxVal, pq.top().second);\n pq.pop();\n }\n\n ans = max(ans, maxVal + value);\n pq.push({end, value});\n }\n\n return ans;\n }\n};\n```\n\n```python []\nimport heapq\n\nclass Solution:\n def maxTwoEvents(self, events):\n events.sort()\n pq = []\n max_val = 0\n ans = 0\n\n for start, end, value in events:\n while pq and pq[0][0] < start:\n max_val = max(max_val, heapq.heappop(pq)[1])\n ans = max(ans, max_val + value)\n heapq.heappush(pq, (end, value))\n\n return ans\n```\n\n```java []\nimport java.util.*;\n\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n Arrays.sort(events, (a, b) -> Integer.compare(a[0], b[0]));\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));\n int maxVal = 0, ans = 0;\n\n for (int[] event : events) {\n int start = event[0], end = event[1], value = event[2];\n\n while (!pq.isEmpty() && pq.peek()[0] < start) {\n maxVal = Math.max(maxVal, pq.poll()[1]);\n }\n\n ans = Math.max(ans, maxVal + value);\n pq.add(new int[]{end, value});\n }\n\n return ans;\n }\n}\n```\n\n```javascript []\n/**\n * @param {number[][]} events\n * @return {number}\n */\nvar maxTwoEvents = function(events) {\n events.sort((a, b) => a[0] - b[0]);\n const n = events.length;\n const prefixMax = new Array(n).fill(0);\n \n prefixMax[n - 1] = events[n - 1][2];\n for (let i = n - 2; i >= 0; i--) {\n prefixMax[i] = Math.max(prefixMax[i + 1], events[i][2]);\n }\n \n let maxResult = 0;\n \n for (let i = 0; i < n; i++) {\n const currValue = events[i][2];\n const currEnd = events[i][1];\n \n let left = i + 1, right = n - 1;\n let maxNextValue = 0;\n \n while (left <= right) {\n const mid = Math.floor((left + right) / 2);\n if (events[mid][0] > currEnd) {\n maxNextValue = Math.max(maxNextValue, prefixMax[mid]);\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n \n maxResult = Math.max(maxResult, currValue + maxNextValue);\n }\n \n return maxResult;\n};\n```\n\n# Intuition \nTo solve the problem, we need to find two non-overlapping events that maximize the total value. Sorting the events by start time helps us efficiently determine which events can be paired. \n\n# Approach \n1. Sort the events based on their start time. \n2. Use a priority queue to keep track of events that end before the current event starts. \n3. Track the maximum value of completed events (`maxVal`) to calculate the best combination with the current event. \n4. Update the global maximum (`ans`) and continue processing. \n\n# Complexity \n- Time complexity: \n $$O(n \\log n)$$ (due to sorting and priority queue operations). \n\n- Space complexity: \n $$O(n)$$ (to store events in the priority queue). \n\n### *If you have any questions or need further clarification, feel free to drop a comment! \uD83D\uDE0A* | 20 | 0 | ['Array', 'Binary Search', 'Dynamic Programming', 'Sorting', 'Heap (Priority Queue)', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 9 |
two-best-non-overlapping-events | Python | Greedy & Binary Search | python-greedy-binary-search-by-khosiyat-8zru | see the Successfully Accepted Submission\n\n# Code\npython3 []\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n # Step 1: | Khosiyat | NORMAL | 2024-12-08T03:13:44.919449+00:00 | 2024-12-08T03:13:44.919470+00:00 | 2,341 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/two-best-non-overlapping-events/submissions/1473126424/?envType=daily-question&envId=2024-12-08)\n\n# Code\n```python3 []\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n # Step 1: Sort the events based on their end time\n events.sort(key=lambda x: x[1])\n \n # Step 2: Maintain a list of [endTime, max_value_until_now]\n max_until = []\n max_value = 0\n for _, end, value in events:\n max_value = max(max_value, value)\n max_until.append((end, max_value))\n \n # Step 3: Find the maximum sum of two events\n result = 0\n for start, end, value in events:\n # Option 1: Take the current event alone\n result = max(result, value)\n \n # Option 2: Take another event that ends before this one starts\n idx = bisect.bisect_left(max_until, (start, 0)) - 1\n if idx >= 0:\n result = max(result, value + max_until[idx][1])\n \n return result\n\n```\n\n# Explanation \n\n## Sorting the Events:\n- The events are sorted by their end times to facilitate the lookup of non-overlapping events.\n\n## Precomputing Maximum Values:\n- We maintain a list `max_until` where each entry `(endTime, max_value_until_now)` represents the maximum value achievable by any event ending on or before that time.\n- This is updated iteratively as we traverse the sorted events.\n\n## Binary Search:\n- For each event, we use binary search (`bisect_left`) to find the last event in `max_until` that ends before the current event\'s start time.\n- This ensures that the selected events are non-overlapping.\n\n## Result Calculation:\n- The result is updated with the maximum of:\n 1. The value of the current event alone.\n 2. The sum of the current event and the maximum value of a non-overlapping event.\n\n## Complexity:\n### Time Complexity:\n- **Sorting the events**: \\(O(n \\log n)\\)\n- **For each event, a binary search**: \\(O(n \\log n)\\)\n- **Overall**: \\(O(n \\log n)\\)\n\n### Space Complexity:\n- \\(O(n)\\) due to the `max_until` list.\n\n\n | 20 | 1 | ['Python3'] | 4 |
two-best-non-overlapping-events | Multiple Approaches | Heap Based || DP + Binary Search || C++ Clean Code | multiple-approaches-heap-based-dp-binary-u7og | Approach 1: Sorting + Priority Queue\n\nThis approach is best suited when we have just "at most 2" events to attend.\n\n# Code : \n\n\nint maxTwoEvents(vector<v | i_quasar | NORMAL | 2021-11-18T02:19:19.489263+00:00 | 2021-11-19T16:59:53.429100+00:00 | 1,184 | false | **Approach 1: Sorting + Priority Queue**\n\nThis approach is best suited when we have just **"at most 2"** events to attend.\n\n# Code : \n\n```\nint maxTwoEvents(vector<vector<int>>& events) {\n \n\tint n = events.size();\n\n\tpriority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq; // <endTime, value>\n\n\tsort(events.begin(), events.end());\n\n\tint maxVal = 0, maxSum = 0;\n\n\tfor(auto& event : events) {\n\t\twhile(pq.size() && pq.top().first < event[0]) {\n\t\t\tmaxVal = max(maxVal, pq.top().second);\n\t\t\tpq.pop();\n\t\t}\n\n\t\tmaxSum = max(maxSum, maxVal + event[2]);\n\n\t\tpq.push({event[1], event[2]});\n\t}\n\n\treturn maxSum;\n}\n```\n\n**Complexity:**\n\n* **Time** : `O(N log N + 2N)` ,\n\t* `N log N` : Sorting and Priority Queue\n\t* `2N` : Since we are poping events from heap to process, so each events is processed twice.\n\t\n* **Space** : `O(N)`, storing events into heap\n\n----------------------------------------------------------------------------------------------------------------------------\n\n**Follow Up Question** : How will you solve this problem when you can attend **at most K** events? \n\nWe cannot use previous approach if we have K events to attend. So how we will solve this? \nLets look at another approach !!\n\n----------------------------------------------------------------------------------------------------------------------------\n\n**Approach 2: DP(Memoization) + Binary Search**\n\n\n# Code: \n\n```\nclass Solution {\npublic:\n \n int getNextIndex(vector<vector<int>>& events, int idx, const int& n) {\n \n int endTime = events[idx][1];\n \n int lo = idx+1, hi = n-1;\n \n int ans = n;\n \n while(lo <= hi) {\n int mid = (lo + hi) >> 1;\n \n if(events[mid][0] > endTime) {\n ans = mid;\n hi = mid-1;\n }\n else {\n lo = mid+1;\n }\n }\n \n return ans;\n }\n \n int attendEvents(vector<vector<int>>& events, vector<vector<int>>& dp, int idx, int k, const int& n) {\n if(k == 0 || idx == n) return 0;\n \n if(dp[idx][k] != -1) return dp[idx][k];\n \n // Include : attend current event\n int nextIdx = getNextIndex(events, idx, n); \n\n int incl = events[idx][2] + attendEvents(events, dp, nextIdx, k-1, n);\n \n // Exclude : skip current event\n int excl = attendEvents(events, dp, idx+1, k, n);\n \n return dp[idx][k] = max(incl, excl);\n }\n \n int maxTwoEvents(vector<vector<int>>& events) {\n \n int n = events.size(), k = 2;\n sort(events.begin(), events.end());\n \n \n vector<vector<int>> dp(n+1, vector<int>(k+1, -1));\n \n return attendEvents(events, dp, 0, k, n);\n }\n};\n```\n**Complexity:**\n\n* **Time** : `O(N log N)` , sorting , attending events and searching for next nearest event\n* **Space** : `O(N * k)`, for memoization \n\n\n----------------------------------------------------------------------------------------------------------------------------\n\n**Similar Problems :**\n\n* [Maximum Earnings from Taxi](https://leetcode.com/problems/maximum-earnings-from-taxi/)\n* [Maximum Profit Job Scheduling](https://leetcode.com/problems/maximum-profit-in-job-scheduling/)\n\n***If you find this post helpful, do give it a like :)*** | 19 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'Heap (Priority Queue)', 'Binary Tree'] | 1 |
two-best-non-overlapping-events | JAVA || Sorting || PriorityQueue || O(NlogN) | java-sorting-priorityqueue-onlogn-by-chi-b9sb | This problem can be solved with the help of Sorting and Heap - \n\nFirst sort all events by start time. If start time of two events are equal, sort them by end | chirag_103 | NORMAL | 2022-05-11T07:48:37.261695+00:00 | 2022-05-11T07:48:37.261735+00:00 | 1,637 | false | This problem can be solved with the help of Sorting and Heap - \n\nFirst sort all events by start time. If start time of two events are equal, sort them by end time.\nThen take a priority queue that takes an array containing [endtime, value]. Priority queue will sort elements on the basis of end time.\nIterate through events, for each event, calculate maximum value from all events that ends before current events start time and store this value in max variable.\n\n```\nclass Solution {\n public int maxTwoEvents(int[][] events) \n {\n Arrays.sort(events , (a,b)-> a[0]!=b[0]?a[0]-b[0]:a[1]-b[1]);\n PriorityQueue<int []> pq = new PriorityQueue<>((a,b)->a[0]-b[0]);\n \n int max = 0 , ans = 0;\n pq.add(new int[]{events[0][1] , events[0][2]});\n \n for(int i=1 ; i<events.length ; i++)\n {\n while(!pq.isEmpty() && pq.peek()[0]<events[i][0])\n {\n int a[] = pq.poll();\n max = Math.max(max , a[1]);\n }\n ans = Math.max(ans , max + events[i][2]);\n pq.add(new int[]{events[i][1] , events[i][2]});\n }\n while(!pq.isEmpty())\n {\n ans = Math.max(ans , pq.poll()[1]);\n }\n \n return ans;\n }\n}\n```\n**Do Upvote if u like the solution!** | 18 | 1 | ['Sorting', 'Heap (Priority Queue)', 'Java'] | 1 |
two-best-non-overlapping-events | [Python3] binary search | python3-binary-search-by-ye15-eran | \n\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n time = []\n vals = []\n ans = prefix = 0\n for st | ye15 | NORMAL | 2021-10-30T16:13:23.853976+00:00 | 2021-11-04T03:39:53.417061+00:00 | 1,954 | false | \n```\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n time = []\n vals = []\n ans = prefix = 0\n for st, et, val in sorted(events, key=lambda x: x[1]): \n prefix = max(prefix, val)\n k = bisect_left(time, st)-1\n if k >= 0: val += vals[k]\n ans = max(ans, val)\n time.append(et)\n vals.append(prefix)\n return ans \n```\n\n```\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n ans = most = 0 \n pq = []\n for st, et, val in sorted(events): \n heappush(pq, (et, val))\n while pq and pq[0][0] < st: \n _, vv = heappop(pq)\n most = max(most, vv)\n ans = max(ans, most + val)\n return ans \n``` | 18 | 0 | ['Python3'] | 1 |
two-best-non-overlapping-events | 📌📌 Heap || very-Easy || Well-Explained 🐍 | heap-very-easy-well-explained-by-abhi9ra-hh78 | IDEA:\nThis question is same as https://leetcode.com/problems/maximum-profit-in-job-scheduling/ .\n\n In this we have to consider atmost two events. So we will | abhi9Rai | NORMAL | 2021-10-30T17:43:20.332694+00:00 | 2021-10-30T17:43:20.332733+00:00 | 1,519 | false | ## IDEA:\n**This question is same as https://leetcode.com/problems/maximum-profit-in-job-scheduling/ .**\n\n* In this we have to consider atmost two events. So we will only put the cureent profit in heap.\n\n* Maintain one variable res1 for storing the maximum value among all the events ending before the current event gets start.\n* Another variable res2 store the maximum profit according the given condition.\n\n\'\'\'\n\n\tclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n \n events.sort()\n heap = []\n res2,res1 = 0,0\n for s,e,p in events:\n while heap and heap[0][0]<s:\n res1 = max(res1,heapq.heappop(heap)[1])\n \n res2 = max(res2,res1+p)\n heapq.heappush(heap,(e,p))\n \n return res2\n\n### Thanks and Upvote If you like the Idea !!\uD83E\uDD1E | 17 | 2 | ['Heap (Priority Queue)', 'Python', 'Python3'] | 2 |
two-best-non-overlapping-events | Understanding the pattern | Java Solution | Recursion + Memoization | understanding-the-pattern-java-solution-ezq90 | I wanted to solve binary search + dp problems and was looking for similar patterns.\nAfter few hours of grilling and understanding patterns between \nhttps://l | shadowpint | NORMAL | 2022-08-24T22:50:23.614252+00:00 | 2022-08-24T22:50:23.614291+00:00 | 871 | false | I wanted to solve binary search + dp problems and was looking for similar patterns.\nAfter few hours of grilling and understanding patterns between \nhttps://leetcode.com/problems/maximum-number-of-events-that-can-be-attended-ii/\nhttps://leetcode.com/problems/two-best-non-overlapping-events/\nhttps://leetcode.com/problems/maximum-profit-in-job-scheduling/\nWill add more problems to this template\n\nI came up with following template -\nSolution for https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended-ii/\n```\nclass Solution {\n public int maxValue(int[][] events, int k) {\n //here k is optional maximum capacity of like knapsack \n int n=events.length;\n \n Arrays.sort(events, (a, b) -> Integer.compare(a[0], b[0]) );\n Integer[][] dp=new Integer[n][k];\n return dfs(events,0,0,n,k,dp);\n }\n \n public int dfs(int[][] events, int idx,int choose, int n,int k,Integer[][] dp){\n if(idx>=n)return 0;\n if(choose>=k)return 0;\n if(dp[idx][choose]!=null)return dp[idx][choose];\n int nextIdx=findNext(events, idx,n);\n int pick=events[idx][2]+dfs(events, nextIdx,choose+1, n,k,dp);\n int notPick=dfs(events, idx+1,choose, n,k,dp);\n return dp[idx][choose]= Math.max(pick,notPick);\n }\n public int findNext(int[][] events, int idx, int n){\n int ans=n;\n int l=idx+1;\n int r=n-1;\n while(l<=r){\n int mid=l+(r-l)/2;\n if(events[idx][1]<events[mid][0]){\n ans=mid;\n r=mid-1;\n }else {\n l=mid+1;\n }\n }\n return ans;\n }\n}\n```\n\nFor https://leetcode.com/problems/two-best-non-overlapping-events/ k=2\n\n```\n int n=events.length;\n \n Arrays.sort(events, (a, b) -> Integer.compare(a[0], b[0]) );\n Integer[][] dp=new Integer[n][k];\n return dfs(events,0,0,n,k,dp);\n }\n \n public int dfs(int[][] events, int idx,int choose, int n,int k,Integer[][] dp){\n if(idx>=n)return 0;\n if(choose>=k)return 0;\n if(dp[idx][choose]!=null)return dp[idx][choose];\n int nextIdx=findNext(events, idx,n);\n int pick=events[idx][2]+dfs(events, nextIdx,choose+1, n,k,dp);\n int notPick=dfs(events, idx+1,choose, n,k,dp);\n return dp[idx][choose]= Math.max(pick,notPick);\n }\n public int findNext(int[][] events, int idx, int n){\n int ans=n;\n int l=idx+1;\n int r=n-1;\n while(l<=r){\n int mid=l+(r-l)/2;\n if(events[idx][1]<events[mid][0]){\n ans=mid;\n r=mid-1;\n }else {\n l=mid+1;\n }\n }\n return ans;\n }\n}\n```\n\nThere may be condition when no k boundation is required for example in question https://leetcode.com/problems/maximum-profit-in-job-scheduling/\n\n```\nclass Solution {\n public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {\n int n=startTime.length;\n int[][] events=new int[n][3];\n for(int i=0;i<n;i++){\n events[i][0]=startTime[i];\n events[i][1]=endTime[i];\n events[i][2]=profit[i];\n }\n Arrays.sort(events,(a,b)->Integer.compare(a[0], b[0]));\n Integer[] dp=new Integer[n];\n return dfs(events,0,n,dp);\n }\n \n public int dfs(int[][] events, int idx, int n,Integer[] dp){\n if(idx==n)return 0;\n if(dp[idx]!=null)return dp[idx];\n int nextIdx=findNext(events, idx,n);\n int pick=events[idx][2]+dfs(events, nextIdx, n,dp);\n int notPick=dfs(events, idx+1, n,dp);\n return dp[idx]= Math.max(pick,notPick);\n }\n public int findNext(int[][] events, int idx, int n){\n int ans=n;\n int l=idx+1;\n int r=n-1;\n while(l<=r){\n int mid=(l+r)>>1;\n if(events[idx][1]<=events[mid][0]){\n ans=mid;\n r=mid-1;\n }else {\n l=mid+1;\n }\n }\n return ans;\n }\n}\n``` | 12 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Binary Tree', 'Java'] | 1 |
two-best-non-overlapping-events | C++ || O(NlogN) || DP + Binary Search || Priority Queue || Sorting | c-onlogn-dp-binary-search-priority-queue-pcdm | Connect with me on LinkedIn: https://www.linkedin.com/in/abhay5349singh/\n\nApproach:\n\n1.Sorting array on basis of start time to have sequential acces to all | abhay5349singh | NORMAL | 2021-10-30T16:04:42.683614+00:00 | 2024-04-02T04:05:42.252109+00:00 | 1,451 | false | **Connect with me on LinkedIn**: https://www.linkedin.com/in/abhay5349singh/\n\n**Approach:**\n\n1.Sorting array on basis of start time to have sequential acces to all events.\n2.Each event can be attended in 2 ways: `single` or `pair-up with max profitable non conflicting event`\n\n```\nclass Solution {\npublic:\n \n int nextNonConflictingEvent(vector<vector<int>>& events, int l, int r, int end){\n while(l<r){\n int m = l+(r-l)/2;\n \n if(events[m][0] > end){\n r=m;\n }else{\n l=m+1;\n }\n }\n \n return (events[l][0] > end ? l:-1);\n }\n \n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(), events.end());\n \n int n=events.size();\n vector<int> single(n,0), pair(n,0);\n single[n-1] = pair[n-1] = events[n-1][2];\n \n int ans = events[n-1][2];\n \n for(int i=n-2;i>=0;i--){\n // max profit from 1 event from [i,n-1]\n single[i] = max(events[i][2], single[i+1]);\n \n // max profit from current + most proftable event from [idx,n-1]\n int idx = nextNonConflictingEvent(events, i+1, n-1, events[i][1]);\n pair[i] = events[i][2] + (idx != -1 ? single[idx]:0);\n \n ans = max(ans, max(single[i], pair[i]));\n }\n \n return ans;\n }\n};\n```\n\n**Approach:**\n\n1.Sorting array on basis of start time to have sequential acces to all events.\n2.Keeping track of max value which can be obtained from valid events w.r.t current event\n\n```\nclass Solution {\npublic:\n \n struct node{\n int value;\n int end;\n };\n \n struct pqCompare{\n bool operator()(const node &a, const node &b){\n if(a.end == b.end) return a.value < b.value; // max heap\n return a.end > b.end; // min heap\n }\n };\n \n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(), events.end());\n \n int n=events.size();\n priority_queue<node, vector<node>, pqCompare> pq;\n \n int ans=0;\n int maxPrevValFromValidEvent=0;\n \n for(int i=0;i<n;i++){\n while(pq.size()>0 && pq.top().end < events[i][0]){\n maxPrevValFromValidEvent = max(maxPrevValFromValidEvent, pq.top().value);\n pq.pop();\n }\n \n ans = max(ans, events[i][2]+maxPrevValFromValidEvent);\n pq.push({events[i][2], events[i][1]});\n }\n \n return ans;\n }\n};\n```\n\n**Do upvote if it helps :)** | 12 | 0 | ['Dynamic Programming', 'Sorting', 'Binary Tree', 'C++'] | 4 |
two-best-non-overlapping-events | Simple Java Solution - With Comments (Left Max + Right Max) | simple-java-solution-with-comments-left-030zo | \nclass Solution {\n public int maxTwoEvents(int[][] events) {\n // for any timestamp - find max of values to left and max of values to right\n\n | pavankumarchaitanya | NORMAL | 2021-10-30T16:02:24.776290+00:00 | 2021-10-30T16:02:39.145186+00:00 | 1,009 | false | ```\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n // for any timestamp - find max of values to left and max of values to right\n\n Arrays.sort(events, (a,b)->a[1]-b[1]);// Sort by end time - to know what events happened previously\n TreeMap<Integer, Integer> maxSeenMapOnLeft = new TreeMap<>();\n int result = 0;\n int maxSeenValue = 0;\n for(int[] event: events){\n int eventVal = event[2];\n if(eventVal>=maxSeenValue){\n maxSeenValue= eventVal;\n maxSeenMapOnLeft.put(event[1],maxSeenValue); // save max value event seen so far at end timestamp\n }\n }\n \n Arrays.sort(events, (a,b)->b[0]-a[0]);// Sort by start time but in descending order - as we parse events and store max value of future events to current event start timestamp\n int maxSeenRight = 0;\n for(int[] event: events){\n int eventVal = event[2];\n if(eventVal>=maxSeenRight){\n maxSeenRight= eventVal;\n Integer maxOnLeftKey = (maxSeenMapOnLeft.floorKey(event[0]-1));//skip one timestamp unit as start and end can\'t be same\n if(maxOnLeftKey!=null){\n result = Math.max(result, maxSeenMapOnLeft.get(maxOnLeftKey) + maxSeenRight);\n }\n }\n }\n return Math.max(maxSeenValue,result);\n }\n}\n``` | 12 | 4 | [] | 2 |
two-best-non-overlapping-events | 🔥BEATS 💯 % 🎯 |✨SUPER EASY BEGINNERS 👏 | beats-super-easy-beginners-by-codewithsp-j06r | \n\n## MOST IMP POINT\n### At most two non-overlapping \n\n\n\n\n\n\n---\nHere\u2019s the detailed breakdown of the problem-solving process for maximizing the | CodeWithSparsh | NORMAL | 2024-12-08T09:12:06.753205+00:00 | 2024-12-08T12:44:35.147931+00:00 | 1,043 | false | \n\n## MOST IMP POINT\n### At most two non-overlapping \n\n\n\n\n\n\n---\nHere\u2019s the detailed breakdown of the problem-solving process for maximizing the sum of values of at most two non-overlapping events:\n\n---\n\n# Intuition\nThe goal is to select up to two non-overlapping events such that their combined value is maximized. \n- To efficiently check overlapping conditions, **sorting the events by end time** is beneficial. \n- A **binary search** can be used to quickly find the latest event that does not overlap with the current one. \n- We use a **running maximum array** to keep track of the maximum value from earlier events, ensuring efficient calculation of the maximum sum.\n\n---\n\n# Approach\n### Step 1: Sort Events by End Time\n- Sorting events by their end times helps in managing overlapping efficiently. This way, for each event, we only need to look at earlier events for potential inclusion.\n\n### Step 2: Create a Running Maximum Array\n- A `maxValues` array is used to store the maximum value among all events up to the current event (non-overlapping logic considered via binary search).\n- This allows efficient calculation of the sum for a given pair of events.\n\n### Step 3: Iterate Through Events\n- For each event:\n - Use binary search to find the latest event that ends before the current event starts.\n - Add its value (if it exists) to the current event\'s value.\n - Update the global maximum sum if the resulting sum is larger than the previous maximum.\n\n### Step 4: Binary Search for Non-Overlapping Events\n- The binary search is used to find the index of the latest event that ends before the current event starts. This ensures no overlap between the selected events.\n\n---\n\n# Complexity\n- **Time Complexity:** \n - Sorting: $$O(n \\log n)$$ \n - Binary Search for each event: $$O(n \\log n)$$ \n - Total: $$O(n \\log n)$$.\n\n- **Space Complexity:** \n - Running max array: $$O(n)$$ \n - Total: $$O(n)$$.\n\n---\n\n\n```dart []\nimport \'dart:math\';\n\nclass Solution {\n int maxTwoEvents(List<List<int>> events) {\n // Step 1: Sort events by their end times\n events.sort((a, b) => a[1].compareTo(b[1]));\n\n // Step 2: Create a running max array\n int n = events.length;\n List<int> maxValues = List.filled(n, 0);\n maxValues[0] = events[0][2]; // Value of the first event\n\n // Fill the running max array\n for (int i = 1; i < n; i++) {\n maxValues[i] = max(maxValues[i - 1], events[i][2]);\n }\n\n int maxSum = 0;\n\n // Step 3: Iterate through the events and use binary search\n for (int i = 0; i < n; i++) {\n int start = events[i][0];\n int value = events[i][2];\n\n // Find the latest event that ends before the current event starts\n int idx = binarySearch(events, start - 1);\n\n // If a valid previous event is found, calculate the sum\n int currentSum = value;\n if (idx != -1) currentSum += maxValues[idx];\n\n // Update the global maximum sum\n maxSum = max(maxSum, currentSum);\n }\n\n return maxSum;\n }\n\n // Helper: Binary search to find the latest event that ends <= targetEnd\n int binarySearch(List<List<int>> events, int targetEnd) {\n int start = 0, end = events.length - 1, res = -1;\n\n while (start <= end) {\n int mid = start + (end - start) ~/ 2;\n if (events[mid][1] <= targetEnd) {\n res = mid; // Found a valid event\n start = mid + 1; // Try to find a later one\n } else {\n end = mid - 1;\n }\n }\n\n return res;\n }\n}\n```\n\n\n```python []\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n # Step 1: Sort events by their end times\n events.sort(key=lambda x: x[1])\n\n # Step 2: Create a running max array\n n = len(events)\n maxValues = [0] * n\n maxValues[0] = events[0][2]\n\n for i in range(1, n):\n maxValues[i] = max(maxValues[i - 1], events[i][2])\n\n maxSum = 0\n\n # Step 3: Iterate through the events and use binary search\n for i in range(n):\n start, value = events[i][0], events[i][2]\n idx = self.binarySearch(events, start - 1)\n\n currentSum = value\n if idx != -1:\n currentSum += maxValues[idx]\n\n maxSum = max(maxSum, currentSum)\n\n return maxSum\n\n def binarySearch(self, events, targetEnd):\n start, end = 0, len(events) - 1\n res = -1\n\n while start <= end:\n mid = start + (end - start) // 2\n if events[mid][1] <= targetEnd:\n res = mid\n start = mid + 1\n else:\n end = mid - 1\n\n return res\n```\n\n\n```cpp []\n#include <vector>\n#include <algorithm>\nusing namespace std;\n\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(), events.end(), [](vector<int>& a, vector<int>& b) {\n return a[1] < b[1];\n });\n\n int n = events.size();\n vector<int> maxValues(n);\n maxValues[0] = events[0][2];\n\n for (int i = 1; i < n; ++i) {\n maxValues[i] = max(maxValues[i - 1], events[i][2]);\n }\n\n int maxSum = 0;\n\n for (int i = 0; i < n; ++i) {\n int start = events[i][0];\n int value = events[i][2];\n int idx = binarySearch(events, start - 1);\n\n int currentSum = value;\n if (idx != -1) {\n currentSum += maxValues[idx];\n }\n\n maxSum = max(maxSum, currentSum);\n }\n\n return maxSum;\n }\n\nprivate:\n int binarySearch(vector<vector<int>>& events, int targetEnd) {\n int start = 0, end = events.size() - 1, res = -1;\n\n while (start <= end) {\n int mid = start + (end - start) / 2;\n if (events[mid][1] <= targetEnd) {\n res = mid;\n start = mid + 1;\n } else {\n end = mid - 1;\n }\n }\n\n return res;\n }\n};\n```\n\n\n```javascript []\nvar maxTwoEvents = function(events) {\n // Step 1: Sort events by their end times\n events.sort((a, b) => a[1] - b[1]);\n\n let n = events.length;\n let maxValues = new Array(n).fill(0);\n maxValues[0] = events[0][2]; // Value of the first event\n\n // Fill the running max array\n for (let i = 1; i < n; i++) {\n maxValues[i] = Math.max(maxValues[i - 1], events[i][2]);\n }\n\n let maxSum = 0;\n\n // Step 3: Iterate through the events and use binary search\n for (let i = 0; i < n; i++) {\n let start = events[i][0];\n let value = events[i][2];\n\n // Find the latest event that ends before the current event starts\n let idx = binarySearch(events, start - 1);\n\n let currentSum = value;\n if (idx !== -1) currentSum += maxValues[idx];\n\n maxSum = Math.max(maxSum, currentSum);\n }\n\n return maxSum;\n};\n\n// Helper: Binary search to find the latest event that ends <= targetEnd\nfunction binarySearch(events, targetEnd) {\n let start = 0, end = events.length - 1, res = -1;\n\n while (start <= end) {\n let mid = Math.floor(start + (end - start) / 2);\n if (events[mid][1] <= targetEnd) {\n res = mid;\n start = mid + 1;\n } else {\n end = mid - 1;\n }\n }\n\n return res;\n}\n```\n\n\n```java []\nimport java.util.*;\n\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n // Step 1: Sort events by their end times\n Arrays.sort(events, (a, b) -> Integer.compare(a[1], b[1]));\n\n int n = events.length;\n int[] maxValues = new int[n];\n maxValues[0] = events[0][2]; // Value of the first event\n\n // Fill the running max array\n for (int i = 1; i < n; i++) {\n maxValues[i] = Math.max(maxValues[i - 1], events[i][2]);\n }\n\n int maxSum = 0;\n\n // Step 3: Iterate through the events and use binary search\n for (int i = 0; i < n; i++) {\n int start = events[i][0];\n int value = events[i][2];\n\n // Find the latest event that ends before the current event starts\n int idx = binarySearch(events, start - 1);\n\n int currentSum = value;\n if (idx != -1) currentSum += maxValues[idx];\n\n maxSum = Math.max(maxSum, currentSum);\n }\n\n return maxSum;\n }\n\n // Helper: Binary search to find the latest event that ends <= targetEnd\n private int binarySearch(int[][] events, int targetEnd) {\n int start = 0, end = events.length - 1, res = -1;\n\n while (start <= end) {\n int mid = start + (end - start) / 2;\n if (events[mid][1] <= targetEnd) {\n res = mid;\n start = mid + 1;\n } else {\n end = mid - 1;\n }\n }\n\n return res;\n }\n}\n```\n\n\n```go []\nimport (\n\t"sort"\n)\n\nfunc maxTwoEvents(events [][]int) int {\n\t// Step 1: Sort events by their end times\n\tsort.Slice(events, func(i, j int) bool {\n\t\treturn events[i][1] < events[j][1]\n\t})\n\n\tn := len(events)\n\tmaxValues := make([]int, n)\n\tmaxValues[0] = events[0][2] // Value of the first event\n\n\t// Fill the running max array\n\tfor i := 1; i < n; i++ {\n\t\tmaxValues[i] = max(maxValues[i-1], events[i][2])\n\t}\n\n\tmaxSum := 0\n\n\t// Step 3: Iterate through the events and use binary search\n\tfor i := 0; i < n; i++ {\n\t\tstart := events[i][0]\n\t\tvalue := events[i][2]\n\n\t\t// Find the latest event that ends before the current event starts\n\t\tidx := binarySearch(events, start-1)\n\n\t\tcurrentSum := value\n\t\tif idx != -1 {\n\t\t\tcurrentSum += maxValues[idx]\n\t\t}\n\n\t\tmaxSum = max(maxSum, currentSum)\n\t}\n\n\treturn maxSum\n}\n\n// Helper: Binary search to find the latest event that ends <= targetEnd\nfunc binarySearch(events [][]int, targetEnd int) int {\n\tstart, end, res := 0, len(events)-1, -1\n\n\tfor start <= end {\n\t\tmid := start + (end-start)/2\n\t\tif events[mid][1] <= targetEnd {\n\t\t\tres = mid\n\t\t\tstart = mid + 1\n\t\t} else {\n\t\t\tend = mid - 1\n\t\t}\n\t}\n\n\treturn res\n}\n\n// Utility: Max function\nfunc max(a, b int) int {\n\tif a > b {\n\t\treturn a\n\t}\n\treturn b\n}\n```\n\n\n---\n\n {:style=\'width:250px\'} | 11 | 0 | ['Array', 'Binary Search', 'C', 'Sorting', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'Dart'] | 2 |
two-best-non-overlapping-events | Easy Solution | O(nlogn) | Priority Queue | Maximum Sum | easy-solution-onlogn-priority-queue-maxi-vqjf | Intuition\n Describe your first thoughts on how to solve this problem. \nThe key idea is to sort the events by their start times and use a priority queue to tra | Sachin6763 | NORMAL | 2024-12-08T03:32:45.223661+00:00 | 2024-12-08T03:32:45.223684+00:00 | 2,592 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key idea is to sort the events by their start times and use a priority queue to track the maximum value of events that end before the current event\'s start time. This allows us to efficiently determine the best event to pair with the current event.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort Events: Sort the events by their start time to process them in order.\n2. Priority Queue: Use a priority queue (min-heap) to store the end times and values of events. This helps us efficiently track the maximum value of events that don\'t overlap with the current event.\n3. Iterate Through Events: For each event:\n - Pop events from the queue that end before the current event\'s start time and update the maximum value.\n - Calculate the potential maximum sum by combining the current event\'s value with the maximum value from previous non-overlapping events.\n - Push the current event into the queue.\n4. Track Maximum Sum: Update the answer with the maximum sum found so far.\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nSorting the events takes O(nlogn). Processing each event with a priority queue operation takes O(logn), leading to an overall complexity of O(nlogn).\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n) due to the priority queue.\n\n# Code\n```python []\nimport heapq\n\nclass Solution:\n def maxTwoEvents(self, events):\n events.sort() # Sort by start time\n pq = [] # Priority queue to store (end_time, value)\n max_value = 0\n ans = 0\n \n for start, end, value in events:\n # Remove all events that end before the current event\'s start time\n while pq and pq[0][0] < start:\n max_value = max(max_value, heapq.heappop(pq)[1])\n \n # Update the maximum sum of values\n ans = max(ans, max_value + value)\n \n # Push the current event into the priority queue\n heapq.heappush(pq, (end, value))\n \n return ans\n```\n```cpp []\n#include <vector>\n#include <queue>\n#include <algorithm>\n\nusing namespace std;\n\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(), events.end()); // Sort events by start time\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;\n int maxVal = 0, ans = 0;\n\n for (auto& event : events) {\n int start = event[0], end = event[1], value = event[2];\n\n // Remove events that end before the current event\'s start time\n while (!pq.empty() && pq.top().first < start) {\n maxVal = max(maxVal, pq.top().second);\n pq.pop();\n }\n\n // Update the maximum sum of values\n ans = max(ans, maxVal + value);\n\n // Add the current event to the priority queue\n pq.push({end, value});\n }\n\n return ans;\n }\n};\n```\n```java []\nimport java.util.*;\n\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n Arrays.sort(events, (a, b) -> Integer.compare(a[0], b[0]));\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));\n int maxVal = 0, ans = 0;\n \n for (int[] event : events) {\n int start = event[0], end = event[1], value = event[2];\n \n // Remove all events that end before the current event\'s start time\n while (!pq.isEmpty() && pq.peek()[0] < start) {\n maxVal = Math.max(maxVal, pq.poll()[1]);\n }\n \n // Update the maximum sum of values\n ans = Math.max(ans, maxVal + value);\n \n // Add the current event to the priority queue\n pq.offer(new int[] {end, value});\n }\n \n return ans;\n }\n}\n```\n``` c []\n#include <stdio.h>\n#include <stdlib.h>\n\ntypedef struct {\n int start, end, value;\n} Event;\n\nint compare(const void *a, const void *b) {\n return ((Event *)a)->start - ((Event *)b)->start;\n}\n\ntypedef struct {\n int end, value;\n} QueueNode;\n\nint maxTwoEvents(Event* events, int n) {\n qsort(events, n, sizeof(Event), compare);\n QueueNode* pq = (QueueNode*)malloc(sizeof(QueueNode) * n);\n int size = 0, maxVal = 0, result = 0;\n\n for (int i = 0; i < n; i++) {\n while (size > 0 && pq[0].end < events[i].start) {\n maxVal = pq[--size].value > maxVal ? pq[size].value : maxVal;\n }\n result = result > maxVal + events[i].value ? result : maxVal + events[i].value;\n pq[size++] = (QueueNode){events[i].end, events[i].value};\n }\n\n free(pq);\n return result;\n}\n``` | 10 | 0 | ['C', 'Sorting', 'Heap (Priority Queue)', 'C++', 'Java', 'Python3'] | 5 |
two-best-non-overlapping-events | Python 3 || 11 lines, 2ptrs || T/S: 90% / 26% | python-3-11-lines-2ptrs-ts-90-26-by-spau-1fhp | Here\'s the plan:\n\n1. We unzip events, rezip vals with each beg and end, and then sort each of these lists.\n\n1. We iterate through the lists similtaneously | Spaulding_ | NORMAL | 2024-04-07T00:41:27.710270+00:00 | 2024-06-11T22:31:57.791284+00:00 | 594 | false | Here\'s the plan:\n\n1. We unzip `events`, rezip `vals` with each `beg` and `end`, and then sort each of these lists.\n\n1. We iterate through the lists similtaneously keeping track of the max value of all the events to the left and determining the value immediately to the right; if the sum of the left max value and the immediate right value is greater than those previous, we store it in `ans`.\n\n1. We return ans upon the finish of the iteration.\n```\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n \n mx, ans = 0, 0\n\n beg, end, val = zip(*events)\n beg2ndMtg = sorted(zip(beg, val))\n end1stMtg = iter(sorted(zip(end, val)))\n\n end1st, val1st = next(end1stMtg)\n\n for beg2nd, val2nd in beg2ndMtg:\n\n while end1st < beg2nd:\n mx = max(mx, val1st)\n end1st, val1st = next(end1stMtg)\n\n ans = max(ans, mx + val2nd)\n\n return ans \n```\n[https://leetcode.com/problems/two-best-non-overlapping-events/submissions/1225229981/](https://leetcode.com/problems/two-best-non-overlapping-events/submissions/1225229981/)\n\n\nI could be wrong, but I think that time complexity is *O*(*N* log *N*) and space complexity is *O*(*N*), in which *N* ~ `len(events)`. | 9 | 0 | ['Python3'] | 0 |
two-best-non-overlapping-events | ✅C++ || Recursion->Memoization->Tabulation || 01-Knapsack | c-recursion-memoization-tabulation-01-kn-rgdi | Method - 1 [Recursion]\n\n\nT->O(Expo) && S->O(n) [Recursion stack space]\n\nclass Solution {\npublic:\n int f(int i,int count,vector& st,vector>& eve,int n) | abhinav_0107 | NORMAL | 2022-10-01T12:57:35.236364+00:00 | 2022-10-01T12:57:35.236405+00:00 | 918 | false | # Method - 1 [Recursion]\n\n\n**T->O(Expo) && S->O(n) [Recursion stack space]**\n\nclass Solution {\npublic:\n int f(int i,int count,vector<int>& st,vector<vector<int>>& eve,int n){\n if(i>=n || count==2) return 0;\n int ind=lower_bound(st.begin(),st.end(),eve[i][1]+1)-st.begin();\n int pick = eve[i][2] + f(ind,count+1,st,eve,n);\n int notpick = f(i+1,count,st,eve,n);\n return max(pick,notpick);\n }\n \n int maxTwoEvents(vector<vector<int>>& eve) {\n int n=eve.size();\n sort(eve.begin(),eve.end());\n vector<int> st;\n for(auto i: eve) st.push_back(i[0]);\n return f(0,0,st,eve,n);\n }\n};\n\n# Method - 1 [Memoization]\n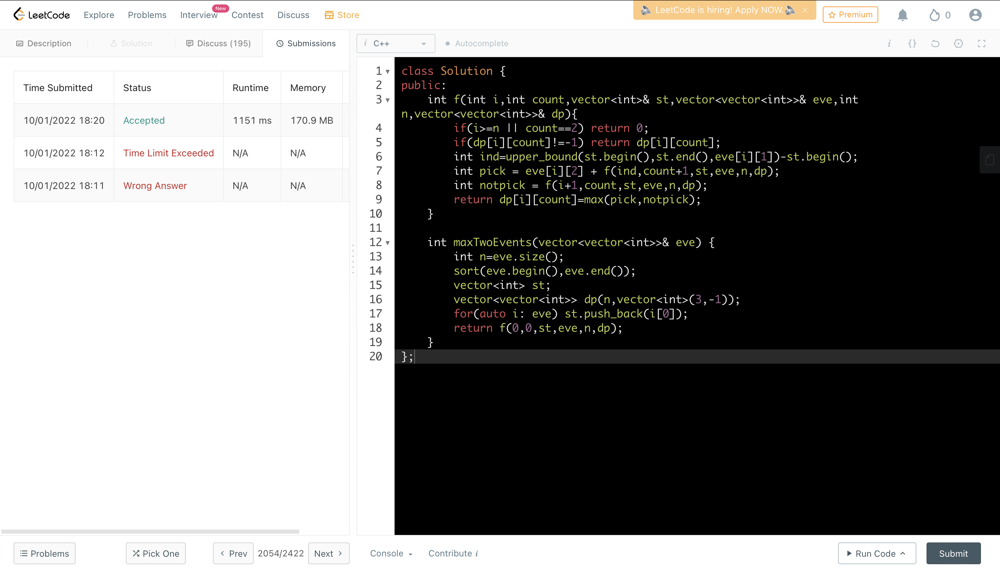\n\n**T->O(3n) && S->O(3n) + O(n) [Recursion stack space]**\n\n\tclass Solution {\n\tpublic:\n\t\tint f(int i,int count,vector<int>& st,vector<vector<int>>& eve,int n,vector<vector<int>>& dp){\n\t\t\tif(i>=n || count==2) return 0;\n\t\t\tif(dp[i][count]!=-1) return dp[i][count];\n\t\t\tint ind=upper_bound(st.begin(),st.end(),eve[i][1])-st.begin();\n\t\t\tint pick = eve[i][2] + f(ind,count+1,st,eve,n,dp);\n\t\t\tint notpick = f(i+1,count,st,eve,n,dp);\n\t\t\treturn dp[i][count]=max(pick,notpick);\n\t\t}\n\n\t\tint maxTwoEvents(vector<vector<int>>& eve) {\n\t\t\tint n=eve.size();\n\t\t\tsort(eve.begin(),eve.end());\n\t\t\tvector<int> st;\n\t\t\tvector<vector<int>> dp(n,vector<int>(3,-1));\n\t\t\tfor(auto i: eve) st.push_back(i[0]);\n\t\t\treturn f(0,0,st,eve,n,dp);\n\t\t}\n\t};\n\t\n# Method -3 [Tabulation]\t\n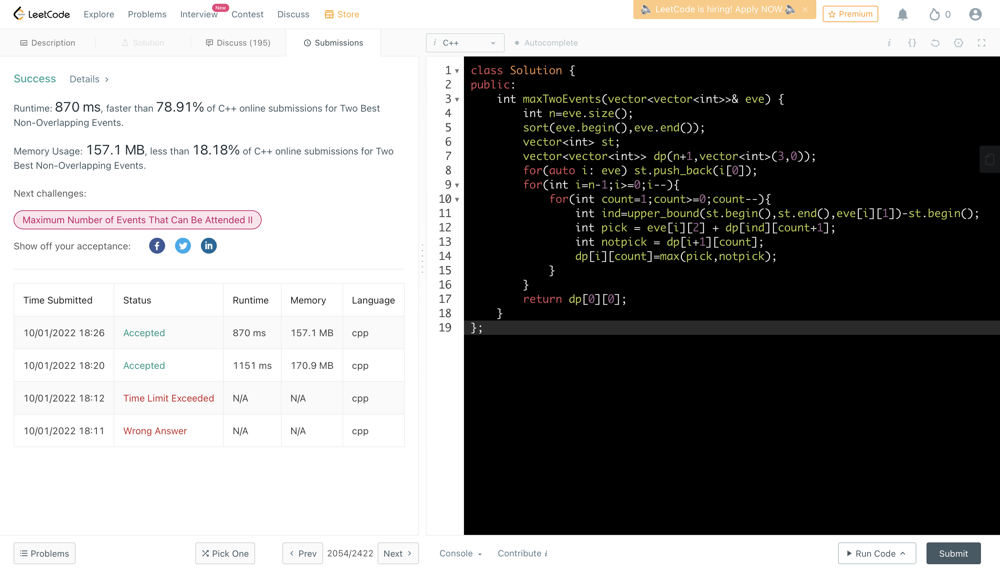\n\n\n**T->O(3n) && S->O(3n)**\n\n\tclass Solution {\n\tpublic:\n\t\tint maxTwoEvents(vector<vector<int>>& eve) {\n\t\t\tint n=eve.size();\n\t\t\tsort(eve.begin(),eve.end());\n\t\t\tvector<int> st;\n\t\t\tvector<vector<int>> dp(n+1,vector<int>(3,0));\n\t\t\tfor(auto i: eve) st.push_back(i[0]);\n\t\t\tfor(int i=n-1;i>=0;i--){\n\t\t\t\tfor(int count=1;count>=0;count--){\n\t\t\t\t\tint ind=upper_bound(st.begin(),st.end(),eve[i][1])-st.begin();\n\t\t\t\t\tint pick = eve[i][2] + dp[ind][count+1];\n\t\t\t\t\tint notpick = dp[i+1][count];\n\t\t\t\t\tdp[i][count]=max(pick,notpick);\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn dp[0][0];\n\t\t}\n\t};\n | 8 | 0 | ['Binary Search', 'Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++'] | 1 |
two-best-non-overlapping-events | Java Concise with Explanation | java-concise-with-explanation-by-adaltio-emxf | \nclass Solution {\n public int maxTwoEvents(int[][] events) {\n // -sort the events by start time\n // -rely on the fact that for any event ev | AdAltioraTendo | NORMAL | 2022-01-04T21:55:32.815731+00:00 | 2022-01-04T21:55:32.815759+00:00 | 442 | false | ```\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n // -sort the events by start time\n // -rely on the fact that for any event events[i], all events after events[i] start at a time\n // after events[i] and so do not overlap with any previous events not overlapping with events[i].\n // hence, we can maintain a PQ of end times for events to keep track of which events don\'t overlap with\n // the current event,\n // and maintain a maximum-valued previous event to combine with curr events[i]\n // answer will either be using two or one event sine value is nonnegative\n \n // sort events by start time\n Arrays.sort(events, (event1, event2) -> Integer.compare(event1[0], event2[0]));\n \n // maintaining the end times of previous events to use for checking overlap\n PriorityQueue<int[]> endTimes = new PriorityQueue<>((event1, event2) -> Integer.compare(event1[1], event2[1]));\n \n // finally, max-valued event we\'ve seen thus far\n int maxValuedEvent = 0;\n int ans = 0;\n \n // now start the iterative process\n for (int[] event : events) {\n while (!endTimes.isEmpty() && endTimes.peek()[1] < event[0]) {\n maxValuedEvent = Math.max(maxValuedEvent, endTimes.poll()[2]);\n }\n ans = Math.max(ans, maxValuedEvent + event[2]);\n endTimes.offer(event);\n }\n return ans;\n }\n}\n``` | 8 | 0 | ['Heap (Priority Queue)', 'Java'] | 0 |
two-best-non-overlapping-events | EASY TO MEDIUM C++ SOLUTION SOLVED || 2054. Two Best Non-Overlapping Events | easy-to-medium-c-solution-solved-2054-tw-v7xn | Intuition\n\nThe goal is to find the maximum value of two non-overlapping events from a list of events, where each event has a start time, end time, and value. | shivambit | NORMAL | 2024-12-08T09:16:17.175190+00:00 | 2024-12-08T09:16:17.175217+00:00 | 471 | false | # Intuition\n\nThe goal is to find the maximum value of two non-overlapping events from a list of events, where each event has a start time, end time, and value. The optimal approach involves sorting the events by their start times and leveraging a priority queue to track the maximum value of events that end before the current event\'s start.\n\n# Approach\n\n1. Sort Events: Sort the events based on their start times to process them in chronological order.\n2. Use a Priority Queue: Use a priority queue (min-heap) to store events as {end time, value}. This allows efficient removal of events that end before the current event\'s start.\n3. Iterate Through Events: For each event: Remove events from the priority queue whose end time is less than the current event\'s start time. While doing so, update maxVal with the maximum value among removed events.\nCalculate the potential maximum value as maxVal + current event value.\nPush the current event into the priority queue.\n4. Update the Answer: Track the maximum value (ans) obtained across all iterations.\n5. Return the Result: Return ans as the maximum value of two non-overlapping events.\n\n# Complexity\n- Time complexity: O(nlogn), Sorting the events takes O(nlogn). Each event is pushed and popped from the priority queue at most once, costing O(logn) per operation.\n\n- Space complexity: O(n), The priority queue can store up to n events in the worst case.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(), events.end()); // Sort events by start time\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;\n int maxVal = 0, ans = 0;\n\n for (auto& event : events) {\n int start = event[0], end = event[1], value = event[2];\n\n // Remove events that end before the current event\'s start time\n while (!pq.empty() && pq.top().first < start) {\n maxVal = max(maxVal, pq.top().second);\n pq.pop();\n }\n\n // Update the maximum sum of values\n ans = max(ans, maxVal + value);\n\n // Add the current event to the priority queue\n pq.push({end, value});\n }\n\n return ans;\n }\n};\n``` | 7 | 0 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 0 |
two-best-non-overlapping-events | ✅ One Line Solution | one-line-solution-by-mikposp-k37h | Binary Search + Right Max \n(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1.1 - Three | MikPosp | NORMAL | 2023-10-19T10:45:13.572403+00:00 | 2024-12-08T10:17:04.499840+00:00 | 594 | false | <!--Binary Search + Right Max-->\n(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1.1 - Three Lines\nTime complexity: $$O(n*log(n))$$. Space complexity: $$O(n)$$.\n```python3\nclass Solution:\n def maxTwoEvents(self, a: List[List[int]]) -> int:\n S,_,V = zip(*(a:=sorted(a)))\n M = [0,*accumulate(V[::-1],max)][::-1]\n return max(v+M[bisect_right(S,e)] for _,e,v in a)\n```\n\n# Code #1.2 - One Line\n```python3\nclass Solution:\n def maxTwoEvents(self, a: List[List[int]]) -> int:\n return max((M:=[0,*accumulate(map(itemgetter(2),(a:=sorted(a))[::-1]),max)][::-1])+[v+M[bisect_right(a,e,key=itemgetter(0))] for _,e,v in a])\n```\n\n# Code #1.3 - Unwrapped\n```python3\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n START, END, VAL = 0, 1, 2\n\n events.sort() \n maxRightVal = [0, *accumulate(map(itemgetter(VAL), events[::-1]), max)][::-1]\n res = 0\n for _, end, val in events:\n j = bisect_right(events, end, key=itemgetter(START))\n res = max(res, val + maxRightVal[j])\n \n return res\n```\n\n# Code #2.1 - Two Lines\nTime complexity: $$O(n*log(n))$$. Space complexity: $$O(n)$$.\n```python3\nclass Solution:\n def maxTwoEvents(self, a: List[List[int]]) -> int:\n t,M = sorted((q[k]+k,k^1,q[2]) for q in a for k in (0,1)),0\n return max(p and v+M or (M:=max(M,v)) for _,p,v in t)\n```\n\n# Code #2.2 - One Line\n```python3\nclass Solution:\n def maxTwoEvents(self, a: List[List[int]]) -> int:\n return (t:=sorted((q[k]+k,k^1,q[2]) for q in a for k in (0,1)),M:=0) and max(p and v+M or (M:=max(M,v)) for _,p,v in t)\n```\n\n(Disclaimer 2: code above is just a product of fantasy packed into one line, it is not claimed to be \'true\' oneliners - please, remind about drawbacks only if you know how to make it better) | 7 | 1 | ['Array', 'Binary Search', 'Sorting', 'Prefix Sum', 'Python', 'Python3'] | 0 |
two-best-non-overlapping-events | Complete Detailed Explanation || Most Intuitive Linear DP + Binary Search Solution || C++ || | complete-detailed-explanation-most-intui-4qdc | Intuition\nFirst Thing WE can understand from the problem is to sort the events first for getting non-overlapping two events. \nThen we can calculate the upperb | brucewayne_5 | NORMAL | 2023-07-15T12:05:59.981628+00:00 | 2023-07-15T12:05:59.981646+00:00 | 591 | false | # Intuition\nFirst Thing WE can understand from the problem is to sort the events first for getting **non-overlapping** two events. \nThen we can calculate the upperbound for current event ending time for choosing next event.\n\n# Approach\nAs mentioned in the intuition we first sort the array.\nThen Here we can observe nonlinearity in the **values** associated with the events.\nExample : events = [[1,3,2],[4,5,2],[1,5,5]]\nAfter Sorting the events became\nevents=[[1,3,2],[1,5,5],[4,5,2]]\nThe Values of Events are in non monotonic nature [2,5,2]\n**Important Observation :**\nconsider the events = [[1,3,2],[4,5,2],[6,7,3],[8,10,100],[11,12,1],[13,20,5]] (arranged in sorted order)\nConsider If we Select the first event now sum=2\nthen what is the next possible event that we can choose OR what are the options we have to choose\n- we can choose event 2 with value 2\n- we can choose event 3 with value 3\n- **we can choose event 4 with value 100**\n- we can choose event 5 with value 1\n- we can choose event 5 with value 5\nWhat is Best Option to choose for getting maximum Sum?\nwe have to choose event 4 .\nwhat can we understand from above example ,\nafter selecting event-1 =[1,3,2]\nthe next should start after ending time of event -1 \nhence events are sorted we can apply upperbound on ending time for getting next event .\nHere for event 1 ending time=3\nupperbound(events,3) = index 1\nwhich form index 1 to n-1 we can select any one event which result maximum sum.\nfor getting that particular event we can precompute the maximum values from the r.h.s **because we don\'t care about which event it was , we just need the maximum value of the event**\nlets compute the maxvalues from the right hand side\ndeclare a maxValues/(u can declare as dp if you wish to) array of size =events.size.\nRun the loop from n-1 to 0\nuse currentMax Variable initialize with zero\n1. at index = 5 , events value = 5 && currentMax=0 \nhence currentMax is less than event value assign \n currentMax=events[index][2] and then \nmaxValues[index]=currentMax\n2.at index = 4 , events value = 1 && currentMax=5 \nhence currentMax is greater than event value we don\'t change currentMax value just assign \nmaxValues[index]=currentMax\n3. at index = 3 , events value = 100 && currentMax=5\nhence currentMax is less than event value assign \n currentMax=events[index][2] and then \nmaxValues[index]=currentMax\nFrom here onwards currentMax value will not get changed \nafter completion for maxValues Computation \nthe maxValues/DP array = [100,100,100,100,5,5]\nNow After Selecting the first event sum=2\nand upperbound(events,endtime) = index 1\nand maxValue[1]=100\nHence For event 1 maximum sum = 102\nLike we can compute maximum sum for every event and return the maximum sum among them.\n**I WISH YOU UNDERSTOOD MY EXPLANATION \n PLEASE UPVOTE IF YOU LIKE MY SOLUTION**\n\n\n# Complexity\n- Time complexity:\n O(NLOGN) for sorting the events \nand we run a loop which for calculating maximum sum runs **n** times in which we use upperbound everytime the loop runs which tooks **logn** time \nhence its results in overall O(nlogn) time complexity\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N) for storing the precomputed maximum values\n\n# Code\n```\nclass Solution {\npublic:\n int upper_bound(vector<vector<int>>& events,int key,int size)\n {\n int low=0,high=size-1,mid;\n while(low<=high)\n {\n mid=(low+high)/2;\n if(events[mid][0]>key) high=mid-1;\n else low=mid+1;\n }\n return low;\n }\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(),events.end());\n int size=events.size(),currMax=0;\n vector<int>maxValue(size,0); //you can declare it as dp\n //now precompute the maximum values\n\n for(int i=size-1;i>=0;i--)\n {\n currMax=max(currMax,events[i][2]);\n maxValue[i]=currMax;\n }\n int maxTwoEventss=0,currTwoEvents=0,nextInd;\n for(int i=0;i<size;i++)\n {\n currTwoEvents=events[i][2];\n nextInd=upper_bound(events,events[i][1],size);\n if(nextInd<size) currTwoEvents+=maxValue[nextInd];\n maxTwoEventss=max(maxTwoEventss,currTwoEvents);\n }\n return maxTwoEventss;\n }\n};\n``` | 7 | 0 | ['Binary Search', 'Dynamic Programming', 'C++'] | 0 |
two-best-non-overlapping-events | C++| 97% faster | 99.26% memory | Binary Search | Explained | c-97-faster-9926-memory-binary-search-ex-4kpy | Steps are explained in comments (If any doubt or any modification please comment)\n\n\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& even | Priyansh_34 | NORMAL | 2021-11-06T20:12:40.958958+00:00 | 2021-11-06T20:16:03.335171+00:00 | 626 | false | **Steps are explained in comments** (If any doubt or any modification please comment)\n\n```\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n ios::sync_with_stdio(false);cin.tie(NULL);\n \n //sort the events according to their start time\n sort(events.begin(),events.end());\n \n int n=events.size();\n //store the maxvalue till that element from right.\n vector<int>R(n,events[n-1][2]);\n for(int i=n-2;i>=0;i--){\n R[i]=max(R[i+1],events[i][2]);\n }\n \n int ans=0;\n for(int i=0;i<n;i++){\n int l=i+1, r=n-1;\n int idx = -1;\n //find first index whose start-time is greater than current event\'s end-time\n while(l <= r){\n int m=(l+r)/2;\n if(events[m][0]>events[i][1]){\n idx=m;\n r=m-1;\n }\n else{\n l=m+1;\n }\n }\n if(idx!=-1){\n ans=max(ans,R[idx]+events[i][2]);\n }\n \n \n }\n //check if there is any single event whose value is greater than the sum of two event\'s value.\n return max(ans,R[0]);\n }\n};\n\n/*\n * Time Complexity - O(nlogn)\n * Space Complexity - O(n)\n * \n*/\n```\n**Do Upvote if you like the solution** | 7 | 0 | ['Binary Tree'] | 2 |
two-best-non-overlapping-events | C++ | Brute force to Binary Search | TC->O(nlogn),SC->O(n) |Commented | c-brute-force-to-binary-search-tc-onlogn-eub4 | \n//Brute Force\nYou must have to undernstand brute force ,if you want to fully get the observation of my binary search solution.\noptimize one will become very | lazy_buddy | NORMAL | 2021-10-31T09:42:53.745270+00:00 | 2021-10-31T13:38:33.802640+00:00 | 344 | false | ```\n//Brute Force\nYou must have to undernstand brute force ,if you want to fully get the observation of my binary search solution.\noptimize one will become very easy ,so get idea about brute fce and jump to optimized one.\n\nint maxTwoEvents(vector<vector<int>>&a) {\n \n int n=a.size();\n int res=INT_MIN;\n int mx=INT_MIN;\n for(int i=0;i<n;i++)\n {\n vector<int>x=a[i];\n int s1=x[0];\n int e1=x[1];\n int val1=x[2];\n for(int j=0;j<n;j++)\n {\n if(j!=i)\n {\n vector<int>v1=a[j];\n int s2=v1[0];\n int e2=v1[1];\n int val2=v1[2];\n if(s2>e1)\n {\n \n res=max(res,val1+val2);\n \n }\n }\n \n }\n mx=max(mx,val1);\n }\n return max(mx,res);\n }\n\tNow think to optimise the above aproach,just we want to remove the repetetive work\n\twe know if we want to get in a range of values in sorted array,we can use binary search\n\tso below is the idea\n\t\n//https://leetcode.com/problems/two-best-non-overlapping-events/\n//sorting based on start time\n//starting time is equal than we will keep the smaller end time first\nstatic bool comp(vector<int>&a,vector<int>&b)\n{\n if(a[0]==b[0])\n return a[1]<b[1];\n return a[0]<b[0];\n}\nint maxTwoEvents(vector<vector<int>>&a)\n{\n \n int n=a.size();\n int res=INT_MIN;\n int mx=INT_MIN;\n sort(a.begin(),a.end(),comp);\n//here I am using maxright to store the max valuefrom the right\n//suppose we landup at middle value and found the starting point greater than end point,so according to logic we want to move our right to mid+1 but \n//There may be the case that we have some starting point after mid which is having value greater than the current mid index\n//so to avoid this conflicts we will store mid max value from the right\n//because we know that after mid all the starting point is going to be greater right\n \n vector<int>maxfromright(n);\n maxfromright[n-1]=a[n-1][2];\n for(int i=n-2;i>=0;i--)\n {\n maxfromright[i]=max(a[i][2],maxfromright[i+1]);\n }\n for(int i=0;i<n;i++)\n {\n //keep all three values\n vector<int>x=a[i];\n int s1=x[0];\n int e1=x[1];\n int val1=x[2];\n //start of binary search\n int l=i+1;\n int r=n-1;\n while(l<=r)\n {\n int mid=l+(r-l)/2;\n vector<int>v1=a[mid];\n //keep all three values\n int s2=v1[0];\n int e2=v1[1];\n int val2=v1[2];\n //start dividing array to get the ans\n int idx=-1;\n if(s2>e1)\n {\n idx=mid;\n r=mid-1;\n \n }\n else\n {\n l=mid+1;\n }\n if(idx!=-1)\n {\n res=max(res,val1+maxfromright[idx]);\n }\n \n }\n//why this,this is because we can take only one events also \n//supose tow events are not giving max but signle events may be max so will keep track of that also\n\n mx=max(mx,val1);\n }\n return max(mx,res);\n}\nTime complexity->O(nlogn)\nSpace complexity->O(n)\n``` | 6 | 1 | ['Array', 'Sorting', 'Binary Tree'] | 0 |
two-best-non-overlapping-events | Binary Search Approach ✅✅ | binary-search-approach-by-arunk_leetcode-xnpr | Intuition\nTo solve this problem, we need to select at most two non-overlapping events to maximize the total value. Sorting the events by start time simplifies | arunk_leetcode | NORMAL | 2024-12-08T16:02:27.759898+00:00 | 2024-12-08T16:03:41.730204+00:00 | 487 | false | # Intuition\nTo solve this problem, we need to select at most two non-overlapping events to maximize the total value. Sorting the events by start time simplifies the problem, allowing efficient checks for overlaps and the use of binary search to find valid second events.\n\n# Approach\n1. **Sort Events**: First, sort the events by their start times.\n2. **Precompute Maximum Values**: Create a `maxValue` array where `maxValue[i]` stores the maximum value from event `i` to the end. This allows for quick access to the best choice for the second event.\n3. **Binary Search for Non-Overlapping Events**: For each event, use binary search to find the next non-overlapping event. Combine the values of the current event and the best non-overlapping event to calculate the maximum value.\n4. **Track Maximum Result**: Update the result iteratively for the best possible outcome.\n\n# Complexity\n- Time complexity: \n Sorting takes $$(O(n \\log n)$$, precomputing the maximum values takes $$(O(n)$$, and binary search for each event takes $$(O(n \\log n)$$. \n Overall: $$(O(n \\log n)$$.\n \n- Space complexity: \n Additional space is used for the `maxValue` array, which is $$O(n)$$\n\n# Code\n``` cpp []\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(), events.end());\n int n = events.size();\n\n vector<int> maxValue(n, 0);\n maxValue[n - 1] = events[n - 1][2];\n for (int i = n - 2; i >= 0; --i) {\n maxValue[i] = max(maxValue[i + 1], events[i][2]);\n }\n\n int result = 0;\n\n for (int i = 0; i < n; ++i) {\n int currValue = events[i][2];\n result = max(result, currValue);\n\n int lo = i + 1, hi = n - 1, nextEvent = -1;\n while (lo <= hi) {\n int mid = lo + (hi - lo) / 2;\n if (events[mid][0] > events[i][1]) {\n nextEvent = mid;\n hi = mid - 1;\n } else {\n lo = mid + 1;\n }\n }\n\n if (nextEvent != -1) {\n result = max(result, currValue + maxValue[nextEvent]);\n }\n }\n\n return result;\n }\n};\n```\n``` Java []\nimport java.util.*;\n\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n Arrays.sort(events, (a, b) -> Integer.compare(a[0], b[0]));\n int n = events.length;\n\n int[] maxValue = new int[n];\n maxValue[n - 1] = events[n - 1][2];\n for (int i = n - 2; i >= 0; --i) {\n maxValue[i] = Math.max(maxValue[i + 1], events[i][2]);\n }\n\n int result = 0;\n\n for (int i = 0; i < n; ++i) {\n int currValue = events[i][2];\n result = Math.max(result, currValue);\n\n int lo = i + 1, hi = n - 1, nextEvent = -1;\n while (lo <= hi) {\n int mid = lo + (hi - lo) / 2;\n if (events[mid][0] > events[i][1]) {\n nextEvent = mid;\n hi = mid - 1;\n } else {\n lo = mid + 1;\n }\n }\n\n if (nextEvent != -1) {\n result = Math.max(result, currValue + maxValue[nextEvent]);\n }\n }\n\n return result;\n }\n}\n\n```\n``` JavaScript []\nvar maxTwoEvents = function(events) {\n events.sort((a, b) => a[0] - b[0]);\n const n = events.length;\n\n const maxValue = new Array(n).fill(0);\n maxValue[n - 1] = events[n - 1][2];\n for (let i = n - 2; i >= 0; --i) {\n maxValue[i] = Math.max(maxValue[i + 1], events[i][2]);\n }\n\n let result = 0;\n\n for (let i = 0; i < n; ++i) {\n const currValue = events[i][2];\n result = Math.max(result, currValue);\n\n let lo = i + 1, hi = n - 1, nextEvent = -1;\n while (lo <= hi) {\n const mid = lo + Math.floor((hi - lo) / 2);\n if (events[mid][0] > events[i][1]) {\n nextEvent = mid;\n hi = mid - 1;\n } else {\n lo = mid + 1;\n }\n }\n\n if (nextEvent !== -1) {\n result = Math.max(result, currValue + maxValue[nextEvent]);\n }\n }\n\n return result;\n};\n\n```\n``` Python []\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n events.sort()\n n = len(events)\n\n maxValue = [0] * n\n maxValue[-1] = events[-1][2]\n for i in range(n - 2, -1, -1):\n maxValue[i] = max(maxValue[i + 1], events[i][2])\n\n result = 0\n\n for i in range(n):\n currValue = events[i][2]\n result = max(result, currValue)\n\n lo, hi, nextEvent = i + 1, n - 1, -1\n while lo <= hi:\n mid = lo + (hi - lo) // 2\n if events[mid][0] > events[i][1]:\n nextEvent = mid\n hi = mid - 1\n else:\n lo = mid + 1\n\n if nextEvent != -1:\n result = max(result, currValue + maxValue[nextEvent])\n\n return result\n\n``` | 5 | 0 | ['Binary Search', 'Python', 'C++', 'Java', 'Python3', 'JavaScript', 'Python ML'] | 1 |
two-best-non-overlapping-events | Solution for waifujahat | C# | 100% Both using Binary Search | solution-for-waifujahat-c-100-both-using-qtky | \n\n---\n\n# How to solve\nThe goal of this task is to find the maximum sum of values by selecting at most two non-overlapping events, I need to ensure the two | waifujahat | NORMAL | 2024-12-08T03:33:15.125103+00:00 | 2024-12-08T13:50:30.437727+00:00 | 212 | false | \n\n---\n\n# How to solve\nThe goal of this task is to find the maximum sum of values by selecting at most two non-overlapping events, I need to ensure the two chosen events don\'t overlap in their time intervals. Like another task I need to pay attention in constraint, it said for each event I choose, I must find another event that doesn\u2019t overlap. So I will make code with `Sorting` and could `Handle Ovelap` because `Sorting` allow us to easily identify future events that start after a given event ends and it make more easy to apply `Binary Search` and Binary Search used to find the earliest valid next event for a current event. Here my plan :\n1. Treat it as the first event\n2. Use Binary Search to find the best second event\n3. Use the suffix array to quickly get the value of the best second event\n4. Keep track of the maximum value across all combinations\n\n---\n\n# About my code\n\n1. Sort events by start time\nSorting the events based on their start times ensures that when I process each event, all possible future events are in order and searching for a valid next event to attend. For each event, the potential future events are guaranteed to come later in the array, the code I make allows me to efficiently search for valid future events using binary search because future events are always sorted by their start time\n2. Prepare a Suffix Array for Maximum Values\nA suffix array stores the maximum value of events that start from a certain index onwards, here `suffix[i]` gives the maximum value of any event that starts at or after `events[i]`. My idea is to quickly find the best future event value when combining two events.\n3. I use Binary Search for Non-Overlapping Events\nI need to find the earliest event whose start time is strictly greater than the end time of the current event so I think Binary search is efficient way for this task because the events are sorted by start time, I could use another method but from the start I had planned to use Binary Search. So I just need to focus what I so i just need to focus on my plan.\n4. Calculate the Maximum Value\nI keep a variable `value` to track the highest sum of values found and I will update it whenever a new valid combination is better than the current maximum, after checking all events, just return the maximum value found.\n\nFor example :\n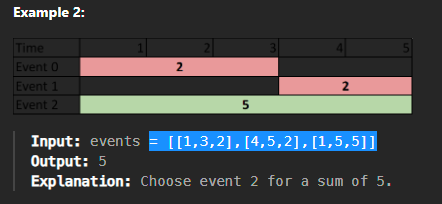\n\nInput = [[1, 3, 2], [4, 5, 2], [1, 5, 5]]\n1. Sorting\n[[1, 3, 2], [1, 5, 5], [4, 5, 2]]\n\n2. Suffix Array\nSuffix[2] = value of event[2] = 2\nSuffix[1] = max(suffix[2], value of event[1] = max(2, 5) = 5\nSuffix[0] = max(suffix[1], value of event[0] = max(5, 2) = 5\n[5, 5, 2]\n\n3. Binary Search\n~ `Event 0` - [1, 3, 2]\nEvents`[mid][0] > 3`\nBinary search find `Event 2` = [4, 5, 2]\nCalculate total value :\nCurrent = 2 | suffix[2]: 2 | 2 + 2 = 4 | current = `4`\n~ `Event 1` - [1, 5, 5]\nEvents`[mid][0] > 5`\nBinary search fails to find a valid next event because no events start after time 5\nCalculate total value :\nCurrent = 5 | No next event to combine | current = `5`\n~ `Event 2` - [4, 5, 2]\nEvents`[mid][0] > 5`\nBinary search fails to find a valid next event because no events start after time 5\nCalculate total value :\nCurrent = 2 | No next event to combine | current = `5`\n\n4. The highest total value of two non overlapping events is 5, achieved by selecting `Event 1` [1, 5, 5], return value = `5`\n\n---\n\n# Code\n```csharp []\npublic class Solution {\n public int MaxTwoEvents(int[][] events) {\n int n = events.Length;\n\n // Step 1\n // Sort events by start time\n Array.Sort(events, (a, b) => a[0].CompareTo(b[0]));\n\n // Step 2\n // Prepare suffix array for maximum future values\n int[] suffix = new int[n];\n suffix[n - 1] = events[n - 1][2];\n\n // Fill the array with the maximum values of events starting after the current event\n // Suffix array from right to left\n for (int i = n - 2; i >= 0; i--) \n {\n suffix[i] = Math.Max(suffix[i + 1], events[i][2]);\n }\n\n // To store or initialize max value\n int value = 0;\n\n // Step 3 \n // Iterate over each event to find the best combination\n for (int i = 0; i < n; i++) \n {\n // Step 4\n // Binary search for the next valid event\n int current = events[i][2];\n // Update max value with current event alone\n value = Math.Max(value, current); \n int low = i + 1;\n int high = n - 1;\n int nextevent = -1;\n\n while (low <= high) \n {\n int mid = low + (high - low) / 2;\n\n // Check if the event at mid starts after the current event ends\n if (events[mid][0] > events[i][1]) \n {\n nextevent = mid;\n high = mid - 1;\n } \n else \n {\n low = mid + 1;\n }\n }\n // Step 5\n // Calculate the sum of current and next events values\n // If a valid next event is found, calculate the total value current + next\n if (nextevent != -1) \n {\n value = Math.Max(value, current + suffix[nextevent]);\n }\n }\n // Return the maximum value found\n return value;\n }\n}\n\n``` | 5 | 0 | ['Array', 'Binary Search', 'Dynamic Programming', 'Sorting', 'Heap (Priority Queue)', 'C#'] | 1 |
two-best-non-overlapping-events | c++ | Memoization+Binary Search | Explaination | c-memoizationbinary-search-explaination-6tkyj | Solution-Memoization + Binary Search\n\nThought Process\n1. For every event, I\'ve two options. Whether I choose that event or not.\n2. If choose, then I add it | ritvikmahajan17 | NORMAL | 2021-11-23T07:09:46.689710+00:00 | 2021-11-23T07:12:21.649213+00:00 | 372 | false | # Solution-Memoization + Binary Search\n\n*Thought Process*\n1. For every event, I\'ve two options. Whether I choose that event or not.\n2. If choose, then I add its value to my answer. If not choosen I move forward to the next event.\n3. Now if I select a event, my next event has to have `start time > end time of choosen event`. Also of all the possible next events I should choose the one with `max value`\n4. To select the next event with `start time > end time of choosen event`, I can do a Binary search.\n5. What to select the `Max value` I can find the value of all legal subsets possible, and select the maximum of all the values.\n\n```\n vector<int> start;\n int dp[100002][2];\n \n int solve(vector<vector<int>>& events, int i, int choose){\n if(i>=events.size()){\n return 0; \n } \n \n if(choose>=2){ // since I cannot chose more than two elemnts.\n return 0;\n }\n \n if(dp[i][choose]!=-1){\n return dp[i][choose];\n }\n \n int idx = upper_bound(start.begin(),start.end(),events[i][1])-start.begin(); // binary search to find the next event\'s index\n \n return dp[i][choose]=max(events[i][2]+solve(events,idx,choose+1),solve(events,i+1,choose)); //either I select an event, or I dont\n \n }\n \n int maxTwoEvents(vector<vector<int>>& events) {\n \n for(int i=0;i<100002;i++){\n for(int j=0;j<2;j++){\n dp[i][j]=-1;\n }\n }\n int n = events.size();\n\t\t//sort elemts acc to start time\n sort(events.begin(),events.end());\n\t\t\n start.clear();\n for(int i=0;i<n;i++){\n start.push_back(events[i][0]); \n }\n \n return solve(events,0,0);\n }\n```\n\n**Time Complexity - O[n*log(n)]** | 5 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'Binary Tree'] | 0 |
two-best-non-overlapping-events | Java O(nlogn) Binary Search + Maximum Caching | java-onlogn-binary-search-maximum-cachin-7f3z | We only need to find a pair of non-overlapping events. Therefore, given one fixed event, we need to find the other event with non-overlapping to form a pair. Fo | gumingdiaoyu | NORMAL | 2021-10-30T16:15:34.428005+00:00 | 2021-10-30T16:45:10.376080+00:00 | 601 | false | We only need to find a pair of non-overlapping events. Therefore, given one fixed event, we need to find the other event with non-overlapping to form a pair. For each pair, we calculate the maximum. However, the complexity will be O(n^2).\n\nTo reduce the complexity, we use binary search to find the other event without overlapping. We first sort the events array based on the starting time. Given a fixed event, once the starting time is sorted, we can use binary search to find the non-overlapping event to form the pair. Moreover, we need an array maxArr to record the maximum value of every event so that we only need O(1) to index.\n\nThe codes are as follows:\n```\n\nclass Solution {\n\n public int maxTwoEvents(int[][] events) {\n if(events == null || events.length < 1) {\n return 0;\n }\n\t\t\n\t\t// Sort the event array based on the starting time\n Arrays.sort(events, (a, b) -> a[0] == b[0] ? b[2] - a[2] : a[0] - b[0]);\n \n\t\t// Use an array to record the maximum value\n int[] maxArr = new int[events.length];\n \n maxArr[events.length - 1] = events[events.length - 1][2];\n for(int i = events.length - 2; i >= 0; i--) {\n maxArr[i] = Math.max(maxArr[i + 1], events[i][2]);\n }\n \n\t\t// The current maximum value is the last event\n int ans = events[events.length - 1][2];\n \n for(int i = 0; i < events.length - 1; i++) {\n int index = find(events, events[i][1], i + 1);\n \n if(index == -1) {\n\t\t\t// If we cannot find a non-overlapping event, the maximum so far is the current event value\n ans = Math.max(ans, events[i][2]);\n } else {\n\t\t\t// The maximum is the current event value plus the nonoverlapping event value\n ans = Math.max(ans, events[i][2] + maxArr[index]);\n }\n }\n \n return ans;\n }\n \n private int find(int[][] events, int target, int left) {\n\t// Binary search to find the first nonoverlapping event\n int right = events.length - 1;\n \n while(left + 1 < right) {\n int mid = left + (right - left) / 2;\n \n if(events[mid][0] <= target) {\n left = mid;\n } else {\n right = mid;\n }\n }\n \n if(events[left][0] > target) {\n return left;\n }\n \n if(events[right][0] > target) {\n return right;\n }\n \n return -1;\n }\n}\n``` | 5 | 0 | ['Sorting', 'Binary Tree', 'Java'] | 2 |
two-best-non-overlapping-events | [Python]: Binary Search + DP | python-binary-search-dp-by-sanathbhargav-n2kk | \nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n def binarySearch(low, high, key):\n if low <= high:\n | sanathbhargav26 | NORMAL | 2021-10-30T16:11:27.474358+00:00 | 2021-10-30T16:11:27.474390+00:00 | 617 | false | ```\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n def binarySearch(low, high, key):\n if low <= high:\n mid = (low+high)//2\n if events[mid][1] >= key:\n return binarySearch(low, mid-1, key)\n else:\n return binarySearch(mid+1, high, key)\n return high\n \n events.sort(key=lambda x: x[1])\n dp = [0 for _ in range(len(events))]\n dp[0] = events[0][2]\n for i in range(1, len(events)):\n dp[i] = max(dp[i-1], events[i][2]) # maximum values if only one selection was allowed \n \n maxi = events[0][2]\n \n for i in range(1, len(events)):\n cur = events[i][2]\n prev = binarySearch(0, len(events), events[i][0]) # previos non-overlapping index\n maxi = max(maxi, cur+dp[prev]) if prev != -1 else max(maxi, cur)\n return maxi\n``` | 5 | 0 | ['Dynamic Programming', 'Binary Tree', 'Python'] | 0 |
two-best-non-overlapping-events | C++ Dynamic Programming | c-dynamic-programming-by-angold4-szjt | Starting from first day, each day has three possible works in this problem:\n\n1. End the first event (Case 1)\n2. Start the second event (Case 2)\n3. Do nothin | angold4 | NORMAL | 2021-10-30T18:21:02.404974+00:00 | 2021-10-31T05:28:06.852719+00:00 | 354 | false | **Starting from first day, each day has three possible works in this problem:**\n\n1. **End the first event** (Case 1)\n2. **Start the second event** (Case 2)\n3. **Do nothing (or in event)** (Case 3)\n\n\n**And their relationship:**\n\n1. **`firstEnd = iValEnd`** (Case 1)\n2. **`secondBegin = max(old_firstEnd + iValBegin, secondBegin)`** (Case 2)\n3. **`old_firstEnd = max(old_firstEnd, firstEnd)`** (Case 3)\n\n#### variables:\n* **`iValEnd`** stands for the maximum value of the events which ends at day i\n* **`iValBegin`** stands for the maximum value of the events which begins at day i\n* **`firstEnd`** stands for the maximum value at day i if you just choose one event to attend\n* **`old_firstEnd`** stands for the yesterday\'s maximum value if you just choose one event to attend\n* **`secondBegin`** stands for the maximum value at day i if you choose the second event to attend\n\n\n```c++\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n int maxDay = 0;\n // Dynamic Programming\n \n unordered_map<int, vector<int>> endDay; // end Day with its value\n unordered_map<int, vector<int>> begDay; // begin Day with its value\n set<int> days;\n \n for (auto event : events) {\n if (event[1] > maxDay) maxDay = event[1];\n endDay[event[1]].push_back(event[2]);\n begDay[event[0]].push_back(event[2]);\n \n days.insert(event[1]);\n days.insert(event[0]);\n }\n int ret = 0;\n \n // Start\n int fee = 0; // first event end\n int seb = 0; // second event begin\n for (auto i : days) {\n int prefee = fee;\n int preseb = seb;\n for (int value : endDay[i]) {\n // first event end today\n fee = max(fee, value);\n }\n \n fee = max(prefee, fee); // do nothing\n \n for (int value : begDay[i]) {\n // second event start today\n seb = max(prefee + value, seb);\n }\n ret = max(ret, max(seb, fee));\n }\n return ret;\n }\n};\n\n \n``` | 4 | 0 | [] | 2 |
two-best-non-overlapping-events | Easy-understood Java solution with sort and postfix array | easy-understood-java-solution-with-sort-xa540 | sort the events by the starting time\n2. create a postfix array to record the largest value after current starting time events[i][0]\n3. use binary search to fi | magi003769 | NORMAL | 2021-10-30T16:19:14.935487+00:00 | 2021-10-30T16:19:14.935521+00:00 | 565 | false | 1. sort the events by the starting time\n2. create a postfix array to record the largest value after current starting time `events[i][0]`\n3. use binary search to find the first event that starting later than the one at current iteration \n\n```\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n Arrays.sort(events, (a, b) -> a[0] - b[0]);\n int onRight = 0, maxOne = 0, n = events.length;\n int[] rightMax = new int[n+1];\n for (int i = n - 1; i >= 0; i--) {\n int start = events[i][0], end = events[i][1], val = events[i][2];\n maxOne = Math.max(val, maxOne);\n rightMax[i] = Math.max(rightMax[i+1], val);\n }\n int two = 0;\n for (int i = 0; i < n; i++) {\n int start = events[i][0], end = events[i][1], val = events[i][2];\n int idx = binarySearch(end, events);\n if (idx < n) {\n two = Math.max(rightMax[idx] + val, two);\n }\n }\n return Math.max(two, maxOne);\n }\n \n public int binarySearch(int end, int[][] arr) {\n int left = 0, right = arr.length;\n while (left < right) {\n int mid = left + (right - left) / 2;\n if (arr[mid][0] > end) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n return left;\n }\n}\n``` | 4 | 0 | ['Binary Search Tree', 'Sorting', 'Java'] | 0 |
two-best-non-overlapping-events | C Solution - Heap | c-solution-heap-by-jafwe-4jqt | c []\nvoid push(int **heap, int *new, int top)\n{\n heap[top] = new;\n int now = top;\n int *temp;\n int next = (top - 1) / 2;\n while (top)\n {\n if ( | jafwe | NORMAL | 2024-12-08T08:28:27.907494+00:00 | 2024-12-08T08:28:27.907522+00:00 | 62 | false | ```c []\nvoid push(int **heap, int *new, int top)\n{\n heap[top] = new;\n int now = top;\n int *temp;\n int next = (top - 1) / 2;\n while (top)\n {\n if (heap[now][2] > heap[next][2])\n {\n temp = heap[next];\n heap[next] = heap[now];\n heap[now] = temp;\n now = next;\n next = (now - 1) / 2;\n }\n else\n return;\n }\n}\n\nvoid pop(int **heap, int top)\n{\n heap[0] = heap[top];\n int now = 0;\n int next;\n int *temp;\n int left = 1;\n int right = 2;\n while (left < top)\n {\n next = top == right ? left : ((heap[left][2] > heap[right][2]) ? left : right);\n if (heap[next][2] > heap[now][2])\n {\n temp = heap[next];\n heap[next] = heap[now];\n heap[now] = temp;\n now = next;\n left = now * 2 + 1;\n right = now * 2 + 2;\n }\n else\n return;\n }\n}\n\nint cmp(const void *ptr1, const void *ptr2)\n{\n int **iptr1 = (int **)ptr1;\n int **iptr2 = (int **)ptr2;\n\n if ((*iptr1)[1] > (*iptr2)[1])\n return 1;\n if ((*iptr1)[1] == (*iptr2)[1] && (*iptr1)[0] > (*iptr2)[0])\n return 1;\n return -1;\n}\n\nint maxTwoEvents(int **events, int eventsSize, int *eventsColSize)\n{\n int ans = 0, top = 0, temp;\n int **heap = (int **)malloc(sizeof(int *) * eventsSize);\n bzero(heap, sizeof(int *) * eventsSize);\n\n // sort by endTime (events[i][1])\n qsort(events, eventsSize, sizeof(int *), cmp);\n\n for (int i = 0; i < eventsSize; i++)\n {\n push(heap, events[i], top++);\n }\n\n for (int i = 0; i < eventsSize; i++)\n {\n while (top > 0 && heap[0][0] <= events[i][1])\n {\n pop(heap, --top);\n }\n\n temp = events[i][2] + (top > 0 ? heap[0][2] : 0);\n ans = ans > temp ? ans : temp;\n }\n\n return ans;\n}\n``` | 3 | 0 | ['C'] | 0 |
two-best-non-overlapping-events | Two Best Non-overlapping Events - Easy Solution - 🌟 Nice Explanation 🌟 | two-best-non-overlapping-events-easy-sol-yxkl | Intuition\n\n1. Sort the 2-D array events with respect to the start_time so we can compare the end time of previous element in the array with the elements in ot | RAJESWARI_P | NORMAL | 2024-12-08T06:54:08.119632+00:00 | 2024-12-08T06:54:08.119666+00:00 | 219 | false | # Intuition\n\n1. Sort the 2-D array events with respect to the start_time so we can compare the end time of previous element in the array with the elements in other index greater than the previous index.\n\n1. Use suffixMax to calculate the maximum value that can be obtained at each index.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n**Initialization and pre-work**:\n\nInitialize no_events to be the no of elements in the events array.\n\n int no_events=events.length;\n\nSort the events array with respect to the startTime which is at 0-th index at each events.\n\n Arrays.sort(events,(a,b)->a[0]-b[0]);\n\nInitialize suffixMax as integer array with the length of the events array.\n \n int[] suffixMax=new int[no_events];\n\nInitialize suffixMax last element as last value of the events array which is sorted by start index.\n\n suffixMax[no_events-1]=events[no_events-1][2];\n\n**Find the maximum value at each index from last**:\n\nIterate through each elements of the events array from the last index of the array and suffixMax is calculated by finding the maximum value of the nextIndex and the current Index\'s value.\n\n for(int i=no_events-2;i>=0;i--)\n {\n suffixMax[i]=Math.max(suffixMax[i+1],events[i][2]);\n }\n\n**Find the maximum value by attending atmost two events**:\n\nInitialize maxSum to be zero.\n\n int maxSum=0;\n\nIterate through all the elements of the events array.\n\n for(int i=0;i<no_events;i++){\n\n**Binary Search to find nextEventIndex**:\n\nUse binary search to find the next non-overlapping element with the highest value by initializing the left index to be index + 1 (i+1) and the right index to be no_events - 1 , then also nextEventIndex to be -1.\n\n int left=i+1,right=no_events-1;\n int nextEventIndex=-1;\n\nIterate from left till the left is less than the right index.\n\n while(left<=right){\n\nFind the mid value by mid=left+(right-left)/2.\n\n int mid=left+(right-left)/2;\n\nCheck if the events[mid][0]>events[i][2] which indicates the non-overlapping index.So the nextEventIndex is updated as mid and the next element can be between left to right=mid-1.\n\n if(events[mid][0]>events[i][1])\n {\n nextEventIndex=mid;\n right=mid-1;\n }\n\nOtherwise, find the nextIndex from left=mid+1 to right.\n\n else\n {\n left=mid+1;\n }\n\n**nextEventIndex is valid or not**:\n\nAt the end of the binary search, if the nextEventIndex is valid,Find the maxSum which is the maximum of the maxSum and the current value plus the maximum value at the index nextEventIndex.\n\n if(nextEventIndex!=-1)\n {\n maxSum=Math.max(maxSum,events[i][2]+suffixMax[nextEventIndex]);\n }\n\nFinally, maxSum to be the maximum of the maxSum and the value of the current event index.\n\n maxSum=Math.max(maxSum,events[i][2]);\n\n**Returning the value**:\n\nThe maxSum contains the maximum value that can be obtained by choosing atmost two non-overlapping events.\n\n return maxSum;\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- ***Time complexity***: **O(nlogn)**.\n n -> number of elements in the events array.\n\n**Sorting Events**: **O(nlogn)**.\n\nThe events are sorted based on **their start times**: **O(nlogn)**.\n\n**Building suffixMax**: **O(n)**.\n\nCalculating the maximum suffix values involves a **single reverse traversal** of the events array: O(n).\n\n**Finding Non-Overlapping Event Using Binary Search**: **O(nlogn)**.\n\nFor each event (n), binary search is performed to find the next non-overlapping event: O(logn) per event.\n\n**Updating maxSum**: **O(n)**.\n\nEach event is checked to **update maxSum: O(n)**.\n\n**Overall Time Complexity**: **O(nlogn)**.\n\nHence the overall Time Complexity can be \n**O(nlogn) + O(n) + O(nlogn)=O(nlogn)**.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- ***Space complexity***: **O(n)**.\n n -> number of elements in the events array.\n\n**Suffix Array**: **O(n)**.\n\nThe suffixMax array requires **O(n) space**.\n\n**Other Variables**: **O(1)**.\n\nA few scalar variables like **maxSum, left, right, etc.: O(1)**.\n\n**Overall Space Complexity**: **O(n)**.\n\nHence overall space complexity is O(n) which is dominated by the **suffixMax array**.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n int no_events=events.length;\n Arrays.sort(events,(a,b)->a[0]-b[0]);\n\n int[] suffixMax=new int[no_events];\n suffixMax[no_events-1]=events[no_events-1][2];\n\n for(int i=no_events-2;i>=0;i--)\n {\n suffixMax[i]=Math.max(suffixMax[i+1],events[i][2]);\n }\n int maxSum=0;\n for(int i=0;i<no_events;i++)\n {\n int left=i+1,right=no_events-1;\n int nextEventIndex=-1;\n\n while(left<=right)\n {\n int mid=left+(right-left)/2;\n if(events[mid][0]>events[i][1])\n {\n nextEventIndex=mid;\n right=mid-1;\n }\n else\n {\n left=mid+1;\n }\n }\n if(nextEventIndex!=-1)\n {\n maxSum=Math.max(maxSum,events[i][2]+suffixMax[nextEventIndex]);\n }\n maxSum=Math.max(maxSum,events[i][2]);\n }\n return maxSum;\n }\n}\n``` | 3 | 0 | ['Array', 'Binary Search', 'Sorting', 'Java'] | 0 |
two-best-non-overlapping-events | C++ | Binary Search | c-binary-search-by-ahmedsayed1-3e2d | Explaining\nfor each index i binary search on the first index greater than i that have start time greater than end time of i\n\n# Complexity\nO(n * log)\n\n# Co | AhmedSayed1 | NORMAL | 2024-12-08T04:59:27.494811+00:00 | 2024-12-08T07:02:03.300061+00:00 | 452 | false | # Explaining\n<h3>for each index i binary search on the first index greater than i that have start time greater than end time of i</h3>\n\n# Complexity\n<h3>O(n * log)</h3>\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& x) {\n sort(x.begin(), x.end());\n\n int n = x.size();\n vector<int>suf(n + 1);\n\n int ans = 0;\n for(int i = n - 1; ~i ;i--)\n suf[i] = max(x[i][2], suf[i + 1]);\n\n for(int i = 0; i < n ;i++){\n int id = upper_bound(x.begin(), x.end(), vector<int>{x[i][1], (int)2e9, (int)2e9}) - x.begin();\n\n ans=max(ans, x[i][2]);\n if(id != n)\n ans = max(ans, x[i][2] + suf[id]);\n }\n return ans;\n }\n};\n\n```\n\n\n | 3 | 0 | ['Binary Search', 'Sorting', 'C++'] | 1 |
two-best-non-overlapping-events | ✅ Easy to Understand | Intuitive Approach with Binary Search with going Greedy | Detailed Video 🔥 | easy-to-understand-intuitive-approach-wi-7bfp | Intuition\nThe problem involves finding the maximum value by selecting one or two non-overlapping events. The key is to leverage the sorted order of events and | sahilpcs | NORMAL | 2024-12-08T03:53:17.118065+00:00 | 2024-12-08T03:53:17.118103+00:00 | 716 | false | # Intuition\nThe problem involves finding the maximum value by selecting one or two non-overlapping events. The key is to leverage the sorted order of events and use an auxiliary array to quickly access the maximum possible value for subsequent events. This helps efficiently calculate the maximum value by combining two non-overlapping events.\n\n# Approach\n1. **Sorting Events**: \n Sort the events by their start time. This ensures that we can use binary search to efficiently find the first valid non-overlapping event.\n\n2. **Suffix Maximum Array**: \n Create a `suffixMax` array where each index stores the maximum event value from that index to the end. This allows us to quickly get the maximum value for any valid non-overlapping event.\n\n3. **Iterate Through Events**: \n For each event, calculate the maximum value by either:\n - Only selecting the current event.\n - Combining the current event\'s value with the maximum value of a valid non-overlapping event (using binary search and `suffixMax`).\n\n4. **Binary Search**: \n Use binary search to find the first event whose start time is greater than the end time of the current event. This ensures no overlap between the two events.\n\n5. **Update Maximum Sum**: \n Keep track of the maximum value across all possible combinations.\n\n# Complexity\n- **Time Complexity**: \n - Sorting the events takes \\(O(n \\log n)\\). \n - Creating the `suffixMax` array takes \\(O(n)\\). \n - For each event, binary search takes \\(O(\\log n)\\), so iterating through all events takes \\(O(n \\log n)\\). \n **Overall**: \\(O(n \\log n)\\).\n\n- **Space Complexity**: \n - The `suffixMax` array requires \\(O(n)\\) space. \n **Overall**: \\(O(n)\\).\n\n\n# Code\n```java []\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n // Step 1: Sort the events by start time\n Arrays.sort(events, (a, b) -> Integer.compare(a[0], b[0]));\n\n int n = events.length;\n\n // Step 2: Create the suffixMax array where suffixMax[i] holds the max value from i to the end\n int[] suffixMax = new int[n];\n suffixMax[n - 1] = events[n - 1][2]; // last event\'s value is the base case\n\n for (int i = n - 2; i >= 0; i--) {\n suffixMax[i] = Math.max(suffixMax[i + 1], events[i][2]);\n }\n\n int maxSum = 0;\n\n // Step 3: For each event, find the maximum sum of choosing one or two non-overlapping events\n for (int i = 0; i < n; i++) {\n // Current event value\n int currentValue = events[i][2];\n\n // Step 4: Perform binary search to find the first event whose start time > current event\'s end time\n int validIndex = binarySearch(events, events[i][1] + 1);\n\n // If such a valid event exists, add its maximum value from suffixMax array\n if (validIndex != -1) {\n currentValue += suffixMax[validIndex];\n }\n\n // Update the maximum sum\n maxSum = Math.max(maxSum, currentValue);\n }\n\n return maxSum;\n }\n\n // Binary search to find the first event whose start time is greater than the given target time\n private int binarySearch(int[][] events, int target) {\n int left = 0, right = events.length - 1;\n while (left <= right) {\n int mid = left + (right - left) / 2;\n\n if (events[mid][0] >= target) {\n right = mid - 1;\n } else {\n left = mid + 1;\n }\n }\n\n // If we find a valid event, return its index; otherwise, return -1\n return (left < events.length) ? left : -1;\n }\n\n}\n\n```\n\nLeetCode 2054 Two Best Non Overlapping Events | Binary Search | Greedy | Razorpay Interview Question\nhttps://youtu.be/QBsf9fVFopg | 3 | 0 | ['Array', 'Binary Search', 'Sorting', 'Java'] | 2 |
two-best-non-overlapping-events | Simplified Sorting Solution without heaps / binary search - beats 96% | simplified-sorting-solution-without-heap-espc | Intuition\n- Brute Force: Sorting + double nested for loop to find the maximum interval before the current one that gives the maximum value.\n- Heap: Sort by st | lecoqif | NORMAL | 2024-12-08T01:19:55.692183+00:00 | 2024-12-08T18:15:58.072410+00:00 | 163 | false | # Intuition\n- Brute Force: Sorting + double nested for loop to find the maximum interval before the current one that gives the maximum value.\n- Heap: Sort by starts and ends, and add all intervals from ends into heap which are less than the current start. \n- Constant to keep track of max: Replace heap with a variable to keep track of max, most optimal solution.\n\n# Complexity\n- Time complexity:\n$$O(nlog(n))$$ --> for sorting the initial arrays by starts and ends\n\n- Space complexity:\n$$O(n)$$ --> extra space to store the sorted arrays\n\n# Code\n```python3 []\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n ends = sorted(events, key=lambda x: x[1])\n starts = sorted(events, key=lambda x: x[0])\n max_val = 0\n end_idx = 0\n res = 0\n\n for i in range(len(starts)):\n while end_idx < len(ends) and ends[end_idx][1] < starts[i][0]:\n max_val = max(max_val, ends[end_idx][2])\n end_idx += 1\n \n res = max(res, starts[i][2] + max_val)\n \n return res\n\n\n\n``` | 3 | 0 | ['Python3'] | 0 |
two-best-non-overlapping-events | (1) Optimized Greedy in Array, (2) Max HeapQueue with Explanation | 1-optimized-greedy-in-array-2-max-heapqu-1v8r | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nGreedy in Array.\n\n# Complexity\n- Time complexity: O(n * log n)\n Add y | stalebii | NORMAL | 2024-12-08T00:45:32.905280+00:00 | 2024-12-08T01:22:15.307261+00:00 | 259 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nGreedy in Array.\n\n# Complexity\n- Time complexity: O(n * log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n event = [] # store (time, load/unload, value)\n\n for start, end, value in events:\n event += [(start, 1, value)]\n event += [(end + 1, -1, value)]\n\n # sort based on the time increasingly\n event = sorted(event)\n\n res = 0 # the maximum aggregation we can build so far\n max_value = 0 # the maximum value seen so far \n\n for time, load, value in event:\n # see a new job, update the aggregation to \n if load == 1:\n res = max(res, max_value + value)\n \n # otherwise, only update max_val seen so far\n else:\n max_value = max(max_value, value)\n\n return res\n```\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nMax HeapQueue.\n\n# Complexity\n- Time complexity: O(n * log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n maxhpq = [(0, float(\'inf\'))] # max heap storing (value, starting time)\n\n for start, _, value in events:\n heappush(maxhpq, (-value, start))\n\n # 1. sort based on the ending time increasingly\n events = sorted(events, key=lambda x: x[1])\n\n res = 0 # the maximum aggregation we can build so far\n max_value = 0 # the maximum value seen so far \n\n # 2. iterate over sorted evnets \n for _, end, value in events:\n # update\n max_value = max(max_value, value)\n\n # clean up max heap if the current and is greater than max heap time\n while maxhpq and end >= maxhpq[0][1]:\n heappop(maxhpq)\n\n # check the aggregation \n res = max(res, max_value - maxhpq[0][0])\n\n return res\n``` | 3 | 0 | ['Array', 'Binary Search', 'Dynamic Programming', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Python', 'Python3'] | 0 |
two-best-non-overlapping-events | Greedy Approach | greedy-approach-by-shivamsingh00141-wyq7 | Intuition\nThe best way to choose an interval works as follows:\n\n-> choose any interval\n-> sum the value of chose events with the maximum value of events whi | shivamsingh00141 | NORMAL | 2023-10-24T18:02:03.565477+00:00 | 2023-10-24T18:02:03.565496+00:00 | 158 | false | # Intuition\nThe best way to choose an interval works as follows:\n\n-> choose any interval\n-> sum the value of chose events with the maximum value of events which ended before it \n-> Now the maximum of the value we obtained in the above step is the answer\n\n# Complexity\n- Time complexity:\nO(nlog(n))\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n vector<pair<int, int>> start, end;\n\n for(const auto &it: events) {\n start.push_back({it[0], it[2]});\n end.push_back({it[1], it[2]});\n }\n\n sort(start.begin(), start.end());\n sort(end.begin(), end.end());\n\n int si = 0, ei = 0, mxe = 0, ans = 0;\n\n while(si < events.size()) {\n while(end[ei].first < start[si].first) {\n mxe = max(mxe, end[ei].second);\n ei++;\n }\n\n ans = max(ans, start[si].second + mxe);\n\n si++;\n }\n\n return ans;\n }\n};\n```\n\nI\'m still learning the best way to share my learnings and approach. Please let me know if there is something I can improve\n | 3 | 0 | ['Greedy', 'C++'] | 0 |
two-best-non-overlapping-events | Python minheap solution | Leetcode 1477 | python-minheap-solution-leetcode-1477-by-u0hq | \ndef maxTwoEvents(self, events: List[List[int]]) -> int:\n\tq, cur, ans = [], 0, 0\n\tfor s, e, v in sorted(events):\n\t\twhile(q and q[0][0]<s):\n\t\t\tcur = | vincent_great | NORMAL | 2022-10-12T05:27:25.910573+00:00 | 2022-10-13T07:34:40.148709+00:00 | 191 | false | ```\ndef maxTwoEvents(self, events: List[List[int]]) -> int:\n\tq, cur, ans = [], 0, 0\n\tfor s, e, v in sorted(events):\n\t\twhile(q and q[0][0]<s):\n\t\t\tcur = max(cur, heappop(q)[1])\n\t\tans = max(ans, cur+v)\n\t\theappush(q, (e, v))\n\treturn ans\n```\nSimilar problem:\n[1477. Find Two Non-overlapping Sub-arrays Each With Target Sum](https://leetcode.com/problems/find-two-non-overlapping-sub-arrays-each-with-target-sum/discuss/2697518/Python-prefix-sum-solution-or-min_heap-or-Leetcode-2054) | 3 | 0 | [] | 0 |
two-best-non-overlapping-events | C++ || Min Heap | c-min-heap-by-narayan1281-ntl5 | \nclass Solution {\npublic:\n \n int maxTwoEvents(vector<vector<int>>& events) {\n int n = events.size();\n priority_queue<pair<int,int>,vec | narayan1281 | NORMAL | 2022-09-18T11:43:02.887399+00:00 | 2022-09-18T11:43:02.887437+00:00 | 289 | false | ```\nclass Solution {\npublic:\n \n int maxTwoEvents(vector<vector<int>>& events) {\n int n = events.size();\n priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> pq;\n // priority queue minheap --> to store endtime and values of the events\n sort(events.begin(),events.end()); // sort according to start time\n \n int result = 0;\n int maxval = 0; // maxvalue stores the maximum value of the values encountered so far and \n // whose ending time is less than the start time of the current event\n for(int i=0; i<n; i++)\n {\n while(!pq.empty() && pq.top().first < events[i][0])\n {\n maxval = max(maxval,pq.top().second);\n pq.pop();\n }\n result = max(result, maxval + events[i][2]);\n pq.push({events[i][1],events[i][2]});\n }\n return result;\n \n }\n};\n``` | 3 | 0 | [] | 1 |
two-best-non-overlapping-events | C++ Memoization code using simple upper bound function || Easy-Understanding | c-memoization-code-using-simple-upper-bo-62vo | \nint dp[100005][3];\n vector<int> vec;\n \n int func( vector<vector<int>> &events , int i , int choose , int n)\n {\n if(i==n)\n {\n | KR_SK_01_In | NORMAL | 2022-03-25T15:04:54.471538+00:00 | 2022-03-25T15:05:33.657650+00:00 | 295 | false | ```\nint dp[100005][3];\n vector<int> vec;\n \n int func( vector<vector<int>> &events , int i , int choose , int n)\n {\n if(i==n)\n {\n return 0;\n }\n \n if(choose>=2)\n {\n return 0;\n }\n \n if(dp[i][choose]!=-1)\n {\n return dp[i][choose];\n }\n \n int val1= func(events , i+1 , choose , n);\n \n int idx=upper_bound(vec.begin(),vec.end() , events[i][1])-vec.begin();\n\t\t\n // upper bound will be implemented in sorted array only \n // as we have to calculate the starting index of that events[i][1] \n // so we will make the vec array \n\t\t\n int val2= events[i][2] + func(events , idx , choose + 1 , n);\n\t\t\n // This is simple knapsack , take it or not take it \n // as we need only at max 2 takes , so we make a choose variable \n // intially choose = 0 , if ( choose >=2) return 0\n\t\t\n return dp[i][choose]=max(val1 , val2);\n }\n int maxTwoEvents(vector<vector<int>>& events) {\n \n int n=events.size();\n \n sort(events.begin(),events.end());\n \n for(int i=0;i<events.size();i++)\n {\n vec.push_back(events[i][0]);\n }\n \n memset( dp , -1 , sizeof(dp));\n \n return func(events ,0 , 0,n);\n \n \n }\n``` | 3 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'Binary Tree', 'C++'] | 0 |
two-best-non-overlapping-events | Explained C++ Min-heap Solution | explained-c-min-heap-solution-by-bishalp-dduy | Sort all the intervals in the events vector based on start time. The reason to sort this using start time will help when we check whether my current interval is | bishalpandit | NORMAL | 2021-11-03T08:49:23.100216+00:00 | 2021-11-03T08:49:23.100243+00:00 | 313 | false | 1. Sort all the intervals in the events vector based on start time. The reason to sort this using start time will help when we check whether my current interval is non-overlapping with the interval at the top of min-heap(priority queue).\n\n2. You have to maintain a `min-heap` which will make sure you can have the interval with least ending time at the top/front so that you will have better chances that your current interval can get a match.\n3. If the current interval\'s start time > end time of interval at top of priority queue, you get a match as they would be non-overlapping. So you maintain a `Max` of the value of intervals from the min-heap. And after getting the ultimate match for every current interval, you maintain a `ans` and update it with `Max + curVal`.\n4. At the end, you push the current interval in the min-heap for that will be checked for pairing for further intervals.\n\n\n```\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n \n sort(events.begin(),events.end());\n \n priority_queue<tuple<int,int,int>> pq;\n int Max = 0, ans = 0;\n for(int i=0;i<events.size();i++) {\n \n while(!pq.empty()) {\n \n auto top = pq.top();\n if(events[i][0] > -get<0>(top)) {\n Max = max(Max,get<2>(top));\n pq.pop();\n continue;\n }\n break;\n }\n \n ans = max(ans, Max + events[i][2]);\n pq.push(make_tuple(-1*events[i][1],events[i][0],events[i][2]));\n }\n \n return ans;\n }\n};\n``` | 3 | 0 | ['Sorting', 'Heap (Priority Queue)'] | 0 |
two-best-non-overlapping-events | [Python] Heap for (end, val) | O(NlogN) | python-heap-for-end-val-onlogn-by-rpashu-ku93 | O(NlogN) | O(N)\n1. Sort by start time\n2. Clean all elements from the heap with end < start and keep max V as res1\n3. Calculate max sum for at most two as res | rpashuto | NORMAL | 2021-10-30T16:45:07.513923+00:00 | 2021-10-30T16:51:13.465232+00:00 | 2,379 | false | O(NlogN) | O(N)\n1. Sort by start time\n2. Clean all elements from the heap with end < start and keep max V as res1\n3. Calculate max sum for at most two as res2, where res1 is largest v with end < current start\n3. Populate the heap at each event with (end, val) to consider it later, after we\'ll reach first start > this end\n\n```\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n events.sort()\n heap = [] # (end, val)\n res1 = res2 = 0 # res1 - max for one, res2 - max sum of at most two\n for s, e, v in events:\n while heap and heap[0][0] < s:\n res1 = max(res1, heapq.heappop(heap)[1])\n res2 = max(res2, res1 + v) \n heapq.heappush(heap, (e, v))\n return res2\n``` | 3 | 1 | [] | 0 |
two-best-non-overlapping-events | c++ solution using binary search not stl | c-solution-using-binary-search-not-stl-b-46oj | \nclass Solution {\npublic:\n static bool cmp(vector<int>&v1,vector<int>&v2)\n {\n return v1[1]<v2[1];\n }\n int maxTwoEvents(vector<vector<i | dilipsuthar17 | NORMAL | 2021-10-30T16:02:53.913301+00:00 | 2021-10-31T09:37:33.504204+00:00 | 405 | false | ```\nclass Solution {\npublic:\n static bool cmp(vector<int>&v1,vector<int>&v2)\n {\n return v1[1]<v2[1];\n }\n int maxTwoEvents(vector<vector<int>>&nums) \n {\n int n=nums.size();\n // vector<int>dp(n+10,0);\n sort(nums.begin(),nums.end(),cmp);\n // dp[0]=nums[0][2];\n int ans=nums[0][2];\n for(int i=1;i<n;i++)\n {\n int s=nums[i][0];\n int e=nums[i][1];\n int cost=nums[i][2];\n nums[i][2]=max(nums[i][2],nums[i-1][2]);\n int l=0;\n int r=i-1;\n int index=-1;\n while(l<=r)\n {\n int mid=(l+r)/2;\n if(nums[mid][1]<s)\n {\n index=mid;\n l=mid+1;\n }\n else\n {\n r=mid-1;\n }\n }\n if(index!=-1)\n {\n cost+=nums[index][2];\n }\n ans=max(ans,cost);\n }\n \n return ans;\n }\n};\n``` | 3 | 0 | ['C', 'Binary Tree', 'C++'] | 2 |
two-best-non-overlapping-events | [ C++ | Java | Kotlin ] Simple binary search solution, detailed explanation, beats 100% 🚀 | c-java-kotlin-simple-binary-search-solut-uv82 | Intuition\nThe key insight is that since we can only select up to two non-overlapping events, we can:\n1. First sort the events by start time to make it easier | DmitryNekrasov | NORMAL | 2024-12-08T15:18:55.826457+00:00 | 2024-12-08T15:31:48.616928+00:00 | 67 | false | # Intuition\nThe key insight is that since we can only select up to two non-overlapping events, we can:\n1. First sort the events by start time to make it easier to find non-overlapping pairs\n2. For each event, try to pair it with the best possible non-overlapping event that comes after it\n3. Use preprocessing to quickly find the maximum value available after any given point\n\n# Approach\n1. Sort Events:\n - Sort all events by their start time to establish a clear timeline\n - This makes it easier to find non-overlapping events since we know all potential second events must start after the first one ends\n\n2. Precompute Maximum Values (maxSuffix array):\n - Create an array that stores the maximum value achievable from each position onwards\n - For each position i, maxSuffix[i] = max(current event value, maxSuffix[i+1])\n - This lets us quickly find the best possible second event after any point\n\n3. Binary Search for Non-overlapping Events:\n - For each event, we need to find the first event that starts after this event ends\n - Use binary search since the events are sorted by start time\n - This is much more efficient than checking each subsequent event ($$O(log(n)$$) vs $$O(n)$$)\n\n4. Calculate Maximum Value:\n - For each event i:\n * Take its value\n * Find the first non-overlapping event after it using binary search\n * Add the maximum possible value from that point (using maxSuffix)\n - Keep track of the maximum sum found\n\n# Complexity\nTime Complexity: $$O(n * log(n))$$ where n is the number of events\n- Sorting: $$O(n * log(n))$$\n- Creating maxSuffix: $$O(n)$$\n- For each event, binary search: $$O(n * log(n))$$\n\nSpace Complexity: $$O(n)$$ for the maxSuffix array\n\nThis solution efficiently handles the constraints of non-overlapping events while finding the maximum possible value using two key optimizations: precomputed maximum values and binary search for finding valid pairs.\n\n# Code\n```kotlin []\nclass Solution {\n fun maxTwoEvents(events: Array<IntArray>): Int {\n events.sortBy { it.first() }\n val n = events.size\n val maxSuffix = IntArray(n)\n maxSuffix[n - 1] = events[n - 1].last()\n for (i in n - 2 downTo 0) {\n maxSuffix[i] = max(maxSuffix[i + 1], events[i].last())\n }\n\n fun binSearch(left: Int, right: Int, target: Int): Int {\n if (left >= right) return right\n val mid = left + (right - left) / 2\n return if (events[mid].first() > target) binSearch(left, mid, target) else binSearch(mid + 1, right, target)\n }\n\n return events.indices.maxOf { i ->\n events[i].last() + binSearch(i + 1, n, events[i][1]).let { if (it < n) maxSuffix[it] else 0 }\n }\n }\n}\n```\n```java []\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n Arrays.sort(events, Comparator.comparingInt(a -> a[0]));\n \n int n = events.length;\n int[] maxSuffix = new int[n];\n \n maxSuffix[n - 1] = events[n - 1][2];\n for (int i = n - 2; i >= 0; i--) {\n maxSuffix[i] = Math.max(maxSuffix[i + 1], events[i][2]);\n }\n \n int maxValue = 0;\n for (int i = 0; i < n; i++) {\n int currentValue = events[i][2];\n int nextEventIndex = binSearch(i + 1, n, events[i][1], events);\n int additionalValue = (nextEventIndex < n) ? maxSuffix[nextEventIndex] : 0;\n maxValue = Math.max(maxValue, currentValue + additionalValue);\n }\n \n return maxValue;\n }\n \n private int binSearch(int left, int right, int target, int[][] events) {\n if (left >= right) {\n return right;\n }\n \n int mid = left + (right - left) / 2;\n if (events[mid][0] > target) {\n return binSearch(left, mid, target, events);\n } else {\n return binSearch(mid + 1, right, target, events);\n }\n }\n}\n```\n```cpp []\nclass Solution {\nprivate:\n int binSearch(int left, int right, int target, const vector<vector<int>>& events) {\n if (left >= right) {\n return right;\n }\n \n int mid = left + (right - left) / 2;\n if (events[mid][0] > target) {\n return binSearch(left, mid, target, events);\n } else {\n return binSearch(mid + 1, right, target, events);\n }\n }\n \npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(), events.end(), \n [](const vector<int>& a, const vector<int>& b) {\n return a[0] < b[0];\n });\n \n int n = events.size();\n vector<int> maxSuffix(n);\n \n maxSuffix[n - 1] = events[n - 1][2];\n for (int i = n - 2; i >= 0; i--) {\n maxSuffix[i] = max(maxSuffix[i + 1], events[i][2]);\n }\n \n int maxValue = 0;\n for (int i = 0; i < n; i++) {\n int currentValue = events[i][2];\n int nextEventIndex = binSearch(i + 1, n, events[i][1], events);\n int additionalValue = (nextEventIndex < n) ? maxSuffix[nextEventIndex] : 0;\n maxValue = max(maxValue, currentValue + additionalValue);\n }\n \n return maxValue;\n }\n};\n```\n\n | 2 | 0 | ['Array', 'Binary Search', 'Sorting', 'C++', 'Java', 'Kotlin'] | 1 |
two-best-non-overlapping-events | Simple Binary search solution | simple-binary-search-solution-by-pranavj-8ft4 | Maximum Sum of Two Non-Overlapping Events\n\n## Problem Description\nGiven an array of events where each event is represented as a triplet \([s, e, v]\): \n- \ | pranavjarande | NORMAL | 2024-12-08T12:34:12.430616+00:00 | 2024-12-08T12:34:12.430656+00:00 | 23 | false | # Maximum Sum of Two Non-Overlapping Events\n\n## Problem Description\nGiven an array of events where each event is represented as a triplet \\([s, e, v]\\): \n- \\(s\\): Start time of the event. \n- \\(e\\): End time of the event. \n- \\(v\\): Value of the event. \n\nThe goal is to find the **maximum sum of values** from two non-overlapping events.\n\n## Approach\n\n### Intuition\nTo maximize the sum of two events, we need to ensure that the two selected events do not overlap. Sorting the events by their start time enables efficient validation of the non-overlapping condition using binary search.\n\n### Algorithm\n1. **Sort Events**: \n Sort the events based on their start time. This simplifies finding a valid second event for a given first event.\n\n2. **Precompute Maximum Values**: \n Use a `maxi` array where `maxi[i]` stores the maximum event value from index \\(i\\) to the end. This allows quick retrieval of the best value for the second event.\n\n3. **Binary Search**: \n For each event, use binary search to find the next valid event (starting after the current event ends). Add the value of this event to the value of the current event.\n\n4. **Iterate and Update Maximum Sum**: \n Iterate through all events to calculate the maximum sum of values from two non-overlapping events.\n\n5. **Return the Result**: \n Return the maximum value obtained.\n\n---\n\n## Complexity\n\n### Time Complexity\n- Sorting the events: \\(O(n \\log n)\\). \n- Computing the `maxi` array: \\(O(n)\\). \n- Performing binary search for each event: \\(O(n \\log n)\\). \n- **Total**: \\(O(n \\log n)\\).\n\n### Space Complexity\n- `maxi` array: \\(O(n)\\). \n- Sorting space overhead: \\(O(n)\\). \n- **Total**: \\(O(n)\\).\n\n---\n\n## Code\n```cpp\nclass Solution {\npublic:\n int n;\n\n int bs(int e, vector<vector<int>>& a, vector<int>& maxi) {\n int l = 0, r = n - 1;\n int ans = INT_MIN;\n while (l <= r) {\n int mid = l + (r - l) / 2;\n if (a[mid][0] >= e) {\n ans = maxi[mid];\n r = mid - 1;\n } else {\n l = mid + 1;\n }\n }\n return ans;\n }\n\n int maxTwoEvents(vector<vector<int>>& a) {\n sort(a.begin(), a.end());\n n = a.size();\n vector<int> maxi(n, 0);\n int ans = INT_MIN;\n\n for (int i = n - 1; i >= 0; i--) {\n ans = max(ans, a[i][2]);\n maxi[i] = max(maxi[i], a[i][2]);\n if (i + 1 < n) maxi[i] = max(maxi[i], maxi[i + 1]);\n }\n\n for (int i = 0; i < n; i++) {\n int ta = a[i][2];\n int en = a[i][1] + 1;\n ta += bs(en, a, maxi);\n ans = max(ans, ta);\n }\n\n return ans;\n }\n};\n | 2 | 0 | ['Binary Search', 'Prefix Sum', 'C++'] | 0 |
two-best-non-overlapping-events | ✅ [Python] - Quick and Easy | python-quick-and-easy-by-danielol-oott | \n# Code\npython3 []\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n \n # Sort events by end time\n events. | DanielOL | NORMAL | 2024-12-08T11:41:13.561709+00:00 | 2024-12-08T11:41:13.561748+00:00 | 110 | false | \n# Code\n```python3 []\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n \n # Sort events by end time\n events.sort(key=lambda x: x[1])\n\n # Store maximum value of events seen so far\n max_value = 0\n result = 0\n\n # Create a list to store the maximum value until each event ends\n max_until = []\n end_times = []\n\n for start, end, value in events:\n\n #Use binary search to find the latest non-overlapping event\n index = bisect.bisect_left(end_times, start) - 1\n max_previous = max_until[index] if index >= 0 else 0\n\n # Update result with the sum of current event value and maximum non-overlapping value\n result = max(result, value + max_previous)\n\n # Update maximum value seen so far\n max_value = max(max_value, value)\n max_until.append(max_value)\n end_times.append(end)\n\n return result\n``` | 2 | 0 | ['Array', 'Binary Search', 'Dynamic Programming', 'Sorting', 'Heap (Priority Queue)', 'Python3'] | 2 |
two-best-non-overlapping-events | Python DP Binary Search 3 lines | python-dp-binary-search-3-lines-by-sonng-iy65 | Intuition\n Describe your first thoughts on how to solve this problem. \n- loop each event\n- val of this event + M := max(all event that have end < this_event. | sonnguyen2201 | NORMAL | 2024-12-08T09:08:57.628480+00:00 | 2024-12-08T09:29:07.232754+00:00 | 131 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- loop each event\n- val of this event + M := max(all event that have end < this_event.start)\n- How to find M?\n - Generate array EV = [[e0,v0],[e1,v1],....[elast,vlast]]\n - we binary search this_event.start in this array EV to find the last ej < start, but the vj is not max. So create another DP from EV\n - DP = [v_max_end_at_0, v_max_end_at_1, ...]\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: NlogN\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: N\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxTwoEvents(self, events):\n ev = sorted([e, v] for s, e, v in events)\n dp = list(accumulate((v for _, v in ev), func=max, initial=0))\n return max(dp[bisect_right(ev, [s, 0])] + v for s, _, v in events)\n``` | 2 | 0 | ['Python3'] | 0 |
two-best-non-overlapping-events | 2054. Two Best Non-Overlapping Events | 2054-two-best-non-overlapping-events-by-bvdac | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | AdilShamim8 | NORMAL | 2024-12-08T07:47:56.974691+00:00 | 2024-12-08T07:47:56.974714+00:00 | 60 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nfrom bisect import bisect_right\n\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n # Sort events by end time\n events.sort(key=lambda x: x[1])\n \n # Store the maximum value at each step\n max_value = 0\n max_sum = 0\n \n # To store end times and cumulative max values\n end_times = []\n cumulative_max = []\n \n for start, end, value in events:\n # Find the index of the last event that ends before the current event\'s start\n idx = bisect_right(end_times, start - 1) - 1\n \n # Calculate max sum with the current event\n if idx >= 0:\n max_sum = max(max_sum, value + cumulative_max[idx])\n else:\n max_sum = max(max_sum, value)\n \n # Update running maximum value and cumulative lists\n max_value = max(max_value, value)\n end_times.append(end)\n cumulative_max.append(max_value)\n \n return max_sum\n\n``` | 2 | 0 | ['Python3'] | 0 |
two-best-non-overlapping-events | Pre Computation + Binary Search || O(n log n) || time better than 93.92% & space 88% | pre-computation-binary-search-on-log-n-t-53kr | \nclass Solution {\n public int maxTwoEvents(int[][] events) {\n Arrays.sort(events,(a,b)->a[0]-b[0]);\n int ans=0;\n int n=events.lengt | Syed_Anwar_leetcode | NORMAL | 2024-12-08T06:59:55.680220+00:00 | 2024-12-08T06:59:55.680255+00:00 | 139 | false | ```\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n Arrays.sort(events,(a,b)->a[0]-b[0]);\n int ans=0;\n int n=events.length;\n int[] maxVal=new int[n];\n maxVal[n-1]=events[n-1][2];\n for(int i=n-2;i>=0;i--)\n maxVal[i]=Math.max(maxVal[i+1],events[i][2]);\n \n for(int i=0;i<n;i++){\n int cur=events[i][2];\n int ind=binarySearch(events,events[i][1],i+1);\n if(ind<n)\n cur+=maxVal[ind];\n ans=Math.max(ans,cur);\n }\n \n return ans;\n }\n \n int binarySearch(int[][] events,int num,int low){\n int ans=events.length;\n int high=events.length-1;\n while(low<=high){\n int mid=(low+high)/2;\n if(events[mid][0]>num){\n ans=mid;\n high=mid-1;\n }else\n low=mid+1;\n }\n return ans;\n }\n}\n``` | 2 | 0 | ['Binary Search', 'Java'] | 0 |
two-best-non-overlapping-events | sort and use priority queue | sort-and-use-priority-queue-by-yanandsin-co0y | \n\nEvents (Sorted) ---> [Start, End, Value]\n\n Time Axis -->\nEvent 1: |------|\nEvent 2: |-------|\nEvent 3: |----|\n\nHeap ---> | yanandsingh1411 | NORMAL | 2024-12-08T05:13:45.249329+00:00 | 2024-12-08T05:13:45.249356+00:00 | 298 | false | \n```\nEvents (Sorted) ---> [Start, End, Value]\n\n Time Axis -->\nEvent 1: |------|\nEvent 2: |-------|\nEvent 3: |----|\n\nHeap ---> Keeps Events Active\n --------------\n | Event End |\n | Max Value |\n --------------\n\nmax_so_far ---> Tracks maximum value from non-overlapping events.\n\nResult ---> max(max_so_far + Current Event Value)\n```\n\n```\ncomplexity - O(nlogn)\n```\n\n# Code\n```cpp []\nclass Solution {\n struct cmp{\n bool operator()(const vector<int> &a, const vector<int> &b){\n return a[1] > b[1];\n }\n };\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n ios_base::sync_with_stdio(false);\n\n sort(events.begin(), events.end());\n priority_queue<vector<int>, vector<vector<int>>, cmp> pQ;\n int res = 0;\n int max_so_far = 0;\n for(const vector<int> &event: events){\n while(!pQ.empty() && pQ.top()[1] < event[0]) { \n max_so_far = max(max_so_far, pQ.top()[2]);\n pQ.pop();\n }\n res = max(res, max_so_far + event[2]);\n pQ.push(event);\n }\n return res;\n }\n};\n\n``` | 2 | 0 | ['Two Pointers', 'Greedy', 'Sliding Window', 'Sorting', 'Heap (Priority Queue)', 'Merge Sort', 'C++'] | 0 |
two-best-non-overlapping-events | Let come up with idea | Share thought | let-come-up-with-idea-share-thought-by-v-3udo | Intuition\n Describe your first thoughts on how to solve this problem. \nYou maybe easily find many solutions, it is not neccessary to share another solution he | vyhv | NORMAL | 2024-12-08T04:56:58.683579+00:00 | 2024-12-08T04:56:58.683604+00:00 | 78 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nYou maybe easily find many solutions, it is not neccessary to share another solution here but I want to share my thought how can I come up to final problem. I hope I can help you.\n\nLet start...\n\nFirstly, I think this problem must to be solved by using Dynamic Programming because I see that one event can be picked or not. So\n- I defined the state of DP likes that: `F(t, i)` which means `"maxVal" after attending "t" events which ends at "i" time`, t = [0..2], i = [1..1e9].\n- Now, if I want to find the `maximum val` after attending the `2nd event` is equal **maximum val after attending 1st event which ends before current 2nd event**: `F(2, endTime) = max(F(2, endTime), F(1, startTime-1) + 2nd_event_val)`\n\nI was happy as I thought this was a solution. I tried to implements like this:\n```\nsort events by end time\n\ndp[3][1e9]\n\nfor (t = 1 .. 2) {\n for (event : events) {\n startTime = event[0], endTime = event[1], val = event[2]\n\n dp[t][endTime] = max(\n dp[t][endTime],\n dp[t-1][startTime-1] + val\n )\n }\n}\n```\nBut it wrong, because I reliased that complexity is 3*1e9 :((\n\nSecondly, I think with the same idea: if choose an event as second event so I must to get the maximum val of event which ends before the current event to get the final answer. So segment tree is data structure I think to `query maximum val of events ending before the current event`. But it didn\'t work because the endTime is in range [1..1e9] it is too large (will be **Memory Limit Exceed**)\n(you can see the code segment tree at the bottom of this solution)\n\nFinnally, I come up with prefix sum, no it is not really prefix sum. I means that I use a array to maintain the maximum val of events ending before current event. And in order to `query maximum val of events ending before the current event`, I use binary search on this prefix array. \n\nAs you can see, I tight up to the idea: `query maximum val of events ending before the current event`, and try to find an efficiency way to implement this.\n\nThanks for your reading. Hope it can help u a little bit\n\n\n# Code\n# sort + prefix + binary search (Passed)\n```cpp []\n#define endTime first\n#define maxVal second\n\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n // sort events by end time\n sort(events.begin(), events.end(), [](auto& e1, auto& e2) {\n return e1[1] < e2[1];\n });\n\n // prefix stores (endTime, maxVal): maxValue of all events ends <= endTime\n vector<pair<int, int>> prefix;\n int res = 0;\n for (vector<int>& event : events) {\n int startTime = event[0], endTime = event[1], val = event[2];\n\n int maxValOfEventLessEndTime = bsearch(prefix, startTime-1);\n\n res = max(res, val + maxValOfEventLessEndTime);\n \n int prevMax = prefix.size() > 0 ? prefix.back().maxVal : 0;\n prefix.push_back({endTime, max(prevMax, val)});\n }\n\n return res;\n }\n\n /**\n Find upper bound: event which has endTime <= startTime-1 param\n Return: maxVal or 0 if can not find any event which has endTime <= startTime-1 param\n */\n int bsearch(vector<pair<int, int>>& prefix, int endTime) {\n int l = 0, r = prefix.size() - 1;\n\n int res = -1;\n while (l <= r) {\n int mid = l + (r - l) / 2;\n\n if (prefix[mid].endTime <= endTime) {\n res = mid;\n l = mid + 1;\n } else {\n r = mid - 1;\n }\n }\n\n if (res == -1) {\n return 0;\n } else {\n return prefix[res].maxVal;\n }\n }\n};\n```\n\nSegment tree solution (Not passed)\n```cpp []\nclass SegmentTree {\nprivate:\n vector<int> tree;\n int n;\n\n void updateTree(int node, int start, int end, int idx, int val) {\n // Base case: if the current segment doesn\'t include the index\n if (start > idx || end < idx) return;\n \n // Update the node with the maximum value\n tree[node] = max(tree[node], val);\n \n // If not a leaf node, recurse on children\n if (start != end) {\n int mid = start + (end - start) / 2;\n updateTree(2 * node, start, mid, idx, val);\n updateTree(2 * node + 1, mid + 1, end, idx, val);\n }\n }\n\n int queryTree(int node, int start, int end, int left, int right) {\n // If the segment is completely outside the query range\n if (start > right || end < left) return 0;\n \n // If the segment is completely inside the query range\n if (left <= start && end <= right) return tree[node];\n \n // Partial overlap, recurse on children\n int mid = start + (end - start) / 2;\n int leftMax = queryTree(2 * node, start, mid, left, right);\n int rightMax = queryTree(2 * node + 1, mid + 1, end, left, right);\n \n return max(leftMax, rightMax);\n }\n\npublic:\n SegmentTree(int size) {\n n = size;\n tree.assign(4L * n + 1, 0);\n }\n\n void update(int endTime, int val) {\n updateTree(1, 1, n, endTime, val);\n }\n\n int query(int end) {\n return queryTree(1, 1, n, 1, end);\n }\n};\n\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n // Find the maximum end time to determine segment tree size\n int maxEndTime = 0;\n for (auto& event : events) {\n maxEndTime = max(maxEndTime, event[1]);\n }\n \n // Create segment tree with maximum end time\n SegmentTree tree(maxEndTime);\n \n // Sort events by end time\n sort(events.begin(), events.end(), [](auto& e1, auto& e2) {\n return e1[1] < e2[1];\n });\n \n int res = 0;\n for (auto& event : events) {\n // Query max value of events ending before current event starts\n int maxPrevValue = tree.query(event[0] - 1);\n \n // Update maximum result\n res = max(res, maxPrevValue + event[2]);\n \n // Update segment tree with current event\'s value\n tree.update(event[1], event[2]);\n }\n \n return res;\n }\n};\n```\n\n | 2 | 0 | ['Binary Search', 'Dynamic Programming', 'Segment Tree', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
two-best-non-overlapping-events | Simple Solution With Added Comments | Binary Search | Sorting | Time Complexity O(nlogn) | | simple-solution-with-added-comments-bina-301u | Intuition\nThe solution aims to maximize the sum of values from two non-overlapping events. Events are sorted by start time for efficient binary search. A right | nvdpsaluja | NORMAL | 2024-12-08T03:53:45.312952+00:00 | 2024-12-08T03:53:45.312981+00:00 | 11 | false | # Intuition\nThe solution aims to maximize the sum of values from two non-overlapping events. Events are sorted by start time for efficient binary search. A right-max array (`rmax`) stores the maximum value of events to the right. For each event, binary search finds the next non-overlapping event, and their values are combined to compute the maximum sum.\n\n# Approach\n### Approach to Solve the Problem:\n\n1. **Sort Events by Start Time**: \n - Sort the events based on their start time to facilitate efficient binary search for non-overlapping intervals.\n\n2. **Create a Right-Max Array `rmax`**: \n - Traverse the events from right to left to compute `rmax`, where `rmax[i]` stores the maximum value of events from index `i` to the end.\n\n3. **Binary Search for Non-Overlapping Events**: \n - For each event, use binary search to find the next event that starts after the current event\'s end time.\n\n4. **Calculate Maximum Value for Two Events**: \n - For each event, calculate the sum of its value and the maximum value (`rmax`) of the non-overlapping event found using binary search.\n\n5. **Track the Overall Maximum**: \n - Update the result with the maximum sum calculated for each event pair.\n\n6. **Return the Result**: \n - Return the highest sum of values from two non-overlapping events.\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n // Time Complexity: O(n log n) (due to sorting and binary search in a loop)\n // Space Complexity: O(n) (for storing the rmax array)\n\n // Binary Search to find the first event whose start time is greater than\n // the end time of the current event\n int bs(int i, vector<vector<int>>& events, int n) {\n int low = i + 1;\n int high = n - 1;\n int mid;\n int ind = -1; // Initialize result as -1 (indicating no suitable event found)\n while (low <= high) {\n mid = low + (high - low) / 2;\n if (events[mid][0] > events[i][1]) {\n ind = mid;\n high = mid - 1;\n } else {\n low = mid + 1;\n }\n }\n return ind;\n }\n\n int maxTwoEvents(vector<vector<int>>& events) {\n int n = events.size();\n // Sort events based on their start time\n // Sorting ensures we can use binary search to find non-overlapping\n // events efficiently\n sort(events.begin(), events.end());\n\n // Create an array rmax to store the maximum value of events from the\n // current index to the end\n vector<int> rmax(n, INT_MIN);\n int maxi = INT_MIN;\n for (int i = n - 1; i >= 0; i--) {\n maxi = max(maxi, events[i][2]);\n rmax[i] = maxi;\n }\n\n // Iterate over each event and calculate the maximum value achievable by\n // selecting two non-overlapping events\n int ans = 0;\n int ind; // To store the index of the next non-overlapping event\n for (int i = 0; i < n; i++) {\n ind = bs(i, events, n);\n int val = events[i][2]; // Value of the current event\n if (ind != -1)\n val += rmax[ind]; // Add the maximum value from the right if a\n // valid index is found\n ans = max(ans, val);\n }\n return ans;\n }\n};\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n\n``` | 2 | 0 | ['C++'] | 0 |
two-best-non-overlapping-events | Simple Line Sweep Algorithm | simple-line-sweep-algorithm-by-up41guy-2xeu | More Line Sweep Problems:\nhttps://leetcode.com/problem-list/a0l633d6/\nhttps://leetcode.com/problem-list/a06u4275/\n\nhttps://carefree-ladka.github.io/js.enigm | Cx1z0 | NORMAL | 2024-12-08T03:10:57.206268+00:00 | 2024-12-08T15:35:57.225063+00:00 | 170 | false | More **Line Sweep** Problems:\nhttps://leetcode.com/problem-list/a0l633d6/\nhttps://leetcode.com/problem-list/a06u4275/\n\nhttps://carefree-ladka.github.io/js.enigma/docs/tutorial-basics/LineSweep\n\n**Intuition:**\n - Take a list with start and end points \n - [start, 1, value] & [end, -1, val] Here 1 means starting an interval and -1 interval end.\n - After pushing events to points list sort it by start time if equal sort by end\n - Now Check type is 1 (starting interval), keep adding val and store in ans\n - If type -1 , it means we have reached an end of an interval, calculate max \n - Return maxTotal \n\n\n---\n\n```javascript []\n/**\n * @param {number[][]} events\n * @return {number}\n */\nvar maxTwoEvents = function (events) {\n //const points = [];\n //events.forEach(([s, e, v]) => points.push([s, 1, v], [e, -1, v]));\n const points = events.flatMap(([s, e, v]) => [[s, 1, v], [e, -1, v]]);\n \n points.sort((a, b) => a[0] - b[0] || b[1] - a[1]);\n\n let maxDone = 0, maxTotal = 0;\n for (const [_, type, val] of points) {\n if (type === 1) maxTotal = Math.max(maxTotal, val + maxDone);\n else maxDone = Math.max(maxDone, val);\n }\n\n return maxTotal\n};\n``` | 2 | 0 | ['Array', 'Line Sweep', 'Sorting', 'JavaScript'] | 1 |
two-best-non-overlapping-events | Kotlin || Binary Search | kotlin-binary-search-by-nazmulcuet11-kq8e | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | nazmulcuet11 | NORMAL | 2024-12-08T02:33:40.914468+00:00 | 2024-12-08T02:33:40.914499+00:00 | 61 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```kotlin []\nclass Solution {\n private fun isOverlapping(a: IntArray, b: IntArray): Boolean {\n return !(a[1] < b[0] || b[1] < a[0])\n }\n\n private fun nextNonOverlappingIndex(events: Array<IntArray>, i: Int): Int {\n var l = i + 1\n var r = events.size - 1\n while (l < r) {\n val m = l + (r - l) / 2\n if (isOverlapping(events[i], events[m])) {\n l = m + 1\n } else {\n r = m\n }\n }\n return l\n }\n\n fun maxTwoEvents(events: Array<IntArray>): Int {\n events.sortBy { it[0] }\n\n val maxValues = mutableListOf<Int>()\n for (i in events.indices.reversed()) {\n if (maxValues.isEmpty()) {\n maxValues.add(events[i][2])\n } else {\n maxValues.add(maxOf(events[i][2], maxValues.last()))\n }\n }\n maxValues.reverse()\n\n var ans = 0\n for (i in events.indices) {\n ans = max(ans, events[i][2])\n val j = nextNonOverlappingIndex(events, i)\n if (j < events.size && !isOverlapping(events[i], events[j])) {\n ans = max(ans, events[i][2] + maxValues[j])\n }\n }\n return ans\n }\n}\n``` | 2 | 0 | ['Binary Search', 'Kotlin'] | 0 |
two-best-non-overlapping-events | Two Pointer w/ on-the-fly prefix sums. 100% | two-pointer-w-on-the-fly-prefix-sums-100-0una | Intuition\nBecause we can only pick two events, first simply the problem to finding a second event which maximizes the value when added to a prefix sum. \n\n# A | conorpo | NORMAL | 2024-12-08T01:24:32.528312+00:00 | 2024-12-08T01:24:32.528333+00:00 | 31 | false | # Intuition\nBecause we can only pick two events, first simply the problem to finding a **second** event which maximizes the value when added to a prefix sum. \n\n# Approach\n- Split events into starts and ends, cloning the value. \n- Sort the vectors.\n- Go left to right on the start list, for each second event cantidate,\n - Compute the prefix-sum on the fly by maxing until your second pointer passes your first. \n - Compute total value and update running max.\n\n\n# Complexity\n- Time complexity:\n$O(n \\cdot logn)$\n- Space complexity:\n$O(n)$\n\n# Code\n```rust []\nimpl Solution {\n pub fn max_two_events(events: Vec<Vec<i32>>) -> i32 {\n let (mut starts, mut ends): (Vec<(i32,i32)>, Vec<(i32,i32)>) = events.into_iter().map(|event| {\n //Start\n ((event[0], event[2]),\n //End\n (event[1], event[2]))\n }).unzip();\n\n starts.sort();\n ends.sort();\n\n let mut first_end_idx = 0;\n let mut cur_first_max = 0;\n let mut total_max = 0;\n\n for (second_start, second_val) in starts {\n while ends[first_end_idx].0 < second_start {\n cur_first_max = cur_first_max.max(ends[first_end_idx].1);\n first_end_idx += 1;\n }\n\n total_max = total_max.max(cur_first_max + second_val);\n }\n\n total_max\n }\n}\n``` | 2 | 0 | ['Rust'] | 0 |
two-best-non-overlapping-events | [JavaScript] 2054. Two Best Non-Overlapping Events | javascript-2054-two-best-non-overlapping-k0wh | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n\nPrevious approach\n\n\n1 only 2 event values needed\n2 their sum must b | pgmreddy | NORMAL | 2023-10-23T16:15:10.533138+00:00 | 2024-12-08T14:37:13.645849+00:00 | 120 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\nPrevious approach\n\n```\n1 only 2 event values needed\n2 their sum must be max\n3 the events must be non-overlapping ( seperate )\n\nsort events by end times\nmaxsum = 0\nfor each event (start, end, value)\n find an event that is before start\n till that event find max of all values - value2\n sum = value + value2\n if (sum > maxsum)\n maxsum = sum\nreturn maxsum\n\nfind an event\n this can be linear ( as given below ) - O(N) - slow\n this can be done via binary search - O(log N) - 10X faster\n\n```\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n**New code** ( since new test cases were added )\n\n---\n\n```\nvar maxTwoEvents = function (events) {\n\tevents.sort((a, b) => a[0] - b[0]); // sort by event start times\n\tconst pqEventEndVal = new PriorityQueue({ compare: (a, b) => a[0] - b[0] });\n\tlet maxPreviousEventVal = 0;\n\tlet maxTwoNonOverlappingEventsValSum = 0;\n\tfor (const [s, e, currentVal] of events) {\n\t\t// remove previous events before current start, from pq, if exists\n\t\twhile (pqEventEndVal.size() && pqEventEndVal.front()[0] < s) {\n\t\t\tconst [prevEventTime, prevEventValue] = pqEventEndVal.dequeue();\n\t\t\tmaxPreviousEventVal = Math.max(maxPreviousEventVal, prevEventValue);\n\t\t}\n\t\tmaxTwoNonOverlappingEventsValSum = //\n\t\t\tMath.max(maxTwoNonOverlappingEventsValSum, maxPreviousEventVal + currentVal);\n\t\tpqEventEndVal.enqueue([e, currentVal]); // for future\n\t}\n\treturn Math.max(maxTwoNonOverlappingEventsValSum, maxPreviousEventVal); // Return the best possible sum\n};\n```\n\n---\n | 2 | 0 | ['JavaScript'] | 1 |
two-best-non-overlapping-events | Java PriorityQueue solution | java-priorityqueue-solution-by-kantariya-k4kp | \n# Code\n\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n int res = 0, maxVal = 0;\n //Min heap by ending time\n Priori | kantariyaraj | NORMAL | 2023-02-07T09:33:26.773634+00:00 | 2023-02-07T09:33:26.773675+00:00 | 274 | false | \n# Code\n```\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n int res = 0, maxVal = 0;\n //Min heap by ending time\n PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));\n //Sort the array by start time\n Arrays.sort(events, Comparator.comparingInt(a -> a[0]));\n for (int[] e : events) {\n //Pop all the finished events and maintain maximum value till now\n while (!pq.isEmpty() && pq.peek()[0] < e[0]) {\n maxVal = Math.max(maxVal, pq.poll()[1]);\n }\n //Check for max value\n res = Math.max(res, maxVal + e[2]);\n pq.offer(new int[]{e[1], e[2]});\n }\n return res;\n }\n}\n``` | 2 | 0 | ['Java'] | 1 |
two-best-non-overlapping-events | easy to understand | easy-to-understand-by-vishwaneet_mishra-9go5 | ```\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n int dp[][] = new int[events.length][3],output = 0;\n for(int row[]:dp) Arra | Vishwaneet_Mishra | NORMAL | 2023-02-06T02:17:12.955560+00:00 | 2023-02-06T02:17:12.955589+00:00 | 305 | false | ```\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n int dp[][] = new int[events.length][3],output = 0;\n for(int row[]:dp) Arrays.fill(row,-1);\n Arrays.sort(events,(a,b)->(a[0]-b[0]));\n int out = find(dp,events,0,2);\n for(int row[]:events) output = Math.max(output,row[2]);\n return Math.max(out,output);\n }\n public int find(int dp[][],int events[][],int n,int count){\n if(count==0) return 0;\n if(n>=events.length||n==-1) return Integer.MIN_VALUE;\n if(dp[n][count]!=-1) return dp[n][count];\n int op = find(dp,events,n+1,count);\n int upper = bisearch(events,events[n][1]);\n int yo = events[n][2]+find(dp,events,upper,count-1);\n return dp[n][count] = Math.max(op,yo);\n }\n public int bisearch(int events[][],int val){\n int top=0,bot=events.length-1;\n while(top<bot){\n int mid = (bot-top)/2+top;\n if(events[mid][0]>val) bot=mid;\n else top = mid+1;\n }\n if(events[bot][0]<=val) return -1;\n return bot;\n }\n}\n//similar question \n//2555. Maximize Win From Two Segments\n//prob. same code\n//answer mentioned in comment in java\n//https://leetcode.com/problems/maximize-win-from-two-segments/discuss/3144297/C%2B%2B-or-or-DP%2BBS-or-or-Memoization-or-or-Well-Explained-Code | 2 | 0 | ['Dynamic Programming', 'Binary Tree', 'Java'] | 0 |
two-best-non-overlapping-events | Golang solution | golang-solution-by-derekmu-ch2a | Intuition\n\nConsider each event ordered by start time while keeping track of the largest already completed event in a copy of the events sorted by end time.\n\ | derekmu | NORMAL | 2023-02-02T05:33:36.354310+00:00 | 2023-02-02T05:33:36.354360+00:00 | 52 | false | # Intuition\n\nConsider each event ordered by start time while keeping track of the largest already completed event in a copy of the events sorted by end time.\n\n# Complexity\n- Time complexity: $$O(nlogn)$$ for sorting.\n\n- Space complexity: $$O(n)$$ for a copy of the events.\n\n# Code\n```\nfunc maxTwoEvents(es [][]int) int {\n // sort events by start time\n\tsort.Slice(es, func(p, q int) bool { return es[p][0] < es[q][0] })\n\n // copy of events sorted by end time\n\tee := append([][]int(nil), es...)\n\tsort.Slice(ee, func(p, q int) bool { return ee[p][1] < ee[q][1] })\n\n // resulting maximum value\n\tr := 0\n // index into ee for the events that have been completed\n\tj := -1\n // the maximum value of events that have been completed\n\tmcv := 0\n\n // consider each event\n\tfor _, e := range es {\n\n // update index and maximum value of completed events\n\t\tfor ee[j+1][1] < e[0] {\n\t\t\tj++\n\t\t\tif ee[j][2] > mcv {\n\t\t\t\tmcv = ee[j][2]\n\t\t\t}\n\t\t}\n\n // value of the current event + the maximum completed event\n\t\tv := e[2] + mcv\n\n\t\tif v > r {\n\t\t\tr = v\n\t\t}\n\t}\n\n\treturn r\n}\n``` | 2 | 0 | ['Go'] | 0 |
two-best-non-overlapping-events | Python - Brute Force ➜ Binary Search ➜ Min Heap ✅ | python-brute-force-binary-search-min-hea-02m4 | 1. BRUTE FORCE APPROACH - O(N^2)\n\nIn Brute Force approach, we just do what the problem asks us to do. We don\'t care about how efficient this solution is. But | itsarvindhere | NORMAL | 2022-10-30T13:33:08.113795+00:00 | 2023-10-09T08:42:09.246525+00:00 | 116 | false | ## **1. BRUTE FORCE APPROACH - O(N^2)**\n\nIn Brute Force approach, we just do what the problem asks us to do. We don\'t care about how efficient this solution is. But if you are able to write a Brute Force Approach, you can think of an Optimized Solution easily.\n\nSince we are asked to find two non overlapping events, we can check for that by making sure that the second event starts after the first has finished. Since it is possible that for any ith event, an event with start time greater than end time of ith event can be before it in the list, we have to traverse the whole array from beginning for every event to find a valid event to pair. \n\nHence, this approach has an O(N^2) complexity. It will not work for large inputs and we will get TLE.\n\n\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n maxSum = 0\n \n # For each event\n for i in range(len(events)): \n sum = events[i][2]\n \n # Try to find the event that can be paired with it to get a maximum sum\n for j in range(len(events)):\n if i != j and events[j][0] > events[i][1]:\n maxSum = max(maxSum, sum + events[j][2]) \n \n # This is for the cases when we cannot find any other event with which this event can be paired\n # It is also possible that a single event has a higher value than any other valid pair combined\n maxSum = max(maxSum, sum)\n return maxSum\n\t\t\n## **2. BINARY SEARCH APPROACH - O(NLogN)**\n\nWe know that if an algorithm has O(N^2) time complexity and it is not working for large inputs, a better approach is to try to make it at least O(NLogN). \n\nConverting that N to LogN complexity means instead of Linear Search in the second for loop, we need to use Binary Search. But to use Binary Search, our array needs to be sorted. \n \nNotice that in Brute Force, one issue is that for each event, we have to traverse the list from the beginning to find an event whose start time is greater than the end time of ith event.\n\n\tNow, just think about it - What if our events list is already sorted based on start time?\n\n\tIn that case, if we can find an event that is valid, then all the events after it are also valid because array is sorted. \n\t\n\tConsider this example ->\n\t\n\t\t\tevents = [[1,3,2],[4,7,3],[5,8,5], [6,4,10]]\n\t\t\t\n\t\t\tIf we take the first event => [1,3,2]\n\t\t\t\n\t\t\tFor it, start time = 1 and end time = 3\n\t\t\t\n\t\t\tIt means, any event that has start time > 3 can be paired with this event.\n\t\t\t\n\t\t\tAnd we see that [4,7,3] is a valid event since its start time is 4 and 4 > 3\n\t\t\t\n\t\t\tBut since our list is already sorted based on start times, \n\t\t\tit also means, all events after [4,7,3] are also valid and can be paired with [1,3,2]\n\t\t\t\n\t\t\tNow you got the idea, right?\n\t\t\t\n\t\t\t\n\tSo, all that we need to find is this leftmost event that is valid \n\tbecause we know all events after it will be valid as well.\n\nOnce we can find such an index, then all that is left to find is what is the maximum possible value in [leftmostindex, end of list] subarray.\n\nBut if we try to find that for each event, that again results in an O(N^2) complexity because to find that max value in a certain interval, we again have to do linear scan as values are not sorted.\n\nHence, the only option is to find a way to precompute this maximum possible value on the right side of each index such that we can find the maximum value in any range [leftmostindex, end of list] in O(1) time.\n\nTherefore, before we even start with Binary Search, we have to precompute the maximum value on the right side for each event.\n\n```\ndef maxTwoEvents(self, events: List[List[int]]) -> int:\n maxSum = 0\n \n n = len(events)\n \n # For Binary Search, we need Sorting first\n # If we apply sort method to events, it will sort the events based on start time\n events.sort()\n \n # Pre compute the maximum value on the right for each event\n maxOnRight = [0] * n\n \n # For last event, there is no event on its right\n # So for it, maximum is its value only\n maxOnRight[- 1] = events[-1][2]\n \n for i in range(n - 2, -1, -1): maxOnRight[i] = max(events[i][2], maxOnRight[i + 1])\n \n # For each event\n for i in range(n): \n sum = events[i][2]\n maxVal = 0\n\n # Now, we can use Binary Search to find the leftmost valid event for ith event\n # Because if we can find such an index, then all events after that index are also valid\n # Because array is sorted based on start time \n # so all events after that index will also have a start time greater than end time of ith event\n start = i + 1\n end = n - 1\n leftmostValid = -1\n \n while start <= end:\n mid = start + (end - start) // 2\n \n # IF mid is a valid event that we can consider pairing\n # We can store this index as it may be the leftmost valid index\n # But we keep searching on left of mid to find the leftmost if there is any other valid event on left\n if events[mid][0] > events[i][1]:\n leftmostValid = mid\n end = mid - 1\n \n # If mid itself is not valid, how can any event before mid can be valid?\n else: start = mid + 1 \n \n # Now, all that we want is what is the maximum value in the [leftmostValid, n - 1] subarray\n # No need to find that again because we have precomputed that in the beginning\n \n if leftmostValid != -1: maxVal = maxOnRight[leftmostValid]\n \n maxSum = max(maxSum, sum + maxVal)\n \n return maxSum\n```\n\n## **3. MIN HEAP APPROACH - O(NLogN)**\n\nI found the minHeap logic to be quite similar to this problem that I did recently - https://leetcode.com/problems/divide-intervals-into-minimum-number-of-groups/\n\nYou can find my solution and explanation here - https://leetcode.com/problems/divide-intervals-into-minimum-number-of-groups/discuss/4134739/python-minheap-approach-explained\n\nIf you compare both the problems and solutions, you will see that one thing that\'s common in both is that we want to avoid overlapping intervals. So, somehow, we want to find a way to quickly check for these overlaps so that we don\'t have to loop over the entire list again and again for every event, something we will do in a Brute Force solution.\n\nOne thing to note is that whenever there is a problem around events/intervals where we have to take care of overlaps, sorting should be the first thing you should do. Why? Because, if we sort the data based on either the "start" or "end" value, then it become easier to check for overlaps. How?\n\n\tLet\'s take an example => events = [[1,3,2],[4,5,2],[2,4,3]]\n\t\n\tHere, in Brute Force approach, I have to take first event [1,3,2]\n\tand then loop over all other events to check for overlaps.\n\n\tSame for [4,5,2]. I will again loop over the entire list to check for overlaps.\n\t\n\tBut, now, sort the events based on their start values\n\t\n\tevents = [[1,3,2], [2,4,3], [4,5,2]]\n\t\n\tNow, since events are sorted by start value, we can say that an event "i" starts after or at the time the event "j" ends.\n\t\n\tAnd they both will overlap based on only one condition -> If event "i" starts before or at the time when event "i - 1" ends.\n\t\n\tIn other words, for both the events to not overlap, event "i" should start "after" event "i-1" ends.\n\t\n\tNow, we can improve our Brute Force solution a bit.\n\t\n\tBecause now, for every event, we just need to loop over all the events before it \n\tand see which "non-overlapping" event has the maximum value.\n\t\n\tBut again, this means, for every event, we have to loop over the entire list on the left.\n\tAnd here comes the minHeap logic.\n\t\nAs the name says, a minHeap will order the elements by some "value" such that the top of minheap has element with the least "value" and bottom has element with the maximum "value".\n\nHow can we use this to our advantage?\n\nFor any event "i", what if we know what is the event with smallest "end" time on its left? In that case, if the event "i" overlaps with the event with the smallest "end" time on its left, we can say that it overlaps with all the events on its left. Makes sense? In this way, there is no need to individually compare the events if we already know that the event "i" overlaps with the event that has smallest "end" value on left.\n\nNow, take the opposite case. If the event "i" does not overlap with the event with smallest "end" value on its left, can we way that all the events after "i" will also not overlap? ABSOLUTELY. Because we already sorted the events by their start values. So, any event after "i" will have a start value greater or equal to it only. \n\nSince we check overlap by checking if "start" of event "i" is greater than "end" of an event on left, this condition will be true for all events on right side of "i" if it is true for "i".\n\nAnd so, we can use a minHeap to quickly get the smallest end value on left so far. And in this way, we can easily get what is the maximum "value" of an event on the left that is not overlapping. Note that if the event with the smallest "end" value on left is not overlapping with an event "i", then we can simply update the maximum value on left so far and now, we no longer require this smallest "end" value event anymore since we know it won\'t be overlapping with any event on right side of "i". So, we can then move on to the next smaller "end" value event.\n\nAnd that\'s the reason we use a minHeap here - To quickly get the smallest end value event so far and compare it with current event.\n\n\n```\ndef maxTwoEvents(self, events: List[List[int]]) -> int:\n \n # Maximum Sum\n maxSum = 0\n \n # Length of the list\n n = len(events)\n \n # A Brute Force solution will fail\n # Because, for every event, we have to loop over the whole list\n # When it comes to intervals and sorting related problems, sorting is something we can use\n # because sorting makes checking for overlaps easier\n \n # Let\'s sort the events by their start values\n events.sort()\n \n # We want to quickly check for overlaps\n # So, let\'s have a minHeap that keeps track of events so far from least end time to maximum\n # Why minHeap? because, if an event overlaps with event on top of minHeap\n # Ofcourse it will also overlap with all other events so far since they have end value\n # greater or equal to what top of heap has \n minHeap = []\n \n # What is the maximum "value" of an event so far before the current event that is not overlapping\n maxValueSoFar = 0\n \n # Loop over the events\n for event in events:\n \n # Our minHeap keeps the events by their "end" time from minimum to maximum\n # So, the top of minHeap at any time has the event with the smallest end time so far\n # So, if the current event overlaps that smallest end time event, ofcourse it will overlap with all events so far\n # So in this way, we don\'t need to compare with all the events that occured so far\n # Similarly, if the current event does not overlap with the top event\n # Then we can say all the events after it also don\'t overlap since events are sorted by start values\n while minHeap and event[0] > minHeap[0][0]: maxValueSoFar = max(maxValueSoFar, heappop(minHeap)[1])\n \n # Once we get the maximum possible "value" so far, we can update our maximum sum for the current "event"\n # And note that this "maxValueSoFar" will remain a possible max value for all upcoming events\n # Because as mentioned above, the list is sorted by "start" value\n # It means, if for an event "i", we have a "maxValueSoFar", \n # Then that will also be valid for any event at index greater than "i"\n maxSum = max(maxSum, event[2] + maxValueSoFar)\n \n # Push the current event to the minHeap as well\n heappush(minHeap, (event[1], event[2]))\n\n # Return the maximum sum\n return maxSum\n```\n\n | 2 | 0 | ['Binary Search', 'Binary Tree', 'Python'] | 1 |
two-best-non-overlapping-events | C++ | DP Memorization + Binary Search | 60% Fast | Easy to Follow Code | c-dp-memorization-binary-search-60-fast-fx5j8 | Please Upvote :)\n\n\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(),events.end());\n vector | ankit4601 | NORMAL | 2022-07-27T10:05:34.954758+00:00 | 2022-07-27T10:05:34.954791+00:00 | 671 | false | Please Upvote :)\n\n```\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(),events.end());\n vector<vector<int>> dp(events.size(),vector<int>(2,-1));\n return fun(events,dp,0,0);\n }\n int fun(vector<vector<int>>& v,vector<vector<int>>& dp,int i,int t)\n {\n if(t==2 || i>=v.size())\n return 0;\n \n if(dp[i][t]!=-1)\n return dp[i][t];\n \n int res=fun(v,dp,i+1,t);\n int next=search(v,v[i][1],i);\n res=max(res,v[i][2]+fun(v,dp,next,t+1));\n \n return dp[i][t]=res;\n }\n int search(vector<vector<int>>& v,int val,int i)\n {\n int l=i+1;\n int r=v.size()-1;\n int res=v.size();\n while(l<=r)\n {\n int mid=(l+r)/2;\n if(v[mid][0]>val)\n {\n res=mid;\n r=mid-1;\n }\n else\n l=mid+1;\n }\n return res;\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'C', 'Sorting', 'Binary Tree', 'C++'] | 0 |
two-best-non-overlapping-events | [C++] Sort + Suffix Max + Binary Search || Very Clean Code || Detailed Explanation | c-sort-suffix-max-binary-search-very-cle-cgtc | We solve the problem in 3 steps:\nStep 1 - Sort the events based on starting time.\n\nStep 2 - For every event (Starting from the last event), we find the maxim | varun09 | NORMAL | 2022-01-15T20:15:19.572024+00:00 | 2022-01-15T20:17:52.290296+00:00 | 147 | false | **We solve the problem in 3 steps:**\n***Step 1*** - Sort the events based on starting time.\n\n***Step 2*** - For every event (Starting from the last event), we find the maximum value we can get if we go to any event starting after that (Including the current event). \nWe store that value in a map, where, Key -> Start time and Value -> Maximum value we can get after attending any event scheduled on or after the start time (key).\n\n***Step 3*** - Now, for every event (say \'curr\'), we find the upper_bound of the end time of curr in the map (which stores the start times as keys). We can attend any event scheduled on/after that time (say \'t\'). Therefore, the current maximum possible score would be m[t] + value of curr.\n\n```\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n int n = events.size();\n\t\t//Step 1\n sort(events.begin(), events.end());\n map<int, int> m;\n \n\t //Step 2\n m[events[n-1][0]] = events[n-1][2];\n int curr = events[n-1][2];\n for(int i = n-2; i>=0; i--) {\n curr = max(curr, events[i][2]);\n m[events[i][0]] = curr;\n }\n \n\t //Step 3\n int res = 0;\n for(int i = 0; i<n; i++) {\n auto it = m.upper_bound(events[i][1]);\n res = max(res, events[i][2]);\n if(it != m.end()) {\n res = max(res, events[i][2] + it -> second);\n }\n }\n \n return res;\n }\n};\n```` | 2 | 0 | ['Binary Search', 'Sorting'] | 0 |
two-best-non-overlapping-events | C# Binary Search + Max Value caching | c-binary-search-max-value-caching-by-cle-rjc8 | \npublic class Solution {\n public int MaxTwoEvents(int[][] events) {\n Array.Sort(events, (x,y) => x[0].CompareTo(y[0]));\n int[] cache = new | clewby | NORMAL | 2021-12-01T20:27:35.055653+00:00 | 2021-12-01T20:29:23.618981+00:00 | 113 | false | ```\npublic class Solution {\n public int MaxTwoEvents(int[][] events) {\n Array.Sort(events, (x,y) => x[0].CompareTo(y[0]));\n int[] cache = new int[events.Length];\n cache[cache.Length-1] = events[events.Length-1][2];\n for(int i = events.Length-2; i >= 0; i--) {\n cache[i] = Math.Max(events[i][2], cache[i+1]); \n\t }\n int res = 0;\n foreach(int[] ev in events)\n {\n int val = ev[2];\n int i = search(ev[1], events);\n if(i != -1) val += cache[i];\n res = Math.Max(res, val);\n }\n return res;\n }\n \n private int search(int target, int[][] events)\n {\n int lo = 0, hi = events.Length-1;\n while(lo < hi)\n {\n int mid = lo + (hi-lo)/2;\n if(events[mid][0] > target)\n hi = mid;\n else\n lo = mid+1;\n } \n return events[lo][0] > target ? lo : -1;\n } \n}\n``` | 2 | 0 | ['Binary Tree'] | 1 |
two-best-non-overlapping-events | Different position of comparator function gives timeout, anyone explain? | different-position-of-comparator-functio-dka7 | First I place comparotor function inside the Solution class in public scope by making the comparator function static, it is giving TLE.\nThen I go through the o | nishantjain1501 | NORMAL | 2021-11-06T12:46:24.321685+00:00 | 2021-11-07T07:13:44.747333+00:00 | 132 | false | First I place comparotor function inside the Solution class in public scope by making the comparator function static, it is giving TLE.\nThen I go through the other solutions and put the comparator function in different structure now code is working fine. Can anyone please explain?\n\n```\nstruct cmp {\n bool operator()(vector<int>& node1, vector<int>& node2) {\n if(node1[1]==node2[1])\n return node1[0] < node2[0]; \n return node1[1] < node2[1]; \n }\n};\n\n\nclass Solution {\n \npublic:\n \n // static bool comp(vector<int> a, vector<int> b) {\n // if (a[1] == b[1])\n // {\n // return a[0] < b[0];\n // }\n // return a[1] < b[1];\n // }\n \n int maxTwoEvents(vector<vector<int>>& events) {\n \n sort(events.begin(), events.end(), cmp());\n vector<int> maxTill(events.size());\n \n int maxVar = 0;\n \n for(int i=0; i<events.size(); i++)\n {\n maxVar = max(events[i][2], maxVar);\n maxTill[i] = maxVar;\n }\n \n int ans = 0;\n \n for(int i=0; i<events.size(); i++)\n {\n \n int index = binarySearch(events, 0, i-1, events[i][0]) ; \n if(index>=0)\n {\n ans = max(ans, events[i][2] + maxTill[index]);\n }\n else\n ans = max(ans, events[i][2]);\n \n }\n \n return ans;\n \n }\n \n int binarySearch(vector<vector<int>>& events, int left, int right, int target)\n {\n while(left<=right)\n {\n int middle = left + (right - left)/2; \n if(events[middle][1]>=target)\n {\n right = middle-1; \n }\n else\n {\n left = middle+1; \n }\n }\n return right; \n \n }\n};\n```\n\nHere when I use the commented function` static bool comp ` in sort function as `sort(events.begin(), events.end(), comp)` it gives TLE.\n | 2 | 0 | ['C', 'Sorting', 'C++'] | 0 |
two-best-non-overlapping-events | c++ simple O(n*logn) solution | c-simple-onlogn-solution-by-hanzhoutang-r8a7 | \nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(),events.end(),[](auto& a, auto& b) {\n re | hanzhoutang | NORMAL | 2021-11-06T03:21:42.397356+00:00 | 2021-11-06T03:21:42.397384+00:00 | 228 | false | ```\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n sort(events.begin(),events.end(),[](auto& a, auto& b) {\n return a[0] < b[0];\n });\n int v = events.back()[2];\n map<int,int> m; \n for(int i = events.size()-1;i>=0;i--) {\n v = max(v,events[i][2]);\n m[events[i][0]] = v; \n }\n sort(events.begin(),events.end(),[](auto& a, auto& b) {\n return a[1] < b[1];\n });\n int ret = 0; \n for(int i = 0;i<events.size();i++) {\n ret = max(ret,events[i][2]);\n auto ptr = m.upper_bound(events[i][1]);\n if(ptr != m.end()) {\n ret = max(ret, events[i][2] + ptr->second);\n }\n }\n return ret; \n }\n};\n``` | 2 | 0 | [] | 1 |
two-best-non-overlapping-events | TreeMap (SortedMap solution) | treemap-sortedmap-solution-by-jay-lkyk | \nimport java.util.Optional;\n\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n // 1. sort by starting time. O(nlogn)\n // 2. ma | jay | NORMAL | 2021-11-05T21:40:25.294019+00:00 | 2021-11-05T21:40:25.294055+00:00 | 124 | false | ```\nimport java.util.Optional;\n\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n // 1. sort by starting time. O(nlogn)\n // 2. map of x -> y meaning for all events starting >=x, y=max value . O(n)\n // 3. iterate again, for each end position, find map.get(end+1).\n Arrays.sort(events, (int[] e1, int[] e2) ->{\n return Integer.compare(e1[0],e2[0]);\n });\n TreeMap<Integer, Integer> navMap = \n new TreeMap<Integer, Integer>();\n int max = Integer.MIN_VALUE;\n for (int i=events.length-1; i>=0; i--) {\n max = Integer.max(max, events[i][2]);\n navMap.put(events[i][0], max);\n }\n \n // 3.\n int res = 0;\n for (int[] event : events) {\n res = Integer.max(res, event[2] + Optional.ofNullable(navMap.ceilingEntry(event[1] +1)) \n .map(e->e.getValue() ).orElse(0) );\n }\n return res;\n }\n}\n``` | 2 | 0 | [] | 1 |
two-best-non-overlapping-events | Very easy c++ solution Check IT ! | very-easy-c-solution-check-it-by-bibhabe-jxe6 | New method to use max-heap queue to min heap \n int maxTwoEvents(vector>& events) {\n int n = events.size();\n int maxValue = 0;\n int ans | BibhabenduMukherjee | NORMAL | 2021-11-03T05:52:27.223784+00:00 | 2021-11-03T05:52:27.223814+00:00 | 81 | false | # New method to use max-heap queue to min heap \n** int maxTwoEvents**(vector<vector<int>>& events) {\n int n = events.size();\n int maxValue = 0;\n int ans = 0;\n // take pq (max heap)\n priority_queue<pair<int, pair<int,int>>> pq;\n sort(events.begin() , events.end());\n // store passion -> in queue ->> {endTime , {startTime , value}}\n \n for(int i = 0 ; i< n ; i++){\n // (-1)* value makes max heap to min heap \n // we want min heap for first event that end earlier\n while(!pq.empty() && (-1* pq.top().first) < events[i][0])\n {\n // take what fist event given me maxValue\n maxValue = max(maxValue , pq.top().second.second);\n pq.pop();\n \n }\n \n // push the first event taking this value as ans\n ans = max(ans , maxValue+events[i][2]);\n pq.push({-1*events[i][1] , {events[i][0], events[i][2]}});\n }\n return ans; \n } | 2 | 0 | [] | 0 |
two-best-non-overlapping-events | Java | sort | sweep line | no DP or BST or TreeMap | java-sort-sweep-line-no-dp-or-bst-or-tre-hur6 | Solution 1 -- sweep line\n\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n List<int[]> list = new ArrayList<>();\n for(int i = | qin10 | NORMAL | 2021-11-02T19:26:40.492981+00:00 | 2021-11-02T19:50:48.658681+00:00 | 127 | false | Solution 1 -- sweep line\n```\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n List<int[]> list = new ArrayList<>();\n for(int i = 0; i < events.length; ++i) {\n int[] arrStart = new int[]{events[i][0], 1, events[i][2]}; // {startTime, 1, value}\n int[] arrEnd = new int[]{events[i][1] + 1, 0, events[i][2]}; // {endTime + 1, 0, value} (+1 for exclusive)\n list.add(arrStart);\n list.add(arrEnd);\n }\n \n Collections.sort(list, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]); //sort by timstamp. if same, put startTime before endTime..\n \n int maxSoFar = 0, maxRes = 0;\n for(int j = 0; j < list.size(); ++j) {\n if(list.get(j)[1] == 1) //startTime\n maxRes = Math.max(maxRes, maxSoFar + list.get(j)[2]);\n else //endTime\n maxSoFar = Math.max(maxSoFar, list.get(j)[2]);\n }\n return maxRes;\n }\n}\n```\n\nsolution2 -- TreeMap\n\n```\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n Arrays.sort(events, (a, b) -> a[1] - b[1]);\n TreeMap<Integer, Integer> map = new TreeMap<>(){{put(0, 0);}};\n \n int maxP = 0;\n for(int[] event : events) {\n maxP = Math.max(maxP, event[2] + map.lowerEntry(event[0]).getValue());\n \n int hi = Math.max(event[2], map.lastEntry().getValue());\n map.put(event[1], hi);\n }\n \n return maxP;\n }\n} | 2 | 0 | [] | 0 |
two-best-non-overlapping-events | C++ with comments | Easy Explanation | Map STL | c-with-comments-easy-explanation-map-stl-7mqb | \nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& e) {\n \n map<int,int>startTimeAndMaxi ; \n \n int maximum = | shreyas_010701 | NORMAL | 2021-10-31T07:32:19.098564+00:00 | 2021-10-31T07:32:19.098608+00:00 | 144 | false | ```\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& e) {\n \n map<int,int>startTimeAndMaxi ; \n \n int maximum = 0 ; \n int answer = 0 ; \n \n sort(e.begin() , e.end()) ; // Sorted acc. to StartTime\n \n int size = e.size() ; \n \n while(size--){\n \n auto itr = startTimeAndMaxi.upper_bound(e[size][1]) ; // itr points to startTime which is next greater than current Endtime (e[size][1]) --> it removes overlapping\n \n maximum = max(maximum, e[size][2]) ; // assuming that curr is the only possible max value\n \n startTimeAndMaxi[e[size][0]] = maximum ; // mapping curr start time with maximum value\n \n if(itr == startTimeAndMaxi.end()){\n answer = max(answer , maximum) ; // itr not able to find the next startTime\n }\n else{\n answer = max(answer , itr->second + e[size][2]) ; // itr found next startTime . Now it will add currVal + maximum value till now\n }\n // answer and maximum keep getting updated\n }\n \n return answer; \n \n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'C'] | 1 |
two-best-non-overlapping-events | Simple code with Explanation and Analysis | Binary search | simple-code-with-explanation-and-analysi-r0a0 | \n\nApproach:\n Sort events by startTime and traverse from event with highest startTime\n While traversing If we can find an event whose startTime > endTime of | bitmasker | NORMAL | 2021-10-31T04:33:35.038060+00:00 | 2021-10-31T04:33:35.038096+00:00 | 125 | false | <br>\n\n**Approach:**\n* Sort events by startTime and traverse from event with highest startTime\n* While traversing If we can find an event whose startTime > endTime of current event then it means we can take these two in our answer set and we will update the answer accordingly\nelse we can only take the current event and update the answer accordingly\n\n<br>\n\n**Will it always give optimal answer ?**\n\nYes, because we are sorting events by startTime and traversing from event with highest startTime, so we will always have the later starting event in our map and apply binary search for endTime of current event on it, \nso we will not miss any two non - overlapping events and also all the events are getting traversed so the case where taking only events is optimal will not be missed.\n\n**Example:** If we currently have [s, e, p] then in map there are events with [s + x, e\', p\'] and only those can be non - overlapping\n<br>\n\n**Time complexity:**\n\nO(n * logn) [sort] + n * (O(logn) [binary search] + O(logn) [insert in map])\n \n = O(n * logn) + n * (2 * O(logn))\n \n = O(n * logn) + 2 * O(n * logn)\n \n ~ **O(n * logn)**\n<br>\n\n**C++ Code:**\n\n\n```\nclass Solution {\npublic:\n int maxTwoEvents(vector<vector<int>>& e) {\n \n int n = e.size();\n int ans = 0, curMax = 0;\n \n // sort events by startTime\n sort(begin(e), end(e));\n \n // mp[i] = j denotes event started at i will give profit of j\n map<int, int> mp;\n \n // start traversing from event with max startTime\n for(int i = n-1; i >= 0; i--) {\n \n // seach for startTime > current endTime\n auto start = mp.upper_bound(e[i][1]);\n \n // current max profit possible (for one event)\n curMax = max(curMax, e[i][2]);\n \n mp[e[i][0]] = curMax;\n \n // if there was no startTime > endTime, we will update answer by taking only current event\n // if we found that, then we will take that event and add current event to it\n if(start == mp.end())\n ans = max(ans, curMax);\n else\n ans = max(ans, e[i][2] + start->second);\n }\n \n return ans;\n }\n};\n```\n\n<br> | 2 | 0 | ['C', 'Sorting', 'Binary Tree'] | 1 |
two-best-non-overlapping-events | C++ || Using Sorting Technique || Simple || | c-using-sorting-technique-simple-by-kund-kvjg | \tclass Solution {\n\tpublic:\n int maxTwoEvents(vector>& events) {\n int res=0;\n int emax=0;\n vector> start;\n vector> end;\n | kundankumar4348 | NORMAL | 2021-10-31T00:22:02.265962+00:00 | 2021-10-31T00:22:02.266021+00:00 | 89 | false | \tclass Solution {\n\tpublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n int res=0;\n int emax=0;\n vector<pair<int,int>> start;\n vector<pair<int,int>> end;\n for(int i=0;i<events.size();++i)\n start.push_back({events[i][0],events[i][2]});\n for(int i=0;i<events.size();++i)\n end.push_back({events[i][1],events[i][2]});\n sort(start.begin(),start.end());\n sort(end.begin(),end.end());\n int j=0;\n for(int i=0;i<start.size();++i){\n res = max(res,start[i].second);\n while(end[j].first < start[i].first){\n emax = max(emax,end[j].second);\n j++;\n }\n res = max(res,start[i].second + emax);\n \n }\n return res;\n }\n\t}; | 2 | 0 | [] | 0 |
two-best-non-overlapping-events | javascript sort + pre max sum 876ms | javascript-sort-pre-max-sum-876ms-by-hen-h7zf | \nconst maxTwoEvents = (a) => {\n let d = [], res = 0, maxPreSum = 0;\n for (const [start, end, sum] of a) {\n d.push([start, sum, 1]);\n d. | henrychen222 | NORMAL | 2021-10-30T16:53:05.134570+00:00 | 2021-10-30T16:53:05.134599+00:00 | 204 | false | ```\nconst maxTwoEvents = (a) => {\n let d = [], res = 0, maxPreSum = 0;\n for (const [start, end, sum] of a) {\n d.push([start, sum, 1]);\n d.push([end, sum, -1])\n }\n d.sort((x, y) => {\n if (x[0] != y[0]) return x[0] - y[0];\n return y[2] - x[2];\n });\n for (const [, sum, flag] of d) {\n if (flag == -1) {\n maxPreSum = Math.max(maxPreSum, sum);\n } else {\n res = Math.max(res, maxPreSum + sum);\n }\n }\n return res;\n};\n``` | 2 | 0 | ['Sorting', 'JavaScript'] | 0 |
two-best-non-overlapping-events | Python | O(nlogn) solution | sort, binary search | python-onlogn-solution-sort-binary-searc-mgrg | \nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n events.sort()\n N = len(events)\n\n start, end, vals = [], | ilyas_01 | NORMAL | 2021-10-30T16:46:36.406962+00:00 | 2021-10-30T18:50:09.828760+00:00 | 160 | false | ```\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n events.sort()\n N = len(events)\n\n start, end, vals = [], [], []\n for s,e,v in events:\n start.append(s)\n end.append(e)\n vals.append(v)\n \n max_at_index = {}\n curr = float("-inf")\n for i in range(N-1,-1,-1):\n curr = max(vals[i], curr)\n max_at_index[i] = curr\n \n ans = float(\'-inf\')\n for i,s in enumerate(start):\n second = bisect.bisect(start, end[i])\n if second < N:\n ans = max(ans, vals[i] + max_at_index[second])\n else:\n ans = max(ans,vals[i])\n return ans\n``` | 2 | 1 | ['Sorting', 'Binary Tree', 'Python'] | 0 |
two-best-non-overlapping-events | [Java] Simple solution using TreeMap - binary search, storing past max profit for the exit time | java-simple-solution-using-treemap-binar-mmrz | Simple Steps:\n1. Split each event into 2 sub events - start and end (identify by -ve value of profit)\n2. If new start sub event comes see if the maxProfit pr | mystic13 | NORMAL | 2021-10-30T16:10:45.810440+00:00 | 2021-10-30T16:14:45.191751+00:00 | 169 | false | **Simple Steps:**\n1. Split each event into 2 sub events - start and end (identify by -ve value of profit)\n2. If new start sub event comes see if the maxProfit present in an end sub event which was before current start using TreeMap lowerEntry function.\n3. When end sub event comes store maxRemoved and make an entry for that end event time in a TreeMap.\n```\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n int n = events.length;\n int[][] inout = new int[2*n][2];\n for(int i=0;i<n;i++) {\n int[] event = events[i];\n inout[i*2] = new int[]{event[0], event[2]};\n inout[i*2 +1] = new int[]{event[1], -event[2]};\n }\n Arrays.sort(inout, (a,b)-> a[0]-b[0]);\n int max = 0, maxRemoved = 0;\n TreeMap<Integer, Integer> maxUntil = new TreeMap<>();\n for(int[] eve : inout) {\n if(eve[1] > 0 ) { // identifying if it is start of event or end of event by -ve value or +ve value\n Map.Entry<Integer, Integer> lower = maxUntil.lowerEntry(eve[0]);\n int lowerProfit = (lower==null? 0 : lower.getValue());\n max = Math.max(max, lowerProfit+eve[1]);\n } else {\n maxRemoved = Math.max(-eve[1], maxRemoved);\n maxUntil.put(eve[0], maxRemoved);\n }\n }\n return max;\n }\n}\n``` | 2 | 0 | ['Binary Tree', 'Java'] | 1 |
two-best-non-overlapping-events | Intuitive way | intuitive-way-by-sohailalamx-g1r9 | IntuitionApproachComplexityCode | sohailalamx | NORMAL | 2025-02-10T19:56:15.824884+00:00 | 2025-02-10T19:56:15.824884+00:00 | 12 | false | # Intuition
1. I took a i'th interval. Now I can take another interval iff
the another one not overlap means eighter that interval will start
after the current's end time or that interval will end before
current's start time.
2. For each interval I will get start, end, value. So
I can keep max value for end < starttime and endtime < start
and track the max value and add up value.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(nlogn)
- Space complexity: O(n)
# Code
```cpp []
class Solution {
public:
int maxTwoEvents(vector<vector<int>>& events) {
map<int, int> st, ed;
unordered_map<int, int> stmax, edmax;
for(vector<int> v:events) {
int stTime = v[0];
int edTime = v[1];
int value = v[2];
st[stTime] = max(st[stTime], value);
ed[edTime] = max(ed[edTime], value);
}
int maxx = 0;
for(auto i = st.rbegin(); i != st.rend(); i++) {
maxx = max(maxx, i -> second);
i -> second = maxx;
}
maxx = 0;
for(auto i = ed.begin(); i != ed.end(); i++) {
maxx = max(maxx, i -> second);
i -> second = maxx;
}
int ans = 0;
for(vector<int> v:events) {
int stTime = v[0];
int edTime = v[1];
int value = v[2];
int maxx = 0;
auto it = st.upper_bound(edTime);
if(it != st.end()) {
maxx = it -> second;
}
it = ed.lower_bound(stTime);
if(it != ed.begin()) {
--it;
maxx = max(maxx, it -> second);
}
ans = max(ans, value+maxx);
}
return ans;
}
};
``` | 1 | 0 | ['C++'] | 0 |
two-best-non-overlapping-events | Easy sorting and min heap solution | easy-sorting-and-min-heap-solution-by-he-9jrd | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | hee_maan_shee | NORMAL | 2025-01-17T09:34:48.286012+00:00 | 2025-01-17T09:34:48.286012+00:00 | 16 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int maxTwoEvents(int[][] events) {
//We are sorting the events based on the START time of the event
Arrays.sort(events, (a, b) -> Integer.compare(a[0], b[0]));
//We are storing in the priority queue based on the END time of the event (min priority queue)
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));
int maxVal = 0, ans = 0;
for (int[] event : events) {
int start = event[0], end = event[1], value = event[2];
while (!pq.isEmpty() && pq.peek()[0] < start) { //maxVal will basically store the maximum "value" of the event having same start time
maxVal = Math.max(maxVal, pq.poll()[1]);
}
ans = Math.max(ans, maxVal + value);
pq.add(new int[]{end, value});
}
return ans;
}
}
``` | 1 | 0 | ['Sorting', 'Heap (Priority Queue)', 'Java'] | 0 |
two-best-non-overlapping-events | C# Solution for Two Best Non-Overlapping Events Problem | c-solution-for-two-best-non-overlapping-mknm1 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is to find the maximum sum of values from two non-overlapping events. Inste | Aman_Raj_Sinha | NORMAL | 2024-12-08T22:05:49.536023+00:00 | 2024-12-08T22:05:49.536051+00:00 | 11 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is to find the maximum sum of values from two non-overlapping events. Instead of comparing every possible pair of events (which would be inefficient), we break events into start and end points and process them in chronological order. This way:\n\u2022\tWe can dynamically keep track of the maximum value of a single event encountered so far.\n\u2022\tWhenever a new event starts, we check if combining it with the best event seen earlier produces a new maximum sum.\n\nThis approach avoids brute-forcing all pairs, leveraging sorted timelines for efficiency\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tTimeline Creation:\n\t\u2022\tFor each event [start, end, value], add two timeline points:\n\t\u2022\t(start, 1, value) for when the event starts.\n\t\u2022\t(end + 1, 0, value) for when the event ends (since the end time is inclusive).\n\t\u2022\tThis splits events into discrete points for easier processing.\n2.\tSorting:\n\t\u2022\tSort the timeline points by time:\n\t\u2022\tPrimary: Time value.\n\t\u2022\tSecondary: Prioritize end points (type == 0) over start points (type == 1) when the times are equal.\n3.\tSweeping Through Points:\n\t\u2022\tUse two variables:\n\t\u2022\tmaxValue: Tracks the maximum single-event value seen so far.\n\t\u2022\tans: Tracks the maximum sum of values of two non-overlapping events.\n\t\u2022\tProcess each point:\n\t\u2022\tFor start points (type == 1): Check if the sum of the current event\u2019s value and maxValue is greater than ans, and update ans if so.\n\t\u2022\tFor end points (type == 0): Update maxValue to include the current event\u2019s value if it\u2019s the largest seen so far.\n4.\tResult:\n\t\u2022\tAfter processing all points, ans contains the maximum sum of two non-overlapping events.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1.\tTimeline Construction:\n\t\u2022\tSplitting each event into two points takes O(n), where n is the number of events.\n2.\tSorting:\n\t\u2022\tSorting the timeline points takes O(2n log (2n)) = O(n log n), as there are 2n points.\n3.\tSweeping Through Points:\n\t\u2022\tProcessing all timeline points takes O(2n) = O(n).\n\nOverall: O(n log n), dominated by the sorting step.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n1.\tAdditional Data Structures:\n\t\u2022\tThe times list stores 2n points: O(n).\n2.\tAuxiliary Variables:\n\t\u2022\tA constant amount of space is used for variables like maxValue and ans.\n\nOverall: O(n).\n\n# Code\n```csharp []\npublic class Solution {\n public int MaxTwoEvents(int[][] events) {\n var times = new List<int[]>();\n\n foreach (var eventData in events) {\n int start = eventData[0];\n int end = eventData[1];\n int value = eventData[2];\n\n times.Add(new int[] { start, 1, value }); \n times.Add(new int[] { end + 1, 0, value }); \n }\n\n times.Sort((a, b) => a[0] == b[0] ? a[1].CompareTo(b[1]) : a[0].CompareTo(b[0]));\n\n int maxValue = 0;\n int ans = 0;\n foreach (var time in times) {\n if (time[1] == 1) {\n ans = Math.Max(ans, time[2] + maxValue);\n } else {\n maxValue = Math.Max(maxValue, time[2]);\n }\n }\n\n return ans;\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
two-best-non-overlapping-events | Java Solution for Two Best Non-Overlapping Events Problem | java-solution-for-two-best-non-overlappi-e3lp | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is to find the maximum sum of values of two non-overlapping events. To solv | Aman_Raj_Sinha | NORMAL | 2024-12-08T22:01:17.884778+00:00 | 2024-12-08T22:01:17.884809+00:00 | 12 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is to find the maximum sum of values of two non-overlapping events. To solve it efficiently:\n\u2022\tWe leverage the timeline of events by breaking them into start and end points.\n\u2022\tBy sweeping through these points in sorted order, we dynamically maintain the maximum value of a single event (maxValue) seen so far.\n\u2022\tWhenever we encounter a new event\u2019s start, we combine its value with maxValue to check if it forms the maximum sum of two non-overlapping events.\n\nThis approach ensures that we process all events in a structured manner without explicitly checking every pair of events, avoiding an O(n^2) complexity.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tEvent Breakdown:\n\t\u2022\tFor each event [start, end, value], split it into two key time points:\n\t\u2022\tA start point (start, 1, value) indicating when the event begins.\n\t\u2022\tAn end point (end + 1, 0, value) indicating when the event ends (end time is inclusive, so we use end + 1).\n\t\u2022\tAdd these points to a list times.\n2.\tSorting:\n\t\u2022\tSort times primarily by the time value.\n\t\u2022\tIf two points have the same time, prioritize end points (type 0) over start points (type 1). This ensures proper updates when events overlap.\n3.\tSweep Line Algorithm:\n\t\u2022\tInitialize:\n\t\u2022\tmaxValue: Tracks the maximum value of a single event seen so far.\n\t\u2022\tans: Tracks the maximum sum of two non-overlapping events.\n\t\u2022\tProcess each point in times:\n\t\u2022\tIf it\u2019s a start point (type == 1), calculate the maximum sum of two events as:\n\t\u2022\tvalue + maxValue (current event + best event seen so far).\n\t\u2022\tUpdate ans with the maximum value of ans and this sum.\n\t\u2022\tIf it\u2019s an end point (type == 0), update maxValue to be the maximum of its current value and the event\u2019s value.\n4.\tResult:\n\t\u2022\tAfter processing all points, ans will contain the maximum sum of two non-overlapping events.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1.\tEvent Processing:\n\t\u2022\tSplitting each event into two points takes O(n), where n is the number of events.\n\t\u2022\tSorting the times array takes O(2n log (2n)) = O(n log n), since it contains 2n elements.\n\t\u2022\tSweeping through times takes O(2n) = O(n).\n2.\tOverall: O(n log n) due to the sorting step.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n1.\tAdditional Data Structures:\n\t\u2022\tThe times list contains 2n elements, requiring O(n) space.\n\t\u2022\tNo other significant space is used.\n2.\tOverall: O(n).\n\n# Code\n```java []\nclass Solution {\n public int maxTwoEvents(int[][] events) {\n List<int[]> times = new ArrayList<>();\n\n for (int[] event : events) {\n times.add(new int[]{event[0], 1, event[2]}); \n times.add(new int[]{event[1] + 1, 0, event[2]}); \n }\n\n times.sort((a, b) -> (a[0] == b[0]) ? Integer.compare(a[1], b[1]) : Integer.compare(a[0], b[0]));\n\n int ans = 0;\n int maxValue = 0;\n\n for (int[] time : times) {\n if (time[1] == 1) {\n ans = Math.max(ans, time[2] + maxValue);\n } else {\n maxValue = Math.max(maxValue, time[2]);\n }\n }\n\n return ans;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
two-best-non-overlapping-events | Swift | Consider all the event points | swift-consider-all-the-event-points-by-p-4qgl | Code\nswift []\nclass Solution {\n func maxTwoEvents(_ events: [[Int]]) -> Int {\n // Every event has 2 points: its start and its end.\n enum E | pagafan7as | NORMAL | 2024-12-08T17:54:21.274531+00:00 | 2024-12-08T18:03:06.304788+00:00 | 17 | false | # Code\n```swift []\nclass Solution {\n func maxTwoEvents(_ events: [[Int]]) -> Int {\n // Every event has 2 points: its start and its end.\n enum EventType: Int { case start = 1, end = 0 }\n typealias EventPoint = (type: EventType, time: Int, value: Int)\n\n // Construct the different event points, sorting them by time.\n let eventPoints = events\n .reduce(into: [EventPoint]()) {\n $0.append(EventPoint(type: .start, time: $1[0], value: $1[2]))\n $0.append(EventPoint(type: .end, time: $1[1] + 1, value: $1[2]))\n }\n .sorted { ($0.time, $0.type.rawValue) < ($1.time, $1.type.rawValue) }\n\n // Go through all the event points, updating the result.\n var bestValue = 0\n var res = 0\n for eventPoint in eventPoints {\n switch eventPoint.type {\n case .start:\n // If the event being started, combined with the best completed\n // event so far, improves the result, update the result.\n res = max(res, bestValue + eventPoint.value)\n case .end:\n // If the event just being completed is better than any\n // previous event, update "bestValue".\n bestValue = max(bestValue, eventPoint.value)\n }\n }\n return res\n }\n}\n``` | 1 | 0 | ['Swift'] | 0 |
two-best-non-overlapping-events | ✅Maximum Sum of Two Non-Overlapping Events Using Binary Search🚀Beats💯 | maximum-sum-of-two-non-overlapping-event-47a8 | Intuition:\n\nTo maximize the sum of values of two non-overlapping events, we need to:\n1. Identify two events such that their times do not overlap (i.e., the s | ranganathv415 | NORMAL | 2024-12-08T17:31:07.747014+00:00 | 2024-12-08T17:31:07.747037+00:00 | 29 | false | # Intuition:\n\nTo maximize the sum of values of two non-overlapping events, we need to:\n1. Identify two events such that their times do not overlap (i.e., the start time of one is after the end time of the other).\n2. Leverage the sorted structure of events to efficiently find compatible pairs, maximizing their combined values.\n\nA **binary search** approach is suitable for finding the latest non-overlapping event efficiently.\n\n# Approach:\n\n1. **Sort Events by End Time**:\n - Sorting events by their end time helps to easily determine compatibility using binary search.\n2. **Binary Search for Compatibility**:\n - For each event, find the latest event (ending before the current event starts) using binary search.\n3. **Precompute Maximum Values**:\n - To optimize the selection of the second event, maintain a prefix array where `maxValues[i]` holds the maximum value of events from the start up to the ith event.\n4. **Iterate Over Events**:\n - For each event:\n - Use binary search to find the latest non-overlapping event.\n - Calculate the maximum sum of the current event and the best earlier event.\n5. **Result**: \n - The result is the maximum of the sums computed during the iteration.\n\n# Complexity:\n\n- **Time Complexity**:\n - Sorting: ***O(n log\u2061 n)***\n - Binary search for each event: ***O(n log \u2061n)***\n - Total: ***O(n log \u2061n)***\n- **Space Complexity**:\n - ***O(n)*** for storing `maxValues` and sorted events.\n\n# Code:\n\n```typescript\nfunction maxTwoEvents(events: number[][]): number {\n // Sort events by endTime\n events.sort((a, b) => a[1] - b[1]);\n\n const n = events.length;\n const maxValues = new Array(n).fill(0);\n\n // Precompute maxValues to store the max value up to each event\n maxValues[0] = events[0][2];\n for (let i = 1; i < n; i++) {\n maxValues[i] = Math.max(maxValues[i - 1], events[i][2]);\n }\n\n let maxSum = 0;\n\n for (let i = 0; i < n; i++) {\n const [startTime, endTime, value] = events[i];\n\n // Binary search to find the last event that ends before startTime\n let low = 0, high = i - 1, lastCompatible = -1;\n while (low <= high) {\n const mid = Math.floor((low + high) / 2);\n if (events[mid][1] < startTime) {\n lastCompatible = mid;\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n\n // If a compatible event exists, calculate the sum\n const currentSum = value + (lastCompatible !== -1 ? maxValues[lastCompatible] : 0);\n\n // Update the maximum sum\n maxSum = Math.max(maxSum, currentSum);\n }\n\n return maxSum;\n};\n\n```\n\n---\n\n### **Example and Explanation Walkthrough**:\n\n#### Example 1:\n\n**Input**:\n```typescript\nevents = [[1,3,2],[4,5,2],[2,4,3]];\n```\n\n**Execution**:\n1. Sort events: `[[1,3,2], [2,4,3], [4,5,2]]`.\n2. Precompute `maxValues`:\n - `maxValues = [2, 3, 3]`.\n3. Iterate over events:\n - For event `[1,3,2]`: No previous compatible event. Max sum = `2`.\n - For event `[2,4,3]`: No previous compatible event. Max sum = `3`.\n - For event `[4,5,2]`: Compatible with `[1,3,2]`. Max sum = `2 + 2 = 4`.\n4. **Output**: `4`.\n\n#### Example 2:\n\n**Input**:\n```typescript\nevents = [[1,5,3],[1,5,1],[6,6,5]];\n```\n\n**Execution**:\n1. Sort events: `[[1,5,3], [1,5,1], [6,6,5]]`.\n2. Precompute `maxValues`:\n - `maxValues = [3, 3, 5]`.\n3. Iterate over events:\n - For event `[1,5,3]`: No previous compatible event. Max sum = `3`.\n - For event `[1,5,1]`: No previous compatible event. Max sum = `3`.\n - For event `[6,6,5]`: Compatible with `[1,5,3]`. Max sum = `3 + 5 = 8`.\n4. **Output**: `8`.\n\n---\n\n### **Key Insights**:\n\n- **Binary Search** ensures efficient compatibility checks.\n- **Precomputing Maximum Values** allows fast retrieval of the best earlier event\'s value.\n- The approach works well within the constraints. | 1 | 0 | ['TypeScript'] | 0 |
two-best-non-overlapping-events | Binary Search & Suffix Array | binary-search-suffix-array-by-himanshu_1-xrzm | Intuition\nThe basic idea is that for every event, the result can either be the current event\'s value or the current event\'s value plus the maximum value of s | himanshu_1998 | NORMAL | 2024-12-08T17:02:15.561178+00:00 | 2024-12-08T17:02:15.561215+00:00 | 10 | false | # Intuition\nThe basic idea is that for every event, the result can either be the current event\'s value or the current event\'s value plus the maximum value of some future non-overlapping event. To efficiently find the next non-overlapping event, we can jump directly to the interval that starts after the current one ends. After that, we can continue linearly.\n\nTo optimize this process, we can use a suffix array. The suffix array stores the maximum value from the current event until the end, allowing us to quickly look up the best future event without having to scan through all future events.\n\n# Complexity\n- Time complexity:\nO(N*Log(N))\n\n- Space complexity:\nO(N)\n\n\n# Code\n```java []\nclass Solution {\n private int upperBound(int lo, int [][] events, int target) {\n int hi = events.length - 1;\n while (lo <= hi) {\n int mid = lo + ((hi - lo) >> 1);\n if (events[mid][0] <= target) {\n lo = mid + 1;\n } else {\n hi = mid - 1;\n }\n } \n return lo;\n }\n public int maxTwoEvents(int[][] events) {\n Arrays.sort(events, (a, b) -> Integer.compare(a[0], b[0]));\n int [] dp = new int [events.length];\n dp[events.length - 1] = events[events.length - 1][2];\n for (int i = events.length - 2; i >= 0; i--) {\n dp[i] = Math.max(dp[i + 1], events[i][2]);\n }\n int result = dp[0];\n for (int i = 0; i < events.length; ++i) {\n int j = upperBound(i + 1, events, events[i][1]);\n if (j < events.length ) {\n result = Math.max(result, dp[j] + events[i][2]);\n } \n }\n return result;\n }\n}\n``` | 1 | 0 | ['Java'] | 1 |
two-best-non-overlapping-events | Two Best Non-Overlapping Events | C++ | Sorting | NlogN | two-best-non-overlapping-events-c-sortin-ml3u | Complexity\n- Time complexity: O(nlogn)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n | JeetuGupta | NORMAL | 2024-12-08T16:18:19.018978+00:00 | 2024-12-08T16:18:19.019014+00:00 | 13 | false | # Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\n int findNextNonOverlapping(vector<vector<int>> &events, int l){\n int start = 0, end = events.size() - 1, ans = end + 1;\n while(start <= end){\n int mid = start + (end - start)/2;\n if(events[mid][0] > l){\n ans = mid;\n end = mid - 1;\n }else start = mid + 1;\n }\n return ans;\n }\npublic:\n int maxTwoEvents(vector<vector<int>>& events) {\n int n = events.size();\n sort(events.begin(), events.end());\n vector<int> maxi(n, 0);\n maxi[n-1] = events[n-1][2];\n for(int i = n-2; i>=0; i--){\n maxi[i] = max(maxi[i+1], events[i][2]);\n }\n int ans = 0;\n for(int i = 0; i<n; i++){\n int ind = findNextNonOverlapping(events, events[i][1]);\n if(ind != n){\n ans = max(ans, events[i][2] + maxi[ind]);\n }else ans = max(ans, events[i][2]);\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.