question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-operations-to-make-the-array-k-increasing
|
✅✅Faster || Easy To Understand || C++ Code
|
faster-easy-to-understand-c-code-by-__kr-jf9g
|
Using Binary Search\n\n Time Complexity :- O(NlogN * K)\n\n Space Complexity :- O(N * K)\n\n\nclass Solution {\npublic:\n int kIncreasing(vector<int>& nums,
|
__KR_SHANU_IITG
|
NORMAL
|
2022-07-04T06:00:11.612637+00:00
|
2022-07-04T06:00:36.532620+00:00
| 141
| false
|
* ***Using Binary Search***\n\n* ***Time Complexity :- O(NlogN * K)***\n\n* ***Space Complexity :- O(N * K)***\n\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& nums, int k) {\n \n int n = nums.size();\n \n // all the k subsets are independent of each other, so we can perform lis on each k subsets independently\n \n // min_count store minimum operations needed\n \n int min_count = 0;\n \n // perform lis on each k subsets\n \n for(int j = 0; j < k; j++) // starting index of subset\n {\n // perform lis\n \n vector<int> lis;\n \n lis.push_back(nums[j]);\n \n // total_element count no of element in each subset\n \n int total_element = 1;\n \n for(int i = j + k; i < n; i += k)\n {\n if(nums[i] >= lis.back()) // push into lis\n lis.push_back(nums[i]);\n \n else // find the correct index in lis for nums[i]\n {\n int idx = upper_bound(lis.begin(), lis.end(), nums[i]) - lis.begin();\n \n lis[idx] = nums[i];\n }\n \n total_element++;\n }\n \n // update result\n \n min_count += total_element - lis.size();\n }\n \n return min_count;\n }\n};\n```
| 0
| 0
|
['Binary Search', 'C', 'Binary Tree']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
python LIS - TC(nlogn)
|
python-lis-tcnlogn-by-vincent_great-7es9
|
\ndef kIncreasing(self, arr: List[int], k: int) -> int: \n\tdef lis(nums):\n\t\tans = [nums[0]]\n\t\tfor n in nums[1:]:\n\t\t\tif ans[-1]<=n:\n\t\t\t\tans.appen
|
vincent_great
|
NORMAL
|
2022-06-30T16:25:57.341528+00:00
|
2022-06-30T16:25:57.341578+00:00
| 58
| false
|
```\ndef kIncreasing(self, arr: List[int], k: int) -> int: \n\tdef lis(nums):\n\t\tans = [nums[0]]\n\t\tfor n in nums[1:]:\n\t\t\tif ans[-1]<=n:\n\t\t\t\tans.append(n)\n\t\t\telse:\n\t\t\t\tidx = bisect.bisect(ans, n)\n\t\t\t\tans[idx] = n\n\t\treturn len(ans)\n\n\tres = 0\n\tfor i in range(k):\n\t\tcans = []\n\t\twhile(i<len(arr)):\n\t\t\tcans.append(arr[i])\n\t\t\ti += k\n\t\tres += (len(cans)-lis(cans))\n\n\treturn res\n```
| 0
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Golang 100/80
|
golang-10080-by-adam-hoelscher-a86y
|
Logic in comments. O(n * log n/k)time; O(n/k) space\n\nfunc kIncreasing(arr []int, k int) int {\n\n // the name of this problem is not optimal. We\'re not ac
|
adam-hoelscher
|
NORMAL
|
2022-06-28T00:46:42.433946+00:00
|
2022-06-28T00:46:42.433978+00:00
| 26
| false
|
Logic in comments. `O(n * log n/k)`time; `O(n/k)` space\n```\nfunc kIncreasing(arr []int, k int) int {\n\n // the name of this problem is not optimal. We\'re not actually trying to make the suqsequences increasing\n // we\'re trying to make them non-decreasing\n\n // the general approach is the same idea as https://leetcode.com/problems/longest-increasing-subsequence/\n // with 2 changes \n // 1) that problem is looking for truly increasing subsequences. the change necessary to move from\n // increasing to non-decreasing is to use strict comparison (>) instead of parial comparison (>=)\n // 2) that problem deals with the full array. this problem asks us to split the full array into k subarrays\n // those subarrays do not intefere with each other in any way. each of those sub-arrays has len n/k or n/k-1\n\n // after accounting for strict vs partial, the only question is whether to work the array from left to right\n // or work with each of the k subarrays. working from left to right requires more memory because we have to\n // maintain a memo for each of the k subarrays as we go. in the worst case, we have to use O(n) memory for that\n // working each subproblem 1 at a time means we only need O(n/k) extra space, since that the is maximum size\n // of the memo for each subarray\n\n // create a variable to store the answer\n var ans int\n\n // start at each pos < k\n for l := 0; l < k; l++ {\n\n // construct a memo to hold the lowest end value for non-dec subseq of each length up to this point\n // at each step len(tails) is the longest subsequence we\'ve built and tails[i] is the lowest value\n // we can have at the end of a subseq of len(i)\n tails := []int{}\n\n // iterate over values of sub-array starting at l\n var r int\n for r = 0; l+k*r < len(arr); r++ {\n // get the value of the sub-array\n x := arr[l+k*r]\n\n // binary search for the len of the longest subseq we can update\n m := sort.Search(len(tails), func(m int) bool {\n // use partial ordering to account for non-decreasing instead of increasing\n return tails[m] > x\n })\n\n if m == len(tails) {\n // if we can add x to the longest subseq, add that to the memo\n tails = append(tails, x)\n } else {\n // otherwise, update the exsisting subseq\'s tail\n tails[m] = x\n }\n\n }\n\n // the number of values we need to change in this sub array is equal to len(subarray) - len(longest subseq)\n // r = len(subarray); len(longest subseq) = len(tails)\n ans += r - len(tails)\n }\n \n return ans\n}\n\n```
| 0
| 0
|
['Binary Search', 'Dynamic Programming']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
K grps LIS
|
k-grps-lis-by-ishubhamrana-6bjp
|
\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n vector<vector<int> > lis(k);\n int N=arr.size();\n \n
|
iShubhamRana
|
NORMAL
|
2022-06-24T05:30:58.906827+00:00
|
2022-06-24T05:30:58.906869+00:00
| 19
| false
|
```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n vector<vector<int> > lis(k);\n int N=arr.size();\n \n for(int i=0;i<N;i++){\n int grp = i%k;\n grp_size[grp]++;\n \n auto &lis_grp = lis[grp];\n \n auto it = upper_bound(lis_grp.begin(),lis_grp.end(),arr[i]);\n \n if(it==lis_grp.end()) lis_grp.push_back(arr[i]);\n else *it = arr[i];\n }\n \n int ans=0;\n for(int i=0;i<k;i++){\n int grp_size = 1 + (N-i-1)/k;\n ans += grp_size- lis[i].size();\n }\n return ans;\n }\n};\n```
| 0
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
[Python 10 lines] Binary Search with thought process when being asked during interviews
|
python-10-lines-binary-search-with-thoug-82fe
|
Binary Search\nLet\'s simply the problem first. What if k is large enough such that there is only one pair for each i to construct the sequence? We just need to
|
jandk
|
NORMAL
|
2022-06-12T10:57:05.684654+00:00
|
2022-06-12T10:57:05.684695+00:00
| 96
| false
|
### Binary Search\nLet\'s simply the problem first. What if `k` is large enough such that there is only one pair for each `i` to construct the sequence? We just need to check each pair to see if it\'s valid or not, and increase the final result by 1 if the pair is invalid.\n\nThen let\'s decrement `k` , the number of integers in each sequence is increased, meaning there is an index `j` exists such that `nums[j - k] <= nums[j] <= nums[j + k]`. More similarly with smaller `k`, there are more integers in the sequence. So we can check each independent sequence to get the result, and then sum up of results for each sequence.\n\nNow the problem is transfered to given a sequence, how many operations we can use to make it increasing? Does it look familar? \n\nNote we can make the sequence valid by changing any invalid integer to be as same as previous integer, for example `[5,2,3,2] => [5,5,5,5]`. So we can just get the increasing sequence and change all of the rest to be equal to any valid integers. \n\nFinally, this problem is converted to finding the longest non decreasing subsequence for each group.\n\n```python\ndef kIncreasing(self, arr: List[int], k: int) -> int:\n\tdef helper(nums):\n\t\tlps = []\n\t\tfor num in nums:\n\t\t\tindex = bisect.bisect(lps, num)\n\t\t\tif index < len(lps):\n\t\t\t\tlps[index] = num\n\t\t\telse: \n\t\t\t\tlps.append(num)\n\t\treturn len(nums) - len(lps)\n\treturn sum(helper([arr[j] for j in range(i, len(arr), k)]) for i in range(k))\n```\n\n*Time Complexity*= **O(NlgN)**\n*Space Complexity* = **O(N)**\n
| 0
| 0
|
['Binary Tree']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
[JAVA] Easy to understand O(NlogN)
|
java-easy-to-understand-onlogn-by-chenya-cxie
|
very very similar to longest increasing subsequence\n\n\nclass Solution {\n public int kIncreasing(int[] A, int k) {\n // Longest increasing subsequen
|
chenyang_johan
|
NORMAL
|
2022-05-11T07:41:34.499707+00:00
|
2022-05-11T07:41:34.499747+00:00
| 144
| false
|
very very similar to longest increasing subsequence\n\n```\nclass Solution {\n public int kIncreasing(int[] A, int k) {\n // Longest increasing subsequence for\n // A[i]..A[i + k].. A[i + 2k]\n int n = A.length;\n // int[] memo = new int[n];\n int res = 0;\n for (int s = 0; s < k; s++) {\n List<Integer> dp = new ArrayList<>();\n for (int i = s; i < n; i += k){\n \n if (!bsearch(dp, A[i])) {\n dp.add(A[i]);\n }\n // System.out.println(A[i] + "-" + i);\n // System.out.println(dp.toString());\n }\n \n // System.out.println(dp.toString());\n res += dp.size();\n }\n return n - res;\n }\n \n private boolean bsearch(List<Integer> dp, int target) {\n if(dp.isEmpty()) {\n return false;\n }\n \n int lo = 0, hi = dp.size() - 1;\n while(lo < hi) {\n int mid = lo + (hi - lo) / 2;\n if (dp.get(mid) <= target) {\n lo = mid + 1;\n } else {\n hi = mid;\n }\n }\n \n if (dp.get(lo) > target){\n dp.set(lo, target);\n return true;\n }\n return false;\n }\n}\n```
| 0
| 0
|
['Binary Tree']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
[C++] LIS with binary search
|
c-lis-with-binary-search-by-kaminyou-b6bi
|
\nclass Solution {\npublic:\n int upperBound(vector<int>& nums, int x) {\n int left = 0;\n int right = nums.size();\n while (left < righ
|
kaminyou
|
NORMAL
|
2022-04-29T16:57:21.787866+00:00
|
2022-04-29T16:57:21.787901+00:00
| 117
| false
|
```\nclass Solution {\npublic:\n int upperBound(vector<int>& nums, int x) {\n int left = 0;\n int right = nums.size();\n while (left < right) {\n int mid = left + (right - left) / 2;\n if (nums[mid] > x) right = mid;\n else left = mid + 1;\n }\n return left;\n }\n int lis(vector<int>& nums) {\n int n = nums.size();\n vector<int> dp;\n for (auto num: nums) {\n int index = upperBound(dp, num);\n if (index == dp.size()) dp.push_back(num);\n else dp[index] = num;\n }\n return n - dp.size();\n }\n int kIncreasing(vector<int>& arr, int k) {\n vector<int> temp;\n int res = 0;\n for (int i = 0; i < k; i++) {\n for (int j = i; j < arr.size(); j += k) {\n temp.push_back(arr[j]);\n }\n res += lis(temp);\n temp.clear();\n }\n return res;\n }\n};\n```
| 0
| 0
|
['C', 'Binary Tree']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
[C++] Beats 97% | LIS | Just ignore K for a while :)
|
c-beats-97-lis-just-ignore-k-for-a-while-zw3u
|
We can skip K for a while, which makes this question as Minimum operations to Make the Array Increasing, which can be solved by finding the LIS (Longest Increas
|
meKabhi
|
NORMAL
|
2022-04-23T12:30:17.820753+00:00
|
2022-04-23T12:30:47.916800+00:00
| 157
| false
|
We can skip `K` for a while, which makes this question as `Minimum operations to Make the Array Increasing`, which can be solved by finding the LIS (Longest Increasing Subsequence), using binary search, and subtracting the size of LIS from size of the array. Performing this step `K` times will give the desired result.\n\n```\n/* \n Time: O(nlogn)\n Space: O(n)\n Tag: DP and Binary Seach (LIS)\n Difficulty: H\n*/\n\nclass Solution {\npublic:\n int kIncreasing(vector<int> &arr, int k) {\n int res = 0;\n vector<int> lis;\n\n for (int i = 0; i < k; i++) {\n int size = 0;\n for (int j = i; j < arr.size(); j += k) {\n size++;\n auto it = upper_bound(lis.begin(), lis.end(), arr[j]);\n if (it == lis.end())\n lis.push_back(arr[j]);\n else\n *it = arr[j];\n }\n res += size - lis.size();\n lis.clear();\n }\n return res;\n }\n};\n```
| 0
| 0
|
['Dynamic Programming', 'C', 'Binary Tree', 'C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ 11 line
|
c-11-line-by-sanzenin_aria-mye8
|
```\n int kIncreasing(vector& arr, int k) {\n int numGood = 0;\n for(int i = 0; i<k; i++){\n vector v;\n for(int j=i;j<ar
|
sanzenin_aria
|
NORMAL
|
2022-04-14T00:54:08.938944+00:00
|
2022-04-14T00:54:08.938985+00:00
| 82
| false
|
```\n int kIncreasing(vector<int>& arr, int k) {\n int numGood = 0;\n for(int i = 0; i<k; i++){\n vector<int> v;\n for(int j=i;j<arr.size();j+=k){\n auto it = upper_bound(v.begin(), v.end(), arr[j]);\n if(it == v.end()) v.push_back(arr[j]);\n else *it = arr[j];\n }\n numGood += v.size();\n }\n return arr.size() - numGood;\n }
| 0
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ lis
|
c-lis-by-wufengxuan1230-n67q
|
\nclass Solution {\npublic:\n int kIncreasing(vector<int>& nums, int k) {\n int res = 0;\n vector<int> lis(nums.size() / k + 2, INT_MAX);\n
|
wufengxuan1230
|
NORMAL
|
2022-03-29T04:44:19.541007+00:00
|
2022-03-29T04:47:56.219112+00:00
| 66
| false
|
```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& nums, int k) {\n int res = 0;\n vector<int> lis(nums.size() / k + 2, INT_MAX);\n for (int i = 0; i < k; ++i) {\n std::fill(lis.begin(), lis.end(), INT_MAX);\n int maxLen = 1;\n lis[maxLen] = nums[i];\n for (int j = i + k; j < nums.size(); j += k) {\n auto it = upper_bound(lis.begin() + 1, lis.begin() + maxLen + 1, nums[j]);\n maxLen = max(maxLen, (int)(it - lis.begin()));\n *it = min(*it, nums[j]);\n }\n res += (nums.size() / k) + (i < (nums.size() % k)) - maxLen;\n }\n return res;\n }\n};\n```
| 0
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Golang LIS Binary Search O(nlog(n)) time complexity
|
golang-lis-binary-search-onlogn-time-com-r2a7
|
\nfunc kIncreasing(arr []int, k int) int {\n buckets := partition(arr, k)\n \n // T -> O(n)\n // S -> O(n)\n var numberOfOperations int\n for
|
alyxjperkins
|
NORMAL
|
2022-03-27T19:24:51.636592+00:00
|
2022-03-27T19:24:51.636635+00:00
| 50
| false
|
```\nfunc kIncreasing(arr []int, k int) int {\n buckets := partition(arr, k)\n \n // T -> O(n)\n // S -> O(n)\n var numberOfOperations int\n for _, bucket := range buckets {\n numberOfOperations += longestIncreasingSequence(bucket)\n }\n \n return numberOfOperations\n}\n\n// T -> O(n)\n// S -> O(n)\nfunc partition(arr []int, k int) [][]int {\n var buckets = make([][]int, 0, k)\n for i := 0; i < k; i++ {\n buckets = append(buckets, []int{})\n }\n \n for i := 0; i < len(arr); i++ {\n bucket := i % k\n buckets[bucket] = append(buckets[bucket], arr[i])\n }\n \n return buckets\n}\n\nfunc longestIncreasingSequence(array []int) int {\n if len(array) == 0 {\n return 0\n }\n \n // T -> O(nlog(n)) where `n` is the length of the array.\n // S -> O(n) worst case the sequence could be the same size as the original array.\n var sequence = []int{array[0]}\n for i := 1; i < len(array); i++ {\n \n currentValue := array[i]\n \n if currentValue >= sequence[len(sequence)-1] {\n sequence = append(sequence, currentValue)\n continue\n }\n \n firstIncreasingElement := bisectLeft(sequence, currentValue)\n if sequence[firstIncreasingElement] == currentValue {\n firstIncreasingElement++\n }\n \n sequence[firstIncreasingElement] = currentValue\n }\n \n \n return len(array) - len(sequence)\n}\n\n// T -> O(log(n))\n// S -> O(1)\nfunc bisectLeft(array []int, target int) int {\n l, r := 0, len(array)\n \n for l < r {\n m := (l + r) / 2\n \n switch {\n case target == array[m]:\n return m\n case target <= array[m]:\n r = m\n default:\n l = m+ 1\n }\n }\n \n return l\n}\n```\n\nHere we do the following:\n1. Partition the array into buckets based on `k` \n2. Perform the LIS (longest increasing subsequence) algorithm on each bucket, with a slight modification\n3. Since the operations cannot be swaps, rather than replace an element in the array with a positive number - we recognise that to make the entire array increasing, we need to make\n len(array) - len(longest increasing subsequence) operations in order to make the full array increasing.
| 0
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
[Java] Clean LC-300 LIS version with Collections.binarySearch
|
java-clean-lc-300-lis-version-with-colle-wywn
|
\nclass Solution {\n private int lis(List<Integer> nums) {\n List<Integer> sub = new ArrayList<>();\n sub.add(nums.get(0));\n \n
|
srinathcoder
|
NORMAL
|
2022-03-22T05:41:59.786653+00:00
|
2022-03-28T02:05:11.321757+00:00
| 186
| false
|
```\nclass Solution {\n private int lis(List<Integer> nums) {\n List<Integer> sub = new ArrayList<>();\n sub.add(nums.get(0));\n \n for (int i = 1; i < nums.size(); i++) {\n int num = nums.get(i);\n if (num >= sub.get(sub.size() - 1)) {\n sub.add(num);\n } else {\n int j = Collections.binarySearch(sub, num) + 1;\n if (j < 0) {\n j = -(j + 1) + 1;\n }\n sub.set(j, num);\n }\n }\n return sub.size();\n }\n \n public int kIncreasing(int[] arr, int k) {\n int total = 0;\n \n for (int i = 0; i < k; i++) {\n List<Integer> nums = new ArrayList<>();\n for (int j = i; j < arr.length; j += k) {\n nums.add(arr[j]);\n }\n total += nums.size() - lis(nums);\n }\n return total;\n }\n}\n```
| 0
| 0
|
['Binary Tree', 'Java']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ | Binary Search | LIS
|
c-binary-search-lis-by-offamikumar-nh0t
|
\nclass Solution {\n int getPos(int val, vector<int>&v) {\n int high = v.size()-1, low = 0; \n int idx{}; \n while (low < high) {\n
|
offamikumar
|
NORMAL
|
2022-03-15T08:23:48.219284+00:00
|
2022-03-15T08:23:48.219317+00:00
| 80
| false
|
```\nclass Solution {\n int getPos(int val, vector<int>&v) {\n int high = v.size()-1, low = 0; \n int idx{}; \n while (low < high) {\n int mid = (low + high) / 2; \n if (val >= v[mid]) {\n low = mid + 1; \n } else {\n high = mid; \n }\n }\n return low;\n }\n int process(vector<int>&v) {\n vector<int>lis; \n int n = 0; \n lis.push_back(v[0]); \n for (int i=1; i<v.size(); ++i) {\n if (v[i] >= lis[n]) {\n lis.push_back(v[i]); \n n++; \n } else {\n int idx = getPos(v[i], lis); \n lis[idx] = v[i]; \n }\n }\n return v.size() - lis.size(); \n }\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int ans = 0; \n for (int i=0; i<k; ++i) {\n vector<int>temp; \n for (int j=i; j<arr.size(); j+=k) {\n temp.push_back(arr[j]); \n }\n ans += process(temp); \n }\n return ans; \n }\n};\n\n```
| 0
| 0
|
['Binary Tree']
| 0
|
binary-prefix-divisible-by-5
|
Detailed Explanation using Modular Arithmetic O(n)
|
detailed-explanation-using-modular-arith-omhg
|
Intuition\n First, let us see how to append an extra bit at the end of a binary number\n Any binary number akak-1...a0 has the form a020 + a121 + ........ a02k
|
just__a__visitor
|
NORMAL
|
2019-03-31T05:02:07.125180+00:00
|
2019-03-31T05:02:07.125242+00:00
| 9,796
| false
|
**Intuition**\n* First, let us see how to append an extra bit at the end of a binary number\n* Any binary number **a<sub>k</sub>a<sub>k-1</sub>...a<sub>0</sub>** has the form a<sub>0</sub>*2<sup>0</sup> + a<sub>1</sub>*2<sup>1</sup> + ........ a<sub>0</sub>*2<sup>k</sup>\n\n\n* To free up an extra slot at the end, we can just multiply the original number by 2.\n* Initially, the contribution of each **a<sub>i</sub>** is 2<sup>i</sup>. If the number is multiplied by 2, the contribution of each a<sup>i</sup> become 2<sup>i+1</sup>.\n* The resulting number is 0*2<sup>0</sup> + a<sub>0</sub>*2<sup>1</sup> + a<sub>1</sub>*2<sup>2</sup> + ........ a<sub>0</sub>*2<sup>k+1</sup>\n* Consider the number **a<sub>k</sub>a<sub>k-1</sub>...a<sub>0</sub>0**. As per the above definition, it is clear that the resulting number is just the decimal representation of this number\n----\n\n* We\'ve seen how to append an extra bit at the end of a binary number. \n* The extra bit appended by the above method is unset (0).\n* How do we append a set bit? Well, we can just free up a slot at the end (by appending 0) and then add 1 to the resulting number.\n* Since the current rightmost bit is zero, therefore there won\'t be any carry-effects. Hence the new number would be **a<sub>k</sub>a<sub>k-1</sub>...a<sub>0</sub>1**\n---\n**Conclusion**\n* For appending a digit **d** at the end of a binary number **old_number** = **a<sub>k</sub>a<sub>k-1</sub>...a<sub>0</sub>**, we can just do **new_number** = old_number*2 + **d**. \n* This gives us the number with binary representation **a<sub>k</sub>a<sub>k-1</sub>...a<sub>0</sub>d**\n---\n**Modular Arithemtic**\n* A number is divisible by 5 **iff** the number is equivalent to **0** in the modular arithemtic of 5.\n---\n**Naive_Algorithm**\n* Since we know how to append any digit at the end, we start with 0 and keep appending digits. We can get all the numbers in this manner.\n* At each step we can take the modulo with respect to 5. If the modulo is zero, we append **true** to our answer.\n---\n**Problems**\n* The problem with the above approach is that the number can overflow easily. (As the largest integer that can be accomodated is of 31 bits in C++).\n---\n**Optimizations**\n* Observe that we only care about the remainder, not the actual number.\n* Use the fact that (a*b + c)%d is same as ((a%d)*(b%d) + c%d)%d.\n* We now have the relation **new_number**%5 = ((old_number%5)*2 + d)%5;\n* This tells us the if we provide the modulo of the old_number instead of the original number, we\'ll get the modulo of the new number.\n* This would prevent overflows, since **new_number** is the equivalent representation of the original number in the modular arithemtic of 5.\n---\n**Optimized Algorithm**\n* Start with **num**=0.\n* For each valid **i** update **num** as **num** = (num*2 + a[i])%5\n* At each stage, if **num** is zero, the substring ending at **i** is divisible by 5.\n---\n**Time Complexity**\n* We pass each element exactly once. Hence *O(n)*.\n```\nclass Solution\n{\npublic:\n vector<bool> prefixesDivBy5(vector<int>& a);\n};\n\nvector<bool> Solution :: prefixesDivBy5(vector<int>& a)\n{\n vector<bool> answer;\n int num=0;\n for(int i=0; i<a.size(); i++)\n {\n num = (num*2 + a[i])%5;\n answer.push_back(num==0);\n }\n return answer;\n}\n```\n
| 147
| 10
|
[]
| 12
|
binary-prefix-divisible-by-5
|
[Java/Python 3] 7/1 liners - left shift, bitwise or, and mod.
|
javapython-3-71-liners-left-shift-bitwis-tgbi
|
Since A includes only 0s and 1s, we can imitate binary operations.\n\njava\n public List<Boolean> prefixesDivBy5(int[] A) {\n int k = 0;\n List
|
rock
|
NORMAL
|
2019-03-31T04:30:38.062831+00:00
|
2022-02-28T18:58:20.309831+00:00
| 5,261
| false
|
Since A includes only `0s` and `1s`, we can imitate binary operations.\n\n```java\n public List<Boolean> prefixesDivBy5(int[] A) {\n int k = 0;\n List<Boolean> ans = new ArrayList<>();\n for (int a : A) {\n k = (k << 1 | a) % 5; // left shift k by 1 bit and plus current element a is the binary number.\n ans.add(k == 0); \n }\n return ans;\n }\n```\n```python\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n ans, b = [], 0\n for a in A:\n b = b << 1 | a\n ans.append(b % 5 == 0)\n return ans\n```\nUse `itertools.accumulate` to make the above 1 liner:\n```python\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n return [x % 5 == 0 for x in itertools.accumulate(A, lambda a, b: a << 1 | b)]\n```\n**Analysis:**\n\nTime & space: O(n), where n = A.length;\n\n**Q & A:**\n\nQ:\nwhy do we need to mod 5 there?\nA: \nThe problem ask if the binary numbers are divisible by 5.\nAlso, mod 5 in each iteration will prevent potential int overflow.\n\nQ: \ncan you give me the explanation for why after mod 5 the value of k plus a can still represent the original value \uFF1F\nA:\n\nRewrite original code as follows, ignore the overflow test cases.\n```\n public List<Boolean> prefixesDivBy5(int[] A) {\n int[] k = new int[A.length + 1];\n List<Boolean> ans = new ArrayList<>();\n for (int i = 0; i < A.length; ++i) {\n k[i + 1] = (k[i] << 1 | a); // left shift k by 1 bit and plus current element a is the binary number.\n ans.add(k[i + 1] % 5 == 0); \n }\n return ans;\n }\n```\n```\n\ni = 0,\n```\nLet F0 = k[0 + 1] / 5,\n r0 = k[0 + 1] % 5,\nDenote k[0 + 1] (= A[0]) = 5 * F0 + r0, \n k[0 + 1] % 5 = r0\n\nsimilarly,\n```\ni = 1,\n```\nk[1 + 1] = 2 * (5 * F0 + r0) + A[1] \n = 2 * 5 * F0 + (**2 * r0 + A[1]**)\n\t\t = 2 * 5 * F0 + (5 * F1 + r1)\nk[1 + 1] % 5 = **(2 * r0 + A[1]) % 5**\n = r1\n```\ni = 2,\n```\nk[2 + 1] = 2 * (2 * 5 * F0 + (5 * F1 + r1)) + A[2] \n = (4 * 5 * F0 + 2 * 5 * F1) + (**2 * r1 + A[2]**)\n = 5 * (4 * F0 + 2 * F1) + (5 * F2 + r2)\nk[2 + 1] % 5 = (**2 * r1 + A[2]**) % 5\n = r2\n\nrepeat the above till the end of the array...\n\nLook at the bold part of the derivation, we can draw a conclusion that **ONLY the remainders such as r<sub>0</sub>,r<sub>1</sub>,r<sub>2</sub>, ...,r<sub>i</sub>..., count; While the part divisible by `5`, like `5 * (4 * F0 + 2 * F1),5 * F1,5 * (4 * F0 + 2 * F1),5 * F2`, does NOT matter.** \nThat is consistent with the original 1st Java code. Let me know if it answers your question.\n\n----\n\nFor more bit shift operations practice and solution, refer to [1290. Convert Binary Number in a Linked List to Integer](https://leetcode.com/problems/convert-binary-number-in-a-linked-list-to-integer/discuss/451815/javapython-3-simulate-binary-operations/434516)
| 66
| 3
|
[]
| 10
|
binary-prefix-divisible-by-5
|
Java solution with best explanation(don't know why some explanation not concise)
|
java-solution-with-best-explanationdont-xp36i
|
Prerequisite\n\nYou need to know how to contruct a number with bits in some numeric representation. \n\nFor example: \n1. Contruct the number from a string in d
|
416486188
|
NORMAL
|
2019-05-21T03:20:34.471163+00:00
|
2020-01-08T21:37:34.805515+00:00
| 2,539
| false
|
**Prerequisite**\n\nYou need to know how to contruct a number with bits in some numeric representation. \n\nFor example: \n1. Contruct the number from a string in decimal like `"12345678"`, key: `num = num * 10 + (c - \'0\')` where `c` is the current character.\n2. Contruct the number from a string in binary like `"01010101"`, key: `num = num * 2 + (c - \'0\')`, and faster: `(num << 1) | (c - \'0\')` where `c` is the current character.\nOr array format like `[0, 1, 0, 1, 0, 1]`, key: `num = (num << 1) | c` where `c` is the current bit. \n\nYou should be already very familar with that.\n\n---\n**Strategy**\n\nIf you know above, then you can just contruct the number `num` and check if `num % 5 = 0` and add it to result `res`. \n\nBut **Trap**:\nIn Java, an integer `int` is a 32-bit number, that\'s why it is in range of `[-2^31, 2^31 - 1]`. So if we use above way, then it can maximumly represent 32 bits in the array `A`. If beyond that, then `overflow` will happen, you may not get correct result. \n\nSo we need to use some **Math Knowledge**(I learnt it from Cryptography Course if my memory services my right):\nConsider the formula below which is the key to this problem:\n```\n(a * b + c) % d = ((a % d) * (b % d) + c % d) % d\n```\n\nSimply say is that we mod each part in `a * b + c`, then mod the result.\n\nSo in this problem, `num = (num << 1) + cur` which can be written as `num = num * 2 + (0 or 1)`. From above trick, we get `num % 5 = (num % 5) * (2 % 5) + (0 or 1) % 5`. Since `2`, `0`, `1` all smaller than 5, so they mod 5 do not cause any difference, we simplify the formula to => `num % 5 = 2 * (num % 5) + (0 or 1)`. \n\nFrom above we know that we can update `num` to `num % 5` each time which then avoids `overflow` for us.\n\n---\n**Final Code**\n\n```java\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n List<Boolean> res = new ArrayList<>();\n int num = 0;\n for(int cur : A){\n num = ((num << 1) + cur) % 5;\n if(num == 0) res.add(true);\n else res.add(false);\n }\n \n return res;\n }\n}\n```\n\n---\nTC: `O(n)` where `n` is the length of `A`\nSC: `O(1)`\n\n---\n**One more thing**\n\nIf you have any confusion or an opinon on the description, please comment, I will insist on updating it for **at least 100 years**.
| 54
| 1
|
[]
| 5
|
binary-prefix-divisible-by-5
|
[Python] Calculate Prefix Mod
|
python-calculate-prefix-mod-by-lee215-1sgk
|
Solution 1\npy\n def prefixesDivBy5(self, A):\n for i in xrange(1, len(A)):\n A[i] += A[i - 1] * 2 % 5\n return [a % 5 == 0 for a in
|
lee215
|
NORMAL
|
2019-03-31T04:03:41.623466+00:00
|
2021-03-29T04:32:25.103402+00:00
| 4,997
| false
|
# Solution 1\n```py\n def prefixesDivBy5(self, A):\n for i in xrange(1, len(A)):\n A[i] += A[i - 1] * 2 % 5\n return [a % 5 == 0 for a in A]\n```\n`O(1)` space\n```\n def prefixesDivBy5(self, A):\n sums = 0\n for i, a in enumerate(A):\n sums = sums * 2 % 5 + a\n A[i] = sums % 5 == 0\n return A\n```\n<br>\n\n# Solution 2: 1 line using accumulate\n**Python3**\n```py\n def prefixesDivBy5(self, A):\n return [x % 5 == 0 for x in accumulate(A, lambda x, y: (x << 1) + y)]\n```\n\n
| 38
| 5
|
[]
| 11
|
binary-prefix-divisible-by-5
|
C++ 4 lines
|
c-4-lines-by-votrubac-owmy
|
Just build your number from the binary string. The only trick here is to track modulo 5, not the actual number, to avoid overflow.\n\nvector<bool> prefixesDivBy
|
votrubac
|
NORMAL
|
2019-03-31T04:27:50.842973+00:00
|
2019-03-31T04:27:50.843024+00:00
| 3,701
| false
|
Just build your number from the binary string. The only trick here is to track modulo 5, not the actual number, to avoid overflow.\n```\nvector<bool> prefixesDivBy5(vector<int>& A, vector<bool> a = {}, int num = 0) {\n for (auto i : A) {\n num = (num * 2 + i) % 5;\n a.push_back(!num);\n }\n return a;\n}\n```
| 31
| 2
|
[]
| 6
|
binary-prefix-divisible-by-5
|
Simple method(Java)
|
simple-methodjava-by-poorvank-087n
|
When a binary number is appended by 0 , the new remainder can be calculated based on current remainder only.\nremainder = (remainder * 2) % 5;\n\nAnd when a bin
|
poorvank
|
NORMAL
|
2019-03-31T04:23:55.131992+00:00
|
2019-03-31T04:23:55.132055+00:00
| 1,685
| false
|
When a binary number is appended by 0 , the new remainder can be calculated based on current remainder only.\nremainder = (remainder * 2) % 5;\n\nAnd when a binary number is appended by 1.\n remainder = (remainder * 2 + 1) % 5;\n \n For example:\n If it is appended by 0 it will become 10 (2 in decimal) means twice of the last value.\n If it is appended by 1 it will become 11(3 in decimal), twice of last value +1.\n \n```\npublic List<Boolean> prefixesDivBy5(int[] A) {\n List<Boolean> list = new ArrayList<>();\n int remainder = 0;\n for(int bit : A) {\n if (bit == 1)\n remainder = (remainder * 2 + 1) % 5;\n if (bit == 0)\n remainder = (remainder * 2) % 5;\n if(remainder%5==0) {\n list.add(true);\n } else {\n list.add(false);\n }\n }\n return list;\n }\n```
| 29
| 3
|
[]
| 3
|
binary-prefix-divisible-by-5
|
C++ and Python simple solution
|
c-and-python-simple-solution-by-tovam-ltcq
|
C++ :\n\n\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n \n vector<bool> res;\n int num;\n \n
|
TovAm
|
NORMAL
|
2021-10-06T10:25:12.370295+00:00
|
2021-10-06T10:25:12.370484+00:00
| 2,688
| false
|
**C++ :**\n\n```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n \n vector<bool> res;\n int num;\n \n for(int i = 0; i < nums.size(); ++i)\n {\n num = (num * 2 + nums[i]) % 5;\n res.push_back(num == 0);\n }\n \n return res;\n }\n};\n```\n\n**Python :**\n\n```\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n res = []\n num = 0\n \n for n in nums:\n num = (num * 2 + n) % 5\n res.append(num == 0)\n \n return res\n```\n\n**Like it? please upvote**
| 28
| 0
|
['C', 'Python', 'C++', 'Python3']
| 2
|
binary-prefix-divisible-by-5
|
Detailed explanation for mod calculation and equation (with super simple Java solution)
|
detailed-explanation-for-mod-calculation-gm4s
|
Java solution\n\njava\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n List<Boolean> result = new ArrayList<>();\n int r =
|
phoenixpan
|
NORMAL
|
2019-04-02T00:32:22.054228+00:00
|
2019-04-02T00:32:22.054270+00:00
| 757
| false
|
**Java solution**\n\n```java\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n List<Boolean> result = new ArrayList<>();\n int r = 0;\n for (int bit : A) {\n r = (r * 2 + bit) % 5;\n result.add(r % 5 == 0);\n }\n return result;\n }\n}\n```\n\nThis question is similar to question 1015. Assume we have the numer 0111, then we will check 0, 01, 011, 0111. For each number, we can carry the result to the next one through mod calculations, so we don\'t need to calculate the entire number again and again. The induction rule is `next = pre * 2 + lastBit`, for example, `0111 = 011 * 2 + 1`. Here\'s the prove: \n```\n011 = 2^2 * 0 + 2^1 * 1 + 2^0 * 1 = 3\n0111 = 011 * 2 + 2^0 * 1 (the extra bit added at the end, either 0 or 1) \n = (2^2 * 0 + 2^1 * 1 + 2^0 * 1) * 2 + 2^0 * 1\n = 2^3 * 0 + 2^2 * 1 + 2^1 * 1 + 2^0 * 1\n = 7\n```\nSince we always append the extra digit (0 or 1) at the end, which is multiplied by 2^0 = 1. Because multiplying by one could be ignored, we will simply add the extra digit at the end. Eventually, we have `next = pre * 2 + bit`. \n\nNext, we need to record the remainder of the number rather than the whole number, as it will go overflow quickly. Here\'s how:\n\nIn general, we know that `(a + b) % k = (a % k + b % k ) % k` and in this question, we already get `next = pre * 2 + bit`. \n\nFirst we assume: \n```\nn % k = r\nn = m * k + r; \n```\nthen we can have: \n```\n2n + lastBit = 2(mk + r) + lastBit\n2n + lastBit = 2mk + 2r + lastBit; \n(2n + lastBit) % k = (2r + lastBit) % k;\n```\nTherefore we know that calculation based on the number itself, `n`, and it\'s remainder, `r`, is the same. In other words, we don\'t have to do `next = pre * 2 + bit`, but rather `remainderOfNext = remainderOfPre * 2 + bit`
| 14
| 0
|
[]
| 1
|
binary-prefix-divisible-by-5
|
[Java] 100% Runtime easy just 1 iteration
|
java-100-runtime-easy-just-1-iteration-b-uw5e
|
\n\nUPVOTE IF YOU FIND IT USEFUL\n\n\n\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n List<Boolean> list = new ArrayList<>();\n
|
pulkitswami7
|
NORMAL
|
2020-09-05T07:06:12.250363+00:00
|
2020-09-05T07:06:12.250424+00:00
| 451
| false
|
<hr>\n\n***UPVOTE IF YOU FIND IT USEFUL***\n<hr>\n\n```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n List<Boolean> list = new ArrayList<>();\n \n int val = 0;\n for(int i=0;i<A.length;i++){\n val = val * 2 + A[i];\n \n if((val %= 5) == 0)\n list.add(true);\n else\n list.add(false);\n \n }\n \n return list;\n }\n}\n```
| 9
| 0
|
[]
| 2
|
binary-prefix-divisible-by-5
|
Simple Java Solution With Explanation
|
simple-java-solution-with-explanation-by-bxgn
|
Idea\ncurr keeping track of decimal representation so far. When scanning from right, if we multiply curr by 2, it will shift all the bits in curr to left to mak
|
naveen_kothamasu
|
NORMAL
|
2019-03-31T05:00:40.870081+00:00
|
2019-03-31T05:00:40.870116+00:00
| 608
| false
|
**Idea**\n`curr` keeping track of decimal representation so far. When scanning from right, if we multiply `curr` by 2, it will shift all the bits in `curr` to left to make place for the incoming digit `i`. That way, we are reusing the computations. We are not interested in the actual number, so to avoid overflow, we can subtract 5 as many times as possible (i.e. modulo by 5) and still validate if it is divisible by 5.\n\n```\npublic List<Boolean> prefixesDivBy5(int[] A) {\n List<Boolean> res = new ArrayList<>();\n int curr = 0;\n for(int i : A){\n curr = 2*curr+i;\n curr %= 5;\n res.add(curr == 0);\n }\n return res;\n }\n```
| 8
| 2
|
[]
| 3
|
binary-prefix-divisible-by-5
|
[Java] 2ms, 100% + math theory
|
java-2ms-100-math-theory-by-stefanelstan-0oyk
|
\nclass Solution {\n /** Algorithm/Theory\n 1. In order to determine if a binary is divisible by 5, we have to build the 10 base & check\n 2. A
|
StefanelStan
|
NORMAL
|
2022-05-27T15:11:31.969295+00:00
|
2022-05-27T15:11:31.969334+00:00
| 997
| false
|
```\nclass Solution {\n /** Algorithm/Theory\n 1. In order to determine if a binary is divisible by 5, we have to build the 10 base & check\n 2. As the problem states, there will be a stream of bits, 1 and 0 that will build n numbers\n In order to build the next number, start with a value of 0, multiply the current value with 2 and and 0 or 1 (depending on current bit)\n EG: 1100\n step1: value = 0. 0 * 2 + 1 = 1; \n step2: value = 1. 1 * 2 + 1 = 3;\n step3: value = 3. 3 * 2 + 0 = 6;\n step4: value = 6. 6 * 2 + 0 = 12.\n 3. Looking at the steps on #2, we can see that no number (1,3,6,12) is divibile by 5\n 4. What if the stream is much longer, like 33,34 bits? The numbers will become 4 bil +\n We need to find a smart approach for this.\n 5. We don\'t really need the whole number, but just it\'s modulo 10.\n EG: value = 6 and the stream continues with [1,1,1,1]\n - 6 * 2 + 1 = 13 => modulo 10 = 3\n 13 * 2 + 1 = 27 => 3 * 2 + 1 = 7\n 27 * 2 + 1 = 55 => 7 * 2 + 1 = 15 mod 10 = 5.\n 6. Thus we observe that the numbers will always be between 0 and 9.\n If current value is 0 or 5, then it divides, if !=, then it doesn\'t divide.\n */\n public List<Boolean> prefixesDivBy5(int[] nums) {\n List<Boolean> divisibleByFive = new ArrayList<>(nums.length);\n int n = 0;\n for(int bit : nums) {\n n = (n * 2 + bit) % 10;\n divisibleByFive.add(n == 5 || n == 0);\n }\n return divisibleByFive;\n }\n}\n```
| 7
| 0
|
['Java']
| 1
|
binary-prefix-divisible-by-5
|
Python3 using yield
|
python3-using-yield-by-wingsoflight2003-w0fy
|
\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n x = 0\n for i in range(len(A)):\n x = x*2+A[i]\n
|
wingsoflight2003
|
NORMAL
|
2020-02-10T15:23:15.525592+00:00
|
2020-02-10T15:23:15.525784+00:00
| 526
| false
|
```\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n x = 0\n for i in range(len(A)):\n x = x*2+A[i]\n yield x%5==0\n```
| 7
| 0
|
['Python3']
| 2
|
binary-prefix-divisible-by-5
|
[C++] Simple Solution
|
c-simple-solution-by-pankajgupta20-ty24
|
\tclass Solution {\n\tpublic:\n\t\tvector prefixesDivBy5(vector& nums) {\n\t\t\tvector res;\n\t\t\tint t = 0;\n\t\t\tfor(int i = 0; i < nums.size(); i++){\n\t\t
|
pankajgupta20
|
NORMAL
|
2021-05-31T11:58:04.882830+00:00
|
2021-05-31T11:58:04.882875+00:00
| 700
| false
|
\tclass Solution {\n\tpublic:\n\t\tvector<bool> prefixesDivBy5(vector<int>& nums) {\n\t\t\tvector<bool> res;\n\t\t\tint t = 0;\n\t\t\tfor(int i = 0; i < nums.size(); i++){\n\t\t\t\tt = (t * 2 + nums[i]) % 5;\n\t\t\t\tres.push_back(t == 0);\n\t\t\t}\n\t\t\treturn res;\n\t\t}\n\t};
| 5
| 0
|
['C', 'C++']
| 2
|
binary-prefix-divisible-by-5
|
1018 | JavaScript 1 Line Solution
|
1018-javascript-1-line-solution-by-spork-1vwz
|
Runtime: 72 ms, faster than 59.00% of JavaScript online submissions\n> Memory Usage: 38.2 MB, less than 92.31% of JavaScript online submissions\n\nNot the faste
|
sporkyy
|
NORMAL
|
2019-08-12T15:06:54.475362+00:00
|
2021-08-31T13:44:28.390736+00:00
| 727
| false
|
> Runtime: **72 ms**, faster than *59.00%* of JavaScript online submissions\n> Memory Usage: **38.2 MB**, less than *92.31%* of JavaScript online submissions\n\nNot the fastest.\n\n```\n/**\n * @param {number[]} A\n * @param {number} acc\n * @return {boolean[]}\n */\nconst prefixesDivBy5 = (A, acc = 0) => A.map(d => !(acc = (acc * 2 + d) % 5));\n```
| 5
| 0
|
['JavaScript']
| 1
|
binary-prefix-divisible-by-5
|
A couple of different solutions in Python
|
a-couple-of-different-solutions-in-pytho-13tk
|
Here is the first solution:\n\npython\nclass Solution:\n def prefixesDivBy5(self, A):\n result = []\n number = 0\n for bit in A:\n
|
lxnn
|
NORMAL
|
2019-07-14T11:52:29.299869+00:00
|
2019-07-14T14:23:55.380058+00:00
| 417
| false
|
Here is the first solution:\n\n```python\nclass Solution:\n def prefixesDivBy5(self, A):\n result = []\n number = 0\n for bit in A:\n number = 2*number + bit\n result.append(number % 5 == 0)\n return result\n```\n\nThe idea is simple: we accumulate the bits into a binary number as we traverse the list. To append another bit to the number you need only to multiply the number by two (equivalent to shifting all the bits left by one place) and then add the bit. We then determine whether the number is divisible by five with the `%` operator.\n\nWe can make this significantly more efficient by storing only the remainder of the number (modulo five). This works because if 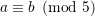, then .\n\n```python\nclass Solution:\n def prefixesDivBy5(self, A):\n result = []\n remainder = 0\n for bit in A:\n remainder = (2*remainder + bit) % 5\n result.append(remainder == 0)\n return result\n```\n\nIn fact, this is essential if you are writing your solution in a language like C, where your integers are at risk of overflowing.\n\n<hr>\n\nAnd here is an alternative one-liner(ish) solution in Python, which takes the same approach but in a more functional-programming style:\n\n```python\nfrom itertools import accumulate\n\nclass Solution:\n def prefixesDivBy5(self, A):\n \n def append_bit_take_mod(num, bit):\n return (2*num + bit) % 5\n \n def equals_zero(num):\n return num == 0\n \n return list(map(equals_zero, accumulate(A, append_bit_take_mod)))\n```
| 5
| 0
|
[]
| 2
|
binary-prefix-divisible-by-5
|
Easy Solution
|
easy-solution-by-algoartisan-q7j6
|
\nvector<bool> prefixesDivBy5(vector<int>& nums) {\n \n vector<bool>v;\n \n int sum=0;\n \n for(auto x : nums){\n
|
AlgoArtisan
|
NORMAL
|
2022-09-10T21:24:43.254888+00:00
|
2022-09-10T21:24:43.254926+00:00
| 921
| false
|
```\nvector<bool> prefixesDivBy5(vector<int>& nums) {\n \n vector<bool>v;\n \n int sum=0;\n \n for(auto x : nums){\n \n sum=(sum*2+x)%5;\n \n v.push_back(sum==0);\n }\n \n return v;\n }\n```
| 4
| 0
|
['C', 'C++']
| 0
|
binary-prefix-divisible-by-5
|
Java Solution with Explanation, faster than 100.00%
|
java-solution-with-explanation-faster-th-fngb
|
\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n int sum = 0;\n int length = nums.length;\n List<Boolean> result
|
kingston880420
|
NORMAL
|
2021-05-29T04:04:49.546906+00:00
|
2021-05-29T04:04:49.546937+00:00
| 500
| false
|
```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n int sum = 0;\n int length = nums.length;\n List<Boolean> result = new ArrayList<>();\n //Go through the nums notice that shifting a binary number to the left is equals to multiplying a decimal number by 2\n for (int i=0; i<length; i++) {\n sum = sum*2 + nums[i];\n if (sum%5==0) {\n result.add(true);\n }\n else {\n result.add(false);\n }\n //This is to prevent it from overflow\n sum = sum%5;\n }\n return result;\n }\n}\n//Time: O(N)\n//Space: O(N)\n```
| 4
| 0
|
['Java']
| 2
|
binary-prefix-divisible-by-5
|
Python | Fast > 99%
|
python-fast-99-by-ddhnnng-feri
|
\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n answer = [None] * len(A)\n S = 0\n for idx, i in enumerate(A
|
ddhnnng
|
NORMAL
|
2021-03-12T21:32:16.498000+00:00
|
2021-03-12T21:33:45.078709+00:00
| 290
| false
|
```\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n answer = [None] * len(A)\n S = 0\n for idx, i in enumerate(A):\n S <<= 1 # bit shift left\n S += i # add new least-sig bit\n S %= 5 # mod math to keep S small (big speed-up)\n answer[idx] = S == 0\n return answer\n```
| 4
| 0
|
['Python']
| 0
|
binary-prefix-divisible-by-5
|
Python O(n) use <<= to solve
|
python-on-use-to-solve-by-abandonblue101-6g1g
|
\ndef prefixesDivBy5(self, A: List[int]) -> List[bool]:\n \n cum = 0\n ans = []\n \n for i in range(len(A)):\n cum
|
abandonblue1015
|
NORMAL
|
2020-07-23T12:31:40.496490+00:00
|
2020-07-23T12:31:40.496519+00:00
| 143
| false
|
```\ndef prefixesDivBy5(self, A: List[int]) -> List[bool]:\n \n cum = 0\n ans = []\n \n for i in range(len(A)):\n cum <<= 1 # based on binary\n cum += (A[i])\n if cum % 5 == 0:\n ans.append(True)\n else:\n ans.append(False)\n return ans\n```
| 4
| 0
|
['Python3']
| 1
|
binary-prefix-divisible-by-5
|
Solution in Python 3 (beats ~98%) (three lines) ( O(1) space )
|
solution-in-python-3-beats-98-three-line-lo0c
|
```\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n \tn = 0\n \tfor i in range(len(A)): A[i], n = (2n + A[i]) % 5 == 0, (2n
|
junaidmansuri
|
NORMAL
|
2019-08-11T14:45:13.659533+00:00
|
2019-08-11T14:46:09.491418+00:00
| 474
| false
|
```\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n \tn = 0\n \tfor i in range(len(A)): A[i], n = (2*n + A[i]) % 5 == 0, (2*n + A[i]) % 5\n \treturn A\n\t\t\n\t\t\n- Junaid Mansuri\n(LeetCode ID)@hotmail.com
| 4
| 1
|
['Python', 'Python3']
| 1
|
binary-prefix-divisible-by-5
|
🔥VERY SIMPLE || JAVA || BEATS 99.11% 🔥
|
very-simple-java-beats-9911-by-tamilselv-ilf1
|
Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n) \n# Code\n\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n L
|
Tamilselvan_Srini
|
NORMAL
|
2024-01-05T10:14:16.904827+00:00
|
2024-01-05T10:20:29.227185+00:00
| 680
| false
|
# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$ \n# Code\n```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n List<Boolean>list=new ArrayList<>();\n int sum=0;\n for(int i=0;i<nums.length;i++)\n {\n sum = (sum * 2 + nums[i]) % 5;\n if(sum!=0)\n {\n list.add(false);\n }\n else\n {\n list.add(true);\n }\n }\n return list;\n }\n}\n```
| 3
| 0
|
['Array', 'Java']
| 1
|
binary-prefix-divisible-by-5
|
|| Easy Solution || DFA ||
|
easy-solution-dfa-by-leetcode_ashutosh-yscp
|
Intuition\nUsing Deterministic Finite Automata \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nConstant\n\n# Code\n\nclass Solution {\n pu
|
leetcode_Ashutosh
|
NORMAL
|
2023-07-19T18:10:48.648386+00:00
|
2023-10-16T15:03:46.150974+00:00
| 173
| false
|
# Intuition\nUsing Deterministic Finite Automata \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nConstant\n\n# Code\n```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n List<Boolean> res = new ArrayList<>();\n int daigram[][] ={{0,1},{2,3},{4,0},{1,2},{3,4}};\n int s = 0;\n for(int a : nums)\n {\n s = daigram[s][a];\n if(s==0)\n res.add(true);\n else\n res.add(false);\n }\n return res;\n }\n}\n```
| 3
| 0
|
['Math', 'Brainteaser', 'C++', 'Java', 'Python3']
| 1
|
binary-prefix-divisible-by-5
|
Java, C++, Python | 🚀 A pinch of math in 7 lines explained
|
java-c-python-a-pinch-of-math-in-7-lines-v8ec
|
\u26A0\uFE0F Disclaimer: The original solution was crafted in Java.\n\nDont forget to upvote if you like the content below. \uD83D\uDE43\n\n# Intuition\nThe tas
|
wallandteen
|
NORMAL
|
2023-05-04T21:16:18.902431+00:00
|
2023-05-09T04:46:05.358313+00:00
| 824
| false
|
> \u26A0\uFE0F **Disclaimer**: The original solution was crafted in Java.\n\nDont forget to upvote if you like the content below. \uD83D\uDE43\n\n# Intuition\nThe task requires us to check whether the binary prefix of each number in an array is divisible by 5. We need to return a boolean array where each index corresponds to the result of the check for the binary prefix ending at the same index in the input array. \n\nThe key insight to solve this problem is to understand that we can keep a running count of the binary number as we iterate through the array and check for divisibility by $$5$$ at each step. As the binary number can be very large, we can take advantage of the fact that $$(a*b) \\mod n==((a \\bmod n)*(b \\mod n)) \\mod n$$.\n\n# Approach\nWe initialize a counter to keep track of the running binary number and an array list to store the results. For each number in the input array, we shift the current counter value to the left by one bit (equivalent to multiplying by $$2$$) and add the current number. We then take the modulus by $$5$$ and check if the result is $$0$$. If it is, we add `true` to the results array; otherwise, we add `false`.\n\n# Complexity Analysis\n- Time complexity: The time complexity is $$O(n)$$, where $$n$$ is the length of the input array, because we make a single pass through the array.\n- Space complexity: The space complexity is $$O(n)$$, where $$n$$ is the length of the input array, because we store a result for each element in the array.\n\n# Code\n```java []\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n var result = new ArrayList<Boolean>(nums.length);\n long counter = 0;\n for (int num : nums) {\n counter = ((counter << 1) + num) % 5;\n result.add(counter == 0);\n }\n return result;\n }\n}\n```\n``` cpp []\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n vector<bool> result;\n int counter = 0;\n for (int num : nums) {\n counter = ((counter << 1) + num) % 5;\n result.push_back(counter == 0);\n }\n return result;\n }\n};\n\n```\n``` python3 []\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n result = []\n counter = 0\n for num in nums:\n counter = ((counter << 1) + num) % 5\n result.append(counter == 0)\n return result\n\n```
| 3
| 0
|
['C++', 'Java', 'Python3']
| 0
|
binary-prefix-divisible-by-5
|
With Explanation Comments: Time: 3 ms (100.00%), Space: 14 MB (46.11%)
|
with-explanation-comments-time-3-ms-1000-f2i3
|
Like it? ->Upvote please! \u30C4\n\n\'\'\'\nclass Solution {\npublic:\n vector prefixesDivBy5(vector& nums) {\n \n //initialize a new vector wi
|
deleted_user
|
NORMAL
|
2022-09-05T19:56:24.177570+00:00
|
2022-09-08T18:53:35.197734+00:00
| 343
| false
|
**Like it? ->Upvote please!** \u30C4\n\n\'\'\'\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n \n //initialize a new vector with boolean values\n vector<bool> res;\n int num=0;\n \n //loop over the whole array numbers\n for(int i=0;i<nums.size();i++){\n /*calculate the current element value added to the last number in the array which is multiplied by 2 as we\'re working with base-2 numbers\n & save the boolean value into the num variable*/\n num=(num*2+nums[i])%5;\n //check if it\'s divisable by 5 or not & insert the resultant boolean value into the new array\n res.push_back(num==0);\n }\n \n //return the new boolean values array\n return res;\n }\n};\n\'\'\'\n\n**Like it? ->Upvote please!** \u30C4\n**If still not understood, feel free to comment. I will help you out**\n**Happy Coding :)**
| 3
| 0
|
['Array', 'C', 'C++']
| 0
|
binary-prefix-divisible-by-5
|
C++|| EASY TO UNDERSTAND || fast and efficient
|
c-easy-to-understand-fast-and-efficient-pdtdg
|
\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n int n=nums.size();\n vector<bool> vec;\n int num=0; \n f
|
aarindey
|
NORMAL
|
2021-10-19T22:09:13.610677+00:00
|
2021-10-19T22:12:29.091601+00:00
| 184
| false
|
```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n int n=nums.size();\n vector<bool> vec;\n int num=0; \n for(int i=0;i<n;i++)\n {\n num=(num*2+nums[i])%10;\n vec.push_back(num%5==0);\n }\n return vec;\n }\n};\n```\n**Please upvote to motivate me in my quest of documenting all leetcode solutions(to help the community). HAPPY CODING:)\nAny suggestions and improvements are always welcome**
| 3
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
C++ || Fast and Easy Method
|
c-fast-and-easy-method-by-suniti0804-hzdi
|
\n vector prefixesDivBy5(vector& A) \n {\n vector res;\n int n = A.size();\n \n int num = 0;\n \n for(int i = 0;
|
suniti0804
|
NORMAL
|
2021-04-13T14:49:18.587362+00:00
|
2021-04-14T17:37:57.121093+00:00
| 271
| false
|
\n vector<bool> prefixesDivBy5(vector<int>& A) \n {\n vector<bool> res;\n int n = A.size();\n \n int num = 0;\n \n for(int i = 0; i < n; i++)\n {\n num = num * 2 + A[i];\n if(num % 5 == 0)\n res.push_back(true);\n else\n res.push_back(false);\n num = num % 5; \n }\n \n return res;\n }\n
| 3
| 0
|
['C', 'C++']
| 0
|
binary-prefix-divisible-by-5
|
Java 100% fast, simple
|
java-100-fast-simple-by-umedjan-0f75
|
\nclass Solution {\n\tpublic List<Boolean> prefixesDivBy5(int[] A) {\n\t\tList<Boolean> result = new ArrayList<>(A.length);\n\t\tint s = 0;\n\t\tfor (int i : A)
|
umedjan
|
NORMAL
|
2021-02-10T09:53:27.520991+00:00
|
2021-02-10T09:53:27.521022+00:00
| 383
| false
|
```\nclass Solution {\n\tpublic List<Boolean> prefixesDivBy5(int[] A) {\n\t\tList<Boolean> result = new ArrayList<>(A.length);\n\t\tint s = 0;\n\t\tfor (int i : A)\n\t\t\tresult.add((s = (s * 2 + i) % 5) == 0);\n\n\t\treturn result;\n\t}\n}\n```
| 3
| 0
|
['Java']
| 3
|
binary-prefix-divisible-by-5
|
C++ 12ms 100% Fast
|
c-12ms-100-fast-by-kumaranuj1303-u9fr
|
\nvector<bool> prefixesDivBy5(vector<int>& A) \n {\n int size = A.size();\n vector<bool> B(size);\n for (auto i = 1; i < size; i++)\n
|
kumaranuj1303
|
NORMAL
|
2020-10-20T13:10:42.541165+00:00
|
2020-10-20T13:10:42.541205+00:00
| 219
| false
|
```\nvector<bool> prefixesDivBy5(vector<int>& A) \n {\n int size = A.size();\n vector<bool> B(size);\n for (auto i = 1; i < size; i++)\n {\n A[i] = (A[i] + A[i-1] * 2) % 10;\n if (A[i] % 5)\n B[i] = 0;\n else\n B[i] = 1;\n }\n if (A[0] == 0)\n B[0] = 1;\n return B;\n }\n```
| 3
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
[Java] Simple bit shifting | O(n) time, O(1) space
|
java-simple-bit-shifting-on-time-o1-spac-ijo7
|
```\nclass Solution {\n public List prefixesDivBy5(int[] A) {\n \n List result = new ArrayList<>(A.length);\n int num = 0;\n for(i
|
mdshahnawaz459
|
NORMAL
|
2020-09-08T12:20:28.273713+00:00
|
2020-09-08T12:23:28.173775+00:00
| 278
| false
|
```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n \n List<Boolean> result = new ArrayList<>(A.length);\n int num = 0;\n for(int i = 0; i < A.length; i++) {\n num <<= 1;\n num |= A[i];\n result.add((num = (num % 5)) == 0 ? true: false);\n }\n return result;\n }\n}
| 3
| 0
|
['Bit Manipulation', 'Java']
| 0
|
binary-prefix-divisible-by-5
|
Javascript simple solution with explanation
|
javascript-simple-solution-with-explanat-3yjk
|
\nvar prefixesDivBy5 = function (A) {\n let stv = 0;\n return A.map((bit) => {\n stv = stv * 2 + bit;\n\t//adding 1 binary bit means whether the number get
|
leomacode
|
NORMAL
|
2020-08-25T18:37:01.540257+00:00
|
2020-08-25T18:40:52.686430+00:00
| 453
| false
|
```\nvar prefixesDivBy5 = function (A) {\n let stv = 0;\n return A.map((bit) => {\n stv = stv * 2 + bit;\n\t//adding 1 binary bit means whether the number gets doubled (if add 0) or gets doubled and plus 1 (if add 1)\n\t//Example: decimal 2 is 10 in binary. If add 0 in binary: 10 will be 100 which is 4 in decimal (the number gets doubled). If add 1 in binary: 10 will be 101 which is 5 in decimal(the number gets doubled and plus 1).\n stv %= 5;\n\t//to prevent overflow\n return stv == 0;\n });\n};\n```
| 3
| 0
|
['JavaScript']
| 0
|
binary-prefix-divisible-by-5
|
Python Simple solution
|
python-simple-solution-by-lokeshsk1-7og0
|
\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n s=\'\';l=[]\n for i in A:\n s+=str(i)\n l.app
|
lokeshsk1
|
NORMAL
|
2020-08-14T08:52:44.943453+00:00
|
2020-08-14T10:25:28.688260+00:00
| 412
| false
|
```\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n s=\'\';l=[]\n for i in A:\n s+=str(i)\n l.append(int(s,2)%5==0)\n return l\n \n```
| 3
| 0
|
['Python', 'Python3']
| 0
|
binary-prefix-divisible-by-5
|
C++ solution
|
c-solution-by-oleksam-u7wm
|
\nvector<bool> prefixesDivBy5(vector<int>& A) {\n\tint iCurr = 0;\n\tvector<bool> vRes;\n\tfor (auto n : A) {\n\t\tiCurr = (iCurr << 1) | n;\n\t\tvRes.push_back
|
oleksam
|
NORMAL
|
2020-06-30T12:49:06.506140+00:00
|
2020-06-30T12:49:06.506173+00:00
| 414
| false
|
```\nvector<bool> prefixesDivBy5(vector<int>& A) {\n\tint iCurr = 0;\n\tvector<bool> vRes;\n\tfor (auto n : A) {\n\t\tiCurr = (iCurr << 1) | n;\n\t\tvRes.push_back(iCurr % 5 == 0);\n\t\tiCurr %= 10;\n\t}\n\treturn vRes;\n}\n```\n
| 3
| 0
|
['C', 'C++']
| 0
|
binary-prefix-divisible-by-5
|
JAVA Solution with a Trick to prevent Overflow
|
java-solution-with-a-trick-to-prevent-ov-7m3z
|
\npublic List<Boolean> prefixesDivBy5(int[] A) {\n\tint currentNum = 0;\n\tList<Boolean> sol = new ArrayList<>();\n\tfor(int a : A) {\n\t\t// (a * b + c) % d =
|
anubhavjindal
|
NORMAL
|
2019-11-16T06:21:50.433788+00:00
|
2019-11-16T06:21:50.433845+00:00
| 227
| false
|
```\npublic List<Boolean> prefixesDivBy5(int[] A) {\n\tint currentNum = 0;\n\tList<Boolean> sol = new ArrayList<>();\n\tfor(int a : A) {\n\t\t// (a * b + c) % d = ((a % d) * (b % d) + c % d) % d\n\t\tcurrentNum = (currentNum << 1 | a)%5;\n\t\tsol.add(currentNum==0);\n\t}\n\treturn sol;\n}\n```
| 3
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
Simple, C++ Solution [beats 98%, 100%]
|
simple-c-solution-beats-98-100-by-pooja0-y5hc
|
Runtime: 8 ms, faster than 98.57% of C++ online submissions for Binary Prefix Divisible By 5.\nMemory Usage: 10.6 MB, less than 100.00% of C++ online submission
|
pooja0406
|
NORMAL
|
2019-09-01T08:18:45.228178+00:00
|
2019-09-01T08:18:45.228210+00:00
| 477
| false
|
Runtime: 8 ms, faster than 98.57% of C++ online submissions for Binary Prefix Divisible By 5.\nMemory Usage: 10.6 MB, less than 100.00% of C++ online submissions for Binary Prefix Divisible By 5.\n\n```\n vector<bool> prefixesDivBy5(vector<int>& A) {\n \n vector<bool> res;\n int n = A.size();\n int num = 0;\n \n for(int i=0; i<n; i++)\n {\n num = num*2 + A[i];\n num %= 5;\n res.push_back(num%5 == 0);\n }\n \n return res;\n }
| 3
| 0
|
['C++']
| 1
|
binary-prefix-divisible-by-5
|
C solution with DFA; general purpose
|
c-solution-with-dfa-general-purpose-by-j-kwo7
|
A general purpose solution written in C with DFA:\n\nc\nbool* prefixesDivBy5(int* A, int ASize, int* returnSize){\n *returnSize = ASize;\n bool *res = (bo
|
jules3in
|
NORMAL
|
2019-08-07T05:18:03.682804+00:00
|
2019-08-07T05:18:03.682840+00:00
| 234
| false
|
A general purpose solution written in C with DFA:\n\n```c\nbool* prefixesDivBy5(int* A, int ASize, int* returnSize){\n *returnSize = ASize;\n bool *res = (bool *)malloc(ASize * sizeof(bool));\n\n int q0 = 0, q1 = 1, q2 = 2, q3 = 3, q4 = 4;\n int DFA[5][2] = { {q0, q1}, {q2, q3}, {q4, q0}, {q1, q2}, {q3, q4} };\n\n int status = q0;\n for (int i = 0; i < ASize; i++) {\n status = DFA[status][A[i]];\n res[i] = status == q0;\n }\n\n return res;\n}\n\n```\n\n For the DFA, see:\n \n* https://www.quora.com/How-do-i-check-if-a-binary-number-is-divisible-by-say-n\n \n* https://stackoverflow.com/questions/21897554/design-dfa-accepting-binary-strings-divisible-by-a-number-n
| 3
| 0
|
['C']
| 0
|
binary-prefix-divisible-by-5
|
Python Solution - Bit shift with mod check
|
python-solution-bit-shift-with-mod-check-vyky
|
Each time you look you add a bit, you are multiplying the previous sum by 2 and adding the value of the current bit. This can be achieved by a simple left bit s
|
raosrika89
|
NORMAL
|
2019-05-26T18:47:06.274556+00:00
|
2019-05-26T19:44:47.826249+00:00
| 320
| false
|
Each time you look you add a bit, you are multiplying the previous sum by 2 and adding the value of the current bit. This can be achieved by a simple left bit shift by 1. \n\nIt is then just a matter of checking if the total is divisible by 5 or not. \n\n```\nclass Solution:\n \n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n \n answer = [False] * len(A)\n total = 0\n \n for i in range(len(A)):\n \n total += A[i] \n \n if total % 5 == 0:\n answer[i] = True\n \n\t\t\t// Left shift by 1 ==> total * (2**1) \n total = total << 1\n \n return answer\n```
| 3
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
JavaScript Solution, Straight forward
|
javascript-solution-straight-forward-by-kmlzs
|
javascript\\\nvar prefixesDivBy5 = function(A) {\n let cur = 0;\n const r = []\n for (const a of A) {\n cur = ((cur << 1) | a) % 5;\n r.p
|
ruinan
|
NORMAL
|
2019-04-21T05:19:31.000013+00:00
|
2019-04-21T05:19:31.000181+00:00
| 282
| false
|
```javascript\\\nvar prefixesDivBy5 = function(A) {\n let cur = 0;\n const r = []\n for (const a of A) {\n cur = ((cur << 1) | a) % 5;\n r.push(cur === 0);\n }\n return r;\n};\n```
| 3
| 0
|
[]
| 1
|
binary-prefix-divisible-by-5
|
个人觉得很好理解的java解法
|
ge-ren-jue-de-hen-hao-li-jie-de-javajie-5313z
|
\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n List<Boolean> result = new ArrayList<>();\n int current = 0;\n for
|
zhf123
|
NORMAL
|
2019-04-17T02:50:20.007613+00:00
|
2019-04-17T02:50:20.007656+00:00
| 248
| false
|
```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n List<Boolean> result = new ArrayList<>();\n int current = 0;\n for (int i:A){\n current = (current*2+i)%10;\n result.add(current%5==0);\n }\n return result;\n}\n}``\n```
| 3
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
Java, simple 3 lines, no modulo
|
java-simple-3-lines-no-modulo-by-jpv-kvmb
|
I see lots of solutions using %, which is an expensive operation. If you have something between 0 and 4, then double it and add 0 or 1, your result is between
|
jpv
|
NORMAL
|
2019-03-31T13:49:57.440502+00:00
|
2019-03-31T13:49:57.440544+00:00
| 355
| false
|
I see lots of solutions using %, which is an expensive operation. If you have something between 0 and 4, then double it and add 0 or 1, your result is between 0 and 9. Just subtracting 5 if needed is cheaper/faster than using modulo.\n```\n public List<Boolean> prefixesDivBy5(int[] A) {\n List<Boolean> ans = new ArrayList<Boolean>( A.length );\n for( int i=0,x=0; i<A.length; x-=(x>4)?5:0,ans.add(x==0),i++ ) x+=x+A[i];\n return ans;\n }\n```
| 3
| 2
|
[]
| 1
|
binary-prefix-divisible-by-5
|
Simple and Easy Java Solution || Beats 99% || With intuition and approach
|
simple-and-easy-java-solution-beats-99-w-myjn
|
🔍 Intuition:
The given binary array represents a number whose digits are read sequentially.
We need to check if the number formed by the prefix (from index0toi)
|
Yashvendra
|
NORMAL
|
2025-02-18T17:45:39.448830+00:00
|
2025-02-18T17:45:39.448830+00:00
| 157
| false
|
## 🔍 Intuition:
- The given binary array represents a number whose digits are read sequentially.
- We need to check if the number formed by the prefix (from index `0` to `i`) is divisible by `5`.
- Instead of converting the entire prefix into an integer (which may cause overflow for large inputs), we can maintain the remainder when divided by `5`.
- Using the property:
- If `(A * 2 + B) % 5 == 0`, then the number is divisible by `5`.
---
## 🛠️ Approach:
1. **Initialize `num = 0`**, which will store the remainder of the number formed so far.
2. Create a **list of Boolean values** to store results for each prefix.
3. **Iterate through `nums`**:
- Update `num` using the formula:
\[
num = (num \times 2 + \text{ele}) \% 5
\]
- Check if `num == 0`, meaning the prefix is divisible by `5`.
- Add the result (`true` or `false`) to the list.
4. **Return the list** containing results for all prefixes.
---
## ⏱️ Complexity Analysis:
- **Time Complexity:**
- We iterate through the `nums` array **once**, performing **O(1)** operations per element.
- **Overall: O(N)**, where `N` is the length of `nums`.
- **Space Complexity:**
- We store `N` boolean values in the list.
- **Overall: O(N)** for the output list.
# Code
```java []
class Solution {
public List<Boolean> prefixesDivBy5(int[] nums) {
int num = 0;
ArrayList<Boolean> list = new ArrayList<>();
for(int ele: nums){
num = (num * 2 + ele)%5;
list.add(num==0);
}
return list;
}
}
```
| 2
| 0
|
['Array', 'Bit Manipulation', 'Java']
| 0
|
binary-prefix-divisible-by-5
|
python solution
|
python-solution-by-bhavanabharatisingh-ybrv
|
Intuitionconvert it into numeric value and check the visibilityComplexity
Time complexity:
O(n)
Space complexity:
O(n)Code
|
bhavanabharatisingh
|
NORMAL
|
2024-12-22T12:20:04.859431+00:00
|
2024-12-22T12:20:04.859431+00:00
| 182
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
convert it into numeric value and check the visibility
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(n)
# Code
```python3 []
class Solution:
def prefixesDivBy5(self, nums: List[int]) -> List[bool]:
str_arr = list()
res = list()
for i in nums:
str_arr.append(str(i))
res.append(int("".join(str_arr), 2) % 5 == 0)
# res.append(True)
return res
```
| 2
| 0
|
['Python3']
| 0
|
binary-prefix-divisible-by-5
|
Two Solutions | Bit Manipulation & DFA | Both O(n)
|
two-solutions-bit-manipulation-dfa-both-fy95r
|
Solution 1 | Bit Manipulation:\n## Intuition\n\nWith each new bit, we can determine the new remainder by left-shifting the new bit onto the existing remainder a
|
SquirtleHerder
|
NORMAL
|
2024-02-23T22:22:53.859215+00:00
|
2024-04-13T04:44:12.891124+00:00
| 631
| false
|
# Solution 1 | Bit Manipulation:\n## Intuition\n\nWith each new bit, we can determine the new remainder by left-shifting the new bit onto the existing remainder and then computing the modulo of the resultant value. \n\nThis approach ensures that the length of the resulting value would remain at most 4 bits vs other bit manipulation approaches. This approach will work on an infinitely long input list regardless of language.\n\n## Approach\n<!-- Describe your approach to solving the problem. -->\nIncrement over each bit in the array and left shift that bit into the last remainder. \n\nMod the new by 5 and store it back into the remainder value.\n\nIf our remainder holds any value other that 0, the number is not divisible by 5.\n\n## Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1):\\ Ignoring\\ the\\ return\\ array$$\n## Python3\n```\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n answer = []\n remainder = 0\n\n for num in nums:\n remainder = (remainder << 1 | num) % 5\n answer.append(not bool (remainder))\n\n return answer\n```\n# C++\n```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& A) {\n vector<bool> answer(A.size());\n int remainder = 0;\n \n for(int i = 0; i < A.size(); i++) {\n remainder = (remainder << 1 | A[i]) % 5;\n answer[i] = !(bool)remainder;\n }\n return answer;\n }\n};\n```\n# C\n```\nbool* prefixesDivBy5(int* nums, int numsSize, int* returnSize) {\n bool* answer = (bool*)malloc(sizeof(bool) * numsSize);\n int remainder = 0;\n \n *returnSize = numsSize;\n for(int i = 0; i < numsSize; i++) {\n remainder = (remainder << 1 | nums[i]) % 5;\n answer[i] = !(bool)remainder;\n }\n\n return answer;\n}\n```\n\n---\n\n# Solution 2: DFA (Deterministic Finite Automaton):\n\n## Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs discussed above, since the new remainder can be obtained by left-shifting the new bit onto the old remainder, we can design a deterministic finite automaton (DFA) with state transitions to achieve this same result.\n\nGiven that there are five potential remainders (0-4), we can establish a DFA comprising five states. The transition table presented below illustrates the state transitions for this DFA.\n\n$$\n\\begin{array}{ccccc}\n\\text{Prev Rem (State)} & \\text{Shift Bit} & \\text{w/ Shift Bit} & \\text{New \\%5 Rem (New State)} \\\\\n\\hline\n0\\| 000 & \\text{0} & 0\\|0000 & 0\\|0000 \\\\\n0\\|000 & \\text{1} & 1\\|0001& 1\\|0001 \\\\\n1\\|001 & \\text{0} & 2\\|0010 & 2\\|0010 \\\\\n1\\|001 & \\text{1} & 3\\|0011& 3\\|0011 \\\\\n2\\|010 & \\text{0} & 4\\|0100 & 4\\|0100 \\\\\n2\\|010 & \\text{1} & 5\\|0101 & 0\\|0000 \\\\\n3\\|011 & \\text{0} & 6\\|0110 & 1\\|0001 \\\\\n3\\|011 & \\text{1} & 7\\|0111 & 2\\|0010 \\\\\n4\\|100 & \\text{0} & 8\\|1000 & 3\\|0011 \\\\\n4\\|100 & \\text{1} & 9\\|1001 & 4\\|0100 \\\\\n\\end{array}\n$$\n\n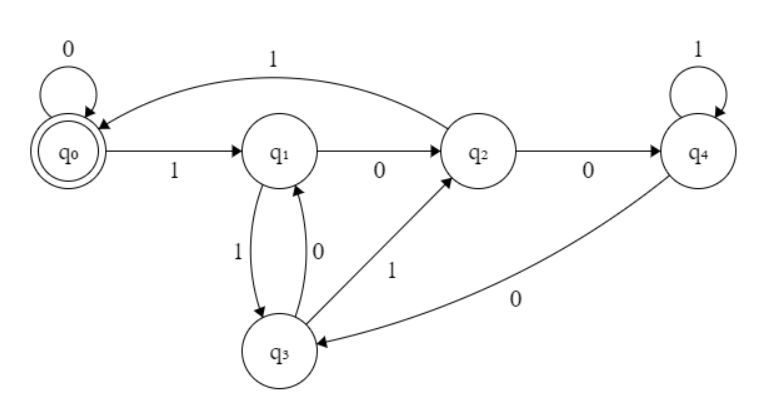\n#####\n\n## Approach\n<!-- Describe your approach to solving the problem. -->\nWe can construct the above DFA using a 2D array.\nEach row represents the states (0-5), and each column represents the next state based on the recieved input (0 or 1).\n\nWe can increment over the input array, and everytime the current state is 0, \'accept\' and append \'true\' onto the answer list otherwise \'reject\' and append \'false\'.\n\n\n## Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1):\\ Ignoring\\ the\\ return\\ array$$\n\n## Python3\n```\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n answer = []\n dfa = [[0,1], [2,3], [4,0], [1,2], [3,4]]\n cur_state = 0\n \n for num in nums:\n cur_state = dfa[cur_state][num]\n answer.append(not bool(cur_state))\n \n return answer\n```\n\n## C++\n\n```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& A) {\n vector<bool> answer(A.size());\n int dfa[5][2] ={{0,1}, {2,3}, {4,0}, {1,2}, {3,4}};\n int curState = 0;\n \n for(int i = 0; i < A.size(); i++) {\n curState = dfa[curState][A[i]];\n answer[i] = !(bool)curState;\n }\n\n return answer;\n }\n};\n```\n\n## C\n```\nbool* prefixesDivBy5(int* nums, int numsSize, int* returnSize) {\n bool* answer = (bool*)malloc(sizeof(bool) * numsSize);\n int dfa[5][2] = {{0,1}, {2,3}, {4,0}, {1,2}, {3,4}};\n int curState = 0;\n \n *returnSize = numsSize;\n for(int i = 0; i < numsSize; i++) {\n curState = dfa[curState][nums[i]];\n answer[i] = !(bool)curState;\n }\n\n return answer;\n}\n```
| 2
| 0
|
['Bit Manipulation', 'C', 'Simulation', 'C++', 'Python3']
| 0
|
binary-prefix-divisible-by-5
|
Solution
|
solution-by-deleted_user-n77d
|
C++ []\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n vector<bool> r;\n int n=0;\n for(int b : nums){\n
|
deleted_user
|
NORMAL
|
2023-05-21T07:25:16.874924+00:00
|
2023-05-21T07:49:00.002614+00:00
| 712
| false
|
```C++ []\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n vector<bool> r;\n int n=0;\n for(int b : nums){\n n = ((n<<1) | b) % 5;\n r.push_back(n==0);\n }\n return r;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n currBinary, result = 0, []\n for bit in nums:\n currBinary = (currBinary * 2 + bit) % 5 \n result.append(currBinary == 0)\n return result\n```\n\n```Java []\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n int c = 0;\n Boolean ans[] = new Boolean[nums.length];\n for(int i=0; i<nums.length; i++){\n c = ((c<<1) + nums[i]) % 5;\n ans[i] = c == 0;\n }\n return Arrays.asList(ans);\n }\n}\n```
| 2
| 0
|
['C++', 'Java', 'Python3']
| 0
|
binary-prefix-divisible-by-5
|
Java && JavaScript Solution does not need to convert anything
|
java-javascript-solution-does-not-need-t-mncq
|
There are many solutions for solving this problem and most of them are awesome. This solution based on that and just modified it to easier and cleaner\n=> Here
|
tonybuidn
|
NORMAL
|
2022-11-26T06:16:58.187901+00:00
|
2023-02-26T15:26:01.924719+00:00
| 713
| false
|
There are many solutions for solving this problem and most of them are awesome. This solution based on that and just modified it to easier and cleaner\n=> Here using loop enhancement instead original loop => because we always to get the value for each index start the first to the end of the array.\n=> so we use loop enhancement just only get the values.\n=> rest of that the logic is similarly: when we move to bit => we will become original * 2: for example: \n+ we have binary 1 => is 1 ( 1 * (2 ^ 0)) => when we move bit 10 => it means that the brevious exponential will become 2 ^ 1. Similarly to other 2 ^ 2, 2 ^ 3.\nHere 1 = (1 * (2 ^ 0)) = 1 , 10 = (1 * (2^1)), 100 = (1*(2^2)), are the same 1 = 1 , 10 = 1 * 2, 100 = 4, 1000 = 8, etc.\n\n**Java**\n```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n LinkedList<Boolean> res = new LinkedList<>();\n\t\t\n int num = 0;\n for(int value : nums){\n num = (num * 2 + value) % 5;\n res.addLast(num == 0);\n }\n\t\t\n\t\treturn res;\n }\n}\n```\n**JavaScript**\n```\n/**\n * @param {number[]} nums\n * @return {boolean[]}\n */\nvar prefixesDivBy5 = function(nums) {\n var result = [];\n const len = nums.length-1;\n\n var num = 0;\n for(var i = 0; i <= len; i++){\n num = (num * 2 + nums[i]) % 5;\n result.push(num == 0);\n }\n return result;\n};\n```
| 2
| 0
|
['Java']
| 1
|
binary-prefix-divisible-by-5
|
C++ || easy and efficient
|
c-easy-and-efficient-by-prakhar_20-i3xo
|
\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n \n vector<bool> v1;\n int sum=0;\n for(int i=0;i
|
prakhar_20
|
NORMAL
|
2022-09-01T19:12:26.420036+00:00
|
2022-09-01T19:12:26.420077+00:00
| 580
| false
|
```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n \n vector<bool> v1;\n int sum=0;\n for(int i=0;i<nums.size();i++)\n { \n sum+=nums[i]; //to check for each element\n sum*=2; // to convert binary to numeric form\n if(sum%5 == 0) \n {\n sum = 0; // if divisible then make it 0\n v1.push_back(true);\n }\n else\n { \n sum = sum%5; //if not divisible then sum= remainder when divided by 5\n v1.push_back(false);\n }\n }\n return v1;\n }\n};\n```\n
| 2
| 0
|
['C++']
| 1
|
binary-prefix-divisible-by-5
|
Least Runtime Solution
|
least-runtime-solution-by-day_tripper-06m3
|
\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n c,l=0,[]\n for i in nums:\n c=(c*2+i)%5\n
|
Day_Tripper
|
NORMAL
|
2022-07-19T09:39:49.620194+00:00
|
2022-07-19T09:39:49.620231+00:00
| 159
| false
|
```\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n c,l=0,[]\n for i in nums:\n c=(c*2+i)%5\n l.append(c==0)\n return l\n```
| 2
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
𝗗𝗲𝘁𝗮𝗶𝗹𝗲𝗱 𝗘𝘅𝗽𝗹𝗮𝗻𝗮𝘁𝗶𝗼𝗻 | Python | C | 𝗢(𝗻) | DFA | Theory | Thought Process
|
detailed-explanation-python-c-on-dfa-the-gp10
|
\u2714 \uD835\uDDD7\uD835\uDDD8\uD835\uDDE7\uD835\uDDD4\uD835\uDDDC\uD835\uDDDF\uD835\uDDD8\uD835\uDDD7 \uD835\uDDD8\uD835\uDDEB\uD835\uDDE3\uD835\uDDDF\uD835\u
|
RohitSgh
|
NORMAL
|
2022-06-02T01:50:35.934185+00:00
|
2023-01-10T20:39:42.305959+00:00
| 377
| false
|
# \u2714 \uD835\uDDD7\uD835\uDDD8\uD835\uDDE7\uD835\uDDD4\uD835\uDDDC\uD835\uDDDF\uD835\uDDD8\uD835\uDDD7 \uD835\uDDD8\uD835\uDDEB\uD835\uDDE3\uD835\uDDDF\uD835\uDDD4\uD835\uDDE1\uD835\uDDD4\uD835\uDDE7\uD835\uDDDC\uD835\uDDE2\uD835\uDDE1 \n\nThis **Solution** will use the concept of **Finite Automaton**, and is similar to <ins>[this][1]</ins> answer. \n> \uD83D\uDC4D\uD83C\uDFFB Those who are well aware of the term can quickly read the post. You will appreciate finding `Practical Application` of `Theory of Automata` \n> \n> \uD83D\uDE44 You haven\'t heard the term? Even you can continue reading! Slowly you will get everything. At last you can dub that you have `learnt new concept the hard way`.\n> \n> \uD83D\uDCDD You will appreciate unique thought process of solving the problem. Make sure to have pen-paper with you. Try to visualize.\n>\n> \uD83D\uDE09 <ins>Solution will slowly build-up `theory`, then we will quickly `analyze problem` and then `code` the thought-process. At last we will try to `optimize` the code.</ins> Last Section of post will take care of Edits and Reply to Comments/Doubts.\n\nWe will simulate a **[Deterministic Finite Automaton (DFA)][1]** that **accepts** Binary Representation of Integers which are divisible by 5, and we want to do this again and again for every substring from index `0` to index `i` \n\n> Now, by **accept**, we mean that when we are done with scanning that particular sub-string, we should be in one of the multiple possible Final States. \n<br>\n\n\n\n----------\n\n\n\n<br>\n\n# \uD83D\uDCD1 \uD835\uDDE7\uD835\uDDDB\uD835\uDDD8\uD835\uDDE2\uD835\uDDE5\uD835\uDDEC\n\n**Approach to Design DFA :** We need to divide the Binary Representation of Integer by 5, and track the remainder. If after consuming/scanning [From MSB to Current LSB, LSB will keep on changing] the entire sub-string, remainder is Zero, then we should end up in Final State [and note down `True`], and if remainder isn\'t zero we should be in Non-Final States [and note down `False`]\n\nNow, DFA is defined by **(Q,q\u2080,F,\u03A3,\u03B4)**. We will obtain these five components step-by-step.\n> Confused? Continue reading, you will enjoy the Journey. \uD83D\uDE0E\n\n\n1. **Q : Finite Set of States** \nWe need to track remainder. On dividing any integer by `5`, we can get remainder as `0,1, 2, 3 or 4`. Hence, we will have Five States `Z, O, T, Th and F` for each possible remainder. \n**Q={Z, O, T, Th, F}** \nIf after scanning certain *part* of Binary String, we are in state `Z`, this means that integer defined from <ins>`Left to this part`</ins> will give remainder `Z`ero when divided by `5`. Similarly, `O` for remainder `O`ne, and so on. \nNow, we can write these three states by [Euclidean Division Algorithm][2] as \n**Z** : 5`m` \n**O** : 5`m`+1 \n**T** : 5`m`+2 \n**Th** : 5`m`+3 \n**F** : 5`m`+4 \nwhere `m` is Integer.\n<br>\n\n2. **q\u2080 : an initial/start state from set Q** \nNow, start state can be thought in terms of empty string (`\u025B`). An `\u025B` directly gets into q\u2080. \nWhat remainder does `\u025B` gives when divided by 5? \nWe can append as many `0s` in left hand side of a *Binary Number*. In the similar fashion, we can append `\u025B` in left hand side of a *Binary String*. Thus, `\u025B` in left can be thought of as `0`. And `0` when divided by `5` gives remainder `0`. Hence, `\u025B` should end in State `Z`. But `\u025B` ends up in q\u2080. <br> \nThus, **q\u2080=Z**\n<br>\n\n3. **F : a set of accept states** \nNow we want all strings which are divisible by 5, **or** which gives remainder 0 when divided by 5, **or** which after complete scanning should end up in state Z, and gets accepted. [`True`]\nHence, \n**F={Z}**\n<br>\n\n4. **\u03A3 : Alphabet (a finite set of input symbols)** \nSince we are scanning/reading a Binary String. Hence,\n**\u03A3={0,1}**\n<br>\n\n5. **\u03B4 : Transition Function (\u03B4 : Q \xD7 \u03A3 \u2192 Q)** \nNow this \u03B4 tells us that if we are in state `x (in Q)` and next input to be scanned is `y (in \u03A3)`, then at which state `z (in Q)` should we go. <br>\n<ins>In context of this problem, if the string upto this point gives remainder `3/Th` when divided by `5`, and if we append `1` to string, then what remainder will resultant string give.</ins> **The Primary Focus of this Problem.** Read This Line Again. \u2714\n<br>\nNow, this can be analyzed by observing *how magnitude of a binary string changes on appending 0 and 1*.<br>\n`a.` \nIn Decimal `(Base-10)`, if we add/append `0`, then magnitude gets multiplied by `10` . 53, on appending 0 it becomes 530 \nAlso, if we append 8 to decimal, then Magnitude gets multiplied by `10`, and then we add `8` to multiplied magnitude.\n<br>`b.` \nIn **Binary (Base-2),** if we **add/append 0**, then magnitude gets multiplied by 2 (The Positional Weight of each Bit get multiplied by 2) \n**Example :** (1010)<sub>2</sub> *[which is (10)<sub>10</sub>]*, on appending 0 it becomes (10100)<sub>2</sub> *[which is (20)<sub>10</sub>]*\nSimilarly, In **Binary**, if we **append 1**, then Magnitude gets multiplied by 2, and then we add 1. \n**Example :** (10)<sub>2</sub> *[which is (2)<sub>10</sub>]*, on appending 1 it becomes (101)<sub>2</sub> *[which is (5)<sub>10</sub>]*\n<br>**Thus, we can say that for Binary String x, \n`-` x0=2|x| \n`-` x1=2|x|+1\n[Key Formula of Problem]**\n<br>We will use these relation to analyze Five States [Read Carefully from <ins>this point</ins> \uD83D\uDC4D\uD83C\uDFFB]\n<br>**Any string in `Z` can be written as `5m`** \n `-` On 0, it becomes `2(5m)`, which is `5(2m)`, nothing but state `Z`. \n `-` On 1, it becomes `2(5m)+1`, which is `5(2m)+1`, that is `O`. *[This can be read as if a Binary String is presently divisible by 5, and we append 1, then resultant string will give remainder as 1]* \n<br>**Any string in `O` can be written as `5m+1`** \n `-` On 0, it becomes `2(5m+1) = 10m+2`, which is `5(2m)+2`, state `T`. \n `-` On 1, it becomes `2(5m+1)+1 = 10m+3`, which is `5(2m)+3`, that is state `Th`. \n<br>**Any string in `T` can be written as `5m+2`**\n `-` On 0, it becomes `2(5m+2) = 10m+4`, which is `5(2m)+4`, state `F`. \n `-` On 1, it becomes `2(5m+2)+1 = 10m+5`, which is `5(2m+1)`, state `Z`. *[If m is integer, so is (2m+1)]* \n <br>**Any string in `Th` can be written as `5m+3`** \n `-` On 0, it becomes `2(5m+3) = 10m+6`, which is `5(2m+1)+1`, state `V`. \n `-` On 1, it becomes `2(5m+3)+1 = 10m+7`, which is `5(2m+1)+2`, that is state `T`. \n<br>**Any string in `F` can be written as `5m+4`** \n `-` On 0, it becomes `2(5m+4) = 10m+8`, which is `5(2m+1)+3`, state `Th`. \n `-` On 1, it becomes `2(5m+4)+1 = 10m+9`, which is `5(2m+1)+4`, that is state `F`. \n\n**Hence, the final DFA combining Everything (creating using [Tool](https://ivanzuzak.info/noam/webapps/fsm_simulator/))** \n\n\n<br>\n\n\n\n----------\n\n\n\n<br>\n\n# \uD83D\uDDEF\uD835\uDDD4\uD835\uDDE1\uD835\uDDD4\uD835\uDDDF\uD835\uDDEC\uD835\uDDED\uD835\uDDDC\uD835\uDDE1\uD835\uDDDA \uD835\uDDE3\uD835\uDDE5\uD835\uDDE2\uD835\uDDD5\uD835\uDDDF\uD835\uDDD8\uD835\uDDE0 \uD835\uDDEE\uD835\uDDFB\uD835\uDDF1 \uD835\uDDE5\uD835\uDDD8\uD835\uDDDF\uD835\uDDD4\uD835\uDDE7\uD835\uDDDC\uD835\uDDE1\uD835\uDDDA \uD835\uDE04\uD835\uDDF6\uD835\uDE01\uD835\uDDF5 \uD835\uDDD7\uD835\uDDD9\uD835\uDDD4\n\n> `x\u1D62` is the number whose binary representation is subarray `nums[0..i]` (from most-significant-bit to least-significant-bit). Return an *array of booleans* `answer` where `answer[i]` is `true` if `x\u1D62` is divisible by 5.\n \n Thus, we have to simulate entire array `nums` on DFA, but after scanning every character, if it\'s in state `Z`, then we should append `True` in Answers, else append `False`. \uD83D\uDE09\n \n**Examples:** \n- **[0,1,1]** \nIn State `Z` (Starting State), scan 0, go to `Z`, add `true`\nIn `Z`, scan 1, go to `O`, add `false`\nIn `O`, scan 1, go to `Th`, add `false`\n**Output :** `[true, false, false]`\n\n- **[1,1,1]** \nIn `Z`, scan 1, go to `O`, add `false`\nIn `O`, scan 1, go to `Th`, add `false`\nIn `Th`, scan 1, go to `T`, add `false`\n**Output :** `[false, false, false]`\n\n- **[1,0,1,0,1,1,1]** \nIn `Z`, scan 1, go to `O`, add `false`\nIn `O`, scan 0, go to `T`, add `false`\nIn `T`, scan 1, go to `Z`, add `true` [101, i. e. 5 is divisble by 5]\nIn `Z`, scan 0, go to `Z`, add `true` [1010 (Ten) is divisble by 5]\nIn `Z`, scan 1, go to `O`, add `false` \nIn `O`, scan 1, go to `Th`, add `false` \nIn `Th`, scan 1, go to `T`, add `false` \n**Output :** `[false, false, true, true, false, false, false]`\n\n<br>\n\n\n\n----------\n\n\n\n<br>\n\n# \uD83D\uDCBB \uD835\uDDE4\uD835\uDDE8\uD835\uDDDC\uD835\uDDD6\uD835\uDDDE-\uD835\uDDD6\uD835\uDDE2\uD835\uDDD7\uD835\uDDD8\nHere is the non-optimized code using the same concept. Comments to clarify things.\n\n**Python**\n```python\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]: \n\t\n #To store transition Function. Key is Current State. Index of Value represents input symbol. \n\t\t#ELement at index represents Next State\n D = {\'Z\':[\'Z\',\'O\'], \'O\':[\'T\',\'Th\'], \'T\':[\'F\',\'Z\'], \'Th\':[\'O\',\'T\'], \'F\':[\'Th\',\'F\']}\n \n #Will Store Current State\n q = \'Z\'\n \n answer = []\n \n for i in nums:\n\t\t\n answer.append(D[q][i]==\'Z\')\n #Now D[q] is a List. i will be either 0 or 1, so is index of list. \n\t\t\t#We have to check if next state is Z or not.\n \n q = D[q][i]\n #Go to Next State\n \n return answer\n``` \n\n\u23F3 **Time Complexity :** `O(n)` where `n` is number of elements in `nums`\n*[Assigning `D`,`q`, and `answer` is `O(1)`, and now `for` loop runs `n` times. Every Statement inside `for` loop is of `O(1)` ]*\n\n\u2328 **Space Complexity :** `O(n)` where `n` is number of elements in `nums`\n*[`D` and `q` will consume constant space. `answer` will store `n` elements, which depends on input. Although, since we are returning allocated memory, many text will claim Space Complexity to be `O(1)`]*\n\n<br>\n\n\n\n----------\n\n\n\n<br>\n\n# \uD83D\uDC68\uD83C\uDFFB\u200D\uD83D\uDCBB\uD835\uDDE2\uD835\uDDE3\uD835\uDDE7\uD835\uDDDC\uD835\uDDE0\uD835\uDDDC\uD835\uDDED\uD835\uDDDC\uD835\uDDE1\uD835\uDDDA/\uD835\uDDE9\uD835\uDDD4\uD835\uDDE5\uD835\uDDDC\uD835\uDDD4\uD835\uDDE7\uD835\uDDDC\uD835\uDDE2\uD835\uDDE1\uD835\uDDE6\nWe surely can optimize the code in both, time and space dimensions. Here are some pointers. We can combine multiple pointers to produce different variations. \uD83D\uDE0E\n\n- **Not consuming Extra Space** : This can be done by modifying array in-place.\n```python \n def prefixesDivBy5(self, nums: List[int]) -> List[bool]: \n D = {\'Z\':[\'Z\',\'O\'], \'O\':[\'T\',\'Th\'], \'T\':[\'F\',\'Z\'], \'Th\':[\'O\',\'T\'], \'F\':[\'Th\',\'F\']}\n cur = \'Z\'\n \n for i in range(len(nums)):\n nxt = D[cur][nums[i]]\n nums[i] = nxt==\'Z\'\n cur = nxt\n \n return nums\n```\n\nUsing only one variable `cur`, we can have \n```python\ncur=D[cur][nums[i]]\nnums[i] = cur==\'Z\'\n```\n\n- Instead of using Alphabets for State [which represents Remainder], we can directly use Numeric Value of Remainder. Thinking Further, we can use **Arithmetic** to replace Dictionary with List/Array. [Without Arithmetic, one can use 2D Array instead of Dictionary]\n```python\n #Current State\n q=0\n \n #Instead of using Dictionary, we can use List. Here\'s How.\n \'\'\'\n Our Dictionary looked like\n D = {0 : [0,1], 1: [2,3], 2: [4,0], 3:[1,2], 4;[3,4]}\n\t\t\n\t\t#indexV (index of Value in Key-Value Pair) [which is a List] represents input symbol. \n\t\t#ELement at index represents Next State\n\t\t\n\t\t\n\t\t\n\t\t2D-Array will look like\n\t\tT = [ [0,1] , [2,3] , [4,0] , [1,2] , [3,4] ]\n \n\t\n\t Now, preparing 1-D Array. Writing only Values in List\n L = [0,1, 2,3, 4,0, 1,2, 3,4]\n indexL = 0 1 2 3 4 5 6 7 8 9\n Key = 0 1 2 3 4\n \n Noticed Any Pattern?\n \n I. From Key, we can get indexL (index of List) by Multiplying Key by 2, \n and adding the indexV (which can be 0 or 1, input symbol)\n \n OR\n \n II. From Key, we can directly get element of List (instead of indexL)\n by Multipling Key by 2, adding indexV and taking mod 5\n \n \n Using Approach-I here\n \n \'\'\'\n \n #Transtition Function\n L = [0,1,2,3,4,0,1,2,3,4]\n \n n = len(nums)\n answer = [False]*n\n \n for i in range(n):\n \n #indexL will be multiplying current key/state by 2, and adding nums[i] (input)\n #We want element at indexL, which will be next state.\n q = L [2*q + nums[i] ]\n \n \n #If Next State is Zero, it\'s negation will be True\n if not q:\n answer[i]=True\n \n return answer\n \n```\n- We can modifiy many components of code\n```if not q: answer[i]=True``` can be written as ```answer[i] = q==0 ```\nAnd, ```q = L [2*q + nums[i] ]``` using bitwise operator can be written as ```q = L [q<<1 | nums[i] ]``` \n\n- Using `Approach-II` as mentioned in previous code comment, we can ultimately get rid of constant-sized list by using **Modular Arithmetic** and bit of **Bit-Manipulation**. More in Comments.\n ```python\n class Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n #Current State\n q=0\n \n #Instead of using Dictionary, we can use List. Here\'s How.\n \'\'\'\n Our Dictionary looked like\n D = {0 : [0,1], 1: [2,3], 2: [4,0], 3:[1,2], 4;[3,4]}\n \n #indexV (index of Value in Key-Value Pair) [which is a List] represents input symbol. \n\t\t#ELement at index represents Next State\n \n Writing only Values in List\n L = [0,1, 2,3, 4,0, 1,2, 3,4]\n Key = 0 1 2 3 4\n \n From Key, we can directly get element of List\n by Multipling Key by 2, adding indexV/input Symbol and taking mod 5.\n This is concept of Modular Arithmetic\n \n Now, key multiplied by 2 will be Even. LSB of Even is 0. \n Thus Even|1 increments number. Even|0 makes no change. (| is Bitwise OR)\n Thus, instead of adding input Symbol, we will take OR.\n This is Concept of Bit Manipulation\n \n And since we can get element of List, we don\'t have to allocate\n space to List :)\n \'\'\'\n \n #Transtition Function\n \n n = len(nums)\n answer = [False]*n\n \n for i in range(n):\n \n #next State will be multiplying current key/state by 2, ORing nums[i] (input)\n #Then taking mod 5\n #q will always be from {0,1,2,3,4}\n q = (q<<1 | nums[i])%5\n \n #If Next State is Zero, means Divisible. True.\n answer[i]=q==0\n \n return answer\n \n ```\n \n ---------- \n \n# \uD83D\uDE0E \uD835\uDDD6\uD835\uDDE2\uD835\uDDE1\uD835\uDDD6\uD835\uDDDF\uD835\uDDE8\uD835\uDDE6\uD835\uDDDC\uD835\uDDE2\uD835\uDDE1\n\nHence, starting from the very theoretical basics, we have build DFA, Coded it, and Provided it\'s different variations. There are more than average comment in code to clarify each and every line. Solution in `python` is written in such a way that it can be converted to other languages easily. Here is one of the Final [but not claiming to be most optimized] Code, with `O(n)` Time Complexity and `O(1)` Space Complexity.\n\n**Python**\n\n```python\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n q=0 \n for i in range(len(nums)):\n q = (q<<1 | nums[i])%5\n nums[i]= q==0\n \n return nums\n```\n\nQuickly Converting \u2B50\n\n```c []\nbool* prefixesDivBy5(int* nums, int numsSize, int* returnSize)\n{\n *returnSize=numsSize;\n int q=0;\n\t\n\t//Using `answer`, as `int array` is different from demanded `bool array`\n bool* answer=(bool *)malloc(numsSize*sizeof(bool));\n\t\n for(register int i=0 ; i<numsSize; i++)\n {\n q = ((q<<1) | nums[i]) % 5;\n answer[i] = (q==0);\n }\n \n return answer;\n}\n```\n```python3 []\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n q=0 \n for i in range(len(nums)):\n q = (q<<1 | nums[i])%5\n nums[i]= q==0\n \n return nums\n```\n\n\n\n<br>\n\n- \u2B06\uFE0F If you have gained some insights, feel free to upvote. Button Below \n- \u2B50 Feel free to add to your Favorite Solutions by clicking on Star.\n- \uD83D\uDE15 If you are confused, or have some doubts, post comments.\n- \uD83D\uDCA1 Any mistake or Have another idea? Share in Comments. \n\n\n----\n\n\n# \uD83E\uDD16 \uD835\uDDD8\uD835\uDDF1\uD835\uDDF6\uD835\uDE01\uD835\uDE00/\uD835\uDDE5\uD835\uDDF2\uD835\uDDFD\uD835\uDDF9\uD835\uDE06\uD835\uDDF6\uD835\uDDFB\uD835\uDDF4 \uD835\uDE01\uD835\uDDFC \uD835\uDDE4\uD835\uDE02\uD835\uDDF2\uD835\uDDFF\uD835\uDDF6\uD835\uDDF2\uD835\uDE00\n\n\n**Isn\'t it too much for a `Easy` Problem?**\nWell, I guess it isn\'t too much. The solution tries to relate with `Theory of Computation`, a core subject offered in Computer Science Courses. The solution isn\'t tough. It slowly, and step-by-step tries to build widely submitted solution [as evident from Discussion]. It is written in such a way that even a novice can understand it. Hence, ideally it isn\'t too much.\n\n---------- \n <br>\n \n [1]: https://stackoverflow.com/a/72594907/15845697\n [2]: https://en.wikipedia.org/wiki/Euclidean_division#Division_theorem\n
| 2
| 0
|
['C', 'Python']
| 0
|
binary-prefix-divisible-by-5
|
Simple C++ Solution
|
simple-c-solution-by-nikhilgupta25-spd6
|
\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n vector<bool>ans;\n int dec=0;\n for(int i=0;i<nums.size
|
NikhilGupta25
|
NORMAL
|
2022-04-14T10:30:42.975446+00:00
|
2022-04-14T10:30:42.975486+00:00
| 332
| false
|
```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n vector<bool>ans;\n int dec=0;\n for(int i=0;i<nums.size();i++){\n dec = dec * 2 + nums[i];\n if(dec%5==0){\n ans.push_back(true);\n }\n else{\n ans.push_back(false);\n }\n dec= dec%5;\n }\n return ans;\n }\n};\n```
| 2
| 0
|
['C', 'C++']
| 0
|
binary-prefix-divisible-by-5
|
Easy Python code for beginners
|
easy-python-code-for-beginners-by-vistri-elgf
|
\ndef prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n l=[]\n su=""\n for i in nums:\n su+=str(i)\n if int(su,2
|
vistrit
|
NORMAL
|
2021-11-24T07:23:06.602663+00:00
|
2021-11-24T07:23:06.602699+00:00
| 195
| false
|
```\ndef prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n l=[]\n su=""\n for i in nums:\n su+=str(i)\n if int(su,2)%5==0:\n l.append(True)\n else:\n l.append(False)\n return l\n```
| 2
| 0
|
['Python', 'Python3']
| 0
|
binary-prefix-divisible-by-5
|
Java O(n) solution with explaination
|
java-on-solution-with-explaination-by-ak-1jr0
|
\n\n/* \n * First thing first, note that by adding a zero bit digit to any binary\n * number, we get a new binary number that represent double of the original b
|
aknuclear
|
NORMAL
|
2021-06-12T03:43:20.411419+00:00
|
2021-06-12T03:43:33.765006+00:00
| 132
| false
|
```\n\n/* \n * First thing first, note that by adding a zero bit digit to any binary\n * number, we get a new binary number that represent double of the original binary value.\n * Similarly, adding a 1 bit digit yields original value * 2 + 1.\n * So we can walk the binary array nums from left to right,\n * starting from the first binary value at nums[0], and then\n * obtain the binary value of each next iteration with one additional\n * bit added to the end from (previousBinaryValue*2)+newBinaryValueAddedAtEnd\n * \n * Furthermore, we don\'t even need to store each of those binary value fully.\n * Decimal number are only divisible by 5 iff it have either 0 or \n * 5 as their least signficant digit. and the least signficiantly bit\n * of each number is the only information one needed to get the least signficant bit\n * of the result value evaulated using addition and multiplication, i.e. the above\n * next iteration calculation formula. So we only need to store the lsd value of previous\n * value at each iteration, which is constant memory and also constant arithmetic\n * cost with all party involves always being 1 bit in size. This makes this algorithmn\n * scale signficantly better with large input, placing it at\n * O(n) both in terms of runtime and space.\n *\n * For further explaination on only needing the least signficant digit / last digit for each\n * calculation, think that no matter what digit value in any other significant position of \n * any decimal number, only the lsd of the number affects the lsd of\n * the new number produced in any addition and multiplciation arithmetic: \n * 2+7 = 9, 4372859(2) + 497346(7) = 4870205(9),\n * 4*6 = 2(4), 674995(4) * 764249(6) = 5158649644518(4)\n */\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n if(nums.length == 0)\n throw new Error("empty binary array input");\n \n int lastDigit = 0; // (0 * 2)+nums[0] = nums[0], initialize to 0 so as to not affect first iteration\n List<Boolean> result = new ArrayList<>();\n \n /* walk the array, calculate binary value at each interval, and determine if it\'s divisible by 5 */\n for(int i = 0; i < nums.length; i++){\n lastDigit = (lastDigit*2 + nums[i]) % 10; // trim off unnecessary bits\n if(lastDigit == 0 || lastDigit == 5){\n result.add(true);\n }\n else{\n result.add(false);\n }\n }\n // done\n return result;\n }\n}\n```
| 2
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
Python3 simple solution
|
python3-simple-solution-by-eklavyajoshi-lnvl
|
\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n res = []\n n = 0\n for i in nums:\n n *= 2\n
|
EklavyaJoshi
|
NORMAL
|
2021-05-26T03:36:50.010714+00:00
|
2021-05-26T03:36:50.010749+00:00
| 96
| false
|
```\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n res = []\n n = 0\n for i in nums:\n n *= 2\n if i == 1:\n n += 1\n res.append(n % 5 == 0)\n return res\n```\n**If you like this solution, please upvote for this**
| 2
| 0
|
['Python3']
| 0
|
binary-prefix-divisible-by-5
|
Java solution with given hint
|
java-solution-with-given-hint-by-ayansam-m7d7
|
class Solution {\n\n\n public List prefixesDivBy5(int[] a) {\n List l = new ArrayList<>();\n long num = a[0];\n l.add(num%5 == 0?true:fa
|
ayansam
|
NORMAL
|
2021-04-22T08:11:30.521418+00:00
|
2021-04-22T08:11:30.521471+00:00
| 100
| false
|
class Solution {\n\n\n public List<Boolean> prefixesDivBy5(int[] a) {\n List<Boolean> l = new ArrayList<>();\n long num = a[0];\n l.add(num%5 == 0?true:false);\n for(int i=1;i<a.length;i++){\n num = 2*num +a[i];\n l.add(num%5 == 0?true:false);\n num = num%10;\n }\n return l;\n }\n}
| 2
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
java-solution
|
java-solution-by-meteor18-talj
|
\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n int temp = 0;\n List<Boolean> result = new ArrayList<Boolean>(A.length);\
|
meteor18
|
NORMAL
|
2019-12-27T02:58:47.958033+00:00
|
2019-12-27T02:58:47.958070+00:00
| 190
| false
|
```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] A) {\n int temp = 0;\n List<Boolean> result = new ArrayList<Boolean>(A.length);\n for (int i = 0; i < A.length; i++) {\n temp = (temp * 2 + A[i]) % 5;\n if (temp == 0)\n result.add(i, Boolean.TRUE);\n else result.add(i, Boolean.FALSE);\n }\n return result;\n }\n}\n```
| 2
| 0
|
['Java']
| 1
|
binary-prefix-divisible-by-5
|
[JavaScript] Beats 100% Time and Memory
|
javascript-beats-100-time-and-memory-by-2jw93
|
Bit shift only to least significant digit to avoid overflow. Current number is divisible by 5 if LSD is 0 or 5.\n\njavascript\nvar prefixesDivBy5 = function(A)
|
ethan-marsh
|
NORMAL
|
2019-09-27T04:09:33.993199+00:00
|
2019-09-27T04:09:33.993242+00:00
| 373
| false
|
Bit shift only to least significant digit to avoid overflow. Current number is divisible by 5 if LSD is 0 or 5.\n\n```javascript\nvar prefixesDivBy5 = function(A) {\n let lsd = 0;\n return A.map((bit) => {\n lsd <<= 1;\n lsd += bit;\n lsd %= 10;\n return lsd === 0 || lsd === 5;\n });\n};\n```
| 2
| 1
|
['JavaScript']
| 1
|
binary-prefix-divisible-by-5
|
Go golang solution
|
go-golang-solution-by-leaf_peng-nvhb
|
Runtime: 332 ms, faster than 71.93% of Go online submissions for Binary Prefix Divisible By 5.\nMemory Usage: 8.2 MB, less than 40.00% of Go online submissions
|
leaf_peng
|
NORMAL
|
2019-09-22T02:28:27.270286+00:00
|
2019-09-22T02:28:27.270335+00:00
| 88
| false
|
>Runtime: 332 ms, faster than 71.93% of Go online submissions for Binary Prefix Divisible By 5.\nMemory Usage: 8.2 MB, less than 40.00% of Go online submissions for Binary Prefix Divisible By 5.\n\n```go\nfunc prefixesDivBy5(A []int) []bool {\n\n\tans := []bool{}\n\tn := 0\n\n\tfor _, v := range A {\n\t\tn = (n<<1 + v) % 5\n\t\tif n == 0 {\n\t\t\tans = append(ans, true)\n\t\t} else {\n\t\t\tans = append(ans, false)\n\t\t}\n\t}\n\treturn ans\n}\n```
| 2
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
javascript
|
javascript-by-huihancarl188-a9fv
|
\nvar prefixesDivBy5 = function(A) {\n // i => current binary number;\n let cur = 0;\n let res = [];\n for(let i = 0 ; i < A.length; i++) {\n
|
huihancarl188
|
NORMAL
|
2019-05-26T04:28:19.159410+00:00
|
2019-05-26T04:28:19.159459+00:00
| 164
| false
|
```\nvar prefixesDivBy5 = function(A) {\n // i => current binary number;\n let cur = 0;\n let res = [];\n for(let i = 0 ; i < A.length; i++) {\n cur = cur << 1;\n cur = cur % 5;\n cur += A[i];\n res.push(cur % 5 === 0);\n }\n return res;\n};\n```
| 2
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
Weird Javascript Question, can anyone explain? (Solved)
|
weird-javascript-question-can-anyone-exp-ehug
|
If I write my code like this\n\nvar prefixesDivBy5 = function(A) {\n let res = [];\n let remainder = 0;\n for(let i=0; i<A.length; i++){\n remai
|
0618
|
NORMAL
|
2019-03-31T14:47:53.906920+00:00
|
2019-03-31T14:47:53.906967+00:00
| 302
| false
|
If I write my code like this\n```\nvar prefixesDivBy5 = function(A) {\n let res = [];\n let remainder = 0;\n for(let i=0; i<A.length; i++){\n remainder = remainder*2 + A[i];\n res.push(remainder%5===0);\n\t\tif(remainder%5===0) remainder = 0;\n }\n\n return res;\n};\n```\nI can\'t pass test case like \n```\n[0,0,1,1,0,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,1,0,1,0,0,1,0,0,1,0,0,1,1,1,1,0,1,1,1,0,0,1,0,1,0,1,1,1,0,0,0,1,0,0,0,0,0,0,0,1,0,1,0,0,1,0,1,0,1,0,1,0,1,1,0,0,1,1,1,0,0,1,0,0,1,1,1,1,1,1,1,0,1,0,0,1,1,0,0,1,0,0,0,0,1,0,1,1,1,0,0,1,0,0,0,1,0,0,0,0,1,1,0,1,1,0,1,0,1,1,0,0,1,1,0,1,1,1,0,0,1,1,1,0,0,1,0,1,1,0,0,1,0,0,1,0,0,1,1,0,1,1,1,0,1,0,0,0,0,0,0,0,0,0,0,1,0,0,1,1,0,1,0,0,0,0,0,1,0,1,0,0,1,1,0,1,0,1,1,1,0,1,0,1,0,1,1,1,1,0,1,1,1,1,0,1,0,1,0,1,0,1,0,0,1,1,0,1,1,0,1,0,1,1,0,0,1,0,1,0,1,0,1,1,1,1,0,0,1,0,1,0,1,0,0,0,1,1,1,0,0,0,1,0,0,0,1,0,1,1,1,0,0,0,1,0,0,1,1,1,1,0,0,0,1,0,1,1,0,1,1,1,1,0,0,0,0,1,1,1,1,0,1,0,1,0,1,1,1,0,0,1,1,1,0,0,0,1,1,1,0,1,1,1,0,1,0,0,1,1,0,1,0,0,1,1,1,1,0,0,1,1,0,0,1,0,1,1,1,0,1,1,0,1,0,0,1,0,1,0,1,0,1,1,0,1,0,1,0,0,1,1,0,1,0,1,1,0,1,1,1,0,1,0,1,0,0,1,0,0,0,1,1,0,1,0,0,0,0,1,0,0,1,0,0,1,1,1,1,1,1,0,0,1,1,0,1,0,1,1,0,0,1,0,1,0,0,0,1,0,0,1,0,0,0,1,0,0,0,0,1,1,1,1,0,1,0,1,0,0,0,0,1,0,0,0,0,1,0,1,1,1,1,1,1,1,0,0,1,1,1,0,1,0,1,1,0,1,1,0,0,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1,0,1,1,1,0,1,1,0,1,1,0,1,0,1,0,0,1,1,1,1,1,0,1,1,0,1,1,0,0,0,1,0,1,0,1,0,1,0,0,0,1,1,1,1,0,0,1,1,0,1,0,0,0,1,0,1,1,1,0,0,1,1,1,1,1,0,1,1,1,0,0,1,0,1,0,0,1,0,1,0,1,1,0,0,1,1,1,0,1,1,1,1,1,1,0,1,0,1,1,0,0,0,1,0,1,0,1,1,0,1,1,1,0,0,1,0,1,0,1,1,0,1,0,1,0,0,0,0,0,0,1,1,1,1,0,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,1,1,1,1,0,1,1,0,0,0,0,1,1,0,1,1,0,1,0,1,0,0,0,0,1,0,0,1,1,0,1,0,0,1,0,1,0,0,0,1,1,1,1,0,0,1,0,0,1,0,0,1,1,1,1,1,0,1,1,0,0,0,1,1,1,0,0,0,0,0,1,1,1,0,0,0,1,1,0,1,1,0,0,1,0,0,0,0,0,1,0,1,0,1,1,1,1,1,1,0,1,1,1,0,0,1,0,0,1,1,1,0,0,1,1,0,1,1,0,0,1,0,0,0,1,1,1,0,1,1,1,1,0,0,1,1,1,1,0,1,0,1,1,0,1,1,1,0,0,1,1,1,1,1,0,1,0,0,1,1,0,0,1,0,0,0,1,1,1,1,0,1,0,1,0,1,0,1,0,0,0,1,1,0,1,1,1,0,0,1,0,1,1,0,0,0,0,0,1,0,0,1,0,0,0,1,1,0,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,1,1,1,0,1,1,1,1,1,1,1,1,1,0,0,1,0,1,1,1,1,0,1,1,1,0,0,0,0,0,1,0,0,0,0,1,0,1,0,1,0,1,1,0,0,1,1,0,1,1,1,1,1,1,0,1,1,0,0,1,0,1,1,1,0,1,1,0,1,0,1,1,0,0,0,1,0,0,0,0,0,0,1,1,1,0,1,0,1,1,0,1,1,1,0,1,1,0,1,1,1,0,0,0,0,1,0,0,0,0,0,0,1,0,1,1,1,0,0,0,0,1,1,0,1,1,0,0,1,0,0,0,1,1,1,0,1,1,0,1,1,0,1,1,0,0,1,1,1,1,1,0,0,0,1,1,0,0,0,0,1,0,1,1,1,0,1,1,0,0,1,0,1,0,0,1,0,1,0,0,1,1,0,1,0,1,0,1,1,0,1,0,1,0,0,0,1,0,1,0,0,0,1,1,0,0,1,0,0,1,1,0,1,1,0,1,0,1,1,0,0,1,0,1,1,0,1,0,0,1,1,1,0,0,0,0,0,1,0,1,0,1,0,0,1,0,1,1,0,1,1,0,0,0,1,1,1,1,1,1,1,0,1,1,0,1,0,0,0,1,0,1,0,1,1,0,0,0,0,1,1,1,0,0,0,0,0,1,1,1,1,1,1,1,0,1,0,1,0,1,1,1,0,0,1,1,1,1,0,1,1,1,0,1,1,1,0,1,0,0,1,1,0,1,1,0,1,0,1,0,1,1,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,1,0,1,1,1,0,1,1,0,1,0,1,1,1,0,1,0,1,1,1,0,1,0,0,1,0,1,0,0,1,0,1,0,1,1,1,1,1,0,0,1,0,1,0,1,1,0,1,1,0,1,1,0,1,1,0,0,0,0,0,1,1,1,0,1,1,1,0,0,0,0,1,1,0,1,0,0,0,1,0,1,1,0,0,0,1,1,0,0,1,1,0,0,1,0,0,1,1,1,0,1,0,0,1,1,0,0,0,0,0,1,1,1,1,0,1,0,1,0,0,0,1,0,0,0,0,0,1,0,1,1,1,0,1,1,1,0,1,1,0,1,0,1,0,1,0,1,1,0,1,0,1,1,1,1,0,1,0,1,1,1,1,0,0,1,0,1,1,1,1,1,0,0,1,0,1,0,1,0,0,0,0,0,0,1,0,0,0,1,0,1,1,0,0,0,0,1,1,0,0,0,0,0,1,0,1,0,0,1,0,0,1,0,1,1,1,0,0,1,0,1,0,1,0,1,1,0,1,1,0,0,0,1,1,0,0,1,0,1,1,0,1,1,0,1,0,1,0,0,1,1,1,1,0,0,0,0,0,1,1,1,1,0,0,1,1,0,1,0,1,0,0,1,0,1,1,1,1,0,0,0,1,0,1,0,0,0,1,1,1,1,1,1,0,1,0,0,0,1,0,1,1,1,0,1,1,1,1,1,0,1,0,1,1,1,1,1,0,0,0,0,1,0,1,0,1,1,0,1,1,1,0,0,0,0,1,1,0,0,1,0,1,0,0,1,0,0,1,1,0,0,0,0,1,1,0,1,1,1,0,1,0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0,1,1,0,1,1,0,1,1,1,1,1,0,0,1,0,0,1,1,0,0,0,0,0,1,1,0,1,1,1,0,1,1,0,0,1,0,1,1,0,0,1,0,1,1,1,1,0,0,1,1,0,1,0,1,1,0,0,0,1,1,1,0,0,1,1,1,1,1,0,0,1,1,0,0,1,1,1,1,1,0,1,0,0,1,1,1,1,1,1,0,1,1,1,0,1,0,1,0,1,0,1,1,0,0,1,0,0,1,0,1,1,0,0,0,0,0,0,0,1,1,0,0,1,0,1,0,0,1,0,0,0,1,1,0,0,1,0,0,1,1,0,1,0,0,1,0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,1,1,0,1,0,0,0,0,1,0,0,1,0,0,1,0,1,1,0,0,0,1,1,0,0,0,0,0,0,0,0,1,1,0,0,1,1,0,0,1,1,0,1,0,0,0,1,0,1,1,1,1,1,0,1,1,1,1,1,1,1,0,0,1,0,1,1,1,0,0,0,1,1,0,1,1,0,1,0,0,1,0,0,1,0,0,1,0,1,1,0,1,0,1,0,1,0,0,1,1,1,0,0,0,1,0,0,1,0,0,1,1,0,1,1,1,1,0,1,1,0,0,0,0,0,0,1,1,0,1,0,0,0,0,0,0,1,1,1,1,0,0,1,1,0,1,0,1,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,1,0,0,0,0,1,1,0,0,1,0,1,1,0,0,1,0,0,0,1,0,1,0,0,1,0,1,1,1,1,0,0,0,0,1,1,1,1,0,1,1,0,0,0,0,0,0,0,0,0,0,1,1,0,1,1,1,0,0,1,0,1,1,1,0,1,1,1,0,0,0,0,1,0,1,0,0,0,0,1,0,0,1,1,0,1,0,0,0,0,0,1,0,0,1,1,1,1,0,1,1,0,0,1,1,0,0,1,1,1,1,1,0,0,1,0,1,0,1,1,0,0,1,0,0,1,1,0,1,0,1,0,1,1,1,1,0,1,0,0,0,1,1,0,1,1,0,1,0,1,0,0,1,0,0,0,1,0,0,1,1,1,1,0,1,0,1,1,0,0,1,0,1,0,0,0,1,1,1,0,0,1,1,0,0,1,0,1,0,1,0,1,0,1,0,1,1,0,0,1,1,1,0,1,0,1,1,1,1,1,0,1,1,1,1,1,0,1,1,0,1,0,1,0,0,0,0,1,1,1,1,0,1,1,1,1,0,1,1,0,0,0,1,1,0,1,0,0,1,1,1,0,0,1,1,0,0,0,0,1,0,1,0,0,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,1,0,1,1,0,0,1,0,1,0,1,0,1,1,0,1,0,1,1,1,0,1,0,1,1,1,1,1,0,1,0,1,1,0,0,1,1,0,0,0,0,1,1,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,1,1,1,1,0,1,0,1,0,1,1,0,0,1,0,0,1,1,1,0,0,1,1,1,0,1,1,1,0,1,0,0,0,1,1,0,0,0,1,0,0,0,0,0,0,0,1,1,1,1,0,1,1,0,1,1,0,1,1,0,1,0,1,1,1,0,1,1,0,0,0,0,1,1,1,0,0,1,1,1,1,1,0,1,1,1,0,1,0,1,0,0,1,1,0,0,1,0,1,1,0,1,0,0,1,0,1,0,1,1,0,0,1,1,0,1,0,0,1,0,1,1,1,0,1,0,0,1,0,1,1,0,0,1,1,0,1,1,0,1,1,0,1,0,1,0,0,0,1,0,0,0,1,1,1,1,0,1,1,1,1,0,0,1,1,1,1,0,1,0,1,0,1,1,0,0,0,1,0,0,0,1,1,0,0,0,0,1,0,1,1,1,0,0,1,1,0,0,1,1,1,1,0,1,1,0,1,1,1,0,1,1,1,1,0,1,1,1,0,0,1,0,1,1,1,1,1,0,1,0,0,0,1,1,1,0,1,1,1,1,0,1,1,0,0,1,1,1,1,0,0,0,0,1,1,1,0,0,0,0,0,1,0,1,1,0,0,0,0,1,1,1,1,1,1,0,1,0,0,0,0,1,1,0,0,1,0,0,1,1,0,1,0,0,1,0,1,1,1,1,1,1,0,1,1,0,0,1,0,0,0,1,1,1,1,1,1,0,1,1,0,0,1,0,0,0,0,1,0,0,0,0,1,1,1,1,1,1,0,1,0,0,1,0,0,1,0,1,1,0,1,0,0,0,0,0,0,1,0,0,1,1,0,0,0,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,0,0,1,1,0,0,1,1,1,0,0,0,0,0,1,0,1,1,1,1,1,0,0,1,0,1,1,0,0,1,1,1,1,1,0,1,1,1,1,1,0,0,0,0,0,0,0,1,1,0,0,1,1,0,0,1,1,0,0,0,0,0,1,0,1,0,1,1,0,0,0,0,1,0,1,1,1,0,0,0,1,1,0,0,1,0,0,1,0,0,1,1,0,0,1,0,0,0,0,0,0,1,0,0,0,0,1,0,1,0,0,0,1,0,0,1,1,0,1,1,1,0,0,1,0,1,0,0,1,1,1,0,1,0,1,0,1,1,1,0,0,1,1,1,1,1,1,1,1,0,1,0,0,0,0,1,1,0,1,1,1,0,0,1,0,1,0,0,1,0,1,1,1,1,1,0,1,1,1,0,0,1,0,0,1,1,0,1,0,1,0,1,0,0,1,0,1,0,0,0,1,0,0,0,1,1,0,0,1,1,0,0,1,1,1,0,1,1,1,1,1,1,1,0,0,1,1,0,0,0,1,0,1,0,1,1,0,1,0,1,0,1,1,1,0,1,1,1,0,0,0,1,1,1,1,1,0,1,0,1,1,1,1,0,1,1,1,0,1,1,0,1,0,1,1,0,1,0,0,1,1,1,0,1,0,0,1,1,0,0,1,1,0,1,1,0,0,0,1,0,1,0,1,1,1,0,0,0,1,0,0,0,0,1,0,1,0,1,0,0,0,1,1,1,1,1,0,1,1,1,0,0,0,1,1,1,0,1,0,1,1,1,1,1,1,0,0,0,0,1,1,1,0,1,0,1,1,0,0,1,0,0,1,0,0,1,1,0,0,0,0,0,1,1,0,1,0,1,1,0,1,1,1,0,0,0,0,1,0,0,0,1,1,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,1,0,1,0,1,1,1,1,0,1,1,1,0,1,0,1,1,1,1,1,0,0,1,1,1,1,1,0,0,0,0,0,0,1,0,1,0,1,1,1,1,1,0,1,0,0,0,1,1,0,1,0,0,1,1,1,1,1,0,0,0,0,0,0,0,1,1,1,1,0,1,1,1,0,0,1,1,0,1,1,1,0,0,1,0,0,1,0,0,1,1,0,0,0,0,1,1,1,1,0,1,1,0,1,1,0,1,0,1,1,0,1,1,1,1,0,0,0,1,1,0,1,1,1,1,1,1,1,0,0,0,0,0,0,1,1,0,1,0,1,1,1,1,1,0,1,1,0,0,1,0,0,0,0,0,1,1,1,1,0,1,0,1,0,0,1,0,1,0,0,0,0,1,1,0,0,1,1,0,0,1,0,0,1,0,1,1,0,0,0,1,1,0,1,0,1,0,1,1,1,1,0,1,1,1,0,0,0,0,0,0,0,1,1,0,1,0,0,0,0,1,1,0,1,1,1,1,1,1,1,1,1,0,1,1,1,1,0,0,1,1,0,0,0,1,0,0,0,0,1,1,0,1,0,0,0,0,1,0,1,1,1,1,0,0,0,0,0,1,0,1,0,1,1,1,1,0,1,0,1,0,1,1,1,0,1,1,0,1,0,1,0,1,1,1,0,1,0,1,1,1,0,0,0,1,0,1,0,0,0,0,1,0,1,1,1,0,0,1,0,1,0,0,0,1,0,1,1,1,1,1,1,0,0,0,1,1,1,0,1,1,1,0,0,1,1,1,1,0,1,1,1,0,1,0,1,1,0,0,0,1,1,0,0,0,1,0,0,1,0,1,0,1,1,0,0,1,1,1,1,1,0,0,1,0,0,1,0,0,0,1,0,1,0,1,0,1,0,0,0,0,1,0,1,1,0,1,0,0,0,0,1,1,0,1,0,0,0,1,1,1,1,0,1,1,1,1,0,0,1,1,1,1,0,0,0,0,1,1,0,1,1,1,0,0,1,0,1,1,1,1,0,0,1,1,1,1,1,0,1,0,0,1,1,0,1,0,1,1,0,0,0,1,0,0,1,1,0,1,1,1,0,0,1,1,0,1,1,1,0,0,1,1,0,0,0,1,1,1,0,0,1,1,0,0,1,1,1,0,0,1,0,1,1,0,0,1,1,1,0,1,1,0,0,0,0,1,1,1,0,0,0,1,1,1,0,0,1,1,0,0,1,0,0,0,0,0,1,1,1,1,0,0,1,0,1,0,1,1,1,1,1,0,0,1,1,0,0,0,1,1,0,0,1,1,0,0,1,0,1,1,0,1,0,0,0,0,1,0,0,0,0,1,1,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,1,1,0,0,1,1,0,1,1,1,1,1,0,0,1,0,1,1,1,1,1,0,0,0,0,1,1,0,0,0,0,0,1,0,0,0,1,0,1,0,1,1,0,0,0,0,1,0,0,1,1,0,0,1,1,0,1,1,0,0,0,1,0,1,0,1,0,1,0,0,1,0,0,1,1,1,1,0,1,1,1,0,0,0,0,0,1,1,0,0,0,1,0,1,1,1,0,0,1,1,1,0,1,1,0,1,0,0,0,0,1,0,1,0,0,1,0,1,0,1,0,1,1,1,0,0,1,1,1,1,1,1,1,1,0,0,1,0,1,1,1,0,1,0,0,0,0,1,1,0,1,0,0,1,0,1,0,1,0,1,0,1,0,0,0,0,0,0,0,1,1,1,0,1,0,0,0,1,1,0,0,1,1,1,1,0,0,1,0,0,1,1,0,1,1,0,0,0,0,1,1,1,1,1,0,0,0,0,0,1,1,1,0,0,0,1,0,0,1,1,0,1,1,0,1,1,0,1,0,1,0,0,0,0,1,1,0,1,0,0,1,0,1,1,1,0,0,0,1,1,1,1,1,1,0,1,0,1,1,0,1,0,0,1,1,0,1,1,1,0,1,1,1,0,1,0,0,1,0,0,1,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,0,1,0,0,1,0,1,1,0,0,1,1,0,1,0,0,0,0,1,1,1,0,0,1,1,1,1,1,0,1,0,1,1,0,1,1,0,1,0,1,1,1,0,0,1,1,1,1,0,0,1,0,0,0,1,0,1,0,0,1,1,1,0,0,1,0,0,0,0,0,1,0,1,1,1,1,1,0,0,1,0,0,0,0,0,1,1,1,0,1,0,1,1,1,1,1,0,1,1,1,0,0,0,0,0,1,1,1,0,0,1,0,1,0,1,0,1,1,0,0,1,1,0,1,0,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1,1,1,0,1,1,1,1,1,0,1,1,0,1,1,0,0,0,1,1,0,1,1,1,1,1,1,0,1,0,0,0,0,1,0,1,1,0,1,0,1,0,0,1,1,0,1,0,1,0,1,1,1,0,0,1,0,1,1,1,1,1,1,1,1,1,0,0,0,1,1,0,0,1,0,0,1,1,1,1,1,1,1,1,0,0,0,1,1,1,0,0,0,1,1,0,1,1,1,1,0,1,0,1,0,1,0,1,1,0,0,1,1,1,1,0,1,0,0,0,1,1,0,0,1,0,1,0,1,1,1,0,0,0,0,0,0,1,0,0,0,1,1,1,0,0,0,1,0,1,0,1,1,0,1,1,0,1,0,1,1,0,1,0,1,1,1,0,1,0,0,1,0,0,0,0,1,1,0,1,1,1,0,0,1,1,0,0,1,0,0,1,0,0,0,0,1,0,0,1,1,0,0,1,1,1,1,0,0,1,0,0,0,0,1,1,1,1,0,0,1,0,0,1,0,0,0,0,0,1,1,0,1,1,0,1,0,0,1,1,1,0,1,0,0,0,0,1,0,0,1,1,0,0,1,0,1,0,1,0,1,1,1,0,0,0,0,1,0,0,1,0,1,1,1,1,1,0,0,1,1,0,1,1,1,0,1,0,0,0,0,1,1,1,1,1,0,0,1,1,1,1,1,0,0,0,0,0,1,1,0,1,0,1,1,0,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,1,0,1,1,1,1,0,0,1,0,1,1,1,0,1,1,0,1,0,0,1,0,1,1,0,1,1,1,1,1,0,1,1,1,0,1,1,1,0,1,0,1,0,0,1,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,1,1,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1,1,0,1,1,1,0,1,0,1,0,1,1,1,0,0,1,0,1,0,1,1,0,0,1,0,0,1,0,1,1,1,1,1,0,1,0,0,0,0,1,1,0,1,1,0,1,1,0,1,0,1,1,1,0,0,1,0,1,1,0,0,0,0,1,1,0,1,1,1,0,1,1,1,1,0,0,1,1,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,1,0,0,1,1,1,0,0,0,1,0,1,1,1,0,0,0,0,0,1,1,0,1,0,0,0,0,1,1,0,0,1,0,1,0,0,1,1,1,0,1,0,1,1,0,0,1,1,0,1,1,0,0,0,0,0,0,0,1,0,1,1,0,1,1,0,0,0,0,0,0,1,0,1,1,0,1,1,0,1,0,1,1,1,0,1,1,1,1,0,1,1,0,1,1,1,0,0,1,0,1,1,1,1,0,0,0,0,0,1,1,0,1,1,1,1,1,1,1,1,1,0,1,1,0,1,0,0,1,1,1,0,0,0,0,1,0,1,0,0,0,1,0,0,1,1,1,1,1,0,1,0,1,0,0,0,0,0,1,0,0,1,0,0,1,1,0,0,1,1,0,1,0,1,1,0,1,1,1,1,1,0,1,0,0,0,0,0,1,0,0,1,0,1,1,0,0,1,1,0,0,1,1,1,1,1,0,1,1,1,0,1,0,0,1,0,0,1,0,0,1,0,0,0,0,0,0,0,1,0,1,1,1,0,1,0,0,0,1,1,1,1,1,0,0,1,0,1,1,0,1,1,1,1,0,0,0,0,1,0,0,1,1,0,1,0,0,1,0,1,1,1,1,1,0,1,1,1,0,0,0,1,1,1,1,1,1,1,0,0,0,1,0,1,0,0,0,1,1,1,0,0,0,0,1,0,1,0,0,1,0,1,1,0,0,1,1,0,0,1,1,0,1,1,1,0,0,1,0,1,1,0,0,1,1,0,1,0,0,1,0,1,1,0,0,0,0,1,0,1,0,1,0,0,0,1,0,0,0,1,0,1,0,0,0,0,1,1,0,0,1,1,1,1,1,0,1,0,0,1,1,0,0,0,1,1,0,1,1,0,1,1,1,0,0,0,1,1,0,1,0,1,0,1,1,0,0,1,0,0,1,1,1,1,0,0,0,0,0,1,0,1,0,0,1,0,0,0,1,0,0,1,0,1,0,1,1,1,1,0,1,0,1,1,0,0,1,1,0,0,0,1,1,1,0,0,0,0,1,0,1,1,1,0,0,0,1,1,0,1,1,1,1,1,1,1,0,1,1,0,0,1,0,1,0,0,0,0,1,1,1,0,0,1,0,0,0,1,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,1,1,1,1,0,0,1,1,0,0,0,1,0,0,1,0,1,1,1,0,0,1,1,1,0,0,0,0,1,1,0,0,1,0,1,1,1,0,0,0,1,0,1,1,0,0,0,0,0,0,0,1,0,0,1,0,1,1,0,1,1,1,1,1,1,0,0,0,1,1,1,0,1,1,0,0,0,0,0,0,0,1,0,0,1,1,0,0,1,0,1,0,0,1,0,1,0,0,1,0,1,0,0,0,0,0,0,0,0,0,1,1,0,1,1,0,1,1,0,0,1,0,0,1,0,1,1,0,0,0,0,0,1,1,1,1,0,1,1,1,1,0,1,0,0,1,1,1,0,0,0,0,0,1,1,0,0,0,0,0,1,0,1,0,1,0,1,1,0,0,1,0,1,0,0,0,0,1,1,0,1,1,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,1,1,1,0,1,0,1,1,1,0,1,1,0,1,1,1,0,1,0,1,0,0,1,1,1,1,1,0,1,0,1,0,1,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,1,0,0,1,0,1,0,1,0,0,0,0,1,1,1,0,0,0,0,1,1,0,0,0,1,1,1,0,0,0,0,1,1,0,1,1,1,0,0,1,1,1,0,0,0,0,0,1,1,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,1,1,1,0,0,1,1,1,1,1,0,1,1,1,1,1,1,0,1,0,0,1,0,0,0,0,1,0,0,1,1,1,1,0,0,1,0,1,1,0,1,1,0,1,0,0,1,0,1,1,1,0,0,1,0,0,0,0,1,0,1,1,0,1,1,0,1,0,0,1,0,0,1,0,1,0,1,0,0,1,1,1,0,0,0,1,0,1,0,0,0,0,1,0,1,1,1,1,0,0,1,0,0,0,1,1,0,0,1,1,0,1,1,1,0,0,0,0,0,1,0,1,0,1,1,0,0,1,1,1,0,1,1,1,0,1,1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,1,0,1,1,1,1,1,1,1,1,0,1,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,1,1,1,1,0,0,1,0,0,1,1,0,0,0,1,1,0,1,1,0,0,0,1,1,1,1,1,1,1,0,1,1,1,0,1,0,1,0,1,1,0,1,0,0,1,0,0,1,0,0,1,1,0,1,1,0,1,0,0,0,0,1,0,0,1,1,1,1,0,1,0,1,0,1,1,1,0,0,0,0,1,1,0,1,0,1,0,1,0,1,0,1,1,1,0,0,1,0,0,0,0,1,1,0,0,0,0,1,0,1,0,1,1,0,0,1,0,0,1,1,0,0,1,0,0,0,1,1,1,0,0,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,0,0,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,0,0,0,0,0,1,0,1,0,1,0,0,0,0,1,1,0,1,0,1,0,0,0,1,0,1,1,1,1,1,0,0,1,0,0,1,1,1,1,0,0,1,1,0,0,0,0,1,1,1,1,1,0,0,1,0,1,0,0,0,0,1,0,1,1,1,0,0,0,1,1,1,1,0,0,0,1,1,0,0,0,1,1,0,1,1,0,1,1,1,1,0,0,0,1,0,0,1,1,1,1,1,1,1,0,0,1,0,0,0,0,1,0,1,0,1,1,1,0,0,0,1,0,1,0,0,1,1,1,1,1,1,0,1,1,0,0,1,0,1,0,0,1,1,1,1,1,1,0,1,1,1,1,0,1,0,0,1,1,0,1,0,0,1,0,1,1,0,1,0,1,1,1,1,1,0,0,1,1,0,1,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,1,1,0,0,1,0,0,1,0,1,1,1,1,1,0,0,0,0,0,0,1,0,1,1,1,0,0,1,0,1,0,1,1,1,1,1,1,1,0,1,0,1,1,0,0,0,0,0,0,0,1,0,1,0,0,1,0,1,1,0,0,0,1,1,1,0,1,1,0,0,1,1,1,1,1,1,0,0,0,1,0,0,1,0,1,0,0,1,1,0,0,1,0,0,1,1,0,0,1,0,0,1,0,1,1,1,1,1,0,0,1,1,1,0,0,1,0,0,1,0,0,1,0,1,0,1,1,1,0,0,0,1,1,0,0,1,1,1,1,1,0,0,1,0,0,1,1,1,0,0,1,0,0,0,1,0,0,1,0,0,0,1,1,1,0,0,1,1,1,1,1,1,0,0,0,0,0,0,1,1,1,0,1,1,0,0,1,0,0,1,1,0,0,1,0,0,1,0,1,0,1,1,0,1,0,0,1,0,0,1,0,0,1,1,0,0,0,0,1,1,0,0,1,1,0,0,0,0,1,0,1,0,1,0,0,0,0,0,1,1,0,0,1,0,1,0,0,0,0,1,0,0,1,0,1,0,1,0,1,0,1,0,0,0,1,1,1,1,0,0,0,0,0,0,1,1,0,1,1,1,1,1,0,0,1,1,1,0,0,0,1,1,1,0,0,1,1,0,0,1,1,1,0,1,1,0,0,1,0,0,0,1,0,0,1,0,1,0,0,1,0,1,1,1,1,0,1,1,0,1,0,1,1,1,0,0,1,0,0,1,0,0,0,1,1,0,0,0,0,0,0,0,1,1,0,0,0,0,1,0,0,1,1,0,0,0,1,0,1,0,0,0,1,1,1,0,0,0,1,0,0,1,0,1,1,1,0,1,1,1,1,0,0,0,0,1,1,1,1,1,0,1,0,0,1,0,0,0,0,1,1,1,1,1,0,0,0,0,1,0,1,1,0,0,0,1,0,0,1,1,0,0,0,0,0,0,0,0,1,1,0,1,1,1,0,1,0,0,1,0,0,0,1,0,1,1,0,1,0,0,0,0,1,0,1,1,0,0,0,1,0,0,0,1,0,1,1,0,0,0,1,1,0,0,0,1,0,1,0,0,1,1,0,1,1,1,0,0,0,0,0,1,0,0,0,1,1,0,0,0,0,1,0,0,1,0,1,1,1,1,0,0,0,1,0,1,0,1,0,1,0,0,1,0,0,1,1,1,1,0,1,1,0,1,1,1,1,0,0,0,1,0,0,0,1,1,1,0,0,1,1,0,1,0,1,1,1,1,0,0,1,1,0,0,1,0,0,0,1,0,1,0,0,0,1,1,1,0,1,0,0,0,1,1,1,0,1,1,1,1,1,1,1,1,1,0,1,0,1,1,0,0,1,0,1,1,1,1,0,0,0,1,1,0,1,0,1,1,1,1,0,0,0,1,1,1,1,1,1,0,1,0,0,0,1,1,1,1,1,0,1,1,1,0,1,1,1,0,0,1,1,1,0,0,0,0,0,0,0,1,1,1,1,1,1,0,1,1,0,1,0,1,0,0,1,0,0,0,0,0,0,0,1,1,0,1,0,0,1,1,1,1,1,1,0,1,0,1,1,1,0,0,0,1,1,0,0,1,1,1,1,0,1,1,1,0,1,0,1,1,0,0,1,0,1,0,1,0,0,0,0,1,0,0,1,0,1,1,1,0,1,0,1,1,1,1,1,0,1,0,0,0,1,1,0,0,1,1,1,1,1,1,1,1,1,0,1,0,1,1,0,0,0,1,1,1,1,0,0,0,0,1,0,0,1,1,0,1,1,1,1,0,0,0,0,0,1,1,1,0,0,1,1,1,0,0,0,0,0,1,0,1,1,1,0,1,0,0,0,0,0,0,1,1,1,0,1,1,0,1,0,0,0,0,1,1,0,1,1,1,1,1,0,1,1,1,0,0,1,1,0,0,0,1,0,0,0,0,1,0,0,0,0,0,1,0,1,0,1,1,0,1,0,1,0,0,0,0,0,1,1,0,0,1,0,0,0,1,0,0,1,1,0,0,0,0,1,0,1,1,1,1,1,0,1,0,0,1,1,0,1,0,0,0,0,1,0,1,1,0,0,0,1,0,1,0,1,0,1,0,1,1,0,1,1,0,1,1,1,0,0,1,0,0,0,0,0,1,0,0,0,0,0,1,1,1,0,1,1,0,0,0,1,0,1,1,0,0,0,0,0,1,1,0,1,0,0,1,0,0,0,1,0,1,0,1,0,0,1,1,0,1,0,1,1,1,1,0,1,1,1,0,0,0,1,0,1,1,1,0,1,0,0,0,1,0,1,1,1,0,0,1,0,0,0,0,1,0,0,0,1,1,0,1,1,1,1,1,0,1,1,0,1,1,0,0,0,0,0,0,0,1,0,0,0,1,0,1,0,1,0,0,0,0,1,0,1,0,0,1,0,0,0,1,1,0,1,1,1,1,1,0,1,1,1,0,1,0,0,0,0,0,0,1,0,1,0,1,0,0,1,1,0,0,1,0,0,0,1,1,0,1,0,1,1,1,0,1,1,0,0,0,1,1,1,1,0,1,1,0,1,1,1,0,1,0,1,0,0,1,1,1,1,0,0,0,0,0,0,1,1,1,0,0,0,0,1,0,1,0,0,1,1,0,1,0,1,1,0,1,1,1,1,0,0,1,0,0,1,0,1,1,0,0,0,1,0,0,0,1,1,0,0,0,0,0,1,1,0,1,0,1,0,1,1,0,1,1,1,1,1,1,1,0,0,0,1,0,1,1,1,0,0,0,1,1,1,1,0,0,1,1,0,1,1,0,1,0,1,0,0,1,0,0,1,0,1,1,1,0,1,0,1,1,1,1,0,1,1,1,0,0,1,1,0,1,1,0,1,0,0,1,0,1,0,0,1,0,0,1,0,0,1,1,0,0,0,1,0,0,0,1,1,1,0,1,1,1,1,1,1,0,0,1,0,0,0,1,0,1,1,1,1,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,0,1,0,1,1,0,0,1,1,0,1,0,0,0,1,1,0,1,0,0,1,0,1,0,1,1,1,0,0,1,0,1,1,1,1,1,0,1,0,0,1,0,0,1,0,1,1,0,1,0,1,1,0,1,1,0,1,1,1,0,0,1,0,1,0,0,0,1,0,0,1,1,0,0,1,1,0,0,0,1,1,0,1,0,0,1,1,1,0,0,1,0,0,1,0,0,0,1,0,0,0,1,0,0,1,0,1,0,0,0,0,1,1,1,1,1,1,0,0,0,0,1,1,0,1,1,0,1,1,1,0,1,1,1,0,1,1,1,0,1,0,0,0,1,1,0,0,0,0,1,1,1,0,1,1,0,0,1,0,1,1,0,1,0,1,0,1,0,0,0,1,1,1,0,1,1,1,1,1,0,0,1,0,0,1,0,0,0,1,1,0,0,1,0,0,1,1,1,1,1,0,1,0,0,1,0,1,1,1,0,0,0,1,0,0,0,1,0,1,0,1,1,0,0,0,0,0,1,0,0,1,0,0,0,1,0,1,1,1,0,1,1,1,1,1,0,1,0,0,0,0,1,0,1,1,0,0,1,0,0,0,1,1,0,1,0,0,0,0,1,1,0,1,0,1,0,1,0,1,0,1,1,1,1,0,0,1,1,1,1,0,1,1,0,1,1,1,0,1,1,0,1,1,0,0,1,0,0,0,1,1,0,0,1,0,1,0,0,1,1,0,0,1,1,1,1,1,1,0,1,0,1,1,0,0,0,0,1,1,0,0,1,0,1,1,0,1,1,1,1,0,0,1,1,1,0,1,0,1,1,1,0,0,0,0,0,1,1,0,0,1,0,1,0,0,1,0,0,0,1,1,0,0,1,1,1,0,0,0,0,1,0,1,0,1,1,0,1,0,0,0,0,0,1,0,1,0,1,1,0,1,1,1,0,1,1,1,0,1,0,1,1,0,0,0,0,1,1,1,0,1,0,0,0,0,1,0,1,1,0,0,1,1,1,1,1,1,0,0,0,1,0,0,0,1,0,1,0,1,0,1,0,1,0,1,1,0,0,1,0,0,0,0,0,1,1,1,0,1,0,1,0,0,0,1,1,0,1,0,1,0,0,0,1,1,1,0,1,0,1,1,0,0,1,1,1,1,0,0,1,0,0,1,1,0,0,1,0,1,0,1,1,0,0,1,1,1,1,0,1,0,1,1,0,0,0,0,0,1,0,1,0,0,1,1,1,0,0,0,1,1,0,1,0,0,1,1,1,1,1,1,0,0,0,0,1,0,0,0,0,0,0,1,0,0,1,1,0,1,0,1,0,0,0,1,1,1,1,1,1,0,0,1,0,0,1,0,1,1,1,1,1,1,0,0,0,1,1,1,1,1,1,0,1,1,0,1,1,1,0,1,0,1,0,0,1,0,0,1,0,1,1,1,0,0,0,0,1,1,1,0,0,1,0,1,1,1,1,1,0,0,1,1,1,0,1,1,1,1,1,0,1,0,1,1,0,1,0,1,1,0,1,1,0,1,1,0,0,0,1,0,0,0,1,0,1,1,0,1,1,1,1,0,1,1,0,1,1,1,0,0,0,1,0,0,0,1,0,1,1,0,1,1,0,0,0,0,1,1,1,0,0,1,1,1,0,1,0,1,1,1,0,0,0,0,1,1,0,0,0,0,1,0,1,1,1,1,0,0,0,1,0,1,0,0,1,1,0,0,1,1,0,1,1,1,0,1,0,1,0,1,1,0,0,1,1,1,1,1,0,1,1,0,1,0,0,0,1,1,0,1,0,1,1,1,1,1,1,0,1,1,0,1,0,1,0,1,0,0,1,1,1,1,0,1,0,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,1,0,1,0,0,1,0,1,1,1,0,1,0,1,1,1,0,0,0,1,0,1,1,1,0,1,1,1,0,0,0,1,1,0,0,1,1,0,1,1,0,1,0,0,1,1,1,1,1,0,1,1,1,0,0,1,0,1,0,1,0,1,0,1,0,0,1,1,0,0,1,0,0,0,1,1,1,0,1,0,0,0,1,0,0,1,1,1,0,1,1,1,0,1,1,1,0,1,0,1,1,1,0,0,1,1,1,1,0,1,0,1,0,0,1,0,0,1,0,1,1,0,1,1,0,0,0,1,0,0,0,1,0,0,0,1,1,0,1,0,0,1,0,1,1,1,0,1,1,0,0,1,1,0,1,1,0,1,1,1,1,1,1,1,1,0,0,0,1,1,0,0,0,0,1,0,0,1,1,0,1,1,1,1,0,0,1,0,0,0,0,1,1,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,0,1,0,1,1,0,1,1,0,0,1,1,1,0,0,1,1,0,1,0,1,0,1,0,1,0,0,0,1,0,1,1,1,0,1,1,1,0,1,0,0,0,0,0,0,1,0,0,1,1,0,0,0,1,0,1,1,0,1,1,0,0,1,1,1,0,1,0,0,1,0,1,0,1,1,1,1,1,0,0,0,0,1,0,1,0,0,0,0,0,1,1,0,0,1,1,1,1,1,0,1,0,0,0,0,1,0,1,0,0,0,1,0,1,1,0,0,0,1,0,1,0,0,1,1,1,1,0,0,0,1,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,1,1,1,1,1,0,1,1,1,0,0,1,1,0,0,0,1,1,1,0,1,1,0,1,1,1,1,0,0,0,1,1,1,0,0,1,1,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,1,0,1,1,1,1,1,1,1,1,0,1,1,1,1,0,1,0,1,0,1,1,0,0,1,0,1,1,0,1,1,1,1,1,0,1,0,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,1,1,0,1,0,0,1,0,0,1,1,1,0,0,0,0,0,1,1,1,0,0,0,0,1,1,1,0,1,0,1,1,0,0,0,0,1,0,1,0,0,0,1,0,0,1,0,1,0,0,1,0,0,1,0,0,0,1,1,1,0,1,1,1,0,0,0,0,1,1,0,1,1,1,1,1,0,0,1,1,0,0,0,1,0,0,0,0,0,1,0,0,0,1,1,1,1,0,0,1,1,1,0,1,0,0,1,1,0,0,0,0,0,0,0,0,0,0,1,0,1,1,1,0,0,1,1,1,0,1,1,0,1,0,0,0,0,1,1,1,0,1,0,0,1,1,0,1,0,1,1,1,1,1,1,1,0,0,1,1,0,0,1,0,1,1,1,1,1,1,1,1,0,0,1,0,1,1,0,0,0,1,1,0,1,1,0,1,0,0,1,1,1,1,0,1,0,1,1,1,1,0,1,1,0,0,1,0,1,0,0,1,0,1,1,1,0,0,0,1,1,1,0,1,1,0,1,0,1,0,0,0,0,1,0,1,0,1,1,1,0,0,0,1,1,0,1,0,0,0,0,1,1,0,0,1,0,0,1,1,0,1,1,1,1,1,0,1,1,1,0,0,0,0,0,0,1,0,1,1,0,0,1,0,1,0,0,0,1,1,0,0,1,1,1,1,1,0,1,1,1,1,0,1,1,1,0,1,1,1,1,0,0,0,1,1,0,1,1,0,1,0,0,0,1,1,0,0,1,0,0,0,0,1,1,0,0,1,1,0,1,0,1,1,0,0,0,1,0,1,1,1,0,0,0,0,1,0,0,0,1,0,0,0,1,1,0,1,0,0,1,1,1,0,0,0,1,0,1,1,1,1,0,0,1,1,1,0,1,1,0,0,1,1,1,1,1,1,0,0,1,1,1,0,1,1,0,0,0,0,1,0,0,0,0,0,0,1,1,0,1,0,1,0,0,1,0,0,0,1,1,1,1,1,0,1,1,1,1,0,1,0,0,1,0,0,0,1,1,1,1,1,0,0,1,0,0,0,0,0,1,1,0,0,1,0,0,0,1,1,0,0,0,1,0,0,1,0,1,0,0,1,1,0,1,1,0,0,0,1,1,1,0,0,1,0,0,1,1,0,0,1,0,1,1,1,0,1,1,0,0,0,1,1,1,1,0,1,1,0,1,1,1,0,1,0,0,0,0,0,0,1,0,1,1,1,0,1,1,1,1,0,1,1,0,1,0,0,1,1,0,0,1,0,0,1,1,0,0,0,1,1,0,0,0,1,0,0,1,1,1,0,1,1,0,1,0,1,1,0,0,0,1,1,0,0,1,0,1,1,0,0,0,1,1,1,1,1,0,1,1,1,0,1,0,0,0,0,1,1,1,0,1,0,0,1,0,0,1,0,0,1,0,1,0,1,1,0,1,1,0,1,0,0,1,1,1,1,1,1,0,0,0,0,0,0,1,1,0,1,0,0,0,0,0,0,1,1,0,1,0,0,1,0,0,1,1,0,1,0,0,1,1,0,0,0,1,1,0,0,1,1,1,1,1,0,1,1,1,1,1,0,0,1,0,0,0,1,0,0,1,0,1,0,0,0,1,1,1,0,0,0,0,0,1,1,1,0,0,0,1,1,1,1,0,0,1,0,1,0,0,0,0,0,0,1,1,1,0,0,1,0,0,1,1,1,0,0,1,1,1,0,0,1,1,1,1,1,1,1,1,0,0,1,1,0,1,0,0,1,0,1,1,0,0,0,0,1,0,0,0,1,0,1,0,1,1,0,1,1,0,1,0,1,1,1,0,0,0,1,1,0,1,0,1,0,0,1,0,0,1,0,0,1,1,0,1,0,1,1,1,0,1,0,1,0,1,0,1,1,1,0,1,1,1,0,0,1,1,0,1,0,0,1,1,0,0,0,0,0,0,1,0,1,0,1,1,0,0,0,1,0,1,1,0,1,1,0,1,1,0,1,0,0,0,1,0,0,1,1,0,1,0,0,0,1,1,1,0,1,1,0,0,1,0,0,0,0,0,0,0,0,1,0,0,1,1,0,0,1,0,1,1,0,0,0,1,0,1,0,1,0,1,1,1,0,1,0,0,0,0,0,0,1,0,1,1,1,0,1,1,1,0,1,1,0,1,1,1,0,1,1,0,0,0,0,1,0,1,1,1,1,0,1,1,1,0,1,1,0,0,1,0,1,0,0,1,1,1,0,1,0,0,0,1,1,0,1,0,0,0,1,1,0,0,0,1,0,1,0,1,1,1,0,1,0,0,0,1,1,0,0,0,1,0,1,1,1,0,0,0,1,0,1,1,0,0,1,1,1,0,1,1,1,1,1,0,1,1,1,0,1,1,1,0,1,1,1,1,0,1,0,0,0,0,0,0,0,1,0,0,1,0,1,1,0,0,0,1,0,1,0,1,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,0,1,0,1,1,0,1,0,0,0,0,0,0,1,1,1,1,1,1,0,0,1,0,0,0,1,0,0,0,1,0,1,0,1,0,1,0,1,1,1,1,1,0,0,1,1,1,0,1,0,0,1,0,0,0,0,1,1,1,0,0,0,1,1,0,1,1,0,1,1,0,1,1,1,0,1,1,0,0,0,1,1,1,1,1,1,0,0,1,1,1,1,0,0,0,0,0,0,1,1,0,0,1,0,1,1,0,0,0,1,0,0,1,1,1,0,1,0,1,0,0,0,1,0,1,1,0,0,0,0,0,1,0,0,0,0,0,0,1,0,1,0,0,0,1,1,0,0,1,0,0,1,0,0,0,1,0,1,1,1,0,0,1,0,1,0,1,0,0,1,0,0,1,1,0,0,1,0,0,0,0,0,1,1,0,0,0,1,1,1,1,0,0,1,1,0,1,1,0,1,1,1,1,0,0,0,0,0,0,1,1,0,0,1,1,1,1,0,1,0,0,0,1,0,0,1,0,1,1,1,1,1,0,1,0,0,1,1,0,0,1,0,0,1,1,0,0,0,1,0,0,0,0,0,0,1,1,0,0,0,0,1,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,0,1,0,1,1,1,0,0,0,1,0,1,1,1,0,1,0,0,0,1,0,1,1,1,1,0,0,1,1,0,0,1,0,0,0,1,1,0,1,1,1,1,1,1,1,0,1,1,0,1,1,1,1,1,0,0,0,0,1,1,1,0,1,1,0,0,1,1,0,1,1,0,0,1,0,0,1,1,1,0,1,0,0,0,1,1,1,0,1,0,1,1,1,1,0,1,1,1,0,0,0,0,0,0,0,1,0,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,0,0,1,1,1,1,0,1,0,1,1,1,1,1,1,1,1,0,0,1,0,1,0,0,0,1,0,0,1,0,1,1,1,0,1,1,1,1,1,1,0,1,1,0,1,1,0,0,1,1,1,1,0,0,1,1,0,0,0,1,0,0,1,1,1,0,0,1,0,0,0,0,0,1,1,0,0,0,1,0,0,1,1,1,1,1,0,0,1,1,1,0,1,1,1,0,0,1,0,1,1,1,0,0,1,0,0,1,0,1,0,1,1,1,1,1,1,1,0,1,0,0,0,0,1,0,1,0,0,1,1,1,1,1,0,1,1,1,1,0,0,1,1,0,1,1,0,1,0,1,1,1,0,1,0,1,0,1,1,1,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,1,1,0,1,0,1,0,1,0,1,0,1,0,0,0,1,1,0,1,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,1,1,1,0,1,1,1,0,1,0,0,0,0,1,0,1,0,0,1,1,1,1,1,1,1,0,1,1,0,1,1,1,0,0,1,1,1,1,0,1,0,1,0,0,1,0,1,0,0,0,0,0,1,0,1,0,1,1,0,0,1,0,0,1,1,1,1,1,0,0,0,0,0,0,0,1,1,1,0,0,1,1,0,1,1,1,1,1,1,0,0,0,0,0,1,1,1,0,1,0,0,0,1,0,0,1,0,1,1,1,1,1,0,0,1,0,0,1,1,1,1,0,1,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,1,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,1,1,1,0,1,0,0,1,0,0,0,0,1,0,0,0,0,1,0,1,0,1,0,0,0,1,0,0,1,1,0,1,0,1,1,0,0,0,1,0,0,1,1,1,0,1,0,1,1,0,1,0,0,0,1,0,1,1,0,1,1,1,0,1,1,0,1,0,0,1,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,1,0,0,1,0,1,0,0,1,0,0,1,1,1,0,1,0,0,0,1,0,0,1,1,0,0,1,1,0,1,1,0,1,0,0,0,0,1,0,0,1,1,0,1,1,0,0,0,1,1,1,0,0,1,0,1,1,1,1,0,0,0,1,1,0,0,0,0,1,0,0,1,1,1,1,1,0,0,1,1,0,0,1,1,0,0,1,1,1,0,0,0,0,1,1,1,1,0,1,0,1,1,1,1,0,0,1,1,1,1,1,1,0,1,0,0,0,0,0,1,0,1,1,1,1,0,0,1,1,0,1,1,0,1,1,1,0,1,0,0,0,0,0,1,0,0,1,1,1,0,1,0,1,0,1,0,0,0,0,0,0,1,0,0,1,1,0,0,1,1,1,0,1,0,1,1,0,1,1,1,0,0,1,1,1,1,0,0,1,0,0,0,0,1,1,1,1,0,1,0,0,0,1,1,0,1,1,1,1,1,0,0,1,0,0,0,1,0,1,1,0,0,0,0,0,1,0,0,0,1,1,1,0,0,0,0,1,1,0,0,1,0,0,0,0,1,1,1,1,0,0,1,1,0,0,1,1,1,1,0,1,0,0,1,1,0,0,0,0,0,1,1,1,0,0,0,0,1,1,1,1,1,1,1,0,1,1,0,1,0,0,0,1,0,1,1,1,1,0,1,0,1,1,0,1,0,1,1,0,1,0,1,0,1,0,1,1,0,0,0,0,1,1,0,0,1,0,0,1,1,1,1,0,1,0,1,1,1,1,1,0,0,0,1,0,1,1,1,1,1,1,0,1,1,0,0,0,1,1,0,0,0,1,1,0,0,0,1,0,1,0,1,0,0,0,1,0,0,0,1,0,0,0,0,0,1,0,1,1,1,0,0,0,1,0,0,0,1,1,0,1,0,1,0,1,1,1,0,0,0,0,1,0,0,0,1,0,0,1,0,0,0,1,1,1,1,1,0,1,1,0,1,1,1,1,0,0,0,1,1,0,0,1,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,1,0,1,0,0,1,0,1,0,1,1,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,1,1,0,1,1,1,0,1,1,0,1,0,0,1,0,1,1,0,0,0,1,0,1,0,0,0,0,0,0,0,1,0,0,1,0,1,0,1,0,0,0,0,0,1,1,1,0,1,1,0,0,0,1,0,1,1,0,1,0,0,0,0,0,0,1,0,0,0,0,1,1,0,1,1,1,0,0,0,0,0,1,0,1,1,1,1,1,1,1,0,1,0,1,1,0,1,1,0,0,1,0,1,1,0,0,1,1,1,1,1,0,1,1,0,1,0,0,0,0,0,1,0,0,0,1,1,1,1,1,0,0,1,1,1,1,1,1,0,0,0,0,1,0,0,1,1,0,0,0,1,0,1,0,0,1,0,1,0,0,1,1,1,1,1,0,1,0,1,1,1,1,1,0,1,1,1,1,0,1,1,0,0,0,0,1,1,0,0,1,1,1,1,1,1,0,1,0,1,0,1,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,1,0,1,1,1,0,0,1,1,0,0,1,0,1,1,1,0,1,1,1,0,1,1,1,1,0,0,0,0,1,0,0,0,1,0,1,1,0,1,0,1,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,1,1,0,0,1,0,0,1,1,1,1,0,0,1,1,0,1,0,0,0,1,1,1,1,1,0,1,0,0,0,0,0,1,1,0,1,0,0,0,0,1,1,1,1,1,0,0,1,0,0,1,1,0,1,1,0,0,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,0,1,0,0,1,1,0,1,1,1,1,0,1,1,1,0,0,0,1,1,0,0,1,0,0,0,1,1,0,0,1,0,1,1,0,0,0,1,1,1,0,1,1,0,0,0,0,1,1,0,0,1,0,0,1,1,1,0,1,0,0,0,0,1,1,1,0,0,0,1,0,1,0,0,0,1,1,0,0,0,1,1,0,0,1,1,0,0,0,1,0,1,0,0,1,1,0,1,0,0,0,1,0,1,0,1,0,1,1,1,1,0,1,0,0,0,1,1,1,1,0,1,1,1,0,1,0,0,0,0,0,0,1,1,1,1,0,1,1,1,0,0,1,1,0,1,0,0,1,1,0,0,1,1,1,0,0,0,1,1,0,0,0,1,1,1,1,1,0,0,0,0,1,0,1,1,0,0,0,0,0,1,0,0,0,1,0,1,1,1,0,1,1,0,0,0,1,1,1,1,1,0,0,0,1,1,0,1,1,0,1,0,0,1,0,0,1,1,1,1,0,0,1,0,1,0,0,1,1,1,0,0,0,0,1,1,0,0,0,0,0,0,0,0,1,1,1,0,0,1,0,0,0,0,0,1,0,0,1,0,1,0,0,0,1,0,1,0,0,0,0,0,0,0,1,0,0,1,0,0,1,1,1,0,0,0,0,0,0,0,1,0,1,0,1,0,0,0,1,0,1,0,0,1,1,0,0,0,0,1,0,1,0,1,1,1,1,0,0,1,0,0,1,1,1,1,0,0,0,0,1,1,0,1,0,1,0,1,1,1,1,0,1,1,1,0,1,0,0,0,0,1,1,0,0,0,1,0,0,0,0,0,0,1,0,0,0,1,1,0,0,1,1,0,0,1,1,0,0,0,1,1,0,1,0,1,0,0,0,0,1,0,0,0,1,1,1,1,0,0,0,1,1,0,1,0,0,0,0,1,0,1,1,1,1,0,1,1,1,1,0,1,0,0,0,1,1,0,0,1,0,1,0,0,0,1,0,1,1,0,1,0,1,0,0,1,0,1,0,1,1,1,1,1,1,0,1,0,1,0,0,0,1,0,0,0,0,1,0,1,1,1,0,0,1,0,0,0,1,1,0,1,1,1,0,1,0,1,0,1,0,1,1,1,1,1,1,0,0,0,1,0,1,0,1,1,1,1,0,0,0,1,1,1,0,0,0,0,0,1,1,0,1,0,1,0,1,1,1,0,0,1,0,0,1,0,0,0,0,1,1,1,0,1,0,1,0,0,1,0,0,1,0,0,0,0,1,1,1,0,0,0,0,0,1,0,0,1,1,1,0,1,1,0,0,0,0,1,0,1,0,1,1,1,0,1,1,1,1,1,1,1,0,1,1,1,0,1,1,1,0,0,1,1,0,0,0,0,1,1,1,0,0,0,0,1,0,0,1,1,1,1,0,1,0,0,0,0,1,0,1,1,0,0,0,1,1,1,0,1,1,0,1,1,0,0,0,1,0,0,0,1,1,0,1,0,1,1,1,1,0,1,1,0,1,0,0,1,1,1,1,0,1,0,0,1,1,1,0,1,0,1,1,0,1,0,1,0,1,1,1,0,1,0,0,0,0,0,1,1,0,1,0,0,0,0,0,1,0,0,0,1,1,1,1,0,1,1,0,0,0,0,0,0,1,0,0,1,1,0,0,1,0,0,1,1,0,0,0,0,1,1,1,0,0,1,0,0,0,1,0,0,1,0,0,1,1,1,0,0,0,0,1,0,0,0,0,0,1,0,1,1,1,0,1,0,1,1,0,0,0,1,1,0,1,0,0,1,1,0,1,0,1,0,0,0,1,1,0,1,1,0,1,1,0,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1,1,0,1,1,0,0,1,0,1,0,1,0,1,0,1,1,1,0,1,0,0,1,1,1,1,0,0,0,1,1,1,0,0,1,0,1,1,1,0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,1,1,0,1,0,1,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,1,1,0,1,1,0,0,1,0,1,0,1,0,0,0,1,1,1,1,0,0,0,1,0,0,0,1,0,1,1,1,0,0,1,1,0,1,1,0,0,0,0,1,0,0,0,0,1,1,1,1,0,1,1,0,0,1,1,0,0,0,1,1,0,1,1,0,1,1,0,0,0,1,1,0,0,0,0,1,1,1,0,0,0,1,1,0,1,0,1,0,0,1,0,1,1,1,1,1,0,0,1,1,1,0,0,0,0,1,0,1,0,0,0,0,0,0,1,1,0,1,0,0,1,0,0,0,0,0,1,0,1,0,0,1,1,1,1,0,0,1,0,0,0,1,0,0,0,1,1,0,0,0,1,1,1,1,1,0,0,1,1,1,1,1,1,1,0,0,1,1,0,1,1,1,1,1,1,1,0,1,1,0,1,1,0,1,1,1,0,1,1,1,1,0,0,1,0,1,1,0,0,0,1,0,1,1,0,1,1,1,1,0,0,0,1,0,1,1,0,1,1,0,1,0,1,1,1,1,1,1,1,0,1,0,0,0,1,0,0,1,0,0,1,0,0,0,1,0,1,1,0,1,1,0,0,0,0,1,1,0,1,0,0,0,1,0,1,1,1,1,1,0,1,1,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,1,1,0,0,0,0,0,1,0,1,0,1,1,1,1,0,1,0,0,0,1,1,0,0,1,1,0,0,1,0,0,0,0,1,1,0,0,0,1,0,1,0,1,0,0,1,1,1,1,1,1,0,1,1,1,1,1,0,1,1,0,0,0,0,1,0,0,0,1,0,0,1,0,1,0,0,0,0,0,0,1,0,0,1,1,0,0,1,0,0,0,1,1,1,0,1,1,0,1,1,0,0,1,1,1,1,0,0,0,1,1,0,0,0,1,1,0,1,1,1,0,0,0,0,0,1,1,1,1,1,0,1,1,0,0,0,0,1,1,1,1,0,1,0,0,1,0,1,0,0,1,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,0,0,1,0,1,1,1,0,1,1,1,1,0,1,1,1,1,0,1,1,0,0,1,0,1,1,0,0,0,0,0,1,1,1,1,1,0,0,0,0,1,1,1,1,0,0,1,0,0,0,1,0,1,0,0,1,1,1,1,0,0,1,0,0,0,0,0,0,1,1,1,0,1,1,0,0,1,0,0,1,1,1,1,1,1,1,0,1,0,1,0,0,1,0,0,1,0,1,0,0,1,1,0,0,0,0,0,1,0,1,1,1,0,1,1,0,1,0,0,0,0,1,0,1,0,0,1,1,1,0,0,0,0,0,0,1,0,1,1,0,0,0,0,1,1,1,0,0,0,0,1,1,0,0,0,0,1,1,0,0,0,0,1,1,0,0,1,0,1,0,0,1,1,1,1,1,1,0,1,1,0,1,0,1,1,0,1,1,0,1,1,0,1,0,1,0,0,0,1,0,0,1,0,0,0,0,0,0,1,0,0,0,1,1,0,0,1,1,0,0,0,1,1,1,0,1,0,0,1,1,1,0,1,1,1,1,1,0,1,0,1,1,1,0,1,0,0,1,1,0,1,0,1,0,0,0,1,1,1,0,1,1,0,1,0,0,1,0,0,0,0,1,1,0,0,1,1,1,0,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,1,1,0,0,0,1,1,1,0,1,0,1,1,1,0,0,0,1,0,0,1,0,1,1,1,1,0,1,0,1,0,1,0,1,1,0,0,1,0,1,0,0,1,0,0,1,1,0,1,1,1,0,1,0,0,1,1,1,0,0,1,0,0,0,1,0,0,1,0,1,0,1,0,1,0,1,1,1,0,1,1,1,1,0,0,1,1,0,0,0,0,0,1,0,1,1,1,0,0,1,1,1,1,1,1,1,1,0,0,0,1,0,1,0,0,1,1,1,0,1,0,0,0,0,0,1,0,0,0,0,1,1,1,1,1,1,1,0,0,0,1,0,0,1,0,1,1,1,0,1,0,1,0,0,0,0,1,0,1,1,0,1,1,0,0,0,1,1,0,0,0,1,1,0,1,0,0,0,1,1,1,0,1,0,1,1,0,0,1,0,1,0,0,1,0,0,1,1,0,1,0,1,1,1,1,0,0,0,1,1,0,1,1,0,0,1,1,1,1,1,0,0,1,1,1,0,1,1,1,1,0,0,0,0,0,1,1,0,0,0,0,1,0,0,1,1,0,0,0,1,1,1,0,0,1,1,1,1,1,0,0,1,1,1,1,0,0,0,1,1,1,0,1,1,0,1,0,1,1,1,1,1,0,1,0,0,1,0,0,1,0,0,0,0,0,0,1,1,1,0,1,0,0,0,0,1,1,1,0,1,1,1,1,1,1,0,0,1,0,1,1,0,1,1,0,1,0,1,1,0,1,0,1,1,1,1,1,1,1,1,1,0,1,1,0,0,1,0,0,1,1,0,1,1,1,1,1,0,1,1,0,0,1,0,1,0,0,0,0,0,0,0,1,0,1,1,0,1,0,1,0,1,0,1,0,0,0,1,1,1,0,0,0,1,0,0,0,1,1,1,1,0,1,0,1,0,0,1,0,0,1,0,0,0,1,0,1,1,0,0,0,1,1,1,1,1,0,0,0,0,0,0,1,0,1,0,0,0,1,1,1,1,0,0,0,0,1,1,0,0,0,0,1,1,0,1,1,1,1,0,1,1,1,0,1,1,0,1,0,0,1,1,1,1,1,1,1,1,1,0,1,1,0,0,1,1,0,0,1,1,0,0,0,1,1,0,1,1,0,1,0,0,1,1,0,1,0,1,1,1,0,0,0,0,0,0,0,1,0,0,0,1,1,1,0,0,0,0,1,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,0,1,0,0,1,1,1,0,0,1,0,1,1,0,0,0,0,1,0,0,1,0,1,0,1,0,0,0,1,1,1,1,0,0,1,0,1,1,0,0,1,0,1,0,0,0,0,0,1,1,1,0,1,0,0,0,0,0,0,1,1,0,1,1,1,1,0,0,0,0,1,0,1,1,0,0,1,1,1,1,0,1,0,1,1,1,1,1,1,0,0,1,0,1,1,0,1,1,1,1,0,1,0,0,1,1,0,0,0,1,0,0,1,1,1,1,0,1,0,0,1,0,0,0,0,1,0,0,0,1,0,1,1,1,1,1,1,0,1,1,1,1,1,1,1,0,0,1,0,1,0,0,1,1,0,0,0,1,1,1,1,0,0,0,0,0,0,1,1,1,1,1,1,0,1,0,0,1,1,0,0,1,0,0,1,1,1,0,0,1,1,0,1,0,0,1,0,1,0,0,0,1,1,0,1,0,1,1,1,0,1,0,0,1,0,1,1,0,1,1,0,1,0,0,0,1,0,0,0,0,1,1,1,0,0,1,1,0,1,0,1,1,0,0,0,1,0,0,0,1,1,1,0,0,0,1,0,1,0,0,0,1,0,1,1,0,0,1,1,0,1,1,0,1,1,0,0,1,0,1,0,1,0,1,0,1,1,0,0,1,1,0,0,1,0,0,0,1,0,0,0,0,1,1,0,1,0,0,0,1,0,0,0,0,0,0,0,0,0,1,1,0,0,1,1,1,1,1,0,0,0,0,1,0,1,0,0,1,1,1,0,0,0,0,1,0,1,0,1,1,0,0,1,0,1,0,0,1,1,1,1,0,0,0,0,0,1,1,0,1,0,0,1,0,0,0,1,0,0,1,1,1,1,0,1,0,0,0,1,1,0,0,0,0,0,1,1,0,1,1,0,0,1,0,1,0,1,0,0,1,0,1,1,0,0,0,1,1,0,0,0,0,1,0,0,0,0,1,1,1,0,0,0,1,0,0,0,1,0,0,1,1,1,1,1,1,1,0,1,1,0,0,0,1,1,1,1,0,0,0,1,1,1,0,0,0,0,1,1,1,1,1,1,1,1,0,1,1,0,0,0,0,0,0,1,0,0,0,0,1,1,1,1,0,0,1,0,1,1,0,1,0,1,0,0,1,1,0,1,0,0,1,1,0,0,1,0,1,1,0,0,1,1,1,1,1,1,0,1,1,0,1,0,0,0,1,0,1,1,0,1,0,0,0,1,0,1,1,0,1,1,1,0,1,0,0,0,1,1,0,1,1,1,1,1,0,0,0,0,0,1,1,1,0,1,0,1,1,0,1,1,1,0,0,1,0,1,0,1,0,1,0,1,1,0,0,0,1,0,0,1,1,1,1,0,1,1,0,0,1,1,0,1,1,0,1,0,0,1,0,1,1,1,0,0,1,1,0,1,0,1,1,1,0,1,0,0,1,0,1,1,1,0,0,1,1,0,0,1,1,0,1,1,0,1,0,0,0,0,0,1,1,1,0,0,1,1,1,0,0,0,0,0,0,0,1,0,1,0,1,1,0,0,1,0,1,0,1,1,1,1,1,1,0,0,0,1,0,0,0,1,1,0,1,0,0,0,0,0,1,0,0,0,1,0,0,1,0,0,1,0,0,1,1,0,0,1,1,1,1,0,1,1,0,1,1,1,1,0,0,1,1,0,1,1,0,1,1,0,1,0,1,1,1,0,1,0,1,1,1,0,0,0,0,0,0,1,0,1,1,0,1,1,1,0,1,0,1,1,1,1,0,1,0,0,1,0,1,1,0,0,1,0,0,1,1,0,0,1,0,1,1,1,1,1,0,0,0,1,0,1,0,1,0,1,0,1,1,0,1,1,1,0,0,0,1,1,0,0,1,1,0,0,0,0,0,0,1,1,0,0,1,1,0,1,1,0,1,0,1,1,0,1,0,0,0,1,1,0,0,1,0,1,1,0,0,1,1,1,0,1,0,1,1,1,0,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,0,1,1,1,0,0,1,0,0,1,1,0,0,0,1,0,1,1,1,1,0,1,1,0,0,1,0,0,0,1,0,1,0,1,0,0,0,0,1,1,1,0,1,0,1,1,1,0,0,0,0,0,1,0,0,1,1,0,0,1,0,0,1,0,0,1,1,0,0,0,1,1,1,0,1,1,1,1,0,1,0,0,0,1,0,0,0,0,1,1,1,1,1,0,0,0,0,0,1,1,0,0,1,1,1,1,0,1,0,0,1,0,0,0,0,1,1,1,1,0,0,1,1,0,0,1,1,1,1,0,0,0,0,0,0,1,0,1,0,1,0,0,1,0,0,1,1,0,1,1,0,1,1,0,1,0,0,0,0,1,0,1,0,1,0,1,0,1,0,1,1,0,0,1,0,1,0,1,1,0,0,1,0,0,1,1,0,0,1,0,1,1,1,0,0,0,1,0,0,0,1,0,1,0,1,0,0,1,0,0,0,0,1,0,1,1,0,0,0,1,0,0,1,0,0,0,1,0,1,1,1,0,0,1,1,0,1,0,0,1,0,1,1,0,1,0,1,0,0,1,1,1,1,0,0,1,0,1,1,0,1,0,1,0,0,0,0,1,0,1,1,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0,1,0,1,0,1,0,1,0,0,1,1,1,0,1,0,1,1,0,1,1,1,0,0,1,0,0,0,1,0,1,0,1,0,1,0,1,1,0,1,0,1,1,1,1,0,0,0,1,0,1,1,0,0,0,0,1,0,1,0,1,1,0,0,1,1,1,0,0,1,1,1,0,1,0,1,0,0,0,1,0,1,0,0,1,1,0,1,0,0,1,1,1,1,0,1,1,0,0,1,1,0,0,1,0,0,1,0,1,0,0,0,0,1,0,1,0,0,1,1,0,0,0,0,0,1,0,0,0,1,1,1,0,1,0,1,1,0,1,0,0,0,1,1,0,0,1,1,0,0,1,0,0,0,0,0,1,1,0,0,0,0,0,1,1,0,0,0,0,0,0,1,1,0,1,0,0,0,1,0,0,1,1,1,1,0,0,1,0,1,0,0,1,0,1,0,1,1,1,0,1,0,0,0,0,0,1,0,0,0,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,0,0,0,1,0,0,0,0,1,0,1,1,1,1,1,1,0,0,0,0,0,0,1,0,1,1,0,1,0,1,0,0,1,1,1,1,1,0,0,0,0,1,0,1,1,0,0,1,0,1,1,1,1,0,0,1,1,1,1,1,0,1,1,1,0,0,0,0,1,0,0,0,0,1,0,0,1,0,0,0,1,0,0,1,0,0,0,1,1,1,0,0,0,0,1,0,0,1,1,1,0,0,0,0,0,1,1,1,1,1,0,1,0,1,1,1,1,1,1,0,1,1,1,1,1,1,0,1,1,1,1,1,0,0,0,1,0,0,0,1,1,1,1,1,0,0,0,1,0,1,1,1,1,1,1,0,0,1,1,0,0,1,1,1,0,0,1,0,0,0,0,0,0,1,0,0,1,0,0,1,1,0,1,1,1,1,1,1,1,0,1,1,1,0,0,1,1,1,0,1,1,1,1,1,0,1,1,0,1,1,1,1,0,1,0,0,1,0,1,1,0,0,1,1,0,1,0,0,1,1,1,0,0,0,1,1,0,1,1,0,1,1,0,1,1,1,0,1,0,0,0,1,0,0,1,0,1,1,1,0,0,0,0,0,1,0,1,0,0,1,0,1,0,1,0,1,1,0,0,0,0,0,0,1,0,1,1,1,0,1,1,1,1,1,0,1,0,1,1,0,0,1,0,1,0,0,1,0,0,0,1,1,1,0,1,1,0,1,0,0,1,1,1,0,1,1,1,0,0,0,1,1,0,1,0,1,1,0,1,0,1,0,1,1,0,0,0,0,0,1,0,1,1,1,0,0,0,0,0,0,1,1,1,0,0,0,1,1,0,0,1,0,1,1,0,1,0,0,0,1,1,1,0,0,0,0,0,1,1,1,0,1,0,0,1,0,0,0,1,1,0,0,0,1,0,1,0,0,1,0,1,0,0,1,1,1,1,1,0,1,0,1,1,1,0,0,1,1,1,0,1,0,1,0,0,1,0,0,0,1,0,0,1,1,1,0,1,0,1,0,0,1,1,0,1,1,1,0,0,0,1,1,1,1,1,0,1,0,0,1,1,1,1,1,1,1,0,1,0,0,0,1,0,0,1,0,1,1,1,0,0,1,0,1,1,0,1,0,0,1,0,1,1,1,0,1,0,0,0,1,1,1,0,1,1,0,1,1,0,0,1,0,0,0,1,0,0,1,0,0,0,0,0,0,1,1,0,1,0,1,0,1,0,0,1,0,0,1,1,0,0,1,0,1,1,1,1,1,1,1,0,1,1,1,0,0,0,0,0,0,1,1,0,0,0,1,0,1,0,0,1,0,1,1,0,0,1,0,0,0,1,1,1,1,1,0,0,0,0,0,1,0,0,0,0,1,0,0,0,1,1,0,1,1,0,1,1,1,0,1,1,0,1,1,0,0,1,1,0,1,1,1,1,1,0,0,1,0,1,1,1,0,1,1,1,0,0,0,1,0,0,1,1,0,0,1,0,1,1,0,1,1,1,0,0,1,1,0,1,0,0,0,0,0,0,0,1,0,1,1,1,0,0,0,0,1,1,0,1,1,0,0,1,0,1,0,0,1,1,1,1,1,0,1,0,0,1,1,0,1,1,0,0,0,1,0,0,0,0,1,1,0,1,1,1,1,0,1,0,0,1,1,0,1,0,1,1,1,1,0,0,1,1,1,1,0,1,0,1,0,0,0,1,1,1,0,0,1,0,0,1,0,0,0,0,1,0,0,1,1,0,0,1,0,0,1,0,0,1,1,0,0,1,1,0,0,1,0,0,0,0,1,1,0,0,1,1,0,0,1,0,0,1,0,0,1,0,0,1,1,0,1,0,0,1,1,0,1,0,1,1,0,1,0,1,1,0,1,0,0,1,0,1,1,0,0,0,1,1,1,1,0,0,1,1,0,1,1,0,0,1,1,0,0,1,0,1,1,0,0,0,0,1,1,1,0,1,0,1,0,0,1,1,0,1,0,0,1,0,1,0,1,0,0,1,1,0,0,1,0,0,0,1,0,1,0,0,0,0,1,1,1,0,0,1,0,0,0,1,1,0,1,0,0,1,1,0,1,0,1,0,1,1,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,1,1,0,1,0,0,1,0,1,1,1,0,0,1,1,0,0,1,1,1,0,0,1,1,0,0,0,1,1,0,0,0,0,1,1,0,0,1,0,1,1,1,0,1,1,0,1,1,1,1,0,0,1,0,0,0,0,0,0,0,1,1,0,1,1,1,0,0,0,0,1,1,1,1,1,1,1,0,1,0,0,0,0,1,0,1,0,0,1,1,1,1,0,1,0,1,0,0,1,1,1,1,0,1,1,1,1,0,1,0,0,1,0,1,1,0,1,0,0,0,1,0,0,0,0,0,1,0,1,0,1,1,0,1,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,1,1,0,0,1,0,1,0,1,0,0,1,1,1,0,0,0,0,1,0,0,1,0,0,0,0,0,0,1,1,0,0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,1,0,0,1,0,0,1,1,0,1,0,1,0,0,0,0,0,1,1,1,1,0,0,1,1,1,0,0,1,1,0,1,1,1,1,0,0,1,1,1,1,0,0,0,0,0,1,1,1,0,1,1,1,0,1,0,0,0,1,0,1,1,0,0,1,1,1,0,0,0,1,0,1,1,0,1,0,0,0,0,1,1,0,0,0,0,0,1,1,1,0,0,0,0,0,1,0,0,1,1,0,0,0,0,1,1,1,0,0,1,0,1,1,0,0,1,0,0,1,1,1,0,1,0,1,0,0,0,0,1,0,1,0,0,0,0,1,0,1,0,0,1,0,0,0,0,1,1,1,1,0,0,0,1,0,0,1,0,1,0,0,0,0,0,1,0,1,1,1,1,1,1,0,0,0,1,0,1,0,0,0,1,0,1,0,1,0,1,0,1,0,0,1,1,0,1,0,0,0,1,0,1,1,0,0,1,0,1,1,0,0,0,0,0,1,1,0,1,0,1,0,0,0,0,1,0,0,1,1,1,0,0,0,0,1,0,1,1,0,0,0,0,0,0,0,1,1,0,1,1,0,0,0,1,0,0,0,1,0,0,1,0,1,1,0,0,1,1,1,0,0,1,0,1,0,1,0,1,1,0,1,1,0,1,1,0,1,1,0,0,0,1,0,1,1,1,1,1,1,1,1,0,0,0,1,1,0,1,0,0,0,0,0,0,1,1,1,0,1,0,0,0,0,1,0,0,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1,1,0,0,1,1,0,0,0,1,1,1,1,1,0,0,0,0,1,1,0,0,0,0,1,1,1,0,1,0,0,1,1,0,0,0,1,0,1,1,1,0,0,0,1,1,1,0,1,0,0,0,1,1,0,0,0,1,0,1,0,0,1,1,1,1,1,0,0,1,0,0,0,1,0,1,1,1,1,0,1,0,1,1,0,0,0,1,1,1,1,0,0,1,0,0,1,0,1,0,1,1,0,1,0,1,1,0,0,0,0,0,0,0,0,1,1,0,0,0,1,1,1,0,1,0,0,0,1,1,0,0,0,1,0,0,0,1,0,1,0,0,1,0,1,1,1,1,0,1,1,1,0,1,0,1,0,1,1,0,1,0,0,1,1,1,0,1,1,0,1,0,1,0,1,0,1,1,1,1,1,1,0,1,0,0,0,1,0,0,0,1,1,0,0,1,0,1,0,0,0,1,1,0,1,0,0,0,0,1,1,1,0,0,0,1,1,1,0,1,1,1,0,1,1,1,1,1,1,0,0,0,0,1,1,0,1,0,1,0,0,0,0,1,0,1,0,0,0,0,1,0,1,0,1,0,0,0,1,0,0,1,0,1,0,0,0,0,0,1,0,1,0,0,1,1,1,1,1,1,0,1,1,0,1,1,1,1,0,1,1,0,0,0,0,1,0,1,1,0,0,0,1,1,1,1,1,1,0,0,1,1,1,1,1,0,0,1,1,1,0,0,1,1,1,1,0,1,0,1,1,1,0,1,1,1,1,0,1,0,0,1,1,1,0,1,1,1,0,1,0,0,1,0,1,0,1,1,1,0,1,0,1,0,1,0,1,1,1,0,1,0,1,1,0,1,1,0,1,1,1,1,0,1,1,0,1,0,1,1,0,0,0,0,1,1,1,1,0,1,1,1,1,1,1,0,0,1,0,1,0,0,0,1,1,0,0,1,1,1,0,1,1,0,1,0,1,0,0,0,0,1,1,1,0,0,1,0,1,0,0,1,1,0,0,0,0,1,0,1,1,1,0,1,0,0,0,0,0,0,0,1,1,1,0,1,1,0,0,1,1,1,0,1,0,0,1,0,1,1,0,0,0,0,1,0,0,0,0,0,0,0,0,1,1,1,1,0,0,1,0,0,1,0,1,1,1,1,1,0,0,1,1,0,0,1,0,1,0,0,1,0,0,0,1,0,1,0,0,0,1,1,1,0,0,1,1,0,1,1,1,1,1,1,0,0,0,1,0,0,0,0,0,0,1,0,1,0,0,0,1,1,1,1,0,1,0,1,0,0,1,1,0,1,0,1,1,1,0,1,1,1,1,0,0,0,1,1,1,0,0,0,1,0,1,0,1,0,0,0,0,1,0,0,0,0,1,0,0,1,0,1,0,1,1,1,1,1,0,0,1,1,0,1,1,0,1,0,0,0,1,1,0,0,1,0,1,1,1,1,0,1,0,1,1,1,0,1,1,1,0,1,1,1,0,1,1,1,1,0,1,1,1,1,1,0,1,1,0,0,1,0,1,1,0,0,0,1,1,0,1,1,0,0,1,1,0,0,1,1,0,0,0,1,0,0,1,1,1,1,0,0,1,1,0,1,0,0,0,1,1,1,0,0,1,0,1,1,1,0,0,1,1,0,1,0,0,0,1,1,1,1,1,0,1,1,1,1,1,0,0,0,0,1,0,0,0,0,1,1,0,0,1,0,0,1,1,1,0,0,1,1,0,0,1,1,0,1,1,1,1,1,1,1,0,0,1,1,1,0,0,0,0,1,1,0,1,0,0,1,1,1,1,0,0,0,1,0,0,1,1,1,0,1,1,0,0,1,0,0,0,0,0,1,0,1,1,1,1,1,1,0,0,1,1,0,1,0,0,0,0,1,0,0,1,0,0,1,1,0,0,1,0,1,0,1,1,1,0,0,0,0,1,1,1,0,1,1,0,1,0,0,1,0,1,0,1,1,0,1,1,1,1,0,1,0,0,1,0,0,1,1,1,1,0,1,0,1,1,0,0,0,1,0,1,1,1,0,0,0,0,1,0,0,1,1,0,1,0,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,1,0,0,1,1,1,1,1,1,1,0,0,0,0,1,1,1,0,1,0,1,0,0,1,0,0,1,1,0,0,1,1,1,1,0,1,0,1,1,1,0,0,1,1,0,0,0,0,0,1,0,0,1,1,1,0,0,1,0,1,0,1,1,1,0,1,1,0,1,0,0,0,0,0,1,1,0,0,0,0,1,1,1,0,0,1,0,1,1,0,1,0,1,1,1,0,1,0,0,0,0,1,1,0,1,1,0,0,0,1,1,0,0,1,1,1,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,1,0,1,0,0,1,0,1,1,0,1,1,1,1,0,1,1,0,0,0,1,0,1,0,0,1,0,0,0,1,0,1,0,1,0,1,1,1,1,1,1,1,1,1,1,0,0,1,0,1,0,0,0,0,0,0,0,1,0,1,0,1,0,1,0,0,1,1,1,0,0,0,1,0,1,0,1,1,1,1,1,1,1,0,1,0,1,0,0,1,1,0,0,1,0,0,1,0,0,1,0,0,1,0,1,1,1,0,1,1,0,0,1,0,0,1,1,0,0,0,1,1,0,0,0,1,0,1,0,1,1,1,1,0,0,1,1,0,1,0,1,0,0,1,0,1,1,1,0,1,1,1,0,1,0,1,0,0,0,1,1,1,1,1,1,0,1,0,0,0,1,0,1,1,1,0,0,1,0,1,1,0,0,0,1,1,1,1,0,0,0,0,0,1,1,1,0,0,1,0,0,1,1,0,1,1,1,1,0,0,0,1,0,1,1,0,0,0,1,0,1,1,1,1,1,1,0,1,0,0,1,0,0,0,0,1,1,0,1,1,1,1,1,1,1,0,1,0,1,0,1,1,0,0,1,0,0,0,1,1,0,0,1,0,1,0,0,0,0,0,0,1,1,0,0,1,0,0,0,1,0,0,0,1,1,0,1,1,1,1,1,1,1,0,1,0,1,1,0,0,0,1,0,1,0,1,0,1,1,1,0,0,1,0,0,1,0,1,0,0,1,1,1,0,1,1,0,1,0,1,0,1,1,0,1,1,1,1,1,1,0,0,0,1,1,0,1,1,0,1,0,1,0,1,1,1,0,1,1,1,0,1,0,1,0,0,0,0,1,1,1,0,0,0,1,1,0,0,0,1,1,1,1,0,1,0,0,0,1,0,0,1,0,0,0,0,0,1,0,0,0,1,1,0,1,1,1,0,0,0,0,0,0,0,1,0,0,1,0,1,1,1,1,0,1,0,0,1,1,0,1,0,0,1,1,0,0,1,1,0,0,0,1,0,0,0,1,1,1,0,1,1,0,1,1,0,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,0,1,1,1,0,1,1,0,0,0,1,0,1,0,0,0,1,1,0,1,0,1,1,1,1,1,1,1,0,1,0,0,1,1,1,1,1,1,0,0,1,1,1,0,1,0,1,1,1,0,0,1,0,0,1,0,0,1,1,1,0,1,0,1,1,0,1,0,1,1,0,0,0,0,0,1,1,1,0,1,1,0,1,1,0,0,0,0,1,0,0,1,0,0,1,1,0,1,1,0,0,0,1,1,0,0,1,0,0,1,1,0,0,1,1,1,1,0,1,0,1,1,0,0,0,1,0,1,1,1,1,1,1,0,1,1,0,1,1,1,1,0,0,0,1,0,1,1,1,1,1,0,0,1,1,1,1,1,1,0,1,0,0,0,1,1,1,0,1,1,0,0,0,1,1,0,0,0,0,1,1,1,1,0,0,0,0,0,1,0,1,0,0,0,1,0,0,0,0,1,1,1,0,0,1,1,0,1,1,1,0,1,1,0,1,1,0,0,0,1,1,1,1,0,0,0,1,1,0,1,0,0,0,0,0,0,1,0,0,1,1,1,1,1,1,0,1,0,1,0,1,1,1,1,0,0,0,1,0,1,0,0,1,1,0,0,0,1,1,1,1,0,0,0,0,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,0,1,0,1,0,0,0,0,0,0,1,0,1,1,1,1,0,0,1,1,0,0,0,1,1,1,1,0,1,1,1,1,1,0,0,0,0,1,1,1,0,0,1,1,1,1,0,1,1,0,1,1,0,0,1,0,0,1,1,1,1,0,1,1,0,0,0,1,1,0,1,1,0,0,0,1,0,0,0,1,1,0,0,1,0,0,1,1,0,0,1,0,1,0,1,1,0,1,0,1,0,0,1,0,0,0,1,1,0,0,0,1,1,0,0,1,0,1,0,0,0,0,0,0,1,1,1,0,1,0,0,1,1,1,1,0,1,1,0,1,0,0,1,1,0,0,1,1,0,0,0,1,0,0,0,1,0,1,0,1,0,0,1,1,0,0,1,0,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,0,1,0,1,0,0,1,1,1,0,1,0,0,1,0,0,1,0,0,1,0,0,0,1,1,0,0,0,0,1,0,1,1,1,1,0,0,1,1,1,0,1,1,1,0,0,1,0,0,1,1,1,1,0,1,0,0,0,0,1,1,1,1,0,1,1,0,0,0,1,1,1,0,1,1,0,0,0,0,1,0,1,0,1,1,1,0,0,0,0,0,1,1,0,1,1,0,0,0,0,0,0,0,1,1,0,0,1,0,0,0,1,1,1,1,0,1,1,0,0,0,0,0,1,0,1,1,0,1,0,1,1,1,1,0,1,0,1,0,1,1,1,1,0,1,1,0,1,0,0,0,0,1,1,0,1,1,0,0,0,1,1,0,1,0,1,1,1,1,0,1,1,1,0,1,1,1,1,0,0,0,1,1,0,0,0,1,1,1,1,1,1,0,0,0,0,1,1,0,1,0,1,0,1,0,1,1,0,0,1,0,0,1,1,0,1,1,1,1,1,0,0,1,1,1,0,1,1,0,1,0,1,1,1,0,1,1,0,1,1,0,1,1,1,1,0,1,0,1,0,1,1,0,1,1,1,1,1,1,1,0,1,1,0,0,1,1,0,1,0,1,0,1,1,0,1,1,0,0,1,0,0,1,1,0,0,1,0,0,1,1,0,0,0,0,0,1,1,1,1,0,0,1,1,0,0,0,1,0,0,0,0,0,1,1,0,1,0,0,0,0,1,1,0,0,0,0,0,1,1,1,0,1,0,1,0,0,0,0,0,0,1,0,0,0,0,1,0,1,1,0,1,1,0,0,0,0,0,1,0,1,1,0,1,0,0,1,0,1,0,0,0,0,1,0,0,1,0,1,0,0,1,1,0,0,0,1,0,1,0,1,0,1,1,0,1,1,1,0,1,1,0,1,0,1,0,0,0,1,1,1,0,1,1,0,0,0,1,1,0,0,0,0,1,1,1,1,1,0,1,0,0,1,0,1,0,1,1,1,0,0,1,0,0,0,0,0,1,1,0,1,0,0,0,1,0,0,0,0,1,1,1,0,0,0,0,0,0,0,1,0,1,1,1,0,0,1,0,1,0,0,0,0,0,0,0,1,0,0,0,0,1,0,0,1,1,0,0,1,0,1,0,1,0,1,1,0,0,0,0,1,1,1,1,1,0,1,0,0,1,0,1,1,0,0,0,1,1,1,0,1,0,0,0,0,1,0,1,0,0,1,0,1,0,0,1,0,1,0,1,1,1,1,0,1,1,1,1,0,1,0,1,0,0,1,0,0,0,1,1,0,1,0,0,0,0,1,1,1,0,1,1,0,0,1,0,1,0,1,0,1,1,0,1,1,1,0,1,1,0,0,1,0,1,0,0,0,0,0,0,1,1,0,1,1,1,0,1,0,1,1,0,0,1,1,1,0,1,1,1,0,1,1,1,0,1,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,1,0,1,1,1,1,1,1,0,0,1,0,0,1,0,0,0,0,0,0,0,1,1,1,0,0,0,1,0,0,1,1,1,0,1,0,1,1,1,1,1,0,1,1,0,1,0,1,0,0,1,0,1,0,0,1,1,0,1,0,1,1,0,0,1,0,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1,1,1,1,0,1,0,0,0,1,0,0,1,0,0,0,1,0,0,0,0,0,1,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,1,0,0,1,1,1,0,1,0,1,1,0,0,0,0,1,1,0,1,0,1,0,1,1,1,0,1,1,1,1,0,1,1,0,1,0,0,1,0,0,0,1,1,0,1,1,0,0,0,1,0,1,0,0,0,1,0,0,0,0,1,0,1,0,1,1,1,1,1,1,1,0,0,1,1,0,0,0,1,1,0,1,1,1,1,1,0,1,1,1,0,0,0,0,0,1,0,1,1,1,0,0,0,1,0,0,1,0,1,0,1,1,0,1,1,0,1,0,1,0,1,1,0,1,1,0,1,0,0,0,0,0,1,0,0,0,0,0,0,1,1,1,0,1,0,0,1,1,1,0,0,0,0,1,1,0,1,0,1,0,1,0,0,0,1,0,1,0,0,1,1,1,1,1,1,1,0,0,0,1,1,1,0,1,0,0,1,0,0,0,0,1,0,0,1,0,0,1,0,1,1,0,0,0,0,1,0,1,0,1,0,0,1,1,1,0,0,0,0,1,0,1,0,0,0,1,0,1,1,1,1,1,1,0,1,1,1,1,1,1,0,0,1,1,0,1,1,0,0,0,0,1,1,0,0,1,1,0,1,1,1,0,0,1,0,1,1,1,1,1,0,1,0,0,1,1,1,0,1,1,0,1,0,1,0,0,1,0,1,1,0,0,0,0,1,1,1,1,1,0,1,1,1,1,1,1,1,0,1,0,0,0,0,1,1,0,0,0,1,0,1,0,1,1,0,0,0,1,1,1,1,1,1,1,0,1,1,0,0,0,1,1,0,1,0,0,1,0,1,1,0,0,0,0,0,1,1,1,1,1,0,0,0,0,1,1,0,0,1,1,0,1,0,0,1,0,0,0,1,1,0,0,1,1,0,1,1,0,0,1,1,1,0,0,0,1,0,0,1,1,1,0,0,0,1,1,0,0,1,0,0,0,1,1,1,1,1,0,1,0,0,1,0,1,0,1,1,0,1,0,0,0,1,1,0,0,0,1,0,0,1,1,0,1,0,1,0,0,0,0,1,0,1,1,1,0,1,0,0,1,0,0,0,1,1,0,0,0,0,1,1,0,1,1,1,0,0,0,1,0,0,1,1,1,0,1,0,0,1,0,0,0,1,1,1,1,1,1,1,0,1,1,1,0,0,1,1,1,0,0,0,0,1,1,1,1,0,1,1,0,1,1,1,0,1,1,1,1,1,1,0,0,1,1,1,1,0,0,1,0,1,0,1,1,1,1,0,0,1,1,1,1,1,1,1,1,0,0,1,1,0,0,0,1,1,1,0,0,1,0,0,1,1,1,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,0,1,1,0,0,0,1,0,1,0,0,0,1,1,1,0,1,1,1,0,0,0,1,1,0,0,0,0,0,0,1,1,0,1,0,1,0,1,1,0,1,1,1,0,1,0,1,0,0,1,0,0,1,1,0,1,0,0,1,1,0,0,0,0,1,1,1,0,1,0,1,1,1,0,1,1,1,1,1,0,1,1,0,1,0,1,1,1,1,1,1,1,1,1,0,0,0,1,0,0,1,1,1,0,0,1,0,1,0,1,1,1,1,1,1,0,1,0,0,1,0,1,0,0,0,0,0,0,1,1,1,1,1,1,1,0,1,1,1,0,0,0,0,1,0,1,1,0,0,1,1,1,0,1,0,0,0,0,0,1,0,0,1,0,1,0,1,1,0,1,1,1,0,1,0,1,0,1,1,1,1,1,1,1,1,0,1,1,1,1,0,1,0,0,1,0,1,0,1,1,1,1,0,1,1,0,0,1,0,0,0,1,0,0,1,0,0,0,0,0,1,1,0,0,1,0,1,1,0,0,0,1,1,1,0,1,1,1,1,1,1,0,0,1,1,0,1,0,0,0,0,0,1,1,0,1,0,1,1,1,1,1,0,0,1,0,0,1,0,0,1,1,1,1,0,0,1,0,1,0,1,1,0,1,0,0,0,1,0,1,0,0,0,1,0,0,1,1,1,1,0,1,0,1,1,0,1,0,1,0,0,1,1,1,0,1,0,0,1,0,1,0,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,0,1,1,1,0,1,1,0,0,0,1,1,1,1,0,1,1,0,1,0,1,1,0,0,1,1,0,1,0,1,0,1,1,0,0,1,0,0,0,1,0,1,0,0,0,0,0,0,0,1,0,1,1,0,0,1,0,1,0,1,1,0,0,0,1,0,0,0,0,1,0,1,0,1,0,0,0,1,1,1,1,1,1,0,1,0,1,0,1,1,1,1,0,0,1,1,1,0,1,0,0,1,0,0,1,1,0,1,1,1,1,1,0,1,1,0,1,0,0,1,0,0,1,0,1,0,0,0,0,1,1,0,1,1,1,1,1,0,0,1,1,0,0,0,1,1,0,1,1,1,1,1,1,1,0,0,0,1,0,1,0,1,1,1,0,1,0,0,1,0,0,1,1,1,1,1,0,1,0,1,0,1,0,0,1,0,1,1,1,1,1,0,1,1,0,1,1,1,1,1,1,1,1,0,0,0,0,1,0,0,1,1,0,1,0,1,1,1,1,1,0,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,0,1,1,0,1,1,0,0,1,0,0,1,1,0,0,1,1,1,1,0,0,1,1,1,0,1,0,1,1,1,0,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,1,0,0,1,1,1,0,0,1,0,1,0,1,0,1,0,0,1,1,0,0,1,1,0,0,1,0,0,0,0,1,0,0,1,1,1,0,1,0,0,0,1,0,0,1,1,1,0,0,0,0,0,1,1,0,0,1,0,1,0,1,0,0,0,1,0,0,1,1,1,1,0,0,0,1,1,0,0,0,1,1,0,0,0,1,1,0,0,0,1,0,1,0,1,0,1,1,1,1,1,0,0,1,1,1,1,0,1,0,1,1,1,1,1,0,0,1,1,1,1,1,0,1,1,1,1,0,1,0,0,1,0,0,0,1,0,1,0,1,1,1,1,1,1,1,1,0,0,1,1,1,0,0,1,0,0,1,1,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,1,1,1,0,0,0,1,0,0,1,0,0,0,0,0,1,1,0,0,1,0,0,0,0,1,1,1,0,1,0,0,1,0,1,1,0,1,0,0,0,0,0,0,0,1,0,0,1,1,0,1,1,0,1,1,0,0,1,1,0,1,1,1,1,1,0,1,1,1,1,0,0,1,0,0,0,0,0,1,1,0,1,0,0,1,0,0,0,1,1,1,1,0,0,1,0,0,0,0,0,1,1,1,1,1,1,0,0,0,1,0,0,1,0,0,0,1,0,0,0,0,0,0,1,1,1,0,1,0,0,0,0,0,1,0,1,1,1,0,0,1,1,1,0,1,0,1,0,1,1,1,0,0,0,0,0,1,1,0,0,0,1,0,1,0,0,0,1,0,1,1,1,1,1,0,1,0,0,1,0,1,1,0,0,1,1,0,1,0,0,0,0,0,1,1,0,1,0,1,0,0,0,1,1,1,0,1,0,0,0,0,1,1,1,1,0,0,0,1,1,0,0,1,0,1,0,1,1,0,1,1,0,1,0,0,1,1,0,0,0,1,1,1,0,0,0,0,0,0,1,1,0,1,0,1,1,1,1,0,0,1,0,0,1,1,0,1,1,0,1,1,1,0,1,1,0,1,0,0,1,1,0,0,0,0,1,1,0,0,0,1,0,1,1,1,0,1,0,1,1,1,0,1,1,0,1,0,0,1,1,0,1,1,1,1,0,0,1,1,0,1,0,1,0,1,0,1,0,0,0,0,1,0,0,1,1,0,1,1,1,1,0,0,0,1,0,0,1,1,1,1,1,1,0,0,0,0,1,0,1,0,1,0,1,1,1,1,0,0,1,1,0,0,0,0,1,0,1,0,1,0,1,0,0,0,1,0,0,1,0,1,1,0,0,0,1,1,1,1,0,0,1,1,1,1,1,1,1,0,1,0,0,0,1,1,0,0,0,0,0,1,1,1,1,0,1,1,0,1,0,0,1,1,1,0,0,0,1,0,0,1,0,1,1,1,0,1,1,0,0,1,0,1,1,0,0,0,0,1,0,1,1,0,0,1,1,1,0,0,1,1,1,0,1,0,1,1,1,1,1,1,0,1,0,1,0,0,0,1,0,1,1,1,1,0,0,1,0,0,1,1,0,0,0,0,1,0,0,0,1,0,0,1,0,0,1,1,1,0,1,0,0,1,0,0,1,1,1,0,0,0,0,1,0,0,1,1,0,1,0,1,0,1,1,0,0,1,1,0,0,0,0,0,0,1,0,1,1,1,1,0,1,1,0,1,1,0,0,1,0,0,0,1,0,0,1,1,1,1,0,0,1,0,1,1,0,0,1,0,1,0,1,1,0,0,1,0,0,0,1,1,0,0,1,0,1,0,1,1,0,0,1,0,0,0,0,1,0,1,0,1,0,1,0,1,0,1,1,0,0,0,0,1,0,1,1,1,0,1,1,0,1,0,1,1,1,0,1,0,0,0,0,1,0,1,0,1,1,0,0,0,1,1,0,0,0,1,0,1,0,1,1,0,0,0,0,1,0,0,0,1,0,1,1,1,0,0,1,0,0,1,1,0,1,0,1,1,0,1,1,0,1,1,0,0,0,1,0,0,0,1,1,1,1,1,1,1,1,0,0,0,1,0,1,0,1,1,1,1,0,1,1,0,1,0,0,1,0,1,0,1,1,1,1,0,1,1,0,1,1,0,0,0,0,1,1,1,0,0,1,1,0,0,0,1,1,0,0,1,0,0,1,0,0,1,1,1,0,0,1,0,0,0,1,1,1,1,1,0,0,0,0,0,1,1,0,0,0,0,0,1,0,1,1,1,1,1,1,0,1,1,1,1,1,0,1,1,0,0,1,1,1,0,0,1,1,1,0,0,0,0,0,1,1,1,1,0,0,1,1,1,1,1,0,0,1,0,1,0,1,0,0,0,0,0,0,0,1,1,1,1,0,0,0,1,1,0,1,1,1,1,0,0,0,1,1,1,0,0,0,1,1,0,0,1,0,0,0,1,0,0,1,0,0,0,0,0,1,0,1,0,0,1,0,1,0,1,1,1,0,0,0,0,0,1,0,0,1,1,0,1,0,1,0,0,0,0,0,1,0,0,0,0,1,1,0,0,0,0,0,1,0,1,0,1,1,1,1,1,1,0,0,1,1,0,1,1,0,0,1,0,0,1,1,0,1,0,1,0,1,0,0,1,0,0,0,0,0,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,0,0,0,0,1,1,1,1,1,1,0,1,0,1,1,0,0,0,0,0,0,1,1,1,0,0,0,1,1,1,0,0,1,0,1,0,0,1,0,0,0,0,0,0,1,0,1,0,1,0,0,0,1,0,0,0,0,1,1,0,0,1,0,1,0,1,0,1,1,1,1,0,0,1,0,0,0,0,1,1,0,0,1,0,1,0,1,1,0,1,1,1,0,1,1,0,1,1,1,1,1,0,1,1,1,0,0,1,1,1,0,1,1,1,0,1,0,0,0,1,1,0,0,1,1,1,1,0,0,1,0,0,0,0,0,1,0,1,1,0,0,0,0,1,0,1,0,0,1,1,1,0,1,1,1,0,1,1,1,0,0,0,1,0,0,0,1,1,1,1,0,0,0,0,1,0,1,1,1,0,1,1,1,0,0,1,1,1,1,1,0,0,1,0,0,0,0,0,0,0,0,1,1,1,0,1,1,0,0,1,0,0,0,0,0,1,1,0,0,0,0,1,0,0,1,1,0,1,1,0,1,0,1,1,0,1,0,1,1,0,0,1,1,0,1,1,1,0,1,0,1,1,0,1,1,0,1,0,1,1,1,0,1,0,0,1,0,1,0,0,0,0,1,0,0,0,0,1,1,0,0,1,0,1,0,0,0,0,0,1,0,1,0,0,1,0,1,0,1,0,1,1,0,0,0,1,0,1,1,0,0,0,0,0,1,1,1,1,0,0,0,0,1,0,1,0,1,0,1,1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,1,0,1,1,0,0,0,1,1,1,0,0,0,1,1,0,0,0,1,1,0,1,1,0,1,0,1,1,1,0,0,0,1,1,0,0,1,1,1,1,0,0,1,1,1,0,0,1,0,0,1,0,0,0,0,1,0,1,1,0,0,1,1,1,1,0,0,1,0,1,0,0,1,1,0,1,1,1,1,1,0,1,1,1,1,0,0,1,0,1,0,0,1,1,0,1,1,1,1,1,1,1,1,1,0,0,1,1,1,0,0,0,0,1,0,0,0,0,1,0,0,1,1,1,1,1,1,1,0,0,0,0,1,0,0,1,1,0,0,0,1,1,1,0,0,1,0,0,1,0,1,1,0,0,0,1,1,0,0,0,1,0,1,1,0,0,0,0,0,0,1,1,0,0,0,0,1,1,1,1,0,1,1,0,0,0,0,0,1,0,1,0,0,0,0,1,1,0,0,1,1,1,0,1,1,1,0,0,1,1,1,1,0,1,0,0,1,1,0,1,0,0,0,1,1,0,0,0,0,1,0,1,0,1,0,1,1,1,0,0,1,1,1,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,0,0,1,1,0,0,0,0,1,1,1,1,0,0,1,1,0,0,0,1,0,1,1,1,0,0,1,0,1,0,1,1,1,0,0,0,1,0,1,0,0,1,0,1,1,0,1,1,1,0,0,1,0,0,1,0,1,1,0,1,0,1,0,0,0,1,1,1,1,1,1,0,1,0,1,1,1,0,0,0,0,1,1,0,0,0,0,1,0,1,0,0,1,1,1,1,0,1,0,0,1,0,1,1,0,1,0,0,0,1,1,0,1,0,0,0,0,0,1,0,1,0,1,0,0,1,1,0,0,0,0,1,0,0,0,1,1,0,1,0,1,1,1,1,1,0,1,0,0,0,1,1,0,0,0,0,1,0,1,0,0,1,1,0,0,1,0,0,0,1,1,0,1,1,0,0,0,1,0,1,0,0,1,1,0,1,1,1,0,0,1,0,1,0,0,1,1,0,1,1,1,1,0,1,0,0,0,0,1,0,0,1,1,1,0,0,0,0,0,0,1,1,1,0,1,1,0,0,0,1,0,1,1,1,1,1,0,0,1,1,1,1,0,0,1,0,0,1,1,0,0,1,1,0,0,0,0,0,1,0,0,0,0,0,0,1,1,0,0,1,0,0,0,0,0,1,0,1,0,1,0,1,0,1,0,0,1,1,1,1,1,1,1,0,1,0,1,1,0,1,1,1,0,0,0,0,0,1,1,0,1,0,0,0,1,0,1,1,0,1,1,0,0,0,1,0,1,0,0,0,0,1,1,1,1,1,0,0,1,0,1,0,1,0,0,1,1,0,1,0,1,1,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,1,0,1,0,0,0,1,0,1,0,0,0,0,0,1,1,0,0,1,1,0,0,1,0,1,1,0,1,0,1,1,1,0,0,1,1,0,1,0,1,0,0,1,0,1,0,0,1,0,0,0,0,1,0,0,0,1,1,1,1,0,1,0,0,1,0,0,0,1,0,0,0,0,1,0,0,1,1,0,1,1,1,0,1,0,1,0,0,1,0,1,0,0,0,1,1,1,0,0,0,1,1,1,1,0,0,1,1,1,0,0,1,0,1,1,1,1,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,1,1,1,1,0,0,0,0,1,1,0,1,1,1,0,0,1,1,0,0,0,0,1,1,1,1,0,1,1,1,1,0,0,0,0,1,0,0,0,1,1,1,0,0,0,1,1,1,1,1,1,0,1,1,1,0,1,1,0,1,0,0,0,1,0,1,1,1,0,1,0,1,1,0,1,1,1,1,0,0,1,0,0,0,1,0,0,1,1,0,1,0,0,0,0,1,0,0,1,1,0,0,1,1,0,0,0,0,0,1,1,1,0,1,1,1,0,0,1,0,0,1,0,0,1,1,1,1,0,1,0,1,1,1,1,0,1,1,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,1,1,0,1,0,0,0,0,0,1,0,1,0,0,0,1,1,1,0,1,1,0,1,0,1,0,1,1,1,1,0,1,0,0,1,1,0,0,0,1,1,0,0,1,1,1,1,1,1,0,1,1,1,0,0,1,1,1,0,0,0,1,0,0,1,0,1,0,1,1,1,0,0,1,1,1,0,1,0,0,0,0,0,1,1,0,0,1,1,0,0,0,0,1,1,1,0,0,0,0,1,1,1,1,0,0,0,1,1,0,0,1,1,1,0,1,0,0,1,0,1,0,1,0,1,0,0,1,1,0,1,0,1,1,1,0,1,1,0,1,1,0,1,0,0,1,1,0,0,0,1,0,1,1,0,1,0,0,1,1,1,0,1,0,0,1,0,0,0,0,1,1,0,0,1,0,1,0,0,0,1,0,1,0,0,1,0,1,0,1,0,0,1,1,0,0,0,1,1,0,1,0,0,1,0,1,1,1,1,1,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,1,1,0,0,0,1,1,0,0,1,0,1,0,1,1,1,0,1,0,1,0,0,1,1,1,1,0,1,0,1,0,0,0,1,1,0,1,1,0,0,1,0,0,1,1,0,1,1,1,1,1,1,1,0,1,1,1,0,1,1,1,0,1,0,1,1,1,1,0,1,0,0,1,1,1,0,1,1,0,0,0,0,0,0,1,1,0,0,1,0,1,1,1,0,1,1,0,0,0,0,1,0,0,1,0,1,0,0,0,1,1,1,1,1,0,0,1,0,0,1,1,0,0,1,1,0,0,1,1,0,1,1,1,0,1,1,1,0,0,0,0,0,1,1,0,1,1,1,1,1,1,0,1,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,1,0,1,0,0,0,0,0,1,0,1,1,1,0,0,1,1,0,0,0,0,0,1,1,1,1,0,0,1,0,0,0,0,0,1,0,0,1,1,0,0,0,1,1,0,1,1,1,1,0,1,0,1,1,0,1,1,1,0,0,0,0,0,0,0,0,1,1,1,0,1,0,1,0,0,0,1,0,0,1,0,0,1,1,0,0,1,0,1,0,0,0,1,1,0,1,0,1,1,0,0,0,0,1,1,1,0,0,0,1,1,1,0,0,1,1,0,1,0,1,1,0,0,0,0,0,1,1,1,0,0,1,0,1,0,1,0,1,0,0,1,1,0,1,0,1,0,0,1,0,1,0,1,0,0,1,1,1,1,1,1,0,1,0,0,0,1,0,0,0,0,0,1,1,1,0,1,1,0,1,0,0,1,1,0,1,0,0,0,0,1,0,0,0,0,1,1,0,0,1,0,1,0,0,1,1,1,1,1,0,1,0,1,0,1,0,1,0,0,1,0,1,1,0,1,1,1,0,0,1,0,0,1,1,1,0,1,1,1,0,0,1,1,1,0,0,1,1,0,1,0,0,1,0,1,1,1,0,1,1,1,1,0,1,1,0,0,0,1,0,1,1,0,1,1,0,0,0,1,0,1,0,1,0,0,1,0,0,0,1,1,1,0,0,0,0,1,1,0,0,0,0,1,1,0,0,0,1,0,1,0,0,1,0,1,1,1,1,1,1,1,0,0,0,0,1,0,1,0,0,0,1,1,0,0,1,1,1,0,0,1,0,1,1,0,1,1,0,0,0,1,0,0,0,1,0,1,1,1,0,0,1,1,1,0,1,0,0,1,1,0,0,0,1,0,1,1,0,0,0,1,0,0,1,1,0,1,0,0,0,1,0,1,1,0,1,1,1,0,1,1,0,0,1,0,0,1,1,1,0,0,1,0,0,0,0,1,0,1,1,0,1,1,0,1,1,1,1,1,0,1,1,0,0,0,0,0,0,1,0,0,1,1,1,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,1,1,1,0,1,0,0,0,0,1,0,0,1,0,1,1,1,0,1,1,1,1,0,1,0,1,0,0,1,0,1,1,0,0,1,1,0,0,1,1,0,1,0,0,0,1,0,0,1,0,0,1,0,0,1,1,0,1,1,0,0,0,1,1,0,1,0,0,0,0,1,1,0,1,0,1,1,0,0,1,1,1,1,0,1,1,1,1,1,1,1,0,1,0,1,0,0,1,0,1,1,1,1,0,1,0,0,1,1,1,1,0,1,1,0,1,0,0,0,0,0,1,1,0,0,1,0,1,1,0,1,0,0,1,1,1,0,1,0,0,1,0,0,1,0,1,1,0,0,1,1,1,0,0,0,0,1,1,0,0,0,0,0,1,1,1,1,1,1,0,0,1,1,1,0,0,1,0,0,1,1,1,0,1,1,0,0,1,0,0,0,1,0,0,0,0,0,1,1,0,0,1,0,1,1,1,1,1,1,0,1,1,0,1,1,1,0,0,1,0,1,1,0,1,0,0,1,1,1,1,1,1,0,1,1,0,0,0,1,0,0,0,0,1,0,1,1,0,0,0,0,0,0,1,0,1,0,0,1,1,0,1,1,0,0,1,1,0,0,1,1,0,0,0,0,0,1,1,1,1,1,0,0,1,0,0,1,1,0,0,1,0,1,1,0,1,0,1,0,0,0,1,0,1,1,0,1,1,1,0,1,0,1,0,1,1,1,1,0,1,1,0,0,1,1,1,0,1,0,1,1,0,1,0,0,0,0,0,0,1,1,1,1,1,1,0,1,0,1,0,0,0,1,0,0,1,0,0,0,1,1,0,1,0,1,0,1,1,0,0,0,1,0,0,1,1,1,0,1,1,1,1,1,1,1,1,1,0,0,0,1,1,0,1,0,0,0,0,0,0,1,0,1,1,0,1,1,0,1,1,0,1,0,1,1,0,0,0,0,0,0,1,1,1,1,0,1,0,0,0,0,1,1,1,1,0,1,1,1,1,1,1,0,0,0,1,0,1,0,1,0,1,1,0,0,1,0,1,0,0,0,0,1,0,1,1,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,1,0,1,0,1,1,1,1,1,1,1,0,1,1,0,0,1,1,0,1,0,0,1,0,0,0,0,1,1,1,0,0,1,0,1,1,1,1,0,1,0,0,1,0,1,1,0,1,1,0,1,1,1,0,0,0,1,1,0,0,0,1,0,1,1,0,0,0,0,0,1,0,1,1,1,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,1,0,0,0,1,0,1,0,0,1,1,1,0,0,0,0,1,1,1,1,1,1,0,1,0,0,0,1,1,1,1,0,1,0,0,0,1,1,0,0,1,1,1,0,0,1,0,0,1,0,0,1,1,0,1,1,1,1,1,1,1,0,0,0,1,1,0,1,1,0,1,0,0,0,1,0,1,1,0,0,0,1,0,0,0,0,0,1,1,0,1,1,0,0,0,0,1,1,0,0,0,0,0,0,1,0,0,1,1,1,0,0,0,1,1,0,1,1,1,1,1,0,1,0,1,0,1,0,1,1,0,1,0,1,1,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,1,1,0,1,1,0,1,0,0,1,0,0,1,0,1,1,0,1,1,0,1,1,1,0,1,0,1,1,1,0,0,0,1,1,0,1,1,0,0,0,1,0,1,0,1,1,0,1,0,1,0,0,0,1,1,0,0,1,1,1,0,0,1,1,1,1,1,1,1,0,1,1,0,1,0,0,1,0,1,0,1,0,0,0,0,1,0,0,1,1,0,0,0,1,1,0,1,0,0,0,1,0,0,1,0,0,0,0,0,1,0,0,0,1,1,0,1,1,0,0,0,1,0,0,0,0,1,0,0,0,1,0,1,0,1,1,0,0,1,0,0,1,1,1,1,1,1,0,1,1,0,1,0,1,0,0,0,1,0,1,1,0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,0,1,1,1,1,1,0,1,1,1,1,0,0,0,1,0,1,1,0,0,0,1,0,0,0,1,0,0,1,1,0,1,0,0,1,0,1,1,1,0,1,1,1,0,0,1,0,1,1,0,0,0,1,0,1,0,0,0,0,0,1,1,1,0,0,0,1,0,1,0,0,0,1,1,0,0,0,0,1,1,0,1,1,1,1,0,0,0,1,0,1,1,0,0,1,1,1,0,0,0,1,1,1,1,1,0,1,0,0,0,1,1,1,1,0,1,0,1,1,0,0,1,1,1,0,1,1,1,1,0,0,0,0,1,0,1,0,0,1,1,0,1,0,1,1,1,1,0,1,0,0,1,1,0,0,1,0,1,0,0,1,0,1,0,1,0,1,1,0,1,0,1,0,0,1,1,0,1,0,1,1,1,1,1,0,0,1,0,0,0,0,1,1,1,1,1,0,0,1,1,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,1,1,0,0,0,1,0,1,0,1,0,1,0,0,1,0,1,0,1,0,0,1,1,0,0,0,1,1,0,1,1,0,1,0,1,0,0,0,1,1,0,0,1,1,1,0,1,0,0,1,1,1,0,0,0,0,0,0,0,1,0,1,1,0,1,1,0,0,0,0,0,1,1,0,0,1,1,0,1,0,1,1,0,1,0,1,1,0,0,0,1,0,1,0,0,0,0,0,1,0,0,1,1,1,1,0,0,1,0,1,1,0,0,0,1,0,0,0,1,0,1,1,0,0,1,1,0,1,0,1,1,1,0,1,0,0,0,1,0,1,1,1,0,0,1,1,1,1,0,0,1,0,1,0,0,1,0,1,0,0,1,0,1,1,0,1,0,0,1,1,0,0,1,0,0,1,1,0,0,1,0,1,1,0,0,1,1,0,0,0,1,1,0,1,0,1,0,1,1,1,1,0,0,1,0,1,0,1,0,1,0,0,0,0,1,1,1,0,0,0,0,0,1,1,0,0,1,0,1,0,0,0,0,1,1,0,0,1,1,1,1,0,1,0,0,1,0,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,1,0,0,0,0,1,0,0,1,1,0,1,0,0,1,0,1,1,0,0,1,0,1,0,1,0,1,1,1,1,1,0,0,1,0,1,0,1,0,1,0,1,1,0,0,1,1,1,0,0,0,1,1,1,1,1,1,0,1,1,1,0,0,1,0,0,1,0,0,0,1,0,1,1,0,0,1,1,0,0,1,0,0,0,0,0,0,0,1,1,0,1,1,1,0,1,0,1,1,1,1,1,0,1,1,1,1,0,0,0,1,1,1,1,0,0,1,1,0,0,1,1,0,0,0,0,1,1,1,0,1,0,0,1,0,1,0,1,0,0,1,1,1,1,1,0,0,0,1,0,1,0,1,0,1,0,1,1,0,1,1,0,1,0,1,0,0,1,0,0,0,0,0,1,0,0,1,0,0,0,0,1,1,1,0,1,0,0,0,0,1,1,0,0,1,1,1,0,1,0,1,0,1,1,0,0,0,1,1,1,0,1,1,1,1,0,0,1,0,0,1,1,0,0,0,1,1,0,0,0,0,1,0,0,0,1,0,1,0,0,0,1,0,1,1,0,0,1,1,0,1,0,1,1,1,1,0,0,1,1,0,1,1,1,0,0,1,1,1,0,1,1,1,1,1,0,0,0,0,0,0,0,1,0,0,0,0,1,1,0,1,0,0,1,0,1,0,0,1,0,1,1,1,0,0,1,0,1,0,0,0,0,0,0,1,0,1,1,1,1,1,0,0,1,1,0,0,1,0,0,1,0,0,1,0,1,1,0,1,1,0,1,0,1,1,1,0,0,1,1,1,0,1,0,0,0,1,1,0,0,0,0,0,1,0,1,1,0,1,1,0,0,0,1,0,0,1,1,0,1,0,0,0,1,0,1,1,1,0,1,0,0,1,0,1,0,0,1,1,0,1,1,0,0,0,1,0,0,1,0,1,1,0,0,1,0,0,1,0,1,1,0,0,1,1,1,1,0,1,1,0,1,1,1,1,0,0,0,0,1,0,1,0,0,0,1,1,1,1,0,0,0,1,0,1,0,1,1,0,1,1,0,1,1,1,0,0,1,0,1,0,1,0,1,0,1,1,0,0,1,1,1,1,1,0,0,0,0,0,1,1,1,1,1,0,1,0,1,0,1,0,1,1,1,0,0,1,1,1,0,0,1,1,1,0,1,0,1,1,1,0,1,1,1,1,1,1,0,1,0,1,0,1,1,1,1,0,0,1,0,0,0,0,1,0,0,1,0,0,1,0,1,1,0,0,0,1,1,1,0,0,1,1,1,1,1,1,1,0,0,1,1,1,0,0,1,0,1,0,0,1,0,0,1,0,1,0,0,1,0,1,0,1,1,1,1,1,0,1,1,1,1,0,0,1,0,1,0,0,0,1,1,1,1,0,0,0,1,1,1,1,1,0,1,1,0,0,0,0,0,1,1,0,1,0,1,0,1,0,1,1,1,0,0,0,0,0,0,1,1,0,0,1,0,1,1,1,1,0,0,0,0,0,1,0,0,1,0,0,1,0,0,1,1,1,0,1,0,0,0,1,0,0,1,0,0,1,0,1,1,1,0,1,0,1,0,1,1,0,1,0,1,0,1,0,1,1,1,1,0,1,0,0,0,1,0,0,1,1,0,1,0,0,1,1,0,1,0,1,1,0,0,0,0,1,1,0,0,0,0,0,1,0,0,1,0,0,1,1,1,1,0,0,0,1,1,1,1,0,0,0,0,1,0,1,0,1,1,0,0,0,0,1,0,1,1,1,1,0,0,0,1,0,1,1,0,0,0,0,0,0,1,1,0,0,1,0,1,1,1,1,1,0,1,0,0,0,0,1,1,1,1,0,0,0,1,0,1,1,1,1,0,1,1,1,0,1,1,1,1,0,1,1,1,1,1,1,0,0,0,1,0,1,1,1,0,1,1,1,1,0,1,0,1,0,0,0,1,0,1,0,1,0,0,1,1,1,1,1,0,1,0,1,0,0,1,0,1,0,0,1,0,1,0,1,1,0,1,0,1,0,0,1,0,1,1,0,0,1,1,1,0,0,1,0,0,1,1,1,0,0,0,1,1,1,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,1,1,1,0,0,1,1,1,0,1,0,0,1,0,0,1,1,0,0,1,0,1,1,1,1,1,1,1,0,1,1,0,1,1,0,1,1,1,1,1,1,1,1,1,1,0,0,1,1,0,0,0,1,1,1,1,0,0,1,0,1,1,1,1,1,1,0,0,1,1,1,0,0,1,1,0,0,1,1,1,0,1,0,0,1,1,1,1,0,1,1,1,0,1,0,1,0,1,0,1,1,0,0,1,1,0,1,1,1,1,0,1,0,0,0,0,0,0,1,0,1,1,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,1,0,0,0,0,1,0,1,0,0,1,1,1,0,0,0,0,1,0,0,0,1,1,0,1,0,0,0,0,1,0,0,1,1,1,1,0,0,1,0,0,0,0,1,0,0,1,0,0,1,0,1,1,0,1,0,0,0,0,0,0,1,1,1,0,0,0,1,0,1,1,0,1,1,1,1,1,1,0,1,1,1,0,0,1,0,1,0,1,0,0,0,0,0,0,1,1,0,1,0,0,1,0,0,1,0,0,1,0,1,1,0,1,0,1,0,0,0,0,0,1,1,0,1,0,1,0,0,0,1,0,1,1,1,1,0,0,1,1,1,1,0,0,0,0,1,1,1,1,1,0,0,0,1,1,0,0,1,1,1,1,0,0,0,1,0,1,0,1,0,0,0,1,0,1,1,0,1,1,1,1,0,0,0,0,1,0,1,0,0,1,1,1,0,1,1,1,1,0,1,1,0,0,0,1,0,1,1,0,1,0,1,0,0,1,0,0,0,1,0,1,0,1,0,1,1,0,0,0,0,0,0,0,1,1,0,1,1,0,1,1,1,0,0,1,0,1,1,1,0,0,0,1,0,0,0,1,1,1,1,0,0,0,1,1,0,0,1,1,1,0,0,1,0,1,0,0,0,0,1,1,1,0,0,1,1,0,0,1,0,0,0,1,1,1,0,0,0,0,1,0,1,0,0,1,0,0,1,1,0,0,1,0,1,0,1,1,1,1,0,0,1,0,0,1,1,1,0,1,1,1,0,0,0,1,0,0,1,0,0,1,1,0,1,1,1,1,0,1,0,0,0,1,1,0,1,1,1,0,0,0,1,1,0,0,0,1,0,0,0,1,0,1,1,1,1,0,0,0,0,1,1,1,0,0,1,1,0,0,0,1,0,1,1,1,0,1,1,1,0,1,0,1,1,0,1,1,1,1,0,0,0,1,1,0,0,1,1,1,1,1,0,1,0,0,0,1,1,1,1,1,0,1,1,1,1,0,0,1,1,0,0,0,0,1,0,1,0,1,1,0,0,0,0,0,1,0,0,1,0,0,1,1,0,1,1,0,1,1,0,0,1,1,0,0,1,0,0,0,1,1,0,0,0,1,0,0,0,1,1,1,1,1,0,0,0,0,1,0,0,1,1,0,0,0,0,1,1,0,0,1,0,0,0,0,0,1,0,0,1,1,0,1,0,1,0,1,1,1,0,1,0,1,0,1,0,0,1,1,0,0,1,1,1,1,0,1,1,0,1,1,0,1,0,1,0,0,0,0,1,0,0,0,1,0,1,1,0,0,0,0,1,0,1,1,0,1,0,1,1,1,0,1,1,0,1,0,1,0,1,1,0,1,1,0,0,0,0,1,1,0,0,1,1,0,0,1,0,1,1,1,0,1,1,0,0,0,1,0,0,0,1,0,1,1,0,1,1,1,1,0,1,0,1,1,0,0,1,1,1,1,0,1,0,0,0,1,1,0,1,0,0,1,0,1,1,0,0,1,1,0,0,0,0,1,1,0,0,0,1,0,0,1,0,1,0,0,1,1,0,0,1,1,1,1,0,0,0,1,1,1,1,0,1,0,0,1,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,1,1,1,0,0,0,1,0,1,1,1,1,1,1,0,1,1,0,1,1,0,0,1,1,1,1,1,0,1,0,0,0,1,0,0,1,1,1,0,1,1,0,1,0,1,1,1,0,1,1,1,1,0,1,1,0,1,1,1,0,1,0,0,0,1,1,1,1,1,1,1,0,0,1,1,1,1,0,1,0,0,1,1,0,1,1,1,0,1,0,0,0,0,1,0,0,1,0,1,0,1,1,0,1,0,0,1,0,1,0,1,1,1,0,1,1,1,0,0,1,0,0,1,0,0,1,1,1,0,1,1,0,0,0,1,0,0,1,1,0,0,0,0,0,0,1,1,1,0,1,0,1,0,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,0,1,0,0,1,0,0,1,1,0,0,1,0,1,1,1,0,1,1,1,1,1,0,0,1,1,1,1,0,0,1,0,1,0,0,0,1,1,1,0,0,1,1,1,0,0,0,0,0,1,1,1,1,1,1,1,0,0,1,1,0,1,0,1,0,1,0,1,1,1,1,1,1,0,1,0,0,1,0,1,1,0,1,1,0,0,1,1,0,0,0,1,0,1,0,0,1,0,0,1,0,1,1,0,0,1,0,0,1,0,1,0,0,0,0,1,0,0,0,1,1,0,1,0,1,1,1,1,1,1,0,0,0,0,1,0,1,0,0,0,0,1,0,1,0,0,0,1,0,0,1,1,0,1,1,0,0,0,1,0,1,1,0,1,1,0,0,1,1,1,1,1,0,0,0,0,1,0,1,0,1,1,0,1,0,1,0,0,0,0,0,0,1,1,1,0,1,0,1,1,1,0,0,1,0,1,1,1,1,0,0,1,1,1,1,0,1,0,0,1,1,0,1,0,1,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,1,0,0,1,1,0,1,0,0,1,0,0,0,1,1,0,1,1,1,1,0,1,1,0,1,0,1,1,1,1,1,0,0,0,1,0,0,0,0,0,1,0,1,1,1,0,0,0,0,1,0,1,1,1,0,1,1,0,1,0,1,1,0,1,1,1,1,0,1,1,1,0,0,1,1,0,0,1,1,0,1,1,0,0,1,1,0,1,0,1,0,1,0,0,0,1,1,0,0,0,1,0,1,0,1,0,0,0,1,0,0,0,1,0,1,0,1,0,1,0,1,1,1,0,0,0,1,0,1,1,1,1,0,0,0,0,1,1,0,1,1,1,1,0,1,0,1,0,0,0,0,0,0,0,1,0,0,0,1,1,1,0,1,1,0,1,0,0,1,1,0,0,0,0,1,0,0,1,0,1,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,1,0,1,0,1,1,1,1,0,1,1,1,0,1,0,1,1,1,1,1,0,0,1,1,1,1,1,0,0,0,1,0,0,1,0,0,0,1,1,1,1,0,0,1,0,0,0,1,0,0,1,1,0,1,0,1,1,0,0,0,0,0,0,0,0,1,1,0,1,0,1,1,1,1,0,1,1,0,1,0,1,0,0,1,1,0,1,0,0,1,1,0,0,0,0,1,1,1,1,0,1,0,0,1,1,0,1,0,1,1,1,1,1,1,1,0,0,0,1,0,0,1,1,0,1,1,1,1,1,1,0,0,0,0,0,1,0,1,0,0,0,1,1,1,0,1,1,0,0,1,0,0,1,0,0,0,1,1,1,0,1,1,0,0,0,1,0,0,0,0,1,0,1,1,0,0,0,1,0,0,1,1,0,1,0,0,0,0,0,0,0,1,0,1,0,1,0,1,1,1,1,0,0,1,1,0,0,0,0,1,0,0,1,1,1,1,0,0,0,0,1,0,1,1,0,1,1,1,1,0,1,0,0,1,1,1,0,0,0,1,1,1,0,0,1,0,0,0,1,1,1,0,0,0,1,0,0,1,1,1,1,1,0,1,1,0,0,0,1,1,0,0,1,1,0,1,1,0,0,1,0,1,1,1,0,1,1,0,1,0,1,1,0,1,1,0,0,1,1,1,1,0,0,0,0,1,0,0,1,0,1,0,1,0,0,1,0,0,1,0,1,0,1,0,1,0,1,1,1,0,1,1,0,0,1,1,1,1,0,1,1,1,0,1,0,1,1,0,1,1,1,1,0,1,1,1,1,0,0,0,0,1,0,0,0,1,0,0,1,0,0,0,1,1,1,0,1,1,1,1,0,0,0,1,0,0,1,1,0,0,0,0,1,0,1,0,1,1,1,1,0,0,0,0,1,0,0,1,0,0,0,1,0,0,0,0,0,0,1,1,0,1,0,1,1,1,1,0,0,1,0,0,0,0,1,0,0,0,1,0,1,0,0,0,0,1,0,1,1,1,1,0,0,1,1,1,0,1,0,0,0,0,1,1,0,1,0,0,0,0,0,0,1,0,0,1,0,0,1,1,1,1,0,0,1,0,1,1,1,0,0,1,1,0,0,0,1,1,1,0,0,1,1,1,0,1,1,0,0,1,1,0,1,1,0,0,1,1,0,0,1,1,1,0,0,0,1,1,1,0,0,1,1,1,1,0,0,1,1,1,1,1,0,0,1,0,1,1,0,1,1,0,0,0,0,0,1,0,1,1,0,1,0,0,1,1,0,0,0,0,0,1,0,1,1,0,1,0,0,1,1,0,1,1,0,1,0,0,0,0,0,0,1,1,1,1,0,1,1,1,1,1,1,1,1,0,0,0,1,0,0,0,1,0,0,0,0,0,1,1,0,1,0,1,1,0,0,0,0,1,0,1,1,1,1,0,0,1,1,1,1,0,1,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,1,0,0,1,0,0,0,1,0,0,1,1,0,0,1,1,1,1,1,0,0,1,0,1,1,0,1,1,0,0,1,1,0,1,1,0,0,1,1,0,1,1,0,0,0,1,0,1,0,1,0,0,0,1,0,0,1,1,0,1,0,0,1,0,1,0,0,0,0,0,0,1,0,1,1,0,1,1,0,0,0,0,1,1,0,1,0,1,0,0,1,0,1,1,1,0,1,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,1,1,1,1,0,1,0,1,0,0,1,0,0,1,0,1,0,1,1,1,0,0,1,1,0,0,0,0,0,0,1,1,1,0,1,1,0,1,0,0,0,0,1,1,0,1,1,1,0,0,0,1,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,1,0,1,0,0,0,0,0,1,1,1,0,0,0,1,1,0,1,1,0,1,0,1,1,0,0,0,0,1,1,1,1,1,0,0,0,1,0,0,1,0,0,0,1,0,0,0,0,1,1,1,0,0,1,0,0,1,1,1,1,0,0,1,0,0,0,0,0,1,0,0,1,0,1,1,0,0,0,0,1,1,1,1,0,1,0,0,1,0,0,0,0,0,1,0,1,1,1,1,0,1,0,1,0,0,0,0,0,0,0,1,1,0,0,1,1,1,0,0,0,1,1,1,0,0,1,0,0,0,0,0,0,1,0,1,1,1,1,1,0,1,0,0,0,0,0,1,1,1,0,1,0,0,1,0,1,1,0,1,1,1,0,0,0,1,1,1,0,1,0,0,0,0,1,0,1,0,1,1,0,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,0,0,0,1,1,1,1,0,0,1,0,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,0,0,1,1,0,0,0,1,0,0,1,0,1,0,0,1,0,0,0,1,1,0,1,1,1,0,1,1,1,0,1,0,0,1,1,0,0,1,0,0,1,0,1,1,1,1,1,1,0,0,0,1,1,1,1,0,0,0,1,0,0,1,1,1,0,1,1,1,0,1,1,0,1,0,0,1,1,1,1,0,1,1,1,0,0,1,0,0,0,0,1,1,1,1,1,0,1,0,0,0,0,1,0,0,1,1,0,1,0,0,0,1,1,0,0,1,1,0,1,1,0,0,0,1,1,0,1,0,0,0,1,0,1,1,0,1,0,1,0,1,0,1,0,0,1,0,0,0,0,1,0,0,1,0,0,1,0,0,0,1,0,0,1,1,1,0,1,1,1,1,1,0,0,1,0,1,1,0,1,1,1,0,1,1,1,1,0,1,0,1,0,0,0,1,1,0,1,1,0,0,0,0,1,1,1,0,0,0,1,0,0,1,1,1,0,0,0,0,0,0,1,0,1,0,0,1,0,1,1,1,1,1,0,0,0,1,1,0,0,1,1,0,1,1,1,1,1,1,1,1,0,0,0,0,0,1,0,1,1,0,1,1,0,1,1,1,1,1,0,0,0,0,1,1,0,1,1,1,0,0,0,0,0,1,0,1,0,1,1,1,0,1,1,0,1,0,1,1,1,0,1,1,0,0,1,1,0,1,1,0,1,1,1,0,0,0,1,0,1,1,0,1,1,0,1,1,0,1,1,1,0,1,1,1,0,1,0,1,0,0,0,0,1,1,0,0,0,0,1,0,1,0,1,0,1,1,1,0,1,0,0,0,0,0,0,0,1,1,0,0,1,1,1,1,1,0,1,0,1,1,1,1,1,0,0,1,0,1,0,1,1,1,0,0,0,1,0,1,1,1,0,0,0,0,0,1,1,1,0,0,1,0,0,1,0,1,0,1,1,0,0,1,0,1,1,0,1,1,0,1,1,0,0,1,0,1,1,1,1,1,0,1,1,1,0,1,0,0,0,1,1,1,0,1,0,1,0,1,1,0,0,0,0,0,0,0,0,1,1,0,0,0,1,0,1,0,0,1,1,0,0,0,0,1,0,1,0,1,0,1,0,1,0,0,0,0,0,1,0,1,1,0,1,0,0,1,1,0,0,1,0,1,0,1,0,0,0,1,1,1,1,0,1,1,0,0,1,1,0,0,1,1,1,0,0,1,0,0,1,0,0,1,0,1,1,0,0,0,0,0,1,0,0,0,1,0,0,1,1,1,0,1,1,1,1,0,1,0,1,0,1,1,0,1,1,1,0,0,0,1,0,0,1,1,1,0,0,0,0,1,1,0,1,0,0,0,0,0,1,0,1,0,1,1,0,1,1,0,1,1,1,0,0,0,0,1,0,1,0,0,1,1,0,0,1,1,1,1,1,1,0,0,1,0,0,0,0,0,1,0,0,1,0,0,1,1,0,1,0,1,0,1,0,1,0,0,0,1,1,0,1,0,1,0,1,0,0,0,1,0,0,1,0,1,0,1,1,1,1,0,0,1,1,1,1,1,0,1,1,0,0,1,1,0,1,0,1,1,0,0,1,0,0,0,0,0,0,0,1,0,1,1,0,1,1,0,0,0,1,1,1,1,1,1,0,1,0,1,1,0,0,1,0,0,0,1,0,0,1,0,0,1,1,0,0,1,0,1,0,1,1,1,0,1,0,1,1,1,0,1,1,1,0,1,1,1,0,1,0,1,0,1,0,1,0,0,0,1,1,0,1,0,0,1,1,0,1,1,0,0,0,1,1,0,0,0,1,0,0,1,1,0,1,1,1,0,0,1,0,1,1,1,0,1,1,1,1,0,1,1,1,1,1,0,0,0,0,1,0,0,1,1,1,0,0,0,1,0,0,1,0,1,0,0,0,1,0,1,0,0,1,0,1,1,1,0,0,0,0,1,1,0,0,1,1,1,0,1,1,0,0,1,1,0,0,1,1,1,1,1,0,1,1,1,1,0,0,1,0,0,1,0,0,1,1,1,0,0,1,1,0,0,0,0,1,0,0,0,1,1,0,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,0,1,0,1,0,0,0,1,1,0,0,0,1,0,1,1,1,0,0,0,1,1,1,0,1,1,1,1,1,0,0,1,0,1,1,0,0,1,0,0,0,1,1,0,1,1,0,0,0,0,0,0,1,1,0,1,0,0,0,1,1,1,1,0,0,1,0,0,1,1,1,0,0,0,1,0,0,0,0,1,0,1,1,0,1,1,1,1,0,1,1,1,1,0,0,0,0,0,0,0,1,0,1,0,1,0,0,0,1,0,1,0,1,0,0,1,0,1,0,1,0,0,0,0,1,1,0,1,0,1,1,1,1,0,0,1,1,1,0,0,1,1,0,1,0,0,1,0,0,1,0,0,0,1,1,0,1,0,1,1,0,0,1,0,1,1,0,0,0,1,0,0,0,1,1,1,0,1,0,1,1,0,1,0,0,1,0,1,1,0,1,1,0,1,1,0,1,0,0,1,1,1,1,1,0,1,0,1,1,0,1,0,0,1,1,1,0,0,1,0,0,1,1,0,0,1,0,0,1,0,1,0,1,0,1,1,0,0,1,1,1,0,0,0,0,0,1,1,0,1,0,0,0,1,0,1,1,1,0,0,1,1,1,0,0,0,0,1,1,0,0,1,0,1,1,1,1,1,0,1,0,1,0,1,0,1,0,0,1,1,1,1,1,0,1,0,1,0,1,1,1,1,1,1,1,1,1,0,0,1,0,0,1,0,1,1,0,0,0,1,0,1,0,1,0,0,0,0]\n```\n\nBut if I change it to the following, the solution got accepted...\n```\nvar prefixesDivBy5 = function(A) {\n let res = [];\n let remainder = 0;\n for(let i=0; i<A.length; i++){\n remainder = (remainder * 2 + A[i]) % 5;\n res.push(!remainder)\n }\n return res;\n};\n```\n\nCan anyone help me understand it?\n\nThanks in advance!
| 2
| 0
|
[]
| 2
|
binary-prefix-divisible-by-5
|
Python straightforward bit manipulation
|
python-straightforward-bit-manipulation-0jke7
|
On each iteration, num bits shift 1 index to left while least-significant bit is A[i].\n\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bo
|
cenkay
|
NORMAL
|
2019-03-31T04:27:57.284956+00:00
|
2019-03-31T04:27:57.284989+00:00
| 188
| false
|
* On each iteration, num bits shift 1 index to left while least-significant bit is A[i].\n```\nclass Solution:\n def prefixesDivBy5(self, A: List[int]) -> List[bool]:\n num = 0\n for i in range(len(A)):\n num = (num << 1) + A[i]\n A[i] = num % 5 == 0\n return A\n```\nTime complexity: O(N)\nSpace complextiy: O(1)
| 2
| 2
|
[]
| 0
|
binary-prefix-divisible-by-5
|
Simple C++ Solution || Beats 100%
|
simple-c-solution-beats-100-by-devanshv1-ynbn
|
IntuitionThe problem requires checking whether the binary number formed by each prefix of the given array (nums) is divisible by 5. Instead of constructing larg
|
Devanshv123
|
NORMAL
|
2025-03-01T14:26:10.961546+00:00
|
2025-03-01T14:26:10.961546+00:00
| 43
| false
|
# Intuition
The problem requires checking whether the binary number formed by each prefix of the given array (nums) is divisible by 5. Instead of constructing large numbers explicitly (which could lead to overflow), we can track only the remainder when divided by 5.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<bool> prefixesDivBy5(vector<int>& nums) {
vector<bool> v;
long long ans = 0;
for(int ele:nums){
ans = (ans*2+ele)%5;
v.push_back(ans==0);
}
return v;
}
};
```
| 1
| 0
|
['Array', 'Bit Manipulation', 'C++']
| 0
|
binary-prefix-divisible-by-5
|
Simple C++ Solution || Beats 100%
|
simple-c-solution-beats-100-by-devanshv1-xt6a
|
IntuitionThe problem requires checking whether the binary number formed by each prefix of the given array (nums) is divisible by 5. Instead of constructing larg
|
Devanshv123
|
NORMAL
|
2025-03-01T14:26:07.802732+00:00
|
2025-03-01T14:26:07.802732+00:00
| 30
| false
|
# Intuition
The problem requires checking whether the binary number formed by each prefix of the given array (nums) is divisible by 5. Instead of constructing large numbers explicitly (which could lead to overflow), we can track only the remainder when divided by 5.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<bool> prefixesDivBy5(vector<int>& nums) {
vector<bool> v;
long long ans = 0;
for(int ele:nums){
ans = (ans*2+ele)%5;
v.push_back(ans==0);
}
return v;
}
};
```
| 1
| 0
|
['Array', 'Bit Manipulation', 'C++']
| 0
|
binary-prefix-divisible-by-5
|
Java Solution
|
java-solution-by-hksuthar12-t6fv
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Hksuthar12
|
NORMAL
|
2025-02-03T12:14:14.144809+00:00
|
2025-02-03T12:14:14.144809+00:00
| 79
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public List<Boolean> prefixesDivBy5(int[] nums) {
List<Boolean> isDivisible = new ArrayList<>();
int num = 0;
for(int i=0; i<nums.length; i++) {
num = (num * 2 + nums[i])%5;
isDivisible.add(num==0);
}
return isDivisible;
}
}
```
| 1
| 0
|
['Java']
| 0
|
binary-prefix-divisible-by-5
|
EASY SOLUTION IN JAVA BEATING 98.16% IN 3ms
|
easy-solution-in-java-beating-9816-in-3m-66ac
|
IntuitionThe problem asks us to determine whether the number represented by the binary subarray nums[0..i] (where i ranges from 0 to n-1) is divisible by 5. The
|
arshi_bansal
|
NORMAL
|
2025-02-03T06:47:04.671421+00:00
|
2025-02-03T06:47:04.671421+00:00
| 68
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem asks us to determine whether the number represented by the binary subarray nums[0..i] (where i ranges from 0 to n-1) is divisible by 5. The binary number formed from nums[0..i] is built progressively as we move through the array.
# Approach
<!-- Describe your approach to solving the problem. -->
1. **Initialization:** Start with num = 0. This will represent the binary number at the current index modulo 5.
2. **Progressively Build the Binary Number:** For each bit in nums:
- Shift the previous number left (multiply by 2).
- Add the current bit.
- Take modulo 5 to keep the result within a manageable range.
3. **Check Divisibility:** For each new num, check if it is divisible by 5. If it is, append true to the result list; otherwise, append false.
4. **Return Result:** Once the entire array has been processed, return the list of boolean values.
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public List<Boolean> prefixesDivBy5(int[] nums) {
List<Boolean> result = new ArrayList<>();
int num = 0;
for (int i = 0; i < nums.length; i++) {
num = (num * 2 + nums[i]) % 5; // Build the number modulo 5
result.add(num == 0); // Check if divisible by 5
}
return result;
}
}
```
| 1
| 0
|
['Array', 'Bit Manipulation', 'Java']
| 0
|
binary-prefix-divisible-by-5
|
O(n)
|
on-by-bhavanabharatisingh-w2fh
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTake each number from the array nums and convert into decimal and check its divisiabli
|
bhavanabharatisingh
|
NORMAL
|
2024-10-01T04:15:54.151698+00:00
|
2024-10-01T04:15:54.151730+00:00
| 33
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTake each number from the array nums and convert into decimal and check its divisiablity with 5\n \n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\n- O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n str_arr = []\n res = []\n for i in range(0,len(nums)):\n str_arr.append(str(nums[i]))\n num = int(\'\'.join(str_arr), 2)\n if num % 5 == 0:\n res.append(True)\n else:\n res.append(False)\n return res\n \n\n \n```
| 1
| 0
|
['Python3']
| 0
|
binary-prefix-divisible-by-5
|
easy-peasy solution | O(n) time complexity
|
easy-peasy-solution-on-time-complexity-b-vgie
|
Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
ilovevectors
|
NORMAL
|
2024-09-09T18:48:01.472457+00:00
|
2024-09-09T18:48:01.472495+00:00
| 274
| false
|
# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n vector<bool> ret;\n int x = 0 ;\n for(int i=0;i<nums.size();i++)\n {\n x = (x*2+nums[i])%5;\n ret.push_back(x==0);\n }\n return ret;\n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
binary-prefix-divisible-by-5
|
EASY SOLUTION USING ONLY ONE WHILE LOOP IN C++
|
easy-solution-using-only-one-while-loop-7gi5b
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vasu049
|
NORMAL
|
2024-08-23T16:26:56.841103+00:00
|
2024-08-23T16:26:56.841133+00:00
| 20
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n int sum=0, i=0;\n vector<bool> ans(nums.size());\n\n while(i<nums.size())\n {\n sum=(sum*2 + nums[i]) % 5;\n ans[i]=(sum==0 ? true : false);\n \n i++;\n }\n\n return (ans);\n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
binary-prefix-divisible-by-5
|
Python Easy Approach
|
python-easy-approach-by-_ss_official_006-sgon
|
Code\n\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n Integer=[]\n output=[]\n Final=[]\n for i in
|
_ss_official_006
|
NORMAL
|
2024-08-10T08:17:56.846253+00:00
|
2024-08-10T08:17:56.846278+00:00
| 168
| false
|
# Code\n```\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n Integer=[]\n output=[]\n Final=[]\n for i in nums:\n Integer.append(str(i))\n for i in range(len(Integer)):\n output.append(int("".join(Integer[:i+1]),2))\n for i in output:\n if i%5==0:\n Final.append(True)\n else:Final.append(False)\n return Final\n```
| 1
| 0
|
['Array', 'Bit Manipulation', 'Python3']
| 1
|
binary-prefix-divisible-by-5
|
Simple java code for beginners
|
simple-java-code-for-beginners-by-arobh-o0yc
|
\n# Complexity\n- \n\n# Code\n\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n ArrayList<Boolean> ans = new ArrayList<>();\n
|
Arobh
|
NORMAL
|
2024-01-07T03:36:22.099830+00:00
|
2024-01-07T03:36:22.099852+00:00
| 35
| false
|
\n# Complexity\n- \n\n# Code\n```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n ArrayList<Boolean> ans = new ArrayList<>();\n int num = 0;\n for(int i = 0 ; i<nums.length ; i++){\n num = (num*2 + nums[i])%5;\n ans.add(num==0);\n }\n return ans;\n }\n}\n```
| 1
| 0
|
['Java']
| 0
|
binary-prefix-divisible-by-5
|
Simple C# solution
|
simple-c-solution-by-dmitriy-maksimov-aled
|
Complexity\n- Time complexity: O(n)\n- Space complexity: O(n)\n\n# Code\n\npublic class Solution\n{\n public IList<bool> PrefixesDivBy5(int[] nums)\n {\n
|
dmitriy-maksimov
|
NORMAL
|
2023-09-06T01:59:33.491451+00:00
|
2023-09-06T01:59:33.491478+00:00
| 28
| false
|
# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\npublic class Solution\n{\n public IList<bool> PrefixesDivBy5(int[] nums)\n {\n var result = new List<bool>();\n var num = 0;\n foreach (var n in nums)\n {\n num = (num * 2 + n) % 5;\n result.Add(num == 0);\n }\n\n return result;\n }\n}\n```
| 1
| 0
|
['C#']
| 0
|
binary-prefix-divisible-by-5
|
Simple Javascript solution
|
simple-javascript-solution-by-kamalbhera-zpfh
|
\n# Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n
|
kamalbhera
|
NORMAL
|
2023-05-16T01:37:30.366102+00:00
|
2023-05-16T01:37:30.366151+00:00
| 161
| false
|
\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[]} nums\n * @return {boolean[]}\n */\nvar prefixesDivBy5 = function(nums) {\n let result = [];\n let binary = 0;\n for(let num of nums){\n binary = (binary % 5) * 2 + num;\n let checkBinary = ( binary % 5 == 0);\n result.push(checkBinary);\n }\n return result\n};\n```
| 1
| 0
|
['JavaScript']
| 0
|
binary-prefix-divisible-by-5
|
Python3 Solution || Beats 99.30% || Prefix Approach
|
python3-solution-beats-9930-prefix-appro-rgmw
|
python\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n currBinary, result = 0, []\n for bit in nums:\n
|
Heber_Alturria
|
NORMAL
|
2023-02-24T02:41:39.625254+00:00
|
2023-02-24T02:42:31.996141+00:00
| 656
| false
|
```python\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n currBinary, result = 0, []\n for bit in nums:\n currBinary = (currBinary * 2 + bit) % 5 \n result.append(currBinary == 0)\n return result\n```
| 1
| 0
|
['Array', 'Prefix Sum', 'Python']
| 0
|
binary-prefix-divisible-by-5
|
Java and Python Solution
|
java-and-python-solution-by-a_shekhar-ymag
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
a_shekhar
|
NORMAL
|
2022-10-11T16:46:41.474064+00:00
|
2023-10-03T16:27:46.843363+00:00
| 482
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n int val = 0;\n List<Boolean> list = new ArrayList<>();\n for(int num : nums){\n // % 5 to prevent integer overflow, otherwsie will need to use BigInteger\n val = ((val * 2) + num) % 5;\n list.add(val == 0);\n }\n return list;\n }\n}\n```\n\n# Python\n\n```\ndef prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n result = list()\n res = str(nums[0])\n result.append(True) if int(res) == 0 else result.append(False)\n for j in range(1, len(nums)):\n res += str(nums[j])\n if int(res, 2) % 5 == 0:\n result.append(True)\n else:\n result.append(False)\n return result\n```
| 1
| 0
|
['Python', 'Java', 'Python3']
| 1
|
binary-prefix-divisible-by-5
|
[C++] Faster than 98%
|
c-faster-than-98-by-nil24-ok90
|
\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n int n=0;\n vector<bool> res;\n\t\t\n for(int i=0;i<nums
|
Nil24
|
NORMAL
|
2022-08-17T08:55:54.330319+00:00
|
2022-08-17T08:55:54.330367+00:00
| 347
| false
|
```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n int n=0;\n vector<bool> res;\n\t\t\n for(int i=0;i<nums.size();i++){\n n=(n<<1)+nums[i];\n res.push_back(n%5==0);\n n=n%5;\n }\n\t\t\n return res;\n }\n};\n```
| 1
| 0
|
['C']
| 1
|
binary-prefix-divisible-by-5
|
java solution | 100% efficient
|
java-solution-100-efficient-by-aayushkum-tno9
|
\nclass Solution {\n func prefixesDivBy5(_ nums: [Int]) -> [Bool] {\n var divisibleByFive = [Bool]()\n var n = 0\n for bit in nums {\n
|
aayushkumar20
|
NORMAL
|
2022-07-19T18:59:55.692192+00:00
|
2022-07-19T18:59:55.692238+00:00
| 147
| false
|
```\nclass Solution {\n func prefixesDivBy5(_ nums: [Int]) -> [Bool] {\n var divisibleByFive = [Bool]()\n var n = 0\n for bit in nums {\n n = (n * 2 + bit) % 10\n divisibleByFive.append(n == 5 || n == 0)\n }\n return divisibleByFive\n }\n}\n```
| 1
| 0
|
['Swift']
| 1
|
binary-prefix-divisible-by-5
|
C++ simple solution
|
c-simple-solution-by-osmanay-pedp
|
\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n \n int n = nums.size();\n vector<bool> res(n);\n
|
osmanay
|
NORMAL
|
2022-07-02T23:30:06.654306+00:00
|
2022-07-02T23:30:06.654344+00:00
| 92
| false
|
```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n \n int n = nums.size();\n vector<bool> res(n);\n \n int num = 0;\n \n for(int i=0; i<n; i++)\n {\n num = num*2 + nums[i];\n num %= 5;\n res[i] = num == 0;\n \n }\n \n return res; \n }\n};\n```
| 1
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
Java | 3 liner | Explained
|
java-3-liner-explained-by-prashant404-c81j
|
Idea: Iterate over the array, form the new number and check for divisibility by 5. Mod by 5 at every iteration to avoid overflows\n>T/S: O(n)/O(1), where n = si
|
prashant404
|
NORMAL
|
2022-03-07T02:08:31.188053+00:00
|
2022-03-07T02:09:41.834256+00:00
| 194
| false
|
**Idea:** Iterate over the array, form the new number and check for divisibility by 5. Mod by 5 at every iteration to avoid overflows\n>**T/S:** O(n)/O(1), where n = size(nums). Ignoring space for output\n```\npublic List<Boolean> prefixesDivBy5(int[] nums) {\n\tvar answer = new ArrayList<Boolean>(nums.length);\n\tfor (int i = 0, n = 0; i < nums.length; i++) \n\t\tanswer.add((n = (n << 1 | nums[i]) % 5) == 0);\n\treturn answer;\n}\n```\n***Please upvote if this helps***
| 1
| 0
|
['Java']
| 0
|
binary-prefix-divisible-by-5
|
[ Problem No. 1018 ] Easy solution for beginners | C++
|
problem-no-1018-easy-solution-for-beginn-bikh
|
\nclass Solution {\npublic:\n\tvector<bool> prefixesDivBy5(vector<int>& nums) {\n\t\tvector<bool> res;\n\t\tint t = 0;\n\t\tfor(int i = 0; i < nums.size(); i++)
|
rakibhasan1030
|
NORMAL
|
2022-03-01T18:35:13.335117+00:00
|
2022-03-01T18:35:13.335158+00:00
| 141
| false
|
```\nclass Solution {\npublic:\n\tvector<bool> prefixesDivBy5(vector<int>& nums) {\n\t\tvector<bool> res;\n\t\tint t = 0;\n\t\tfor(int i = 0; i < nums.size(); i++){\n\t\t\tt = (t * 2 + nums[i]) % 5;\n\t\t\tres.push_back(t == 0);\n\t\t}\n\t\treturn res;\n\t}\n};\n```\n***Please upvote if it was helpful for you, thank you!***
| 1
| 0
|
['Array', 'C', 'C++']
| 0
|
binary-prefix-divisible-by-5
|
Simple Python Solution
|
simple-python-solution-by-idebbarh-x4io
|
\n def prefixesDivBy5(self, nums):\n output = []\n nums = "".join([str(i) for i in nums])\n for i in range(0,len(nums)) :\n i
|
idebbarh
|
NORMAL
|
2022-02-28T11:27:13.890599+00:00
|
2022-02-28T11:27:13.890639+00:00
| 48
| false
|
```\n def prefixesDivBy5(self, nums):\n output = []\n nums = "".join([str(i) for i in nums])\n for i in range(0,len(nums)) :\n if int(nums[0:i+1], 2)%5==0 :\n output.append(True)\n else :\n output.append(False)\n return output\n```
| 1
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
(C++) 1018. Binary Prefix Divisible By 5
|
c-1018-binary-prefix-divisible-by-5-by-q-uh13
|
\n\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n vector<bool> ans; \n int prefix = 0; \n for (auto& x
|
qeetcode
|
NORMAL
|
2022-02-02T21:17:45.986963+00:00
|
2022-02-02T21:17:45.986995+00:00
| 166
| false
|
\n```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n vector<bool> ans; \n int prefix = 0; \n for (auto& x : nums) {\n prefix = (2*prefix + x) % 5; \n ans.push_back(!prefix); \n }\n return ans; \n }\n};\n```
| 1
| 0
|
['C']
| 0
|
binary-prefix-divisible-by-5
|
Golang easy solution 8ms 100%
|
golang-easy-solution-8ms-100-by-fshiori-1rct
|
\nfunc prefixesDivBy5(nums []int) []bool {\n ans := make([]bool, len(nums))\n var t int\n for i, num := range nums {\n t = t << 1 + num\n
|
fshiori
|
NORMAL
|
2021-12-26T13:15:40.404183+00:00
|
2021-12-26T13:15:40.404223+00:00
| 136
| false
|
```\nfunc prefixesDivBy5(nums []int) []bool {\n ans := make([]bool, len(nums))\n var t int\n for i, num := range nums {\n t = t << 1 + num\n if t % 5 == 0 {\n ans[i] = true\n t = 0\n } else {\n t %= 5\n }\n }\n return ans\n}\n```
| 1
| 0
|
['Go']
| 0
|
binary-prefix-divisible-by-5
|
Binary Prefix Divisible By 5: Combining a bit shift with modulo
|
binary-prefix-divisible-by-5-combining-a-7mzn
|
This solution has a space complexity of O(n) because the length of the list returned is n. But if we use a generator instead, this becomes O(1). We iterate thro
|
jodawill
|
NORMAL
|
2021-12-07T20:40:38.882876+00:00
|
2021-12-07T20:40:38.882908+00:00
| 65
| false
|
This solution has a space complexity of `O(n`) because the length of the list returned is `n`. But if we use a generator instead, this becomes `O(1)`. We iterate through each bit in the list, shifting as we go, and adding true or false to the results, based on whether `n % 5 == 0`. So the time complexity is also `O(n)`.\n\n```\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n results = []\n n = 0\n for bit in nums:\n n <<= 1\n n += bit\n results.append(n % 5 == 0)\n return results\n```
| 1
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
Python: 5 lines of code with bad explanation
|
python-5-lines-of-code-with-bad-explanat-e7ol
|
python\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n n = 0\n for i, bit in enumerate(nums):\n n = (n
|
ctonic
|
NORMAL
|
2021-12-06T20:04:31.252818+00:00
|
2021-12-06T20:04:31.252856+00:00
| 100
| false
|
```python\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n n = 0\n for i, bit in enumerate(nums):\n n = (n << 1) + bit\n nums[i] = not (n % 5)\n return nums`\n```\n\nReuse the list to save space\nIDK if (n << 1) or (n * 2) is faster
| 1
| 0
|
['Python3']
| 0
|
binary-prefix-divisible-by-5
|
O(n) time, O(n) space.
|
on-time-on-space-by-yayarokya-7byy
|
\npublic class Solution {\n public IList<bool> PrefixesDivBy5(int[] nums) {\n var res = new List<bool>();\n int curr = 0;\n foreach(var
|
yayarokya
|
NORMAL
|
2021-09-10T06:14:27.890789+00:00
|
2021-09-10T06:19:16.431115+00:00
| 99
| false
|
```\npublic class Solution {\n public IList<bool> PrefixesDivBy5(int[] nums) {\n var res = new List<bool>();\n int curr = 0;\n foreach(var n in nums) {\n curr = (2*curr + n) % 5;\n res.Add(curr == 0);\n }\n return res;\n }\n}\n```
| 1
| 1
|
[]
| 0
|
binary-prefix-divisible-by-5
|
Python simple solution O(n)
|
python-simple-solution-on-by-doya1-gc1o
|
\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n answer = []\n start = 1\n val = 0\n for i in nums:
|
doya1
|
NORMAL
|
2021-07-26T05:01:55.450139+00:00
|
2021-07-26T05:01:55.450188+00:00
| 68
| false
|
```\nclass Solution:\n def prefixesDivBy5(self, nums: List[int]) -> List[bool]:\n answer = []\n start = 1\n val = 0\n for i in nums:\n val += i\n if val%5==0:\n answer.append(True)\n else:\n answer.append(False)\n val *= 2\n \n return answer\n\n```
| 1
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
Java Simple Solution
|
java-simple-solution-by-kunalojha1999-yn13
|
\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n int cur = 0;\n ArrayList<Boolean> res = new ArrayList<>();\n \n
|
kunalojha1999
|
NORMAL
|
2021-07-22T15:45:35.357586+00:00
|
2021-07-22T15:45:35.357638+00:00
| 178
| false
|
```\nclass Solution {\n public List<Boolean> prefixesDivBy5(int[] nums) {\n int cur = 0;\n ArrayList<Boolean> res = new ArrayList<>();\n \n for(int i = 0 ; i < nums.length ; i++){\n cur = (2 * cur + nums[i]) % 5;\n if(cur == 0)\n res.add(true);\n else\n res.add(false);\n }\n return res;\n }\n}\n```
| 1
| 0
|
[]
| 0
|
binary-prefix-divisible-by-5
|
Java | Bit-manipulation
|
java-bit-manipulation-by-tangjiawei18-0s32
|
\n public List<Boolean> prefixesDivBy5(int[] nums) {\n int a = 0;\n List<Boolean> res = new ArrayList<>();\n for (int i :nums) {\n
|
tangjiawei18
|
NORMAL
|
2021-06-29T07:05:10.178541+00:00
|
2021-06-29T07:05:10.178600+00:00
| 97
| false
|
```\n public List<Boolean> prefixesDivBy5(int[] nums) {\n int a = 0;\n List<Boolean> res = new ArrayList<>();\n for (int i :nums) {\n a = (a << 1 | i) % 5;\n res.add(a == 0);\n }\n return res;\n }\n```
| 1
| 0
|
['Bit Manipulation']
| 0
|
binary-prefix-divisible-by-5
|
C++ ||Clean Code|| Easy explanation||Short| T: 90%, Mem:100%
|
c-clean-code-easy-explanationshort-t-90-udlzx
|
the intution is based on storing prefix sum, but instead of sum, i am storing the number upto that point.\nIt would be easier to understand if we consider decim
|
DivyanshuCS
|
NORMAL
|
2021-06-21T19:23:54.502129+00:00
|
2021-06-21T19:23:54.502171+00:00
| 108
| false
|
the intution is based on storing prefix sum, but instead of sum, i am storing the number upto that point.\nIt would be easier to understand if we consider decimal number system.\nImagine nums represet a decimal number array instead of binary and you have an array like\n1 0 2 3 8 9 0 1\nso at index 0, the number it will form will be simply nums[0] itself.\nbut at index 1, you will first multiply the previous number by 10(base of decimal number system) and then add it to get 10.\nSimilary, at index 2, you will multiply this 10 by 10 and add 2 to get 102.\nat index 3, we multiply 102 by 10 and 3 to get 1023.\nand so on ..\n\nusing this intution, we can easily get the number upto that index in the binary system as well. The only change is instead of multiplying it by base 10, we need to multiply it by 2 (base of binary number system).\n\nNow, this promptly leads to the problem of integer overflow, and that\'s where modulo comes in. Once we start storing the decimal represent of binary numbers at each index, we don\'t really need the whole number, only it\'s modulo-5 as in next step we are simply multiplying it by 2 (not a factor of 5) and only change that occur in it\'s state is due to addition. So we can safely store only moudlo 5 values. This ensures that we only need to store the digits [0,4] and thus avoid the overflow problem\n\n```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n vector<bool> ans;\n ans.push_back(nums[0]%5==0);\n \n for(int i=1;i<nums.size();i++)\n {\n nums[i-1]*=2;//multiplying the starting bits by corresponding base power\n nums[i]+=nums[i-1];//adding the LSB\n ans.push_back(nums[i]%5==0); //checking if it\'s divisible by 5\n nums[i]%=5; //storing only the remainder since rest is not required\n }\n return ans;\n }\n};\n```
| 1
| 0
|
['C++']
| 1
|
binary-prefix-divisible-by-5
|
100% FASTER || c++ SOLUTION || SIMPLE 5 LINES SOLUTION
|
100-faster-c-solution-simple-5-lines-sol-ili8
|
```\nclass Solution {\npublic:\n vector prefixesDivBy5(vector& nums) {\n vectorans;\n int sum=0;\n \n \n for(int i=0;i<num
|
SJ4u
|
NORMAL
|
2021-05-30T19:01:41.494150+00:00
|
2021-05-30T19:01:41.494185+00:00
| 124
| false
|
```\nclass Solution {\npublic:\n vector<bool> prefixesDivBy5(vector<int>& nums) {\n vector<bool>ans;\n int sum=0;\n \n \n for(int i=0;i<nums.size();i++)\n {\n sum*=2;\n sum+=nums[i];\n sum=sum%5;\n ans.push_back(sum%5==0);\n }\n \n return ans;\n }\n};\n````
| 1
| 1
|
['C']
| 0
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.