question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
concatenated-words | C++ || Simple DP (With Full Explanation) || Beats 99% 🏁🔥 | c-simple-dp-with-full-explanation-beats-cj40x | Intuition\nThe intuition behind this solution is to use dynamic programming to check if a word can be constructed by the concatenation of other words in the set | ufoblivr | NORMAL | 2023-01-27T01:29:10.761505+00:00 | 2023-01-27T02:22:37.663535+00:00 | 25,185 | false | # Intuition\nThe intuition behind this solution is to use dynamic programming to check if a word can be constructed by the concatenation of other words in the set.\n\n# Approach\nFirst, the input list of words is converted into an unordered_set, which is an efficient data structure for checking if a word is in the set in constant time. Then, an empty vector res is created to store the concatenated words that are found.\n\nThe code then iterates over the input list of words. For each word, it creates a vector dp of size n+1 where n is the length of the word. This vector is used to store whether it is possible to construct the word until a certain index by concatenating other words in the set. The vector is initially set to 0 for all indices, except for the first element, which is set to 1.\n\nThe code then iterates over the word again, and for each index i, it checks if the dp value at index i is 1, which means it is possible to construct the word until this index by concatenating other words. If so, it checks if there is a word in the set that starts from this index and has a length j - i, where j is the next index. If such a word is found, it updates the dp value at index j to 1.\n\nFinally, after iterating over the word, the code checks if the dp value at the last index is 1, which means that the word can be constructed by the concatenation of other words in the set. If so, it adds the word to the result vector.\n\nAfter iterating over all the words, the code returns the result vector, which contains all the concatenated words in the input list of words.\n\n\uD83D\uDCCD Here is an example of how the code would work for the word "catdog" and the set of words {"cat","dog"}:\n1. First, the input list of words is converted into an unordered_set, which is an efficient data structure for checking if a word is in the set in constant time.\n2. Then, an empty vector res is created to store the concatenated words that are found.\n3. The code then iterates over the input list of words. For each word "catdog", it creates a vector dp of size n+1 where n is the length of the word. This vector is used to store whether it is possible to construct the word until a certain index by concatenating other words in the set. The vector is initially set to 0 for all indices, except for the first element, which is set to 1.\n ```\n dp = [1, 0, 0, 0, 0, 0, 0]\n\n ```\n4. The code then iterates over the word again, and for each index i, it checks if the dp value at index i is 1, which means it is possible to construct the word until this index by concatenating other words. If so, it checks if there is a word in the set that starts from this index and has a length j - i, where j is the next index. If such a word is found, it updates the dp value at index j to 1.\n ```\n i = 0, j = 3, check if "cat" is in set: Yes, update dp[3] = 1\n i = 3, j = 6, check if "dog" is in set: Yes, update dp[6] = 1\n ```\n5. Finally, after iterating over the word, the code checks if the dp value at the last index is 1, which means that the word can be constructed by the concatenation of other words in the set. If so, it adds the word to the result vector.\n ```\n dp = [1, 0, 0, 1, 0, 0, 1]\n\n ```\n\nAs the dp array\'s last index is 1, which means the word "catdog" can be constructed by the concatenation of other words in the set, so it\'s added to the result vector.\n\nIn this way, this approach is checking if a word is a concatenated word by breaking it down into substrings and checking if each substring is a word in the set, making use of a dp array to store intermediate results. This method is much more efficient than checking all possible concatenations of words.\n\n# Complexity\n- **Time complexity:**\nThe time complexity of this solution is **O(n * L^2)**, where n is the number of words in the input list and L is the maximum length of the words.\nThe main source of the time complexity is the nested loops that iterate over the words and the characters of the words. The outer loop iterates over the words and has a time complexity of O(n). The inner loop iterates over the characters of the words and has a time complexity of O(L). The inner loop also performs additional operations, such as checking if a word is in the set and updating the dp array, which also contribute to the overall time complexity.\n\n- **Space complexity:**\nThe space complexity is **O(n * L)**, where n is the number of words in the input list and L is the maximum length of the words. The main source of the space complexity is the dp array, which is created for each word and has a size of L. Additionally, creating a unordered_set of all the words also takes O(n) space.\n\n# Code\n```\nclass Solution {\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n unordered_set<string> words_set;\n for (string word : words) words_set.insert(word);\n vector<string> res;\n \n for (string word : words) {\n int n = word.size();\n vector<int> dp(n + 1, 0);\n dp[0] = 1;\n for (int i = 0; i < n; i++) {\n if (!dp[i]) continue;\n for (int j = i + 1; j <= n; j++) {\n if (j - i < n && words_set.count(word.substr(i, j - i))) {\n dp[j] = 1;\n }\n }\n if (dp[n]) {\n res.push_back(word);\n break;\n }\n }\n }\n return res;\n }\n};\n```\n\n\n\n | 537 | 1 | ['String', 'Dynamic Programming', 'Depth-First Search', 'C++'] | 15 |
concatenated-words | Java DP Solution | java-dp-solution-by-shawngao-h7fv | Do you still remember how did you solve this problem? https://leetcode.com/problems/word-break/\n\nIf you do know one optimized solution for above question is u | shawngao | NORMAL | 2016-12-18T05:35:57.320000+00:00 | 2018-10-20T22:49:26.044921+00:00 | 70,677 | false | Do you still remember how did you solve this problem? https://leetcode.com/problems/word-break/\n\nIf you do know one optimized solution for above question is using ```DP```, this problem is just one more step further. We iterate through each ```word``` and see if it can be formed by using other ```words```.\n\nOf course it is also obvious that a ```word``` can only be formed by ```words``` shorter than it. So we can first sort the input by length of each ```word```, and only try to form one ```word``` by using ```words``` in front of it.\n```\npublic class Solution {\n public static List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> result = new ArrayList<>();\n Set<String> preWords = new HashSet<>();\n Arrays.sort(words, new Comparator<String>() {\n public int compare (String s1, String s2) {\n return s1.length() - s2.length();\n }\n });\n \n for (int i = 0; i < words.length; i++) {\n if (canForm(words[i], preWords)) {\n result.add(words[i]);\n }\n preWords.add(words[i]);\n }\n \n return result;\n }\n\t\n private static boolean canForm(String word, Set<String> dict) {\n if (dict.isEmpty()) return false;\n\tboolean[] dp = new boolean[word.length() + 1];\n\tdp[0] = true;\n\tfor (int i = 1; i <= word.length(); i++) {\n\t for (int j = 0; j < i; j++) {\n\t\tif (!dp[j]) continue;\n\t\tif (dict.contains(word.substring(j, i))) {\n\t\t dp[i] = true;\n\t\t break;\n\t\t}\n\t }\n\t}\n\treturn dp[word.length()];\n }\n}\n``` | 466 | 5 | [] | 60 |
concatenated-words | Python DFS readable solution | python-dfs-readable-solution-by-kv391p-1l3v | \nclass Solution(object):\n def findAllConcatenatedWordsInADict(self, words):\n """\n :type words: List[str]\n :rtype: List[str]\n | kv391p | NORMAL | 2018-08-13T02:39:02.659235+00:00 | 2018-09-01T14:39:40.220553+00:00 | 28,843 | false | ```\nclass Solution(object):\n def findAllConcatenatedWordsInADict(self, words):\n """\n :type words: List[str]\n :rtype: List[str]\n """\n d = set(words)\n \n def dfs(word):\n for i in range(1, len(word)):\n prefix = word[:i]\n suffix = word[i:]\n \n if prefix in d and suffix in d:\n return True\n if prefix in d and dfs(suffix):\n return True\n if suffix in d and dfs(prefix):\n return True\n \n return False\n \n res = []\n for word in words:\n if dfs(word):\n res.append(word)\n \n return res\n``` | 412 | 12 | [] | 53 |
concatenated-words | Java Common template - Word Break I, Word Break II, Concatenated Words | java-common-template-word-break-i-word-b-590g | Word Break I - Link\n Word Break II - Link \n Concatenated Words - Link\n\nCommon approach for Word Break I, Word Break II, and Concatenated Words problems. \nC | bluesky299 | NORMAL | 2019-08-01T22:17:50.618360+00:00 | 2021-02-09T17:15:02.111962+00:00 | 20,591 | false | * Word Break I - [Link](https://leetcode.com/problems/word-break/)\n* Word Break II - [Link](https://leetcode.com/problems/word-break-ii/) \n* Concatenated Words - [Link](https://leetcode.com/problems/concatenated-words/)\n\nCommon approach for Word Break I, Word Break II, and Concatenated Words problems. \nConcatenated Words is the reverse process of Word Break I, hence can be broken down to Word Break I.\n\n1. Word Break I \n This is the top-Down approach\n\t \n\t class Solution { \n\t \n\t public boolean wordBreak(String s, List<String> wordDict) {\n \n // Need to use Boolean[] memo instead of boolean[], because we store both "true" and "false" in this array\n // and need to return our pre-calculated result of "true/"false" when we hit the scenario,\n // if it is not yet precomputed, the value will be "null"\n \n // If boolean[] is used, then the array will be initialized with "false", \n // this might not be the pre-computed "false"\n return topDown(s, new HashSet<>(wordDict), 0, new Boolean[s.length()]);\n }\n \n \n\t private boolean topDown(String s, Set<String> wordDict, int startIndex, Boolean[] memo) {\n \n\t\t// if we reach the beyond the string, then return true\n // s = "leetcode" when "code" is being checked in the IF() of the loop, we reach endIndex == s.length(), \n // and wordDict.contains("code") => true and topDown(s, wordDict, endIndex, memo) needs to return true. \n if(startIndex == s.length()) {\n return true;\n }\n \n // memo[i] = true means => that the substring from index i can be segmented. \n // memo[startIndex] means => wordDict contains substring from startIndex and it can be segemented.\n if(memo[startIndex] != null) { //Boolean[] array\'s default value is "null"\n return memo[startIndex];\n }\n \n for(int endIndex = startIndex + 1; endIndex <= s.length(); endIndex++) {\n if(wordDict.contains(s.substring(startIndex, endIndex)) && topDown(s, wordDict, endIndex, memo)) {\n memo[startIndex] = true;\n return true;\n }\n }\n memo[startIndex] = false;\n return false;\n }\n }\n\t Time Complexity : O(n^3)\n\t \n\t \n\t This is the bottom-up approach, where base case is dp[0] = true, because string of length 0 (empty string) is present in wordDict.\n\t dp[i] = true => means a valid word (word that exists in wordDict) ends at index i.\n\n class Solution {\n\t\n public boolean wordBreak(String s, List<String> wordDict) {\n boolean[] dp = new boolean[s.length() + 1]; //DP array to store previous results.\n dp[0] = true; //default value.\n \n for(int i=1; i <= s.length(); i++){\n for(int j=0; j < i; j++){\n if(dp[j] && wordDict.contains(s.substring(j, i))){\n dp[i] = true;\n break;\n }\n }\n }\n return dp[s.length()];\n }\n }\n\nTime Complexity : O(n^3) since substring() in Java version > 7 takes O(n) time.\n\n\n\n\n2. Word Break II - use a HashMap to store previously computed results. You check given string starts with any of the words from wordDict, instead of checking every prefix of \'s\' in wordDict.\n\n \n\t class Solution {\t\n public List<String> wordBreak(String s, List<String> wordDict) {\t\n return DFS(s, wordDict, new HashMap<String, List<String>>());\n }\n \n\t public List<String> DFS(String s, List<String> wordDict, Map<String, List<String>> map){\n \n if(map.containsKey(s)) return map.get(s);\n \n List<String> result = new ArrayList<>();\n for(String word : wordDict){\n if(s.startsWith(word)){\n String nextWord = s.substring(word.length());\n if(nextWord.length() == 0) \n result.add(word);\n else{\n for(String w : DFS(nextWord, wordDict, map)) \n result.add(word + " " + w);\n } \n } \n }\n map.put(s, result);\n return result;\n }\n }\n\t \nTime Complexity: O(n^3).\nThis approach is too time consuming if the wordDict has millions of words.\n\nAnother approach based on Word Break I, where we check if every prefix of given string exists in wordDict -\n\n class Solution {\n \n public Map<String, List<String>> memo = new HashMap<String, List<String>>(); \n \n public List<String> wordBreak(String s, List<String> wordDict) {\n return topDown(s, new HashSet<>(wordDict), memo);\n }\n \n private List<String> topDown(String s, Set<String> wordDict, Map<String, List<String>> memo) {\n \n if(memo.containsKey(s)) {\n return memo.get(s);\n }\n \n List<String> result = new ArrayList<String>();\n if(wordDict.contains(s)) {\n result.add(s);\n }\n \n for(int endIndex = 1; endIndex <= s.length(); endIndex++) {\n if(wordDict.contains(s.substring(0, endIndex))) {\n for (String ss : topDown(s.substring(endIndex), wordDict, memo)) {\n result.add(s.substring(0, endIndex) + " " + ss);\n }\n }\n }\n memo.put(s, result);\n return result;\n }\n }\n\n\n3. Concatenated Words - Call Word Break I function to check if a word can be concatenated by the list of words in preWords set.\n \n\t This is the top-down approach - \n\n class Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n //sort the array in asc order of word length, since longer words are formed by shorter words.\n Arrays.sort(words, (a,b) -> a.length() - b.length());\n\n List<String> result = new ArrayList<>();\n\n //list of shorter words \n HashSet<String> preWords = new HashSet<>();\n\n for(int i=0; i< words.length; i++){\n //Word Break-I problem.\n if(topDown(words[i], preWords, 0, new Boolean[words[i].length()])) {\n result.add(words[i]);\n }\n preWords.add(words[i]);\n }\n return result;\n }\n \n private boolean topDown(String s, HashSet<String> wordDict, int startIndex, Boolean[] memo) {\n if(wordDict.isEmpty()) {\n return false;\n }\n // if we reach the beyond the string, then return true\n // s = "leetcode" when "code" is being checked in the IF() of the loop, we reach endIndex == s.length(), \n // and wordDict.contains("code") => true and topDown(s, wordDict, endIndex, memo) needs to return true. \n if(startIndex == s.length()) {\n return true;\n }\n \n // memo[i] = true means => that the substring from index i can be segmented. \n // memo[startIndex] means => wordDict contains substring from startIndex and it can be segemented.\n if(memo[startIndex] != null) { //Boolean[] array\'s default value is "null"\n return memo[startIndex];\n }\n \n for(int endIndex = startIndex + 1; endIndex <= s.length(); endIndex++) {\n if(wordDict.contains(s.substring(startIndex, endIndex)) && topDown(s, wordDict, endIndex, memo)) {\n memo[startIndex] = true;\n return true;\n }\n }\n memo[startIndex] = false;\n return false;\n }\n } \n\n\t \nThis is the bottom-up approach - \n\n class Solution {\t \n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n\t \n //sort the array in asc order of word length, since longer words are formed by shorter words.\n Arrays.sort(words, (a,b) -> a.length() - b.length());\n \n\t\tList<String> result = new ArrayList<>();\n \n //list of shorter words \n HashSet<String> preWords = new HashSet<>();\n \n for(int i=0; i< words.length; i++){\n //Word Break-I problem.\n if(wordBreak(words[i], preWords)) result.add(words[i]);\n preWords.add(words[i]);\n }\n return result;\n }\n \n\t private boolean wordBreak(String s, HashSet<String> preWords){\n if(preWords.isEmpty()) return false;\n \n boolean[] dp = new boolean[s.length() + 1];\n dp[0] = true;\n \n for(int i = 1; i <= s.length(); i++){\n for(int j = 0; j < i; j++){\n if(dp[j] && preWords.contains(s.substring(j, i))){\n dp[i] = true;\n break;\n }\n }\n }\n return dp[s.length()];\n }\n }\n\t \n\t \nTime Complexity: O(total no.of words * (n^3)) where n = avg length of each word.\n\n | 247 | 1 | ['Dynamic Programming', 'Depth-First Search', 'Java'] | 16 |
concatenated-words | Day 27 || Simple Recursion - DFS || Easiest Beginner Friendly Sol | day-27-simple-recursion-dfs-easiest-begi-sm2n | Intuition of this Problem:\nWe can solve this problem using various methods:\n- Trie data strucutre\n- dynamic programming\n\nBut I solved this problem using si | singhabhinash | NORMAL | 2023-01-27T01:38:38.003349+00:00 | 2023-04-01T10:51:40.329638+00:00 | 9,329 | false | # Intuition of this Problem:\nWe can solve this problem using various methods:\n- Trie data strucutre\n- dynamic programming\n\nBut I solved this problem using simple recursion - dfs.\n\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Create an empty set \'s\' to store all the words in the given array of strings.\n2. Iterate through the array of strings and insert each word into the set \'s\'.\n3. Create an empty vector \'concatenateWords\' to store all the concatenated words.\n4. Iterate through the array of strings again, for each word, check if it is a concatenated word using the function \'checkConcatenate(word)\'.\n5. In the \'checkConcatenate(word)\' function, use a for loop to iterate through each substring of the word, starting from index 1 to the second last index of the word.\n6. For each substring, check if the prefix and suffix of the substring exists in the set \'s\'.\n7. If the prefix and suffix both exist in the set \'s\', then return true, indicating that the word is a concatenated word.\n8. If the function \'checkConcatenate(word)\' returns true, then insert the word into the \'concatenateWords\' vector.\n9. Return the \'concatenateWords\' vector.\n<!-- Describe your approach to solving the problem. -->\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n set<string> s;\n bool checkConcatenate(string word) {\n for(int i = 1; i < word.length(); i++) {\n string prefixWord = word.substr(0, i);\n string suffixWord = word.substr(i, word.length()-i);\n if(s.find(prefixWord) != s.end() && (s.find(suffixWord) != s.end() || checkConcatenate(suffixWord)))\n return true;\n }\n return false;\n }\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n vector<string> concatenateWords;\n for(string word : words)\n s.insert(word);\n for(string word : words) {\n if(checkConcatenate(word) == true)\n concatenateWords.push_back(word);\n }\n return concatenateWords;\n }\n};\n```\n```Java []\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n Set<String> s = new HashSet<>();\n List<String> concatenateWords = new ArrayList<>();\n for(String word : words)\n s.add(word);\n for(String word : words) {\n if(checkConcatenate(word, s) == true)\n concatenateWords.add(word);\n }\n return concatenateWords;\n }\n public boolean checkConcatenate(String word, Set<String> s) {\n for(int i = 1; i < word.length(); i++) {\n String prefixWord = word.substring(0, i);\n String suffixWord = word.substring(i, word.length());\n if(s.contains(prefixWord) && (s.contains(suffixWord) || checkConcatenate(suffixWord, s)))\n return true;\n }\n return false;\n }\n}\n\n```\n```Python []\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n s = set()\n concatenateWords = []\n for word in words:\n s.add(word)\n for word in words:\n if self.checkConcatenate(word, s) == True:\n concatenateWords.append(word)\n return concatenateWords\n def checkConcatenate(self, word: str, s: set) -> bool:\n for i in range(1, len(word)):\n prefixWord = word[:i]\n suffixWord = word[i:]\n if prefixWord in s and (suffixWord in s or self.checkConcatenate(suffixWord, s)):\n return True\n return False\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(n^2*m)** //where n is the number of words in the input array and m is the average length of the words.\n\nThe checkConcatenate() function is called for each word in the input array, and for each call, it iterates through the word to check for possible concatenation, which takes O(m) time. The find() function of the set data structure takes O(log(n)) time on average. So, the total time complexity of the checkConcatenate() function is **O(n*m*log(n))**. Since this function is called for each word in the input array, the total time complexity of the findAllConcatenatedWordsInADict() function is **O(n^2*m*log(n))**.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(n*m)** //where n is the number of words in the input array and m is the average length of the words.\n\nThe space complexity **O(nm)**, where n is the number of words in the input array and m is the average length of the words. The set data structure is used to store all the words in the input array, which takes O(nm) space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nReference Video Link - https://www.youtube.com/watch?v=RLc0SyvDjrI | 140 | 0 | ['Depth-First Search', 'Python', 'C++', 'Java'] | 18 |
concatenated-words | 102ms java Trie + DFS solution. With explanation, easy to understand. | 102ms-java-trie-dfs-solution-with-explan-beqk | \npublic List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> res = new ArrayList<String>();\n if (words == null || words | futurehau | NORMAL | 2017-01-12T02:32:27.881000+00:00 | 2018-08-28T22:42:24.104899+00:00 | 27,508 | false | ```\npublic List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> res = new ArrayList<String>();\n if (words == null || words.length == 0) {\n return res;\n }\n TrieNode root = new TrieNode();\n for (String word : words) { // construct Trie tree\n if (word.length() == 0) {\n continue;\n }\n addWord(word, root);\n }\n for (String word : words) { // test word is a concatenated word or not\n if (word.length() == 0) {\n continue;\n }\n if (testWord(word.toCharArray(), 0, root, 0)) {\n res.add(word);\n }\n }\n return res;\n }\n public boolean testWord(char[] chars, int index, TrieNode root, int count) { // count means how many words during the search path\n TrieNode cur = root;\n int n = chars.length;\n for (int i = index; i < n; i++) {\n if (cur.sons[chars[i] - 'a'] == null) {\n return false;\n }\n if (cur.sons[chars[i] - 'a'].isEnd) {\n if (i == n - 1) { // no next word, so test count to get result.\n return count >= 1;\n }\n if (testWord(chars, i + 1, root, count + 1)) {\n return true;\n }\n }\n cur = cur.sons[chars[i] - 'a'];\n }\n return false;\n }\n public void addWord(String str, TrieNode root) {\n char[] chars = str.toCharArray();\n TrieNode cur = root;\n for (char c : chars) {\n if (cur.sons[c - 'a'] == null) {\n cur.sons[c - 'a'] = new TrieNode();\n }\n cur = cur.sons[c - 'a'];\n }\n cur.isEnd = true;\n }\n}\nclass TrieNode {\n TrieNode[] sons;\n boolean isEnd;\n public TrieNode() {\n sons = new TrieNode[26];\n }\n``` | 129 | 5 | [] | 27 |
concatenated-words | Trie with Explanations | trie-with-explanations-by-gracemeng-tyhn | \nA concatenated word is a word add other word(words) as prefix.\n\nWe have to answer a question recursively: is a substring(word[x, word.length()-1]) prefixed | gracemeng | NORMAL | 2018-10-02T16:23:22.658797+00:00 | 2020-03-31T17:00:36.942007+00:00 | 14,464 | false | ```\nA concatenated word is a word add other word(words) as prefix.\n\nWe have to answer a question recursively: is a substring(word[x, word.length()-1]) prefixed with another word in words?\n\nThat\'s natural to prefix tree(trie). \n\nWe can build a trie using words and search for concatenated words in the trie. \n\nWe have to make a decision when we meet a node that meets the end of a word (with en in the example below). We can\n - either take the current node\'s associated word as prefix (and restart at root for another word) \n - or not take the current node\'s associated word as prefix (i.e. move further within the same branch).\nFor example,\n root \n /\\\n c d\n / \\\n a o\n / \\\n t(en) g(en)\n / \n s(en) \n \nTo concatenate catsdogcats using {cat, cats, dog}\nsearch tree: (-\'s in the same vertical line are sibling nodes)\n root - c - a - t(en) - X [to take cat as prefix doesn\'t work]\n - s(en) - d - o - g(en) - c - a - t - s(en) DONE!\n - X [not to take dog as prefix doesn\'t work]\n - [not to take cats as prefix doesn\'t work]\n```\n****\n```\nclass Solution {\n private static Node root;\n \n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n if (words == null || words.length == 0)\n return new ArrayList<>();\n \n root = new Node();\n buildTrie(words);\n \n List<String> result = new LinkedList<>();\n for (String word : words) {\n if (isConcatenated(word, 0, 0))\n result.add(word);\n }\n return result;\n }\n \n // Return true if word starting from index is concatenated\n boolean isConcatenated(String word, int index, int countConcatenatedWords) {\n if (index == word.length())\n return countConcatenatedWords >= 2;\n \n Node ptr = root;\n for (int i = index; i < word.length(); i++) {\n if (ptr.children[word.charAt(i) - \'a\'] == null) \n return false;\n ptr = ptr.children[word.charAt(i) - \'a\'];\n \n if (ptr.isWordEnd)\n if (isConcatenated(word, i + 1, countConcatenatedWords + 1))\n return true;\n }\n \n return false;\n }\n \n private void buildTrie(String[] words) {\n Node ptr;\n for (String word : words) {\n ptr = root;\n for (char ch : word.toCharArray()) {\n int order = ch - \'a\';\n if (ptr.children[order] == null) {\n ptr.children[order] = new Node();\n } \n ptr = ptr.children[order];\n }\n ptr.isWordEnd = true;\n }\n }\n \n class Node {\n Node[] children;\n boolean isWordEnd;\n \n public Node() {\n children = new Node[26];\n isWordEnd = false;\n }\n }\n}\n```\n | 117 | 4 | [] | 18 |
concatenated-words | Python Template - Word Break I, Word Break II, Concatenated Words | python-template-word-break-i-word-break-35hco | Code & Idea for questions :\n1. Word Break : Ques No. 139\n2. Word Break II : Ques No. 140\n3. Concatenated Words : Ques No. 472\n\nBasic idea is same for all, | aayuskh | NORMAL | 2020-09-08T19:36:15.555035+00:00 | 2020-09-08T19:36:15.555087+00:00 | 8,330 | false | Code & Idea for questions :\n1. [Word Break : Ques No. 139](http://leetcode.com/problems/word-break/)\n2. [Word Break II : Ques No. 140](http://leetcode.com/problems/word-break-ii/)\n3. [Concatenated Words : Ques No. 472](http://leetcode.com/problems/concatenated-words/)\n\nBasic idea is same for all, find if string can be broken down to smaller string. Word Break I template follows other two.\n\n### Word Break I\nUsing dynamic programming to calculate if word break is possible or not\n\n```\nclass Solution(object):\n def wordBreak(self, s, wordDict):\n """\n :type s: str\n :type wordDict: List[str]\n :rtype: bool\n """\n dp = [False] * (len(s) + 1)\n dp[0] = True\n wordDict = set(wordDict)\n \n for i in range(len(s)+1):\n for j in range(i):\n if dp[j] and s[j:i] in wordDict:\n dp[i] = True\n return dp[-1]\n```\n\n### Word Break II\nThis is backtracking plus dynamic programming. We use dp array generated from word break I to figure out remaining string can be splitted or not, this reduces lot of backtracking calls. \n```\nclass Solution(object):\n def wordBreak(self, s, wordDict):\n """\n :type s: str\n :type wordDict: List[str]\n :rtype: List[str]\n """\n if not s:\n return [""]\n \n self.res = []\n self.wordDict = set(wordDict)\n self.dp = self.isWordBreak(s, wordDict)\n self.backtrack(s, 0, [])\n \n return self.res\n \n def backtrack(self, s, idx, path):\n # Before we backtrack, we check whether the remaining string \n # can be splitted by using the dictionary,\n # in this way we can decrease unnecessary computation greatly.\n if self.dp[idx+len(s)]: # if word break possible then only proceed\n if not s:\n self.res.append(\' \'.join(path))\n else:\n for i in range(1, len(s)+1):\n if s[:i] in self.wordDict:\n self.backtrack(s[i:], idx+i, path + [s[:i]])\n \n # this is from Word Break I\n def isWordBreak(self, s, wordDict):\n dp = [False] * (len(s) + 1)\n dp[0] = True\n \n for i in range(len(s)+1):\n for j in range(i):\n if dp[j] and s[j:i] in wordDict:\n dp[i] = True\n return dp\n```\n\n### Concatenated Words\nConcatenated Words is the reverse of Word Break I, so can be broken down to Word Break I. \n1. Sort the words according to shortest length since short ones form long words\n2. for each word start building our dictionary of words and check if word split is possible or not\n\n```\nclass Solution(object):\n def findAllConcatenatedWordsInADict(self, words):\n """\n :type words: List[str]\n :rtype: List[str]\n """\n res = []\n preWords = set()\n \n # asc order of word length, since longer words are formed by shorter words\n words.sort(key = len)\n \n # for each short word start building preWords\n for word in words:\n if self.wordBreak(word, preWords):\n res.append(word)\n preWords.add(word)\n \n return res\n \n # Word Break I template\n def wordBreak(self, string, words):\n if not words:\n return False\n \n dp = [False] * (len(string) + 1)\n dp[0] = True\n \n for i in range(len(string)+1):\n for j in range(i):\n if dp[j] and string[j:i] in words:\n dp[i] = True\n break\n \n return dp[-1]\n``` | 102 | 0 | ['Dynamic Programming', 'Depth-First Search', 'Python'] | 10 |
concatenated-words | [Java] DFS + Memoization - Clean code | java-dfs-memoization-clean-code-by-hiepi-z09o | Solution 1: Straigtforward DFS + Memoization\njava\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<St | hiepit | NORMAL | 2020-03-16T15:07:55.260629+00:00 | 2020-03-17T16:00:29.580904+00:00 | 8,630 | false | **Solution 1: Straigtforward DFS + Memoization**\n```java\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> ans = new ArrayList<>();\n HashSet<String> wordSet = new HashSet<>(Arrays.asList(words));\n HashMap<String, Boolean> cache = new HashMap<>();\n for (String word : words) if (dfs(word, wordSet, cache)) ans.add(word);\n return ans;\n }\n boolean dfs(String word, HashSet<String> wordSet, HashMap<String, Boolean> cache) {\n if (cache.containsKey(word)) return cache.get(word);\n for (int i = 1; i < word.length(); i++) {\n if (wordSet.contains(word.substring(0, i))) {\n String suffix = word.substring(i);\n if (wordSet.contains(suffix) || dfs(suffix, wordSet, cache)) {\n cache.put(word, true);\n return true;\n }\n }\n }\n cache.put(word, false);\n return false;\n }\n}\n```\n\n**Solution 2: Concise**\n```java\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> ans = new ArrayList<>();\n HashSet<String> wordSet = new HashSet<>(Arrays.asList(words));\n for (String word : words) if (dfs(word, wordSet)) ans.add(word);\n return ans;\n }\n boolean dfs(String word, HashSet<String> wordSet) {\n for (int i = 1; i < word.length(); i++) {\n if (wordSet.contains(word.substring(0, i))) {\n String suffix = word.substring(i);\n if (wordSet.contains(suffix) || dfs(suffix, wordSet)) {\n wordSet.add(word); // can treat concatenated word as a new word for quickly lookup later\n return true;\n }\n }\n }\n return false;\n }\n}\n```\n**Solution 3: Cache nonCombination**\n```java\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> ans = new ArrayList<>();\n HashSet<String> wordSet = new HashSet<>(Arrays.asList(words));\n HashSet<String> nonCombination = new HashSet<>();\n for (String word : words) if (dfs(word, wordSet, nonCombination)) ans.add(word);\n return ans;\n }\n boolean dfs(String word, HashSet<String> wordSet, HashSet<String> nonCombination) {\n if (nonCombination.contains(word)) return false;\n for (int i = 1; i < word.length(); i++) {\n if (wordSet.contains(word.substring(0, i))) {\n String suffix = word.substring(i);\n if (wordSet.contains(suffix) || dfs(suffix, wordSet, nonCombination)) {\n wordSet.add(word); // can treat concatenated word as a new word for quickly lookup later\n return true;\n }\n }\n }\n nonCombination.add(word);\n return false;\n }\n}\n```\n\n**Solution 4: Trie**\n```java\nclass Solution {\n class TrieNode {\n TrieNode[] children = new TrieNode[26];\n boolean isWord;\n }\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n TrieNode root = new TrieNode();\n for (String word : words) {\n TrieNode current = root;\n for (char c : word.toCharArray()) {\n if (current.children[c-\'a\'] == null) current.children[c-\'a\'] = new TrieNode();\n current = current.children[c-\'a\'];\n }\n if (current != root) current.isWord = true;\n }\n List<String> ans = new ArrayList<>();\n for (String word : words) if (dfs(root, word.toCharArray(), 0, word.length() - 1)) ans.add(word);\n return ans;\n }\n boolean dfs(TrieNode root, char[] cstr, int left, int right) {\n TrieNode current = root;\n for (int i = left; i <= right; i++) {\n char c = cstr[i];\n if (current.children[c-\'a\'] == null) return false;\n current = current.children[c-\'a\'];\n if (current.isWord) { // prefix\n if (isWord(root, cstr, i + 1, right) || dfs(root, cstr, i + 1, right))\n return true;\n }\n }\n return false;\n }\n boolean isWord(TrieNode root, char[] cstr, int left, int right) {\n TrieNode current = root;\n for (int i = left; i <= right; i++) {\n char c = cstr[i];\n if (current.children[c-\'a\'] == null) return false;\n current = current.children[c-\'a\'];\n }\n return current.isWord;\n }\n}\n```\n\nSmilliar problems:\n- [139. Word Break](https://leetcode.com/problems/word-break/)\n- [140. Word Break II](https://leetcode.com/problems/word-break-ii/) | 98 | 2 | [] | 14 |
concatenated-words | ✅C++💯💯image detailed explanation ✅✅ recursion | cimage-detailed-explanation-recursion-by-f7rz | \n\n\n\nNOTE:-here emoji says that ""ca","t" and "dogcats" all are present in set and returning true. if some part like tdogcats did not returened true as it wa | sonal91022 | NORMAL | 2023-01-27T06:02:42.850459+00:00 | 2023-05-12T05:41:07.713177+00:00 | 2,948 | false | \n\n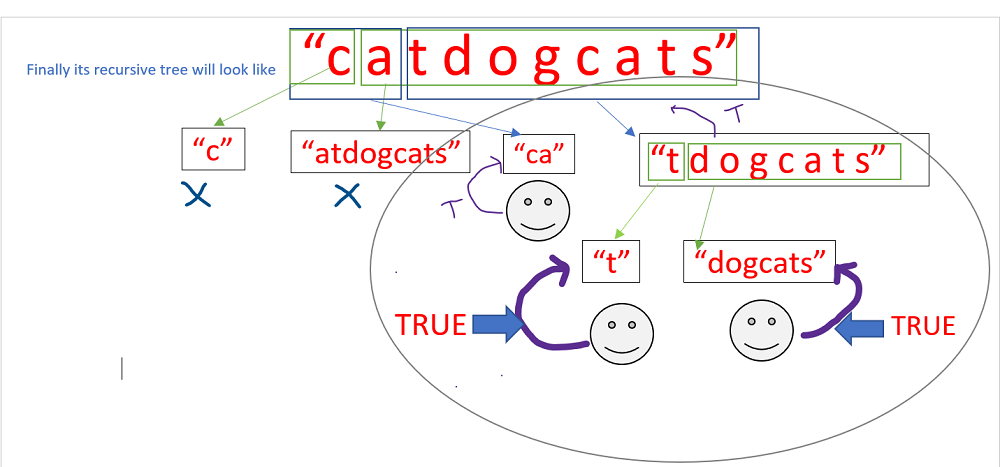\n\n**NOTE:-**here emoji says that "**"ca"**,**"t"** and **"dogcats"** all are present in set and returning true. if some part like **tdogcats** did not returened true as it was not present in our map .then we breaked it as the same way we did earlier so ,simply pass it to recursive function.. when it returns true from both side only then add that word to our answer.. \n\n\n**i draw all this things for you..so that you feel the problem.if you gain something then please motivate me by upvoting my solution.**\n\nLets Connect On Linkedin https://www.linkedin.com/in/sonal-prasad-sahu-78973a229/\n\n\n# Code\n```\nclass Solution {\npublic: bool concat_possible(string &word,vector<string>& words, unordered_map<string,int>&mp){\n int size=word.size();\n for(int i=1;i<size;++i){ \n string prefix=word.substr(0,i);// left subpart\n string suffix=word.substr(i); // right subpart\n if(mp[prefix] && (mp[suffix] || concat_possible(suffix,words,mp))){ /*checking if left and right subpart is present in map or not .\nif one subpart is present(lets say prefix) and other is not(lets say suffix) then recursively check the suffix subpart .if both subparts is present then return true*/\n return true;\n }\n }\n return false;\n}\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n vector<string>ans;\n unordered_map<string,int>mp; \n for(auto string:words){ //storing each words into unordered_map\n mp[string]++;\n }\n\n\n for(auto &word:words){ //check for each word .if its return true then add it into our solution\n if(concat_possible(word,words,mp)){\n ans.push_back(word);\n }\n }\n return ans;\n }\n};\n```\n\n | 60 | 0 | ['Recursion', 'C++'] | 6 |
concatenated-words | Clean Codes🔥🔥|| Full Explanation✅|| Trie & DFS✅|| C++|| Java || Python3 | clean-codes-full-explanation-trie-dfs-c-fundv | Intuition :\n- We can use the data structure trie to store the words. Then for each word in the list of words, we use depth first search to see whether it is a | N7_BLACKHAT | NORMAL | 2023-01-27T02:57:59.955780+00:00 | 2023-01-29T09:59:26.106606+00:00 | 5,962 | false | # Intuition :\n- We can use the data structure trie to store the words. Then for each word in the list of words, we use depth first search to see whether it is a concatenation of two or more words from the list.\n\n- We first build a trie structure that stores the list of words. In every trie node, we use an array of length 26 to store possible next trie node, and a flag to indicate whether the trie node is the last letter of a word in the dictionary.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach :\n- Suppose we have a list of words like this, words = [\u201Ccat\u201D, \u201Ccats\u201D, \u201Ccatsdogcats\u201D, \u201Cdog\u201D, \u201Cdogcatsdog\u201D, \u201Chippopotamuses\u201D, \u201Crat\u201D, \u201Cratcatdogcat\u201D]. The trie structure we build looks like the following. If the node is an end of a word, there is a * next to it.\n```\n c d h r\n | | | |\n a o i a\n | | | |\n t* g* p t*\n | | | |\n s* c p c\n | | | |\n d a o a\n | | | |\n o t p t\n | | | |\n g s o d\n | | | |\n c d t o\n | | | |\n a o a g\n | | | |\n t g* m c\n | | |\n s* u a\n | |\n s t*\n |\n e\n |\n s*\n```\n- Next, for each word in the sentence, we search whether the word is a concatenation of two or more other words from the list. We can use depth first search here.\n\n- For each word, we start from the root node of the trie and the first letter of the word. If the letter is not null in the current trie node, we go to the next trie node of that letter. We keep searching until the trie node is an end of a word (with a * in the above graph). \n\n- We increase the count of words the comprise the current word. Then we start from the root node of the trie again, and keep on searching until we reach the end of the current word. If we cannot find the letter in the trie, we go backtrack to the last run of trie nodes and continue the search.\n\n- If we can find a concatenation of words that reaches the end of the current word, we check how many words are concatenated. If it is greater than 2, we put the current word to the final answer\n<!-- Describe your approach to solving the problem. -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n# Codes for above Explained Approach :\n```C++ []\nclass Solution {\nstruct TrieNode {\n TrieNode* arr[26];\n bool is_end;\n TrieNode() {\n for (int i = 0; i < 26; i ++) arr[i] = NULL;\n is_end = false;\n } \n};\n\nvoid insert(TrieNode* root, string key) {\n TrieNode* curr = root;\n for (int i = 0; i < key.size(); i ++) {\n int idx = key[i] - \'a\';\n if (curr->arr[idx] == NULL)\n curr->arr[idx] = new TrieNode();\n curr = curr->arr[idx];\n }\n curr->is_end = true;\n}\n\nbool dfs(TrieNode* root, string key, int index, int count) {\n if (index >= key.size())\n return count > 1;\n TrieNode* curr = root;\n for (int i = index; i < key.size(); i ++) {\n int p = key[i] - \'a\';\n if (curr->arr[p] == NULL) {\n return false;\n }\n curr = curr->arr[p];\n if (curr->is_end) {\n if (dfs(root, key, i+1, count+1))\n return true;\n }\n }\n return false;\n}\npublic:\nvector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n TrieNode* root = new TrieNode();\n for (int i = 0; i < words.size(); i ++) {\n insert(root, words[i]);\n }\n vector<string> ans;\n for (int i = 0; i < words.size(); i ++) {\n if (dfs(root, words[i], 0, 0))\n ans.push_back(words[i]);\n }\n return ans; \n}\n};\n```\n```Java []\nimport java.util.List;\nimport java.util.ArrayList;\n\nclass Solution {\n class TrieNode {\n TrieNode[] arr = new TrieNode[26];\n boolean is_end;\n TrieNode() {\n for (int i = 0; i < 26; i ++) arr[i] = null;\n is_end = false;\n } \n };\n\n void insert(TrieNode root, String key) {\n TrieNode curr = root;\n for (int i = 0; i < key.length(); i ++) {\n int idx = key.charAt(i) - \'a\';\n if (curr.arr[idx] == null)\n curr.arr[idx] = new TrieNode();\n curr = curr.arr[idx];\n }\n curr.is_end = true;\n }\n\n boolean dfs(TrieNode root, String key, int index, int count) {\n if (index >= key.length())\n return count > 1;\n TrieNode curr = root;\n for (int i = index; i < key.length(); i ++) {\n int p = key.charAt(i) - \'a\';\n if (curr.arr[p] == null) {\n return false;\n }\n curr = curr.arr[p];\n if (curr.is_end) {\n if (dfs(root, key, i+1, count+1))\n return true;\n }\n }\n return false;\n }\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n TrieNode root = new TrieNode();\n for (int i = 0; i < words.length; i ++) {\n insert(root, words[i]);\n }\n List<String> ans = new ArrayList<String>();\n for (int i = 0; i < words.length; i ++) {\n if (dfs(root, words[i], 0, 0))\n ans.add(words[i]);\n }\n return ans; \n }\n}\n```\n```Python3 []\nclass TrieNode:\n def __init__(self):\n self.children = [None] * 26\n self.is_end = False\n\nclass Solution:\n def __init__(self):\n self.root = TrieNode()\n \n def insert(self, root, key):\n curr = root\n for i in range(len(key)):\n idx = ord(key[i]) - ord(\'a\')\n if not curr.children[idx]:\n curr.children[idx] = TrieNode()\n curr = curr.children[idx]\n curr.is_end = True\n\n def dfs(self, root, key, index, count):\n if index >= len(key):\n return count > 1\n curr = root\n for i in range(index, len(key)):\n p = ord(key[i]) - ord(\'a\')\n if not curr.children[p]:\n return False\n curr = curr.children[p]\n if curr.is_end:\n if self.dfs(root, key, i+1, count+1):\n return True\n return False\n\n def findAllConcatenatedWordsInADict(self, words):\n for i in range(len(words)):\n self.insert(self.root, words[i])\n ans = []\n for i in range(len(words)):\n if self.dfs(self.root, words[i], 0, 0):\n ans.append(words[i])\n return ans\n```\n# For the 42/43 test case passing issue in C++ : Use this code\n```\nclass Solution {\nprivate:\n struct Trie\n {\n vector<Trie*> children{26};\n bool end{false};\n };\n \n Trie* root;\n \n void insert(string& s)\n {\n if (s.empty()) return;\n Trie* cur = root;\n for (char c:s)\n {\n if (cur->children[c-\'a\'] == nullptr)\n cur->children[c-\'a\'] = new Trie();\n cur = cur->children[c-\'a\'];\n }\n cur->end = true;\n }\n \n bool dfs(Trie* root, Trie* node, string& word, int idx, int count)\n {\n if (!node)\n return false;\n \n if (idx >= word.size())\n {\n if (node->end && count >=1 )\n return true;\n else\n return false;\n }\n \n if (node->end && dfs(root, root, word, idx, count+1))\n return true;\n return dfs(root, node->children[word[idx]-\'a\'], word, idx+1, count);\n }\n \npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n sort(words.begin(), words.end(), [](const string& w1, const string& w2) {\n return w1.size() < w2.size();\n });\n \n vector<string> ret;\n root = new Trie();\n \n for(auto &w: words)\n {\n if (w.empty()) continue;\n if(dfs(root, root, w, 0, 0)) \n ret.push_back(w);\n else \n insert(w);\n }\n \n return ret;\n }\n};\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n\n | 48 | 0 | ['Trie', 'Python', 'C++', 'Java', 'Python3'] | 5 |
concatenated-words | Accepted (192ms) C++ solution using DP and Trie | accepted-192ms-c-solution-using-dp-and-t-d2z2 | Following is pretty straight-forward, kind-of brute-force approach that result to TLE upon submission. Almost all the solution-posts follow this approach and re | mango_pickle | NORMAL | 2021-08-13T13:22:55.530879+00:00 | 2021-08-19T05:17:59.650069+00:00 | 4,335 | false | Following is pretty straight-forward, kind-of brute-force approach that result to TLE upon submission. Almost all the solution-posts follow this approach and result to TLE with newly added test-cases. \n```\nclass Solution {\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n sort(words.begin(), words.end(), [](string& w1, string& w2){\n return (w1.length() <= w2.length());\n });\n \n vector<string> ret;\n unordered_set<string> m;\n \n for(string w : words) {\n vector<bool> dp(w.length()+1, false);\n dp[0] = true;\n for(int i = 0; i < w.length(); i++) {\n for(int j = i; j >= 0; j--) {\n string s = w.substr(j, i-j+1); // O(length) operation\n if(dp[j] && m.find(s) != m.end()) {\n dp[i+1] = true;\n break;\n }\n }\n }\n \n if(dp[w.length()])\n ret.push_back(w);\n \n m.insert(w);\n }\n \n return ret;\n }\n};\n```\n\nTime complexity : *O(N * L^3)*, where N = number of words and L = length of word. \n\nWhile applying DP for each of the word, we are using `substr` to calculate the suffix and then searching it on `map`. We can use a `trie` instead to check if current suffix is a valid smaller word. That will bring down the complexity from `O(length)` to `O(1)`. \n\nSo, following snippet\n```\nfor(int j = i; j >= 0; j--) {\n string s = w.substr(j, i-j+1); // O(length) operation\n if(dp[j] && m.find(s) != m.end()) {\n dp[i+1] = true;\n break;\n }\n}\n``` \ncan be replaced with (provided that the word has been inserted into trie in reverse order)\n```\ntrie* node = root;\nfor(int j = i; j >= 0; j--) {\n if(node->arr[w[j]-\'a\'] == NULL)\n break;\n node = node->arr[w[j]-\'a\'];\n if(dp[j] && node->end) {\n dp[i+1] = true;\n break;\n }\n}\n```\n\nHere is the final accepted version,\n```\nclass Solution {\n struct trie{\n\t struct trie* arr[26];\n\t bool end = false;\n\t trie() {\n\t\t memset(arr,0,sizeof(arr));\n\t\t end = false;\n\t }\n };\n\n trie* root;\n\n void insert(string s){\n trie* node = root;\n /* \n * inserting the string in reverse order as we will search from the\n * end (i.e. suffix) of the word while using DP.\n */\n for(int i = s.length()-1; i >= 0; i--) {\n char ch = s[i];\n if(!node->arr[ch-\'a\']) {\n node->arr[ch-\'a\'] = new trie();\n }\n node = node->arr[ch-\'a\'];\n }\n node->end = true;\n }\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n /* \n * every word can be generated by concatinating smaller words only,\n * so smaller words will be processed and inserted into trie first \n */\n sort(words.begin(), words.end(), [](const string& w1, const string& w2) {\n return (w1.size() < w2.size());\n });\n \n vector<string> ret;\n root = new trie();\n \n for(string w : words) {\n if(w.length() == 0)\n continue;\n \n vector<bool> dp(w.length()+1, false);\n dp[0] = true;\n for(int i = 0; i < w.length(); i++) {\n trie* node = root;\n for(int j = i; j >= 0; j--) {\n /* \n * instead of keeping the smaller words into a map and \n * searching in the map after doing substr() which is O(n)\n * operation, trie is being used here to achieve constant \n * time search operation of current suffix\n */ \n if(node->arr[w[j]-\'a\'] == NULL)\n break;\n node = node->arr[w[j]-\'a\'];\n if(dp[j] && node->end) {\n dp[i+1] = true;\n break;\n }\n }\n }\n \n if(dp[w.length()])\n ret.push_back(w);\n \n insert(w);\n }\n \n return ret;\n }\n};\n```\n\nTime complexity : *O(N * L^2)*, where N = number of words and L = length of word. | 37 | 1 | ['Dynamic Programming', 'Trie', 'C'] | 4 |
concatenated-words | C++ 772 ms dp solution | c-772-ms-dp-solution-by-hcisly-phwk | For any qualified word, there must be at least 3 indexes (at least 1 besides 0 and n-1 which n is the length of the word), which can be used to split the whole | hcisly | NORMAL | 2016-12-20T04:37:45.828000+00:00 | 2016-12-20T04:37:45.828000+00:00 | 10,236 | false | For any qualified word, there must be at least 3 indexes (at least 1 besides 0 and n-1 which n is the length of the word), which can be used to split the whole string to at least two sub strings and all sub strings can be found in words.\nE.g. input ```["cat","cats", "dog", "sdog","dogcatsdog"]```, for word ```dogcatsdog```, there are 2 sets of numbers: ```[0, 3, 6, 10]``` and ```[0, 3, 7, 10]``` which can be formed by concatenating ```[dog, cat, sdog]``` and ```[dog, cats, dog]``` respectively.\nSo, we can use a ```vector<int> dp(n+1)``` to store if ```w.substr(0, i)``` can be formed by existing words. Once ```i``` reach to ```n``` and it is not the word itself, we put the word to results.\n\n```\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n unordered_set<string> s(words.begin(), words.end());\n vector<string> res;\n for (auto w : words) {\n int n = w.size();\n vector<int> dp(n+1);\n dp[0] = 1;\n for (int i = 0; i < n; i++) {\n if (dp[i] == 0) continue;\n for (int j = i+1; j <= n; j++) {\n if (j - i < n && s.count(w.substr(i, j-i))) dp[j] = 1;\n }\n if (dp[n]) { res.push_back(w); break; }\n }\n }\n return res;\n }\n``` | 35 | 4 | [] | 14 |
concatenated-words | Python Explanation | python-explanation-by-awice-o3ok | Let's discuss whether a word should be included in our answer.\nConsider the word as a topologically sorted directed graph, where each node is a letter, and an | awice | NORMAL | 2016-12-18T04:52:06.675000+00:00 | 2018-10-03T18:57:56.014312+00:00 | 10,431 | false | Let's discuss whether a word should be included in our answer.\nConsider the word as a topologically sorted directed graph, where each node is a letter, and an edge exists from i to j if word[i:j] is in our wordlist, [and there is no edge from i=0 to j=len(word)-1]. We want to know if there is a path from beginning to end. If there is, then the word can be broken into concatenated parts from our wordlist. To answer this question, we DFS over this graph.\n\nCode:\n```\nS = set(A)\nans = []\nfor word in A:\n if not word: continue\n stack = [0]\n seen = {0}\n M = len(word)\n while stack:\n node = stack.pop()\n if node == M:\n ans.append(word)\n break\n for j in xrange(M - node + 1):\n if (word[node:node+j] in S and \n node + j not in seen and\n (node > 0 or node + j != M)):\n stack.append(node + j)\n seen.add(node + j)\n\nreturn ans\n``` | 33 | 2 | [] | 11 |
concatenated-words | Simple Recursion and Optimization | Java C++ | simple-recursion-and-optimization-java-c-86lf | Intution\nFirst lets approach the easiest ones.\n\n1. Solution 1: a sub problem\n\tThe simple idea is we will break a string into 2 Strings and see if they are | jeevankumar159 | NORMAL | 2023-01-27T01:02:57.238395+00:00 | 2023-01-27T03:58:32.793328+00:00 | 3,355 | false | Intution\nFirst lets approach the easiest ones.\n\n1. Solution 1: a sub problem\n\tThe simple idea is we will break a string into 2 Strings and see if they are they are there in the array\n\teg [cat, s, cats]; \n\t\n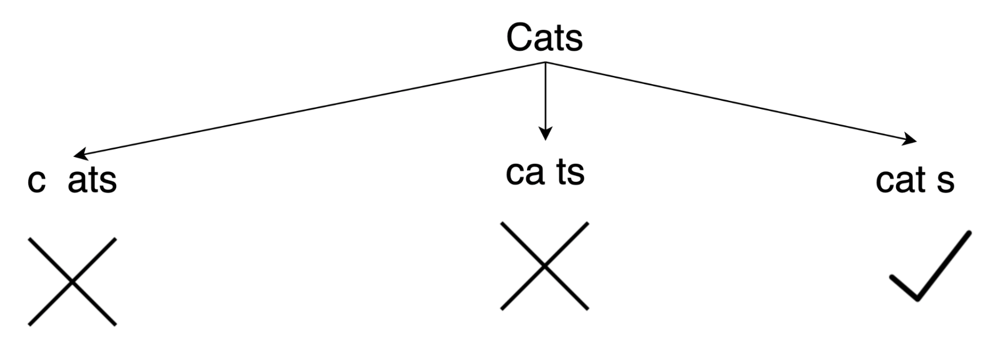\n\nHowever the second part need not always be there in the array, but it can aslo be a comination of words, but simple idea is to pass the right part again to function. If left is in dict and right can be formed or is in dict we have a word that can be formed.\n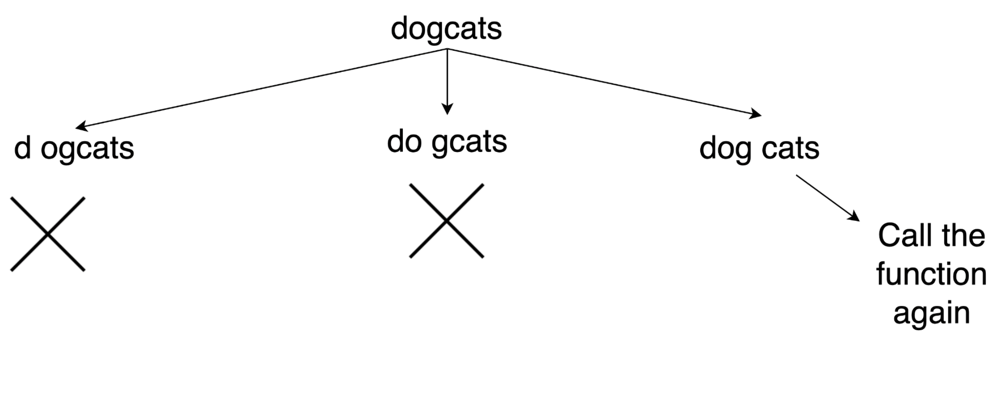\n\nThe approach is simple, we pass the words to canBeformed function and check and then add to result;\n\nFurther optimization\n\nWe are recalculating can be formed for the same word multiple time i.e cat can be passed to canBeformed multiple times. We can simple store already formed words in hashSet\n\nhttps://youtu.be/BThdNPvJrpQ\n\n\n\n\n\tSet<String> dict;\n Set <String> formedWords;\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> result = new ArrayList<>();\n dict = new HashSet<>(Arrays.asList(words));\n formedWords = new HashSet<>();\n \n \n for(String word:words){\n if(canbeFormed(word)){\n result.add(word);\n }\n }\n return result;\n }\n \n public boolean canbeFormed(String s){\n if(formedWords.contains(s)) return true;\n \n for(int i = 1;i<s.length();i++){\n String s1 = s.substring(0,i);\n String s2 = s.substring(i);\n if(dict.contains(s1)){\n if(dict.contains(s2) || canbeFormed(s2)) {\n formedWords.add(s);\n return true;\n }\n }\n }\n return false;\n }\n\n\n\n```\nunordered_set<string> dict;\nunordered_set<string> formedWords;\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n \n vector<string> result;\n dict = unordered_set<string>(words.begin(), words.end());\n formedWords = unordered_set<string>();\n \n for (auto word : words) {\n if (canbeFormed(word)) {\n result.push_back(word);\n }\n }\n return result;\n}\n\nbool canbeFormed(std::string s) {\n if (formedWords.count(s)) return true;\n\n for (int i = 1; i < s.length(); i++) {\n string s1 = s.substr(0, i);\n string s2 = s.substr(i);\n if (dict.count(s1)) {\n if (dict.count(s2) || canbeFormed(s2)) {\n formedWords.insert(s);\n return true;\n }\n }\n }\n return false;\n}\n```\n\n\n | 32 | 1 | ['C', 'Java'] | 4 |
concatenated-words | Python3 Solution beats 100% | python3-solution-beats-100-by-wsteg-7px9 | This is the python version of this post written by @JayS03. Surprisingly, the runtime beats 100% of python 3 submissions.\n\nclass Solution:\n def findAllCon | wsteg | NORMAL | 2017-11-09T07:53:55.419000+00:00 | 2017-11-09T07:53:55.419000+00:00 | 4,331 | false | This is the python version of [this post](https://discuss.leetcode.com/topic/95747/having-been-troubled-by-this-for-a-long-time-here-is-my-pretty-short-java-code-beats-78-quite-easy-no-comlicated-data-structure) written by @JayS03. Surprisingly, the runtime beats 100% of python 3 submissions.\n```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words):\n """\n :type words: List[str]\n :rtype: List[str]\n """\n res = []\n words_dict = set(words)\n for word in words:\n words_dict.remove(word)\n if self.check(word, words_dict) is True:\n res.append(word)\n words_dict.add(word)\n return res\n \n def check(self, word, d):\n if word in d:\n return True\n \n for i in range(len(word),0, -1):\n if word[:i] in d and self.check(word[i:], d):\n return True\n return False\n``` | 32 | 1 | [] | 12 |
concatenated-words | Easyway Explanation every step | easyway-explanation-every-step-by-paul_d-j7qo | \nfor word in words:\n if dfs(word):\n\n\n# Taking word from wods list /array one by one\n\n\ndef dfs(word):\n for i in range(1, len(word) | paul_dream | NORMAL | 2020-09-30T11:45:52.600941+00:00 | 2020-10-24T04:23:35.533723+00:00 | 2,611 | false | ```\nfor word in words:\n if dfs(word):\n```\n\n# Taking word from wods list /array one by one\n\n```\ndef dfs(word):\n for i in range(1, len(word)):\n```\n.\n# travesing one by character which selecte from word list every time \n\n```\nprefix = word[:i]\n suffix = word[i:]\n```\n.\n# divide the word \n.\n# word =prefix [0:i ] +suffix [i :n]\n.\n```\nif prefix in d and suffix in d:\n return True\n\t\t\t\t\t\n \n```\n# if prefix and suffix present then return ture\n .\n```\n\t\t\t\t\t\n if prefix in d and dfs(suffix):\n return True\n \n \n return False\n```\n \n# or if prefix present then searching suffix parts .if you find suffix is present in wordlist return true\n.\n# else false\n\n``` # Explanation \n#Input: ["cat","cats","catsdogcats","dog","dogcatsdog","hippopotamuses","rat","ratcatdogcat"]\n\n\n \n>>>>cat \n\nword= cat\nprefix= c suffix= at\nprefix= ca suffix= t\n\n>>>>>cats\n\n\nword= cats\nprefix= c suffix= ats\nprefix= ca suffix= ts\nprefix= cat suffix= s\n\nsending suffix= s\nword= s\n return dfs suffix= s False\n\n>>>>>>catsdogcats \n\n\nword= catsdogcats\nprefix= c suffix= atsdogcats\nprefix= ca suffix= tsdogcats\nprefix= cat suffix= sdogcats\n\nsending suffix= sdogcats\nword= sdogcats\nprefix= s suffix= dogcats\nprefix= sd suffix= ogcats\nprefix= sdo suffix= gcats\nprefix= sdog suffix= cats\nprefix= sdogc suffix= ats\nprefix= sdogca suffix= ts\nprefix= sdogcat suffix= s\n return dfs suffix= sdogcats False\nprefix= cats suffix= dogcats\n\nsending suffix= dogcats\nword= dogcats\nprefix= d suffix= ogcats\nprefix= do suffix= gcats\nprefix= dog suffix= cats\nsuffix and prefix both present= dog cats\n return dfs suffix= dogcats True\n\n>>>>>>dog \n\nword= dog\nprefix= d suffix= og\nprefix= do suffix= g\n\n>>>>>>dogcatsdog \n\nword= dogcatsdog\nprefix= d suffix= ogcatsdog\nprefix= do suffix= gcatsdog\nprefix= dog suffix= catsdog\n\nsending suffix= catsdog\nword= catsdog\nprefix= c suffix= atsdog\nprefix= ca suffix= tsdog\nprefix= cat suffix= sdog\n\nsending suffix= sdog\nword= sdog\nprefix= s suffix= dog\nprefix= sd suffix= og\nprefix= sdo suffix= g\n return dfs suffix= sdog False\nprefix= cats suffix= dog\nsuffix and prefix both present= cats dog\n return dfs suffix= catsdog True\n\n>>>>>> hippopotamuses\n\n\nword= hippopotamuses\nprefix= h suffix= ippopotamuses\nprefix= hi suffix= ppopotamuses\nprefix= hip suffix= popotamuses\nprefix= hipp suffix= opotamuses\nprefix= hippo suffix= potamuses\nprefix= hippop suffix= otamuses\nprefix= hippopo suffix= tamuses\nprefix= hippopot suffix= amuses\nprefix= hippopota suffix= muses\nprefix= hippopotam suffix= uses\nprefix= hippopotamu suffix= ses\nprefix= hippopotamus suffix= es\nprefix= hippopotamuse suffix= s\n\n>>>>rat\n\n\nword= rat\nprefix= r suffix= at\nprefix= ra suffix= t\n\n>>>>> ratcatdogcat\n\n\nword= ratcatdogcat\nprefix= r suffix= atcatdogcat\nprefix= ra suffix= tcatdogcat\nprefix= rat suffix= catdogcat\n\nsending suffix= catdogcat\nword= catdogcat\nprefix= c suffix= atdogcat\nprefix= ca suffix= tdogcat\nprefix= cat suffix= dogcat\n\nsending suffix= dogcat\nword= dogcat\nprefix= d suffix= ogcat\nprefix= do suffix= gcat\nprefix= dog suffix= cat\nsuffix and prefix both present= dog cat\n return dfs suffix= dogcat True\n return dfs suffix= catdogcat True\n\n[\'catsdogcats\', \'dogcatsdog\', \'ratcatdogcat\']\n\n \n \n```\n\n\n```\n# python code\nclass Solution(object):\n def findAllConcatenatedWordsInADict(self, words):\n """\n :type words: List[str]\n :rtype: List[str]\n """\n d = set(words)\n \n def dfs(word):\n for i in range(1, len(word)):\n prefix = word[:i]\n suffix = word[i:]\n \n if prefix in d and suffix in d:\n return True\n\t\t\t\t\t\n if prefix in d and dfs(suffix):\n return True\n \n \n return False\n \n res = []\n for word in words:\n if dfs(word):\n res.append(word)\n \n return res\n\t\t\n``` | 31 | 1 | ['Python', 'Python3'] | 12 |
concatenated-words | having been troubled by this for a long time.... here is my pretty short java code beats 78% quite easy no comlicated data structure | having-been-troubled-by-this-for-a-long-ix3fq | ```\npublic List findAllConcatenatedWordsInADict(String[] words) {\n List list = new ArrayList<>();\n Set dictionary = new HashSet<>();\n f | jays03 | NORMAL | 2017-07-12T23:46:59.315000+00:00 | 2018-10-10T22:42:07.399446+00:00 | 4,082 | false | ```\npublic List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> list = new ArrayList<>();\n Set<String> dictionary = new HashSet<>();\n for(String string : words) dictionary.add(string);\n for(String word:words) {\n dictionary.remove(word);\n if(check(word,dictionary)) list.add(word);\n dictionary.add(word);\n }\n return list;\n }\n \n private boolean check(String word,Set<String> dictionary) {\n if(dictionary.contains(word)) return true;\n int i = word.length() - 1;\n while(i >= 1) {\n if(dictionary.contains(word.substring(0,i)) && check(word.substring(i),dictionary)) return true;\n i--;\n }\n return false;\n } | 29 | 2 | [] | 14 |
concatenated-words | 20 line C++ 169 ms Beats 100% & Why I think this problem is not properly judged. | 20-line-c-169-ms-beats-100-why-i-think-t-e4qa | The following simple naive brutal force easily beats 100% C++ submission from the past 6 months!\n\nYou know why your algorithm was slower?\nBecause you are too | fentoyal | NORMAL | 2017-05-19T08:51:44.967000+00:00 | 2018-10-24T22:10:18.813121+00:00 | 4,947 | false | The following simple naive brutal force easily beats 100% C++ submission from the past 6 months!\n\n**You know why your algorithm was slower?**\n**Because you are too smart!**\n\n DO NOT memoize the intermediate results and DO NOT use trie. The additional data structure slows the algorithm down!!\n\nThis is why I think this problem is not properly judged. The judge system should favor smarter solutions, like DP (DFS with memoization) or Trie over a naive solution like mine. \n\nAnd truth to be told, this brutal force naive one is actually my 3rd attempts: Trie is MLE, DFS with memoization is too slow (220 ms)...\n```\nclass Solution {\n vector<string> results;\n unordered_set<string> dict;\n int min_len = 1;\n bool isConcatenated(string const & word)\n {\n if (dict.count(word)) return true;\n for (int i = min_len; i < word.size() - min_len + 1 ; ++ i)\n if (dict.count(word.substr(0, i)) > 0 && isConcatenated(word.substr(i, word.size() - i)))\n return true;\n return false;\n }\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n sort(words.begin(), words.end(), [](const string &lhs, const string &rhs){return lhs.size() < rhs.size();});\n min_len = max(1ul, words.front().size());\n for (int i = 0; i < words.size(); dict.insert(words[i++]))\n if (words[i].size() >= min_len * 2 && isConcatenated(words[i]))\n results.push_back(words[i]);\n return results;\n }\n};\n```\n\nThis is my Trie which got a MLE\n```\n///Passed all cases but last one got a MLE (memory limit exceeded).\nstruct TrieNode\n{\n const static char BEGC = \'`\', ENDC = \'{\';\n TrieNode * m_children[27] = {nullptr};\n TrieNode(char c = BEGC)\n {\n }\n inline const TrieNode * operator[](char c) const\n {\n return m_children[c - \'a\'];\n }\n inline TrieNode *& operator[](char c)\n {\n return m_children[c - \'a\'];\n }\n virtual ~TrieNode ()\n {\n for (auto ptr : m_children)\n delete ptr;\n }\n};\nstruct Trie\n{\n TrieNode* root;\n const static char BEGC = TrieNode::BEGC, ENDC = TrieNode::ENDC;\n virtual ~Trie()\n {\n delete root;\n }\n Trie()\n {\n root = new TrieNode();\n }\n void insert(const string & word)\n {\n TrieNode *cur_node_ptr = root;\n for (const auto c : word)\n {\n TrieNode &cur_node = *cur_node_ptr;\n if (cur_node[c] == nullptr)\n cur_node[c] = new TrieNode(c);\n cur_node_ptr = cur_node[c];\n }\n TrieNode &cur_node = *cur_node_ptr;\n if (cur_node[ENDC] == nullptr)\n cur_node[ENDC] = new TrieNode(ENDC);\n }\n};\nclass Solution {\n vector<string> results;\n Trie trie;\n bool isConcatenated(string const & word, int start)\n {\n TrieNode * cur_node_ptr = trie.root;\n for (int i = start; i < word.size(); ++i)\n {\n TrieNode & cur_node = *cur_node_ptr;\n if (cur_node[Trie::ENDC] != nullptr && isConcatenated(word, i))\n return true;\n cur_node_ptr = cur_node[word[i]];\n if (cur_node_ptr == nullptr)\n return false;\n }\n if ((*cur_node_ptr)[Trie::ENDC] != nullptr)\n return true;\n return false;\n }\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n sort(words.begin(), words.end(), [](const string &lhs, const string &rhs){return lhs.size() < rhs.size();});\n for (auto word : words)\n {\n if (word.empty())\n continue;\n if (isConcatenated(word, 0))\n results.push_back(word);\n trie.insert(word);\n }\n return results;\n }\n};\n``` | 27 | 3 | [] | 8 |
concatenated-words | [PYTHON] , VERY EASY,DP, RECURSION, MEMOISATION, Space and time optimised | python-very-easydp-recursion-memoisation-t8ib | First Lets look at the recursion solution so that we get the clarity and then we can move to dp solution\n\nclass Solution:\n def findAllConcatenatedWordsInA | abhinay-thor | NORMAL | 2023-01-27T01:33:38.281549+00:00 | 2023-01-27T01:35:46.436770+00:00 | 2,955 | false | First Lets look at the recursion solution so that we get the clarity and then we can move to dp solution\n```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n # helper function to check if a given word can be formed by concatenating \n # two or more words in the input list\n def can(w,dit):\n for i in range(1,len(w)):\n # check the left part of the word\n lf=w[:i]\n # check the right part of the word\n rt=w[i:]\n if lf in dit:\n # if left part of the word is in the input set, check if the right part is in the set\n # or can be formed by concatenating other words in the set\n if rt in dit or can(rt,dit):\n return True\n return False\n # initialize an empty list to store concatenated words\n res=[]\n # create a set of all words from the input list to improve lookup time\n dit = set(list(words))\n for w in words:\n # check if the word can be formed by concatenating other words in the set\n if can(w,dit):\n # if it can, add it to the list of concatenated words\n res.append(w)\n \n return res\n```\n\nNow lets look a bit space optimized solution\n**Space optimized**\n```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n def can(w,dit):\n for i in range(mini,len(w)):\n lf=w[:i]\n rt=w[i:]\n if lf in dit:\n if rt in dit or can(rt,dit):\n return True\n return False\n res=[]\n dit = set(list(words))\n mini=10000\n for w in words:\n mini=min(len(w),mini)\n for w in words:\n if can(w,dit):\n res.append(w)\n \n return res\n```\nNow lets look at the most optimized\n**DP solution most optimize**\n```\nclass Solution:\ndef findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n\tdef can(w,dit):\n\t\tif w in dp:\n\t\t\treturn True\n\t\tfor i in range(mini,len(w)):\n\t\t\tlf=w[:i]\n\t\t\trt=w[i:]\n\t\t\tif lf in dit:\n\t\t\t\tif rt in dit or can(rt,dit):\n\t\t\t\t\tdp.append(w)\n\t\t\t\t\treturn True\n\t\treturn False\n\tres=[]\n\tdit = set(list(words))\n\tmini=10000\n\tdp=[]\n\tfor w in words:\n\t\tmini=min(len(w),mini)\n\tfor w in words:\n\t\tif can(w,dit):\n\t\t\tres.append(w)\n\n\treturn res\n```\nHope it helps \n**UPVOTE** if helped\nfeel free to post query \n\t | 26 | 1 | ['Dynamic Programming', 'Recursion', 'Python'] | 5 |
concatenated-words | C++ || Easy || NO DP | c-easy-no-dp-by-jenish_09-s3mb | \n\n# Code\n\nclass Solution {\npublic:\n map<string,int> m;\n bool cal(string &str,int idx,int cnt)\n {\n if(idx==str.size())\n retu | jenish_09 | NORMAL | 2023-01-27T05:19:47.650494+00:00 | 2023-01-27T05:19:47.650547+00:00 | 2,093 | false | \n\n# Code\n```\nclass Solution {\npublic:\n map<string,int> m;\n bool cal(string &str,int idx,int cnt)\n {\n if(idx==str.size())\n return cnt>1; // check atleat two string are concate\n string tmp="";\n for(int i=idx;i<str.size();i++)\n {\n tmp+=str[i];\n if(m.find(tmp)!=m.end())\n {\n // if string found then check with next index\n bool flag=cal(str,i+1,cnt+1);\n if(flag)\n return true;\n }\n }\n return false;\n }\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n for(auto x:words)\n m[x]++;\n vector<string> ans;\n for(auto x:words)\n {\n bool flag=cal(x,0,0);\n // if given string satisfy the condition then add it to our answer\n if(flag)\n ans.push_back(x);\n }\n return ans;\n }\n};\n``` | 21 | 0 | ['String', 'C++'] | 4 |
concatenated-words | Simple Java Trie + DFS solution 144ms | simple-java-trie-dfs-solution-144ms-by-h-i5sl | Most of lines are adding words into Trie Tree \nThis solution is like putting two pointers to search through the tree. When find a word, put the other pointer b | huiyuyang | NORMAL | 2016-12-18T17:58:38.568000+00:00 | 2016-12-18T17:58:38.568000+00:00 | 10,562 | false | Most of lines are adding words into Trie Tree \nThis solution is like putting two pointers to search through the tree. When find a word, put the other pointer back on root then continue searching.\nBut I'm not sure about the time complexity of my solution. Suppose word length is len and there are n words. Is the time complexity O(len * n ^ 2)?\n```\npublic class Solution {\n class TrieNode {\n TrieNode[] children;\n String word;\n boolean isEnd;\n boolean combo; //if this word is a combination of simple words\n boolean added; //if this word is already added in result\n public TrieNode() {\n this.children = new TrieNode[26];\n this.word = new String();\n this.isEnd = false;\n this.combo = false;\n this.added = false;\n }\n }\n private void addWord(String str) {\n TrieNode node = root;\n for (char ch : str.toCharArray()) {\n if (node.children[ch - 'a'] == null) {\n node.children[ch - 'a'] = new TrieNode();\n }\n node = node.children[ch - 'a'];\n }\n node.isEnd = true;\n node.word = str;\n }\n private TrieNode root;\n private List<String> result;\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n root = new TrieNode();\n for (String str : words) {\n if (str.length() == 0) {\n continue;\n }\n addWord(str);\n }\n result = new ArrayList<>();\n dfs(root, 0);\n return result;\n }\n private void dfs(TrieNode node, int multi) {\n \t//multi counts how many single words combined in this word\n if(node.isEnd && !node.added && multi > 1) {\n node.combo = true;\n node.added = true;\n result.add(node.word);\n }\n searchWord(node, root, multi);\n }\n private void searchWord(TrieNode node1, TrieNode node2, int multi) {\n if (node2.combo) {\n return;\n }\n if (node2.isEnd) {\n //take the pointer of node2 back to root\n dfs(node1, multi + 1);\n }\n for (int i = 0; i < 26; i++) {\n if (node1.children[i] != null && node2.children[i] != null) {\n searchWord(node1.children[i], node2.children[i], multi);\n }\n }\n }\n}\n``` | 20 | 1 | [] | 17 |
concatenated-words | Python Trie solution explained | python-trie-solution-explained-by-skdoos-gy94 | This question is very similar to 208. Implement Trie (Prefix Tree) with one modification. Apart from searching for a word in the trie, we should also keep track | skdoosh | NORMAL | 2020-07-31T19:03:06.388159+00:00 | 2020-07-31T19:13:53.038182+00:00 | 2,090 | false | This question is very similar to [208. Implement Trie (Prefix Tree)](http://leetcode.com/problems/implement-trie-prefix-tree/) with one modification. Apart from searching for a word in the trie, we should also keep track of smaller words encountered during the search. \n\n1. We insert all the words into the `trie`. \n2. Iterate through each word and check if we can successfully perform `DFS`.\n\t2.1 If yes, add the word to `result`\n3. Return the `result`\n\nDuring the `DFS`, we keep track of 4 parameters: \n`word` - word to be searched\n`start` - to track the current character of the `word` \n`root` - root of the `trie`\n`count` - number of smaller words encountered so far\n\nWe iterate through the characters of the `word` one by one starting from `start`. Check if the current character is a word ending and also if it is the last character of the `word`. We make a decision based on the `count` value. Otherwise, we recur for remaining indices of the `word` with `count ` increased by 1. \n\nHead over to [link](http://skdoosh-leetcode.herokuapp.com) for more python solutions to leetcode problems and star my [github repo](https://github.com/Anirudh-Muthukumar/Leetcode-Solutions) if you like my work. \n\n```\nimport collections\n\nclass TrieNode:\n def __init__(self):\n self.children = collections.defaultdict(TrieNode)\n self.isEnd = False\n\nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n \n def insert(self, word):\n marker = self.root\n for ch in word:\n marker = marker.children[ch]\n marker.isEnd = True\n\n\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words):\n \n def dfs(word, start, root, count):\n n = len(word)\n marker = root\n for i in range(start, n):\n marker = marker.children[word[i]]\n if marker.isEnd: # smaller word encountered\n if i == n-1: # leaf node\n return count>=1\n elif dfs(word, i+1, root, count+1): # increment the count and start a new DFS\n return True\n return False\n \n res = []\n trie = Trie()\n for word in words:\n trie.insert(word)\n\n for word in words:\n if dfs(word, 0, trie.root, 0):\n res += word,\n \n return res\n```\n \n \n\n \n \n \n\n\n | 19 | 1 | ['Depth-First Search', 'Trie', 'Recursion', 'Python3'] | 6 |
concatenated-words | Python solutions: top-down DP, Trie + DFS | python-solutions-top-down-dp-trie-dfs-by-j7wg | Please see and vote for my Python DP solutions for\n139. Word Break\n140. Word Break II\n472. Concatenated Words\n\nMethod 1: top-down DP (444 ms, beat 52%)\nLe | otoc | NORMAL | 2019-06-28T22:36:16.776235+00:00 | 2022-08-16T04:29:03.819016+00:00 | 1,366 | false | Please see and vote for my Python DP solutions for\n[139. Word Break](https://leetcode.com/problems/word-break/discuss/322388/Standard-DP-solutions-(Bottom-up-Top-down))\n[140. Word Break II](https://leetcode.com/problems/word-break-ii/discuss/322400/Standard-Python-DP-solutions-(Bottom-up-Top-down))\n[472. Concatenated Words](https://leetcode.com/problems/concatenated-words/discuss/322444/Python-solutions%3A-top-down-DP-Trie)\n\nMethod 1: top-down DP (444 ms, beat 52%)\nLet dp[i] = whether s[i:len(s)] can be segmented into a space-separated sequence of words, i=0,1,2,..., len(s).\nThe possible values of dp[i] are: \n0 means s[i:len(s)] cannot be sucessfully segmented, \n1 means s[i:len(s)] is in words and cannot be sucessfully segmented,\n2 means s[i:len(s)] can be segmented into a space-spearated sequence of at least two words.\n```\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n def recursive(s, i, n):\n if i in dp:\n return dp[i]\n j = i + 1\n while j <= n:\n if s[i:j] in word_set and recursive(s, j, n):\n dp[i] = 2 if j < n else 1\n return dp[i]\n j += 1\n dp[i] = 0\n return dp[i]\n \n word_set = set(words)\n res = []\n for w in words:\n n = len(w)\n dp = {n: 1}\n if recursive(w, 0, n) > 1:\n res.append(w)\n return res\n```\n\nMethod 2: implement same algorithm via Trie + DFS (1616 ms, beat 6.95%)\n\nPlease see and vote for my solutions for\n[208. Implement Trie (Prefix Tree)](https://leetcode.com/problems/implement-trie-prefix-tree/discuss/320224/Simple-Python-solution)\n[1233. Remove Sub-Folders from the Filesystem](https://leetcode.com/problems/remove-sub-folders-from-the-filesystem/discuss/409075/standard-python-prefix-tree-solution)\n[1032. Stream of Characters](https://leetcode.com/problems/stream-of-characters/discuss/320837/Standard-Python-Trie-Solution)\n[211. Add and Search Word - Data structure design](https://leetcode.com/problems/add-and-search-word-data-structure-design/discuss/319361/Simple-Python-solution)\n[676. Implement Magic Dictionary](https://leetcode.com/problems/implement-magic-dictionary/discuss/320197/Simple-Python-solution)\n[677. Map Sum Pairs](https://leetcode.com/problems/map-sum-pairs/discuss/320237/Simple-Python-solution)\n[745. Prefix and Suffix Search](https://leetcode.com/problems/prefix-and-suffix-search/discuss/320712/Different-Python-solutions-with-thinking-process)\n[425. Word Squares](https://leetcode.com/problems/word-squares/discuss/320916/Easily-implemented-Python-solution%3A-Backtrack-%2B-Trie)\n[472. Concatenated Words](https://leetcode.com/problems/concatenated-words/discuss/322444/Python-solutions%3A-top-down-DP-Trie)\n[212. Word Search II](https://leetcode.com/problems/word-search-ii/discuss/319071/Standard-Python-solution-with-Trie-%2B-Backtrack)\n[336. Palindrome Pairs](https://leetcode.com/problems/palindrome-pairs/discuss/316960/Different-Python-solutions%3A-brute-force-dictionary-Trie)\n\n```\nclass TrieNode():\n def __init__(self):\n self.children = {}\n self.isEnd = False\n\nclass Trie():\n def __init__(self, words):\n self.root = TrieNode()\n for w in words:\n if w:\n self.insert(w)\n \n def insert(self, word):\n node = self.root\n for char in word:\n if char not in node.children:\n node.children[char] = TrieNode()\n node = node.children[char]\n node.isEnd = True\n\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n def dfs(node, i, w, space_inserted):\n if i == len(w):\n return node.isEnd and space_inserted\n if node.isEnd:\n if dfs(trie.root, i, w, True):\n return True\n if w[i] not in node.children:\n return False\n else:\n return dfs(node.children[w[i]], i + 1, w, space_inserted)\n \n trie = Trie(words)\n res = []\n for w in words:\n if dfs(trie.root, 0, w, False):\n res.append(w)\n return res\n``` | 19 | 1 | [] | 5 |
concatenated-words | Simple solution. Javascript Beats 90% with explanation | simple-solution-javascript-beats-90-with-pb36 | \n1. Use a set for quick lookup\n2. Call isConcat on each word. If a word\'s prefix is in the dictionary, see if the suffix can also be concatenated.\n3. You c | kenhufford | NORMAL | 2020-04-10T22:59:39.271071+00:00 | 2020-04-10T22:59:39.271111+00:00 | 1,483 | false | \n1. Use a set for quick lookup\n2. Call isConcat on each word. If a word\'s prefix is in the dictionary, see if the suffix can also be concatenated.\n3. You can use the dictionary as a memo, when you find a word that can be made via concatenation, you can store it in the dictionary\n4. When you loop through the words, remember to delete and add the word from the set before and after the isConcat call\n\n```\nlet findAllConcatenatedWordsInADict = (words) => {\n const dict = new Set(words);\n const isConcat = (word) => {\n if(dict.has(word)) return true;\n for(let i = 0; i < word.length; i++){\n let prefix = word.slice(0,i+1);\n if(dict.has(prefix)){\n let suffix = word.slice(i+1);\n let result = isConcat(suffix);\n if(result){\n dict.add(word);\n return true;\n }\n }\n }\n return false;\n }\n const results = [];\n for(const word of words){\n dict.delete(word);\n if(isConcat(word)) results.push(word);\n dict.add(word);\n }\n return results;\n};\n``` | 18 | 1 | ['Depth-First Search', 'Recursion', 'JavaScript'] | 4 |
concatenated-words | A review of top solutions | a-review-of-top-solutions-by-yu6-ffbo | After studying the top solutions, I might not be the only one wondering which is the best and why. So I would like to share my understanding with this post.\n\n | yu6 | NORMAL | 2017-02-09T19:38:17.105000+00:00 | 2017-02-09T19:38:17.105000+00:00 | 2,600 | false | After studying the top solutions, I might not be the only one wondering which is the best and why. So I would like to share my understanding with this post.\n\nOne sub problem is word break. There are three ways to solve word break,[ DFS, BFS and DP](https://discuss.leetcode.com/topic/66356/evolve-from-brute-force-to-optimal). DFS is the best way because it terminates as soon as it finds one way to break the word. DP and BFS checks all the substrings thus less efficient. Combined with the sorting idea by [@shawngao ](https://discuss.leetcode.com/topic/72113/java-dp-solution) is the best I have.\n```\n struct comp {\n bool operator()(string &s1, string &s2) {\n return s1.size()<s2.size();\n }\n };\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n unordered_set<string> ht; \n vector<string> res;\n sort(words.begin(),words.end(),comp());\n for(auto &s:words) {\n if(s.empty()) continue;\n if(canbrk(0,s,ht)) res.push_back(s);\n ht.insert(s);\n }\n return res;\n }\n bool canbrk(int p, string &s, unordered_set<string>& ht) {\n int n = s.size();\n if(p==n) return 1;\n string sub;\n for(int i=p;i<n;i++) if(ht.count(sub+=s[i])&&canbrk(i+1,s,ht)) return 1;\n return 0;\n }\n```\nAnother improve is to use trie instead of hash table to save memory. However, looks like all c++ solution with trie gets memory limit exceeded. I think the oj bug needs to be fixed @administrators \n```\n struct Node {\n Node():end(),nxt() {};\n bool end;\n Node* nxt[26];\n };\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n vector<string> res;\n sort(words.begin(),words.end(),comp());\n Node *root = new Node();\n for(auto &s:words) {\n if(s.empty()) continue;\n if(canbrk(0,s,root)) res.push_back(s);\n addWord(s,root);\n }\n destroy(root);\n return res;\n }\n bool canbrk(int p, string &s, Node *r) {\n int n = s.size();\n if(p==n) return 1;\n string sub;\n for(int i=p;i<n;i++) if(search(sub+=s[i], r)&&canbrk(i+1,s,r)) return 1;\n return 0;\n }\n void addWord(string word, Node *p) {\n for(char c:word) {\n Node *&nxt = p->nxt[c-'a'];\n if(!nxt) nxt = new Node();\n p = nxt;\n }\n p->end = 1;\n }\n bool search(string& word, Node *r) {\n for(char c:word) {\n Node *&nxt = r->nxt[c-'a'];\n if(!nxt) return 0;\n r = nxt;\n }\n return r->end;\n }\n void destroy(Node* r) {\n if (!r) return;\n for (int i = 0; i < 26; i++) destroy(r->nxt[i]);\n delete r;\n }\n``` | 17 | 0 | ['C'] | 2 |
concatenated-words | java 41ms trie and dfs solution which beats 97% | java-41ms-trie-and-dfs-solution-which-be-kqnw | We can solve the problem in two steps:\n1. put the given words in a trie;\n2. For each word, dfs the trie (traverse characters in the word one by one). If the t | pangeneral | NORMAL | 2019-04-24T13:58:30.943419+00:00 | 2019-04-24T13:58:30.943464+00:00 | 1,946 | false | We can solve the problem in two steps:\n1. put the given words in a trie;\n2. For each word, dfs the trie (traverse characters in the word one by one). If the trie node of current character represent a word, then for next character, we search from the root node of trie. \n\n```\npublic List<String> findAllConcatenatedWordsInADict(String[] words) {\n Trie root = new Trie();\n for(int i = 0; i < words.length; i++) {\n if( words[i].length() > 0 )\n buildTrie(root, words[i]);\n }\n\n List<String> resultList = new ArrayList<String>();\n for(int i = 0; i < words.length; i++)\n if( search(root, words[i], 0, 0) )\n resultList.add(words[i]);\n return resultList;\n}\n\npublic void buildTrie(Trie root, String word) {\n Trie current = root;\n for(int i = 0; i < word.length(); i++) {\n int index = word.charAt(i) - \'a\';\n if( current.array[index] == null )\n current.array[index] = new Trie();\n current = current.array[index];\n }\n current.isWord = true;\n}\n\n// num represent the number of words that current word can be comprised of\npublic boolean search(Trie root, String word, int begin, int num) {\n Trie current = root;\n for(int i = begin; i < word.length(); i++) {\n int index = word.charAt(i) - \'a\';\n if( current.array[index] == null )\n return false;\n current = current.array[index];\n if( current.isWord && search(root, word, i + 1, num + 1) ) \n return true;\n }\n return num >= 1 && current.isWord;\n}\n\nclass Trie {\n Trie array[] = new Trie[26];\n boolean isWord = false;\n}\n``` | 16 | 0 | ['Depth-First Search', 'Trie', 'Java'] | 4 |
concatenated-words | java hashset 48ms beats 100% | java-hashset-48ms-beats-100-by-lolozo-dc5n | \npublic class Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> ret = new ArrayList<>();\n Set | lolozo | NORMAL | 2018-07-04T22:28:36.096921+00:00 | 2018-07-04T22:28:36.096921+00:00 | 1,930 | false | ```\npublic class Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> ret = new ArrayList<>();\n Set<String> set = new HashSet<>();\n for (String word : words) {\n set.add(word);\n }\n for (String word : words) {\n if (isConcatenated(set, word)) ret.add(word);\n }\n return ret;\n }\n \n private boolean isConcatenated(Set<String> set, String s) {\n for (int i = 1; i < s.length(); i++) {\n if (set.contains(s.substring(0, i))) {\n String rightStr = s.substring(i);\n if (set.contains(rightStr) || isConcatenated(set, rightStr))\n return true;\n }\n }\n return false;\n }\n}\n``` | 16 | 0 | [] | 5 |
concatenated-words | Fast Python DP solution | fast-python-dp-solution-by-hongsenyu-2ni7 | \n\'\'\'\nIf a word can be Concatenated from shorter words, then word[:i] and word[i:] must also be Concatenated from shorter words.\nBuild results of word from | hongsenyu | NORMAL | 2020-02-26T06:35:48.466271+00:00 | 2020-02-26T06:35:48.466307+00:00 | 783 | false | ```\n\'\'\'\nIf a word can be Concatenated from shorter words, then word[:i] and word[i:] must also be Concatenated from shorter words.\nBuild results of word from results of word[:i] and word[i:]\nIterate i from range(1, len(word)) to avoid a word is Concatenated from itself.\nUse memorization to avoid repeat calculation.\nTime: O(n*l)\nSpace: O(n)\n\'\'\'\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n mem = {}\n words_set = set(words)\n return [w for w in words if self.check(w, words_set, mem)]\n \n def check(self, word, word_set, mem):\n if word in mem:\n return mem[word]\n mem[word] = False\n for i in range(1, len(word)):\n if word[:i] in word_set and (word[i:] in word_set or self.check(word[i:], word_set, mem)):\n mem[word] = True\n break\n return mem[word]\n``` | 15 | 0 | ['Dynamic Programming'] | 3 |
concatenated-words | C++ Solutions, Backtrack, DP, or Trie. | c-solutions-backtrack-dp-or-trie-by-wang-8og0 | First, I provide my working solution using unorederd_set. But I think a better solution should use Trie. Though it passed all test cases, I always get MLE. But | wangxinbo | NORMAL | 2016-12-19T23:52:15.506000+00:00 | 2018-08-23T16:55:48.631569+00:00 | 5,210 | false | First, I provide my working solution using unorederd_set. But I think a better solution should use Trie. Though it passed all test cases, I always get MLE. But the java solution using Trie can be accepted. Did anybody have any suggestions about this? I have already made some optimization on it, e.g., a word that can be concatenated by shorter words will not be inserted into the Trie. But I still get MLE.\n\nunordered_set solution 486 ms\n```\nvector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n vector<string> result;\n if(words.empty()) return result; \n auto mycomp = [&](const string& str1, const string& str2){return str1.size() < str2.size();};\n sort(words.begin(), words.end(), mycomp);\n unordered_set<string> mp;\n for(auto& word: words) {\n string path = "";\n if(dfs(word, 0, path, 0, mp)) result.push_back(word); // We don't need to insert this word, because it can be concatenated from other words.\n else mp.insert(word); \n }\n return result;\n }\n \nprivate:\n bool dfs(string& word, int pos, string& path, int nb, unordered_set<string>& mp) {\n if(pos == word.size()) {\n if(mp.find(path) != mp.end() && nb > 0) return true;\n else return false;\n }\n path.push_back(word[pos]);\n if(mp.find(path) != mp.end()) {\n string temp = "";\n if(dfs(word, pos+1, temp, nb+1, mp)) return true;\n }\n if(dfs(word, pos+1, path, nb, mp)) return true;\n else return false;\n }\n```\n\nDP solution based on Word Break 739 ms\n```\nvector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n vector<string> result;\n if(words.empty()) return result; \n auto mycomp = [&](const string& str1, const string& str2){return str1.size() < str2.size();};\n sort(words.begin(), words.end(), mycomp);\n unordered_set<string> mp;\n for(auto& word: words) {\n string path = "";\n if(wordBreak(word, mp)) result.push_back(word); // We don't need to insert this word, because it can be concatenated from other words.\n else mp.insert(word); \n }\n return result;\n }\n \nprivate:\n bool wordBreak(string& s, unordered_set<string>& wordDict) {\n if(s.empty() || wordDict.empty()) return false;\n vector<bool> dp(s.size()+1, false);\n dp[0] = true;\n for(int i = 1; i <= s.size(); i++) {\n for(int k = i-1; k >= 0; k--) {\n if(dp[k] && wordDict.find(s.substr(k, i-k)) != wordDict.end()) {\n dp[i] = true;\n break;\n }\n }\n }\n return dp[s.size()];\n }\n```\n\nHere I provide my Trie-based solution, but it gets MLE.\n```\nclass Solution {\npublic:\n struct TrieNode {\n bool isWord;\n unordered_map<char, TrieNode*> children;\n TrieNode(): isWord(false) {};\n };\n\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n vector<string> result;\n if(words.empty()) return result; \n auto mycomp = [&](const string& str1, const string& str2){return str1.size() < str2.size();};\n sort(words.begin(), words.end(), mycomp);\n \n root = new TrieNode();\n for(auto& word: words) {\n if(dfs(word, 0, root, 0)) result.push_back(word);\n else insert(word);\n }\n return result;\n }\n \nprivate:\n TrieNode* root;\n \n void insert(string& word) {\n auto run = root;\n for(char c: word) {\n if(run->children.find(c) == run->children.end()) {\n TrieNode* newnode = new TrieNode();\n run->children[c] = newnode;\n }\n run = run->children[c];\n }\n run->isWord = true;\n }\n \n bool dfs(string& word, int pos, TrieNode* node, int nb) {\n if(pos == word.size()) {\n if(node->isWord && nb > 0) return true;\n else return false;\n }\n \n if(node->children.find(word[pos]) == node->children.end()) return false;\n auto next = node->children[word[pos]];\n if(next->isWord) {\n if(dfs(word, pos+1, root, nb+1)) return true;\n }\n if(dfs(word, pos+1, next, nb)) return true;\n else return false;\n }\n};\n``` | 14 | 0 | [] | 7 |
concatenated-words | ✅ fast C++ code | fast-c-code-by-coding_menance-44zy | Solution Code\nC++ []\nclass Solution {\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n unordered_set<string> wor | coding_menance | NORMAL | 2023-01-27T04:02:56.146265+00:00 | 2023-01-27T10:04:00.640925+00:00 | 956 | false | # Solution Code\n``` C++ []\nclass Solution {\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n unordered_set<string> words_set;\n for (string word : words) words_set.insert(word);\n vector<string> res;\n \n for (string word : words) {\n int n = word.size();\n vector<int> dp(n + 1, 0);\n dp[0] = 1;\n for (int i = 0; i < n; i++) {\n if (!dp[i]) continue;\n for (int j = i + 1; j <= n; j++) {\n if (j - i < n && words_set.count(word.substr(i, j - i))) {\n dp[j] = 1;\n }\n }\n if (dp[n]) {\n res.push_back(word);\n break;\n }\n }\n }\n return res;\n }\n};\n```\n\n\n | 13 | 0 | ['C++'] | 3 |
concatenated-words | 51ms easy Java Trie solution | 51ms-easy-java-trie-solution-by-bianhit-agg2 | \nclass Solution {\n TrieNode root = new TrieNode();\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> res = n | bianhit | NORMAL | 2018-08-14T18:27:42.757871+00:00 | 2018-09-30T21:18:37.871954+00:00 | 1,467 | false | ```\nclass Solution {\n TrieNode root = new TrieNode();\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> res = new ArrayList<>();\n build(words);\n for (String word : words) \n if (search(root,word,0,0))\n res.add(word);\n return res;\n }\n \n public void build(String[] dict) {\n for (String word : dict) {\n if (word == null || word.length() == 0) continue;\n TrieNode temp = root;\n int len = word.length();\n for (int i = 0; i < len; i++) {\n char c = word.charAt(i);\n if (temp.children[c-\'a\'] == null) temp.children[c-\'a\'] = new TrieNode();\n temp = temp.children[c-\'a\'];\n }\n temp.isWord = true;\n }\n }\n \n public boolean search(TrieNode temp, String word, int index, int curr) {\n int len = word.length();\n for (int i = index; i < len; i++) {\n if (temp.children[word.charAt(i)-\'a\'] == null) return false;\n temp = temp.children[word.charAt(i)-\'a\'];\n if (temp.isWord && search(root,word,i+1,curr+1)) return true;\n }\n return curr >= 1 && temp.isWord;\n }\n}\n\nclass TrieNode {\n boolean isWord;\n TrieNode[] children;\n public TrieNode(){\n isWord = false;\n children = new TrieNode[26];\n }\n}\n``` | 13 | 0 | [] | 1 |
concatenated-words | C++ 200ms straightforward Trie+DFS solution without DP | c-200ms-straightforward-triedfs-solution-urlz | \nclass Solution {\nprivate:\n struct Trie\n {\n vector<Trie*> children{26};\n bool end{false};\n };\n \n Trie* root;\n \n vo | ilovehawthorn | NORMAL | 2021-11-07T05:28:37.070688+00:00 | 2021-11-07T05:29:20.459563+00:00 | 816 | false | ```\nclass Solution {\nprivate:\n struct Trie\n {\n vector<Trie*> children{26};\n bool end{false};\n };\n \n Trie* root;\n \n void insert(string& s)\n {\n if (s.empty()) return;\n Trie* cur = root;\n for (char c:s)\n {\n if (cur->children[c-\'a\'] == nullptr)\n cur->children[c-\'a\'] = new Trie();\n cur = cur->children[c-\'a\'];\n }\n cur->end = true;\n }\n \n bool dfs(Trie* root, Trie* node, string& word, int idx, int count)\n {\n if (!node)\n return false;\n \n if (idx >= word.size())\n {\n if (node->end && count >=1 )\n return true;\n else\n return false;\n }\n \n if (node->end && dfs(root, root, word, idx, count+1))\n return true;\n return dfs(root, node->children[word[idx]-\'a\'], word, idx+1, count);\n }\n \npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n sort(words.begin(), words.end(), [](const string& w1, const string& w2) {\n return w1.size() < w2.size();\n });\n \n vector<string> ret;\n root = new Trie();\n \n for(auto &w: words)\n {\n if (w.empty()) continue;\n if(dfs(root, root, w, 0, 0)) \n ret.push_back(w);\n else \n insert(w);\n }\n \n return ret;\n }\n};\n```\n\nThe keys to pass the unit tests.\n1) sort words.\n2) only build trie with un-concatenated words.\n3) handle empty string. | 12 | 1 | ['Depth-First Search', 'Trie', 'C'] | 2 |
concatenated-words | c++(124ms 98%) sorting & Trie & memorisation | c124ms-98-sorting-trie-memorisation-by-z-as9h | New version : fixed for new cases. In old version I want to not use memorisation, but for NEW case of test I need to do it and I done it\nRuntime: 164 ms, faste | zx007pi | NORMAL | 2021-10-26T08:37:21.607311+00:00 | 2022-02-09T15:31:37.740356+00:00 | 918 | false | **New version : fixed for new cases. In old version I want to not use memorisation, but for NEW case of test I need to do it and I done it**\nRuntime: 164 ms, faster than 97.29% of C++ online submissions for Concatenated Words.\nMemory Usage: 242.3 MB, less than 49.85% of C++ online submissions for Concatenated Words.\n```\nclass Trie {\npublic:\n struct Node{\n bool eow;\n Node* nb[26];\n Node(){eow = false; for(int i=0;i!=26;i++) nb[i] = NULL;}\n };\n Node *root;\n\n Trie() {root = new Node(); root->eow = true;}\n \n void insert(string &word) {\n Node *tmp = root;\n \n for(int j = 0, idx ;j < word.size(); j++)\n if(tmp->nb[idx = word[j] - \'a\']) tmp = tmp->nb[idx]; //if this node present\n else //if not\n for(int idx; j != word.size(); j++, tmp = tmp->nb[idx])\n tmp->nb[idx = word[j] - \'a\'] = new Node();\n\n tmp->eow = true;\n }\n \n bool is_concatenated(string &sample, int j, vector<int> &hash){ //check : is the sample concatenation of words from Trie ? \n Node *tmp = root;\n if(hash[j]) return false; \n hash[j] = 1;\n for(int idx; j < sample.size(); j++){ \n if(tmp->nb[idx = sample[j] - \'a\']) tmp = tmp->nb[idx]; \n else return false;\n if(tmp->eow && (j + 1 == sample.size() || is_concatenated(sample, j + 1, hash)) ) return true; \n }\n return false; \n }\n};\n\nclass Solution {\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n sort(words.begin(), words.end(), [](string &a, string &b) -> bool{return a.size() < b.size();});\n Trie t;\n vector<string> answer;\n vector<int> hash;\n \n for(auto &w: words){\n hash.clear(); //hash for indexes\n hash.resize(w.size()+1, 0); //for next word\n if(t.is_concatenated(w,0,hash)) answer.push_back(w);\n else t.insert(w);\n }\n \n return answer; \n }\n};\n```\n\n**Good day !!! FOR NEW CASE OF TEST IT HAVE TLE !!! I try to fix it !!!**\nRuntime: 124 ms, faster than 98.20% of C++ online submissions for Concatenated Words.\nMemory Usage: 241.7 MB, less than 63.26% of C++ online submissions for Concatenated Words.\n**General idea:**\n**1.** Sort our words from array from the smallest to the largest and will consider from the smallest\n**2.** take our current word from array and check : is this word the concatenation of words or not ? if yes : put it into answer **AND NOT PUT INTO Trie** ; if not : add this word into Trie\n**3.** I use my own realisation of Trie from https://leetcode.com/problems/implement-trie-prefix-tree/discuss/1110993/c%2B%2B(44ms-99)-classical-(with-comments)\n```\nclass Trie {\npublic:\n struct Node{\n bool eow;\n Node* nb[26];\n Node(){eow = false; for(int i=0;i!=26;i++) nb[i] = NULL;}\n };\n Node *root;\n\n Trie() {root = new Node(); root->eow = true;}\n \n void insert(string &word) {\n Node *tmp = root;\n \n for(int j = 0, idx ;j < word.size(); j++)\n if(tmp->nb[idx = word[j] - \'a\']) tmp = tmp->nb[idx]; //if this node present\n else //if not\n for(int idx; j != word.size(); j++, tmp = tmp->nb[idx])\n tmp->nb[idx = word[j] - \'a\'] = new Node();\n\n tmp->eow = true;\n }\n \n bool is_concatenated(string &sample, int j){ //check : is the sample concatenation of words from Trie ? \n Node *tmp = root;\n for(int idx; j < sample.size(); j++){\n if(tmp->nb[idx = sample[j] - \'a\']) tmp = tmp->nb[idx]; \n else return false;\n if(tmp->eow && (j + 1 == sample.size() || is_concatenated(sample, j + 1)) ) return true; \n }\n return false; \n }\n};\n\nclass Solution {\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n sort(words.begin(), words.end(), [](string &a, string &b) -> bool{return a.size() < b.size();});\n Trie t;\n vector<string> answer;\n \n for(auto &w: words)\n if(t.is_concatenated(w,0)) answer.push_back(w);\n else t.insert(w);\n \n return answer; \n }\n};\n``` | 12 | 0 | ['C', 'C++'] | 4 |
concatenated-words | 🔥C++|Template for Word Break I,II,Concatenated-words|All U Need✅ | ctemplate-for-word-break-iiiconcatenated-apib | Intuition\n Describe your first thoughts on how to solve this problem. \nIntuition for all the problems:\nAll the three given problems can be divided into sub- | Xahoor72 | NORMAL | 2023-01-27T21:27:25.000706+00:00 | 2023-01-27T21:27:25.000735+00:00 | 332 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIntuition for all the problems:\nAll the three given problems can be divided into sub-problems .And If these subproblems individually satisfy the required conditions, then complete problem will also satisfy the same. And hence we can say whether it is true to find the word in the dictionary or not.\n\n# Approach\n- **Naive Approach**: Use recursion and backtracking. For finding the solution, we check every prefix of the string in the word_dict of words, if it is found , then the recursive function is called for the remaining portion of that string. But this will be$$ 2^n$$ so will give tle . SO we can optimize using memoization or dp.\n- **DP**: So as we can see that in recurion we call for evrery prefix substring and check if its presnt and like this the we check the whole is present or not .So similarly we can store the same ,like upto certain index whether the substring upto that index is present or not . In this way our dp array will be filled with 0\'s and 1\'s representing whether the substring upto that index is present or not . And at last if last index is true i.e dp[n] is true this means whole string is presnt .\n- So applying this logic we can do all the three problems with a little modification based on requirements.\n<!-- Describe your approach to solving the problem. -->\n# **For Word Break I**\n\n# Code\n\n```\n bool wordBreak(string s, vector<string>& wordDict) {\n unordered_set<string>word_set(wordDict.begin(),wordDict.end());\n int n=s.size();\n vector<bool>dp(n+1,0);\n dp[0]=1;\n for(int i=0;i<n;i++){\n if(!dp[i])continue;\n for(int j=i+1;j<=n;j++){\n if( word_set.count(s.substr(i,j-i)))\n dp[j]=1;\n }\n }\n return dp[n];\n }\n```\n# Complexity\n- Time complexity:$$O(N^3)$$\n - $$N^2$$ for two loops and N for `substr`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# **For Word Break II**\n```\nvector<string> wordBreak(string s, vector<string>& wordDict) {\n int n=s.size();\n unordered_set<string>word_Set(wordDict.begin(),wordDict.end());\n vector<vector<string>>dp(n+1,vector<string>());\n dp[0].push_back("");\n \n for(int i = 0; i < n; ++i){\n for(int j = i+1; j <= n; ++j){\n string temp = s.substr(i, j-i);\n if(word_Set.count(temp)){\n for(auto x : dp[i]){\n dp[j].emplace_back(x + (x == "" ? "" : " ") + temp); \n }\n }\n }\n }\n return dp[n];\n }\n```\n# Complexity\n- Time complexity:$$O(N^3)$$\n - $$N^2$$ for two loops and N for `substr`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(N^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# **For concatenated Words**\n```\nclass Solution {\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n unordered_set<string>word_set(words.begin(),words.end());\n vector<string>ans;\n for(auto w:words){\n int n=w.size();\n vector<bool>dp(n+1,false);\n dp[0]=1;\n for(int i=0;i<n;i++){\n if(!dp[i])continue;\n for(int j=i+1;j<=n;j++){\n if(j-i<n and word_set.count(w.substr(i,j-i)))\n dp[j]=1;\n }\n }\n if(dp[n]==1)ans.push_back(w);\n }\n return ans;\n }\n};\n```\n# Complexity\n- Time complexity:$$O(N*W^3)$$\n - where `N=word.length and W = words[i].length`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(N*W)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n | 11 | 0 | ['Hash Table', 'Dynamic Programming', 'Backtracking', 'Depth-First Search', 'C++'] | 0 |
concatenated-words | 472. Concatenated Words - Analysis | 472-concatenated-words-analysis-by-hamle-x8ov | Concatenated Words \nGiven a list of words (without duplicates), please write a program that returns all concatenated words in the given list of words.\nA conca | hamlet_fiis | NORMAL | 2019-02-17T07:16:24.031105+00:00 | 2019-02-17T07:16:24.031183+00:00 | 3,954 | false | <h2>Concatenated Words</h2>\nGiven a list of words (<b>without duplicates</b>), please write a program that returns all concatenated words in the given list of words.\nA concatenated word is defined as a string that is comprised entirely of at least two shorter words in the given array.\n\n**Example**\n<pre><strong>Input:</strong> ["cat","cats","catsdogcats","dog","dogcatsdog","hippopotamuses","rat","ratcatdogcat"]\n<strong>Output: </strong>["catsdogcats","dogcatsdog","ratcatdogcat"]\n<strong>Explanation: </strong> "catsdogcats" can be concatenated by "cats", "dog" and "cats"; \n "dogcatsdog" can be concatenated by "dog", "cats" and "dog"; \n"ratcatdogcat" can be concatenated by "rat", "cat", "dog" and "cat".\n</pre>\n\n<h2 id="solution">Solution</h2>\n<hr>\n<h4>Approach 1: Dynamic Programming</h4>\n<strong>Intuition and Algorithm</strong>\n<p>\nA concatenated word must be formed by 2 or more shorter words. We will iterate through each word and see if this is a <code>concatenated word</code>.\n</p>\n<p>\nLet\'s try for a dynamic programming (DP) solution.\nGiven the input\n\n<code>Words = ["cat","cats","catsdogcats","dog","dogcatsdog","hippopotamuses","rat","ratcatdogcat"]</code>\nWe are going to check, for example, if the word <code>W = ratcatdogcat</code> is concatenated.\nGiven a prefix of size <code>K</code> of the word <code>W</code>, <code>dp[k]</code> returns a boolean if this prefix can be formed by other words in the dictionary. We have:\n</p>\n\n* <code>dp[0] = True,</code> (empy string) base case\n* <code>dp[1] = False,</code> prefix <code>"r" </code> is not formed by other words \n* <code>dp[2] = False,</code> prefix <code>"ra" </code> is not formed by other words\n* <code>dp[3] = True,</code> prefix <code>"rat" </code> exists in W (dictionary)\n* <code>dp[4] = False,</code> prefix <code>"ratc" </code> is not formed by other words\n* <code>dp[5] = False,</code> prefix <code>"ratca" </code> is not formed by other words \n* <code>dp[6] = False,</code> prefix <code>"ratcat" </code> Its formed by 2 words in W <code>rat + cat</code>\n* <code>dp[7] = dp[8] =False,</code> \n* <code>dp[9] = True,</code> prefix <code>"ratcatdog" </code> Its formed by 3 words in W <code>rat + cat +dog</code>\n* <code>dp[10] = dp[11] =False,</code> \n* <code>dp[12] = True,</code> prefix <code>"ratcatdogcat" </code> Its formed by 4 words in W <code>rat + cat +dog + cat</code> (It\'s allowed to repeat a word as <code>cat</code>).\n\nA word is concatenated if <code>dp[N] is true </code> where N is the size of W.\n<code>\n\n\t\tclass Solution {\n\t\tpublic:\n\t\t\n\t\tvector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n\t\t\tvector<string> ans;\n\t\t\tunordered_set<string>dict(words.begin(),words.end());\n\t\t\t\t\n\t\t\tfor(auto w : words){\n\t\t\t\tint n = w.size();\n\t\t\t\tif(n == 0) continue;\n\t\t\t\tbool dp[n+1];\n\t\t\t\tmemset(dp,false,sizeof(dp));\n\t\t\t\tdp[0] = true;\n\t\t\t\n\t\t\t\tfor(int i=0; i<n; i++){\n\t\t\t\t\tif(dp[i] == false) continue;\n\t\t\t\t\tstring generate="";\n\t\t\t\t\n\t\t\t\t\tfor(int j=i; j<n; j++){\n\t\t\t\t\t\tgenerate += w[j];\n\t\t\t\t\t\tif(dp[j+1])continue;\n\t\t\t\t\t\tif(i==0 && j==n-1)continue;\n\t\t\t\t\t\tif(dict.find(generate) != dict.end())\n\t\t\t\t\t\t\tdp[j+1]=true;\n\t\t\t\t\t}\n\t\t\t\t\t\n\t\t\t\t\tif(dp[n]){\n\t\t\t\t\t\tans.push_back(w);\n\t\t\t\t\t\tbreak;\n\t\t\t\t\t}\n\t\t\t\t} \n\t\t\t}\n\t\t\t\t\t\n\t\t\treturn ans;\n\t\t}\n\t};\n</code>\n\n<b>Complexity time </b>\n* O(m * n^3) where m is the length of words and n is the average length of words.\n \nBecause of our improvements, the complexity analysis corresponds to the worst case.\n\n<h4>Approach 2: Trie + Dynamic Programming</h4>\n<strong> Algorithm</strong>\n<p>\nFrom the previous algorithm, in this line, <code>if(dict.find(generate) != dict.end()) </code>. We check if a substring is a word in the dictionary using <code> unordered_set</code>. We could improved it using <b>Trie</b> in constant time.\n</p>\n\n<i>\nThe improvement is not significant, due to the additional memory used to create the Trie, in addition to the weak test cases..\n</i>\n\n<code>\n\n\tclass Solution {\n\tpublic:\t\n\t\tstruct TrieNode { \n\t\t\tTrieNode *children[26];\n\t\t\tbool isTerminal; \n\t\t}; \n\t\n\t\tstruct TrieNode *getNode(void){ \n\t\t\tTrieNode *p = new TrieNode; \n\t\t\tp->isTerminal = false; \n\t\t\tfor (int i = 0; i < 26; i++) \n\t\t\t\tp->children[i] = NULL;\n\t\t\treturn p; \n\t\t} \n\t\t\n\t\tvoid add(TrieNode *p, string w){ \n\t\t\tint n = w.size(); \n\t\n\t\t\tfor (int i = 0; i < n; i++) { \n\t\t\t\tint index = w[i]-\'a\'; \n\t\t\t\tif (!p->children[index]) \n\t\t\t\t\tp->children[index] = getNode(); \n\t\t\t\tp = p->children[index]; \n\t\t\t}\n\t\n\t\t\tp->isTerminal = true; \n\t\t} \n\t\t\n\t\tvector<string> findAllConcatenatedWordsInADict(vector<string>& words){\n\t\t\tTrieNode *root = getNode();\n\t\t\t\n\t\t\tfor (int i = 0; i < words.size(); i++) \n\t\t\t\tadd(root, words[i]);\n\t\t\t\n\t\t\tvector<string> ans;\n\t\t\t\t\t\n\t\t\tfor(auto w : words){\n\t\t\t\tint n = w.size();\n\t\t\t\tif(n == 0) continue;\n\t\t\t\tbool dp[n+1];\n\t\t\t\tmemset(dp,false,sizeof(dp));\n\t\t\t\tdp[0] = true;\n\t\t\t\t\n\t\t\t\tfor(int i=0; i<n; i++){\n\t\t\t\t\tif(dp[i] == false) continue;\n\t\t\t\t\tTrieNode *p = root;\n\t\t\t\t\t\n\t\t\t\t\tfor(int j=i;j<n;j++){\n\t\t\t\t\t\tif (!p->children[w[j]-\'a\'])break;\n\t\t\t\t\t\tp = p->children[w[j]-\'a\'];\n\t\t\t\t\t\tif(i==0 && j==n-1)continue;\n\t\t\t\t\t\tif(p->isTerminal)\n\t\t\t\t\t\t\tdp[j+1]=true;\n\t\t\t\t\t}\n\t\t\t\t\t\n\t\t\t\t\tif(dp[n]){\n\t\t\t\t\t\tans.push_back(w);\n\t\t\t\t\t\tbreak;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t\t\n\t\t\treturn ans;\n\t\t}\n\t};\n\n</code>\n\n<b>Complexity time </b>\n\n* O(m * n^2 + K*26) where <code>m</code> is the length of words ,<code> n</code> is the average length of words and <code>K</code> is the number of nodes in the trie.\n \n The second term represents Trie construction, 26 is the alphabet size. \nBecause of our improvements, the complexity analysis corresponds to the worst case.\n\nAnother implementation, without pointers, (number of nodes in the Trie is setted in <code>50000</code> because of weak cases. \n\n<code>\n\n\tint trie[50000][26];\n\tbool terminal[50000];\n\tclass Solution {\n\tpublic:\n\t\tint node;\n\t\t\n\t\tvoid add(string s){\n\t\t\tint tam = s.size();\n\t\t\tint p = 0; \n\t\t\tfor(int i=0;i<tam;i++){\n\t\t\t\tif(trie[p][s[i]-\'a\'] != 0){\n\t\t\t\t\tp = trie[p][s[i]-\'a\'];\n\t\t\t\t}else{\n\t\t\t\t\tp = trie[p][s[i]-\'a\'] = node++;\n\t\t\t\t}\n\t\t\t}\n\t\t\t\n\t\t\tterminal[p]= true;\n\t\t}\n\t\t\n\t\tvector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n\t\t\tnode = 1;\n\t\t\tvector<string> ans;\n\t\t\tmemset(trie,0,sizeof(trie));\n\t\t\tmemset(terminal,false,sizeof(terminal));\n\t\t\t\n\t\t\tfor(int i=0;i<words.size();i++)\n\t\t\t\tadd(words[i]);\n\t\t\t\n\t\t\tfor(auto w : words){\n\t\t\t\tint n = w.size();\n\t\t\t\tif(n == 0) continue;\n\t\t\t\tbool dp[n+1];\n\t\t\t\tmemset(dp,false,sizeof(dp));\n\t\t\t\tdp[0] = true;\n\t\t\t\t\n\t\t\t\tfor(int i=0; i<n; i++){\n\t\t\t\t\tif(dp[i] == false) continue;\n\t\t\t\t\tint index = 0;\n\t\t\t\t\t\n\t\t\t\t\tfor(int j=i;j<n;j++){\n\t\t\t\t\t\tindex = trie[index][w[j]-\'a\'];\n\t\t\t\t\t\tif(index == 0)break;\n\t\t\t\t\t\tif(i==0 && j==n-1)continue;\n\t\t\t\t\t\tif(terminal[index])\n\t\t\t\t\t\t\tdp[j+1]=true;\n\t\t\t\t\t}\n\t\t\t\t\t\n\t\t\t\t\tif(dp[n]){\n\t\t\t\t\t\tans.push_back(w);\n\t\t\t\t\t\tbreak;\n\t\t\t\t\t}\n\t\t\t\t} \n\t\t\t}\n\t\t\t\n\t\t\treturn ans;\n\t\t}\n\t};\n</code>\n\n | 11 | 2 | ['Dynamic Programming', 'Trie'] | 4 |
concatenated-words | Simple DFS || No Trie || No DP || Easy to understand | simple-dfs-no-trie-no-dp-easy-to-underst-5wk2 | \nclass Solution {\npublic:\n int solve(set<string>&st, string& word, int start)\n {\n if (start >= word.size()) return 0;\n\n string strTil | mohakharjani | NORMAL | 2023-01-27T01:27:51.009418+00:00 | 2023-01-27T01:37:16.933168+00:00 | 1,438 | false | ```\nclass Solution {\npublic:\n int solve(set<string>&st, string& word, int start)\n {\n if (start >= word.size()) return 0;\n\n string strTillPivot = "";\n int mx = INT_MIN;\n for (int pivotIdx = start; pivotIdx < word.size(); pivotIdx++)\n {\n strTillPivot.push_back(word[pivotIdx]);\n if (st.find(strTillPivot) == st.end()) continue;\n \n int nextPartitionCount = solve(st, word, pivotIdx + 1);\n if (nextPartitionCount == INT_MIN) continue;\n\t\t\t//INT_MIN defines that the nextString cannot form a valid partition\n\t\t\t\n int totalPartitions = 1 + nextPartitionCount;\n mx = max(mx, totalPartitions);\n }\n return mx;\n }\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) \n {\n set<string>st;\n for (string& word : words) st.insert(word);\n vector<string>ans;\n for (string word : words)\n {\n int partitionCount = solve(st, word, 0);\n if (partitionCount >= 2) ans.push_back(word); //If we can partition the word in >=2 parts\n }\n return ans;\n \n }\n};\n``` | 9 | 1 | ['Depth-First Search', 'C', 'C++'] | 1 |
concatenated-words | [C++] Simple C++ Code || No Trie || 73% time || 78% space | c-simple-c-code-no-trie-73-time-78-space-sx37 | If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.\n\nclass Solution {\n unord | _pros_ | NORMAL | 2022-07-19T07:27:02.049837+00:00 | 2022-07-19T07:28:04.247062+00:00 | 463 | false | # **If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.**\n```\nclass Solution {\n unordered_map<string, int> um;\n vector<string> ans;\n bool dfs(string &str, int i)\n {\n if(i == str.size())\n {\n return true;\n }\n string tmp = "";\n for(int j = i; j < str.size(); j++)\n {\n tmp += str[j];\n if(j == str.size()-1 && i == 0)\n return false;\n else if(um.count(tmp))\n {\n if(dfs(str, j+1)) return true;\n }\n }\n return false;\n }\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n for(string &str : words)\n um[str]++;\n for(string &str : words)\n {\n if(dfs(str, 0))\n ans.push_back(str);\n }\n return ans;\n }\n};\n``` | 9 | 0 | ['Backtracking', 'Recursion', 'C'] | 1 |
concatenated-words | Python Fast Simple Top-Down Dynamic Programming | python-fast-simple-top-down-dynamic-prog-psjp | python\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n wordset = set(words)\n @cache\n de | ashkan-leo | NORMAL | 2022-05-11T01:54:09.257339+00:00 | 2022-05-11T01:54:09.257369+00:00 | 606 | false | ```python\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n wordset = set(words)\n @cache\n def iscat(word):\n for i in range(1, len(word)):\n if word[:i] in wordset and (word[i:] in wordset or iscat(word[i:])):\n return True\n return False\n \n return [word for word in words if iscat(word)]\n``` | 9 | 0 | ['Python'] | 3 |
concatenated-words | JAVA DP + Trie 75ms | java-dp-trie-75ms-by-guiguia-pyor | Step 1: created Trie from words\nStep 2: check each word\n\tdp[i]: number of concatenated words for substring of word[i, word.length() - 1]\n\tfor each index i | guiguia | NORMAL | 2021-08-11T19:20:09.325434+00:00 | 2021-08-11T19:20:09.325463+00:00 | 373 | false | Step 1: created Trie from words\nStep 2: check each word\n\tdp[i]: number of concatenated words for substring of word[i, word.length() - 1]\n\tfor each index i at each word, check the second part of word[i, n -1] is a word.\n\tdp[i] >= 2 means it can be concatenated from two words \n\t\nTime complexity: O(m * n^2). Geneate Trie. O(m * n). dp check each word O(n^2). m loops\nSpace complexity: O(m * n*). O(m*n) for Trie and O(n) for dp\n\nm: words.length\nn: maximum word length\n```\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n TrieNode root = new TrieNode();\n\t\t//put each word in the Trie\n for(String word : words) {\n insertWord(root, word);\n }\n List<String> result = new ArrayList<>();\n\t\t//check each word\n for (String word : words) {\n if (isConcatenated(word, root)){\n result.add(word);\n }\n }\n return result;\n }\n private boolean isConcatenated(String word, TrieNode root) {\n int[] dp = new int[word.length() + 1];\n dp[word.length()] = 0;\n for (int i = word.length() - 1; i >= 0; i--) {\n TrieNode cur = root;\n dp[i] = -1;\n\t\t\t//check word substring from right to left\n for (int j = i; j < word.length(); j++) {\n cur = cur.children[word.charAt(j) - \'a\'];\n if (cur == null) {\n break;\n }\n\t\t\t\t//if prefix does not exist, no need to check further\n if (cur.isWord && dp[j + 1] != -1) {\n dp[i] = dp[j + 1] + 1;\n if (dp[i] >= 2) {\n break;\n }\n\t\t\t\t\t//once found it can be composed by two words, break\n }\n }\n }\n return dp[0] >= 2;\n }\n private void insertWord(TrieNode root, String word) {\n TrieNode cur = root;\n for (char c : word.toCharArray()) {\n TrieNode next = cur.children[c - \'a\'];\n if (next == null) {\n next = new TrieNode();\n cur.children[c - \'a\'] = next;\n }\n cur = next;\n }\n cur.isWord = true;\n }\n private class TrieNode {\n TrieNode[] children = new TrieNode[26];\n boolean isWord = false;\n }\n}\n``` | 9 | 0 | [] | 0 |
concatenated-words | ✅C++|Very Simple DP |Beats 90%🔥✔ | cvery-simple-dp-beats-90-by-xahoor72-a7ih | Intuition\n Describe your first thoughts on how to solve this problem. \nIdea is to check if a word can be constructed by the concatenation of other words in t | Xahoor72 | NORMAL | 2023-01-27T14:46:22.749063+00:00 | 2023-01-27T14:46:22.749096+00:00 | 718 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIdea is to check if a word can be constructed by the concatenation of other words in the set. Actually first fill all the word in aset that is a perfect data structure to check if a word s present or not . \n# Approach\n<!-- Describe your approach to solving the problem. -->\nSo here we have to check for substring of a word is presnt or not if starting substring is not present then no need to get further if presnt then we add up and atlast check if dp[n] is true or not ,if yes then we push the word in ans vector. \nActually DP array will track the substring upto some index is present or not and at n the index if it is true in dp array then whole word is found and then we push_back that word.\n# Complexity\n- Time complexity:$$O(N*W^3)$$\n - where N=words.length() and W=words[i].length()\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(N*W)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n unordered_set<string>word_set(words.begin(),words.end());\n vector<string>ans;\n for(auto w:words){\n int n=w.size();\n vector<bool>dp(n+1,false);\n dp[0]=1;\n for(int i=0;i<n;i++){\n if(!dp[i])continue;\n for(int j=i+1;j<=n;j++){\n if(j-i<n and word_set.count(w.substr(i,j-i)))\n dp[j]=1;\n }\n }\n if(dp[n]==1)ans.push_back(w);\n }\n return ans;\n }\n};\n``` | 8 | 0 | ['Hash Table', 'String', 'Dynamic Programming', 'Depth-First Search', 'C++'] | 0 |
concatenated-words | ✅ [C++]Easy solution with explanation ✅ | ceasy-solution-with-explanation-by-upadh-8wdh | Intuition\nYou don\'t need to find all the words you just need to check whether the words are made or not , so simply check for the word form (i to j) and then | upadhyayabhi0107 | NORMAL | 2023-01-27T05:56:15.037325+00:00 | 2023-01-27T06:40:54.991922+00:00 | 500 | false | # Intuition\nYou don\'t need to find all the words you just need to check whether the words are made or not , so simply check for the word form (i to j) and then call the check for j + 1;\n\n# Approach\nWhat Function findWord is doing ?\nIt makes a word from i till j where there is word , \neg : [cat , catanddog , and , dog]\nAt catanddog\nc -> not found\n ca -> not found\n cat call for(anddog)-> found then it checks whether there exist a word from after cat and calls for it and before that it increses the count for word and if not found then it decrements the word count.\n\nSimilarly it\'ll check for all the words and call for the next part of the string and check for words in it.\n\n# Complexity\n- Time Complexity : O(words.size() + (words[i].size() * log(words[i].size()))\n\n- Space Complexity : O(words.size())\n# Code\n```\nclass Solution {\npublic:\n bool findWord(set<string>& mp , int i , string & str , int &cnt){\n if(i >= str.size() ){\n return true;\n }\n string temp = "";\n for(int j = i ; j < str.size() ; j++){\n temp += str[j];\n if(mp.find(temp) != mp.end()){\n //cout<<temp<<" : sub\\n";\n cnt++;\n if(findWord(mp , j + 1 , str , cnt)){\n return true;\n }\n cnt--;\n }\n }\n return false;\n }\n vector<string> findAllConcatenatedWordsInADict(vector<string>& wd) {\n int n = wd.size();\n set<string> words;\n vector<string> ans;\n for(auto it : wd){\n words.insert(it);\n }\n int cnt = 0;\n for(int i = 0 ; i < n ; i++){\n string str = wd[i];\n int cnt = 0;\n if(findWord(words , 0 , str , cnt) && cnt >= 2){\n ans.push_back(str);\n }\n }\n return ans;\n }\n};\n``` | 8 | 1 | ['Dynamic Programming', 'Depth-First Search', 'C++'] | 0 |
concatenated-words | Javascript 98.11% fast very very easy to understand solution with video explanation!!! | javascript-9811-fast-very-very-easy-to-u-4icr | If you like my video and explanation, Subscribe please!!! Thank you!!\n\nhttps://youtu.be/LRhVY83R9cI\n\n\n# Code\n\n/**\n * @param {string[]} words\n * @return | rlawnsqja850 | NORMAL | 2023-01-27T01:06:28.011483+00:00 | 2023-01-27T01:06:28.011513+00:00 | 1,042 | false | If you like my video and explanation, Subscribe please!!! Thank you!!\n\nhttps://youtu.be/LRhVY83R9cI\n\n\n# Code\n```\n/**\n * @param {string[]} words\n * @return {string[]}\n */\nvar findAllConcatenatedWordsInADict = function(words) {\n const set = new Set(words);\n let res = []\n\n let isValid = (word) =>{\n if(word.length == 0) return true;\n for(let i =1; i<=word.length;i++){\n let value = word.slice(0,i);\n if(set.has(value)){\n let check = isValid(word.slice(i))\n if(check) return true;\n }\n }\n return false;\n }\n\n for(let word of words){\n set.delete(word);\n if(isValid(word)) res.push(word)\n set.add(word)\n }\n return res;\n};\n``` | 8 | 0 | ['JavaScript'] | 2 |
concatenated-words | Java | Trie & Sort & DFS | 91ms | Some thoughts. | java-trie-sort-dfs-91ms-some-thoughts-by-ri0b | Sort it by length in ascending order because we only need to try to form the current string with shorter strings.\nThen we construct the trie as we go and do a | Student2091 | NORMAL | 2022-07-05T07:19:40.199767+00:00 | 2022-07-05T07:42:19.606088+00:00 | 565 | false | Sort it by length in ascending order because we only need to try to form the current string with shorter strings.\nThen we construct the trie as we go and do a dfs on each word.\n\nFor the DFS, we generally have two possible options:\n- Continue with the current word\n- If the current index has a valid word ended there, start a new DFS from the root Trie.\n\nHere is the normal version that **passed** it in 91ms, but it has a fatal flaw and **should NOT have passed**.\nCould you see where the problem is?\n```Java\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> ans = new ArrayList<>();\n Trie root = new Trie();\n Arrays.sort(words, Comparator.comparingInt(o->o.length()));\n for (String s : words){\n if (dfs(0,s,root,root)){ // check for current word\n ans.add(s);\n }\n Trie cur = root;\n for (char ch : s.toCharArray()){ // build tree\n if (cur.nodes[ch-\'a\']==null){\n cur.nodes[ch-\'a\']=new Trie();\n }\n cur=cur.nodes[ch-\'a\'];\n }\n cur.isWord=true;\n }\n return ans;\n }\n\n private boolean dfs(int idx, String s, Trie cur, Trie root){\n if (cur==null){\n return false;\n }\n if (idx==s.length()){\n return cur.isWord;\n }\n return cur.isWord && dfs(idx,s,root,root)||dfs(idx+1,s,cur.nodes[s.charAt(idx)-\'a\'],root); // two options.\n }\n\n private class Trie {\n Trie[] nodes = new Trie[26];\n boolean isWord;\n Trie(){}\n }\n}\n```\n*Answer:*\nOne may notice that it got TLE for this test case that I discovered:\n```\n["aaaaaaaaaaaaaaaaaaaaaaaaaaab","a","aa","aaa","aaaa","aaaaa","aaaaaa","aaaaaaa","aaaaaaaa","aaaaaaaaa","aaaaaaaaaa","aaaaaaaaaaa","aaaaaaaaaaaa","aaaaaaaaaaaaa","aaaaaaaaaaaaaa","aaaaaaaaaaaaaaaa","aaaaaaaaaaaaaaaaa"]\n```\nHence, we need to add memo to avoid it.\n- In particular, we will not allow DFS to start **anew** at an index that was previous explored anew as well.\n- If you don\'t like to reallocate at most 30 new bytes per word, use `int[]` and a rolling `id` to mark as seen.\n- Byte? isn\'t boolean in Java bit? No, JVM usually reserves 1 byte for boolean.\n```Java\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> ans = new ArrayList<>();\n Trie root = new Trie();\n Arrays.sort(words, Comparator.comparingInt(o->o.length()));\n for (String s : words){\n if (dfs(0,s,root,root, new boolean[s.length()])){\n ans.add(s);\n }\n Trie cur = root;\n for (char ch : s.toCharArray()){\n if (cur.nodes[ch-\'a\']==null){\n cur.nodes[ch-\'a\']=new Trie();\n }\n cur=cur.nodes[ch-\'a\'];\n }\n cur.isWord=true;\n }\n return ans;\n }\n\n private boolean dfs(int idx, String s, Trie cur, Trie root, boolean[] seen){\n if (cur==null){\n return false;\n }\n if (idx==s.length()){\n return cur.isWord;\n }\n if (cur==root){ // memo\n if (seen[idx]){\n return false;\n }\n seen[idx]=true;\n }\n return cur.isWord && dfs(idx,s,root,root,seen)||dfs(idx+1,s,cur.nodes[s.charAt(idx)-\'a\'],root,seen);\n }\n\n private class Trie {\n Trie[] nodes = new Trie[26];\n boolean isWord;\n Trie(){}\n }\n}\n``` | 8 | 0 | ['Trie', 'Java'] | 1 |
concatenated-words | [Python]14 line DP with inline explanation | python14-line-dp-with-inline-explanation-rd95 | \nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n \n wordSet = set(words)\n ans = []\n | diihuu | NORMAL | 2021-02-09T19:07:13.958599+00:00 | 2021-03-03T04:25:21.702074+00:00 | 609 | false | ```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n \n wordSet = set(words)\n ans = []\n # 1) For each word w, For loop w[:i] \n # 2) check if the front segment[0:j] is in wordSet and if the [j+1: i] is in the wordset\n # EDGE CASE: cats is in wordSet but not concatenated, catsdog is in wordSet but also concatenated\n # SOLUTION to edge case: instead of storing True/False, store the concatenated time, base is 1, and 2 means it is\n # concatenated with "" + word, which is the word itself\n # 3) If yes:w[:i] is concatenated=> dp[-1] > 2, append to ans, BREAK(to pass the edge case full of "a")\n \n for i, w in enumerate(words):\n dp = [0] * (len(w) + 1)\n dp[0] = 1\n for i in range(1, len(w) + 1):\n for j in range(i):\n if dp[j] and w[j: i] in wordSet:\n dp[i] = max(dp[i], dp[j] + 1)\n if dp[i] > 2:\n break\n if dp[-1] > 2:\n ans.append(w)\n return ans\n \n``` | 8 | 0 | [] | 1 |
concatenated-words | Easy Python | 100% Speed | Highly Optimized | easy-python-100-speed-highly-optimized-b-0ajx | Easy Python | 100% Speed | Highly Optimized\n\nThe Python code below corresponds to a simple solution based on:\n\n1. Matching substrings against a global set ( | aragorn_ | NORMAL | 2020-07-20T21:33:58.436965+00:00 | 2020-09-04T23:06:02.323722+00:00 | 1,784 | false | **Easy Python | 100% Speed | Highly Optimized**\n\nThe Python code below corresponds to a simple solution based on:\n\n1. Matching substrings against a global set (I experimented using "Tries" originally, but they don\'t provide any benefits).\n\n2. Using Binary Search to look for compatible substring lengths (the process is still O(n), but it\'s a significant boost).\n\n3. Using Depth-First Search to look for complete matches for a word.\n\nThe comments inside the code provide further insights. I hope you find it helpful. Cheers,\n\nPS. Those notes about bisect_right, and bisect_left changed my life lol\n```\n# Python 2/3\nfrom bisect import bisect_right,bisect_left\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words):\n words = set([word for word in words if word]) # Filter Empty Words\n #\n # Find Compatible substring lengths using binary search\n nlens = sorted( set(map(len,words)) )\n def getsizes(L,i):\n # BISECT USAGE:\n # bisect_left -> a[lo:i] < x <= a[i:hi]\n # bisect_right -> a[lo:i] <= x < a[i:hi]\n if i:\n Lj = bisect_right(nlens,L) # include L\n else:\n Lj = bisect_left(nlens,L) # exclude L\n # Yield Reversed without delay\n for j in range(Lj-1,-1,-1):\n yield nlens[j]\n #\n # DFS matching function:\n def dfs(i,word,L):\n if i == L:\n return True\n #\n for a in getsizes(L-i,i):\n if word[i:i+a] in words and dfs(i+a,word,L):\n return True\n return False\n #\n # Final Loop:\n res = []\n for word in words:\n if dfs(0,word,len(word)):\n res.append(word)\n #\n return res\n``` | 8 | 1 | ['Python', 'Python3'] | 5 |
concatenated-words | Short and easy recursive solution | short-and-easy-recursive-solution-by-ani-9kmh | Use ranges to split a particular word into two: w[..i] and w[i..]:\ncsharp\npublic class Solution\n{\n public IList<string> FindAllConcatenatedWordsInADict(s | anikit | NORMAL | 2023-01-27T11:05:58.225271+00:00 | 2023-01-27T11:30:52.046667+00:00 | 1,394 | false | Use ranges to split a particular word into two: `w[..i]` and `w[i..]`:\n```csharp\npublic class Solution\n{\n public IList<string> FindAllConcatenatedWordsInADict(string[] words)\n {\n HashSet<string> ws = new(words);\n return words.Where(w => IsConcatenated(w)).ToList();\n\n bool IsConcatenated(string w, int count = 0)\n {\n if (w.Length == 0) return count > 1;\n\n for (int i = 1; i <= w.Length; i++)\n {\n if (ws.Contains(w[..i]) && IsConcatenated(w[i..], count + 1)) return true;\n }\n \n return false;\n }\n }\n}\n```\n\nThe same logic can be expressed in a more concise way, looks horrible though:\n```csharp\npublic class Solution\n{\n public IList<string> FindAllConcatenatedWordsInADict(string[] words)\n {\n HashSet<string> ws = new(words);\n return words.Where(w => IsConcatenated(w)).ToList();\n\n bool IsConcatenated(string w, int count = 0) =>\n w.Length == 0 && count > 1\n || Enumerable.Range(1, w.Length)\n .Where(i => ws.Contains(w[..i]) && IsConcatenated(w[i..], count + 1))\n .Any();\n }\n}\n``` | 7 | 0 | ['Depth-First Search', 'Recursion', 'C#'] | 0 |
concatenated-words | JAVA || EASY UNDERSTAING || USING RECURSION || DFS | java-easy-understaing-using-recursion-df-raqo | Code\n\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String>al=new ArrayList<>();\n Set<Stri | shaikhu3421 | NORMAL | 2023-01-27T03:15:30.453714+00:00 | 2023-01-27T03:15:30.453765+00:00 | 1,856 | false | # Code\n```\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String>al=new ArrayList<>();\n Set<String>hs=new HashSet<>();\n for(String i:words) hs.add(i);\n Map<String,Integer>hm=new HashMap<>();\n for(String i:words) if(check(i,hs,hm)) al.add(i);\n return al;\n }\n public static boolean check(String i,Set<String>hs,Map<String,Integer>hm){\n if(hm.containsKey(i)) return hm.get(i)==1;\n for(int z=0;z<i.length();z++){\n if(hs.contains(i.substring(0,z))){\n String s1=i.substring(z);\n if(hs.contains(s1)||check(s1,hs,hm)){\n hm.put(i,1);\n return true;\n }\n }\n }\n hm.put(i,0);\n return false;\n }\n}\n```\nUPVOTE IF U LIKE THE APPROACH | 7 | 0 | ['Depth-First Search', 'Java'] | 4 |
concatenated-words | ✔️ [Python3] TRIE WITH RECURSION ᕕ( ᐛ )ᕗ, Explained | python3-trie-with-recursion-fi-waa-fo-ex-jqvr | UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.\n\nWe create a trie data structure from all given words. Then w | artod | NORMAL | 2022-06-24T04:05:10.750492+00:00 | 2022-06-24T04:05:10.750525+00:00 | 566 | false | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nWe create a trie data structure from all given words. Then we iterate over the characters of every word. When we see that a current prefix is in the trie, we call a recursive function asking whether the slice of the word starting after the prefix is a concatenated word.\n\nTime: **O(n)**\nSpace: **O(n)**\n\n```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n ddic = lambda: defaultdict(ddic)\n trie = ddic()\n \n for word in words:\n cur = trie\n for char in word:\n cur = cur[char]\n\n cur[\'end\'] = True\n \n def isConcat(word, start):\n cur = trie\n for i in range(start, len(word)):\n char = word[i]\n if char not in cur:\n return False\n cur = cur[char]\n\n if \'end\' in cur:\n if i + 1 == len(word):\n # tricky part that helps us distinguish simple word from concat word\n return start != 0\n \n if isConcat(word, i + 1):\n return True\n\n return False\n \n return [word for word in words if isConcat(word, 0)]\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 7 | 0 | ['Python3'] | 0 |
concatenated-words | C++ Soln || Trie + DFS | c-soln-trie-dfs-by-mitedyna-5l2m | \nclass Solution {\npublic:\n struct trie{\n trie* child[26];\n bool isend;\n };\n trie* root;\n trie* getnode(){\n trie* node= | mitedyna | NORMAL | 2021-05-30T23:29:14.543466+00:00 | 2021-05-30T23:29:14.543507+00:00 | 767 | false | ```\nclass Solution {\npublic:\n struct trie{\n trie* child[26];\n bool isend;\n };\n trie* root;\n trie* getnode(){\n trie* node=new trie;\n for(int i=0;i<26;i++){\n node->child[i]=NULL;\n }\n node->isend=false;\n return node;\n }\n void addword(string s){\n trie *cur=root;\n for(int i=0;i<s.length();i++){\n if(!cur->child[s[i]-\'a\'])cur->child[s[i]-\'a\']=getnode();\n cur=cur->child[s[i]-\'a\'];\n }\n cur->isend=true;\n }\n bool search(string w) {\n trie* cur=root;\n for(int i=0;i<w.length();i++){\n if(!cur->child[w[i]-\'a\'])return false;\n cur=cur->child[w[i]-\'a\'];\n }\n return (cur!=NULL && cur->isend);\n }\n vector<string> res;\n bool sol(string word, int count){\n if(count>1 && search(word))return true;\n for(int j=0;j<word.length()-1;j++){\n string left=word.substr(0,j+1);\n string right=word.substr(j+1);\n if(search(left) && sol(right, count+1)) return true;\n \n }\n return false;\n }\n \n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n root=getnode();\n bool flag=false;\n vector<string> ans;\n for(int i=0;i<words.size();i++){\n if(words[i]=="")continue;\n addword(words[i]);\n \n }\n for(auto &w:words){\n if(w=="")continue;\n if(sol(w,1))ans.push_back(w);\n }\n return ans;\n \n }\n};\n``` | 7 | 2 | ['Depth-First Search', 'Trie', 'C'] | 2 |
concatenated-words | [Recursion, Memoization] JS Solution | recursion-memoization-js-solution-by-hbj-25s8 | \nvar findAllConcatenatedWordsInADict = function(words) {\n let m = new Map(), memo = new Map();\n let res = [];\n for (let i = 0; i < words.length; i+ | hbjorbj | NORMAL | 2020-11-13T04:02:29.298713+00:00 | 2020-11-17T22:41:17.811743+00:00 | 807 | false | ```\nvar findAllConcatenatedWordsInADict = function(words) {\n let m = new Map(), memo = new Map();\n let res = [];\n for (let i = 0; i < words.length; i++) {\n m.set(words[i], 1);\n }\n for (let i = 0; i < words.length; i++) {\n if (isConcat(words[i], m, memo)) res.push(words[i]);\n }\n return res;\n};\n\nfunction isConcat(word, m, memo) {\n if (memo.has(word)) return memo.get(word);\n for (let i = 1; i < word.length; i++) {\n let prefix = word.slice(0, i);\n let suffix = word.slice(i);\n if (m.has(prefix) && (m.has(suffix) || isConcat(suffix, m, memo))) {\n memo.set(word, true);\n return true;\n }\n }\n \n memo.set(word, false);\n return false;\n};\n\n// Time Complexity: O(n*k^2) where k is the maximum length of word\n// Space Complexity: O(max(n, k)) because call stack can go as much as k\n``` | 7 | 0 | ['JavaScript'] | 3 |
concatenated-words | 📌📌Python3 || ⚡347 ms, faster than 91.39% of Python3 | python3-347-ms-faster-than-9139-of-pytho-i1vb | \ndef findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n wordset = set(words)\n result = []\n def dfs(word, wordset):\ | harshithdshetty | NORMAL | 2023-01-27T12:33:07.958861+00:00 | 2023-01-27T12:33:07.958926+00:00 | 1,003 | false | ```\ndef findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n wordset = set(words)\n result = []\n def dfs(word, wordset):\n if word == "":\n return True\n for i in range(len(word)):\n if word[:i+1] in wordset:\n if dfs(word[i+1:], wordset):\n return True\n return False\n for word in words:\n wordset.remove(word)\n if dfs(word, wordset):\n result.append(word)\n wordset.add(word)\n return result\n``` | 6 | 1 | ['Depth-First Search', 'Ordered Set', 'Python', 'Python3'] | 1 |
concatenated-words | ✅ C++ || ✅ Explained || ✅ Simple approach ||🚀 EASY RECURSION || Using SET | c-explained-simple-approach-easy-recursi-r1l9 | PLZ UPVOTE\n\n\n# Code\n\nclass Solution {\npublic:\n\n //Our lc function breaks the word into two parts left and right\n // and check if these are alread | Sarthakberi | NORMAL | 2023-01-27T06:34:45.307019+00:00 | 2023-01-27T06:35:55.437649+00:00 | 750 | false | # PLZ UPVOTE\n\n\n# Code\n```\nclass Solution {\npublic:\n\n //Our lc function breaks the word into two parts left and right\n // and check if these are already present in our dictionary \n //or can be formed using the words presnt in dictionary\n\n bool lc(string s , set<string>&dictionary){\n\n for(int i=1; i<s.size(); ++i){\n\n string left=s.substr(0,i);\n string right=s.substr(i);\n \n //iterators for the string to check their presence\n auto ii=dictionary.find(left);\n auto j=dictionary.find(right);\n \n // if left is found then right is also found \n //or our right can be made\n\n if(ii!=dictionary.end()){\n if(j!=dictionary.end() or lc(right,dictionary)) return true;\n }\n }\n\n return false;\n }\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n \n //Made for storing the answer\n vector<string> beri;\n\n //Making a set of the string (dictionary) for all the words \n set<string> dictionary;\n for(auto i:words) dictionary.insert(i);\n \n //we are checking if the particular word can be made\n // from other words presnt inside the dictionary\n for(auto i :words){\n if(lc(i,dictionary)) beri.push_back(i);\n }\n\n return beri;\n }\n};\n```\n | 6 | 0 | ['Array', 'String', 'Recursion', 'Ordered Set', 'C++'] | 1 |
concatenated-words | C++ || EASY TO UNDERSTAND || Simple BackTracking Siolution | c-easy-to-understand-simple-backtracking-rb1q | \nclass Solution {\npublic:\n set<string> dict;\n bool check(string &word,int c)\n {\n if(word.size()==0)\n {\n // cout<<c<<en | aarindey | NORMAL | 2022-07-08T01:09:05.435990+00:00 | 2022-07-08T01:09:05.436032+00:00 | 320 | false | ```\nclass Solution {\npublic:\n set<string> dict;\n bool check(string &word,int c)\n {\n if(word.size()==0)\n {\n // cout<<c<<endl;\n if(c>=2)\n return true;\n \n return false;\n }\n\n for(int i=1;i<=word.size();i++)\n {\n string left=word.substr(0,i);\n string right=word.substr(i);\n if(dict.find(left)!=dict.end())\n {\n ++c;\n if(check(right,c))\n {\n return true;\n }\n --c;\n }\n }\n return false;\n }\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n vector<string> ans;\n for(auto &word:words)\n {\n dict.insert(word);\n }\n for(auto &word:words)\n {\n if(check(word,0))\n {\n ans.push_back(word);\n }\n }\n return ans;\n }\n};\n```\n**Please upvote to motivate me in my quest of documenting all leetcode solutions. HAPPY CODING:)\nAny suggestions and improvements are always welcome**\n | 6 | 0 | [] | 1 |
concatenated-words | My simple Java Solution using DP. No sort. | my-simple-java-solution-using-dp-no-sort-ufqx | \nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> result = new ArrayList<>();\n Set<Str | sumitrawat | NORMAL | 2020-09-05T08:34:03.233003+00:00 | 2020-09-05T08:34:03.233050+00:00 | 842 | false | ```\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> result = new ArrayList<>();\n Set<String> set = new HashSet<>();\n for(String word: words)\n set.add(word);\n for(String word: words){\n if(helper(word, set)){\n result.add(word);\n }\n }\n return result;\n }\n private boolean helper(String s, Set<String> set){\n int len = s.length();\n if(len == 0)\n return false;\n boolean[] dp = new boolean[len + 1];\n dp[0] = true;\n for(int i = 0; i <= len; i++){\n for(int j = i - 1 ; j >= 0; j--){ // running this loop in the backwards direction saves time\n if(i == len && j == 0) // we can\'t consider the string to be made up of itself i.e we ignore s.substring(0, len)\n continue;\n if(dp[j] && set.contains(s.substring(j,i))){\n dp[i] = true;\n break;\n } \n }\n }\n return dp[len];\n }\n}\n```\nThe time complexity of this solution is O( N * len^3) were N is the size of words array and len is the length of the string | 6 | 0 | ['Dynamic Programming', 'Java'] | 5 |
concatenated-words | Java Nice & Small, whats the TimeComplexity? | java-nice-small-whats-the-timecomplexity-y3fh | \nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> aList = new ArrayList<>();\n if(words | nirmal4343 | NORMAL | 2020-05-17T22:08:09.784089+00:00 | 2020-05-17T22:08:09.784166+00:00 | 617 | false | ```\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> aList = new ArrayList<>();\n if(words.length == 0) return aList;\n Set<String> wordSet = new HashSet<>();\n for (String string : words) {\n wordSet.add(string);\n }\n for (String word : words) {\n if(canConcatinate(word, wordSet)) {\n aList.add(word);\n }\n }\n return aList;\n }\n\n private boolean canConcatinate(String word, Set<String> wSet) {\n for (int i = 1 ; i < word.length(); i++) {\n String prefix = word.substring(0 , i);\n String suffix = word.substring(i , word.length());\n if(wSet.contains(prefix) && (wSet.contains(suffix) || canConcatinate(suffix, wSet))) {\n return true;\n }\n }\n return false;\n }\n}\n``` | 6 | 0 | ['Java'] | 2 |
concatenated-words | python concise dfs solution | python-concise-dfs-solution-by-nio_up_to-60pp | ```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:#dfs to search.\n def dfs(w,oneGood):#return True or F | NIO_up_to_moon | NORMAL | 2019-11-07T00:18:18.117086+00:00 | 2019-11-07T00:18:18.117134+00:00 | 408 | false | ```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:#dfs to search.\n def dfs(w,oneGood):#return True or False\n if w in Set and oneGood:\n return True\n if w in memo:\n return memo[w]\n for i in range(len(w)-1):#[:i+1] and [i+1:] part \n if w[:i+1] in Set and dfs(w[i+1:],True):\n memo[w]=True\n return True\n memo[w]=False\n return False \n \n memo={}#cache visited word\'s result \n res=[]\n Set=set(words)\n for w in words:\n if dfs(w,False):\n res.append(w)\n return res | 6 | 0 | [] | 0 |
concatenated-words | python trie solution | python-trie-solution-by-shuuchen-bp45 | sort words by word length, so that short words are inserted firstly\n* insert words into trie one by one, if all of sub-words already exist in trie, return Fals | shuuchen | NORMAL | 2019-10-31T06:20:21.385113+00:00 | 2019-10-31T06:20:21.385163+00:00 | 460 | false | * sort words by word length, so that short words are inserted firstly\n* insert words into trie one by one, if all of sub-words already exist in trie, return False.\n\n```\nclass TrieNode:\n def __init__(self):\n self.isWord = False\n self.children = collections.defaultdict(TrieNode)\n\nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n \n def insert(self, word):\n node = self.root\n for i, c in enumerate(word):\n node = node.children[c]\n if node.isWord:\n if self.exists(word[i+1:]):\n return False\n else:\n continue\n node.isWord = True\n return True\n \n def exists(self, word):\n node = self.root\n for i, c in enumerate(word):\n if c in node.children:\n node = node.children[c]\n if node.isWord:\n if i == len(word)-1 or self.exists(word[i+1:]):\n return True\n else:\n continue\n else:\n return False\n\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n \n trie = Trie()\n \n return [word for word in sorted(words, key=len) if not trie.insert(word)] | 6 | 0 | [] | 1 |
concatenated-words | O(N*L) | O(N*L) | Python Solution | Explained | onl-onl-python-solution-explained-by-tfd-eprj | Hello Tenno Leetcoders, \n\nFor this problem, we want to return all non duplicated concatenated words\n\nThis problem has the same logic as 139. Word Break. Th | TFDLeeter | NORMAL | 2023-01-27T18:25:30.926957+00:00 | 2023-01-27T18:25:46.928429+00:00 | 482 | false | Hello **Tenno Leetcoders**, \n\nFor this problem, we want to return all non duplicated `concatenated words`\n\nThis problem has the same logic as `139. Word Break`. This problem has its differences though because we want only words that are concatenated by 2 or more other words\n\nWe can use `Dynamic Programming` to break the problem down and try to form a single word by using words in our array.\n\n### Dynamic Programming\n\n1) Iterate over our given array and try to form a word by checking if each given word is a `concatenation` of other words\n\n2) If we found a word that is a concatenation of other words, we will add it to our result\n\n\n\n### Code\n```\ndef findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n \n words_set = set(words)\n \n result = []\n \n def dfs(word):\n for i in range(len(word)):\n \n if word[:i+1] in words_set and word[i+1:] in words_set:\n return True\n\t\t\t\t\t\n if word[:i+1] in words_set and dfs(word[i+1:]):\n return True\n\n return False\n \n for word in words:\n if dfs(word):\n result.append(word)\n return result\n```\n\n#### Time Complexity: O(N*L)\n#### Space Complexity: O(N*L)\n\n\n***Upvote if this tenno\'s discussion helped you in some type of way***\n \n***Warframe\'s short pvp clip of the day***\n\n | 5 | 0 | ['Dynamic Programming', 'Python', 'Python3'] | 3 |
concatenated-words | C++ || Simple || Brute Force Recursion with Memoization || 🔥🔥 | c-simple-brute-force-recursion-with-memo-v84p | Intuition\nWe check for each word given and if it is comprised entirely of at least two shorter words in the given array then we store it in our ans vector.\n\n | i_anurag_mishra | NORMAL | 2023-01-27T16:35:39.294393+00:00 | 2023-08-07T10:16:34.641159+00:00 | 235 | false | # Intuition\nWe check for each word given and if it is comprised entirely of at least two shorter words in the given array then we store it in our ans vector.\n\n# Approach\nIterate through the each word. If upto any particular index, it is present in given vector then call recursively for next indices. Cnt shows how much time recursive function is called (cnt>1 shows every word concatenates at least two words given in array).\n\n\n# Code\n```\nclass Solution {\n unordered_set<string> st;\n int dp[10000][30][31];\n bool check(int idx, vector<string>& words, int i, int cnt)\n {\n if(idx==words[i].size())\n {\n if(cnt>1) return true;\n return false;\n }\n if(dp[i][idx][cnt]!=-1) return dp[i][idx][cnt];\n for(int k=idx; k<words[i].size(); k++)\n {\n string t=words[i].substr(idx, k-idx+1);\n if(st.find(t) != st.end() && check(k+1, words, i, cnt+1)) \n {\n return dp[i][idx][cnt] = 1;\n }\n }\n return dp[i][idx][cnt] = 0;\n }\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) \n {\n int n=words.size();\n vector<string> ans;\n for(auto &w: words) st.insert(w);\n memset(dp, -1, sizeof(dp));\n for(int i=0; i<n; i++)\n {\n if(check(0, words, i, 0)) ans.push_back(words[i]);\n } \n return ans; \n }\n};\n``` | 5 | 0 | ['Dynamic Programming', 'Recursion', 'C++'] | 2 |
concatenated-words | JAVA | Simple Recursion | Explained ✅ | java-simple-recursion-explained-by-souri-nbc2 | ---\n# Please Upvote \uD83D\uDE07\n---\njava []\nclass Solution {\n // globally declare a hashset to store all the words \n private Set<String> set = new | sourin_bruh | NORMAL | 2023-01-27T16:31:28.189099+00:00 | 2023-01-28T11:04:30.861867+00:00 | 852 | false | ---\n# Please Upvote \uD83D\uDE07\n---\n``` java []\nclass Solution {\n // globally declare a hashset to store all the words \n private Set<String> set = new HashSet<>();\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n // add the words to the set\n for (String w : words) {\n set.add(w);\n }\n\n // initialise answer arraylist\n List<String> ans = new ArrayList<>();\n // iterate over words[]\n for (String w : words) {\n if (isConcat(w)) { // if the method returns a true,\n ans.add(w); // we add the word to answer list\n }\n }\n\n return ans;\n }\n\n // this method tells us if the word is a concatenation of other words\n private boolean isConcat(String s) {\n // we will partition the word into 2 words\n for (int i = 0; i < s.length(); i++) {\n String prefix = s.substring(0, i); // first part\n String suffix = s.substring(i); // second part\n // if both the parts are present in set means that\n // the original word is a concatenation\n // if the prefix is not in set, we will create the next prefix\n // s = "catsdogcats", we have the prefix "cat" which is not in set\n // so we would make the next prefix "cats", which is present in set\n // we are left with "dogcats" as suffix. It is not present in set\n // (if it were present in set we would have got our answer)\n // Now we would recusively call isConcat() to partition "dogcats" the way we did "catsdogcats"\n // it\'ll make further partitions of the suffix and check if the partitions are present in set\n if (set.contains(prefix) && (set.contains(suffix) || isConcat(suffix))) {\n return true; // return true if we find that the word is a concatenation\n }\n }\n\n // no partitioning could create the word, means no concatenation possible\n return false; // so return false\n }\n}\n\n// TC: O(n * k), SC: O(n)\n```\n---\n### Clean solution:\n``` java []\nclass Solution {\n private Set<String> set = new HashSet<>();\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n for (String w : words) {\n set.add(w);\n }\n\n List<String> ans = new ArrayList<>();\n for (String w : words) {\n if (isConcat(w)) { \n ans.add(w); \n }\n }\n\n return ans;\n }\n\n private boolean isConcat(String s) { \n for (int i = 0; i < s.length(); i++) {\n String prefix = s.substring(0, i); \n String suffix = s.substring(i); \n if (set.contains(prefix) && (set.contains(suffix) || isConcat(suffix))) {\n return true; \n }\n }\n\n return false; \n }\n}\n```\n---\n#### Time complexity: $$O(n * k)$$\n`n` be the number of strings in the `word` array. \n`k`be the length of each individual word in words array.\n#### Space complexity: $$O(n)$$\nWe are creating a hashset and putting all the words (from words array) into it.\n | 5 | 0 | ['String', 'Recursion', 'Java'] | 3 |
concatenated-words | Java dp 22 lines and beat 90% with comments | java-dp-22-lines-and-beat-90-with-commen-ny7u | This is the medium question "139. Word Break" + a for loop. \nIf the input size of the list is N and the average of the word length is M.\nTo solve Leetcode 139 | yupeng1127 | NORMAL | 2022-03-07T06:42:48.345937+00:00 | 2022-03-07T06:42:48.345962+00:00 | 642 | false | This is the medium question "139. Word Break" + a for loop. \nIf the input size of the list is N and the average of the word length is M.\nTo solve Leetcode 139, we have two dp approaches:\n1.For each position in a word, we loop through all the words in the List and update the dp arrays. BigO: N * M * N\n2.For each word, we loop through all the possible sub strings to find a match in the List and update the dp arrays. BigO: N * M * M\nFor this one, since N is bigger than M, so we use the 2nd approach.\n(I have also tried the 1 approach, and I got a ETL).\n\n```\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> result = new ArrayList<>();\n HashSet<String> set = new HashSet<>();\n for(String word : words) set.add(word); \n for(String word : words) helper(result, set, word); \n return result;\n } \n private void helper(List<String> list, HashSet<String> set, String word){\n if(word.length() == 0) return;\n boolean[] dp = new boolean[word.length() + 1];\n dp[0] = true;\n for(int i = 0; i < word.length(); i++){\n if(!dp[i]) continue;\n for(int j = i + 1; j < dp.length; j++){\n if(i == 0 && j == word.length()) continue;\n if(set.contains(word.substring(i,j)))dp[j] = true; \n }\n } \n if(dp[dp.length - 1]) list.add(word); \n }\n}\n\n\n``` | 5 | 0 | ['Dynamic Programming', 'Java'] | 1 |
concatenated-words | Python | Trie | python-trie-by-__aj-d15d | \tclass Trie:\n\n\t\tdef init(self):\n\t\t\tself.root = dict()\n\n\t\tdef insert(self, words):\n\t\t\tfor word in words:\n\t\t\t\tcurrent = self.root\n\t\t\t\tf | __AJ__ | NORMAL | 2021-12-20T09:37:27.905289+00:00 | 2021-12-20T09:37:27.905430+00:00 | 1,139 | false | \tclass Trie:\n\n\t\tdef __init__(self):\n\t\t\tself.root = dict()\n\n\t\tdef insert(self, words):\n\t\t\tfor word in words:\n\t\t\t\tcurrent = self.root\n\t\t\t\tfor char in word:\n\t\t\t\t\tif char not in current:\n\t\t\t\t\t\tcurrent[char] = dict()\n\t\t\t\t\tcurrent = current[char]\n\t\t\t\tcurrent[\'*\'] = \'*\'\n\n\t\t@lru_cache()\n\t\tdef search(self, target):\n\t\t\tif target == \'\':\n\t\t\t\treturn True\n\n\t\t\tresult = False\n\t\t\tnode = self.root\n\n\t\t\tfor index, char in enumerate(target):\n\t\t\t\tif char not in node:\n\t\t\t\t\tbreak\n\t\t\t\tnode = node[char]\n\t\t\t\tif \'*\' in node:\n\t\t\t\t\tresult = result or self.search(target[index+1:])\n\t\t\t\t\tif result:\n\t\t\t\t\t\tbreak\n\t\t\treturn result\n\n\tclass Solution:\n\t\tdef findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n\t\t\tobj = Trie()\n\t\t\tobj.insert(words)\n\t\t\tfinal = []\n\t\t\tfor word in words:\n\t\t\t\tnode = obj.root\n\t\t\t\tfor index , char in enumerate(word):\n\t\t\t\t\tnode=node[char]\n\t\t\t\t\tif "*" in node:\n\t\t\t\t\t\tif index!=len(word)-1 and obj.search(word[index+1:]):\n\t\t\t\t\t\t\tfinal.append(word)\n\t\t\t\t\t\t\tbreak\n\t\t\treturn final\n\t\t\t\n**If You Like The Solution Upvote.** | 5 | 1 | ['Trie', 'Python', 'Python3'] | 1 |
concatenated-words | Java: Trie | java-trie-by-ankurpremi-30pt | Note: With the new test cases this solution gives TLE.\n\n\n\n\npublic List<String> findAllConcatenatedWordsInADict(String[] words) {\n TrieNode root = b | ankurpremi | NORMAL | 2020-12-06T18:42:24.895938+00:00 | 2020-12-28T17:31:11.369099+00:00 | 463 | false | Note: With the new test cases this solution gives TLE.\n\n\n```\n\npublic List<String> findAllConcatenatedWordsInADict(String[] words) {\n TrieNode root = buildTrie(words);\n List<String> result = new ArrayList();\n for(String word : words){\n if(searchWords(root, word, 0, 0))\n result.add(word);\n }\n return result;\n }\n \n private boolean searchWords(TrieNode root, String word, int idx, int count){\n\n int n = word.length();\n TrieNode node = root;\n for(int i=idx ; i<n ; i++){\n char c = word.charAt(i);\n node = node.next[c - \'a\'];\n if(node == null) return false;\n \n if(node.isWord){\n //check at the end\n if(i == n-1){\n //check at least this word is made of more than 1 word\n return count >= 1;\n } else{\n if(searchWords(root, word, i+1, count+1))\n return true;\n }\n }\n \n }\n return false;\n }\n \n private TrieNode buildTrie(String[] words){\n TrieNode root = new TrieNode();\n for(String word : words){\n if(word.isEmpty()) continue;\n TrieNode node = root;\n for(int i=0 ; i<word.length() ; i++){\n char c = word.charAt(i);\n if(node.next[c - \'a\'] == null){\n node.next[c - \'a\'] = new TrieNode();\n }\n node = node.next[c - \'a\'];\n }\n node.isWord = true;\n }\n return root;\n }\n \n class TrieNode{\n TrieNode[] next = new TrieNode[26];\n boolean isWord;\n }\n\n``` | 5 | 0 | [] | 1 |
concatenated-words | [Java] Clean code with Trie | java-clean-code-with-trie-by-algorithmim-xko7 | \npublic List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> result = new ArrayList<>(); \n Trie root = new Trie();\ | algorithmimplementer | NORMAL | 2020-01-26T18:41:58.301695+00:00 | 2020-01-26T18:43:32.974392+00:00 | 308 | false | ``` \npublic List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> result = new ArrayList<>(); \n Trie root = new Trie();\n // Insert each word \n for (String word : words) {\n if (word.length() == 0) continue;\n Trie node = root; \n for (char c : word.toCharArray()) {\n if (node.next[c - \'a\'] == null) \n node.next[c - \'a\'] = new Trie();\n node = node.next[c - \'a\'];\n }\n node.word = word;\n } \n for (String word : words)\n if (search(word, 0, root, root))\n result.add(word);\n \n return result;\n }\n \n private boolean search(String word, int index, Trie node, Trie root) {\n // tricky : the last word of the concatenated word is definitely storing the last word\n if (index == word.length())\n return node.word != null && !node.word.equals(word); \n \n Trie current = node.next[word.charAt(index) - \'a\'];\n \n if (current == null) return false;\n \n // only time when you found word and the search for the rest of the words are true which is searched from the root\n if (current.word != null && \n search(word, index + 1, root, root)) return true;\n \n // Keep moving with the next index\n return search(word, index + 1, current, root);\n }\n \n class Trie {\n Trie[] next = new Trie[26];\n String word;\n }\n``` | 5 | 0 | [] | 0 |
concatenated-words | 💡JavaScript Solution | javascript-solution-by-aminick-0c3b | The idea\n1. Sort the array by length\n2. Use dynamic programming (bottom up) to check whether array[0,i-1] is a concatenated word\n3. Build the dp array as we | aminick | NORMAL | 2019-12-05T11:17:11.341210+00:00 | 2019-12-05T11:17:11.341243+00:00 | 641 | false | ### The idea\n1. Sort the array by length\n2. Use dynamic programming (bottom up) to check whether array[0,i-1] is a concatenated word\n3. Build the dp array as we iterate through the word from left to right using `end` pointer. Iterate array[0, end-1] use another point `start`. This way, we essentially split the question into 2 parts, array[0,start-1] (which is just dp[start])and array[start, end-1].\n``` javascript\nvar findAllConcatenatedWordsInADict = function(words) {\n words.sort((a,b)=>a.length-b.length);\n let wordList = new Set();\n let allConcat = [];\n let isConcat = function(word) {\n if (!word) return false;\n let dp = new Array(word.length+1).fill(false);\n dp[0] = true;\n for (let end=1;end<=word.length;end++) {\n for (let start=0;start<end;start++) {\n if (dp[start] && wordList.has(word.slice(start, end))) {\n dp[end] = true;\n break;\n }\n }\n }\n return dp.pop();\n }\n\n for (let i=0;i<words.length;i++) {\n if(isConcat(words[i])) {\n allConcat.push(words[i]);\n }\n wordList.add(words[i]);\n }\n return allConcat;\n};\n``` | 5 | 0 | ['JavaScript'] | 1 |
concatenated-words | [Kotlin] Dynamic Programming Word Concatenation Finder | kotlin-dynamic-programming-word-concaten-asdu | Intuition\nTo solve this problem, we can use dynamic programming. We iterate through each word in the input list and check if it can be formed by concatenating | teogor | NORMAL | 2024-04-14T12:02:24.541308+00:00 | 2024-04-14T12:02:24.541339+00:00 | 10 | false | # Intuition\nTo solve this problem, we can use dynamic programming. We iterate through each word in the input list and check if it can be formed by concatenating shorter words from the list.\n\n# Approach\n1. **Word Set Creation**: We start by creating a set called `wordSet` to store all the words in the input list. This set will allow us to efficiently check if a word exists in the list.\n\n2. **Iterating Through Words**: We iterate through each word in the input list. For each word, we temporarily remove it from the `wordSet` to prevent self-concatenation.\n\n3. **Dynamic Programming Check**: We use dynamic programming to check if the current word can be formed by concatenating shorter words from the `wordSet`. We initialize a dynamic programming array called `dp` with a length one more than the length of the current word. We set `dp[0] = true` to indicate that an empty string can be formed. Then, we iterate through each position in the word and check if the substring up to that position can be formed by concatenating shorter words. If we find a match, we set `dp[i] = true`.\n\n4. **Result Construction**: After checking all positions in the word, if `dp[word.length]` is true, it means the entire word can be formed by concatenating shorter words. In this case, we add the word to the result list.\n\n5. **Restore Word to Set**: Finally, we restore the word to the `wordSet` to maintain its presence for subsequent iterations.\n\n# Complexity Analysis\n- **Time complexity**: \n - Creating the `wordSet` takes `O(n)` time, where `n` is the number of words.\n - Iterating through each word and performing dynamic programming check takes `O(n * l^2)` time, where `l` is the average length of words.\n - Overall, the time complexity is `O(n^2 * l^2)`.\n\n- **Space complexity**: \n - The word set `wordSet` requires `O(n)` space.\n - The dynamic programming array `dp` requires `O(l)` space.\n - Overall, the space complexity is `O(n + l)`.\n\n# Code\n```\nclass Solution {\n fun findAllConcatenatedWordsInADict(words: Array<String>): List<String> {\n val result = mutableListOf<String>()\n val wordSet = words.toHashSet()\n for (word in words) {\n wordSet.remove(word)\n if (canForm(word, wordSet)) {\n result.add(word)\n }\n wordSet.add(word)\n }\n return result\n }\n \n private fun canForm(word: String, wordSet: Set<String>): Boolean {\n if (word.isEmpty()) return false\n val dp = BooleanArray(word.length + 1)\n dp[0] = true\n for (i in 1..word.length) {\n for (j in 0 until i) {\n if (dp[j] && wordSet.contains(word.substring(j, i))) {\n dp[i] = true\n break\n }\n }\n }\n return dp[word.length]\n }\n}\n\n``` | 4 | 0 | ['Array', 'String', 'Dynamic Programming', 'Kotlin'] | 0 |
concatenated-words | 472: Solution with step by step explanation | 472-solution-with-step-by-step-explanati-sjff | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. Create a set of all words in the given list.\n2. Define a recursive fu | Marlen09 | NORMAL | 2023-03-10T17:29:50.349903+00:00 | 2023-03-10T17:29:50.349944+00:00 | 489 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create a set of all words in the given list.\n2. Define a recursive function called isConcat to check if a word is concatenated.\n3. Memoize the isConcat function using the functools.lru_cache decorator to cache its results and improve performance.\n4. For a given word, try all possible splits of the word by iterating over its characters using a for loop.\n5. For each split, get the prefix and suffix of the split using string slicing.\n6. Check if the prefix is in the wordSet.\n7. If the prefix is in the wordSet, check if the suffix is either in the wordSet or can be formed by concatenating other words by recursively calling the isConcat function on the suffix.\n8. If the suffix is either in the wordSet or can be formed by concatenating other words, then the word is concatenated and we can return True from the isConcat function.\n9. If none of the splits result in a concatenated word, then the word is not concatenated and we can return False from the isConcat function.\n10. Use a list comprehension to get all concatenated words by iterating over the words in the input list and calling the isConcat function on each word.\n11. Return the list of concatenated words.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n # Create a set of all words in the given list\n wordSet = set(words)\n\n # Define a recursive function to check if a word is concatenated\n @functools.lru_cache(None) # Memoize the function with least-recently-used cache\n def isConcat(word: str) -> bool:\n for i in range(1, len(word)): # Try all possible splits of the word\n prefix = word[:i] # Get the prefix of the split\n suffix = word[i:] # Get the suffix of the split\n if prefix in wordSet and (suffix in wordSet or isConcat(suffix)):\n # If the prefix is in the wordSet and the suffix is either in the wordSet\n # or can be formed by concatenating other words, then the word is\n # concatenated\n return True\n return False\n\n # Use a list comprehension to get all concatenated words\n return [word for word in words if isConcat(word)]\n\n``` | 4 | 0 | ['Array', 'Dynamic Programming', 'Depth-First Search', 'Python', 'Python3'] | 0 |
concatenated-words | 🗓️ Daily LeetCoding Challenge January, Day 27 | daily-leetcoding-challenge-january-day-2-46wr | This problem is the Daily LeetCoding Challenge for January, Day 27. Feel free to share anything related to this problem here! You can ask questions, discuss wha | leetcode | OFFICIAL | 2023-01-27T00:00:32.246772+00:00 | 2023-01-27T00:00:32.246844+00:00 | 3,267 | false | This problem is the Daily LeetCoding Challenge for January, Day 27.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/concatenated-words/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain this 0 approach in the official solution</summary>
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br> | 4 | 0 | [] | 18 |
concatenated-words | JAVA || HashSet || EFFICIENT APPOACH || LEARNER FRIENDLY || RECURSION | java-hashset-efficient-appoach-learner-f-wbqg | \nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> result = new ArrayList<>();\n \n | duke05 | NORMAL | 2022-10-10T18:09:29.843141+00:00 | 2022-10-10T19:16:35.992778+00:00 | 660 | false | ```\nclass Solution {\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n List<String> result = new ArrayList<>();\n \n Set<String> dict = new HashSet<>(Arrays.asList(words));\n \n for (String word : words) {\n if(form(word, dict)) {\n result.add(word);\n }\n }\n return result ;\n }\n \n public boolean form(String word, Set<String> dict) {\n for (int i=1; i<word.length(); i++) {\n String left = word.substring(0, i) ;\n String right = word.substring(i) ;\n\n if(dict.contains(left)) {\n if(dict.contains(right) || form(right, dict)) {\n return true;\n }\n }\n }\n return false;\n }\n}\n```\n\n | 4 | 0 | ['Recursion', 'Java'] | 0 |
concatenated-words | Concatenated Words | Python3 Solution | with comments | Time complexity analysis | concatenated-words-python3-solution-with-jaqi | \'\'\'\n\n\tdef findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n # creating a hashset of words for faster look-up\n wordset | tushar_goel | NORMAL | 2021-11-30T18:11:53.405656+00:00 | 2021-11-30T18:11:53.405701+00:00 | 266 | false | \'\'\'\n\n\tdef findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n # creating a hashset of words for faster look-up\n wordset = set(words)\n # List to store the final desired output\n result = []\n # Hashmap for keeping account of word of the wordset\n dict_map = {}\n \n # DfS algorithm for calculating concatenated words\n def dfs(word):\n # if the word is already present in the hashMap, return its value\n if word in dict_map:\n return dict_map[word]\n \n # Going over the prefix and suffix of the given word to check whether they exist in the wordset\n # If yes, then return True and update the hashMap value of that word to True\n for indx in range(1,len(word)):\n prefix = word[:indx]\n suffix = word[indx:]\n \n if prefix in wordset and suffix in wordset:\n dict_map[word] = True\n return True\n elif prefix in wordset and dfs(suffix):\n dict_map[word] = True\n return True\n \n dict_map[word] = False\n return False\n # Going over each word in words list\n for word in words:\n if dfs(word):\n # Appending the word to the result \n result.append(word)\n return result\n \nTime Complexity:- O(MN)\nHere,\nM --> Number of words in a word list\nN --> Length of word\n\nHope this helps. Thanks! | 4 | 0 | ['Depth-First Search', 'Recursion', 'Ordered Set'] | 1 |
concatenated-words | Python | Beats 97% runtime | Trie | python-beats-97-runtime-trie-by-rajatrai-k7wt | \nclass Solution:\ndef findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n\ttrie={}\n\tfor w in words:\n\t\troot=trie\n\t\tfor s in w:\n\t\t | rajatrai1206 | NORMAL | 2021-11-12T07:02:02.512582+00:00 | 2021-11-12T07:02:02.512625+00:00 | 682 | false | ```\nclass Solution:\ndef findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n\ttrie={}\n\tfor w in words:\n\t\troot=trie\n\t\tfor s in w:\n\t\t\tif s not in root:\n\t\t\t\troot[s]={}\n\t\t\troot=root[s]\n\t\troot["$"]=True\n\n\t@lru_cache(None)\n\tdef find(w):\n\t\tif not w:\n\t\t\treturn True\n\t\ttmp=trie\n\t\tval=False\n\t\tfor i,s in enumerate(w):\n\t\t\tif s not in tmp:\n\t\t\t\tbreak\n\t\t\ttmp=tmp[s]\n\t\t\tif "$" in tmp:\n\t\t\t\tval|= find(w[i+1:])\n\t\t\t\tif val:\n\t\t\t\t\tbreak\n\t\treturn val\n\n\tres=[]\n\tfor w in words:\n\t\troot=trie\n\t\tfor i,s in enumerate(w):\n\t\t\troot=root[s]\n\t\t\tif "$" in root:\n\t\t\t\tif i!=len(w)-1 and find(w[i+1:]):\n\t\t\t\t\tres.append(w)\n\t\t\t\t\tbreak\n\treturn res\n\n```\n | 4 | 0 | ['Trie', 'Python'] | 0 |
concatenated-words | (C++) 472. Concatenated Words | c-472-concatenated-words-by-qeetcode-n4xe | \n\nclass TrieNode {\npublic: \n TrieNode* children[26] = {nullptr}; \n bool word = false; \n ~TrieNode() {\n for (auto& child : children) \n | qeetcode | NORMAL | 2021-09-15T01:25:08.341873+00:00 | 2021-09-15T01:25:08.341906+00:00 | 532 | false | \n```\nclass TrieNode {\npublic: \n TrieNode* children[26] = {nullptr}; \n bool word = false; \n ~TrieNode() {\n for (auto& child : children) \n delete child; \n }\n}; \n\nclass Trie {\n TrieNode* root = nullptr; \npublic: \n Trie() { root = new TrieNode(); }\n \n ~Trie() { delete root; }\n \n void insert(string word) {\n TrieNode* node = root; \n for (int i = word.size()-1; i >= 0; --i) {\n if (!node->children[word[i] - \'a\'])\n node->children[word[i] - \'a\'] = new TrieNode(); \n node = node->children[word[i] - \'a\']; \n }\n node->word = true; \n }\n \n bool search(string word) {\n vector<bool> dp(1 + word.size()); \n dp[0] = true; \n for (int i = 0; i < word.size(); ++i) {\n TrieNode* node = root; \n for (int j = i; j >= 0; --j) {\n if (!node->children[word[j] - \'a\']) break; \n node = node->children[word[j] - \'a\']; \n if (dp[j] && node->word) {\n dp[i+1] = true; \n break; \n }\n }\n }\n return dp.back(); \n }\n}; \n\n\nclass Solution {\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n sort(words.begin(), words.end(), [](const string& w1, const string& w2) { return (w1.size() < w2.size()); });\n vector<string> ans;\n \n Trie* trie = new Trie(); \n for (auto& word : words) \n if (word.size()) {\n if (trie->search(word)) ans.push_back(word); \n trie->insert(word); \n }\n \n delete trie; \n return ans;\n }\n};\n``` | 4 | 0 | ['C'] | 1 |
concatenated-words | [Python3] hash | python3-hash-by-ye15-p3kn | \n\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n seen = set(words)\n \n @cache\n | ye15 | NORMAL | 2021-09-14T22:20:02.151032+00:00 | 2021-09-15T01:43:39.197435+00:00 | 421 | false | \n```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n seen = set(words)\n \n @cache\n def fn(word):\n """Return True if input is a concatenated word."""\n for i in range(1, len(word)): \n prefix = word[:i]\n suffix = word[i:]\n if prefix in seen and (suffix in seen or fn(suffix)): return True \n return False \n \n ans = []\n for word in words: \n if fn(word): ans.append(word)\n return ans \n```\n\n```\nclass Trie: \n \n def __init__(self): \n self.root = {}\n \n def insert(self, word): \n node = self.root\n for ch in reversed(word): \n node = node.setdefault(ch, {})\n node["#"] = True\n \n def search(self, word): \n """Return True if input is a concatenated word."""\n dp = [True] + [False] * len(word)\n for i in range(len(word)): \n node = self.root\n for j in reversed(range(i+1)): \n if word[j] not in node: break \n node = node[word[j]]\n if dp[j] and node.get("#"):\n dp[i+1] = True \n break \n return dp[-1]\n\n\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n ans = []\n trie = Trie()\n for word in sorted(words, key=len): \n if word: \n if trie.search(word): ans.append(word)\n trie.insert(word)\n return ans\n``` | 4 | 0 | ['Python3'] | 2 |
concatenated-words | Two Approaches 1.) Memo + DFS 2.) DP | two-approaches-1-memo-dfs-2-dp-by-agingw-j472 | Memo + DFS:\n\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n wordSet = set(words)\n rv = []\n | agingwolverine | NORMAL | 2021-09-08T02:34:35.906276+00:00 | 2021-09-08T02:41:15.870113+00:00 | 695 | false | Memo + DFS:\n```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n wordSet = set(words)\n rv = []\n for wd in words:\n memo = {}\n wordSet.remove(wd)\n if len(wd) > 0 and self.dfs(wd, wordSet, memo):\n rv.append(wd)\n wordSet.add(wd) \n return rv\n \n def dfs(self, s, wordSet, memo):\n if len(s) == 0:\n return True\n \n if s in memo:\n return memo[s]\n \n result = False\n nw = \'\'\n for c in s:\n nw += c\n if nw in wordSet and self.dfs(s[len(nw):], wordSet, memo):\n result = True\n break\n \n memo[s] = result\n return result \n```\t\t\n\t\nDP:\n```\n\tclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n wordSet = set(words)\n rv = []\n for wd in words:\n if len(wd) == 0:\n continue\n wordSet.remove(wd)\n dp = [False for _ in range(len(wd)+1)]\n dp[0] = True\n for i in range(len(wd)):\n for j in range(i+1, len(wd)+1):\n ss = wd[i:j]\n if ss in wordSet and dp[i]:\n dp[j] = True\n wordSet.add(wd)\n if dp[len(wd)]:\n rv.append(wd)\n return rv\n```\t\t\n\t\t | 4 | 0 | ['Depth-First Search', 'Python'] | 0 |
concatenated-words | C# DP solution | c-dp-solution-by-newbiecoder1-d83l | \npublic class Solution {\n public IList<string> FindAllConcatenatedWordsInADict(string[] words) {\n \n List<string> res = new List<string>();\ | newbiecoder1 | NORMAL | 2021-07-05T22:13:49.379846+00:00 | 2021-07-05T22:13:49.379876+00:00 | 396 | false | ```\npublic class Solution {\n public IList<string> FindAllConcatenatedWordsInADict(string[] words) {\n \n List<string> res = new List<string>();\n if(words == null || words.Length == 0)\n return res;\n \n HashSet<string> wordSet = new HashSet<string>();\n Array.Sort(words, (a,b) => a.Length - b.Length);\n foreach(var word in words)\n {\n if(IsConcatenated(word, wordSet))\n res.Add(word);\n \n wordSet.Add(word);\n }\n \n return res;\n }\n \n public bool IsConcatenated(string word, HashSet<string> wordSet)\n {\n if(wordSet.Count == 0)\n return false;\n \n bool[] dp = new bool[word.Length + 1];\n dp[0] = true;\n \n // check substrings starting with length 1 for current word\n for(int i = 1; i <= word.Length; i++)\n {\n // check if the substring is concatenated\n // divide the substring into 2 parts, the 1st part has length j\n for(int j = 0; j < i; j++)\n { \n if(dp[j] && wordSet.Contains(word.Substring(j, i - j)))\n {\n dp[i] = true;\n break;\n }\n }\n }\n \n return dp[word.Length];\n }\n}\n``` | 4 | 0 | [] | 1 |
concatenated-words | Java || DFS || Similar to Word Break | java-dfs-similar-to-word-break-by-legend-kb8b | \n\t// O(log(words.lengthlog(words.length)) + O(words.lengthwords[i].length^2))\n\tpublic List findAllConcatenatedWordsInADict(String[] words) {\n\n\t\tList res | LegendaryCoder | NORMAL | 2021-02-27T03:44:51.522889+00:00 | 2021-02-27T05:14:09.518989+00:00 | 425 | false | \n\t// O(log(words.length*log(words.length)) + O(words.length*words[i].length^2))\n\tpublic List<String> findAllConcatenatedWordsInADict(String[] words) {\n\n\t\tList<String> res = new ArrayList<String>();\n\t\tif (words.length == 1)\n\t\t\treturn res;\n\n\t\tArrays.sort(words, new Comparator<String>() {\n\t\t\t@Override\n\t\t\tpublic int compare(String o1, String o2) {\n\t\t\t\treturn o1.length() - o2.length();\n\t\t\t}\n\t\t});\n\n\t\tHashSet<String> dict = new HashSet<String>();\n\t\tfor (String word : words) {\n\t\t\tif (word.length() != 0 && wordBreak(word, dict))\n\t\t\t\tres.add(word);\n\t\t\tdict.add(word);\n\t\t}\n\n\t\treturn res;\n\t}\n\n\t// O(s.length^2)\n\tpublic boolean wordBreak(String s, HashSet<String> dict) {\n\t\tint[] memo = new int[s.length()];\n\t\tint len = s.length();\n\t\treturn wordBreakDFS(len - 1, s, dict, memo);\n\t}\n\n\t// O(s.length^2)\n\tpublic boolean wordBreakDFS(int start, String s, HashSet<String> dict, int[] memo) {\n\n\t\tif (start == -1)\n\t\t\treturn true;\n\n\t\tif (memo[start] == 1)\n\t\t\treturn false;\n\n\t\tboolean ans = false;\n\t\tfor (int i = start; i >= 0; i--) {\n\t\t\tif (dict.contains(s.substring(i, start + 1))) {\n\t\t\t\tans = wordBreakDFS(i - 1, s, dict, memo);\n\t\t\t\tif (ans)\n\t\t\t\t\treturn true;\n\t\t\t}\n\t\t}\n\t\tmemo[start] = 1;\n\t\treturn false;\n\t}\n\n | 4 | 0 | [] | 0 |
concatenated-words | Trie + DFS Solution [C++] | trie-dfs-solution-c-by-kalel_ms-33qu | \nclass TrieNode {\npublic:\n bool isKey = false;\n TrieNode* child[26];\n};\n\nclass Solution {\npublic:\n TrieNode* root = new TrieNode();\n \n | kalEl_ | NORMAL | 2020-09-08T05:20:13.041815+00:00 | 2020-09-08T05:20:13.041868+00:00 | 433 | false | ```\nclass TrieNode {\npublic:\n bool isKey = false;\n TrieNode* child[26];\n};\n\nclass Solution {\npublic:\n TrieNode* root = new TrieNode();\n \n void addWord (string word) {\n TrieNode* curr = root;\n for(char c : word) {\n if(!curr->child[c - \'a\'])\n curr->child[c - \'a\'] = new TrieNode();\n curr = curr->child[c - \'a\'];\n }\n curr->isKey = true;\n }\n \n bool search (string word, int index, int count) {\n if(index >= word.size()) return count >= 2;\n \n TrieNode* curr = root;\n \n for(int i = index; i < word.size(); i++) {\n char c = word[i];\n if(!curr->child[c - \'a\'])\n return false;\n curr = curr->child[c - \'a\'];\n if(curr->isKey) {\n if(search(word, i + 1, count + 1))\n return true;\n }\n }\n return false;\n }\n \n vector<string> findAllConcatenatedWordsInADict (vector<string>& words) {\n vector<string> res;\n if(words.size() == 0) \n return res;\n for(string s : words)\n addWord(s);\n for(string s : words) {\n if(search(s, 0, 0))\n res.push_back(s);\n }\n return res;\n }\n};\n``` | 4 | 0 | ['Depth-First Search', 'Trie', 'Recursion', 'C++'] | 2 |
concatenated-words | Python | Trie + Memo | Simple | python-trie-memo-simple-by-ared25-gg4e | \nclass Solution:\n def findAllConcatenatedWordsInADict(self, words):\n t, memo, res = Trie(), {}, []\n for word in words:\n t.add(w | ared25 | NORMAL | 2020-02-17T07:17:13.330974+00:00 | 2021-11-16T00:24:13.593942+00:00 | 1,289 | false | ```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words):\n t, memo, res = Trie(), {}, []\n for word in words:\n t.add(word)\n for word in words:\n if t.helper(word, 0, len(word) - 1, 0, memo):\n res.append(word)\n return res\n\n\nclass Node:\n def __init__(self):\n self.children = {}\n self.is_end = False\n\n\nclass Trie:\n def __init__(self):\n self.root = Node()\n\n def add(self, word):\n p = self.root\n for c in word:\n if c not in p.children:\n p.children[c] = Node()\n p = p.children[c]\n p.is_end = True\n\n\n def helper(self, word, st, end, cnt, memo):\n p = self.root\n curr = word[st: end + 1]\n if curr in memo: \n return memo[curr]\n \n for x in range(st, end + 1):\n if word[x] in p.children:\n p = p.children[word[x]]\n if p.is_end:\n if x == end:\n return cnt >= 1\n if self.helper(word, x + 1, end, cnt + 1, memo):\n memo[curr] = True\n return True\n else:\n break\n \n memo[curr] = False\n return False\n``` | 4 | 0 | ['Trie', 'Recursion', 'Python'] | 7 |
concatenated-words | Python DP Simple Solution with 3 Lines | python-dp-simple-solution-with-3-lines-b-f52e | \nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n s = set(words)\n \n memo = {}\n d | thseong | NORMAL | 2019-11-22T09:50:57.674787+00:00 | 2019-11-28T09:04:21.770813+00:00 | 635 | false | ```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n s = set(words)\n \n memo = {}\n def isConcatenatedWord(w):\n if w in memo: return memo[w]\n \n for i in range(1, len(w)):\n if w[:i] not in s: continue\n \n r = w[i:]\n if r in s or isConcatenatedWord(r):\n memo[w] = True\n return True\n \n memo[w] = False\n return False\n \n return filter(isConcatenatedWord, words)\n```\n\n3 lines Solution :P\n```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n s, m = set(words), {}\n dp = lambda w: m[w] if w in m else any(w[:i] in s and (w[i:] in s or dp(w[i:])) for i in range(1, len(w)))\n return filter(dp, words)\n``` | 4 | 0 | ['Dynamic Programming', 'Python3'] | 1 |
concatenated-words | Python naive solution beats 99% and 100% | python-naive-solution-beats-99-and-100-b-gkvg | \nclass Solution(object):\n def findAllConcatenatedWordsInADict(self, words):\n words = set(words)\n\t\t\n def is_concatenated(word):\n | jdjw | NORMAL | 2019-10-20T04:37:10.677725+00:00 | 2019-10-20T04:37:29.302051+00:00 | 334 | false | ```\nclass Solution(object):\n def findAllConcatenatedWordsInADict(self, words):\n words = set(words)\n\t\t\n def is_concatenated(word):\n for i in range(1, len(word)):\n if word[:i] in words and (word[i:] in words or is_concatenated(word[i:])):\n return True\n return False\n \n return [word for word in words if is_concatenated(word)]\n``` | 4 | 0 | [] | 0 |
concatenated-words | very simple and clean solutions on Java (2 approaches) | very-simple-and-clean-solutions-on-java-5voev | \n\tApproach #1 Backtracking:\n \n\tpublic List findAllConcatenatedWordsInADict(String[] words) {\n Set hash = new HashSet<>(Arrays.asList(words));\n\n | jisqaqov | NORMAL | 2019-10-06T08:22:05.621525+00:00 | 2019-10-06T08:22:35.556186+00:00 | 537 | false | \n\tApproach #1 Backtracking:\n \n\tpublic List<String> findAllConcatenatedWordsInADict(String[] words) {\n Set<String> hash = new HashSet<>(Arrays.asList(words));\n\n List<String> list = new ArrayList<>();\n for (String word : words) {\n if (concatenated(word, 0, hash)) {\n list.add(word);\n }\n }\n\n return list;\n }\n\n private boolean concatenated(String word, int i, Set<String> words) {\n StringBuilder sb = new StringBuilder();\n\n for (int k = i; k < word.length(); k++) {\n sb.append(word.charAt(k));\n if (words.contains(sb.toString())) {\n if (concatenated(word, k + 1, words)) {\n return true;\n }\n }\n }\n\n return sb.length() > 0 && sb.length() < word.length() && words.contains(sb.toString());\n }\n\t\n\tApproach #2 Trie + DFS:\n\t\n\tpublic List<String> findAllConcatenatedWordsInADict(String[] words) {\n Trie trie = new Trie();\n\n for (String word : words) {\n trie.addWord(word);\n }\n\n List<String> solution = new ArrayList<>();\n\n for (String word : words) {\n if (isConcatenated(trie.root, word, 0)) {\n solution.add(word);\n }\n }\n\n return solution;\n }\n\n private boolean isConcatenated(TrieNode root, String word, int index) {\n int counter = 0;\n\n TrieNode node = root;\n\n for (int i = index; i < word.length(); i++) {\n counter++;\n\n char ch = word.charAt(i);\n\n if (!node.map.containsKey(ch)) {\n return false;\n }\n\n node = node.map.get(ch);\n if (node.isWord) {\n if (i == word.length() - 1 && counter < word.length()) {\n return true;\n } else if (i < word.length() - 1 && isConcatenated(root, word, i + 1)) {\n return true;\n }\n }\n }\n\n return false;\n }\n\n private static class Trie {\n private TrieNode root = new TrieNode();\n\n private void addWord(String word) {\n TrieNode node = root;\n\n for (int i = 0; i < word.length(); i++) {\n char ch = word.charAt(i);\n\n if (node.map.containsKey(ch)) {\n node = node.map.get(ch);\n } else {\n node.map.put(ch, new TrieNode());\n node = node.map.get(ch);\n }\n }\n\n node.isWord = true;\n }\n }\n\n private static class TrieNode {\n Map<Character, TrieNode> map = new HashMap<>();\n boolean isWord = false;\n } | 4 | 0 | ['Backtracking', 'Depth-First Search', 'Trie'] | 2 |
concatenated-words | C# HashSet + WordBreak | c-hashset-wordbreak-by-bacon-pp0j | \npublic class Solution {\n public IList<string> FindAllConcatenatedWordsInADict(string[] words) {\n var result = new List<string>();\n if (wor | bacon | NORMAL | 2019-07-31T03:57:02.665885+00:00 | 2019-07-31T03:57:02.665940+00:00 | 550 | false | ```\npublic class Solution {\n public IList<string> FindAllConcatenatedWordsInADict(string[] words) {\n var result = new List<string>();\n if (words.Length <= 2) return result;\n\n var wordSet = new HashSet<string>(words);\n foreach (var word in words) {\n if (word == "") continue;\n\n wordSet.Remove(word);\n\n var canBreak = WordBreak(word, wordSet);\n\n if (canBreak) result.Add(word);\n wordSet.Add(word);\n }\n\n return result;\n }\n\n private bool WordBreak(string s, HashSet<string> dict) {\n if (s.Length == 0) return false;\n\n var n = s.Length;\n var dp = new bool[n + 1];\n dp[n] = true;\n\n for (int i = n - 1; i >= 0; --i) {\n for (int j = i; j < n; ++j) {\n if (dp[j + 1] && dict.Contains(s.Substring(i, j - i + 1))) {\n dp[i] = true;\n break;\n }\n }\n }\n\n return dp[0];\n }\n}\n``` | 4 | 0 | [] | 0 |
concatenated-words | Python DFS Solution | python-dfs-solution-by-ycyc-sfnr | \nclass Solution(object):\n def findAllConcatenatedWordsInADict(self, words):\n """\n :type words: List[str]\n :rtype: List[str]\n | ycyc | NORMAL | 2016-12-29T01:28:15.776000+00:00 | 2016-12-29T01:28:15.776000+00:00 | 1,206 | false | ```\nclass Solution(object):\n def findAllConcatenatedWordsInADict(self, words):\n """\n :type words: List[str]\n :rtype: List[str]\n """\n word_set = set(words)\n ans = []\n def helper(w, cur, cnt):\n if cur == len(w):\n if cnt > 1:\n return True\n else:\n return False\n for i in xrange(cur + 1, len(w) + 1):\n if w[cur : i] in word_set and helper(w, i, cnt + 1):\n return True\n return False\n for w in words:\n if helper(w, 0, 0):\n ans.append(w)\n return ans\n\n``` | 4 | 0 | [] | 2 |
concatenated-words | [Python3] Simple DFS & Set: 111ms | Beats 91.31% | python3-beats-90-simple-dfs-set-solution-p27f | IntuitionThe key insight is that each word in the list can potentially be formed by concatenating other words from the list. We need to check if we can split a | Leo_Ouyang | NORMAL | 2024-12-26T21:06:21.824411+00:00 | 2025-01-08T21:38:44.119323+00:00 | 330 | false | # Intuition
The key insight is that each word in the list can potentially be formed by concatenating other words from the list. We need to check if we can split a word into multiple valid words that exist in our dictionary. This is a perfect case for using recursion with dynamic programming principles.
# Approach
1. First, convert the list of words into a set for O(1) lookup times
2. Create a helper function `dfs()` that will:
- Try to split the current word at every possible position
- Check if the prefix exists in our word set
- Recursively check if the remaining suffix can be formed from dictionary words
3. For each word:
- Remove it from the set (to avoid using the word itself)
- Check if it can be formed by concatenating other words
- Add it back to the set
4. Use a set to memoize incorrect combinations to avoid redundant work
# Code
```python
class Solution:
def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:
res = []
word_set = set(words)
incorrect = set()
def dfs(word):
if word in word_set:
return True
elif word in incorrect:
return False
else:
for i in range(1, len(word)):
if word[:i] in word_set:
if dfs(word[i:]):
return True
else:
incorrect.add(word[i:])
incorrect.add(word)
return False
for word in words:
word_set.remove(word)
if dfs(word):
res.append(word)
word_set.add(word)
return res
```
# Complexity
- Time complexity: $$O(n * 2^m)$$ where n is the number of words and m is the length of the longest word.
- Space complexity: $$O(n)$$ for the word_set and incorrect set, plus $$O(m)$$ for the recursion stack depth. | 3 | 0 | ['Python3'] | 0 |
concatenated-words | Clean Java Solution With Trie + DP | clean-java-solution-with-trie-dp-by-bard-0te9 | Intuition\nBuild the Trie with the Input words, then recursively check whether each word can be broken down such that all partitions are present in the Trie\n\n | bardock | NORMAL | 2023-11-05T00:18:49.584966+00:00 | 2023-11-05T00:18:49.584989+00:00 | 229 | false | # Intuition\nBuild the Trie with the Input words, then recursively check whether each word can be broken down such that all partitions are present in the Trie\n\n# Approach\nI did not come up with this, original solution is by @gracemeng\n\n\n# Code\n```\nclass Solution {\n class Trie {\n Map<Character, Trie> children;\n String word;\n Trie() {\n this.children = new HashMap<>();\n this.word = null;\n }\n void add(String s) {\n Trie node = this;\n for(char c : s.toCharArray()) {\n node = node.children.computeIfAbsent(c, k->new Trie());\n }\n node.word = s;\n }\n }\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n Trie root = new Trie();\n for(String word : words) {\n root.add(word);\n }\n List<String> result = new ArrayList<>();\n\n for(String word : words) {\n Boolean[] dp = new Boolean[word.length()];\n boolean count = isWordConcatenated(root, word, 0, 0, dp);\n if(count) {\n result.add(word);\n }\n }\n \n return result;\n \n }\n \n boolean isWordConcatenated(Trie root, String word, int idx, int wordsSoFar, Boolean[] dp) {\n if(idx == word.length())\n return wordsSoFar > 1;\n \n if(dp[idx] == null) {\n Trie node = root;\n for(int i = idx; i < word.length(); i++) {\n if(!node.children.containsKey(word.charAt(i))) {\n dp[idx] = false;\n break;\n }\n node = node.children.get(word.charAt(i));\n if(node.word != null) {\n boolean found = isWordConcatenated(root, word, i + 1, wordsSoFar+1, dp);\n if(found) {\n dp[idx] = true;\n break;\n }\n }\n }\n dp[idx] = dp[idx] == null ? false : dp[idx];\n }\n return dp[idx];\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
concatenated-words | [C++] | Trie solution | c-trie-solution-by-ometek-3njb | Intuition\nBy storing the data in a Trie tree structure we will be able to check the presence of the word in O(s) time, where s is the lenghts of the word. As t | Ometek | NORMAL | 2023-01-27T13:53:10.932990+00:00 | 2023-01-27T13:53:10.933020+00:00 | 43 | false | # Intuition\nBy storing the data in a Trie tree structure we will be able to check the presence of the word in O(s) time, where s is the lenghts of the word. As the words are relatively short - 30 characters max - this structure allows us to do that very efficiently.\n\n# Approach\n1. Initialize a trie tree\n2. Add elements to the trie tree-> appendToTrie()\n3. For each word check if it can be created by concatenation of shorter words \n\nTo execute step 3 we can follow a simple DFS approach:\n1. If there exists a word that ends in a particular place, run DFS from the root of the tree.\n2. If no words end, go to the next letter of the word in the tree if it exists.\n3. Remember how many words have already ended\n4. Check stop conditions -> if the entire word has been checked or the answer has already been found\n\n# Complexity\n- Time complexity: O(n * s^2)\n \n- Space complexity: O(M)\n\nn - number of words\ns - maximum word length\nM - sum of all word lengths\n\n# Code\n```\nclass Solution {\npublic:\n struct trieNode {\n int letters[26];\n bool end = false;\n };\n\n void appendToTrie(vector<trieNode>& trie, int trieIndex, string& word, int wordIndex) {\n if (word.size() == wordIndex) {\n trie[trieIndex].end = true;\n return;\n }\n if (trie[trieIndex].letters[word[wordIndex] - \'a\'] == 0) {\n trie[trieIndex].letters[word[wordIndex] - \'a\'] = trie.size();\n trie.push_back({});\n }\n appendToTrie(trie, trie[trieIndex].letters[word[wordIndex] - \'a\'], word, wordIndex + 1);\n }\n\n void checkInTrie(vector<trieNode>& trie, int trieIndex, string& word, int wordIndex, bool& ok, int cnt) {\n if (word.size() == wordIndex && trie[trieIndex].end && cnt > 0)\n ok = true;\n if (ok)\n return;\n if (word.size() == wordIndex)\n return;\n if (trie[trieIndex].end)\n checkInTrie(trie, 0, word, wordIndex, ok, cnt + 1);\n if (trie[trieIndex].letters[word[wordIndex] - \'a\'])\n checkInTrie(trie, trie[trieIndex].letters[word[wordIndex] - \'a\'], word, wordIndex + 1, ok, cnt);\n }\n\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n vector<trieNode> trie;\n trie.push_back({});\n\n for (auto word : words) \n appendToTrie(trie, 0, word, 0);\n\n vector<string> ans;\n\n for (auto word : words) {\n bool ok = false;\n checkInTrie(trie, 0, word, 0, ok, 0);\n if (ok)\n ans.push_back(word);\n }\n\n return ans;\n }\n};\n``` | 3 | 0 | ['Depth-First Search', 'Trie', 'C++'] | 0 |
concatenated-words | ✅Accepted || ✅Short & Simple || ✅Best Method || ✅Easy-To-Understand | accepted-short-simple-best-method-easy-t-y7il | \n# Code\n\nclass Solution {\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n unordered_set<string> st(words.begin | sanjaydwk8 | NORMAL | 2023-01-27T08:02:19.040735+00:00 | 2023-01-27T08:02:19.040775+00:00 | 217 | false | \n# Code\n```\nclass Solution {\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n unordered_set<string> st(words.begin(), words.end());\n vector<string> ans;\n unordered_map<string, int> mp;\n for(string s:st)\n mp[s]++;\n for(string s:st)\n {\n int n=s.size();\n vector<bool> dp(n+1);\n dp[0]=true;\n for(int i=1;i<=n;i++)\n {\n for(int j=0;j<i;j++)\n {\n if(dp[j])\n {\n string sub=s.substr(j, i-j);\n if(mp.find(sub)!=mp.end() && sub!=s)\n {\n dp[i]=true;\n break;\n }\n }\n }\n if(dp[n])\n ans.push_back(s);\n }\n }\n return ans;\n }\n};\n```\nPlease **UPVOTE** if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!! | 3 | 0 | ['C++'] | 0 |
concatenated-words | Maps cpp solve✅✅ Map+Recursive Solve | maps-cpp-solve-maprecursive-solve-by-mil-4qqg | Intuition\n Describe your first thoughts on how to solve this problem. \nMap stores the words \n# Approach\n Describe your approach to solving the problem. \nre | milan2001 | NORMAL | 2023-01-27T06:59:04.162894+00:00 | 2023-01-27T06:59:19.201408+00:00 | 515 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMap stores the words \n# Approach\n<!-- Describe your approach to solving the problem. -->\nrecursive approaches\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool solve(string s,vector<string>& words,map<string,int>& mapp,string r,int vals){\n if(s.size()==0&&vals>=2)\n {\n return true;\n }\n else if(s.size()==0)\n return false;\n for(int p=1;p<=s.size();p++){\n if(mapp.count(s.substr(0,p))>0){\n if(solve(s.substr(p),words,mapp,r,vals+1))\n {return true;}\n }}\n return false;}\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n vector<string> sols;\n map<string,int> mapp;\n for(int p=0;p<words.size();p++){\n mapp[words[p]]++;\n }\n for(int po=0;po<words.size();po++){\n if(solve(words[po],words,mapp,"",0))\n sols.push_back(words[po]);\n }\n return sols;\n }\n};\n``` | 3 | 0 | ['Ordered Map', 'C++'] | 0 |
concatenated-words | ✅C++|| Recursion || Memoization || Very Easy || Approach || Complexity | c-recursion-memoization-very-easy-approa-qixf | Intuition\n Describe your first thoughts on how to solve this problem. \nRecursion\n\n# Approach\n Describe your approach to solving the problem. \n- store all | sunnyjha1512002 | NORMAL | 2023-01-27T06:50:21.816048+00:00 | 2023-01-27T06:50:21.816110+00:00 | 321 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRecursion\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- store all strings in set to find it in fast.\n- traverse on each word\n - check if it can func(concat) or not\n - push in ans\n\n\n## concat function\n- traverse on each char of word\n- pick up prefix string \n- check if (curr string (0,idx) is present in set && prefix string is present || call concat function on prefix).\n - if yes return true\n- after end of loop return false bcz we not find 2 or more words in that word.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(exponential)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n*max.word.length) + O(n)$$\n\n# Code\n```\nclass Solution {\nprivate:\nbool isConcat(string word,unordered_set<string>& st){\n int n = word.size();\n for(int i=1;i<n;i++){\n string prefix = word.substr(i);\n if(st.count(word.substr(0,i))&&(st.count(prefix)||isConcat(prefix,st)))return true;\n }\n return false;\n}\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n if(words.size()==0)return {};\n unordered_set<string> st;\n vector<string> ans;\n for(auto word:words)st.insert(word);\n for(auto word:words){\n if(isConcat(word,st))ans.push_back(word);\n }\n return ans;\n }\n};\n```\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- just apply memoization on Upper solution.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n*(max.len.word)^3)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n*max.word.length) + O(n)$$\n\n# Code\n\n```\nclass Solution {\nprivate:\nbool isConcat(string word,unordered_set<string>& st,unordered_map<string,bool>& mp){\n int n = word.size();\n if(mp.count(word))return mp[word];\n for(int i=1;i<n;i++){\n string prefix = word.substr(i);\n if(st.count(word.substr(0,i))&&(st.count(prefix)||isConcat(prefix,st,mp)))return mp[word] = true;\n }\n return mp[word] = false;\n}\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n if(words.size()==0)return {};\n unordered_set<string> st;\n unordered_map<string,bool> mp;\n vector<string> ans;\n for(auto word:words)st.insert(word);\n for(auto word:words){\n if(isConcat(word,st,mp))ans.push_back(word);\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 0 |
concatenated-words | Partition Dp Solution || C++ || Easy Understanding | partition-dp-solution-c-easy-understandi-32te | \n\nT.C : O(n*s[i].length)\nS.C : O(n * s[i].length)\n\n\n\nclass Solution {\npublic:\n unordered_set<string> mp;\n // dp[i] = number of ways to partition | krunal_078 | NORMAL | 2023-01-27T05:49:43.172128+00:00 | 2023-01-27T05:53:01.002802+00:00 | 168 | false | \n\n**T.C : O(n*s[i].length)\nS.C : O(n * s[i].length)**\n\n\n```\nclass Solution {\npublic:\n unordered_set<string> mp;\n // dp[i] = number of ways to partition strings such that each substring is in the words;\n int rec(string &s,int n,int i,vector<int> &dp){\n if(i>=n) return true;\n if(dp[i]!=-1) return dp[i];\n dp[i] = 0;\n for(int j=i;j<n;j++){\n string tmp = s.substr(i,j-i+1);\n if(mp.count(tmp)){ // if substring is in words.\n dp[i] += rec(s,n,j+1,dp);\n }\n }\n return dp[i];\n }\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words){\n mp.clear();\n vector<string> ans;\n for(auto &ele:words) mp.insert(ele);\n for(auto &ele:words){\n vector<int> dp(ele.size()+1,-1);\n int ways = rec(ele,ele.size(),0,dp);\n if(ways>1){ // we can always partition whole string so that way is not considered.\n ans.push_back(ele);\n }\n }\n return ans;\n }\n};\n```\n\nPlease upvote if you like the solution !! | 3 | 0 | ['Dynamic Programming', 'C'] | 0 |
concatenated-words | ✔️ | C++ | TRIE + DFS | Easy Solution | c-trie-dfs-easy-solution-by-code_alone-vl56 | Approach\n Use Trie Data Structure and do dfs to find the count of words that are used to make the current word\n\n# Complexity\n- Time complexity:\n- O(N^ | code_alone | NORMAL | 2023-01-27T05:06:07.950886+00:00 | 2023-01-27T05:06:07.950929+00:00 | 780 | false | # Approach\n Use Trie Data Structure and do dfs to find the count of words that are used to make the current word\n\n# Complexity\n- Time complexity:\n- O(N^2)\n\n- Space complexity:\n- O(26*N)\n# Code\n```\n\nstruct Node{\n bool end = false;\n Node* next[26] = { NULL };\n};\n\nclass Solution {\npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n root = new Node();\n for(const auto& word : words)\n add(word);\n\n for(const auto& word : words){\n if(dfs(0, 0, word.size(), word))\n ans.push_back(word);\n }\n return ans;\n }\n\nprivate:\n Node* root;\n vector<string> ans;\n void add(const string& str) {\n auto cur = root;\n for(auto& ch : str) {\n if(!cur->next[ch-\'a\']) cur->next[ch-\'a\'] = new Node();\n cur = cur->next[ch-\'a\'];\n }\n cur->end = true;\n }\n\n bool dfs(int i, int cnt, int n, const string& s){\n if(i == n) return cnt > 1;\n auto cur = root;\n while(i<n && cur->next[s[i]-\'a\'] != NULL) {\n cur = cur->next[s[i] - \'a\'];\n i++;\n if(cur->end) {\n if(dfs(i, cnt+1, n, s)) return true;\n }\n }\n return false;\n }\n};\n``` | 3 | 0 | ['Trie', 'C++'] | 1 |
concatenated-words | Easy C++ recursive code 864 ms . | easy-c-recursive-code-864-ms-by-akt617-blfn | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. Simple approach with take | akt617 | NORMAL | 2023-01-27T04:31:21.365725+00:00 | 2023-01-27T04:31:21.365763+00:00 | 175 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->Simple approach with take and not take method.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(n)\n\n# Code\n```\nclass Solution {\npublic:\n map<string,int> mp; //to store all word,in order to access them in O(1) when require. \n bool f(int i,string &s,int cnt,string q){\n if(i == s.size()){\n if(cnt > 1 && q == ""){\n return true;\n }\n return false;\n }\n q += s[i];\n string g;\n //take\n if(mp[q]){\n return (f(i+1,s,cnt+1,g)||f(i+1,s,cnt,q));\n }\n //not take\n return f(i+1,s,cnt,q);\n }\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n \n vector<string> ans;\n for(auto it : words){\n mp[it]++;\n }\n for(auto x : words){\n string temp = x;\n string q;\n //f checks whether given condition in problem is satisfying or not.\n if(f(0,x,0,q)){\n ans.push_back(x); //if yes append it to ans.\n }\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
concatenated-words | Clean & Optimized Code + Commented | clean-optimized-code-commented-by-nextth-du0g | \nclass Solution {\npublic:\n bool check(string word, unordered_set<string>& dict, unordered_map<string, bool> &ump){\n if(ump.find(word) != ump.end | NextThread | NORMAL | 2023-01-27T04:29:17.675922+00:00 | 2023-01-27T04:29:17.675973+00:00 | 47 | false | ```\nclass Solution {\npublic:\n bool check(string word, unordered_set<string>& dict, unordered_map<string, bool> &ump){\n if(ump.find(word) != ump.end()) return ump[word];\n for(int i = 1 ; i < word.size() ; ++i) {\n string substring = word.substr(0, i); // check for every substring\n if(dict.count(substring)) { // if substring is pre-stored\n string nextpart = word.substr(i); // the rest substring\n if(dict.count(nextpart) || check(nextpart, dict, ump)) // check if the next substring is been there in our map already or using the next part we can do the same operation(recursive call) and is possible\n {\n ump.insert({word, true});\n return true;\n }\n }\n }\n ump.insert({word, false});\n return false;\n }\n \n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n vector<string> res;\n unordered_set<string> dict(words.begin(), words.end()); // let\'s remove duplicate words first\n unordered_map<string, bool> mp;\n for(string word : words)\n if(check(word, dict, mp)) res.push_back(word);\n return res;\n }\n};\n``` | 3 | 0 | ['C', 'Ordered Set'] | 0 |
concatenated-words | 📌📌 C++ || DFS || Hashset || Faster || Easy To Understand | c-dfs-hashset-faster-easy-to-understand-yk49q | Using DFS && Hashset\n\n Time Complexity :- O(N * L * L)\n\n Space Complexity :- O(N * L), Where L is the size of the string\n\n\nclass Solution {\npublic:\n | __KR_SHANU_IITG | NORMAL | 2023-01-27T02:51:17.292938+00:00 | 2023-01-27T02:51:17.292983+00:00 | 231 | false | * ***Using DFS && Hashset***\n\n* ***Time Complexity :- O(N * L * L)***\n\n* ***Space Complexity :- O(N * L), Where L is the size of the string***\n\n```\nclass Solution {\npublic:\n \n // set will store all the words of words\n \n unordered_set<string> s;\n \n bool helper(string& str, int i, int n)\n {\n // base case\n \n if(i == n)\n return true;\n \n // partition str at j and call for next\n \n for(int j = i; j < n; j++)\n {\n if(str.substr(i, j - i + 1) != str && s.count(str.substr(i, j - i + 1)))\n {\n if(helper(str, j + 1, n))\n return true;\n }\n }\n \n return false;\n }\n \n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n \n // insert all the word of words into s\n \n for(auto word : words)\n {\n s.insert(word);\n }\n \n vector<string> res;\n \n // iterate over words and check for each word is it concatenated or not\n \n for(auto word : words)\n { \n if(helper(word, 0, word.size()))\n res.push_back(word);\n }\n \n return res;\n }\n};\n``` | 3 | 0 | ['Depth-First Search', 'C', 'C++'] | 0 |
concatenated-words | Go - Easy to understand O(n**2) Approach✅ | go-easy-to-understand-on2-approach-by-si-37pw | Complexity\n- Time complexity: O(n^2*m)\n Add your time complexity here, e.g. O(n) \n\n# Code\n\nfunc findAllConcatenatedWordsInADict(words []string) []string { | sinistersup2001 | NORMAL | 2023-01-27T02:17:50.875045+00:00 | 2023-01-27T02:17:50.875078+00:00 | 997 | false | # Complexity\n- Time complexity: O(n^2*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunc findAllConcatenatedWordsInADict(words []string) []string {\n s := make(map[string]bool)\n concatenateWords := []string{}\n for _, word := range words {\n s[word] = true\n }\n for _, word := range words {\n if checkConcatenate(word, s) {\n concatenateWords = append(concatenateWords, word)\n }\n }\n return concatenateWords\n}\n\nfunc checkConcatenate(word string, s map[string]bool) bool {\n for i := 1; i < len(word); i++ {\n prefixWord := word[:i]\n suffixWord := word[i:]\n if s[prefixWord] && (s[suffixWord] || checkConcatenate(suffixWord, s)) {\n return true\n }\n }\n return false\n}\n``` | 3 | 0 | ['Go'] | 0 |
concatenated-words | python3 | sort and use trie. | python3-sort-and-use-trie-by-iter_next-rdv1 | If there is word whose substrings are already in array, the length of each substring would be <= len(word) itself. Here is the logic below. \n1. Sort the array | iter_next | NORMAL | 2023-01-27T02:16:38.526434+00:00 | 2023-01-27T02:16:38.526462+00:00 | 1,177 | false | If there is word whose substrings are already in array, the length of each substring would be <= len(word) itself. Here is the logic below. \n1. Sort the array based on length of word.\n2. Identify if trie contains already a list of words that make up the word we are looking for using recursion. \n3. If (2) is true, add the word to list ans.\n4. Regardless of (3) add the word to the trie and mark the end of a word by using \'#\'\n\n```\nclass Solution:\n def check(self, trie, word, widx):\n if widx == len(word): \n return True\n \n t = trie\n ret = False\n \n for cidx in range(widx, len(word)):\n if word[cidx] in t:\n t = t[word[cidx]]\n else: \n return False \n \n if \'#\' in t: \n ret |= self.check(trie, word, cidx+1)\n \n if ret: \n return ret\n \n return ret\n \n def insert(self, word, trie):\n t = trie\n for c in word:\n if c not in t:\n t[c] = {}\n \n t = t[c]\n t[\'#\'] = {}\n \n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n words.sort(key=lambda x: len(x))\n t = {}\n ans = []\n for w in words:\n if self.check(t, w, 0):\n ans.append(w)\n self.insert(w, t)\n \n return ans\n | 3 | 0 | ['Trie', 'Recursion', 'Python3'] | 1 |
concatenated-words | Python Short Brute Force 85% Time | python-short-brute-force-85-time-by-8by8-n872 | ```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n # Check if current word can be made from smaller wo | 8by8 | NORMAL | 2023-01-27T02:13:57.984953+00:00 | 2023-01-27T02:13:57.984981+00:00 | 681 | false | ```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n # Check if current word can be made from smaller words\n def check(word):\n if word in s:\n return True\n # If prefix is seen, recurse on rest of word\n return any(check(word[i:]) for i in range(1, len(word)) if word[:i] in s)\n \n s = set()\n res = []\n for word in sorted(words, key=lambda x:len(x)):\n if check(word):\n res.append(word)\n s.add(word)\n return res | 3 | 0 | ['Recursion', 'Python', 'Python3'] | 2 |
concatenated-words | [Python] Straightforward brute-force solution without memoization/trie/DFS/BFS | python-straightforward-brute-force-solut-fga4 | A simple brute-force solution without memoization works for me. The algorithm is straightforward:\n1. Construct a dictionary/hashmap of words to enable O(1) loo | ardulat | NORMAL | 2023-01-27T01:50:01.143796+00:00 | 2023-01-27T01:50:01.143832+00:00 | 481 | false | A simple brute-force solution without memoization works for me. The algorithm is straightforward:\n1. Construct a dictionary/hashmap of words to enable O(1) lookup.\n2. For each word, check if the given word is concatenated:\n - Start with an empty subword\n - For each character `word[i]` in the given word, append the character to the end of the subword\n - If you can find the subword in the dictionary of words we previously created, recurse to check if `word[i + 1:]` (the rest of the word) is a concatenated word\n - Maintain the count of subwords found so far\n - Recursion terminates when you reach the end of the word and the count of subwords is at least two\n3. Return the list of found concatenated words.\n\nHere is the code for the above algorithm:\n\n```python\nclass Solution(object):\n def findAllConcatenatedWordsInADict(self, words):\n """\n :type words: List[str]\n :rtype: List[str]\n """\n def is_concatenated(word, count):\n if word == "" and count >= 2:\n return True\n \n subword = ""\n for i in range(len(word)):\n subword += word[i] # append char to the end of the subword\n if subword in self.words_dict:\n if is_concatenated(word[i + 1:], count + 1):\n return True\n\n # nothing found at this point\n return False\n \n # construct a dict of words to enable O(1) lookup\n self.words_dict = dict()\n for w in words:\n self.words_dict[w] = True\n \n res = []\n for w in words:\n if is_concatenated(w, 0):\n res.append(w)\n \n return res\n``` | 3 | 0 | ['Recursion', 'Python'] | 1 |
numbers-with-repeated-digits | Solution | solution-by-deleted_user-ejr2 | C++ []\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int n) {\n vector<int> digits{};\n int temp = n + 1;\n while (temp > 0) {\n | deleted_user | NORMAL | 2023-05-20T07:50:23.316211+00:00 | 2023-05-20T08:23:12.211778+00:00 | 5,239 | false | ```C++ []\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int n) {\n vector<int> digits{};\n int temp = n + 1;\n while (temp > 0) {\n digits.emplace_back(temp % 10);\n temp /= 10;\n }\n int result = 0;\n int len = digits.size();\n int curr = 9;\n for (int i = 0; i < len - 1; i++) {\n result += curr;\n curr *= 9 - i;\n }\n curr /= 9;\n vector<bool> seen(10, false);\n for (int i = 0; i < len; i++) {\n int d = digits[len - i - 1];\n\n for (int j = i == 0 ? 1 : 0; j < d; j++) if (!seen[j]) result += curr;\n curr /= 9 - i;\n\n if (seen[d]) break;\n seen[d] = true;\n }\n return n - result;\n }\n};\n```\n\n```Python3 []\nfrom math import perm\n\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n digits = list(map(int, str(n + 1)))\n nl = len(digits)\n res = sum(9 * perm(9, i) for i in range(nl - 1))\n s = set()\n for i, x in enumerate(digits):\n for y in range(i == 0, x):\n if y not in s:\n res += perm(9 - i, nl - i - 1)\n if x in s:\n break\n s.add(x)\n return n - res\n```\n\n```Java []\nclass Solution {\n public int numDupDigitsAtMostN(int N) {\n ArrayList<Integer> L = new ArrayList<Integer>();\n for (int x = N + 1; x > 0; x /= 10)\n L.add(0, x % 10);\n\n int res = 0, n = L.size();\n for (int i = 1; i < n; ++i)\n res += 9 * A(9, i - 1);\n\n HashSet<Integer> seen = new HashSet<>();\n for (int i = 0; i < n; ++i) {\n for (int j = i > 0 ? 0 : 1; j < L.get(i); ++j)\n if (!seen.contains(j))\n res += A(9 - i, n - i - 1);\n if (seen.contains(L.get(i))) break;\n seen.add(L.get(i));\n }\n return N - res;\n }\n public int A(int m, int n) {\n return n == 0 ? 1 : A(m, n - 1) * (m - n + 1);\n }\n}\n``` | 442 | 0 | ['C++', 'Java', 'Python3'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.