question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
number-of-subsequences-that-satisfy-the-given-sum-condition | Image Explanation🏆- [Binary Exponentiation || Two Pointers || Pre-Computation] - C++/Java/Python | image-explanation-binary-exponentiation-sx7ub | Video Solution (Aryan Mittal) - Link in LeetCode Profile\nNumber of Subsequences That Satisfy the Given Sum Condition by Aryan Mittal\n\n\n\n# Approach & Intuti | aryan_0077 | NORMAL | 2023-05-06T01:51:10.796303+00:00 | 2023-05-06T02:01:25.107587+00:00 | 29,324 | false | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Number of Subsequences That Satisfy the Given Sum Condition` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n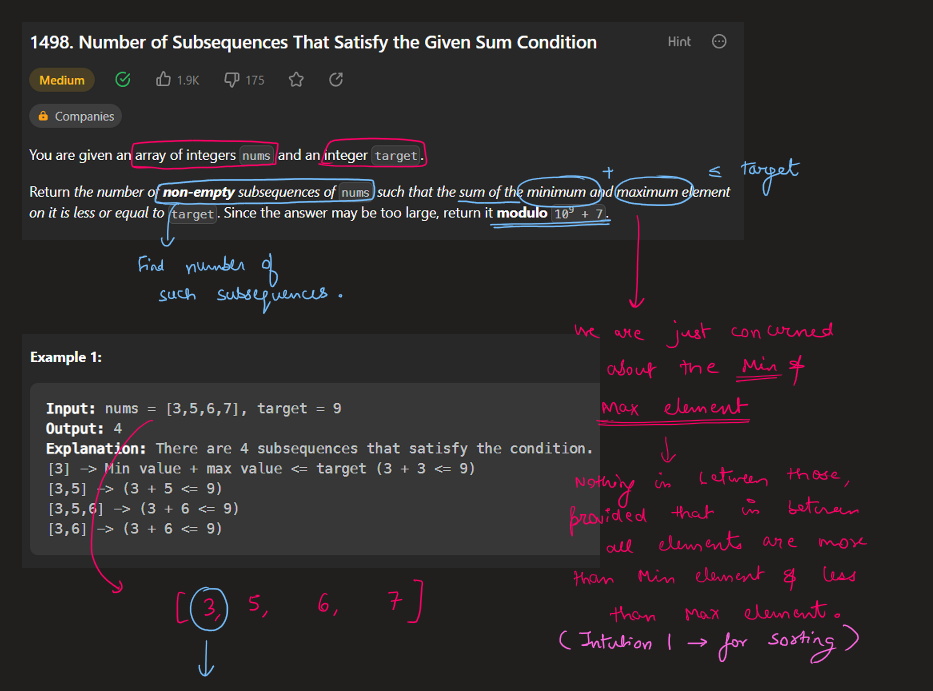\n\n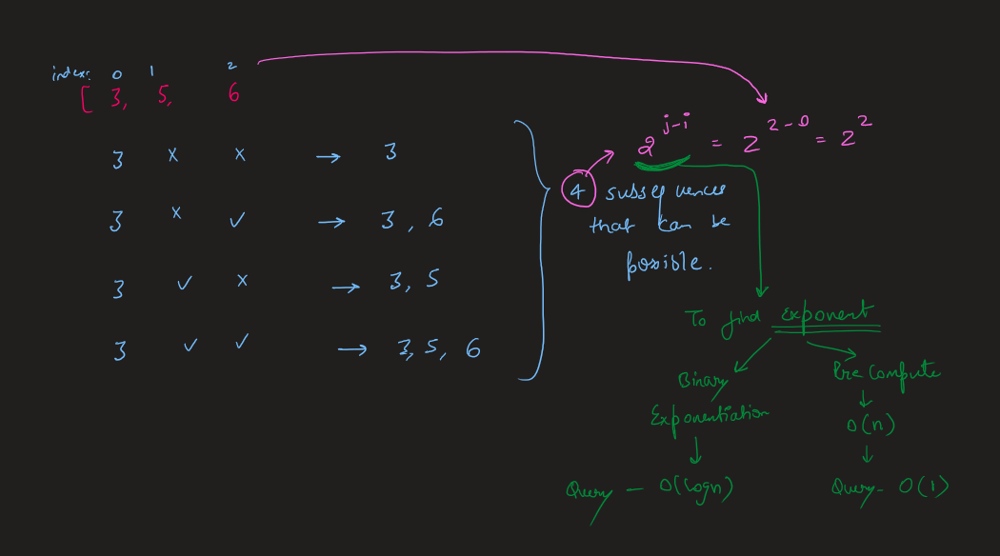\n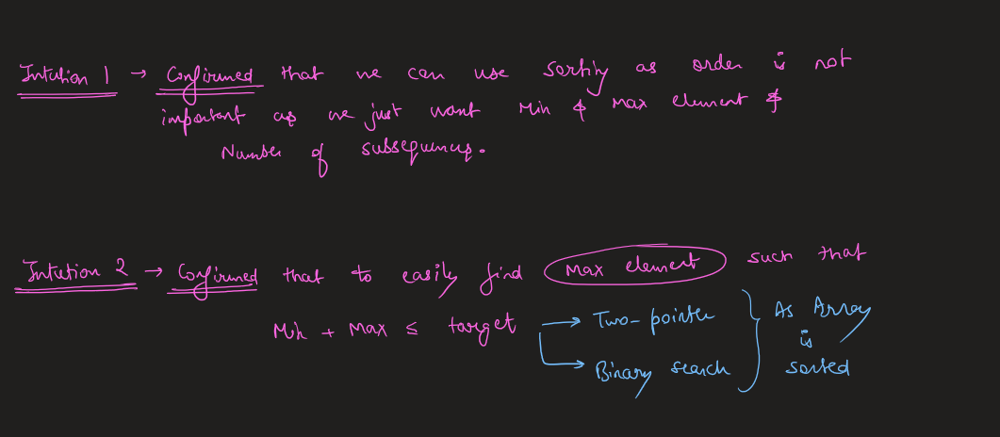\n\n\n# How to Code in Different ways\n\n\n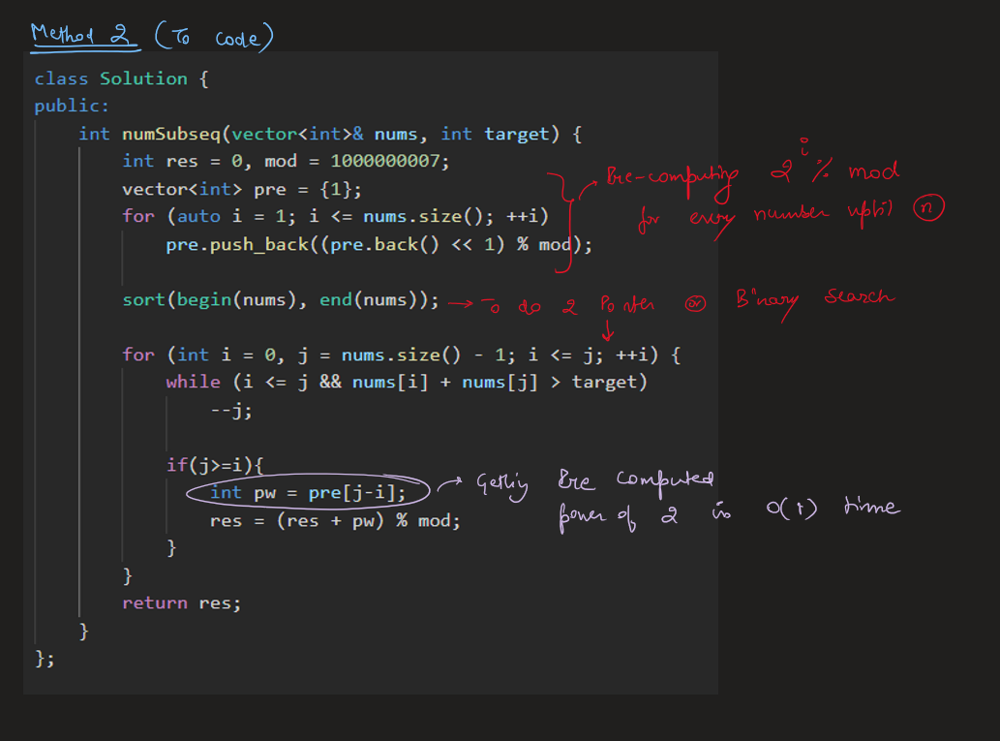\n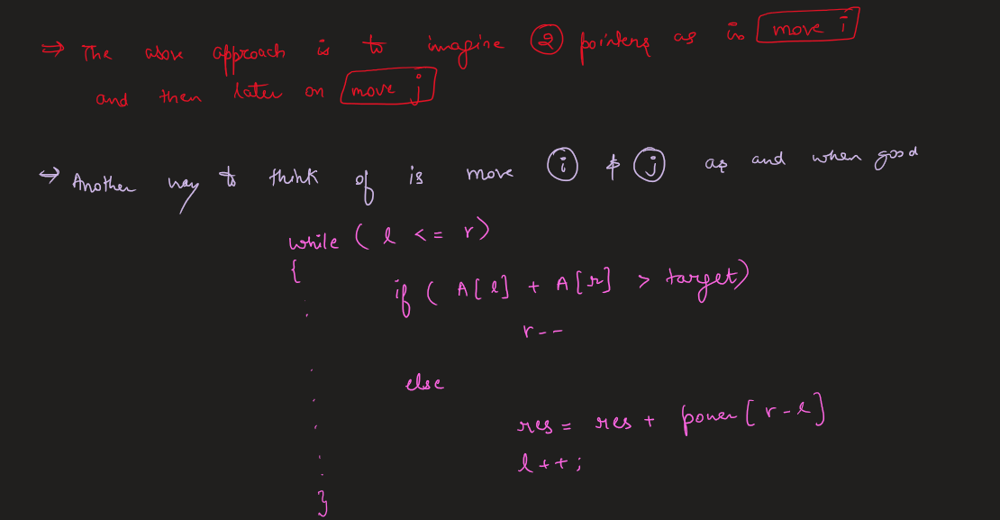\n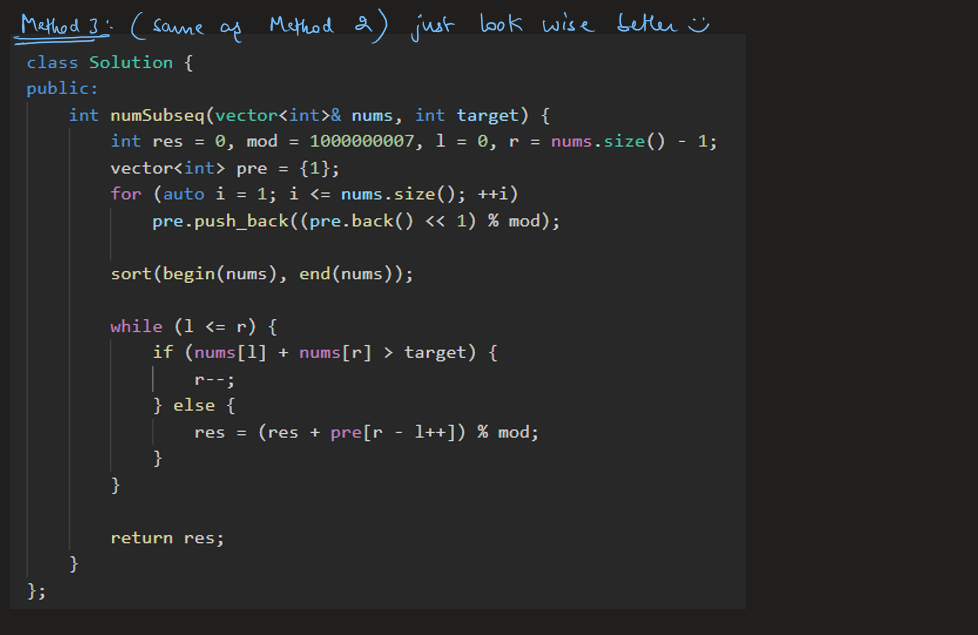\n\n\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n int res = 0, mod = 1000000007, l = 0, r = nums.size() - 1;\n vector<int> pre = {1};\n for (auto i = 1; i <= nums.size(); ++i)\n pre.push_back((pre.back() << 1) % mod); \n \n sort(begin(nums), end(nums));\n \n while (l <= r) {\n if (nums[l] + nums[r] > target) {\n r--;\n } else {\n res = (res + pre[r - l++]) % mod;\n }\n }\n\n return res;\n }\n};\n```\n```Java []\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n int res = 0, mod = 1000000007, l = 0, r = nums.length - 1;\n List<Integer> pre = new ArrayList<>();\n pre.add(1);\n for (int i = 1; i <= nums.length; ++i) {\n pre.add((pre.get(i - 1) << 1) % mod);\n }\n\n Arrays.sort(nums);\n\n while (l <= r) {\n if (nums[l] + nums[r] > target) {\n r--;\n } else {\n res = (res + pre.get(r - l++)) % mod;\n }\n }\n\n return res;\n }\n}\n```\n```Python []\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n res, mod = 0, 1000000007\n l, r = 0, len(nums) - 1\n pre = [1]\n for i in range(1, len(nums) + 1):\n pre.append((pre[-1] << 1) % mod)\n \n nums.sort()\n \n while l <= r:\n if nums[l] + nums[r] > target:\n r -= 1\n else:\n res = (res + pre[r - l]) % mod\n l += 1\n\n return res\n``` | 175 | 2 | ['Array', 'Two Pointers', 'C++', 'Java', 'Python3'] | 11 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ very simple solution | c-very-simple-solution-by-himansh9968-10hq | Here we need to find out subsequence so that now we can sort the array. \nAlgo - \n1. We first sort the array.\n2. Use 2 pointers approach let say i and j.\n\t\ | himanshsh1704 | NORMAL | 2021-08-02T21:42:41.991906+00:00 | 2021-08-03T21:51:40.128200+00:00 | 11,456 | false | Here we need to find out subsequence so that now we can sort the array. \nAlgo - \n1. We first sort the array.\n2. Use 2 pointers approach let say i and j.\n\t\ti=0 and j=n-1;\n\tnow if(nums[i]+nums[j]<=target) then we can make substrings out of that \n\t\t\tnext thing from this how many substrings we can make we need to maintain nums[i[ as minimum we need to take it and the maximum element can be any from i+1 to j\n\tSo, for every element we have two choices whether to take or not so, we have 2^(j-i) substrings out of that. and i++;\n\telse j--\n\n\n```\nclass Solution {\npublic:\n int mod=1000000007;\n int numSubseq(vector<int>& nums, int target) \n {\n sort(nums.begin(),nums.end());\n int res=0,n=nums.size(),i=0,j=n-1;\n vector<int>pow2(n+1,1);\n for(int i=1;i<=n;i++)\n {\n pow2[i]=(2*pow2[i-1])%mod;\n }\n while(i<=j)\n {\n if(nums[j]+nums[i]<=target)\n {\n res=(res+pow2[j-i])%mod;\n i++;\n }\n else\n j--;\n }\n return res;\n }\n};\n```\n\nIt would be great if you upvote.\n\t | 60 | 1 | ['C', 'C++'] | 3 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Python Two pointers Complete Explanation | python-two-pointers-complete-explanation-dsr8 | Show some love with upvotes if you found this helpful.Now,into the solution ===>\n\nSort the array, because subsequence is nothing but a subset.\n\nreason: A wi | akhil_ak | NORMAL | 2020-07-01T01:13:52.930558+00:00 | 2020-07-01T01:13:52.930591+00:00 | 7,885 | false | Show some love with upvotes if you found this helpful.Now,into the solution ===>\n\nSort the array, because subsequence is nothing but a subset.\n\nreason: A window can be maintained [imin,j] such that\nif A[imin]+A[j]<=target\n then,\n for all i such that imin<=i<j\n A[imin]+A[i] <= target is true.\n\n \nThe idea is to find the imin for every j.\nThen,add all the possible subsequences that can be generated from this [imin,j] window.\n\nfor a window [imin,j], we can change the max by reducing j.\nBut,when imin changes the window shifts and the min+max<=target may not\nbe true anymore.\n\n```\nNo of subsequences for a window of [imin,j] are calculated as below:\n Example:\n sorted nums : [a,b,c,d]\n lets say a+d<=target.\n no of subsequences are:\n 1)when max reduces the min+max cant exceed target,so\n [a,b,c,d], [a,b,c],[a,b],[a] => 3\n 2)[a,b,c,d] gives [a,b,d],[a,c,d],[a,d] with same min+max\n 3)[a,b,c] gives [a,c] with same min+max\n 4)[a,b] doesnt give anything new\n 5)[a] also remains same\n\n The key thing to observe here is that, [a ,......] is the pattern\n for every subsequence.\n The no of subsets of the rest of the numbers\n is the total no of subsequnces. i.e 1<<(numberofelements) or power(2,numberoflements)\n```\n\nTime : O(nlogn)\nSpace:O(1)\n\n```python\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n nums.sort()\n n = len(nums)\n res = 0\n #one length subsequence\n mod = 10**9 + 7\n i,j = 0,n-1\n \n \n for i in range(n):\n while i<=j and nums[i]+nums[j] > target:\n j-=1\n \n if i<=j and nums[i] + nums[j] <= target:\n res += pow(2,(j-i) , mod)\n res %= mod\n \n return res\n``` \n | 48 | 7 | [] | 7 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ Precomputed Pow | c-precomputed-pow-by-votrubac-4l3y | Similar to the other solutions, but with precomputing power of 2 modulo 10 ^ 9 + 7.\n\nWell, Python folks are in luck. In C++, computing 2 ^ n inline gives TLE. | votrubac | NORMAL | 2020-06-28T05:28:30.163989+00:00 | 2020-06-28T05:53:32.877480+00:00 | 7,727 | false | Similar to the other solutions, but with precomputing power of 2 modulo `10 ^ 9 + 7`.\n\nWell, Python folks are in luck. In C++, computing `2 ^ n` inline gives TLE. I could not find an efficient modulo power function. So, I just precomputed the `pow(i, 2) % mod` values iterativelly.\n\n```cpp\nint numSubseq(vector<int>& nums, int target) {\n int res = 0, mod = 1000000007;\n vector<int> pre = {0, 1};\n for (auto i = pre.size(); i <= nums.size(); ++i)\n pre.push_back((pre.back() << 1) % mod); \n sort(begin(nums), end(nums));\n for (int i = 0, j = nums.size() - 1; i <= j; ++i) {\n while (i <= j && nums[i] + nums[j] > target)\n --j;\n res = (res + pre[j - i + 1]) % mod;\n }\n return res;\n}\n``` | 47 | 9 | [] | 5 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | pythonjavacsimple-solutioneasy-to-unders-cmki | !! BIG ANNOUNCEMENT !!\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies relat | techwired8 | NORMAL | 2023-05-06T00:09:04.137864+00:00 | 2023-05-06T01:27:28.664094+00:00 | 9,096 | false | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. I planned to give for next 10,000 Subscribers as well. If you\'re interested **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# Video Solution \n\n# Search \uD83D\uDC49 `Number of Subsequences That Satisfy the Given Sum Condition by Tech Wired `\n\n# or\n\n# Click the Link in my Profile\n\n# Approach:\n\n- Sort the given array in non-decreasing order.\n- Initialize two pointers left and right to the first and last indices of the array respectively.\n- Initialize a variable count to 0.\n- Iterate the loop until left is less than or equal to right.\n- If the sum of elements at indices left and right is greater than the given target, decrement the right pointer.\n- Otherwise, the subsequence formed by elements at indices left and right and all the possible subsequences formed by the elements between them (i.e., from left+1 to right-1) will satisfy the given sum condition.\n- The number of possible subsequences that can be formed by the elements between left and right is equal to 2^(right-left).\n- Increment count by the number of possible subsequences and move left to the right.\n- After the loop, return the value of count-1 modulo 10^9 + 7.\n\n# Intuition:\n\nThe approach uses the fact that a subsequence can be formed by selecting any number of elements from a given array, without changing their relative order. Since the array is sorted in non-decreasing order, we can use a two-pointer approach to identify the elements that can be included in a subsequence that satisfies the given sum condition. We start by considering the first and last elements of the array. If their sum is greater than the given target, we decrement the last pointer. Otherwise, we include the last element in all possible subsequences that can be formed with the first element, and move the first pointer to the right. We repeat this process until the first pointer reaches the last pointer. Finally, we subtract 1 from the count to exclude the empty subsequence, and return the result modulo 10^9 + 7.\n\n```Python []\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n nums.sort()\n left, right = 0, len(nums) - 1\n count = 0\n mod = 10 ** 9 + 7\n \n while left <= right:\n if nums[left] + nums[right] > target:\n right -= 1\n else:\n count += pow(2, right - left, mod)\n left += 1\n \n return count % mod\n\n\n```\n```Java []\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int res = 0, n = nums.length, left = 0, right = n - 1, mod = (int)1e9 + 7;\n int[] pows = new int[n];\n pows[0] = 1;\n for (int i = 1 ; i < n ; ++i)\n pows[i] = pows[i - 1] * 2 % mod;\n while (left <= right) {\n if (nums[left] + nums[right] > target) {\n right--;\n } else {\n res = (res + pows[right - left++]) % mod;\n }\n }\n return res;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end());\n int res = 0, n = nums.size(), left = 0, right = n - 1, mod = 1e9 + 7;\n vector<int> pows(n);\n pows[0] = 1;\n for (int i = 1 ; i < n ; ++i)\n pows[i] = pows[i - 1] * 2 % mod;\n while (left <= right) {\n if (nums[left] + nums[right] > target) {\n right--;\n } else {\n res = (res + pows[right - left++]) % mod;\n }\n }\n return res;\n }\n};\n\n```\n# An Upvote will be encouraging \uD83D\uDC4D | 45 | 1 | ['Binary Search', 'Sorting', 'C++', 'Java', 'Python3'] | 5 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Two Sum,Python solution, explained, O(nlogn) | two-sumpython-solution-explained-onlogn-i4lpx | 1.This problem is a manipulation of Two sum problem.\n\t2. In this problem, order of numbers of a subsequence doesn\'t matter as we just have to consider max an | avinashgaur | NORMAL | 2020-06-29T10:52:37.981272+00:00 | 2020-06-29T12:43:08.623037+00:00 | 4,788 | false | 1.This problem is a manipulation of Two sum problem.\n\t2. In this problem, order of numbers of a subsequence doesn\'t matter as we just have to consider max and min of subsequence.Therefore, a subsequence from i to j in original array is equivalent to array having same elements and same minimum and maximum value. For e.g consider, nums = [3,7,6,5] and target = 10.For eg, In this a subsequence [3,7,6] is equivalent to subsequence [3,6,7] of [3,5,6,7]. Therefore, result of nums is equal to result of sorted[nums].\n3. For each index "i" in sorted_nums, find maximum "j" such that sorted_nums[i] + sorted_nums[j] <= target and j >= i.\n4. From i+1 to j, we can either pick or leave each element.\n5. Therefore, res += 2**(j-i)\n```\n \n\t res = 0\n end = len(nums)-1\n nums.sort()\n for i in range(len(nums)):\n while nums[i] + nums[end] > target:\n if end > i:\n end = end-1\n else:\n return res % (10**(9)+7)\n res += pow(2, end - i)\n return res % (10**(9)+7)\n```\nUpvote if you like the solution :) | 31 | 3 | ['Sliding Window', 'Python3'] | 6 |
number-of-subsequences-that-satisfy-the-given-sum-condition | BEST ANS EASIEST TWO POINTER APPROACH | best-ans-easiest-two-pointer-approach-by-fspx | Intuition\n Describe your first thoughts on how to solve this problem. \nTwo Pointer Approach as we have to make sure that our window\'s max-min<=target.\n\n# A | Carpediem02 | NORMAL | 2023-05-06T02:56:21.513867+00:00 | 2023-05-06T02:56:21.513903+00:00 | 5,572 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTwo Pointer Approach as we have to make sure that our window\'s max-min<=target.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe have to sort the given nums array so that we can apply two pointer approach.For the window that has max-min<=target will have a length of r-l+1,but the first element should be included that is the minimum of window to have all the unique possible answers. Therefore for that window we can have 2^r-l valid subsequence because for every element in the window we can have 2 options to include it or not.\n\n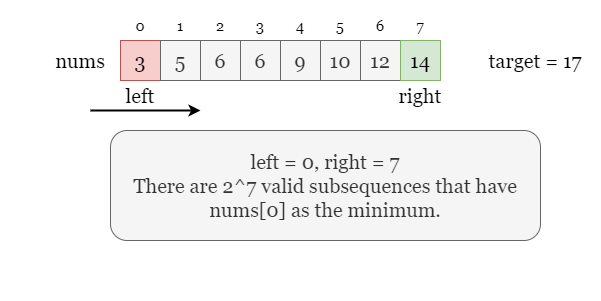\n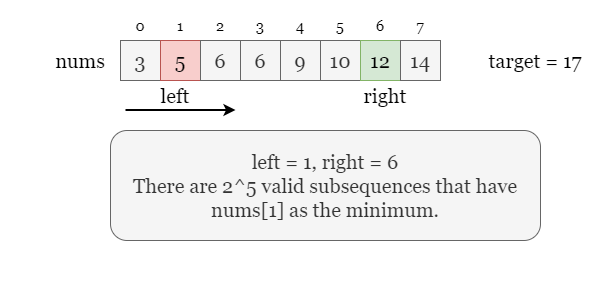\n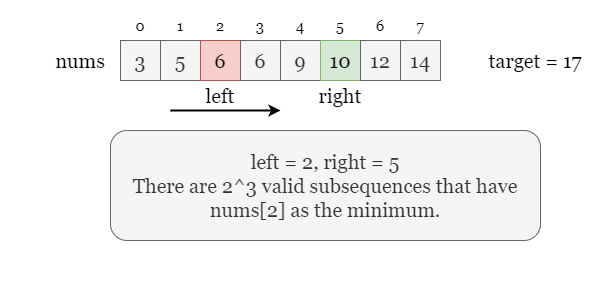\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n```\nO(N*LOG(N)) Sorting takes N*log(n) \n```\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n```\nO(N)\n```\n\n# Code\n```\nconst int MOD = 1000000007;\n\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end());\n int ans = 0;\n int l = 0, r = nums.size() - 1;\n \n vector<int>powerof2(nums.size());\n powerof2[0] = 1;\n for(int i = 1; i < nums.size(); i++) {\n powerof2[i] = (powerof2[i-1] * 2)%MOD;\n }\n while(l <= r) {\n if(nums[l] + nums[r] <= target) {\n ans += powerof2[r - l];\n ans %= MOD;\n l++;\n } else {\n r--;\n }\n }\n\n return ans;\n }\n};\n``` | 30 | 0 | ['C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Code + Login Explanation | Python | code-login-explanation-python-by-morning-v9s4 | \nThe solution to the question lies in finding the number of possible subsequence between \nstart and end pointer.\n\nLet the first pointer be at index 0 and l | morningstar317 | NORMAL | 2021-01-07T18:39:46.858680+00:00 | 2021-01-07T18:40:10.180418+00:00 | 1,824 | false | ```\nThe solution to the question lies in finding the number of possible subsequence between \nstart and end pointer.\n```\nLet the first pointer be at index ```0``` and last pointer be at index ```n-1```.\n\nSteps to follow:\n1. Sort the array\n2. Find the ```start and end ```index such that ```A[start] + A[end] <= target``` \n3. Let\'s say we have the required start index ```i``` and end index ```j```. \n\ta. For all the index starting from ```i+1``` to ```j```, we can choose either include it our set or ignore it\n\tb. Meaning for every index from ```i+1``` to ```j``` we have two options\n\tc. Therefore the total count of subsets would be ```2**(j-i)```\n\t\n\t\n```\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n \n left = 0\n right = len(nums)-1\n nums.sort()\n ans = 0\n while left <= right:\n val = nums[left] + nums[right]\n if val > target:\n right-=1\n else:\n ans += pow(2,right-left,10**9+7)\n left+=1\n return ans % (10**9 + 7)\n\t\t\n\t\n\tUpvote if this helps !\n\t\n | 20 | 0 | ['Python'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java - O(n log(n)) - Binary Search | java-on-logn-binary-search-by-toberank1-6196 | \nIdea:\n\n1. Sort the array firstly, because of the binary search.\n2. Each time we fix a starting point, then use binary search to find the ending point\n3. o | toberank1 | NORMAL | 2020-06-28T10:10:14.881334+00:00 | 2020-06-28T10:11:43.643613+00:00 | 3,476 | false | \nIdea:\n\n1. Sort the array firstly, because of the binary search.\n2. Each time we fix a starting point, then use binary search to find the ending point\n3. once we got starting and endinng point, 2^(end-start) makes sense, because for each element we select or not to select\n\nTime Complexity: O(n log(n))\nSpace Complexity: O(n) // because of the powDP[], but I guess in Python, we can fulfill O(1)Space?\n\nTIPS for JAVA USERS:\nIt is impossible to use 2^n in Java when n is very large(overflow), but Python can. So we need to use DP-method to pre-calculate 2^n % 1e9+7\n\n```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int res=0;\n int toMod=(int)1e9+7;\n //It is impossible to use 2^n in Java when n is very large, but Python can\n //So we need to use DP-method to pre-calculate 2^n % 1e9+7\n int[] powDP = new int[nums.length];\n powDP[0] = 1;\n for(int i=1; i<powDP.length; i++) powDP[i] = (powDP[i-1]*2)%toMod;\n //each time we fix a starting point\n for(int start=0; start<nums.length; start++){\n //like two-sum, we use binary search to find the nums[end] <= target-nums[start]\n //in other word, we use binary search to find the ending point\n int l=start, r=nums.length-1;\n //"end" is to memorize the largest element satisfying our requirement\n //and its initial value -1 is important as well\n int end = -1;\n while(l<=r){\n int mid = l+(r-l)/2;\n if(nums[start]+nums[mid]<=target){\n l=mid+1;\n end=mid;\n }\n else r=mid-1;\n }\n //so we\'ve got starting and ending points\n \n //we have to consider a situation that we didn\'t find an element satisfying(nums[end] <= target-nums[start])\n //Then we can stop the iteration and return the result\n if(end==-1) break;\n res = (res + powDP[end-start])%toMod;\n }\n \n return res;\n }\n}\n``` | 19 | 1 | [] | 4 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ | Unique solution✅✅ | c-unique-solution-by-pathrinarayananmdu-z4pb | \nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n int count =0 ; \n int n = nums.size();\n vector<int>pow(n | pathrinarayananmdu | NORMAL | 2023-05-06T04:23:53.925706+00:00 | 2023-05-06T14:47:41.166243+00:00 | 2,327 | false | ```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n int count =0 ; \n int n = nums.size();\n vector<int>pow(n,1);\n sort(nums.begin(), nums.end());\n for(int i =1;i<n;i++){\n pow[i] = (pow[i-1] * 2) % (1000000007 );\n }\n int left =0 ; int right = n-1;\n while(left<=right){\n if(nums[left] + nums[right] > target) right--;\n else{\n count = (count + pow[right-left] ) % (1000000007 );\n left++;\n }\n }\n return count;\n }\n};\n```\n\n | 15 | 0 | ['C'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | ✅ C++ | 2 pointers Simple Explanation | c-2-pointers-simple-explanation-by-ashok-5mxr | As we care about only min & max of a subseq ... we need not bother about the ordering of elems . so just sort the array and apply two pointers to count subseq t | ashoknitw | NORMAL | 2022-06-27T07:37:50.434747+00:00 | 2022-08-08T12:39:19.843137+00:00 | 3,729 | false | **As we care about only min & max of a subseq ... we need not bother about the ordering of elems . so just sort the array and apply two pointers to count subseq that has the i\'th elem as minimum and j\'th elem as the maximum**\n\n**proof :**\n```\n/*\n [3 5 6 6]\n i j\nsay i at 3 and j at 6.. rem 3 elem after 3 are 5,6,6\n\nTotal subseq having elems from [i,j] = 2 power(j-i) \nbelow are possible subseq that includes ith elem :\n\n1 len = (3) need 0 more from rem 3 elem (5,6,6)=> 3c0 = 1\n2 len = (3,5) (3,6) (3,6) => 1 from rem 3 => 3c1 = 3\n3 len = (3,5,6) (3,5,6) (3 6 6) => 2 from rem 3 => 3c2 = 3 \n4 len = (3,5,6,6) => 3 from rem 3 => 3c3 = 1\n\nwe know Nc0 + Nc1 + Nc2..+NcN = 2^N\n\n*/\n\nclass Solution {\npublic: int mod = 1e9+7;\n int numSubseq(vector<int>& a, int k) {\n vector<int> twopower{1}; //precompute pow of 2 \n \n for(int i = 0;i<a.size();i++){\n twopower.push_back((twopower.back()*2)%mod);\n }\n \n sort(begin(a),end(a)); int ans = 0;\n \n int i = 0,j = a.size()-1; \n \n while(i<=j){\n \n if(a[i]+a[j]>k){\n j--;\n }\n else{\n int rem = j-i,r = 0;\n ans = (ans + twopower[rem]) % mod;\n i++;\n }\n }\n return ans;\n } \n};\n``` | 15 | 0 | ['Two Pointers', 'C'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Python || 96.44% Faster || Two Pointers || Sorting | python-9644-faster-two-pointers-sorting-y6phz | \nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n i,j=0,len(nums)-1\n c,mod=0,(10**9+7)\n nums.sort()\n | pulkit_uppal | NORMAL | 2022-11-27T17:50:17.877852+00:00 | 2022-11-27T17:53:40.795604+00:00 | 2,131 | false | ```\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n i,j=0,len(nums)-1\n c,mod=0,(10**9+7)\n nums.sort()\n while i<=j:\n if nums[i]+nums[j]<=target:\n c+=pow(2,(j-i),mod)\n i+=1\n else:\n j-=1\n return c%mod\n```\n\n**An upvote will be encouraging** | 13 | 1 | ['Two Pointers', 'Sorting', 'Python', 'Python3'] | 2 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java solution | Easy to understand |beats 100% | Beginner friendly | java-solution-easy-to-understand-beats-1-142t | Intuition\n Describe your first thoughts on how to solve this problem. \nProblem requires finding the number of subsequences of the given array nums whose sum i | antovincent | NORMAL | 2023-05-06T08:40:55.078457+00:00 | 2023-05-06T08:40:55.078489+00:00 | 2,655 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nProblem requires finding the number of subsequences of the given array nums whose sum is less than or equal to target. Sorting the array nums in non-decreasing order allows us to apply a two-pointer approach to count such subsequences efficiently. Specifically, we use two pointers l and r that point to the leftmost and rightmost elements of the sorted array, respectively. We then iterate while l is less than or equal to r and count the number of subsequences that can be formed with the first element pointed to by l and the last element pointed to by r. If the sum of these elements is less than or equal to target, then we can include all the subsequences that can be formed with these two elements and any element between them. We use a precomputed array p to calculate the number of subsequences that can be formed with a given range of indices.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Sort the given array nums in non-decreasing order.\n- Initialize two pointers l and r to the first and last elements of the sorted array, respectively.\n- Initialize a variable ans to 0 to store the number of subsequences whose sum is less than or equal to target.\n- Compute an array p such that p[i] stores 2^i modulo 1000000007.\n- Iterate while l is less than or equal to r.\n- If the sum of the elements pointed to by l and r is less than or equal to target, then we can include all the subsequences that can be formed with these two elements and any element between them. Add the number of such subsequences to ans. This number is given by p[r-l].\n- If the sum of the elements pointed to by l and r is greater than target, then decrement r. Otherwise, increment l.\n- Return ans modulo 1000000007.\n\n# Complexity\n- Time complexity:O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int l=0,r=nums.length,ans=0;\n int [] p =new int[r];\n p[0]=1;\n for(int i=1;i<r;i++)p[i] = (p[i-1]*2)%1000000007;\n r--;\n while(l<=r){\n if(nums[l]+nums[r]<=target){\n ans+=p[r-l];\n ans%=1000000007;\n l++;\n }\n else\n r--;\n }\n return ans;\n }\n}\n```\nUpvotes are Encouraging | 12 | 0 | ['Java'] | 2 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java two pointer with explanation | java-two-pointer-with-explanation-by-ank-74b1 | \nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums); //Sorting so that we can get the min and max directly\n | ankitkumarmahato | NORMAL | 2022-01-17T18:15:04.143219+00:00 | 2022-01-17T18:15:04.143269+00:00 | 3,041 | false | ```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums); //Sorting so that we can get the min and max directly\n int i=0,j=nums.length-1,count=0,mod=(int)1e9 + 7;\n int[] power=new int[nums.length]; //Calculating the power in the power array.\n power[0]=1; // no. of subsequences formed using one no. is 1\n for(int idx=1;idx<nums.length;idx++)\n power[idx]=(power[idx-1]*2)%mod; \n\t\t\t//Now if i is at 0 and j is at 3 then the no. of \n\t\t\t//subsequences keeping the first no. that is at i fixed we can form 8 subsequences, similarly for different values of i and j the no. of subsequences varies.\n\t\t\t// if this is the array\n\t\t // 3 5 6 7\t\t\t\n\t\t // i j j-i=3.\n\t\t // then no. of subsequences formed keeping 3 constant is 8 which is stored in the power array (power[j-i]=8) just do a dry run of the formula. you will get 8 for gap of 3\n\t\t\t//3\n\t\t\t//3 5 6 7\n\t\t\t//3 5 6\n\t\t\t//3 5 7\n\t\t\t//3 6 7\n\t\t\t//3 5\n\t\t\t//3 6\n\t\t\t//3 7\n while(i<=j){\n if(nums[i]+nums[j]<=target){\n count=(count+power[j-i])%mod;\n i++;\n }else if(nums[i]+nums[j]>target)\n j--;\n }\n return count;\n }\n}\n``` | 10 | 0 | ['Two Pointers', 'Java'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | 🔥🔥 3-D Dynamic Programming Solution 🔥🔥 | 3-d-dynamic-programming-solution-by-nama-6env | Intuition\nExplore all sub sequencs\nKeep track of min and max element in subsequence\n\n\n# Approach\nBy the way this will give TLE \u203C\n\nAt each index mak | namanchandak | NORMAL | 2023-05-06T06:16:35.030457+00:00 | 2023-05-06T06:36:18.510110+00:00 | 1,781 | false | # Intuition\nExplore all sub sequencs\nKeep track of min and max element in subsequence\n\n\n# Approach\nBy the way this will give TLE \u203C\n\nAt each index make 2 calls\n 1 for pick the element into subsequence\n 2 for not pick the element into subsequence\n\nreturn all the cases where minimum and maximum element has sum not greater than target\n\nthis question has 3-d dp approach\n\n\nAlso at the begining of code I put up 2 elements in nums\n1e9, -1e9 so that if the subset is empty then minimum element is 1e9 and maximum will be -1e9; and hence in base case we have terms like ind==nums.size()-2 (we substract 2 because of the 2 value we put in nums).\n\n# Complexity\n- Time complexity:\no(nxnxn)\n\n- Space complexity:\no(nxnxn)\n\n# Code\n```\nclass Solution {\npublic:\nint mod=1000000007;\n long long int sol(vector<int>& nums, int target,int ind,int maxi,int mini,vector<vector<vector<long long int>>>&dp)\n {\n\n //// base cases\n if(ind>nums.size()-2 )\n return 0;\n\n // cout<<ind<<endl;\n \n if(nums[maxi]+nums[mini]<=target && nums[maxi]!=-1e9 && ind==nums.size()-2)\n return 1;\n else if(ind==nums.size()-1)\n return 0;\n\n \n if(dp[ind][maxi][mini]!=-1)\n return dp[ind][maxi][mini];\n\n\n /////pick,not pick\n long long int notpick=sol(nums,target,ind+1,maxi,mini,dp)%mod;\n\n ///// update min and max values\n maxi=nums[maxi]>nums[ind]?maxi:ind;\n mini=nums[mini]<nums[ind]?mini:ind;\n long long int pick=sol(nums,target,ind+1,maxi,mini,dp)%mod;\n\n return dp[ind][maxi][mini]= pick+notpick%mod;\n\n }\n\n int numSubseq(vector<int>& nums, int target) {\n int n=nums.size();\n nums.push_back(-1e9);\n nums.push_back(1e9);\n vector<vector<vector<long long int>>>dp(n+3,vector<vector<long long int>>(n+3,vector<long long int>(n+3,-1)));\n return sol(nums,target,0,n,n+1,dp)%mod;\n }\n};\n``` | 8 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 2 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Easy Explanation🔥Two Pointers | Cpp | Java | Python | Javascript🔥 | easy-explanationtwo-pointers-cpp-java-py-uoa9 | Intuition\nThe main idea behind this approach is to use two pointers to form pairs of indices (left, right) such that the sum of the minimum and maximum element | nandini-gangrade | NORMAL | 2023-05-06T01:47:17.477923+00:00 | 2023-05-06T01:52:49.197697+00:00 | 2,197 | false | # Intuition\nThe main idea behind this approach is to use two pointers to form pairs of indices (left, right) such that the sum of the minimum and maximum element in the subsequence formed by using the elements from nums[left] to nums[right] is less than or equal to the given target. To count all the subsequences that can be formed using the elements from nums[left+1] to nums[right], we can use the formula 2^(right-left), because for each element in this range, we can either choose to include it or exclude it from the subsequence, thus giving us 2 choices, and we have (right-left) such elements, hence the total number of subsequences that can be formed is 2^(right-left).\n\n# Approach\n- Sort the given array in non-decreasing order.\n- Traverse through the array using two pointers, one pointing to the left end and the other pointing to the right end.\n- For each pair of indices (left, right), if nums[left] + nums[right] <= target, then count all the subsequences of nums that can be formed using the elements from nums[left+1] to nums[right], and add it to the final result.\n- To count all the subsequences that can be formed using the elements from nums[left+1] to nums[right], we can use the formula 2^(right-left), because for each element in this range, we can either choose to include it or exclude it from the subsequence, thus giving us 2 choices, and we have (right-left) such elements, hence the total number of subsequences that can be formed is 2^(right-left).\n- Return the final result.\n\n# Complexity\n- Time complexity: O(nlogn), where n is the length of the given array. This is because we first sort the given array in non-decreasing order, which takes O(nlogn) time, and then we traverse through the array using two pointers, which takes O(n) time in the worst case.\n\n- Space complexity: O(1), since we only use a constant amount of extra space to store the two pointers and the final result.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n const int mod = 1e9 + 7;\n sort(nums.begin(), nums.end());\n int left = 0, right = nums.size() - 1;\n int result = 0;\n while (left <= right) {\n if (nums[left] + nums[right] <= target) {\n result = (result + pow(2, right - left, mod)) % mod;\n left++;\n } else {\n right--;\n }\n }\n return result;\n }\n};\n```\n```java []\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int n = nums.length;\n int left = 0, right = n - 1;\n int res = 0;\n int mod = 1000000007;\n while (left <= right) {\n if (nums[left] + nums[right] <= target) {\n res = (res + (int)Math.pow(2, right - left)) % mod;\n left++;\n } else {\n right--;\n }\n }\n return res;\n }\n}\n\n```\n```python []\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n nums.sort()\n n = len(nums)\n left, right = 0, n - 1\n res = 0\n mod = 10**9 + 7\n while left <= right:\n if nums[left] + nums[right] <= target:\n res = (res + pow(2, right - left, mod)) % mod\n left += 1\n else:\n right -= 1\n return res\n\n```\n```javascript []\nvar numSubseq = function(nums, target) {\n nums.sort((a, b) => a - b);\n let n = nums.length;\n let left = 0, right = n - 1;\n let res = 0;\n let mod = 1000000007;\n while (left <= right) {\n if (nums[left] + nums[right] <= target) {\n res = (res + (2 ** (right - left)) % mod) % mod;\n left++;\n } else {\n right--;\n }\n }\n return res;\n};\n\n```\n**Please Upvote If You Found It Helpful**\n | 8 | 4 | ['Two Pointers', 'C++', 'Java', 'Python3', 'JavaScript'] | 6 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java | Two pointers | Beats 100% | 15 lines | java-two-pointers-beats-100-15-lines-by-sbc7k | Complexity\n- Time complexity: O(n*log(n))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \ | judgementdey | NORMAL | 2023-05-06T00:47:49.419940+00:00 | 2023-05-06T00:49:41.478414+00:00 | 3,856 | false | # Complexity\n- Time complexity: $$O(n*log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n var n = nums.length;\n Arrays.sort(nums);\n\n var exp = new int[n];\n exp[0] = 1;\n\n for (var i=1; i<n; i++)\n exp[i] = (exp[i-1] * 2) % 1000000007;\n\n int i = 0, j = n-1, cnt = 0;\n\n while (i <= j) {\n if (nums[i] + nums[j] <= target) {\n cnt = (cnt + exp[j-i]) % 1000000007;\n i++;\n } else {\n j--;\n }\n }\n return cnt;\n }\n}\n```\nIf you like my solution, please upvote it! | 8 | 1 | ['Array', 'Two Pointers', 'Sorting', 'Java'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ Solution || Sliding Window || Easy to understand | c-solution-sliding-window-easy-to-unders-ylbj | we first sort the array to keep out minimum element at position and find the maximum subarrays that follow the condition.\nthe approach is similar to that of th | ngaur6834 | NORMAL | 2021-05-15T18:08:15.636267+00:00 | 2021-05-15T18:08:15.636308+00:00 | 1,889 | false | we first sort the array to keep out minimum element at position and find the maximum subarrays that follow the condition.\nthe approach is similar to that of the sliding window solution of the two sum problem.\nWhenever our sum is less than or equals to the target sum then we count the number of the subarrays.\n\nLets say our (right - left) is of length l then the solution in this array will be 2^(right - left) (take the element or dont take the element).\n\t\n\tint numSubseq(vector<int>& nums, int target) {\n int n = nums.size();\n \n sort(nums.begin(), nums.end());\n int l = 0;\n int r = n-1;\n int ans = 0;\n int mod = 1e9 + 7;\n \n vector<int> pow(n,1);\n \n for(int i=1; i<n; i++){\n pow[i] = (pow[i-1] * 2) % mod; \n }\n \n while(l <= r){\n if(nums[l] + nums[r] > target){\n r--;\n }\n else{\n ans = (ans + pow[r - l]) % mod;\n l++;\n }\n }\n \n return ans;\n } | 8 | 1 | ['C', 'Sliding Window'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C#, and TypeScript Solution 🔥🚀 with approach. ❇️✅ | c-and-typescript-solution-with-approach-4fsm9 | \u2B06\uFE0FLike|\uD83C\uDFAFShare|\u2B50Favourite\n\n\n\n# Complexity\n- Time complexity:\nO(n log n)\n\n- Space complexity:\n O(n)\n\ncsharp []\npublic class | arafatsabbir | NORMAL | 2023-05-06T05:36:15.372918+00:00 | 2023-05-06T05:36:15.372946+00:00 | 2,125 | false | # \u2B06\uFE0FLike|\uD83C\uDFAFShare|\u2B50Favourite\n\n\n\n# Complexity\n- Time complexity:\nO(n log n)\n\n- Space complexity:\n O(n)\n\n```csharp []\npublic class Solution {\n public int NumSubseq(int[] nums, int target) {\n // Sort the array in non-decreasing order\n Array.Sort(nums);\n\n // Initialize variables\n int mod = 1000000007;\n int n = nums.Length;\n int ans = 0;\n\n // Calculate powers of 2 modulo mod\n int[] pow2 = new int[n];\n pow2[0] = 1;\n for (int i = 1; i < n; i++) {\n pow2[i] = (pow2[i - 1] * 2) % mod;\n }\n\n // Use two pointers to find subsequences\n int left = 0, right = n - 1;\n while (left <= right) {\n // If the sum of the minimum and maximum values is less than or equal to target,\n // add the number of subsequences of length (right - left) to the answer\n if (nums[left] + nums[right] <= target) {\n ans = (ans + pow2[right - left]) % mod;\n left++;\n }\n // Otherwise, move the right pointer to the left\n else {\n right--;\n }\n }\n\n return ans;\n }\n}\n```\n```typescript []\nfunction numSubseq(nums: number[], target: number): number {\n nums.sort((a, b) => a - b); // sort array in non-decreasing order\n\n const mod = 1e9 + 7;\n const n = nums.length;\n let ans = 0;\n\n // calculate powers of 2 modulo mod\n const pow2: number[] = new Array(n);\n pow2[0] = 1;\n for (let i = 1; i < n; i++) {\n pow2[i] = (pow2[i - 1] * 2) % mod;\n }\n\n // use two pointers to find subsequences\n let left = 0, right = n - 1;\n while (left <= right) {\n // if the sum of the minimum and maximum values is less than or equal to target,\n // add the number of subsequences of length (right - left) to the answer\n if (nums[left] + nums[right] <= target) {\n ans = (ans + pow2[right - left]) % mod;\n left++;\n }\n // otherwise, move the right pointer to the left\n else {\n right--;\n }\n }\n\n return ans;\n};\n``` | 7 | 0 | ['Array', 'Two Pointers', 'Sorting', 'TypeScript', 'C#'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Easy JS solution Beats 95% online submissions | easy-js-solution-beats-95-online-submiss-joso | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Viraj_Patil_092 | NORMAL | 2023-05-06T04:33:19.716428+00:00 | 2023-05-06T04:33:19.716479+00:00 | 2,088 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[]} nums\n * @param {number} target\n * @return {number}\n */\nvar numSubseq = function(nums, target) {\n let pow = [];\n pow.push(1);\n\n nums.sort((a,b)=>{return a-b;})\n\n const mod = 1e9+7;\n\n for(let i = 1;i < nums.length;i++){\n pow.push((pow[pow.length-1]*2) % mod);\n }\n\n let i = 0, j = nums.length-1, res = 0;\n\n while(i <= j){\n if(nums[i]+nums[j] > target){\n j--;\n }\n else{\n res = (res+pow[j-i++]) % mod;\n }\n }\n\n return res;\n};\n``` | 7 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'Sorting', 'JavaScript'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | [ C++ ] | Binary Search + Binary Exponentiation | Easy Explanation | c-binary-search-binary-exponentiation-ea-tqk8 | Intuition\n Describe your first thoughts on how to solve this problem. \nSince we have to find Subsequences, Sorting will not hamper the result\n\nFor each inte | kshzz24 | NORMAL | 2023-05-06T04:32:30.508895+00:00 | 2023-05-06T04:32:30.508929+00:00 | 1,013 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince we have to find Subsequences, Sorting will not hamper the result\n\nFor each integer if we found the maximum value which can be accepted under the given conditions we can find all subsequences starting from that integer.\n\n# Prerequisites \n\n[ Binary Exponentiation](https://leetcode.com/problems/powx-n/)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSort the Array,then for each element find the maximum accepted value\n\nwe only have to consider those cases where `target-nums[currIndex]>=nums[currIndex]` because then only we can find a possible answer\n\n\n\n## How will Upper Bound work\nUpper bound will return the index of the element which is just greater than the maximum accepted value\n\nIf Upper Bound returns `currIndex` means that there is no integer `>` nums[currIndex] we have to skip those case.\n\nOtherwise calculate the all the subsequences\n\nNo. of Subsequences will be `2^(Length of array)`\n\n\n\n# Complexity\n- Time complexity: $$O(nLogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define ll long long\nclass Solution {\npublic:\n // Define a constant M for modular arithmetic\n int M = 1e9+7;\n \n // Define a function for efficient modular exponentiation\n ll binpow(ll a, ll b) {\n ll res = 1;\n while (b > 0) {\n if (b & 1)\n res = (res * a)%M;\n a = (a * a)%M;\n b >>= 1;\n }\n return res;\n }\n \n int numSubseq(vector<int>& nums, int target) {\n int n = nums.size();\n int ans = 0;\n \n // Sort the input array\n sort(nums.begin(), nums.end());\n\n // Iterate over each element of the array\n for(int i = 0;i<n;i++){\n int currIndex = i;\n \n // If the current element is less than or equal to half the target\n if(target-nums[currIndex]>=nums[currIndex]){\n \n // Use upper_bound to find the index of the largest element in the array\n // that is less than or equal to the target minus the current element\n int index = upper_bound(nums.begin()+currIndex, nums.end(), (target-nums[currIndex]))-nums.begin();\n \n // If such an element exists\n if(index!=currIndex){\n \n // Compute the number of subsequences that can be formed using the current\n // element and all elements up to and including the target minus the current element\n ans = ans%M+ binpow(2, (index-1-currIndex))%M;\n }\n }\n }\n \n return ans;\n }\n};\n\n``` | 7 | 0 | ['Binary Search', 'Sorting', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ solution (sorting + sliding window protocol) | c-solution-sorting-sliding-window-protoc-x8yt | \nCode:\nclass Solution {\npublic:\n \n int numSubseq(vector& nums, int target) {\n \n sort(nums.begin(), nums.end());\n \n in | pazamour | NORMAL | 2020-06-29T06:47:10.477529+00:00 | 2020-06-29T06:47:45.302427+00:00 | 1,884 | false | \nCode:\nclass Solution {\npublic:\n \n int numSubseq(vector<int>& nums, int target) {\n \n sort(nums.begin(), nums.end());\n \n int l = 0;\n int r = nums.size()-1;\n int ans = 0;\n long long por[nums.size()+1];\n por[0]=1;\n\t\t\n\t\t/// Also, we can reduce the no.calculations for calculating power as well (I just didn\'t do it here)\n for (int i=1; i<=nums.size(); i++) {\n por[i] = (2*por[i-1])%1000000007;\n }\n while(l<=r) {\n int sum = nums[l]+nums[r];\n if (sum<=target) {\n ans = ((ans + por[r-l])%1000000007);\n l++;\n } else {\n r--;\n }\n }\n return ans;\n }\n}; | 7 | 0 | [] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Easy Java solution || beginner friendly | easy-java-solution-beginner-friendly-by-9jhwj | Please UPVOTE if you like my solution!\n\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int mod = 10 | gau5tam | NORMAL | 2023-05-06T17:25:17.901441+00:00 | 2023-05-06T17:25:17.901474+00:00 | 255 | false | Please **UPVOTE** if you like my solution!\n```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int mod = 1000000007;\n int [] arr =new int[nums.length];\n arr[0]=1;\n for(int i=1;i<nums.length;i++){\n arr[i] = (arr[i-1]*2)%mod;\n }\n\n int i = 0;\n int j = nums.length-1;\n int count = 0;\n while(i<=j){\n if(nums[i]+nums[j]<=target){\n count+=arr[j-i];\n count%=mod;\n i++;\n }\n else\n j--;\n }\n return count;\n }\n}\n``` | 6 | 0 | ['Two Pointers', 'Sorting', 'Java'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java 27 ms Faster than 99.87% online submissions using sliding window and Sorting | java-27-ms-faster-than-9987-online-submi-4q2s | \nclass Solution {\n public int numSubseq(int[] nums, int target) {\n final int MODULO = 1000000007;\n int length=nums.length;\n Arrays. | tarushi | NORMAL | 2021-02-25T22:30:05.984555+00:00 | 2021-02-25T22:33:06.744622+00:00 | 2,091 | false | ```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n final int MODULO = 1000000007;\n int length=nums.length;\n Arrays.sort(nums);\n int[] power2 = new int[length + 1];\n power2[0] = 1;\n for (int i = 1; i <= length; i++)\n power2[i] = (power2[i - 1] * 2) % MODULO;\n int l=0; int r=length-1; int ans=0;\n while(l<=r){\n if(nums[l]+nums[r]<=target){\n ans=(ans+power2[r-l])%MODULO;\n l+=1;\n }else{\n r-=1;\n }\n }\n \n return ans;\n }\n}\n```\n//this question in java can work with Math.pow function also but Math.pow returns double value and then that gets converted to int thus deviates the value of ans ...and so power2 is pre-computed in here\n``` | 6 | 0 | ['Sliding Window', 'Sorting', 'Java'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Two-Pointers Approach || Easy to Understand | two-pointers-approach-easy-to-understand-ztvq | Solution:\n\nThe given problem can be solved using two pointer technique.\n\nFirst, sort the given array.\n\nThen, we can consider each element in the array as | IAmMADMAX | NORMAL | 2023-05-06T08:35:43.543140+00:00 | 2023-05-06T08:35:43.543178+00:00 | 428 | false | **Solution:**\n\nThe given problem can be solved using two pointer technique.\n\nFirst, sort the given array.\n\nThen, we can consider each element in the array as the minimum element of a subsequence, and find the maximum element that can be included in the subsequence such that the sum of the minimum and maximum element is less than or equal to the target. We can use a pointer for this.\n\nFor each minimum element, we can calculate the number of subsequences that can be formed using the maximum element pointer. This can be calculated as 2^(j-i), where i is the index of the minimum element and j is the index of the maximum element.\n\nFinally, we can add up the number of subsequences for each minimum element and return the result modulo 10^9 + 7.\n\nHere\'s the implementation of the above approach:\n\n````\nclass Solution:\n\tdef numSubseq(self, nums: List[int], target: int) -> int:\n nums.sort()\n i, j = 0, len(nums)-1\n ans = 0\n while i <= j:\n if nums[i] + nums[j] <= target:\n ans += pow(2, j-i, 10**9+7)\n i += 1\n else:\n j -= 1\n return ans % (10**9+7)\n```` | 5 | 0 | ['Two Pointers', 'Python3'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Optimized solution using Two Pointers with Binary Exponentiation | Solution explained in detail. | optimized-solution-using-two-pointers-wi-x470 | \n\n# Approach\nThe given problem requires counting the number of non-empty subsequences of an array of integers nums such that the sum of the minimum and maxim | priyanshu11_ | NORMAL | 2023-05-06T07:26:53.805508+00:00 | 2023-05-06T07:28:06.651270+00:00 | 2,109 | false | \n\n# Approach\nThe given problem requires counting the number of non-empty subsequences of an array of integers nums such that the sum of the minimum and maximum element on it is less than or equal to a given integer target. Since the answer may be large, the final result must be returned modulo 10^9 + 7.\n\nThe solution starts by sorting the input array in non-decreasing order, allowing us to easily compare the minimum and maximum elements of any subsequence.\n\nNext, two pointers, left and right, are initialized at the beginning and the end of the sorted array, respectively. The idea is to consider all possible subsequences of nums by varying the left and right endpoints, while counting only those that satisfy the given condition. Specifically, for any pair of indices (left, right) such that nums[left] + nums[right] \u2264 target, we add 2^(right-left) to the answer ans to count the number of subsequences that can be formed between these indices.\n\nThe factor of 2^(right-left) corresponds to the number of ways to choose any subset of elements between left and right, i.e., the number of non-empty subsequences. The running sum of this quantity is maintained in ans. Whenever the sum nums[left] + nums[right] is greater than target, we decrement right, since the minimum and maximum elements in any valid subsequence must add up to less than or equal to target. If nums[left] + nums[right] is less than or equal to target, we increment left and add 2^(right-left) to the answer.\n\nFinally, the function returns the value of ans modulo 10^9 + 7 as required.\n\n# Complexity\n- Time complexity:\nSorting the array takes O(nlogn) time, where n is the length of the input array. The while loop takes O(n) time, since each pointer moves at most n times. The time complexity of the power function is O(log mod) since it uses the binary exponentiation algorithm. Therefore, the overall time complexity is O(nlogn).\n\n- Space complexity:\nThe solution uses constant space, except for the space used to store the sorted array, which takes O(n) space. Therefore, the space complexity of this solution is O(n).\n\n# Code\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n const int MOD = 1e9 + 7;\n int n = nums.size();\n sort(nums.begin(), nums.end());\n int left = 0, right = n - 1;\n long long ans = 0;\n while (left <= right) {\n if (nums[left] + nums[right] > target) {\n right--;\n } else {\n ans = (ans + power(2, right - left, MOD)) % MOD;\n left++;\n }\n }\n return ans;\n }\n \n int power(int base, int exp, int mod) {\n long long res = 1;\n while (exp > 0) {\n if (exp % 2 == 1) {\n res = (res * (long long)base) % mod;\n }\n base = ((long long)base * base) % mod;\n exp /= 2;\n }\n return (int)res;\n }\n\n};\n\n``` | 5 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'C++', 'Java'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ || BINARY SEARCH || SORT || EASY TO UNDERSTAND | c-binary-search-sort-easy-to-understand-69rys | Intuition\n\nhere we need to find all subsequece.\nso find biggest element for (v[i]+x)<=target\nall element between [v[i] to x] possible ans v[i] must be inclu | ganeshkumawat8740 | NORMAL | 2023-05-06T06:55:41.646711+00:00 | 2023-05-06T07:12:16.051965+00:00 | 2,085 | false | # Intuition\n\nhere we need to find all subsequece.\nso find biggest element for (v[i]+x)<=target\nall element between [v[i] to x] possible ans v[i] must be included in subsequence.\n\n# Approach\nSORT ARRAY\nfind upper bound of target-v[i]. let\'s upperbound\'s index equal to x\nif(x<i)break;\nelse increment ans by (1LL<(x-i-1)) \n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nCONSTANT SPACE\n\n# Code\n```\n//IF ANY SUGGETION INFORM ME \n//AND UPVOTE THIS SOLUTION\nclass Solution {\npublic:\n int po(int x){\n int y = 1, mod = 1e9+7,z = 2;\n while(x){\n if(x&1){\n y = (y*1LL*z)%mod;\n }\n x >>= 1;\n z = (z*1LL*z)%mod;\n }\n return y;\n }\n int numSubseq(vector<int>& nums, int target) {\n int mod = 1e9+7;\n sort(nums.begin(),nums.end());\n for(auto &i: nums)cout<<i<<" ";\n int ans = 0;\n int i,x,n=nums.size();\n for(i = 0; i < n; i++){\n x = upper_bound(nums.begin(),nums.end(),target-nums[i])-nums.begin();//find an element x index for that v[i]+x>target\n \n if(x-i-1<0)break;\n ans = (ans + po(x-i-1)%mod)%mod;//get all possible ans for an sorted subarray\n }\n return ans;\n }\n};\n``` | 5 | 0 | ['Binary Search', 'Sorting', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | ✅C++ || Two-pointer || Set Theory || Sorting | c-two-pointer-set-theory-sorting-by-abhi-verz | \n\nT->O(n * log n) && S->O(n) [For storing the power of 2\'s in vector\n\n\tclass Solution {\n\tpublic:\n\t\tint numSubseq(vector& nums, int target) {\n\t\t\ti | abhinav_0107 | NORMAL | 2022-07-07T20:42:04.084134+00:00 | 2022-07-07T20:42:04.084181+00:00 | 1,537 | false | \n\n**T->O(n * log n) && S->O(n) [For storing the power of 2\'s in vector**\n\n\tclass Solution {\n\tpublic:\n\t\tint numSubseq(vector<int>& nums, int target) {\n\t\t\tint mod=1e9+7,n=nums.size();\n\t\t\tsort(nums.begin(),nums.end());\n\t\t\tvector<int> p(n,1);\n\t\t\tfor(int i=1;i<n;i++) p[i]=(2*p[i-1])%mod;\n\t\t\tint i=0,j=n-1,count=0;\n\t\t\twhile(j>=i){\n\t\t\t\tif(nums[i]+nums[j]<=target){\n\t\t\t\t\tcount+=p[j-i];\n\t\t\t\t\ti++;\n\t\t\t\t}\n\t\t\t\telse j--;\n\t\t\t}\n\t\t\treturn count; \n\t\t}\n\t}; | 5 | 0 | ['Two Pointers', 'C', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | JavaScript (JS) solution 🔥🔥🔥 Ultrafast 💯💯💯 | javascript-js-solution-ultrafast-by-abas-xmio | JavaScript solution\n\n\nvar numSubseq = function(nums, target) {\n const MOD = 1000000007;\n\n nums = nums.sort((a, b) => a - b);\n\n const pows = [1] | abashev | NORMAL | 2022-06-17T04:42:59.613381+00:00 | 2022-06-17T04:44:28.985461+00:00 | 1,212 | false | JavaScript solution\n\n```\nvar numSubseq = function(nums, target) {\n const MOD = 1000000007;\n\n nums = nums.sort((a, b) => a - b);\n\n const pows = [1];\n \n for (let i = 1; i < nums.length; i++) {\n pows.push(pows[i - 1] * 2 % MOD);\n }\n \n let left = 0;\n let right = nums.length - 1;\n let ans = 0;\n\n while (left <= right) {\n if (nums[left] + nums[right] > target) {\n right--;\n } else {\n ans = (ans + pows[right - left]);\n left++;\n }\n }\n\n return ans % MOD;\n};\n``` | 5 | 1 | ['Two Pointers', 'Binary Search', 'Binary Tree', 'JavaScript'] | 3 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ | Two Pointer Solution | O(nlogn) | Explained | c-two-pointer-solution-onlogn-explained-erfry | Approach\n1. Sort the given nums array.\n2. For every index i from 0 to n-1 find the index j of largest number.\n3. The number of valid subsequences are 2^(j - | nikhil682 | NORMAL | 2021-10-26T05:45:53.073021+00:00 | 2021-10-26T05:45:53.073068+00:00 | 1,202 | false | Approach\n1. Sort the given nums array.\n2. For every index i from 0 to n-1 find the index j of largest number.\n3. The number of valid subsequences are 2^(j - i)\n\nI have stored the values from 2^0 to 2^(n-1) to avoid repeated computations.\n\n```\n int numSubseq(vector<int>& nums, int target) {\n \n int mod = 1000000007;\n \n //sort the given array\n int n = nums.size();\n sort(nums.begin(), nums.end());\n \n //store 2^power to decrease computations\n vector<int> power = {1};\n for(int i = power.size(); i < n; i++){\n power.push_back((power.back() << 1)%mod);\n }\n \n //store the result in res\n int res = 0;\n \n //Initialize a pointer j pointing to the last element\n int j = n - 1;\n for(int i = 0; i < n; i++){\n \n // Decrement j until condition satisfies\n while(nums[i] + nums[j] > target && i < j) j--;\n \n // Add 2^(j - i) to the result\n if(nums[i] + nums[j] <= target){\n res = (res%mod + power[j - i]%mod)%mod;\n }\n }\n \n return res;\n }\n``` | 5 | 0 | [] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | FASTER THAN 100% TIME +100% SPACE | faster-than-100-time-100-space-by-shivam-3p4p | JAVA CODE IS:\n# \n\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int res=0,mod=1000_000_000+7;\n | shivam_gupta_ | NORMAL | 2021-03-27T06:08:02.009534+00:00 | 2021-03-27T06:08:02.009562+00:00 | 790 | false | JAVA CODE IS:\n# \n```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int res=0,mod=1000_000_000+7;\n int pow[]=new int[nums.length+1];\n pow[0]=1;\n for(int i=1;i<=nums.length;i++)\n pow[i]=(pow[i-1]*2)%mod;\n int i=0,j=nums.length-1;\n while(i<=j){\n if(nums[i]+nums[j]<=target) res=(res+pow[j-i++])%mod;\n else j--;\n }\n return res;\n }\n}\n```\nTIME : O(nlogn)\nSPACE : O(n)\n***PLEASE,UPVOTE IF THIS IS HELPFUL*** | 5 | 1 | [] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java+two pointer approch | javatwo-pointer-approch-by-puskin123-grsa | class Solution {\n public int numSubseq(int[] nums, int target) {\n\n//basically the total subsequences possible from start to end is the ans of that particu | puskin123 | NORMAL | 2020-09-04T10:18:33.685758+00:00 | 2020-09-05T13:13:21.496085+00:00 | 1,244 | false | class Solution {\n public int numSubseq(int[] nums, int target) {\n\n//basically the total subsequences possible from start to end is the ans of that particular start index\n \n\tArrays.sort(nums);\n int sp=0;\n int ans=0;\n int ep=nums.length-1;\n while(sp<=ep){\n if(nums[sp]+nums[ep]<=target){\n ans+=help(2,ep-sp);//to calculate Math.pow(2,ep-sp) reduce to logn \n ans=ans%1000000007;\n sp++;\n }else{\n ep--;\n }\n }\n return ans;\n }\n public long help(int x,int y){\n if(y==1)\n return x;\n if(y==0)\n return 1;\n long ans=1;\n if(y%2==0){\n ans=help(x,y/2);\n ans*=ans;\n }else{\n ans=help(x,y-1);\n ans=ans*x;\n ans=ans%1000000007;\n }\n return ans%1000000007;\n \n }\n} | 5 | 2 | [] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java Solution | java-solution-by-mycafebabe-a58z | \nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int ans = 0;\n int n = nums.length;\n | mycafebabe | NORMAL | 2020-07-10T07:07:47.201027+00:00 | 2020-07-10T07:07:47.201074+00:00 | 1,024 | false | ```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int ans = 0;\n int n = nums.length;\n int mod = (int)(1e9 + 7);\n int[] pows = new int[n];\n pows[0] = 1;\n for (int i = 1; i < n; i++) {\n pows[i] = (pows[i - 1] * 2) % mod;\n }\n int i = 0, j = n - 1;\n while (i <= j) {\n if (nums[i] + nums[j] <= target) {\n ans = (ans + pows[j - i]) % mod;\n i++;\n } else {\n j--;\n }\n }\n return ans;\n }\n}\n``` | 5 | 1 | [] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java Very Clean solution faster than 100% speed and space using Two Pointer O(nlogn) time | java-very-clean-solution-faster-than-100-7adc | \nclass Solution {\n private static final int MOD = 1000000007;\n public int numSubseq(int[] nums, int target) {\n long[] modPow = new long[nums.le | nambk314 | NORMAL | 2020-06-28T07:02:06.649834+00:00 | 2020-06-28T07:02:30.050459+00:00 | 2,101 | false | ```\nclass Solution {\n private static final int MOD = 1000000007;\n public int numSubseq(int[] nums, int target) {\n long[] modPow = new long[nums.length + 1];\n modPow[0] = 1;\n for (int i = 1; i < modPow.length; i++) {\n modPow[i] = 2 * modPow[i-1] % MOD;\n }\n \n Arrays.sort(nums);\n int low = 0;\n int high = nums.length -1;\n long result = 0;\n while (low <= high) {\n if (nums[low] + nums[high] > target) {\n high--;\n } else {\n long curPower = modPow[high-low];\n result += curPower%MOD;\n low++;\n }\n }\n result = result%MOD;\n return (int) result;\n }\n}\n``` | 5 | 1 | [] | 7 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C# 2 Pointer solution | c-2-pointer-solution-by-leoooooo-bl15 | \npublic class Solution\n{\n public int NumSubseq(int[] nums, int target)\n {\n Array.Sort(nums);\n long mod = (long)Math.Pow(10, 9) + 7;\n\ | leoooooo | NORMAL | 2020-06-28T05:15:23.852463+00:00 | 2020-06-28T05:25:12.899185+00:00 | 547 | false | ```\npublic class Solution\n{\n public int NumSubseq(int[] nums, int target)\n {\n Array.Sort(nums);\n long mod = (long)Math.Pow(10, 9) + 7;\n\t\t//Pre compute 2^N, since N is big in this question.\n long[] cnt = new long[nums.Length];\n cnt[0] = 1;\n for (int i = 1; i < nums.Length; i++)\n {\n cnt[i] = cnt[i - 1] * 2 % mod;\n }\n \n long res = 0;\n int left = 0;\n int right = nums.Length - 1;\n while (left <= right)\n {\n if (nums[left] + nums[right] > target)\n right--;\n else\n {\n\t\t\t\t//The combination of sub sequence starting from nums[left] is 2 ^ (right - left)\n res += cnt[right - left];\n left++;\n }\n }\n\n return (int)(res % mod);\n }\n}\n``` | 5 | 2 | [] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | JAVA CODE || Properly Explained With Diagram || Modified Two Sum Approach || | java-code-properly-explained-with-diagra-3cje | Intuition\n Describe your first thoughts on how to solve this problem. \nwe can use modified two sum approach to solve this.\n\n# Approach\n Describe your appro | shiivamtaneja | NORMAL | 2023-08-15T13:50:37.867409+00:00 | 2023-08-15T13:50:37.867434+00:00 | 391 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe can use modified two sum approach to solve this.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirstly we need to ensure that the array is sorted for this approach to work.\nNow we create a new array of the same size as the input array, this array stores the power of 2 , \neg- [$$2^0$$, $$2^1$$, $$2^2$$, $$2^3$$, $$2^4$$ and so on ]\n\n\n powerValues = [1, 2, 4, 8, 16...]\n \n`(powerValues[i - 1] * 2) % mod` is done to avoid integer overflow, the dry run for filling the powerValues array is\n\n at i = 0\n powerValues[0] = 1\n\n at i = 1\n powerValues[1] = (powerValues[0] * 2) % (10^9 + 7)\n i.e. powerValues[1] = 2\n\nnow we just modify the two sum approach to solve this question.\nlets consider - \n\n arr - [3, 5, 6, 7] target = 9\n | |\n left right\n\nsince `nums[left] + nums[right] <= target` then that means that we can find `2^(right- left)`different number of Subsequences which satisfy the above condition.\n\nwe got `2^(right- left)`different number of Subsequences because -\n`total number of ways to select n elements = 2 ^ n` this also includes those cases where we don\'t select any element and we aren\'t allowed to pick non-empty subsequences.\n\nso we fix the smallest element, then we only have the choice to select or not select those elements ranging from `left + 1` to `right`\n\n eg - \n arr - [1, 2, 6, 7]\n | |\n left right\n \nif`1`is fixed, then we only have option for`2`, and `6` either to `select them` or `not select them`. So,\n\n`total number of ways to select n elements = 2 ^ (right - (left + 1) + 1)` (+ 1 at the end for 0 based indexing.)\n\nso instead of calculating all the number of Subsequences, we use the powerValues array to find number, then we modulo it with `10^9 + 7` to avoid integer overflow\n\n# Complexity\n- Time complexity:\nSorting - $$O(n*logn)$$\nSaving the power of 2 - $$O(n)$$\nModified Two Sum approach - $$O(n)$$\n\nOverall Time Complexity - $$O(n*logn)$$ + $$O(n)$$ + $$O(n)$$ = $$O(n*logn)$$\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n // Sorting the array\n Arrays.sort(nums);\n int n = nums.length;\n \n int[] powerValues = new int[n];\n int mod = (int) 1e9 + 7;\n\n // Filling the array with power of 2\'s\n for(int i = 0; i < n; i++) {\n powerValues[i] = i == 0 ? 1 : (powerValues[i - 1] * 2) % mod;\n }\n\n // Modified Two sum approach\n int left = 0;\n int right = n - 1;\n int counter = 0;\n\n while(left <= right) {\n if(nums[left] + nums[right] > target) {\n right--;\n } else {\n // Using the stored value of power of 2\n // to find the number of Subsequences\n counter = (counter + powerValues[right - left]) % mod;\n left++;\n }\n }\n\n return counter;\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Easy Solution | C++ | Two pointer | Exponentiation | Beginner Friendly | easy-solution-c-two-pointer-exponentiati-ngly | \n\n# Approach\n- First, we sort the array.\n- We use the 2 pointer approach to check if the first and last element is greater or less than the target\n- If the | kvkvvats | NORMAL | 2023-05-06T14:00:56.311527+00:00 | 2023-05-06T17:00:40.338666+00:00 | 632 | false | \n\n# Approach\n- First, we sort the array.\n- We use the 2 pointer approach to check if the first and last element is greater or less than the target\n- If the condition is satisfied then we calculate the number of non-empty subsequences\n- Number of sequences is equal to 2^n where n is the difference b/w the first and the last pointer\n- We calculate the power using Exponentiation to avoid TLE as it uses logn complexity.\n\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity: \nO(1)\n\n# Code\n```\nclass Solution {\nprivate:\n long long power(long long base,long long n, long long mod){\n long long ans=1;\n while(n!=0){\n if(n%2==1){\n ans=(ans*base)%mod;\n n--;\n }else{\n base=(base*base)%mod;\n n=n/2;\n }\n }\n return ans;\n }\npublic:\n int numSubseq(vector<int>& nums, int target) {\n\n int start=0;\n int end=nums.size()-1;\n\n sort(nums.begin(),nums.end());\n\n int mod=1000000007;\n\n int count=0;\n\n //number of subsequences is 2^n here, n is the range b/w the first and last element index\n\n while(start<=end){\n\n if(nums[start]+nums[end]<=target){\n long long totalsubseq=power(2,end-start,mod);\n count=(count+totalsubseq)%mod;\n start++;\n }\n else{\n end--;\n }\n\n }\n\n return count;\n }\n};\n``` | 4 | 0 | ['Two Pointers', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | To Find Number of Subsequences That Satisfy the Given Sum Condition | to-find-number-of-subsequences-that-sati-w0kz | Approach\nFirstly sort the given array. Now set a right pointer to n-1 and left pointer to 0. Now check if nums[left] +nums[right] >target. This is because afte | _parthiv_saikia_ | NORMAL | 2023-05-06T13:20:43.372454+00:00 | 2023-05-06T13:33:18.279458+00:00 | 1,042 | false | # Approach\nFirstly sort the given array. Now set a right pointer to n-1 and left pointer to 0. Now check if nums[left] +nums[right] >target. This is because after sorting the smallest element will at left and largest element is on the right. If the sum is greater than target decrease the right pointer. If the sum is less than or equal to target add it to answer as ans+=(2^(right-left))%mod. Example if the right pointer is on 2nd index and left pointer on the 0th index then the total number of elements is 2-0+1=3 and the total number of subsequences possible is 2^2=4 of (2^(right-left)) %mod. Then increase the left pointer by one. Repeat this step until left pointer is smaller or equal to right pointer. This while loop will run in O(n) time complexity but we had sort the array in the beginning so the overall time complexity of the entire program will be O(nlogn).\n# Complexity\n- Time complexity:\nO(nlogn) for sorting\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n int mod=1e9+7;\n int ans=0;\n int n=nums.size();\n int left=0,right=n-1;\n sort(nums.begin(),nums.end());\n vector<int> pow(n,1);\n for(int i=1;i<n;i++)\n {\n pow[i]=pow[i-1]*2%mod;\n }\n while(left<=right)\n {\n if((nums[left]+nums[right])>target)\n {\n right-=1;\n }\n else\n {\n ans=(ans+(pow[right-left]%mod))%mod;\n left+=1;\n }\n }\n return ans%mod;\n }\n};\n``` | 4 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'Sorting', 'C++'] | 2 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Very Easy Way || Precomputing || sorting || Binary Search || CPP | very-easy-way-precomputing-sorting-binar-m25z | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shubham7447 | NORMAL | 2023-05-06T08:27:04.604240+00:00 | 2023-05-06T08:27:04.604285+00:00 | 416 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define mod 1000000007\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n int n=nums.size();\n vector<int>v(n);\n int p=1;\n for(int i=0;i<n;i++){\n v[i]=p;\n p=2*p;\n p=p%mod;\n }\n sort(nums.begin(),nums.end());\n int ans=0;\n for(int i=0;i<n;i++){\n if(nums[i]+nums[i]>target){\n break;\n }\n if(i==n-1){\n ans++;\n return ans;\n }\n \n int s=i+1;\n int e=n-1;\n int m=(s+e)/2;\n while(s<=e){\n // cout<<s<<" "<<e<<" "<<i<<endl;\n if(nums[m]<=target-nums[i]){\n s=m+1;\n }\n else if(nums[m]>target-nums[i]){\n e=m-1;\n }\n m=(s+e)/2;\n }\n int a=m-i;\n ans=(ans%mod+(v[a]%mod))%mod;\n // cout<<m<<endl;\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Math', 'Binary Search', 'Sorting', 'C++'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | [ C++ ] [ Dynamic Programming ] [ DP + Binary Search ] | c-dynamic-programming-dp-binary-search-b-uie7 | Code\n\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end());\n int n = nums.size();\n | Sosuke23 | NORMAL | 2023-05-06T04:02:41.243023+00:00 | 2023-05-06T06:56:06.450377+00:00 | 2,102 | false | # Code\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end());\n int n = nums.size();\n long res = 0;\n int k = 1\'000\'000\'007;\n vector<long> dp(n + 1, 1);\n for(int i = 1; i <= n; ++i){\n dp[i] = (dp[i - 1] << 1) % k;\n }\n for(int i = 0, j = n - 1; i < n; ++i){\n while(j >= i && nums[i] + nums[j] > target) {\n --j;\n }\n if(i > j) {\n continue;\n } \n res = (res + dp[j - i]) % k; \n }\n return res;\n }\n};\n```\n# UPD ( Binary Search to Speed Up the Process )\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end());\n int n = nums.size();\n long res = 0;\n int k = 1\'000\'000\'007;\n vector<long> dp(n + 1, 1);\n for(int i = 1; i <= n; ++i){\n dp[i] = (dp[i - 1] << 1) % k;\n }\n int lo = 0, hi = n - 1;\n while (lo <= hi) {\n if (nums[lo] + nums[hi] > target) {\n hi -= 1;\n } \n else {\n (res += (dp[hi - lo])) %= k;\n lo += 1;\n }\n }\n return res;\n }\n};\n``` | 4 | 0 | ['Binary Search', 'Dynamic Programming', 'C++'] | 2 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ Easy Binary Search Solution | c-easy-binary-search-solution-by-beast_3-4tnx | So let us first look at the logic part, so consider an array [2,3,4,5] and target value 7 for this array . Now we know that for the first element i.e., 2 the up | Beast_376 | NORMAL | 2022-07-14T15:23:25.175972+00:00 | 2022-07-16T05:58:02.208741+00:00 | 877 | false | So let us first look at the logic part, so consider an array [2,3,4,5] and target value 7 for this array . Now we know that for the first element i.e., 2 the upper_bound value would be 5 (target-a[i]) . So we would add pow(2,3-0) in our answer (3 is index of 5 and 0 is index of 2). But the question arises why we considered all the subsequences with max length 3, why not 4, we all know that if we are considering a particular element then if we want any subsequence to satisy this condition of ***(max-min<=target)*** we would have to consider that element in every subsequence so originally if we would have take subsequences of max length 4 then there would be some subsequence like [3,4,5] which would have been taken into consideration but this subsequence does not have min value as 2 so therfore to eleminate such subsequences we have taken one length less than the actual length.\nFollow the below steps to get an idea on how to approach this question:\n1. Firstly we will Sort the array.\n1. After that we will compute and store the powers of 2 for values till 100001 with mod. \n1. Now we will perform binary search on every element to find the upper_bound of (target-a[i]). If we find any such value then we will add powers[ind-i] to our answer. Here we will make use of the powers array which we made in previous step.\n\n\n``` \nclass Solution {\npublic:\n int numSubseq(vector<int>& a, int t) {\n \n sort(a.begin(),a.end());\n \n // powers array to precomputer powers of 2 with mod\n int powers[100001]={};\n \n // pow(2,0)=1\n powers[0]=1;\n \n int mod=1000000007;\n \n for(int i=1;i<100001;i++){\n // calculating power for every i\n powers[i]=(powers[i-1]*2)%mod;\n }\n \n long long int ans=0;\n \n for(int i=0;i<a.size();i++){\n \n // defining ranges for every i\n int l=i,r=a.size()-1,ind=-1;\n \n while(l<=r){\n int mid=(l+r)/2;\n \n // if a[mid]+a[i]<=target then we can increase the value of l \n if(a[mid]+a[i]<=t){\n ind=max(ind,mid);\n l=mid+1;\n }\n \n // else we have to decrease value of r \n else{\n r=mid-1;\n }\n }\n \n // edge case (if there is no such value (target-a[i]) does not exist then we will not compute for this i and every i greater than this one\n if(ind!=-1){\n \n \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0// subtract the value of i from ind and add the power to the answer \n ind-=i;\n \n ans=(ans+powers[ind])%mod;\n \n }\n \n else{\n break;\n }\n }\n \n return ans;\n }\n};\n```\nIf you have liked my explanation for this question, then please ***upvote***. \nIf you have any ***doubts*** then you can ask in the comments section.\nHappy Coding! | 4 | 0 | ['Binary Search', 'Sorting', 'Binary Tree'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | python easy two-pointers + sorting solution | python-easy-two-pointers-sorting-solutio-vw1a | \nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n n = len(nums)\n \n nums.sort()\n i, j = 0, n-1\n | byuns9334 | NORMAL | 2022-01-20T05:59:24.395907+00:00 | 2022-01-20T05:59:24.395950+00:00 | 1,287 | false | ```\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n n = len(nums)\n \n nums.sort()\n i, j = 0, n-1\n \n \n res = 0 \n NUM = 10**9+7\n while i <= j:\n if nums[i] + nums[j] > target:\n j -= 1\n elif nums[i] + nums[j] <= target:\n res += pow(2, j-i, NUM)\n i += 1\n #else: # nums[i] + nums[j] == target\n \n \n \n return res % NUM\n``` | 4 | 0 | ['Two Pointers', 'Sorting', 'Python', 'Python3'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ two pointer approach , Time-O(nlogn) | c-two-pointer-approach-time-onlogn-by-dh-0gzs | class Solution {\npublic:\n int calpow(int a,int b)\n {\n if(b==0)return 1;\n \n int res=calpow(a,b/2);\n \n if(b%2==0) | dhruvjain04 | NORMAL | 2022-01-14T08:19:12.264546+00:00 | 2022-01-14T08:19:12.264577+00:00 | 841 | false | class Solution {\npublic:\n int calpow(int a,int b)\n {\n if(b==0)return 1;\n \n int res=calpow(a,b/2);\n \n if(b%2==0)\n {\n res=res*res;\n }\n else\n {\n res=res*a*res;\n }\n return res;\n }\n \n int numSubseq(vector<int>& nums, int target) \n {\n int mod=1000000007;\n int n=nums.size();\n int i=0,j=n-1;\n int ans=0;\n \n vector<int> pow(n,1);\n \n for(int i=1; i<n; i++)\n {\n pow[i] = (pow[i-1] * 2) % mod; \n }\n \n sort(nums.begin(),nums.end());\n \n while(i<=j)\n {\n if(nums[i]+nums[j]>target)j--;\n \n else\n {\n ans=(ans+pow[j-i])%mod;\n i++;\n }\n }\n return ans;\n }\n}; | 4 | 0 | ['Sorting'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | very easy cpp solution || 98 % faster | very-easy-cpp-solution-98-faster-by-vvd4-avdo | \nclass Solution {\npublic:\n \n \n \n int numSubseq(vector<int>& nums, int target) {\n long long power[100005], ans=0,n=nums.size();;\n | vvd4 | NORMAL | 2021-01-22T11:07:52.989771+00:00 | 2021-01-22T11:07:52.989805+00:00 | 470 | false | ```\nclass Solution {\npublic:\n \n \n \n int numSubseq(vector<int>& nums, int target) {\n long long power[100005], ans=0,n=nums.size();;\n \n power[0]=1;\n for(int i=1;i<n;i++)\n power[i]=(power[i-1]*2)%1000000007;\n \n sort(nums.begin(),nums.end());\n int start=0,end=n-1;\n while(start<=end)\n {\n if(nums[start]+nums[end]<=target)\n {\n ans+=power[end-start];\n start++;\n }\n else\n end--;\n ans%=1000000007;\n \n }\n return ans;\n }\n};\n``` | 4 | 0 | [] | 2 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Go - O(N * log N) | go-on-log-n-by-p_a_r_u_s-6e5x | I don\'t think this one are medium complexity solutions. Hope nobody ask this during interview or just to 100% fail candidate.\nJust watch this video: https://w | p_a_r_u_s | NORMAL | 2020-09-17T05:42:45.717511+00:00 | 2020-09-17T06:07:43.780803+00:00 | 255 | false | I don\'t think this one are medium complexity solutions. Hope nobody ask this during interview or just to 100% fail candidate.\nJust watch this video: https://www.youtube.com/watch?v=xCsIkPLS4Ls\n\n```\nfunc numSubseq(nums []int, target int) int {\n\tconst MOD = 1000000007\n\texps := make([]int, len(nums))\n\tfor i:= range exps {\n\t\texps[i] = 1\n\t}\n\n\tfor i:=1; i < len(exps); i++ {\n\t\texps[i] = (2 * exps[i - 1]) % MOD\n\t}\n\n\tsort.Ints(nums)\n\tleft := 0\n\tright := len(nums)-1\n\tcount := 0\n\n\tfor left <= right {\n\t\tif nums[left] + nums[right] > target {\n\t\t\tright--\n\t\t} else {\n\t\t\tcount = count + exps[right - left]\n\t\t\tleft++\n\t\t}\n\t}\n\n\treturn count % MOD\n}\n```\n\n**Unit Tests**\n```\nfunc Test_Number_of_Subsequences_That_Satisfy_the_Given_Sum_Condition(t *testing.T) {\n\ttestCases := []struct{\n\t\tnums []int\n\t\ttarget int\n\t\tresult int\n\t} {\n\t\t{ []int{3,5,6,7}, 9, 4,},\n\t\t{ []int{3,3,6,8}, 10, 6,},\n\t\t{ []int{2,3,3,4,6,7}, 12, 61,},\n\t\t{ []int{5,2,4,1,7,6,8}, 16, 127,},\n\t\t{ []int{14,4,6,6,20,8,5,6,8,12,6,10,14,9,17,16,9,7,14,11,14,15,13,11,10,18,13,17,17,14,17,7,9,5,10,13,8,5,18,20,7,5,5,15,19,14}, 22, 272187084,},\n\t}\n\n\tfor _, tc := range testCases {\n\t\tr := numSubseq(tc.nums, tc.target)\n\t\tif r != tc.result {\n\t\t\tt.Errorf("Source: %2d, target:%2d\\n Expected: %2d\\n Actual: %2d\\n",\n\t\t\t\ttc.nums,\n\t\t\t\ttc.target,\n\t\t\t\ttc.result,\n\t\t\t\tr)\n\t\t}\n\t}\n}\n``` | 4 | 0 | [] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java simple sort and count | java-simple-sort-and-count-by-hobiter-cogp | See comments for explanation\n1, sort the array from min to max;\n\n2. for each different right tail number tail = nums[r], \nwe find the highest left head numb | hobiter | NORMAL | 2020-06-28T19:18:40.380514+00:00 | 2020-06-28T19:24:29.718875+00:00 | 873 | false | See comments for explanation\n1, sort the array from min to max;\n\n2. for each different right tail number tail = nums[r], \nwe find the highest left head number head = nums[l]:\nthat head + tail <= target (t for short); \nThen we can form a valid subsequence: head ... tail; \nany numver between tail and head could be contained or not contained in the subsequence, then wen can get f(l) = 2^(r - l - 1) different subsequences.\n\n3, then any number nums[i] <= head, that is i <= l, all the subsequence start from nums[i], end with nums[r], will be valid subsequence;\nthere will be f(i) = 2^(r - i - 1) those subsquence; \nfor each different r, there will be (l + 1) different i, where i = 0, 1, 2,..., l;\nthe total count will be:\n```\nsigma (f(i)) = f(l) * (2 ^ (l + 1) - 1) \nthat is:\nsigma (f(i)) = 2 ^ (r - l - 1) * (2 ^ (l + 1) - 1);\n```\n\nprove of sigma (f(i)) = 2 ^ (r - l - 1) * (2 ^ (l + 1) - 1):\n```\nsigma (f(i)) = f(0) + f(1) + .. + f(l) = 2 ^ (l - 0) * f(l) + 2 ^ (l -1) * f(l)... + f(l)\n= f(l) * (2 ^ (l - 0) + 2 ^ (l -1) + ... + 1) \n= f(l) * (2 ^ (l + 1) - 1)\nsince f(l) = 2^(r - i - 1) \nsigma (f(i)) = 2 ^ (r - l - 1) * (2 ^ (l + 1) - 1)\n```\n\n\n\ncode:\n```\n public int numSubseq(int[] nums, int t) {\n Arrays.sort(nums);\n int n = nums.length, l = 0, r = n - 1, mod = (int)1e9 + 7;\n long res = 0, pow[] = new long[n + 1];\n pow[0] = 1;\n for (int i = 1 ; i <= n ; ++i) pow[i] = pow[i - 1] * 2 % mod;\n while(l <= r && nums[r] + nums[l] > t) r--; // find the first right pointer;\n while(l <= r){\n while (l <= r && nums[r] + nums[l] <= t) l++;\n l--;\n if (r == l) res = (res + pow[l + 1] - 1) % mod; // corner casem \n else res = (res + pow[r - l - 1] * (pow[l + 1] - 1)) % mod; //sigma(f(l))\n r--;\n }\n return (int) res;\n }\n``` | 4 | 2 | [] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Easy C++ Solution | Easy to Understand | easy-c-solution-easy-to-understand-by-sh-so6a | \n# Code\n\n#define mod 1000000007\nclass Solution {\npublic:\n long long power(long long base,long long n){\n long long ans=1;\n while(n!=0){\ | shubhaamtiwary_01 | NORMAL | 2023-10-11T12:17:45.624915+00:00 | 2023-10-11T12:17:45.624933+00:00 | 337 | false | \n# Code\n```\n#define mod 1000000007\nclass Solution {\npublic:\n long long power(long long base,long long n){\n long long ans=1;\n while(n!=0){\n if(n%2==1){\n ans=(ans*base)%mod;\n n--;\n }else{\n base=(base*base)%mod;\n n=n/2;\n }\n }\n return ans;\n }\n int numSubseq(vector<int>& nums, int target) {\n int i=0;\n int j=nums.size()-1;\n sort(nums.begin(),nums.end());\n long long ans=0;\n\n while(i<=j){\n if(nums[i]+nums[j]<=target){\n long long temp=power(2,j-i);\n ans=(ans+temp)%mod;\n i++;\n }\n else {\n j--;\n }\n }\n\n return ans;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | [Python 3] From Brute force to Two Pointers Solution - Clean & Concise | python-3-from-brute-force-to-two-pointer-lqda | \u274C Solution 1: Brute force (TLE)\n- We try all non-empty subsequences of the nums array, finding the min and max elements within each subsequence. We then c | hiepit | NORMAL | 2023-08-28T09:02:53.271443+00:00 | 2023-08-29T17:09:30.289947+00:00 | 242 | false | **\u274C Solution 1: Brute force (TLE)**\n- We try all non-empty subsequences of the `nums` array, finding the `min` and `max` elements within each subsequence. We then check if `min + max <= target`; if so, the subsequence is valid.\n- If nums has N elements, then there will be `2^N` subsequences.\n\n```python\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n n = len(nums)\n MOD = int(1e9) + 7\n ans = 0\n for mask in range(1, 1 << n):\n minElement = math.inf\n maxElement = -math.inf\n for i in range(n):\n if (mask >> i) & 1:\n minElement = min(minElement, nums[i])\n maxElement = max(maxElement, nums[i])\n \n if minElement + maxElement <= target:\n ans = (ans + 1) % MOD\n\n return ans\n```\nComplexity:\n- Time: `O(N * 2^N)`, where `N <= 10^5` is length of `nums` array.\n- Space: `O(1)`\n\n---\n**\u2714\uFE0F Solution 2: Two Pointers**\n- In this problem, we count number of valid subsequences, which also means counting number of valid subsets in `nums` array.\n- We count all the subsets where the `min` is the smallest element and `max` is the largest element in the subset, such that `min + max <= target`.\n- The idea is to sort the `nums` array in non-descending order (no need to worry about the original order anymore)\n- We implement two pointers, where `left` is the index pointing to the first element, and `right` is the index pointing to the last element.\n- If `nums[left] + nums[right] <= target`, then we have subsets that take elements within the range `nums[left..right]` to form valid subsets that satisfy the problem requirements.\n - To count the number of valid subsets efficiently, we assume the subsets always contains the `nums[left]` element, combined with all possible subsets (including empty ones) of the elements in the range `nums[left+1...right]`. \n - Thus, there will be `2^(right - left)` total subsets. It\'s because there are `2^(right-left)` subsets of elements in `nums[left+1..right]`.\n - After counting `nums[left]`, we increment `left` by 1.\n- Otherwise, if `nums[left] + nums[right] > target`, then we decrement `right` by 1 to reduce the sum.\n\n```python\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n nums.sort()\n MOD = int(1e9) + 7\n n = len(nums)\n POW2 = [1] * (n+1)\n for i in range(n):\n POW2[i+1] = POW2[i] * 2 % MOD\n\n left = 0\n right = len(nums) - 1\n ans = 0\n while left <= right:\n if nums[left] + nums[right] <= target:\n ans = (ans + POW2[right - left]) % MOD\n left += 1\n else:\n right -= 1\n return ans\n```\nComplexity:\n- Time: `O(NlogN)`, where `N <= 10^5` is length of `nums` array.\n- Space: `O(N)`\n\n\n\nCertainly! Here\'s the translation of the Vietnamese explanation into English:\n\n---\n**Let analyze an example for better understanding:** \nExample: nums = [1, 1, 3, 5, 7], target = 6\n\n**Step 1: left = 0, right = 4**\nnums[0] + nums[4] = 1 + 7 > 6\n\n- There are no valid subsequences that take `nums[0]` as the minimum and `nums[4]` as the maximum. So, decrement `right` by 1 (`right -= 1`).\n\n**Step 2: left = 0, right = 3**\nnums[0] + nums[3] = 1 + 5 <= 6\n- Always pick `nums[0]`\n- Consider all subsequences from elements in `nums[1...3]`:\n - []\n - [nums[1]]\n - [nums[2]]\n - [nums[3]]\n - [nums[1], nums[2]]\n - [nums[1], nums[3]]\n - [nums[2], nums[3]]\n - [nums[1], nums[2], nums[3]]\n- When combined with `nums[0]`, the valid subsequences are:\n - [nums[0]]\n - \\[nums\\[0\\], nums\\[1\\]\\]\n - \\[nums\\[0\\], nums\\[2\\]\\]\n - \\[nums\\[0\\], nums\\[3\\]\\]\n - \\[nums\\[0\\], nums\\[1\\], nums\\[2\\]\\]\n - \\[nums\\[0\\], nums\\[1\\], nums\\[3\\]\\]\n - \\[nums\\[0\\], nums\\[2\\], nums\\[3\\]\\]\n - \\[nums\\[0\\], nums\\[1\\], nums\\[2\\], nums\\[3\\]\\]\n- We have considered all the valid subsequences containing `nums[0]`, so increment `left` by 1 (`left += 1`).\n \n**Step 3: left = 1, right = 3**\nnums\\[1\\] + nums\\[3\\] = 1 + 5 <= 6\n\n- Always pick `nums[1]`\n- Consider all subsequences from elements in `nums[2..3]`:\n - \\[\\]\n - \\[nums\\[2\\]\\]\n - \\[nums\\[3\\]\\]\n - \\[nums\\[2\\], nums\\[3\\]\\]\n- When combined with `nums[1]`, the valid subsequences are:\n - \\[nums\\[1\\]\\]\n - \\[nums\\[1\\], nums\\[2\\]\\]\n - \\[nums\\[1\\], nums\\[3\\]\\]\n - \\[nums\\[1\\], nums\\[2\\], nums\\[3\\]\\]\n- We have considered all the valid subsequences containing `nums[1]`, so increment `left` by 1 (`left += 1`).\n \n\n**Step 4: left = 2, right = 3**\nnums\\[2\\] + nums\\[3\\] = 3 + 5 > 6\n- There are no valid subsequences that take `nums[2]` as the minimum and `nums[3]` as the maximum. So, decrement `right` by 1 (`right -= 1`).\n\n**Step 5: left = 2, right = 2**\nnums\\[2\\] + nums\\[2\\] = 3 + 3 <= 6\n\n- Always pick `nums[2]`\n- Consider all subsequences from elements in `nums[3..2]`:\n - \\[\\]\n- When combined with `nums[2]`, the valid subsequences are:\n - \\[nums\\[2\\]\\]\n- We have considered all the valid subsequences containing `nums[2]`, so increment `left` by 1 (`left += 1`).\n \n\n**End of Program** | 3 | 0 | ['Two Pointers', 'Python3'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Beats 99.7% || C++ || Significance of 'int' and 'long long' || Binary Search | beats-997-c-significance-of-int-and-long-g6nl | \n Describe your first thoughts on how to solve this problem. \n\n# Approach\nTo start, we arrange the numbers in the nums array in ascending order. This helps | AY73 | NORMAL | 2023-08-14T14:12:02.528101+00:00 | 2023-08-14T15:19:30.550188+00:00 | 48 | false | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTo start, we arrange the numbers in the nums array in ascending order. This helps us navigate through the array more effectively.\n\nWe place i at the beginning of the array and j at the end.\n\nAs we move forward with the pointers, we keep track of how many valid subsequences we encounter. For each position of i, we move j backwards while adding up the numbers at nums[i] and nums[j]. This helps us find subsequences where the sum meets our condition.\n\n**The number of subsequences of length \\(j - i\\) is given by \\(2^{j - i - 1}\\). This can be understood using a simple observation. When constructing a subsequence of length \\(j - i\\), each element has two choices: either include it in the subsequence or exclude it. This binary choice applies to each element in the subsequence, resulting in a total of \\(2^{j - i}\\) possible subsequences of length \\(j - i\\). However, since we are counting subsequences where element at i should be included for sure, we subtract one to obtain \\(2^{j - i - 1}\\) as the final count.**\n\nNote :-\nTo make our calculations faster and more accurate, we use a trick with powers of 2.This allows us to efficiently count the number of subsequences without getting into complex calculations.\n\nThroughout our process, we make sure our calculations don\'t become too large by applying modular arithmetic. This means we only keep the remainder when dividing by a certain number, which helps us avoid big and unwieldy numbers.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n) {Assuming given arrays are already sorted.}\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end());\n int n = nums.size();\n const int MOD = 1e9 + 7;\n long long ans = 0;\n int i = 0;\n int j = n - 1; \n\n vector<long long> powers(n);\n powers[0] = 1;\n for (int k = 1; k < n; ++k) {\n powers[k] = (powers[k - 1] * 2) % MOD;\n }\n\n while (i <= j) {\n if (nums[i] + nums[j] <= target) {\n ans = (ans + powers[j - i]) % MOD;\n i++;\n } else {\n j--;\n }\n }\n\n return ans;\n }\n};\n\n``` | 3 | 0 | ['Two Pointers', 'Binary Search', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | 🐍 [ Python ] Simple Solution | 🚀 Optimal | 🔢 Two Pointer Sum Approach | ⏱️ O(n*log(n)) Approach | python-simple-solution-optimal-two-point-x3vf | Runtime: 832 ms, faster than 68.92% of Python3 online submissions for Number of Subsequences That Satisfy the Given Sum Condition.\nMemory Usage: 29.5 MB, less | godemode12 | NORMAL | 2023-05-06T11:18:01.910409+00:00 | 2023-05-06T11:18:39.034469+00:00 | 77 | false | *Runtime: 832 ms, faster than 68.92% of Python3 online submissions for Number of Subsequences That Satisfy the Given Sum Condition.\nMemory Usage: 29.5 MB, less than 8.18% of Python3 online submissions for Number of Subsequences That Satisfy the Given Sum Condition.*\n\nhere\'s a step-by-step explanation of the solution with some intuition behind each step:\nangelscript\n\n```\nclass Solution:\n def numSubseq(self, nums: List[int], t: int) -> int:\n if len(nums)==1:\n return 1 if 2*nums[0]<=t else 0\n```\n\nThe function begins by checking if the input list nums contains only one element. If it does, the function returns 1 if the element is less than or equal to t/2, since the element itself is a valid subsequence that satisfies the condition. Otherwise, it returns 0, since there are no valid subsequences that satisfy the condition.\n\n\tnums.sort()\n\tl=0\n\tr=len(nums)-1\n\tc=0\n\tMOD = 10**9 + 7\n\n\nIf the input list nums contains more than one element, the function first sorts the list in non-decreasing order. This is necessary for the two-pointer approach to work correctly. The function initializes the left and right pointers l and r to the beginning and end of the sorted array, respectively. It also initializes a counter c to 0 and a constant MOD to 10^9 + 7.\n\n\twhile (l<=r):\n\t\tif nums[l]+nums[r]>t:\n\t\t\tr-=1\n\t\telse:\n\t\t\tc = (c + pow(2, r - l, MOD)) % MOD\n\t\t\tl += 1\n\n\nThe function then enters a loop that continues as long as the left pointer l is less than or equal to the right pointer r. Within the loop, the function checks if the sum of the elements pointed to by l and r is greater than t. If it is, the function decrements the right pointer r to move it closer to the left pointer l. This is because if the sum of the elements pointed to by l and r is greater than t, then moving the right pointer r to the left can only decrease the sum and make it more likely to satisfy the condition.\n\nIf the sum of the elements pointed to by l and r is less than or equal to t, the function updates the counter c to include all valid subsequences that start with the element pointed to by l. The number of such subsequences is 2^(r-l), since each element between nums[l+1] and nums[r] can either be included or excluded from the subsequence. The function uses modular arithmetic to compute 2^(r-l) % MOD, and adds the result to the counter c.\n\nAfter updating the counter c, the function increments the left pointer l to move it closer to the right pointer r. This is because if the sum of the elements pointed to by l and r is less than or equal to t, then moving the left pointer l to the right can only increase the sum and make it less likely to satisfy the condition.\n\n\treturn c\n\n\nFinally, after the loop has terminated, the function returns the counter c, which represents the total number of valid subsequences that satisfy the condition.\n\n```\nclass Solution:\n def numSubseq(self, nums: List[int], t: int) -> int:\n if len(nums)==1:\n return 1 if 2*nums[0]<=t else 0\n nums.sort()\n l=0\n r=len(nums)-1\n c=0\n MOD = 10**9 + 7\n while (l<=r):\n if nums[l]+nums[r]>t:\n r-=1\n else:\n c = (c + pow(2, r - l, MOD)) % MOD\n l += 1\n return c\n```\n\nA simple upvote would make my day ... Thank You | 3 | 0 | ['Array', 'Two Pointers', 'Sorting', 'Python'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Almost like editorial version but in JavaScript. :). Just watch. | almost-like-editorial-version-but-in-jav-492o | \n# Code\n\n/**\n * @param {number[]} nums\n * @param {number} target\n * @return {number}\n */\nvar numSubseq = function(nums, target) {\n let n = nums. | AzamatAbduvohidov | NORMAL | 2023-05-06T09:11:22.166099+00:00 | 2023-05-06T09:11:22.166144+00:00 | 726 | false | \n# Code\n```\n/**\n * @param {number[]} nums\n * @param {number} target\n * @return {number}\n */\nvar numSubseq = function(nums, target) {\n let n = nums.length;\n let mod = 1_000_000_007;\n nums.sort((a,b) => a - b);\n \n // Precompute the value of 2 to the power of each value.\n let power = [];\n power[0] = 1;\n for (let i = 1; i < n; ++i) {\n power[i] = (power[i - 1] * 2) % mod;\n }\n \n let answer = 0;\n let left = 0, right = n - 1;\n\n while (left <= right) {\n if (nums[left] + nums[right] <= target) {\n answer += power[right - left];\n answer %= mod;\n left++;\n } else {\n right--;\n }\n }\n \n return answer;\n};\n``` | 3 | 0 | ['JavaScript'] | 3 |
number-of-subsequences-that-satisfy-the-given-sum-condition | python3 code | python3-code-by-veenaayyannagari-ucei | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | veenaayyannagari | NORMAL | 2023-05-06T08:29:06.088612+00:00 | 2023-05-06T08:29:06.088649+00:00 | 2,155 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n nums.sort()\n left, right = 0, len(nums) - 1\n count = 0\n mod = 10 ** 9 + 7\n \n while left <= right:\n if nums[left] + nums[right] > target:\n right -= 1\n else:\n count += pow(2, right - left, mod)\n left += 1\n \n return count % mod\n\n``` | 3 | 0 | ['Python3'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | 2 Pointers easy approach | 2-pointers-easy-approach-by-sowjanyasank-x7zm | Intuition\n Describe your first thoughts on how to solve this problem. \nWe need to think of the subsequences having sum of minimum and maximum element less tha | sowjanyasanku | NORMAL | 2023-05-06T06:58:35.298834+00:00 | 2023-05-06T06:58:35.298930+00:00 | 55 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to think of the subsequences having sum of minimum and maximum element less than the target. For this we use the two pinter approach.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initially we consider 2 pointers low and high pointing to first element and last element\n2. If the sum of those is greater than target, we decrement the high pointer\n3. Else we will find out the number of subsequences generated with the formula 2 power n\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long int MOD = 1e9+7;\n int numSubseq(vector<int>& nums, int target) {\n int N = nums.size();\n int l = 0, h = N-1;\n int ans=0;\n \n vector<int> p(N,1);\n p[0]=1;\n for(int i=1;i<N;i++)\n p[i] = (p[i-1]*2)%MOD;\n\n sort(nums.begin(),nums.end());\n while(l<=h)\n {\n int req = nums[l] + nums[h];\n if(req>target)\n {\n h--;\n }\n else\n {\n ans += p[h-l];\n ans %= MOD;\n\n l++;\n }\n }\n\n return ans;\n }\n};\n``` | 3 | 0 | ['C++'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Easy C++ solution using 2 pointers | easy-c-solution-using-2-pointers-by-anwe-6i0b | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | anwendeng | NORMAL | 2023-05-06T02:07:35.177480+00:00 | 2023-05-06T02:07:35.177511+00:00 | 1,318 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n const int mod=1e9+7;\n sort(nums.begin(), nums.end());\n\n int n=nums.size(); \n vector<int> pow2mod(n+1, 1);\n for (int exp=1; exp<=n; exp++)\n pow2mod[exp]=(pow2mod[exp-1]<<1)%mod;\n \n int l=0, r=n-1;\n int result=0;\n while(l<=r){\n if( nums[l]+nums[r]<=target){\n result=(result+pow2mod[r-l])%mod;\n l++;\n }\n else r--;\n }\n return result;\n }\n};\n``` | 3 | 0 | ['Array', 'Two Pointers', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Beats 100%, check it out. | beats-100-check-it-out-by-seekerofmiracl-af7k | \n\n# Complexity\n- Time complexity: O(n * log(n)) - Time complexity of this function is dominated by the sorting operation. That is O(n*log n)\n- Space complex | SeekerOfMiracle | NORMAL | 2023-05-06T01:54:05.349473+00:00 | 2023-05-06T01:54:05.349505+00:00 | 3,105 | false | \n\n# Complexity\n- Time complexity: O(n * log(n)) - Time complexity of this function is dominated by the sorting operation. That is O(n*log n)\n- Space complexity: O(n) - array `arr` is created with `n` elements, where `n` is the length of the input `nums`. \n\n# Code\n```\n/**\n * @param {number[]} nums\n * @param {number} target\n * @return {number}\n */\n \nvar numSubseq = function(nums, target) \n{\n const mod = 1000000007, arr = [];\n let num = 1;\n\n for (let i = 0; i < nums.length; i++) \n {\n arr.push(num);\n num = num * 2 % mod;\n }\n\n nums.sort((a,b) => a - b);\n\n let count = 0, j = nums.length - 1;\n\n for (let i = 0; i < nums.length && nums[i]*2 <= target; i++) \n {\n while (j && nums[j] + nums[i] > target) \n j--;\n\n count = (count + arr[j - i])%mod;\n }\n return count;\n};\n``` | 3 | 0 | ['JavaScript'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Easy Understand | Simple Method | Binary Exponentiation | Java | Python | C++✅ | easy-understand-simple-method-binary-exp-cuej | Intuition\n Describe your first thoughts on how to solve this problem. \nFirst, the array needs to be sorted so that the array is monotonic so that it easy to b | czshippee | NORMAL | 2023-05-06T00:07:17.229580+00:00 | 2023-05-06T01:43:37.098342+00:00 | 1,839 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst, the array needs to be sorted so that the array is monotonic so that it easy to be operational by binary search\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAfter sorting the array, the array has monotonicity.\n\nWe randomly find a continuous sub-array, the left boundary of this sub-array must be the smallest number in the sub-array (because it has been sorted before), denoted as `L`, and the right boundary of the sub-array must be the largest sub-array denoted as `R`.\n\nIf `L+R<=target`, then we only need to keep the left boundary `L `unchanged, and the right boundary `R` can be any number smaller than `R`.\n\nStep:\n- sort the array `nums`\n- Traverse each number of the array as the left boundary `L`.\n- According to the left boundary `L`, use the binary search to find the qualified right boundary `R`\n- After determining L and R, any permutation and combination of numbers between (L+1)-R meets the requirements (the number is 2 to the power of R-L)\n- Just add all the results together, the specific code is as follows\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nlogn)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n``` Java []\nclass Solution {\n final static int MOD = (int)1e9+7;\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int n = nums.length;\n int[] f = new int[n];\n f[0] = 1;\n for (int i = 1; i < n; i++)\n f[i] = (f[i - 1] << 1) % MOD;\n int l = 0, r = n-1;\n int ans = 0;\n while (l <= r) {\n if (nums[l] + nums[r] > target)\n r--;\n else {\n ans = (ans + f[r - l]) % MOD;\n l++;\n }\n }\n return ans;\n }\n}\n```\n``` Python3 []\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n # Optimized, beats 97%\n MOD = 10**9 + 7\n f = [1] + [0] * (len(nums)-1)\n for i in range(1, len(nums)):\n f[i] = f[i - 1] * 2 % MOD\n nums.sort()\n ans = 0\n for i, num in enumerate(nums):\n if nums[i] * 2 > target:\n break\n maxValue = target - nums[i]\n pos = bisect.bisect_right(nums, maxValue) - 1\n ans += f[pos - i] if pos >= i else 0\n return ans % MOD\n```\n``` C++ []\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n int mod = 1e9 + 7;\n int res = 0, n = nums.size(), l = 0, r = n - 1;\n vector<int> pows(n, 1);\n for (int i = 1 ; i < n ; ++i)\n pows[i] = pows[i - 1] * 2 % mod;\n sort(nums.begin(), nums.end());\n while (l <= r) {\n if (nums[l] + nums[r] > target) {\n r--;\n } else {\n res = (res + pows[r - l]) % mod;\n l++;\n }\n }\n return res;\n }\n};\n``` | 3 | 0 | ['Two Pointers', 'Binary Search', 'C++', 'Java', 'Python3'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | 🗓️ Daily LeetCoding Challenge May, Day 6 | daily-leetcoding-challenge-may-day-6-by-ugty1 | This problem is the Daily LeetCoding Challenge for May, Day 6. Feel free to share anything related to this problem here! You can ask questions, discuss what you | leetcode | OFFICIAL | 2023-05-06T00:00:18.240058+00:00 | 2023-05-06T00:00:18.240151+00:00 | 5,525 | false | This problem is the Daily LeetCoding Challenge for May, Day 6.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/number-of-subsequences-that-satisfy-the-given-sum-condition/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain these 2 approaches in the official solution</summary>
**Approach 1:** Binary Search
**Approach 2:** Two Pointers
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br> | 3 | 0 | [] | 15 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ Recursive Solution but got TLE | c-recursive-solution-but-got-tle-by-susn-r18q | int countSubseq(int index,int n,int sum,int target,vector &nums,vector&subseq){\n if(index == n){\n if(!subseq.empty()){\n int | Susnata_das | NORMAL | 2022-09-10T11:47:44.965196+00:00 | 2022-09-10T11:47:44.965238+00:00 | 1,850 | false | int countSubseq(int index,int n,int sum,int target,vector<int> &nums,vector<int>&subseq){\n if(index == n){\n if(!subseq.empty()){\n int minEle = *min_element(subseq.begin() , subseq.end());\n int maxEle = *max_element(subseq.begin() , subseq.end());\n if(maxEle+minEle <= target) return 1;\n }\n return 0;\n }\n subseq.push_back(nums[index]);\n sum += nums[index];\n int leftSum = countSubseq(index+1,n,sum,target,nums,subseq);\n subseq.pop_back();\n sum -= nums[index];\n int rightSum = countSubseq(index+1,n,sum,target,nums,subseq);\n return leftSum+rightSum;\n } | 3 | 0 | ['Recursion', 'C'] | 2 |
number-of-subsequences-that-satisfy-the-given-sum-condition | [C++] Binary Search | c-binary-search-by-deepesh_dragoneel-l27x | \nclass Solution {\npublic:\n int power(long long x, long long y, long long p)\n {\n long long res = 1;\n x = x % p;\n if (x == 0) re | deepesh_dragoneel | NORMAL | 2022-04-15T07:06:56.716408+00:00 | 2022-04-15T07:06:56.716442+00:00 | 702 | false | ```\nclass Solution {\npublic:\n int power(long long x, long long y, long long p)\n {\n long long res = 1;\n x = x % p;\n if (x == 0) return 0;\n while (y > 0)\n {\n if (y & 1)\n res = (res*x) % p;\n y = y>>1;\n x = ((x%p)*(x%p)) % p;\n }\n return (int)(res%p);\n }\n \n int numSubseq(vector<int>& a, int target) {\n sort(a.begin(), a.end());\n int ans = 0, mod = 1e9+7, l=0, r=a.size();\n for(int i=0;i<r;i++){\n int idx = upper_bound(a.begin(), a.end(), target-a[i]) - a.begin();\n if(a[i]*2<=target) {\n ans+=1;\n }\n if(idx>=0 && idx==a.size() || a[idx] != target-a[i]) idx--;\n if(idx<i) continue;\n ans = ((ans%mod)+(power(2, idx - i, mod)%mod)%mod) - 1;\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['C', 'Binary Tree'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Help me to memorize. | help-me-to-memorize-by-hekarket-69b5 | \nclass Solution {\n public int numSubseqUtil(int min, int max, int i, int[] nums, int target ){\n if(i == nums.length) return 0;\n int newMin | HekarKET | NORMAL | 2022-03-26T15:51:27.838163+00:00 | 2022-03-26T15:52:37.693679+00:00 | 1,553 | false | ```\nclass Solution {\n public int numSubseqUtil(int min, int max, int i, int[] nums, int target ){\n if(i == nums.length) return 0;\n int newMin = Math.min(min, nums[i]);\n int newMax = Math.max(max, nums[i]);\n\t\tint count = 0;\n if(newMax+newMin<=target){\n count += 1;\n } \n return count + numSubseqUtil(newMin, newMax, i+1, nums, target) + numSubseqUtil(min, max, i+1, nums, target);\n }\n \n public int numSubseq(int[] nums, int target) {\n int n = nums.length;\n return numSubseqUtil(1000000, -1000000, 0, nums, target);\n }\n}\n``` | 3 | 0 | ['Recursion', 'Java'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | 2 pointers easy Python solution | 2-pointers-easy-python-solution-by-facep-yv1p | \tnums.sort()\n\tn = len(nums)\n\ti, j = 0, n - 1\n\tresult = 0\n\twhile i <= j:\n\t\tif nums[i] + nums[j] <= target:\n\t\t\tresult += 2 ** (j - i)\n\t\t\ti += | FACEPLANT | NORMAL | 2021-03-26T15:30:10.264915+00:00 | 2021-03-26T15:30:10.264953+00:00 | 348 | false | \tnums.sort()\n\tn = len(nums)\n\ti, j = 0, n - 1\n\tresult = 0\n\twhile i <= j:\n\t\tif nums[i] + nums[j] <= target:\n\t\t\tresult += 2 ** (j - i)\n\t\t\ti += 1\n\t\telse:\n\t\t\tj -= 1\n\treturn result % (10 ** 9 + 7) | 3 | 2 | [] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ | 2 Pointer with easy explanation | upvote if you liked the approach | O(nlogn) time complexity | c-2-pointer-with-easy-explanation-upvote-tyip | \nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n // sort the array, to get the right pairs optimally\n sort(nums. | swapnilkant11 | NORMAL | 2020-09-01T06:59:49.544334+00:00 | 2020-09-14T12:12:12.180862+00:00 | 606 | false | ```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n // sort the array, to get the right pairs optimally\n sort(nums.begin(), nums.end());\n int len = nums.size();\n // take a temp array to store the number values, once taking the number and once ignoring it\n int arrdp[len];\n // using two pointer concept\n int frontptr = 0;\n int backptr = nums.size() - 1;\n int totalsum = 0;\n // allocate each eelement to 1\n for(int i = 0; i < len; i++)\n arrdp[i] = 1;\n int MOD = 1000000007;\n // now, keep checking for the values in the array.\n for(int i = 1; i < len; i++){\n arrdp[i] = arrdp[i - 1] * 2; // taking once the current element and once rejecting the same element\n if(arrdp[i] >= MOD) // if overflow then reduce the value\n arrdp[i] -= MOD;\n \n }\n while(frontptr <= backptr){\n // if the condition is true take it in the final ans\n if(nums[frontptr] + nums[backptr] <= target){\n totalsum += arrdp[backptr - frontptr];\n frontptr++; // taking a pair we will increment the frontptr becuase it is already included\n if(totalsum >= MOD) // if overflow then, reduce the value\n totalsum -= MOD;\n }\n // else drecrement the backptr as, we dont\'t need to include current element\n else\n backptr--;\n }\n return totalsum;\n }\n};\n``` | 3 | 1 | [] | 2 |
number-of-subsequences-that-satisfy-the-given-sum-condition | From brute force backtracking to efficient Two pointer solution | from-brute-force-backtracking-to-efficie-7fvl | Bactracking solution - TLE\n\nclass Solution {\n int count = 0;\n int modulo = (int)Math.pow(10, 9) + 7;\n public int numSubseq(int[] nums, int target) | gagrawa3 | NORMAL | 2020-07-25T17:18:59.998205+00:00 | 2020-07-25T17:18:59.998258+00:00 | 632 | false | Bactracking solution - TLE\n```\nclass Solution {\n int count = 0;\n int modulo = (int)Math.pow(10, 9) + 7;\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n backtrack(new ArrayList<Integer>(), nums, target, 0);\n return count%modulo;\n }\n \n private void backtrack(List<Integer> list, int[] nums, int target, int start) {\n if(list.size() != 0) {\n if(list.get(0) + list.get(list.size()-1) <= target) {\n count = (count + 1) % modulo; \n }\n }\n \n for(int i=start;i<nums.length;i++) {\n list.add(nums[i]);\n backtrack(list, nums, target, i+1);\n list.remove(list.size()-1);\n }\n }\n}\n```\n\nTwo pointer Solution:\n\n```\nclass Solution {\n int modulo = (int)Math.pow(10, 9) + 7;\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int count = 0;\n int[] dp = new int[nums.length];\n dp[0] = 1;\n for(int i=1;i<nums.length;i++) {\n dp[i] = (dp[i-1]*2) % modulo;\n }\n \n int lo = 0, hi = nums.length-1;\n while(lo<=hi) {\n if(nums[lo] + nums[hi] <= target) {\n count = (count + dp[hi-lo++]) % modulo;\n } else {\n hi--;\n }\n }\n \n return count;\n }\n \n}\n``` | 3 | 0 | [] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | cpp solution two pointers + math | cpp-solution-two-pointers-math-by-huowa2-7tz4 | \n\n\nclass Solution {\npublic:\n int numSubseq(vector<int> &nums, int target) {\n sort(nums.begin(), nums.end()); \n long long ret = 0;\n | huowa222 | NORMAL | 2020-07-09T04:48:57.269251+00:00 | 2020-07-09T04:48:57.269299+00:00 | 443 | false | ```\n\n\nclass Solution {\npublic:\n int numSubseq(vector<int> &nums, int target) {\n sort(nums.begin(), nums.end()); \n long long ret = 0;\n int left = 0, right = nums.size() - 1;\n while(left <= right) {\n if(nums[left] + nums[right] > target) right--;\n else {\n ret += exp(2, (right - left++), 1000000007);\n ret %= 1000000007;\n }\n }\n return (int) ret;\n }\nprivate:\n int exp(int b, int exponent, int MOD) {\n int result = 1; \n unsigned long long int base = b % MOD; \n while(exponent > 0) {\n if (exponent % 2 == 1) {\n result = (result * base) % MOD; \n }\n exponent = exponent >> 1; \n base = (base * base) % MOD; \n }\n return result; \n }\n};\n``` | 3 | 0 | [] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Can Somebody Help me with this Code?? | can-somebody-help-me-with-this-code-by-m-qtku | \n\nIs it Overflow? or is the code wrong?\nCan Math.pow() compute values like 2^10000 and hold them??\n\n\nclass Solution \n{\n public int numSubseq(int[] A, | MasterBruce | NORMAL | 2020-06-28T13:53:59.940287+00:00 | 2020-06-28T15:05:32.999727+00:00 | 286 | false | \n\n**Is it Overflow? or is the code wrong?**\n**Can Math.pow() compute values like 2^10000 and hold them??**\n\n```\nclass Solution \n{\n public int numSubseq(int[] A, int target) {\n Arrays.sort(A);\n int res = 0, n = A.length, l = 0, r = n - 1;\n int mod = (int)1e9 + 7;\n \n while (l <= r) {\n if (A[l] + A[r] > target) {\n r--;\n } else {\n res = (int)((res + (long)Math.pow(2, (r-l))%mod) % mod);\n l++;\n }\n }\n return res;\n }\n}\n```\n\n***UPDATE :*** I think such value will be so huge for even LONG to hold.\nAnd the constraints have length upto ```10 ^ 5 ``` So, there are chances for us to calculate 2^10000.\nSo, such values should be calculated along with ``` % 1000000007 ```\n\nTry to print value for ```2^10000``` in Python. The value will be something like this. \n```\n19950631168807583848837421626835850838234968318861924548520089498529438830221946631919961684036194597899331129423209124271556491349413781117593785932096323957855730046793794526765246551266059895520550086918193311542508608460618104685509074866089624888090489894838009253941633257850621568309473902556912388065225096643874441046759871626985453222868538161694315775629640762836880760732228535091641476183956381458969463899410840960536267821064621427333394036525565649530603142680234969400335934316651459297773279665775606172582031407994198179607378245683762280037302885487251900834464581454650557929601414833921615734588139257095379769119277800826957735674444123062018757836325502728323789270710373802866393031428133241401624195671690574061419654342324638801248856147305207431992259611796250130992860241708340807605932320161268492288496255841312844061536738951487114256315111089745514203313820202931640957596464756010405845841566072044962867016515061920631004186422275908670900574606417856951911456055068251250406007519842261898059237118054444788072906395242548339221982707404473162376760846613033778706039803413197133493654622700563169937455508241780972810983291314403571877524768509857276937926433221599399876886660808368837838027643282775172273657572744784112294389733810861607423253291974813120197604178281965697475898164531258434135959862784130128185406283476649088690521047580882615823961985770122407044330583075869039319604603404973156583208672105913300903752823415539745394397715257455290510212310947321610753474825740775273986348298498340756937955646638621874569499279016572103701364433135817214311791398222983845847334440270964182851005072927748364550578634501100852987812389473928699540834346158807043959118985815145779177143619698728131459483783202081474982171858011389071228250905826817436220577475921417653715687725614904582904992461028630081535583308130101987675856234343538955409175623400844887526162643568648833519463720377293240094456246923254350400678027273837755376406726898636241037491410966718557050759098100246789880178271925953381282421954028302759408448955014676668389697996886241636313376393903373455801407636741877711055384225739499110186468219696581651485130494222369947714763069155468217682876200362777257723781365331611196811280792669481887201298643660768551639860534602297871557517947385246369446923087894265948217008051120322365496288169035739121368338393591756418733850510970271613915439590991598154654417336311656936031122249937969999226781732358023111862644575299135758175008199839236284615249881088960232244362173771618086357015468484058622329792853875623486556440536962622018963571028812361567512543338303270029097668650568557157505516727518899194129711337690149916181315171544007728650573189557450920330185304847113818315407324053319038462084036421763703911550639789000742853672196280903477974533320468368795868580237952218629120080742819551317948157624448298518461509704888027274721574688131594750409732115080498190455803416826949787141316063210686391511681774304792596709376\n```\n\n**Correct me if I am wrong. Or if somebody knows better, please share..!!!** | 3 | 1 | [] | 5 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Binary Search | Beats 61% | Python3 | binary-search-beats-61-python3-by-alpha2-9ykt | Please UpvoteCode | Alpha2404 | NORMAL | 2025-03-20T11:01:13.373413+00:00 | 2025-03-20T11:01:13.373413+00:00 | 87 | false | # Please Upvote
# Code
```python3 []
class Solution:
def numSubseq(self, nums: List[int], target: int) -> int:
N = len(nums)
count = 0
MOD = 10**9+7
nums.sort()
for i in range(N):
j = bisect_right(nums,target-nums[i]) - 1
if j >= i:
count += pow(2,j-i,MOD)
return count%MOD
``` | 2 | 0 | ['Array', 'Binary Search', 'Sorting', 'Python3'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | ✅ C++ Solution - 2 pointers O(nlogn) TC O(n) SC ✅ | c-solution-2-pointers-onlogn-tc-on-sc-by-zp6o | Code\n\nclass Solution {\npublic:\n int mod = 1e9+7;\n vector<int> pow(int b,int n){\n vector<int> power(n+1);\n power[0]=1;\n for(in | ADreamOfMine | NORMAL | 2024-10-23T16:10:44.150980+00:00 | 2024-10-23T16:12:47.933902+00:00 | 149 | false | ## Code\n```\nclass Solution {\npublic:\n int mod = 1e9+7;\n vector<int> pow(int b,int n){\n vector<int> power(n+1);\n power[0]=1;\n for(int i=1;i<=n;i++){\n power[i]=(power[i-1]*b)%mod;\n }\n return power;\n }\n int numSubseq(vector<int>& nums, int target) {\n \n int n=nums.size();\n sort(nums.begin(),nums.end());\n\n vector<int> power = pow(2,n);\n\n int count=0;\n //l=min, h=max\n int l=0,h=n-1;\n while(l<=h){\n if(nums[l]+nums[h]<=target){\n count = (count + power[h-l]%mod)%mod; \n //minE should be present for sure\n //rest all can be present or not\n l++;\n }\n else h--;\n }\n return count%mod;\n }\n};\n```\nTo optimise further, use **Binary Exponentiation**. | 2 | 0 | ['Array', 'Two Pointers', 'Sorting', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Number of Subsequences That Satisfy the Given Sum Condition C++ Solution | number-of-subsequences-that-satisfy-the-3j7xz | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rissabh361 | NORMAL | 2023-09-07T05:18:22.867831+00:00 | 2023-09-07T05:18:22.867854+00:00 | 74 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n int n = nums.size();\n int MOD = 1e9+7;\n int ans = 0;\n vector<int> power(n, 1);\n for(int i = 1; i < n; ++i){\n power[i] = (power[i-1] << 1) % MOD;\n }\n \n sort(nums.begin(), nums.end());\n \n for(int l = 0, r = n-1; l <= r; ){\n if(nums[l] + nums[r] > target)\n {--r;\n }else{\n ans = (ans + power[r-l]) % MOD;\n ++l;}\n }\n return ans; \n }};\n``` | 2 | 0 | ['C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java || Recursion&Memo|| Subsequence logic (Explained) || Passes 45/62(TLE) | java-recursionmemo-subsequence-logic-exp-hm65 | ```\nclass Solution {\n private static final int MOD = (int) (1e9 + 7);\n\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n | kurmiamreet44 | NORMAL | 2023-05-21T19:42:34.601467+00:00 | 2023-05-21T19:42:34.601506+00:00 | 1,176 | false | ```\nclass Solution {\n private static final int MOD = (int) (1e9 + 7);\n\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n Map<String, Integer> memo = new HashMap<>();\n long ans = helper(nums, Integer.MAX_VALUE, Integer.MIN_VALUE, 0, target, memo);\n return (int) (ans % MOD);\n }\n\n public long helper(int[] nums, long min, long max, int i, int target, Map<String, Integer> memo) {\n if (i >= nums.length)\n return 0;\n // memoization \n String key = i + "#" + min + "#" + max;\n if (memo.containsKey(key))\n return memo.get(key);\n\n long max1 = max;\n long min1 = min;\n if (nums[i] > max1) {\n max1 = nums[i];\n }\n\n if (nums[i] < min1) {\n min1 = nums[i];\n }\n\n long sum = min1 + max1;\n\n long count = 0;\n// we return 0 as all number are sorted hence later we only get much larger number so no point in checking further \n if (sum > target)\n return 0;\n//**take \n else {\n\t\t// we have updated the max and min with max1 and min1 hence we are including this number in subsequence \n count = 1 + helper(nums, min1, max1, i + 1, target, memo);\n }\n\t\t// **notTake\n// this call is when we are ignoring this number and moving forward hence max and min are same \n count += helper(nums, min, max, i + 1, target, memo);\n\n memo.put(key, (int) (count % MOD));\n return count;\n }\n}\n\n// i think we can ignore duplicates and optiize this more, feel free to add in comments | 2 | 0 | ['Recursion', 'Java'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | 1498. Number of Subsequences That Satisfy the Given Sum Condition | 1498-number-of-subsequences-that-satisfy-wmiz | class Solution {\n int power(int b) {\n long long ans = 1, k = 2, mod = 1e9 + 7;\n while(b) {\n if(b % 2) ans = (ans * k) % mod;\n | pspraneetsehra08 | NORMAL | 2023-05-14T19:26:05.049923+00:00 | 2023-05-14T19:26:05.049965+00:00 | 18 | false | class Solution {\n int power(int b) {\n long long ans = 1, k = 2, mod = 1e9 + 7;\n while(b) {\n if(b % 2) ans = (ans * k) % mod;\n b /= 2;\n k = (k * k) % mod;\n }\n return ans;\n }\npublic:\n int numSubseq(vector<int>& nums, int target) {\n long long n = nums.size(), ans = 0, mod = 1e9 + 7;\n sort(nums.begin(), nums.end());\n\n for(int i=0; i<n; i++) {\n int pos = upper_bound(nums.begin() + i, nums.end(), target - nums[i]) - nums.begin() - 1;\n if(pos - i >= 0) ans = (ans + power(pos - i))% mod;\n }\n return ans;\n }\n}; | 2 | 0 | ['C'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | ex-amazon-explains-a-solution-with-a-vid-3g6t | My youtube channel - KeetCode(Ex-Amazon)\nI create 165 videos for leetcode questions as of May 7, 2023. I believe my channel helps you prepare for the coming te | niits | NORMAL | 2023-05-06T20:06:43.190398+00:00 | 2023-05-06T20:06:43.190447+00:00 | 100 | false | # My youtube channel - KeetCode(Ex-Amazon)\nI create 165 videos for leetcode questions as of May 7, 2023. I believe my channel helps you prepare for the coming technical interviews. Please subscribe my channel!\n\n### Please subscribe my channel - KeetCode(Ex-Amazon) from here.\n\n**I created a video for this question. I believe you can understand easily with visualization.** \n\n**My youtube channel - KeetCode(Ex-Amazon)**\nThere is my channel link under picture in LeetCode profile.\nhttps://leetcode.com/niits/\n\n\n\n\n---\n\n# Intuition\nSort input array and Use two pointers. When we create subsequences, we have two choices. including each number and excluding each number.\n\n# Approach\nThis is based on Python code. Other languages might be different.\n\n1. Sort the given array of integers \'nums\' in non-descending order using the \'sort()\' method of Python.\n\n2. Initialize two pointers, \'left\' and \'right\', pointing to the first and the last element of the sorted array, respectively.\n\n3. Initialize a variable \'ans\' to zero, which will store the number of subsequences that satisfy the given sum condition.\n\n4. Define a constant \'mod\' and assign it a value of 10^9 + 7.\n\n5. Use a while loop to iterate until \'left\' becomes greater than \'right\'.\n\n6. Check if the sum of the current left and right elements of \'nums\' is greater than \'target\'.\n\n7. If the sum is greater, decrement \'right\' by 1 to exclude the largest element and try again.\n\n8. If the sum is less than or equal to \'target\', then increment \'left\' by 1 to exclude the smallest element, and calculate the number of possible subsequences between \'left\' and \'right\'.\n\n9. For calculating the number of subsequences between \'left\' and \'right\', use the \'pow()\' function to calculate 2 raised to the power of \'right - left\' modulo \'mod\', and add the result to \'ans\'.\n\n10. After the while loop terminates, return the value of \'ans\' modulo \'mod\'.\n\n---\n\n**My youtube channel - KeetCode(Ex-Amazon)**\nThere is my channel link under picture in LeetCode profile.\nhttps://leetcode.com/niits/\n\n---\n\n# Complexity\nThis is based on Python code. Other languages might be different.\n\n- Time complexity: O(n log n)\nn is the length of the input array nums. This is because the nums.sort()\n\n- Space complexity: O(1)\nwe only use a constant amount of extra space to store the pointers and variables\n\n# Python\n```\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n nums.sort()\n left, right = 0, len(nums) - 1\n ans = 0\n mod = 10 ** 9 + 7\n\n while left <= right:\n if nums[left] + nums[right] > target:\n right -= 1\n else:\n # pow(x, y, z) = x^y % z\n ans += pow(2, right - left, mod)\n left += 1\n \n return ans % mod\n```\n# JavaScript\n```\n/**\n * @param {number[]} nums\n * @param {number} target\n * @return {number}\n */\nvar numSubseq = function(nums, target) {\n let pow = [];\n pow.push(1);\n\n nums.sort((a, b) => { return a - b; })\n\n const mod = 1e9+7;\n\n for (let i = 1; i < nums.length; i++) {\n pow.push((pow[pow.length - 1] * 2) % mod);\n }\n\n let left = 0, right = nums.length - 1, res = 0;\n\n while (left <= right) {\n if (nums[left] + nums[right] > target) {\n right--;\n } else {\n res = (res + pow[right - left]) % mod;\n left++;\n }\n }\n\n return res;\n};\n\n\n```\n# Java\n```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int[] pow = new int[nums.length];\n pow[0] = 1;\n\n for (int i = 1; i < nums.length; i++) {\n pow[i] = (pow[i - 1] * 2) % 1000000007;\n }\n\n int left = 0, right = nums.length - 1;\n int res = 0;\n\n while (left <= right) {\n if (nums[left] + nums[right] > target) {\n right--;\n } else {\n res = (res + pow[right - left]) % 1000000007;\n left++;\n }\n }\n\n return res; \n }\n}\n```\n# C++\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end());\n int n = nums.size();\n vector<int> pow(n, 1);\n const int mod = 1e9 + 7;\n \n for(int i = 1; i < n; i++){\n pow[i] = (2 * pow[i-1]) % mod;\n }\n \n int left = 0, right = n-1;\n long long res = 0;\n \n while(left <= right){\n if(nums[left] + nums[right] > target){\n right--;\n } else {\n res = (res + pow[right - left]) % mod;\n left++;\n }\n }\n \n return res;\n }\n};\n``` | 2 | 0 | ['C++', 'Java', 'Python3', 'JavaScript'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | CPP SOLUTION PROMINENT | cpp-solution-prominent-by-chayannn-xfmg | \n\n\n# Code\n\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(),nums.end());\n int mod = 1e9+7;\ | Chayannn | NORMAL | 2023-05-06T19:23:34.828058+00:00 | 2023-05-06T19:23:34.828098+00:00 | 36 | false | \n\n\n# Code\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(),nums.end());\n int mod = 1e9+7;\n int i = 0;\n int j = nums.size()-1;\n int ans=0;\n vector<int>subs(nums.size(),0);\n subs[0] = 1;\n for(int i=1;i<nums.size();i++){\n subs[i] = (subs[i-1]*2)%mod;\n }\n while(i<=j){\n if(nums[i]+nums[j]>target)j--;\n else{\n ans = (ans + subs[j-i])%mod;\n i++;\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Easy C++ Solution || Pre-Computation || Two Pointer || T.C- O(nlogn) || S.C- O(n) | easy-c-solution-pre-computation-two-poin-7lsd | \n\n# Complexity\n- Time complexity:O(nlogn)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n)\n Add your space complexity here, e.g. O(n) | karanjangir02 | NORMAL | 2023-05-06T18:27:19.890683+00:00 | 2023-05-06T18:27:19.890726+00:00 | 1,617 | false | \n\n# Complexity\n- Time complexity:O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n int ans=0;\n int n=nums.size();\n int mod=1e9+7;\n sort(nums.begin(),nums.end());\n int l=0,r=n-1;\n\n //pre-computing the power\n vector<int> power(n);\n power[0]=1;\n for(int i=1;i<n;++i)\n {\n power[i]=(power[i-1]*2)%mod;\n }\n\n while(l<=r)\n {\n if(nums[l]+nums[r]<=target)\n {\n int diff=r-l;\n ans=ans%mod+(power[diff])%mod;\n l++;\n }\n else r--;\n }\n\n return ans;\n }\n};\n``` | 2 | 0 | ['Two Pointers', 'C++'] | 2 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C# O(Log N) memory, beats 100% by memory | c-olog-n-memory-beats-100-by-memory-by-d-wer3 | Intuition\nIn this problem, in order to compute powers of 2 for big exponents, most solutions use $O(N)$ memory to store each power of $2$ up to $N$ - length of | danlavrushko | NORMAL | 2023-05-06T18:26:51.063080+00:00 | 2023-05-07T03:59:39.688153+00:00 | 207 | false | # Intuition\nIn this problem, in order to compute powers of 2 for big exponents, most solutions use $O(N)$ memory to store each power of $2$ up to $N$ - length of `nums` array. This could be greatly optimizied, if we store only those powers which itself are powers of $2$, eg $2^1, 2^2, 2^4, 2^8 \\ldots$ and so on. And later use this powers to quickly compute any power of $2$. To get the idea, consider this example: \n\n$$2^{15} = 2^1 \\cdot 2^2 \\cdot 2^4 \\cdot 2^8$$\n\n# Approach\nGeneral approach here is similar to other solutions:\n- Sort the `nums` array\n- Use 2 pointers `min` and `max` as lower and upper bound, and increase/decrease correspondingly until they meet. \n\n# Complexity\n- Time complexity: $$O(N \\log N)$$ - this is required by Sorting.\n\n- Space complexity: $$O(\\log N)$$ - additional space for selected powers of 2\n\n# Code\n```csharp\npublic class Solution {\n const int Mod = 1000_000_007;\n long[] powersOf2 = BuildPowersOf2();\n \n public int NumSubseq(int[] nums, int target) {\n long total = 0;\n \n Array.Sort(nums);\n\n if (nums[0] > target) return 0;\n\n // initially min and max indexes consider whole array\n int min = 0, max = nums.Length - 1;\n\n while (min <= max)\n {\n if (nums[min] + nums[max] > target) // <-- bigger than target\n max--; // <-- decrease upper bound estimate\n else {\n // here we fit the target, increase total count\n total = (total + ToPowerOf2(max - min)) % Mod; // 2^(max - min)\n min++; // <-- current lower bound is used, try increase it\n }\n }\n \n return (int)total;\n }\n\n long ToPowerOf2(int e) {\n if (e < 31) return 1 << e; // 2^(e)\n\n // one of optimal ways to calculate powers of 2 for big exponents\n // to get the idea, consider this example: 2^15 = 2^1 * 2^2 * 2^4 * 2^8\n long pow = 1;\n int i = 0;\n\n while (e > 0) {\n if ((e & 1) == 1) pow = pow * powersOf2[i] % Mod;\n i++;\n e >>= 1;\n }\n\n return pow;\n }\n\n static long[] BuildPowersOf2() {\n var powers = new long[17]; // enough to cover all powers up to 2^100_000\n\n powers[0] = 2;\n\n for (int i = 1; i < powers.Length; i++)\n powers[i] = powers[i - 1] * powers[i - 1] % Mod;\n \n return powers;\n }\n}\n``` | 2 | 0 | ['C#'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Sort + Binary Search | C++ | sort-binary-search-c-by-tusharbhart-tjqj | \nclass Solution {\n int power(int b) {\n long long ans = 1, k = 2, mod = 1e9 + 7;\n while(b) {\n if(b % 2) ans = (ans * k) % mod;\n | TusharBhart | NORMAL | 2023-05-06T18:19:34.720713+00:00 | 2023-05-06T18:19:34.720746+00:00 | 98 | false | ```\nclass Solution {\n int power(int b) {\n long long ans = 1, k = 2, mod = 1e9 + 7;\n while(b) {\n if(b % 2) ans = (ans * k) % mod;\n b /= 2;\n k = (k * k) % mod;\n }\n return ans;\n }\npublic:\n int numSubseq(vector<int>& nums, int target) {\n long long n = nums.size(), ans = 0, mod = 1e9 + 7;\n sort(nums.begin(), nums.end());\n\n for(int i=0; i<n; i++) {\n int pos = upper_bound(nums.begin() + i, nums.end(), target - nums[i]) - nums.begin() - 1;\n if(pos - i >= 0) ans = (ans + power(pos - i))% mod;\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Binary Search', 'Sorting', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | c++ and JAVA sorting + two pointer with explanation | c-and-java-sorting-two-pointer-with-expl-xwi6 | Intuition\n Describe your first thoughts on how to solve this problem. \nhere arr[i] means sum of 2^i + 2^(i-1) + ....2^2 + 2^1 + 1\nThis is just to make the ca | vedantnaudiyal | NORMAL | 2023-05-06T16:24:57.264467+00:00 | 2023-05-06T17:01:26.838166+00:00 | 332 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nhere arr[i] means sum of 2^i + 2^(i-1) + ....2^2 + 2^1 + 1\nThis is just to make the calculations easier.\nWe will soon understand that since the subsequences can be generated using any no irrespective of their place but should be in order in which it appears in the array but a catch here is that since we are just concerned about the min and max element in the subsequence so, whatever the order we arrange it in (in the order in which it appears or in sorted order) does not matter until the no. are same.\nFor Example,\n[7,6,3,5]\nnow sort->[3,5,6,7]\nthe subsequences including 7->(max) and 3->(min) can be easily created using any of the no lieing bw them like \n3,7\n3,6,7\n3,5,7\n3,5,6,7\nfor now assume target to be 10\nnow all these subseq can also be generated int the org array but with diff orders\nlike\n7,3\n7,6,3\n7,3,5\n7,6,3,5\nlook the no of subseq are always the same or we can say that same subsets will be generated from both org and sort arrays\nSo, now we just have to find every pair whose sum <=target and take into account all the subseq formed by elements lienng in bw these pairs lets say nums[i] and nms[j] then all elements bw i...j will create sub this no can be fetched by 2^(no of elem in bw ie; j-i-1) considering every no as present in subseq or not.\nLets say these elem as x\nnow any elem >nums[i] int the right of iand before j will also sum with nums[j] to <target so all those no will also create these sub for that instead of doing their add ups sep we can just add the sum of 2^x +2^(x-1) + 2^(x-2) +--=4+2+1. This is the reason for above arr[i];\nnow a asimple two pointer apprach isused to get those pairs i & j in sorted nums if i & j makes a pair dd its cont and then i++ try bigger i\'s inc the sum if it is greater than target j-- dec the sum \nOne spl case single element becoming min and max of the subseq including themselves is separately taken care of.\nAll the multiplications by 2 can be changed with <<1 to make it more fast as shift operations are faster than multi. operations and long long is also not needed , testcases are such that ans never goes above INT_MAX during any adds. \n\n \n# Approach\n<!-- Describe your approach to solving the problem. -->\nsorting + two approach\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlog(N))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n**PLS UPVOTE IF IT HELPED!**\n\n# JAVA\n```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n int mod=1000000007;\n Arrays.sort(nums);\n int n=nums.length;\n int ans=0;\n if(2*nums[0]<=target) ans++;\n if(n==1) return ans;\n int[] arr=new int[n];\n arr[0]=1;\n for(int i=1;i<n;i++){\n if(2*nums[i]<=target) ans++;\n arr[i]=(((arr[i-1]+1)*2)-1)%mod;\n }\n int i=0;\n int j=n-1;\n while(i<j){\n if(nums[i]+nums[j]<=target){\n ans+=arr[j-i-1];\n ans%=mod;\n i++;\n }else{\n j--;\n }\n }\n return ans;\n }\n}\n```\n# C++\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n int mod=1e9+7;\n sort(nums.begin(),nums.end());\n int n=nums.size();\n long long ans=0;\n if(2*nums[0]<=target) ans++;\n if(n==1) return ans;\n int* arr=new int[n];\n arr[0]=1;\n arr[1]=3;\n if(2*nums[1]<=target) ans++;\n for(int i=2;i<n;i++){\n if(2*nums[i]<=target) ans++;\n arr[i]=((1LL*(arr[i-1]+1)*2)-1)%mod;\n }\n int i=0;\n int j=n-1;\n while(i<j){\n if(nums[i]+nums[j]<=target){\n ans+=arr[j-i-1];\n ans%=mod;\n i++;\n }else{\n j--;\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | TWO POINTER APPROACH | two-pointer-approach-by-priyanka8d19-rqee | \n# Code\n\nconst int MOD = 1000000007;\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end());\ | priyanka8d19 | NORMAL | 2023-05-06T15:03:45.779670+00:00 | 2023-05-06T15:03:45.779701+00:00 | 1,063 | false | \n# Code\n```\nconst int MOD = 1000000007;\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end());\n int ans = 0;\n int l = 0, r = nums.size() - 1;\n \n vector<int>p2(nums.size());\n p2[0] = 1;\n for(int i = 1; i < nums.size(); i++) {\n p2[i] = (p2[i-1] * 2)%MOD;\n }\n while(l <= r) {\n if(nums[l] + nums[r] <= target) {\n ans += p2[r - l];\n ans %= MOD;\n l++;\n } else {\n r--;\n }\n }\n\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Python short and clean. Functional programming. | python-short-and-clean-functional-progra-iw3b | Approach\nTL;DR, Similar to the Editorial solution, but written as a 1-liner.\n\n# Complexity\n- Time complexity: O(n * log(n))\n\n- Space complexity: O(n)\n\nw | darshan-as | NORMAL | 2023-05-06T13:47:04.379611+00:00 | 2023-05-06T13:47:04.379641+00:00 | 400 | false | # Approach\nTL;DR, Similar to the [Editorial solution](https://leetcode.com/problems/number-of-subsequences-that-satisfy-the-given-sum-condition/editorial/), but written as a 1-liner.\n\n# Complexity\n- Time complexity: $$O(n * log(n))$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is length of nums`.\n\n# Code\n```python\nclass Solution:\n def numSubseq(self, nums: list[int], target: int) -> int:\n s_nums = sorted(nums)\n return sum(\n pow(2, bisect.bisect(s_nums, y, i) - 1 - i, 1_000_000_007)\n for i, x in enumerate(s_nums)\n if (y := target - x) >= x\n ) % 1_000_000_007\n\n\n``` | 2 | 0 | ['Two Pointers', 'Binary Search', 'Sorting', 'Python', 'Python3'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | A Game of long long || Upper Bound ||C++ | a-game-of-long-long-upper-bound-c-by-_dr-xc3p | Intuition\n Describe your first thoughts on how to solve this problem. \nIntuition is simple as we need to find upper bound for every digit in nums[i] if nums[i | _drigger | NORMAL | 2023-05-06T12:44:13.420571+00:00 | 2023-05-06T12:44:13.420620+00:00 | 56 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIntuition is simple as we need to find upper bound for every digit in nums[i] if nums[i] is twice greater than target than just return else find upper bound let\'s ay that is pos then find **pow(2,pos-i-1)** after this return ans+=pow. Need to focus on how we find power.\n\n# Complexity\n- Time complexity: O(n long(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution {\npublic:\n\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(),nums.end());\n int ans=0;const unsigned int M = 1000000007;\n for(int i=0;i<nums.size();i++){\n if(2*nums[i]>target)\n return ans;\n int temp=target-nums[i];\n int pos=(upper_bound(nums.begin()+i,nums.end(),temp)-nums.begin());\n int m=pos-i-1;\n long long x=2,val=1;\n while (m != 0) {\n if (m & 1 != 0) {\n // x=(long long)(x) % M;\n val = (long long)(val* x) % M;\n } \n x = (long long)(x* x)%M ;\n m /= 2; \n }\n ans=(int)(ans+val)%M;\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Binary Search', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | GoLang Solution | golang-solution-by-debadev-dfpo | \n# Code\n\nimport(\n "sort"\n "math"\n "fmt"\n)\n\nfunc numSubseq(nums []int, target int) int {\n n, mod :=len(nums), math.Pow(10,9) + 7\n sort. | debadev | NORMAL | 2023-05-06T08:50:22.538296+00:00 | 2023-05-06T08:50:22.538334+00:00 | 277 | false | \n# Code\n```\nimport(\n "sort"\n "math"\n "fmt"\n)\n\nfunc numSubseq(nums []int, target int) int {\n n, mod :=len(nums), math.Pow(10,9) + 7\n sort.Ints(nums)\n\n var ans float64\n left, right := 0,n-1\n power:= make([]float64,n)\n power[0] = 1\n for i:=1;i<n;i++{\n power[i] = math.Mod((power[i-1] * 2),mod)\n }\n for left <= right{\n if nums[left] + nums[right] <=target{\n ans+=power[right-left]\n ans = math.Mod(ans,mod)\n left++\n }else{\n right--\n }\n }\n return int(ans)\n\n}\n``` | 2 | 0 | ['Go'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Short and Easy C++ solution | short-and-easy-c-solution-by-__akash_sin-afod | Intuition\nTwo Pointer and sorting\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nAs we are interested in subsequences, we can sor | __AKASH_SINGH___ | NORMAL | 2023-05-06T08:33:50.445958+00:00 | 2023-05-06T08:33:50.445985+00:00 | 918 | false | # Intuition\nTwo Pointer and sorting\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nAs we are interested in subsequences, we can sort the array,\nNow then we intialise two pointer at both end and find the potential min and max range and then we consider the min element as fix for current subsequence and count total number of subsequence by bin() fun. for current min value and add this for potential candidate in nums.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlog(n) + n), nlogn -> sorting, n->two pointer\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define ll long long\nclass Solution {\npublic:\n ll inf = 1e9+7;\n ll bin(ll a, ll b)\n {\n ll ans = 1;\n while(b)\n {\n if(b&1) ans = (ans * a)%inf;\n a = (a * a)%inf;\n b >>= 1;\n }\n return ans;\n }\n \n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end());\n int n = size(nums),i = 0, ans = 0, j= n-1;\n while(i<=j)\n {\n if(nums[i] + nums[j] > target)--j;\n else ans = (ans + bin(2, j-i)) %inf, ++i;\n }\n return ans;\n }\n};\n// Upvote if you like the solution!!! \uD83D\uDC4D\uD83D\uDC4D\n``` | 2 | 0 | ['C++'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | JAVA/PYTHON SOLUTION || BEATS 100% || EASY TO UNDERSTAND || 2 POINTER | javapython-solution-beats-100-easy-to-un-y6e5 | Approach\n Describe your approach to solving the problem. \nMake an array \'l\' of length n=length of nums,and insert 2^i in it, make sure that 2^i doest not ex | deleted_user | NORMAL | 2023-05-06T08:28:46.335296+00:00 | 2023-05-06T08:28:46.335338+00:00 | 423 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nMake an array \'l\' of length n=length of nums,and insert 2^i in it, make sure that 2^i doest not exceed 10^9+7.Now initialize two pointers left=0 and right=n-1 and check if sum of nums[left] and nums[right] is less than or equal to target or not. If it is less or equal, make count=l[right-left] and if it is greater than 10^9+7\nthen mod it and increment left. If sum is greater than target then decrement right.\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n int [] l=new int[nums.length];\n Arrays.sort(nums);\n l[0]=1;\n int m=(int)1e9+7;\n for(int i=1;i<nums.length;i++){\n l[i]=(l[i-1]*2)%m;\n }\n int i=0,j=nums.length-1,c=0;\n while(i<=j){\n if(nums[i]+nums[j]>target){\n j--;\n }\n else{\n c+=l[j-i];\n c%=m;\n i++;\n }\n }\n return c;\n }\n}\n```\n```python []\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n nums.sort()\n l=[1]\n m=int(1e9+7)\n for i in range(1,len(nums)):\n l.append((l[i-1]*2)%m)\n i=0\n j=len(nums)-1\n c=0\n while i<=j:\n if nums[i]+nums[j]>target:\n j-=1\n else:\n c+=l[j-i]\n c%=m\n i+=1\n return c\n```\n | 2 | 0 | ['Java'] | 2 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java | Python | C++ | Two-Pointer | java-python-c-two-pointer-by-rahulraturi-q9a2 | \nclass Solution\n{\n public:\n int numSubseq(vector<int> &nums, int target)\n {\n int n=nums.size();\n sort(nums.begin() | rahulraturi2002 | NORMAL | 2023-05-06T08:19:35.047149+00:00 | 2023-05-06T10:08:04.218783+00:00 | 516 | false | ```\nclass Solution\n{\n public:\n int numSubseq(vector<int> &nums, int target)\n {\n int n=nums.size();\n sort(nums.begin(), nums.end());\n int l = 0;\n int r = n - 1;\n int ans = 0;\n int mod = 1e9 + 7;\n\n vector<int> pow(n, 1);\n\n for (int i = 1; i < n; i++)\n {\n pow[i] = (pow[i - 1] *2) % mod;\n }\n\n while (l <= r)\n {\n if (nums[l] + nums[r] > target)\n {\n r--;\n }\n else\n {\n ans = (ans + pow[r - l]) % mod;\n l++;\n }\n }\n\n return ans;\n }\n};\n```\n```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n int n = nums.length;\n Arrays.sort(nums);\n int l = 0;\n int r = n - 1;\n int ans = 0;\n int mod = 1000000007;\n \n int[] pow = new int[n];\n pow[0] = 1;\n for (int i = 1; i < n; i++) {\n pow[i] = (pow[i - 1] * 2) % mod;\n }\n \n while (l <= r) {\n if (nums[l] + nums[r] > target) {\n r--;\n } else {\n ans = (ans + pow[r - l]) % mod;\n l++;\n }\n }\n \n return ans;\n }\n}\n```\n```\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n n = len(nums)\n nums.sort()\n l = 0\n r = n - 1\n ans = 0\n mod = int(1e9) + 7\n \n pow = [1] * n\n for i in range(1, n):\n pow[i] = (pow[i - 1] * 2) % mod\n \n while l <= r:\n if nums[l] + nums[r] > target:\n r -= 1\n else:\n ans = (ans + pow[r - l]) % mod\n l += 1\n \n return ans\n``` | 2 | 0 | ['Two Pointers', 'C', 'Python', 'Java'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Easy beginner friendly sollution | easy-beginner-friendly-sollution-by-farh-h392 | \n# Approach\nmodified 2 sum approach\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n int | farhanc | NORMAL | 2023-05-06T08:19:16.108364+00:00 | 2023-05-06T08:19:16.108397+00:00 | 62 | false | \n# Approach\nmodified 2 sum approach\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int mod=1e9+7;\n long power(int x,int y){\n if(y==0)return 1; \n if(y==1) return x;\n long ans=1;\n if(y%2==0){\n ans=power(x,y/2);\n ans*=ans;\n }else{\n ans=power(x,y-1);\n ans*=x;\n }\n return ans%mod;\n }\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(),nums.end());\n int s=0,e=nums.size()-1;\n int ans=0;\n while(s<=e){\n if(nums[s]+nums[e]<=target){\n ans+=power(2,e-s);\n ans%=mod;\n s++;\n }else{\n e--;\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Beginner Friendly || Clean Code || C++ | beginner-friendly-clean-code-c-by-somend-rutg | \n# Complexity\n- Time complexity: O(nLogn)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) | somendrasingh019 | NORMAL | 2023-05-06T06:50:11.660276+00:00 | 2023-05-06T06:50:11.660304+00:00 | 72 | false | \n# Complexity\n- Time complexity: O(nLogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n int n=nums.size(),mod = 1000000007;\n int l=0,r=n-1,ans=0;\n vector<int> power(n,1);\n for(int i=1;i<n;i++) {\n power[i] = (power[i-1]<<1) % mod;\n }\n sort(nums.begin(),nums.end());\n while(l<=r) {\n if(nums[l]+nums[r] > target) {\n r--;\n }\n else {\n ans = (ans+power[r-l++]) % mod;\n }\n }\n return ans;\n }\n};\n\n\n\n\n``` | 2 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'Sorting', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java Solution for Number of Sequences that Satisfy the Given Sum Condition Problem | java-solution-for-number-of-sequences-th-ui3s | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind the solution is to use a two-pointer approach to find all possible | Aman_Raj_Sinha | NORMAL | 2023-05-06T06:34:08.416786+00:00 | 2023-05-06T06:34:08.416818+00:00 | 176 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind the solution is to use a two-pointer approach to find all possible subsequences of the input array nums whose minimum and maximum elements sum up to a value less than or equal to the target.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is to first sort the input array in ascending order. Then, initialize an array pow2 to store the powers of 2 modulo 109 + 7. The program then uses two pointers left and right to iterate through the array. The left pointer starts at the beginning of the array, and the right pointer starts at the end of the array.\nThe program then checks if the sum of the minimum and maximum element of the subsequence formed by the left and right pointers is less than or equal to the target. If it is, the program adds the number of possible subsequences that can be formed by the left and right pointers to the answer. The number of possible subsequences is calculated using the pow2 array. If the sum of the minimum and maximum element of the subsequence is greater than the target, the program moves the right pointer one position to the left. If the sum is less than or equal to the target, the program moves the left pointer one position to the right.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the solution is O(n log n), where n is the length of the input array. This is because the program sorts the input array, which takes O(n log n) time. The two-pointer approach then takes O(n) time to find all possible subsequences.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of the solution is O(n), where n is the length of the input array. This is because the program uses an array pow2 of size n to store the powers of 2 modulo 109 + 7.\n\n# Code\n```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int n = nums.length;\n int mod = 1000000007;\n int[] pow2 = new int[n];\n pow2[0] = 1;\n for (int i = 1; i < n; i++) \n {\n pow2[i] = pow2[i - 1] * 2 % mod;\n }\n int ans = 0;\n int left = 0, right = n - 1;\n while (left <= right) \n {\n if (nums[left] + nums[right] > target) \n {\n right--;\n } \n else \n {\n ans = (ans + pow2[right - left]) % mod;\n left++;\n }\n }\n return ans;\n }\n}\n``` | 2 | 0 | ['Java'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java very easy O(nlogn) solution | java-very-easy-onlogn-solution-by-abhine-w4u5 | Intuition\n Describe your first thoughts on how to solve this problem. \n- We will use two pointer approach to solve this, it is same as two sum\n- Suppose we g | abhineshchandra1234 | NORMAL | 2023-05-06T06:33:22.178778+00:00 | 2023-05-06T06:33:22.178829+00:00 | 91 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- We will use two pointer approach to solve this, it is same as two sum\n- Suppose we got index i & j such that nums[i] + nums[j] <= target. Then no of subsequence will be 2^(j-i).\n- In order to get i & j & apply two pointer we need to have array in sorted order. \n- This will not affect no of subsequence as 3,6,5 & 3,5,6 will have same no of subsequence.\n- Now for above statement\n- like - a=[3,5,6] t=9\n- 3 & 6 satisfy the condition ie 3+6<=9, no of subsequence will be 2^(3-1)=4\n- 3 * _ * _ , 3 * 5 * _, 3 * _ * 6, 3 * 5 * 6\n- For each no we have two option either we can take it or leave it\n- we add this subsequence count in the result for each valid pair and get the final result.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- 2^(j-i) will take O(n) computation time we can reduce it through binary exponentiation\n- 1st method\n- 2^n , 2^5\n- if n is odd\n- n * 2^(n-1) , 2 * 2^4\n- if n is even\n- n * n * 2^(n/2); , 2 * 2 * 2^2\n- we can compute 2^n in O(logn) time.\n- through pre computation\n- 2nd method\n- store the prev result and compute next\n- pows[0] = 1 ,2^0 = 1\n- pows[1] = pows[0] * 2, 2^1 = 2\n- pows[2] = pows[1] * 2, 2^2 = 4\n- it will take O(1) time, we need not compute 2^n everytime just return res at index n.\n- two-pointers\n- l+r>t\n- r-- to reduce the sum\n- else l++ to compute other nos.\n- if we start r again from end for each l++ then it would always be greater than target bcs array is sorted.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- O(nlogn) -> sorting\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- O(n) -> pre-computation\n\n# Code\ncredits @lee215\n```\nclass Solution {\n public int numSubseq(int[] nums, int target) {\n \n Arrays.sort(nums);\n int res=0, n=nums.length, l=0, r=n-1, mod=(int)1e9+7;\n int[] pows=new int[n];\n pows[0]=1;\n for(int i=1; i<n; i++)\n pows[i]=pows[i-1]*2%mod;\n while(l<=r) {\n if(nums[l]+nums[r]>target)\n r--;\n else\n res= (res+pows[r-l++])%mod;\n }\n return res;\n }\n}\n``` | 2 | 0 | ['Array', 'Two Pointers', 'Sorting', 'Java'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Binary Search is good | binary-search-is-good-by-_aman_gupta-4kn8 | # Intuition \n\n\n\n\n\n# Complexity\n- Time complexity: O(n * log(n))\n\n\n- Space complexity: O(log(n))\n\n\n# Code\n\nclass Solution {\n int n, mod = (i | _aman_gupta_ | NORMAL | 2023-05-06T06:16:10.378851+00:00 | 2023-05-06T06:16:10.378894+00:00 | 237 | false | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n * log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(log(n))$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n int n, mod = (int)(1e9 + 7);\n long pow2(int n) {\n if(n == 0)\n return 1;\n long half = pow2(n / 2);\n if(n % 2 == 1)\n return (2 * half * half) % mod;\n return (half * half) % mod;\n }\n int lower_bound(int[] nums, int target) {\n int l = 0, r = n - 1, mid;\n while(l <= r) {\n mid = l + (r - l) / 2;\n if(nums[mid] <= target)\n l = mid + 1;\n else\n r = mid - 1;\n }\n return r;\n }\n public int numSubseq(int[] nums, int target) {\n Arrays.sort(nums);\n int subs = 0, j;\n n = nums.length;\n for(int i = 0; i < n; i++) {\n j = lower_bound(nums, target - nums[i]);\n if(j >= i)\n subs = (int)(subs + pow2(j - i)) % mod;\n }\n return subs;\n }\n}\n``` | 2 | 0 | ['Array', 'Binary Search', 'Sorting', 'Java'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | binary search + python3 | binary-search-python3-by-arana-o3an | Intuition\nSimilar to the editorial solution, but with binary search implemented in details\n\n\n# Complexity\n- Time complexity:\nO(NlogN)\n\n\n\n# Code\n\ncla | arana | NORMAL | 2023-05-06T06:10:37.843360+00:00 | 2023-05-06T06:10:37.843398+00:00 | 72 | false | # Intuition\nSimilar to the editorial solution, but with binary search implemented in details\n\n\n# Complexity\n- Time complexity:\nO(NlogN)\n\n\n\n# Code\n```\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n nums = sorted(nums)\n #binary search, find the range that has minimum and maximum <=9\n l = 0\n r = len(nums)-1\n mod = 10**9+7\n\n def binary_search(l, r, nums, target):\n #Need to find where target - nums[0] is in the array. \n #Need to find the right boundary\n\n #Using the ultimate template\n while l<=r:\n mid = l + (r-l)//2\n if nums[mid] < target:\n l = mid + 1\n elif nums[mid] > target:\n r = mid - 1\n elif nums[mid] == target:\n l = mid + 1\n #Do not need to do edge case check. Because it will be done in the for loop below\n return l-1\n \n res = 0\n for l in range(len(nums)):\n if nums[l]>target:\n break #if the smallest number being checked is already larger than target, there is no chance for getting a meaningful r2 to build subsequences that satisfy the requirement\n r2 = binary_search(l, r, nums, target-nums[l])\n if r2>=l:\n res += pow(2, r2-l, mod)# Note, if we find [2, \'3\', 4, 5, 6, 7, \'8\'] (\'x\' means left and r2, respectively), for the l==3, any subsequence including 4 to 8 (5 numbers) satisfy the requirement. Thus, it is r2-l, because there are this many numbers (5 numbers in this example)\n return res % mod\n``` | 2 | 0 | ['Binary Search', 'Python3'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ Very Simple Solution - Sorting, Two Pointers, Sliding Window, Memoization - Time : O(n*logn) | c-very-simple-solution-sorting-two-point-8vwn | Intuition\n Describe your first thoughts on how to solve this problem. \n1. Problem is to find subsequences. So, Order is not important, I can sort it.\n2. Two | yvrakesh | NORMAL | 2023-05-06T06:05:33.162849+00:00 | 2023-05-06T16:09:03.669632+00:00 | 931 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Problem is to find **subsequences**. So, Order is not important, I can **sort** it.\n2. **Two pointer approach**. Because we need minimum and maximum in that subsequence, Left pointer will be pointing minimum and right pointer pointing maximum.\n3. **Sliding window approach** is used to find the number of subsequences between left and right pointer as the window size changes as the execution processes.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the vector.\n2. Initialize left pointer l = 0 and right pointer r = nums.size() - 1.\n3. Check if nums[l] + nums[r] <= target. Then find the number of subsequences possible from l to r.\n4. We use **Memoization** to precompute all the 2 powers less than max size into a vector. Max size is r-l+1 max value which is nums.size().\n5. If the nums[l] + nums[r] > target then we should choose lesser maximum value so decrement r.\n6. Continue until l > r.\n7. Since the numbers can overflow, mod with 1000000007.\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# CPP Code\n```\nclass Solution {\npublic:\n int mod = 1e9 + 7;\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end());\n int res = 0, n = nums.size(), l = 0, r = n - 1;\n vector<int> pows(n, 1);\n // <<1 is a left shift operator which is equivalent to 2*num\n // Bit shift is comparitively faster than multiplication\n for (int i = 1 ; i < n ; ++i)\n pows[i] = (pows[i - 1]<<1) % mod;\n while (l <= r) {\n if (nums[l] + nums[r] <= target) {\n res = (res + pows[r - l]) % mod;\n l++; \n } else {\n r--;\n }\n }\n return res;\n }\n};\n```\n\n---\n\nGo through the intuition and approach to better understand the solution. Feel free to comment your doubts or findings. \n\n<h2 align="center">Please Upvote if you find this useful. Thank you.</h2> | 2 | 0 | ['Two Pointers', 'Memoization', 'Sliding Window', 'Sorting', 'C++'] | 2 |
number-of-subsequences-that-satisfy-the-given-sum-condition | UPPER_BOUND | C++ | upper_bound-c-by-pajju_0330-qper | Code\n\nclass Solution {\npublic:\nint power(long long x, unsigned int y, int p)\n{\n int res = 1; \n x = x % p; \n if (x == 0) return 0; \n whi | Pajju_0330 | NORMAL | 2023-05-06T04:44:24.833945+00:00 | 2023-05-06T04:44:24.833984+00:00 | 501 | false | # Code\n```\nclass Solution {\npublic:\nint power(long long x, unsigned int y, int p)\n{\n int res = 1; \n x = x % p; \n if (x == 0) return 0; \n while (y > 0)\n {\n if (y & 1)\n res = (res*x) % p;\n y = y>>1; \n x = (x*x) % p;\n }\n return res;\n}\nint MOD = 1e9 + 7;\n int numSubseq(vector<int>& nums, int target) {\n sort(nums.begin(),nums.end());\n int ans = 0;\n for(int i = 0; i < nums.size(); ++i){\n\n int val = target - nums[i];\n int idx = upper_bound(nums.begin(),nums.end(),val) - nums.begin();\n idx--;\n if(idx >= i){\n ans = (ans + power(2,idx-i,MOD))%MOD;\n }\n }\n return ans%MOD;\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | 2_Pointor.py | 2_pointorpy-by-jyot_150-kqdj | Approach\nTwo Pointer\n\n# Complexity\n- Time complexity:\n O(n)\n\n\n# Code\n\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n | jyot_150 | NORMAL | 2023-05-06T04:16:51.756439+00:00 | 2023-05-06T04:16:51.756479+00:00 | 759 | false | # Approach\nTwo Pointer\n\n# Complexity\n- Time complexity:\n $$O(n)$$\n\n\n# Code\n```\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n nums.sort()\n ans=0\n i,j=0,len(nums)-1\n while i<=j:\n if nums[i]+nums[j]>target:\n j-=1\n else:\n ans+=2**(j-i)\n ans=ans%(10**9+7)\n i+=1\n return ans%(10**9+7)\n``` | 2 | 0 | ['Python3'] | 1 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Sorting + Two Pointers technique || Simple And Easy C++ Solution || | sorting-two-pointers-technique-simple-an-z4cr | Intuition\nwe can apply two sum problem logic here for solving it.\n# Approach\n Describe your approach to solving the problem. \nsort the array and apply twosu | brucewayne_5 | NORMAL | 2023-05-06T03:46:58.331859+00:00 | 2023-05-06T03:50:50.680383+00:00 | 162 | false | # Intuition\nwe can apply two sum problem logic here for solving it.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nsort the array and apply twosum problem logic \nthe number of subsequences will be pow(2,subsequence length).\n# Complexity\n- Time complexity:\nO(NLOGN)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int x) {\n int mod=1e9+7;\n int n=nums.size();\n vector<int>pow2(n+1,1);\n //instead of using inbulit function precomputing all powers of 2 upto n\n for(int i=1;i<=n;i++)\n {\n pow2[i]=pow2[i-1]*2%mod;\n }\n //sort the array\n sort(nums.begin(),nums.end());\n long long ans=0;\n //apply two sum logic\n int i=0,j=n-1;\n while(i<=j)\n {\n if((nums[i]+nums[j])<=x)\n {\n \n ans=(ans+(pow2[j-i]%mod)%mod)%mod;\n \n \n \n i++;\n }\n else j--;\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Two Pointers', 'Sorting', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | 📌📌 C++ || Sorting || Two Pointers || Faster || Easy To Understand 🤷♂️🤷♂️ | c-sorting-two-pointers-faster-easy-to-un-87g3 | Sorting + Two Pointers\n\n Time Complexity :- O(NlogN)\n\n Space Complexity :- O(N)\n\n\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int tar | __KR_SHANU_IITG | NORMAL | 2023-05-06T03:15:58.169319+00:00 | 2023-05-06T03:15:58.169352+00:00 | 531 | false | * ***Sorting + Two Pointers***\n\n* ***Time Complexity :- O(NlogN)***\n\n* ***Space Complexity :- O(N)***\n\n```\nclass Solution {\npublic:\n int numSubseq(vector<int>& nums, int target) {\n \n int n = nums.size();\n \n long long mod = 1e9 + 7;\n \n // sort the nums\n \n sort(nums.begin(), nums.end());\n \n // precalculate the power and store in powers array\n \n vector<int> powers(n, 1);\n \n for(int i = 1; i < n; i++)\n {\n powers[i] = (powers[i - 1] % mod * 2 % mod) % mod;\n }\n \n // apply two pointer approach and find possible result\n \n int i = 0, j = n - 1;\n \n int res = 0;\n \n while(i <= j)\n {\n if(nums[i] + nums[j] > target)\n {\n j--;\n }\n else\n {\n res = (res % mod + powers[j - i] % mod) % mod;\n \n i++;\n }\n }\n \n return res;\n }\n};\n``` | 2 | 0 | ['Two Pointers', 'C', 'Sorting', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | DAILY LEETCODE SOLUTION || EASY C++ SOLUTION | daily-leetcode-solution-easy-c-solution-qjc39 | \nconst int MOD=1e9+7;\nclass Solution {\npublic:\n long long powr(long long a,long long b){\n long long res=1;\n while(b){\n if(b&1 | pankaj_777 | NORMAL | 2023-05-06T02:41:42.813160+00:00 | 2023-05-06T02:41:42.813211+00:00 | 451 | false | ```\nconst int MOD=1e9+7;\nclass Solution {\npublic:\n long long powr(long long a,long long b){\n long long res=1;\n while(b){\n if(b&1) res=(res*a)%MOD;\n a=(a*a)%MOD;\n b=b>>1;\n }\n return res;\n }\n int lowerBound(vector<int>& nums,int target){\n int n=nums.size();\n int s=0,e=n-1,res=n;\n while(s<=e){\n int mid=s+(e-s)/2;\n if(nums[mid]==target){\n res=mid;\n s=mid+1;\n }\n else if(nums[mid]<target){\n res=mid;\n s=mid+1;\n }\n else{\n e=mid-1;\n }\n }\n return res;\n }\n int numSubseq(vector<int>& nums, int target) {\n int n=nums.size();\n long long res=0;\n sort(nums.begin(),nums.end());\n for(int i=0;i<n;i++){\n int num=target-nums[i];\n int idx=lowerBound(nums,num);\n if(idx<n){\n if(idx>=i){\n res=(res+powr(2,idx-i))%MOD;\n }\n }\n }\n return (int)res;\n }\n};\n``` | 2 | 1 | ['Array', 'Two Pointers', 'C', 'Sorting', 'Binary Tree'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Python3 solution beats 95.78% 🚀🚀 || quibler7 | python3-solution-beats-9578-quibler7-by-odeoh | \n\n\n# Code\n\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n nums.sort()\n l, r = 0, len(nums) - 1\n re | quibler7 | NORMAL | 2023-05-06T02:16:17.819090+00:00 | 2023-05-06T02:17:40.229828+00:00 | 64 | false | \n\n\n# Code\n```\nclass Solution:\n def numSubseq(self, nums: List[int], target: int) -> int:\n nums.sort()\n l, r = 0, len(nums) - 1\n res = 0\n mod = 10**9 + 7\n while l <= r:\n if nums[l] + nums[r] > target:\n r -= 1\n else:\n res += pow(2, r - l, mod)\n l += 1\n return res % mod\n``` | 2 | 0 | ['Python3'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | C++ || O(n*(log(n) | c-onlogn-by-sagargupta1610-jf33 | Approach\n1. Sort given array.\n2. For each element from 1st onward find target-element index and put all element combination of total element in that range - 1 | Sagargupta1610 | NORMAL | 2023-05-06T02:09:17.630252+00:00 | 2023-05-06T02:14:51.530288+00:00 | 233 | false | # Approach\n1. Sort given array.\n2. For each element from 1st onward find target-element index and put all element combination of total element in that range - 1\n3. For finding all combination we used power of 2 with modulous of 1000000007 and add it in answer. \n\n# Complexity\n- Time complexity: $O(n*log(n))$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int modPow(long long base, int exp) {\n if (exp == 0) return 1;\n else if (exp == 1) return base;\n else if (exp%2 == 0) return modPow((base*base)%1000000007,exp/2);\n else return base*modPow(base,exp-1)%1000000007; \n }\n int numSubseq(vector<int>& nums, int target) {\n int n=nums.size(),i=0;\n sort(nums.begin(),nums.end());\n long long ans=0; int x=upper_bound(nums.begin(),nums.end(),target-nums[i])-nums.begin()-1;\n while(x>=i){\n int y=modPow(2,x-i);\n ans=(ans+y)%1000000007;\n i++;\n while(nums[x]+nums[i]>target) x--;\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Array', 'Two Pointers', 'Binary Search', 'Sorting', 'C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | Java | 2 pointers | Explained | java-2-pointers-explained-by-prashant404-i1eg | Idea:\n sum(min, max) must be \u2264 target, so it doesn\'t matter what the numbers in between are\n Number of subsequences of length n that must start with a g | prashant404 | NORMAL | 2023-05-06T01:56:54.578129+00:00 | 2023-05-06T01:56:54.578164+00:00 | 203 | false | **Idea:**\n* sum(min, max) must be \u2264 target, so it doesn\'t matter what the numbers in between are\n* Number of subsequences of length `n` that must start with a give number = 2 ^ (n - 1). This is because for each number except the first one, there is a choice to include it or exclude it, so 1 x 2 x 2 ... (n - 1) times = 2 ^ (n - 1)\n* If numbers are in sorted order, the first number will be the min and last num will be max in the subsequence\n* Since we\'re counting subsequences, sorting `nums` will not effect the result, so do it\n* Use 2 pointers (L and R) pointing at max and min of the subsequence\n* If `A[L] + A[R] \u2264 T`, then all the possible subsequences are valid, so count them in and increment L\n* Else decrement R\n* Java\'s primitive data types can\'t contain large powers of a number, unless you want to use `BigInteger`, so use an array to store 2\'s powers % MOD\n\n**Example:**\n\n>**T/S:** O(n lg n)/O(n), where n = size(nums)\n```\nprivate static final int MOD = (int) (1e9 + 7);\n\npublic int numSubseq(int[] nums, int target) {\n\tvar count = 0L;\n\tvar n = nums.length;\n\tvar powTwo = getTwoPowers(n);\n\tArrays.sort(nums);\n\n\tfor (int left = 0, right = n - 1; left <= right; ) {\n\t\tif (nums[left] + nums[right] <= target)\n\t\t\tcount += powTwo[right - left++];\n\t\telse\n\t\t\tright--;\n\t}\n\n\treturn (int) (count % MOD);\n}\n\nprivate int[] getTwoPowers(int n) {\n\tvar powTwo = new int[n];\n\tpowTwo[0] = 1;\n\n\tfor (var i = 1; i < n; i++)\n\t\tpowTwo[i] = (powTwo[i - 1] << 1) % MOD;\n\t\t\n\treturn powTwo;\n}\n```\n***Please upvote if this helps*** | 2 | 0 | ['Java'] | 0 |
minimum-elements-to-add-to-form-a-given-sum | [Java/C++/Python] Clean Greedy Solution | javacpython-clean-greedy-solution-by-lee-kltu | Explanation\nCalculate the difference we need to change diff = abs(sum(A) - goal))\nWe can change at most limit once\nResult is the integer ceil of fraction dif | lee215 | NORMAL | 2021-03-07T04:11:11.796147+00:00 | 2021-03-07T04:20:32.885625+00:00 | 4,688 | false | # **Explanation**\nCalculate the difference we need to change `diff = abs(sum(A) - goal))`\nWe can change at most limit `once`\nResult is the integer ceil of fraction `diff / limit`.\nIn math it equals to `(diff + limit - 1) / limit`\n<br>\n\n# **Complexity**\nTime `O(n)`\nSpace `O(1)`\n<br>\n\n**Java**\n```java\n public int minElements(int[] A, int limit, int goal) {\n long sum = 0, diff;\n for (int a : A)\n sum += a;\n diff = Math.abs(goal - sum);\n return (int)((diff + limit - 1) / limit);\n }\n```\n**C++**\n```cpp\n int minElements(vector<int>& A, int limit, int goal) {\n long sum = accumulate(A.begin(), A.end(), 0L), diff = abs(goal - sum);\n return (diff + limit - 1) / limit;\n }\n```\n**Python**\n```py\n def minElements(self, A, limit, goal):\n return (abs(sum(A) - goal) + limit - 1) / limit\n```\n | 57 | 5 | [] | 11 |
minimum-elements-to-add-to-form-a-given-sum | C++ 1-liner | c-1-liner-by-votrubac-qohd | We need to divide the difference between the sum and the goal by your limit. \n\nNote that you need one more element if there is remainder (difference % limit | votrubac | NORMAL | 2021-03-07T16:33:49.686886+00:00 | 2021-03-07T16:33:49.686932+00:00 | 1,632 | false | We need to divide the difference between the sum and the goal by your limit. \n\nNote that you need one more element if there is remainder (`difference % limit != 0`).\n\n```cpp\nint minElements(vector<int>& nums, int limit, int goal) {\n return (abs(accumulate(begin(nums), end(nums), 0l) - goal) + limit - 1) / limit;\n}\n``` | 12 | 1 | [] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.