question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
numbers-with-repeated-digits | [Java/Python] Count the Number Without Repeated Digit | javapython-count-the-number-without-repe-t5eq | Intuition\nCount res the Number Without Repeated Digit\nThen the number with repeated digits = N - res\n\nSimilar as\n788. Rotated Digits\n902. Numbers At Most | lee215 | NORMAL | 2019-03-17T04:01:15.508536+00:00 | 2022-08-14T16:09:31.264170+00:00 | 32,461 | false | # **Intuition**\nCount `res` the Number Without Repeated Digit\nThen the number with repeated digits = N - res\n\nSimilar as\n788. Rotated Digits\n902. Numbers At Most N Given Digit Set\n\n\n# **Explanation**:\n\n1. Transform `N + 1` to arrayList\n2. Count the number with digits < n\n3. Count the number with same prefix\n\nFor example,\nif `N = 8765`, `L = [8,7,6,6]`,\nthe number without repeated digit can the the following format:\n`XXX`\n`XX`\n`X`\n`1XXX ~ 7XXX`\n`80XX ~ 86XX`\n`870X ~ 875X`\n`8760 ~ 8765`\n\n\n# **Time Complexity**:\nthe number of permutations `A(m,n)` is `O(1)`\nWe count digit by digit, so it\'s `O(logN)`\n\n<br>\n\n**Java:**\n```java\n public int numDupDigitsAtMostN(int N) {\n // Transform N + 1 to arrayList\n ArrayList<Integer> L = new ArrayList<Integer>();\n for (int x = N + 1; x > 0; x /= 10)\n L.add(0, x % 10);\n\n // Count the number with digits < N\n int res = 0, n = L.size();\n for (int i = 1; i < n; ++i)\n res += 9 * A(9, i - 1);\n\n // Count the number with same prefix\n HashSet<Integer> seen = new HashSet<>();\n for (int i = 0; i < n; ++i) {\n for (int j = i > 0 ? 0 : 1; j < L.get(i); ++j)\n if (!seen.contains(j))\n res += A(9 - i, n - i - 1);\n if (seen.contains(L.get(i))) break;\n seen.add(L.get(i));\n }\n return N - res;\n }\n\n\n public int A(int m, int n) {\n return n == 0 ? 1 : A(m, n - 1) * (m - n + 1);\n }\n```\n**Python3**\n```py\n def numDupDigitsAtMostN(self, N):\n L = list(map(int, str(N + 1)))\n n = len(L)\n res = sum(9 * perm(9, i) for i in range(n - 1))\n s = set()\n for i, x in enumerate(L):\n for y in range(i == 0, x):\n if y not in s:\n res += perm(9 - i, n - i - 1)\n if x in s: break\n s.add(x)\n return N - res\n```\n | 278 | 9 | ['Python', 'Java'] | 49 |
numbers-with-repeated-digits | Share my O(logN) C++ DP solution with proof and explanation | share-my-ologn-c-dp-solution-with-proof-6tkio | ---\n## 1. Problem\n\n---\nGiven a positive integer N, return the number of positive integers less than or equal to N that have at least 1 repeated digit.\n\nEx | kjer | NORMAL | 2019-03-19T07:52:55.595189+00:00 | 2019-03-19T07:52:55.595234+00:00 | 8,878 | false | ---\n## 1. Problem\n\n---\nGiven a positive integer ```N```, return the number of positive integers less than or equal to ```N``` that have at least 1 repeated digit.\n\n**Example 1:**\n```\nInput: 20\nOutput: 1\nExplanation: The only positive number (<= 20) with at least 1 repeated digit is 11.\n```\n\n**Example 2:**\n```\nInput: 100\nOutput: 10\nExplanation: The positive numbers (<= 100) with at least 1 repeated digit are 11, 22, 33, 44, 55, 66, 77, 88, 99, and 100.\n```\n\n**Example 3:**\n```\nInput: 1000\nOutput: 262\n```\n**Note:**\n* 1 <= N <= 10^9\n\n---\n## 2. Thinking process\n\n---\n#### 2.1 Analysis\n\n---\nThe problem is to return \n\n>#### T(N) = the number of positive integers less than or equal to N that have **at least 1 repeated digit**.\n\nSuppose\n\n>#### S(N) = the number of positive integers less than or equal to N that have **NO repeated digits**.\n\nThe answer can be expressed as\n\n>#### T(N) = N - S(N).\n\nLater, the calculation of S(N) will be focused on.\n\n---\n#### 2.2 Find the rules\n\n---\n\n- From **1** to **9**, there are **9** positive integers that have **NO repeated digits**.\n\n- From **10** to **99**,\n - From **10** to **19**, there are **9** positive integers that have **NO repeated digits**. (Only **11** has repeated digits)\n - From **20** to **29**, there are **9** positive integers that have **NO repeated digits**. (Only **22** has repeated digits)\n - From **30** to **39**, there are **9** positive integers that have **NO repeated digits**. (Only **33** has repeated digits)\n - From **40** to **49**, there are **9** positive integers that have **NO repeated digits**. (Only **44** has repeated digits)\n - From **50** to **59**, there are **9** positive integers that have **NO repeated digits**. (Only **55** has repeated digits)\n - From **60** to **69**, there are **9** positive integers that have **NO repeated digits**. (Only **66** has repeated digits)\n - From **70** to **79**, there are **9** positive integers that have **NO repeated digits**. (Only **77** has repeated digits)\n - From **80** to **89**, there are **9** positive integers that have **NO repeated digits**. (Only **88** has repeated digits)\n - From **90** to **99**, there are **9** positive integers that have **NO repeated digits**. (Only **99** has repeated digits)\n there are **9 \xD7 9 = 81** positive integers that have **NO repeated digits**. \n \n- From **100** to **999**,\n - From **100** to **199**,\n - From **100** to **109**, there are **8** positive integers that have **NO repeated digits**. (**100** and **101** have repeated digits)\n - From **110** to **119**, there are **0** positive integers that have **NO repeated digits**. (**ALL numbers** have repeated digits because of the prefix **11**)\n - From **120** to **129**, there are **8** positive integers that have **NO repeated digits**. (**121** and **122** have repeated digits)\n - From **130** to **139**, there are **8** positive integers that have **NO repeated digits**. (**131** and **133** have repeated digits)\n - From **140** to **149**, there are **8** positive integers that have **NO repeated digits**. (**141** and **144** have repeated digits)\n - From **150** to **159**, there are **8** positive integers that have **NO repeated digits**. (**151** and **155** have repeated digits)\n - From **160** to **169**, there are **8** positive integers that have **NO repeated digits**. (**161** and **166** have repeated digits)\n - From **170** to **179**, there are **8** positive integers that have **NO repeated digits**. (**171** and **177** have repeated digits)\n - From **180** to **189**, there are **8** positive integers that have **NO repeated digits**. (**181** and **188** have repeated digits)\n - From **190** to **199**, there are **8** positive integers that have **NO repeated digits**. (**191** and **199** have repeated digits)\n there are **9 \xD7 8 = 72** positive integers that have **NO repeated digits**.\n - .....\n\nLet\'s think about all positive integers **from 100 to 199**.\n \nThey can be generated by \n\n>#### adding a new digit from **0** to **9** to the end of all positive integers from **10** to **19**.\nIn order to generate a new positive integer that has **NO** repeated digits,\n- To **10**: **10 has NO repeated digits**. There are **8 choices (0 and 1 can NOT be chosen)**.\n- To **11**: **11 has repeated digits**. There are **0 choices (0 to 9 can NOT be chosen)**.\n- To **12**: **12 has NO repeated digits**. There are **8 choices (1 and 2 can NOT be chosen)**.\n- To **13**: **13 has NO repeated digits**. There are **8 choices (1 and 3 can NOT be chosen)**.\n- To **14**: **14 has NO repeated digits**. There are **8 choices (1 and 4 can NOT be chosen)**.\n- To **15**: **15 has NO repeated digits**. There are **8 choices (1 and 5 can NOT be chosen)**.\n- To **16**: **16 has NO repeated digits**. There are **8 choices (1 and 6 can NOT be chosen)**.\n- To **17**: **17 has NO repeated digits**. There are **8 choices (1 and 7 can NOT be chosen)**.\n- To **18**: **18 has NO repeated digits**. There are **8 choices (1 and 8 can NOT be chosen)**.\n- To **19**: **19 has NO repeated digits**. There are **8 choices (1 and 9 can NOT be chosen)**.\n\nAre there rules?\n\n---\n>#### **Rule A:** \n>#### **A k-digit positive integer with NO repeated digits can ONLY be generated from (k - 1)-digit positive integers with NO repeated digits (k > 1).**\n\nProof:\n\nIf a (k - 1)-digit positive integer has repeated digits (e.g. **11**), \nafter adding a digit (**0** to **9**) to its end, the generated k-digit integer (e.g. 110, 111, ..., 119) **STILL has repeated digits**.\nThat\'s to say, a k-digit positive integer with **NO** repeated digits can **ONLY** be generated from (k - 1)-digit positive integers with **NO** repeated digits.\n\n---\n\n>#### **Rule B:** \n>#### **To generate a k-digit positive integer with NO repeated digits,** \n>#### **there are (10 - k + 1) digits that can be added to (k - 1)-digit positive integers with NO repeated digits (k > 1).**\n\nProof:\n\nA (k - 1)-digit positive integer **with NO repeated digits** has **k - 1 distinct digits**.\nWhen generating a k-digit positive integer **with NO repeated digits** from it, \nsince **k - 1** digits in **0** to **9** have been **used**, there are **10 - k + 1** choices for the digit to be added.\n\n\n---\n#### 2.3 Recursion formula\n\n---\nDefinition:\n\n>#### **f(i, j, k): The number of i-digit positive integers with NO repeated digits in the interval [j, k]. (i > 0, j \u2264 k, j and k are i-digit positive integers).**\n\n\nBased on the **Rule A and Rule B in Section 2.2**, the recursion formula is\n\n>#### **f(i, j, k) = k - j + 1. i = 1.**\n>#### **f(i + 1, 10j, 10k + 9) = f(i, j, k) \xD7 (10 - i). others.**\n\n---\n#### 2.4 Normal case analysis\n\n\n---\n\nIn order to illustrate the usage of the recursion formula in Section 2.3, we take a normal case for calculation.\n\nIf **N = 26334**,\n\nFrom **Section 2.3**,\n \n- From **1** to **9**, f(1, 1, 9) = 9.\n- From **10** to **99**, f(2, 10, 99) = f(1, 1, 9) \xD7 (10 - 1) = 9 \xD7 9 = 81.\n- From **100** to **999**, f(3, 100, 999) = f(2, 10, 99) \xD7 (10 - 2) = 81 \xD7 8 = 648.\n- From **1000** to **9999**, f(4, 1000, 9999) = f(3, 100, 999) \xD7 (10 - 3) = 648 \xD7 7 = 4536.\n\nIf all values are added together, the sum is\n\n>#### **S(9999) = f(1, 1, 9) + f(2, 10, 99) + f(3, 100, 999) + f(4, 1000, 9999) = 9 + 81 + 648 + 4536 = 5274.**\n\nNow the number of positive integers **with NO repeated digits less than or equal to 9999** has been calculated, which is the **first part of the whole result**.\n\n\n---\nHow about the rest?\n\nThe rest part is the number of positive integers **with NO repeated digits in interval [10000, 26334]**, which is\n\n>#### **P = f(5, 10000, 26334)**.\n\nHow can the recursion formula be applied here?\n\n---\nSince our target is to **calculate f(5, 10000, 26334)**, the **calculation series** is\n\n>#### **f(1, 1, 2), f(2, 10, 26), f(3, 100, 263), f(4, 1000, 2633), f(5, 10000, 26334).**\n\n\n- From **1** to **2**, **f(1, 1, 2) = 2**.\n\n\n- From **10** to **29**, by applying the recursion formula, **f(2, 10, 29) = f(1, 1, 2) \xD7 (10 - 1) = 2 \xD7 9 = 18**.\n\n - From **27 to 29**, there are **3** positive integers **with NO repeated digits**, which means **f(2, 27, 29) = 3**. \n\n - **f(2, 10, 26) = f(2, 10, 29) - f(2, 27, 29) = 18 - 3 = 15**.\n \n\n- From **100** to **269**, by applying the recursion formula, **f(3, 100, 269) = f(2, 10, 26) \xD7 (10 - 2) = 15 \xD7 8 = 120**.\n\n - From **264 to 269**, there are **5** positive integers **with NO repeated digits** (**except 266**), which means **f(3, 264, 269) = 5**.\n \n - **f(3, 100, 263) = f(3, 100, 269) - f(3, 264, 269) = 120 - 5 = 115**.\n \n \n- From **1000** to **2639**, by applying the recursion formula, **f(4, 1000, 2639) = f(3, 100, 263) \xD7 (10 - 3) = 115 \xD7 7 = 805**.\n\n - From **2634 to 2639**, there are **5** positive integers **with NO repeated digits** (**except 2636**), which means **f(4, 2634, 2639) = 5**.\n \n - **f(4, 1000, 2633) = f(4, 1000, 2639) - f(4, 2634, 2639) = 805 - 5 = 800**. \n\n \n- From **10000** to **26339**, by applying the recursion formula, **f(4, 10000, 26339) = f(4, 1000, 2633) \xD7 (10 - 4) = 800 \xD7 6 = 4800**.\n\n - From **26335 to 26339**, there are **NO** positive integers **with NO repeated digits** (**due to the prefix "2633"**), which means **f(5, 26335, 26339) = 0**.\n \n - **f(5, 10000, 26334) = f(4, 10000, 26339) - f(5, 26335, 26339) = 4800 - 0 = 4800**.\n\nThis is the **second part of the whole result**.\n\n---\nThen\n\n>#### **S(26334) = S(9999) + f(5, 10000, 26334) = 5274 + 4800 = 10074.**\n\n\nThe final answer is\n\n>#### **T(26334) = 26334 - S(26334) = 26334 - 10074 = 16260.**\n\n---\n#### 2.4 Algorithm\n\n\n---\n**Special case**:\n- If N < 10, return 0.\n\n---\n**Get digits**:\n- Initialization:\n\n - Set k = 0. i = N.\n\n- Loop: while i > 0, \n \n - Set k = k + 1. (Now, k is the digit length of N).\n\n - Set i = i / 10. \n \n- Initialization: \n\n - Set j = N.\n\n - Array digit with size = k. (saving all digits in N)\n \n- Loop: iterate i from 0 to k - 1\n\n - Set digit[k - 1 - i] = j mod 10.\n \n - Set j = j / 10.\n\n---\n**Get first part**:\n\n- Initialization: \n\n - Array noDupBase with size = k - 1. \n \n - Set noDupBaseSum = 0. (calculate first part)\n\n- Loop: iterate i from 0 to k - 2.\n\n - If i = 0, noDupBase[i] = 9. Calculate f(1, 1, 9).\n \n - Else, noDupBase[i] = noDupBase[i - 1] \xD7 (10 - i). Calculate f(i, 10^(i - 1), 10^i - 1).\n \n - Set noDupBaseSum = noDupBaseSum + noDupBase[i].\n\n---\n**Get second part**:\n\n- Initialization: \n\n - Set boolean value duplicate = false. (prefix duplicate) \n \n - Array count with size = 10.(record the digits\' count in prefix). \n \n - Array noDupRes with size = k. (calculate second part)\n \n- Loop: iterate i from 0 to k - 1.\n\n - If i = 0, noDupBase[i] = 9. Calculate f(1, 1, 9).\n \n - Else, noDupBase[i] = noDupBase[i - 1] \xD7 (10 - i).\n \n - If NOT duplicate\n \n - Set diff = 0.\n\t\n\t- Loop: iterate j from digit[i] + 1 to 9\n\t\n\t - If count[j] = 0, Set diff = diff + 1.\n\t \n\t- Set noDupRes[i] = noDupRes[i] - diff.\n\t\n\t- Set count[digit[i]] = count[digit[i]] + 1.\n\t\n\t- If count[digit[i]] > 1, Set duplicate = true.\n\n---\n**Get final answer**:\n\t\n- return N - (noDupBaseSum + noDupRes[k - 1]).\n\n\n---\n## 4. Complexity Analysis\n\n---\n\n#### 4.1 Time complexity\n\n---\n\n>#### The time complexity is **O(logN)**.\n\n---\n\n#### 4.2 Space complexity\n\n---\n\n>#### The space complexity is **O(logN)**.\n\n---\n## 5. Code\n\n---\n```\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int N) {\n if(N < 10) return 0;\n int k = 0;\n for(int i = N; i > 0; i /= 10) k++;\n int digit[k] = {0};\n for(int i = 0, j = N; i < k; i++, j /= 10) digit[k - 1 - i] = j % 10;\n \n int noDupBaseSum = 0;\n int noDupBase[k - 1] = {0};\n for(int i = 0; i < k - 1; i++)\n {\n noDupBase[i] = i == 0 ? 9 : noDupBase[i - 1] * (10 - i);\n noDupBaseSum += noDupBase[i];\n }\n \n int count[10] = {0};\n int noDupRes[k] = {0};\n bool duplicate = false;\n for(int i = 0; i < k; i++)\n {\n noDupRes[i] = i == 0 ? 9 : noDupRes[i - 1] * (10 - i);\n if(!duplicate)\n {\n int diff = 0;\n for(int j = digit[i] + 1; j < 10; j++) diff += count[j] == 0;\n noDupRes[i] -= diff;\n count[digit[i]]++;\n if(count[digit[i]] > 1) duplicate = true;\n }\n }\n return N - (noDupBaseSum + noDupRes[k - 1]);\n }\n}; | 184 | 2 | ['Math', 'Dynamic Programming', 'Recursion', 'C++'] | 13 |
numbers-with-repeated-digits | Python O(logN) solution with clear explanation | python-ologn-solution-with-clear-explana-zabx | The number of non-repeated digits can be easily calculated with permutaiton. We only need to exclude all the non-repeated digits to get the answer.\n\nLet\'s fi | heqingy | NORMAL | 2019-03-17T05:55:53.394700+00:00 | 2019-03-17T05:55:53.394754+00:00 | 7,169 | false | The number of non-repeated digits can be easily calculated with permutaiton. We only need to exclude all the non-repeated digits to get the answer.\n\nLet\'s first consider about the cases where N=10^k\n**N=10**\nthe free digits are marked as `*`, so we only need to consider about `*` and `1*`\n* `*`: obviously all 1-digit numbers are non-repeated, so non-repeated number = 9\n* `1*`: we only need to consider about `1* <= 10`, so non-repeated number = 1\n\nThus, the result for N=10 is:\n`N - #non_repeat(*) - #non_repeat(1*) = 10 - 9 - 1 = 0`\n\n**N=100**\nthe free digits are marked as `*`, so we only need to consider about `*`, `**`, and `1**`\n* `*`: obviously all 1-digit numbers are non-repeated, so non-repeated number = 9\n* `**`: this can be calculated with permutation: leading digit has 9 options(1-9) and the last 1 digit has `10-1` options, thus the total permuation is `9 * permutation(9, 1)=81`. i.e: non-repeated number = 81\n* `1**`: we only need to consider about `1**<=100`, so non-repeated number =0\n\nThus, the result for N=100 is:\n`N - #non_repeat(*) - #non_repeat(**) - #non_repeat(1**) = 100 - 9 - 81 = 10`\n\n**N=1000**\n`#non_repeat(***) = 9 * permutation(9, 2) = 9 * 9 * 8 = 648`\nsimilarly, we can get:\n`N - #non_repeat(*) - #non_repeat(**) - #non_repeat(***) - #non_repeat(1***) = 1000 - 9 - 81 - 648 = 282`\n\nNow, let\'s consider a more general case:\n**N=12345**\nactually, we can get the count of non-repeated numbers by counting all non-repeated numbers in following patterns:\n\n```\n *\n **\n ***\n ****\n10***\n11*** (prefix repeated, skip)\n120**\n121** (prefix repeated, skip)\n122** (prefix repeated, skip)\n1230*\n1231* (prefix repeated, skip)\n1232* (prefix repeated, skip)\n1233* (prefix repeated, skip)\n12340\n12341 (prefix repeated, skip)\n12342\n12343\n12344 (prefix repeated, skip)\n12345\n```\n\nand use N to minus the count we will get the answer.\n\nReference implementation:\n```\n# given number n, see whether n has repeated number\ndef has_repeated(n):\n str_n = str(n)\n return len(set(str_n)) != len(str_n)\n\ndef permutation(n, k):\n prod = 1\n for i in range(k):\n prod *= (n-i)\n return prod\n\n# calculate number of non-repeated n-digit numbers\n# note: the n-digit number can\'t start with 0\n# i.e: n_digit_no_repeat(2) calculates the non-repeated\n# numbers in range [10, 99] (inclusive)\ndef n_digit_no_repeat(n):\n if n == 1:\n return 9\n else:\n return 9 * permutation(9, n-1)\n\nclass Solution(object):\n def numDupDigitsAtMostN(self, N):\n """\n :type N: int\n :rtype: int\n """ \n N_str = str(N)\n n_digit = len(N_str)\n digits = map(int, N_str)\n result = N - 1\n prefix = 0\n for i in range(1, n_digit):\n result -= n_digit_no_repeat(i)\n for i in range(n_digit):\n # when we fix the most significant digit, it \n # can\'t be zero\n start = 0 if i else 1\n for j in range(start, digits[i]):\n if has_repeated(prefix * 10 + j):\n continue\n if i != n_digit-1:\n result -= permutation(10-i-1, n_digit-1-i)\n else:\n # optmized from `result -= has_repeated(prefix*10+j)`\n result -= 1\n prefix = prefix*10 + digits[i]\n return result + has_repeated(N)\n``` | 98 | 1 | [] | 10 |
numbers-with-repeated-digits | screencast of LeetCode Weekly Contest 128 | screencast-of-leetcode-weekly-contest-12-i87g | https://www.youtube.com/watch?v=yXKBREQbBOg\n\nenjoy :) | cuiaoxiang | NORMAL | 2019-03-17T10:12:08.334342+00:00 | 2019-03-17T10:12:08.334389+00:00 | 2,361 | false | https://www.youtube.com/watch?v=yXKBREQbBOg\n\nenjoy :) | 33 | 2 | [] | 3 |
numbers-with-repeated-digits | C++ Digit Dp solution | c-digit-dp-solution-by-_awm-u5ko | """\n\n //dp[pos][tight][start][rep][mask];\n int dp[10][2][2][2][1<<10];\n vectornum;\n int solve(int pos,int tight,int start,int rep,int mask)\n | _AWM_ | NORMAL | 2020-03-15T07:51:13.640863+00:00 | 2020-03-15T07:51:13.640919+00:00 | 3,150 | false | """\n\n //dp[pos][tight][start][rep][mask];\n int dp[10][2][2][2][1<<10];\n vector<int>num;\n int solve(int pos,int tight,int start,int rep,int mask)\n {\n if(pos == num.size())\n {\n return rep;\n }\n int &ans= dp[pos][tight][start][rep][mask];\n if(ans!=-1)return ans;\n \n int k = num[pos];\n if(tight)k=9;\n int res=0;\n for(int i=0;i<=k;i++)\n {\n int ns = start||i>0;//number started yet or not\n int nt = tight||i<k;//tight for next number\n if(ns){\n res+=solve(pos+1,nt,ns,rep||(mask&(1<<i)),mask|1<<i);\n }\n else{\n res+=solve(pos+1,nt,0,rep,mask);\n }\n \n }\n ans= res;\n return res;\n }\n int numDupDigitsAtMostN(int N) {\n while(N){\n num.push_back(N%10);\n N/=10;\n }\n reverse(num.begin(),num.end());\n memset(dp,-1,sizeof(dp));\n return solve(0,0,0,0,0);\n }\n}\n""" | 28 | 4 | [] | 3 |
numbers-with-repeated-digits | [Java] Clean Solution || with detailed explanation | java-clean-solution-with-detailed-explan-pgvc | The key to solve this problem is cleverly enumerate all numbers < n without repeated digits. One of the ways is as follow: \n\nStep 1 : count numbers with lengt | xieyun95 | NORMAL | 2021-05-24T22:45:34.891125+00:00 | 2021-05-24T22:51:30.370935+00:00 | 2,338 | false | The key to solve this problem is cleverly enumerate all numbers < n without repeated digits. One of the ways is as follow: \n\n**Step 1 : count numbers with length smaller than n:**\n```\n// return count of numbers with d digits and no repeated digits\nprivate int totalNoRepeat(int d) {\n\tint res = 9; // 0-th digit has 9 choices (1, ..., 9)\n\t\n\t/* 1-st digit has 9 choices <==> (0, ..., 9) except 0-th digit\n\t 2-st digit has 8 choices <==> (0, ..., 9) except 0-th & 1-st digit\n\t ...\n\t i-th digit has (10- i) choices <==> (0, ..., 9) except 0-th & ...& (i-1)-th digit */\n\t\n\tfor (int i = 1; i < d; i++) {\n\t\tres *= (10 - i); \n\t} \n\treturn res;\n}\n```\n**Step 2 : count numbers with length equals to n:**\n```\nCase 1 : n = 3 4 6 5 \n\tpivot index i = 0 should < 3 <==> {1, 2} \n\t\t\t\t\t1 X X X - 2 X X X ==> 2 * 9 * 8 * 7\n pivot index i = 1 should < 4 and not take values of previous indices <==> {0, 1, 2} \n\t\t\t\t\t3 0 X X - 3 3 X X ==> 1 * 3 * 8 * 7 \n\tpivot index i = 2 should < 6 and not take values of previous indices <==> {0, 1, 2, 5} \n\t\t\t\t\t3 4 0 X - 3 4 5 X ==> 1 * 1 * 4 * 7\n pivot index i = 3 should < 5 and not take values of previous indices <==> {0, 1, 2} \n\t\t\t\t\t3 4 6 0 - 3 4 6 5 ==> 1 * 1 * 1 * 3\n\nCase 2 : n = 3 3 5 3\n\tpivot index i = 0 should < 3 <==> {1, 2} \n\t\t\t\t\t1 X X X - 2 X X X ==> 2 * 9 * 8 * 7\n\tpivot index i = 1 should < 3 and not take values of previous indices <==> {0, 1, 2} \n\t\t\t\t\t3 0 X X - 3 2 X X ==> 1 * 3 * 8 * 7\n\tpivot index i = 2 and after should not be consider\n\t\t\t\t\t3 3 X X ==> 0 the number will contain repeated digits\n```\nFrom these two examples, we can see the pattern of choosing digits: \n```\n// i := pivot index \n// d := i-th digit in the original number n\n\ni = 0 <==> choose from {1, 2, ..., d-1}; After the pivot index i = 0: \n\t// 1-st digit has 9 choices <==> (0, ..., 9) except {0-th digit}\n\t// 2-nd digit has 8 choices <==> (0, ..., 9) except {0-th, 1-st digit}\n\t// ...\n\ni = 1 <==> choose from {0, 1, ... , d-1} - {0-th digit}; After the pivot index i = 1: \n\t// 2-nd digit has 8 choices <==> (0, ..., 9) except {0-th, 1-st digit}\n\t// 3-rd digit has 7 choices <==> (0, ..., 9) except {0-th, 1-st, 2-nd digit}\n\t// ...\n\nThus for j-th digit after the pivot index i, \n\t// j-th digit has (10- j) choices <==> (0, ..., 9) except 0-th & ...& (j-1)-th digit \n```\n\n**Final solution:** \n```\nclass Solution {\n public int numDupDigitsAtMostN(int n) {\n String str = String.valueOf(n);\n int len = str.length();\n \n // all number with no repeat and length < len\n int unique = 0;\n for (int i = 1; i < len; i++) {\n unique += totalNoRepeat(i);\n }\n \n\t\t// all number with no repeat and length == len\n Set<Integer> set = new HashSet<>();\n int i = 0;\n for (i = 0; i < len; i++) {\n int d = str.charAt(i) - \'0\';\n \n int temp = pivotChoice(set, d, i == 0);\n for (int j = i+1; j < len; j++) {\n temp *= (10 - j);\n }\n \n unique += temp;\n if (!set.add(d)) break; // no need to continue after seeing repeated digits\n }\n \n if (i == len) unique++; // the number n itself\n \n return n - unique;\n }\n \n private int totalNoRepeat(int d) {\n int res = 9;\n for (int i = 1; i < d; i++) {\n res *= (10 - i);\n }\n return res;\n }\n \n private int pivotChoice(Set<Integer> set, int d, boolean first) {\n int res = 0;\n int i = (first ? 1 : 0);\n \n while (i < d) {\n if (!set.contains(i++)) res++;\n }\n \n return res;\n } \n \n}\n```\n\nThe main function can also be written as following. Here we consider the count of numbers strictly less than (n+1):\n\n```\npublic int numDupDigitsAtMostN(int n) {\n\tString str = String.valueOf(n+1);\n\tint len = str.length();\n\t\n\tint unique = 0;\n\tfor (int i = 1; i < len; i++) {\n\t\tunique += totalNoRepeat(i);\n\t}\n\n\tSet<Integer> set = new HashSet<>();\n\tint i = 0;\n\tfor (i = 0; i < len; i++) {\n\t\tint d = str.charAt(i) - \'0\';\n\n\t\tint temp = pivotChoice(set, d, i == 0);\n\t\tfor (int j = i+1; j < len; j++) {\n\t\t\ttemp *= (10 - j);\n\t\t}\n\n\t\tunique += temp;\n\t\tif (!set.add(d)) break; \n\t}\n\treturn n - unique;\n}\n``` | 17 | 0 | ['Java'] | 2 |
numbers-with-repeated-digits | Backtracking with C++ in a few lines | backtracking-with-c-in-a-few-lines-by-ki-hegr | \nclass Solution {\npublic:\n int uniqueDigits = 0;\n int numDupDigitsAtMostN(int N) {\n backtrack(0,0, N);\n return N - uniqueDigits + 1; / | kirakira | NORMAL | 2019-03-27T09:16:15.636691+00:00 | 2019-03-27T09:16:15.636736+00:00 | 1,884 | false | ```\nclass Solution {\npublic:\n int uniqueDigits = 0;\n int numDupDigitsAtMostN(int N) {\n backtrack(0,0, N);\n return N - uniqueDigits + 1; // +1 as 0 is counted\n }\n \n void backtrack(long cur, int bitmask, int& N){\n if(cur > N) return;\n else uniqueDigits++;\n \n for(int digit=0; digit<10; digit++){\n if(bitmask == 0 && digit == 0) continue;\n if((bitmask & (1<<digit)) > 0) continue; // has repeat digits\n backtrack(cur*10 + digit, bitmask | (1<<digit), N);\n }\n }\n};\n``` | 17 | 0 | [] | 3 |
numbers-with-repeated-digits | C++ digit DP, with bitMask, with comments | c-digit-dp-with-bitmask-with-comments-by-ze50 | \nclass Solution {\npublic:\n\n\tint dp[11][2][2][(1 << 10)];\n\n\n\tint solve(int pos, bool bound, bool hasRepeated, int mask, string &s) {\n\n\t\tif (pos == s | uttu_dce | NORMAL | 2022-06-11T18:33:30.432006+00:00 | 2022-06-11T18:33:30.432035+00:00 | 1,458 | false | ```\nclass Solution {\npublic:\n\n\tint dp[11][2][2][(1 << 10)];\n\n\n\tint solve(int pos, bool bound, bool hasRepeated, int mask, string &s) {\n\n\t\tif (pos == s.length()) {\n\t\t\treturn hasRepeated ? 1 : 0;\n\t\t}\n\n\t\tif (dp[pos][bound][hasRepeated][mask] != -1) return dp[pos][bound][hasRepeated][mask];\n\n\t\tint maxDigit = bound ? s[pos] - \'0\' : 9;\n\n\t\tfor (int digit = 0; digit <= maxDigit; digit++) {\n\n\t\t\t/* if this is a leading zero, then hasRepeated for the the current guy (position) will obviously be false */\n\t\t\tif (digit == 0 && mask == 0) ans += solve(pos + 1, bound && (digit == s[pos] - \'0\'), false, mask, s);\n\n\t\t\t/*\n\t\t\t\tif this particular has already come earlier in this digit, and it is not a leading zero, then clearly, there is a repitition\n\t\t\t\tand we have to pass true in hasRepeated\n\t\t\t*/\n\t\t\telse if ((mask & (1 << digit))) ans += solve(pos + 1, bound && (digit == s[pos] - \'0\'), true, mask, s);\n\n\t\t\t/*\n\t\t\t\tif this guy is coming for the first time, then hasRepeated will be whatever was for the previous guy\n\t\t\t\tand don\'t forget to switch on the bit corresponding to this digit in the mask\n\t\t\t*/\n\t\t\telse ans += solve(pos + 1, bound && (digit == s[pos] - \'0\'), hasRepeated, (mask | (1 << digit)), s);\n\n\t\t}\n\n\t\treturn dp[pos][bound][hasRepeated][mask] = ans;\n\n\t}\n\n\tint numDupDigitsAtMostN(int n) {\n\t\tmemset(dp, -1, sizeof(dp));\n\t\tstring R = to_string(n);\n\t\t// return solve(0, true, false, false, 0, R);\n\t\treturn solve(0, true, false, 0, s);\n\t}\n};\n``` | 13 | 0 | ['Dynamic Programming', 'Bitmask'] | 3 |
numbers-with-repeated-digits | C++ with Alternative Explanation | c-with-alternative-explanation-by-gemisi-qw8j | Really enjoyed working through this problem and pushing myself to better understand permutations because of it, and figured I\'d post my explanation of this pro | gemisis | NORMAL | 2019-03-17T20:18:07.458811+00:00 | 2019-03-17T20:18:07.458850+00:00 | 1,678 | false | Really enjoyed working through this problem and pushing myself to better understand permutations because of it, and figured I\'d post my explanation of this problem here. The basic idea behind this problem is to instead determine how many **invalid** numbers exist from **1-N**, rather than trying to find the valid numbers.\n\nTo do this, we can make heavy use of the permutations formula (see [here](https://www.mathplanet.com/education/algebra-2/discrete-mathematics-and-probability/permutations-and-combinations) for a great explination on it) since it gives us the number permutations of unique numbers. We can start by figure out how many digits are in our number, and varying all of the digits in L-1 (L being the number of digits).\n\nFor example, with the number 350, we have 3 digits, meaning we can start by finding all **invalid** numbers from 0 to 99 (e.g. the first two digits). To start, let\'s assuming we only have 1 digit available. In this case, we can\'t vary any other digits in the number since there are none, and because there is only 1 digit they are all invalid. Thus, since there are 9 total numbers with 1 digit, we have 9 invalid permutations for this digit. Similarly, for 2 digits, we have 1 digit we can vary (e.g. 1x has x that can be varied, 2y has y that can be varied, so on and so forth). Plugging that into our our formula, we have perm(9, 1) which results in 9. Because there are 9 possible digits for the first digit, we can multiply the result by 9 (perm(9, 1) * 9) which gives us 81 invalid digits. Adding that onto our first result of 9, and we get 90 invalid digits for a number range of 1-99 (meaning we have 9 valid digits in that range).\n\nAt this point, for the number 350, we know that thare are at least 90 invalid digits from 1-100 as a result (since 100 is valid). Now however we need to count the number of invalid digits from 100-350. This can be done by varying each of the digits in 351 (e.g. N+1), and finding the valid permutations of that as a result. For example:\n```\n3XX -> perm(9-0, 3-0-1) -> perm(9, 2)\nX5X -> perm(9-1, 3-1-1) -> perm(8, 1)\nXX1 -> perm(9-2, 3-2-1) -> perm(7, 0)\n```\nWe then add this number of invalid permutations to our count based on the number we have. However, if we\'ve previously seen a number in that range, we ignore it. For example, when we get to the 5 in 351, we will only add perm(8, 1)\'s result 4 times, since the third time has already been accounted for when we went over the 3 in 351. Once we\'ve done all of this, we can simply subtract our number of invalid numbers from our original number N to get our result.\n\nHere is what this process looks like in action:\n```\n350 -> 351\ninvalid digits -> 0\n\n1 digit -> X -> perm(9, 0) * 9 -> 9 invalid digits\n2 digits -> YX -> perm(9, 1) * 9 -> 81 invalid digits\ninvalid digits -> 90\n\n0XX -> invalid so don\'t count the invalid digits.\n1XX -> perm(9, 2) -> 72 invalid digits\n2XX -> perm(9, 2) -> 72 invalid digits\n3XX -> stop counting invalid numbers for the first digit.\nX0X -> perm(8, 1) -> 8 invalid digits\nX1X -> perm(8, 1) -> 8 invalid digits\nX2X -> perm(8, 1) -> 8 invalid digits\nX3X -> perm(8, 1) -> 8 invalid digits -> but because we\'ve already looked at the digit 3 previously we can skip this.\nX4X -> perm(8, 1) -> 8 invalid digits\nX5X -> stop counting invalid numbers for the second digit.\nXX0 -> perm(7, 0) -> 1 invalid digit\nXX1 -> stop counting invalid numbers for the third and final digit.\ninvalid digits -> 267\n\nresult -> 350 - 267 = 83\n```\nAnd the full code looks like this:\n```\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int N) {\n int invalid = 0;\n \n // Begin by calculating all of the invalid numbers up to 10^(L-1), where L is the length of our number (e.g. For 350, we would find all invalid numbers between 1 and 99)\n int c = floor(log10(N+1))+1;\n for (int i = 0;i < c-1;i++) {\n invalid += 9 * perm(9, i);\n }\n\n // For each digit, calculate the possible invalid permutations that are available up until that digit.\n int digits = 0;\n for (int i = 0;i < c;i++) {\n // Get the left most digit.\n int digit = ((N+1) / (int)pow(10, c-i-1)) % 10;\n // Count up to the digit. Note that if it\'s the first digit, we start at 1 to avoid finding permutations when the first digit is a 1 since there are none.\n for (int j = (i > 0 ? 0 : 1);j < digit;j++) {\n // If we\'ve had the same digit to the left of it previously, then we don\'t need to count it again.\n // E.g. If our number is 350, when get to 330-339 we\'ve already considered all possible invalid permutations for that number range and can skip it.\n if (((digits >> j) & 1) == 0) {\n invalid += perm(9 - i, c - i - 1);\n }\n }\n // If we end up finding a digit we\'ve already searched, we can finish here.\n if ((digits >> digit) & 1)\n break;\n digits |= 1 << digit;\n }\n\n return N - invalid;\n }\n \n int perm(int m, int n) {\n int out = 1;\n while (m > 1 && n > 0) {\n out *= m;\n m--;\n n--;\n }\n return out;\n }\n};\n```\nSome trickery I used: **log10(N+1) + 1** counts the number of digits we have for us so we don\'t have to do another loop over them. We can then also abuse some other mathematics to quickly iterate over this without any additional memory, resulting in a **O(c) memory usage, where c is a constant value (e.g. O(1))**. The runtime of this is going to be **O(L\xB2) where L is the number of digits** from what I can tell, because our second for loop will iterate over every digital (with a max of 9 being possible), and for each digit will iterate over the range of numbers from 0 to D (D being the digit we are on) which also has a mximum possible value of 9. **My math on the runtime may be off, so please correct me if that\'s the case, as I would like to know the correct runtime.**\n\nAs far as further optimizations on the runtime, I\'m not sure how possible this is since we ultimately need to make sure we don\'t double count any of the previously checked digits. Feedback on this explination would be greatly appreciated as well! | 12 | 1 | ['C++'] | 3 |
numbers-with-repeated-digits | Runtime 75 ms Beats 75.00% [EXPLAINED] | runtime-75-ms-beats-7500-explained-by-r9-7w0o | Intuition\nWhen solving this problem, I want to find out how many numbers from 1 to \uD835\uDC5B have at least one repeated digit. Instead of counting these num | r9n | NORMAL | 2024-09-12T22:12:56.244421+00:00 | 2024-09-12T22:12:56.244442+00:00 | 101 | false | # Intuition\nWhen solving this problem, I want to find out how many numbers from 1 to \uD835\uDC5B have at least one repeated digit. Instead of counting these numbers directly (which is hard), I use a clever trick: I count how many numbers up to \uD835\uDC5B don\'t have repeated digits, and then subtract this from \uD835\uDC5B.\n\n\n# Approach\nConvert n to a String: Makes digit handling easier.\n\nRecursive Search: Explore numbers with unique digits using a bitmask to track used digits and a DP table to avoid redundant work.\n\nCount and Subtract: Count unique-digit numbers and subtract from n.\n\n# Complexity\n- Time complexity:\nO(n x 2d), where d is the number of digits in n.\n\n\n- Space complexity:\nO(d x 2d) for the DP table.\n\n# Code\n```typescript []\nfunction numDupDigitsAtMostN(n: number): number {\n const s = n.toString();\n const len = s.length;\n const dp = Array.from({ length: len }, () => Array(1 << 10).fill(-1));\n \n const dfs = (index: number, mask: number, isLimit: boolean, hasLeadingZeros: boolean): number => {\n // Base case: reached the end of the number\n if (index === len) return hasLeadingZeros ? 0 : 1;\n\n // Return cached result if not constrained by limits\n if (!isLimit && !hasLeadingZeros && dp[index][mask] !== -1) {\n return dp[index][mask];\n }\n\n // Initialize result for the current state\n let count = 0;\n\n // If there are leading zeros, skip to the next digit\n if (hasLeadingZeros) {\n count += dfs(index + 1, mask, false, true);\n }\n\n // Define range for the current digit\n const low = hasLeadingZeros ? 1 : 0;\n const high = isLimit ? +s[index] : 9;\n\n // Try all possible digits for the current position\n for (let digit = low; digit <= high; digit++) {\n if ((mask & (1 << digit)) === 0) { // Check if digit is not used\n count += dfs(index + 1, mask | (1 << digit), isLimit && digit === high, false);\n }\n }\n\n // Cache result for the current state if not constrained by limits\n if (!isLimit && !hasLeadingZeros) {\n dp[index][mask] = count;\n }\n\n return count;\n };\n\n // Total numbers with unique digits up to `n`\n return n - dfs(0, 0, true, true);\n}\n\n``` | 8 | 0 | ['TypeScript'] | 0 |
numbers-with-repeated-digits | ✅ [c++] || Digit DP with Bismasking || recursive+memoization | c-digit-dp-with-bismasking-recursivememo-k3hd | \nclass Solution {\npublic:\n \n int dp[11][2][1024][2]; //dp[pos][strictly][s][repeated]\n //s value can go upto 1024.\n //logic:- if we set all bi | xor09 | NORMAL | 2021-10-15T04:31:33.061290+00:00 | 2021-10-15T04:44:01.124940+00:00 | 1,222 | false | ```\nclass Solution {\npublic:\n \n int dp[11][2][1024][2]; //dp[pos][strictly][s][repeated]\n //s value can go upto 1024.\n //logic:- if we set all bit from (9...0) it gives approx. 1023 \n int solve(string& str, int pos, bool strictly, int s, bool repeated){\n if(pos==str.size()){\n if(repeated) return 1;\n else return 0;\n }\n if(dp[pos][strictly][s][repeated]!=-1) return dp[pos][strictly][s][repeated];\n int cur=0, n=str[pos]-\'0\';\n if(strictly){\n for(int i=0;i<=n;++i){\n if(i==0 and s==0) cur+=solve(str,pos+1,false,s,repeated); //leading zero\n else if(i==n){\n if(s&(1<<i)) cur+=solve(str,pos+1,true,s,true);\n else cur+=solve(str,pos+1,true,s^(1<<i),repeated);\n }else{\n if(s&(1<<i)) cur+=solve(str,pos+1,false,s,true);\n else cur+=solve(str,pos+1,false,s^(1<<i),repeated);\n }\n }\n }else{\n for(int i=0;i<=9;++i){\n if(i==0 and s==0) cur+=solve(str,pos+1,false,s,repeated); //leading zero\n else{\n if(s&(1<<i)) cur+=solve(str,pos+1,false,s,true);\n else cur+=solve(str,pos+1,false,s^(1<<i),repeated);\n }\n }\n }\n return dp[pos][strictly][s][repeated] = cur;\n }\n \n \n int numDupDigitsAtMostN(int n) {\n string str = to_string(n);\n memset(dp,-1,sizeof(dp));\n return solve(str,0,true,0,false);\n }\n};\n```\nPlease **UPVOTE** | 7 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'Bitmask', 'C++'] | 2 |
numbers-with-repeated-digits | C++ | Digit DP | Simplest Solution | Clean Code | c-digit-dp-simplest-solution-clean-code-2o99c | Intuition & Approach\nRather than finding numbers having repetitions, we can find: Total numbers - Numbers with all digits unique.\nMaintain a bitmask to make s | rosegold | NORMAL | 2023-08-20T18:23:21.024022+00:00 | 2023-08-20T18:25:23.642415+00:00 | 556 | false | # Intuition & Approach\nRather than finding numbers having repetitions, we can find: `Total numbers - Numbers with all digits unique`.\nMaintain a bitmask to make sure that we don\'t re-select a digit which has already been included.\n\n# Code\n```\nclass Solution {\npublic:\n int dp[11][2][1025]; // 1025 -> (1 << 10)\n int dfs(int i, int mask, bool tight, string &digits) {\n if(i == digits.size()) {\n return mask == 0 ? 0 : 1;\n }\n\n if(dp[i][tight][mask] != -1) return dp[i][tight][mask];\n\n int limit = 9, res = 0;\n if(tight) limit = (digits[i] - \'0\');\n\n for(int dig = 0; dig <= limit; dig++) {\n // mask = 0 -> No number has been formed yet &\n // dig = 0 -> We can\'t select first digit as 0 \n if(mask == 0 && dig == 0) {\n res += dfs(i + 1, mask, (tight & (limit == dig)), digits);\n continue;\n }\n // Check if the current digit has already been included\n int repeated = mask & (1 << dig);\n // If it hasn\'t, include it and furthur proceed\n if(repeated == 0) {\n res += dfs(i + 1, mask | (1 << dig), (tight & (limit == dig)), digits);\n }\n }\n\n return dp[i][tight][mask] = res;\n }\n int numDupDigitsAtMostN(int n) {\n memset(dp, -1, sizeof dp);\n string x = to_string(n);\n return n - dfs(0, 0, true, x);\n }\n};\n``` | 6 | 0 | ['Dynamic Programming', 'C++'] | 2 |
numbers-with-repeated-digits | Java O(1) 0ms beats all | java-o1-0ms-beats-all-by-limkinghei-0fz3 | This is to count the numbers with all distinct digits.\nWe can separate into two parts... say for N = 6,543,210,\n\nwe\'ll count the distinct one from 1 to 999, | limkinghei | NORMAL | 2019-03-17T22:01:36.172354+00:00 | 2019-03-17T22:01:36.172418+00:00 | 1,785 | false | This is to count the numbers with all distinct digits.\nWe can separate into two parts... say for N = 6,543,210,\n\nwe\'ll count the distinct one from 1 to 999,999, which would be \n\t1-9: 9\n\tplus 10-99: 9 * 9 \n\tplus 100-999: 9 * 9 * 8\n\tplus 1,000 - 9,999: 9 * 9 * 8 * 7\n\t...\n\t100,000 - 999,999: 9 * 9 * 8 * 7 * 6 * 5.\n\t\nThe above part can be done in one for loop with at most 9 iterations : O (1)\t\n\nThen we add the remaining distinct ones (from 1,000,000 to 6,543,210)\n\nFrom 1,000,000 to 5,999,999 : 5 * 9 * 8 * 7 * 6 * 5 * 4\nthen 6,000,000 to 6,499,999: 5 * 9 * 8 * 7 * 6 * 5\nthen 6,500,000 to 6,539,999 and so on... 4 * 9 * 8 * 7 * 6 ...\n\nThe above part takes at most 81 iterations which is also O(1)\n\n```\nclass Solution {\n public int numDupDigitsAtMostN(int N) {\n if (N<=10)\n return 0;\n int[] digits = new int[9];\n int cursor = 0;\n int v = N;\n while (v>0){\n digits[cursor++] = v%10;\n v= v/10;\n }\n //cursor is digit cnt\n return N - countDistinctUpToMsb1(cursor) - countDistinctFromMsb1(digits, cursor);\n }\n \n private int countDistinctUpToMsb1(int digitCnts){\n int total = 9;\n int last = 9;\n int remainingCnt = 9;\n for (int i=1;i<digitCnts-1;i++){\n last = last * remainingCnt;\n total += last;\n remainingCnt--;\n }\n return total;\n }\n \n private int countDistinctFromMsb1(int[] digits, int length){\n //eg 1000 - 2345\n boolean[] digitUsed = new boolean[10];\n int count = 0;\n for (int i=0;i<length;i++){\n int digit = digits[length-i-1];\n count += countDistinct(digitUsed, i, digit, i==0?false:true,length-i-1);\n if (digitUsed[digit])\n break;\n if (i==length-1)\n count++;\n digitUsed[digit] = true;\n }\n return count;\n }\n private int countDistinct(boolean[] digitUsed,int digitUsedCnt, int nextDigit, boolean nextFromZero, int tailingZeros){\n int cnt=0;\n for (int i=nextFromZero?0:1;i<nextDigit;i++){\n if (!digitUsed[i])\n cnt++;\n }\n digitUsedCnt++;\n for (int i=0;i<tailingZeros;i++){\n cnt *= (10 - digitUsedCnt++);\n }\n return cnt;\n }\n}\n``` | 6 | 0 | [] | 0 |
numbers-with-repeated-digits | Very Obvious , Intuitive and Easy 13D - DP :) | very-obvious-intuitive-and-easy-13d-dp-b-lqmq | \n# Code\n\nclass Solution {\npublic:\n string s;\n\n\n int dp[11][2][3][3][3][3][3][3][3][3][3][3][2];\n\n int rec(int index, bool tight, int one, int | sojabhai | NORMAL | 2024-07-01T20:55:16.479675+00:00 | 2024-07-01T20:55:16.479697+00:00 | 420 | false | \n# Code\n```\nclass Solution {\npublic:\n string s;\n\n\n int dp[11][2][3][3][3][3][3][3][3][3][3][3][2];\n\n int rec(int index, bool tight, int one, int two, int three, int four,\n int five, int six, int seven, int eight, int nine, int zero,\n bool lead) {\n\n if (index == s.size()) {\n return one == 2 || two == 2 || three == 2 || four == 2 ||\n five == 2 || six == 2 || seven == 2 || eight == 2 ||\n nine == 2 || zero == 2;\n }\n\n int& ans = dp[index][tight][one][two][three][four][five][six][seven]\n [eight][nine][zero][lead];\n if (ans != -1)\n return ans;\n\n int lb = 0;\n int ub = tight ? s[index] - \'0\' : 9;\n ans = 0;\n\n for (int i = lb; i <= ub; i++) {\n int n_one = one, n_two = two, n_three = three, n_four = four,\n n_five = five, n_six = six, n_seven = seven, n_eight = eight,\n n_nine = nine, n_zero = zero;\n\n if (i == 1)\n n_one++;\n else if (i == 2)\n n_two++;\n else if (i == 3)\n n_three++;\n else if (i == 4)\n n_four++;\n else if (i == 5)\n n_five++;\n else if (i == 6)\n n_six++;\n else if (i == 7)\n n_seven++;\n else if (i == 8)\n n_eight++;\n else if (i == 9)\n n_nine++;\n else if (i == 0 && lead)\n n_zero++;\n\n ans +=\n rec(index + 1, tight && (i == ub), min(n_one, 2), min(n_two, 2),\n min(n_three, 2), min(n_four, 2), min(n_five, 2),\n min(n_six, 2), min(n_seven, 2), min(n_eight, 2),\n min(n_nine, 2), min(n_zero, 2), lead || i > 0);\n }\n\n return ans;\n }\n\n int numDupDigitsAtMostN(int n) {\n for (int i0 = 0; i0 < 11; i0++)\n for (int i1 = 0; i1 < 2; i1++)\n for (int i2 = 0; i2 < 3; i2++)\n for (int i3 = 0; i3 < 3; i3++)\n for (int i4 = 0; i4 < 3; i4++)\n for (int i5 = 0; i5 < 3; i5++)\n for (int i6 = 0; i6 < 3; i6++)\n for (int i7 = 0; i7 < 3; i7++)\n for (int i8 = 0; i8 < 3; i8++)\n for (int i9 = 0; i9 < 3; i9++)\n for (int i10 = 0; i10 < 3;\n i10++)\n for (int i11 = 0; i11 < 3;\n i11++)\n for (int i12 = 0;\n i12 < 2; i12++)\n dp[i0][i1][i2][i3]\n [i4][i5][i6][i7]\n [i8][i9][i10][i11]\n [i12] = -1;\n\n s = to_string(n);\n return rec(0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0);\n }\n};\n``` | 5 | 1 | ['C++'] | 4 |
numbers-with-repeated-digits | C++ || Digit DP Solution || | c-digit-dp-solution-by-viraj7403-a2v5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\nlets build intuition from scratch. \nI will not direct jump into solution. \n(If you | viraj7403 | NORMAL | 2024-04-15T11:49:52.358007+00:00 | 2024-04-15T11:49:52.358037+00:00 | 386 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nlets build intuition from scratch. \nI will not direct jump into solution. \n**(If you don\'t have time to read whole article you can direct go to code).** \n\n\nSo , Let\'s start: \n\n```\nApproach - 1: \n```\n\nIterate from number 1 to n and then check that current number is valid or not ?\n\nThat is too basic right ?? and your n is 1e9 so that won\'t work here. \n\n```\nApproach - 2: \n```\n\nFrom above thing you have core concept like you have to build number and validate it without brutly gnerating whole number range. \n\n..... then what ?? \n\n**(Note : remember one thing . when you know what to do but stuck in complexity thing then just change the way you are iterating).** \n\n\nFirst of all , you are iterate whole number. \ncan you think any other way to build numbers ? \n\nwhat if we iterate on digits ?? \n\nlet say you know size of number string which is 5. \n\n_ , _ , _ , _ , _ . \n\nso for each index you can put digit from (0 to 9) and when you fill up all numbers then you validate is there any repeating digits or not, if yes then increase count. Right ?? \n\n*Yes , this is core logic. Now come to implementation part.* \n\n---\n\n\nThis kind of question you can solve easily with digit DP. \nI\'ll highly recommand to you to go through DIGIT DP thing and learn how to up "tight" , "index" and basic thing. \n\nNow , you can read further. \n\n`\nTask 1) `\n\nFor current index you decide your upper limit via tight varialble and all stuff (will not go into deep in this thing) , and now let say you have taken 3 for current index and have to check in previous index you have taken 3 or not, what is best way to do this ?\n\nYes , you can store bitmask of it and can check by set and unset bit either this digit have been taken or not.\n\nFrom here you know 3 states: \n```\n--> index. \n--> mask. \n--> tight. \n```\n\n\n`Task 2)` \n\nLet say n = 1000 , in digit DP you will take size of number string as length of maximum number and let say you want to generate lesser number then you can put 0 in front. \n\nWe have discussed that for each index we can choose digit from (0 to k) , where k is your upper bound based on tight variable. \n\nsee this case: 0010 , in this number we have taken 0 3 times , is that true ? \nNo. First 2 zeroes are just trailing zeroes and should not consider it into your mask. \n\nSo you have to keep one boolean variable , from left side when you take any noo-zero element then you mark it as 1 and now you have to take 0\'s in consideration. \n\n```\nYou got 4th state: \n--> taken. \n```\n`\nTask 3) `\n\nNow you have your number when you fill all the index, now how will you validate ? \n\nwill you store strings for number ?? No No that will be same as Approach - 1. \n\nNow when at current index from mask when you know that you have seen duplicate Digit , then mark one boolean variable as true to and pass it when you process for further index. \nSo that when you reach at out of bound index , means you have fill all digits. if that boolean variable 1 then you have to consider this otherwise not. \n\n```\nyou got 5th state: \n--> choose. \n```\n\n\n\n**You have 5 state which Generate 5-D DP.\nand then after i have taken standard template for digit DP.** \n\nNow you can go to code. \n\n```\nThanks to read upto here. \n\nDO UPVOTE TO MAKE ME HAPPY :))) \n```\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n[ 10*(1<<10)*(2)*(2)*(2) ] * 10 , here before 10 is our DP table and 10 is like 10 digits. \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nour DP table, 10*(1<<10)*(2)*(2)*(2)\n\n# Code\n```\nclass Solution {\npublic:\n\n long long dp[10][1<<10][2][2][2]; \n\n long long solve(string & s , int index , int mask , int tight , int taken , int choose){\n \n if(index == s.size()) return choose; \n if(dp[index][mask][tight][taken][choose] != -1) return dp[index][mask][tight][taken][choose]; \n\n char k = \'9\'; \n if(tight) k = s[index]; \n\n long long ans = 0; \n for(char c = \'0\' ; c <= k ; c++){\n int ele = c-\'0\'; \n if((1<<ele) & (mask)) \n ans += solve(s , index+1 , ( (mask) | (1<<ele)) , tight && (c == k) , 1 , 1); \n else {\n if((c > \'0\') || (c == \'0\' && taken)){\n ans += solve(s , index+1 , ( (mask) | (1<<ele)) , tight && (c == k) , 1 , choose); \n }\n else ans += solve(s , index+1 , (mask) , tight && (c == k) , 0 , choose);\n }\n }\n return dp[index][mask][tight][taken][choose] = ans;\n }\n int numDupDigitsAtMostN(int n) {\n\n memset(dp , -1 , sizeof(dp)); \n string s = ""; \n while(n){\n s += (n%10 + \'0\'); \n n /= 10;\n }\n reverse(s.begin() , s.end()); \n return solve(s , 0 , 0 , 1 , 0 , 0) ; \n }\n};\n``` | 5 | 0 | ['Math', 'String', 'Dynamic Programming', 'Backtracking', 'Bit Manipulation', 'Recursion', 'Memoization', 'Bitmask', 'C++'] | 0 |
numbers-with-repeated-digits | I spent 4 hours on this shit I hate my life | i-spent-4-hours-on-this-shit-i-hate-my-l-uoj2 | Intuition\n Describe your first thoughts on how to solve this problem. \nIts basically just math, Im gonna die \n# Approach\n Describe your approach to solving | FrostPanda | NORMAL | 2023-02-22T16:08:33.839645+00:00 | 2023-02-22T16:08:33.839677+00:00 | 756 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIts basically just math, Im gonna die \n# Approach\n<!-- Describe your approach to solving the problem. -->\nlet n be a K digit integer\nWe will count the total number of non-duplicated integers\nWe split them up in 2 cases by counting <K digits and K digits\n\nFor < K digits\nI did abit of trial and error for this but the general form that you would get would be for each k number of digits\n$$9\\bullet\\sum^{K-3}_{i=0}\\Pi^9_{j=9-i}j + 9$$\n\nSo how i visualised it was for e.g. we wamt let K = 5 so we want to find all possible non-duplicated integers <10 000 i.e. [1,9 999]\n\nFrom 1000 to 9999 we have 10000 - 1000 = 9000 integers \nwe fix the 1st digit so we have 1XXX then for the 2nd digit we have 9 remaining unique digits so on and so forth. Resulting in 9x8x7 integers\nNow we permutate the first digit to be between 1 to 9\nHence from 1000 - 9999 we have 9x9x8x7 non-duplicated integers\n\nSimilarly, from 100 - 999 we have 9x9x8\nfrom 10 - 99 we have 9x9\nfrom 1 - 9 we have 9\n\nNow if we take the sum we get \n9x9x8x7 9x9x8 + 9x9 + 9\n\n\nFor a fixed length of K digits\nWe store each leading digit in seen\nThen we build the integer up by iterating from 0 (if not first digit) and 1(if first digit) up to the leading digit. If any of the digit was seen before then we skip it. We then permutate the remaining digits left. If the leading digit was already seen we can stop as we know it will no longer give us any non-duplicated integers.\n\nE.g. if we let n = 13579\nWe will calculate this in parts as well specifically from \n1XXXX - 1XXXX\n10XXX - 12XXX\n130XX - 134XX\n1350X - 1356X\n1357X - 13578\n(remember last number not inclusive, pretty sure you can tweak the code to include)\n\nAt the start we have 10 000, since the leading digit is the first digit and is 1 we skip it. We then store 1 inside seen. Now we have fixed the first digit.\n\nFor the second digit, we start building from 0 to 2 so we have 10XXX, 11XXX and 12XXX but since 11XXX is already a duplicate we will skip it. Giving us 2x8x7x6 non-duplicated integers. Now we fix the second digit to be 3\n\nFor the third digit we will consider 130XX, 131XX, 132XX, 133XX, 134XX, w can see that 131XX and 133XX already contains duplicates and hence we will skip them. Giving us 3x7x6. Then we fix the third digit to be 5\n\nSo on and so forth, resulting in a total of 2x8x7x6 + 3x7x6 + 4x6 + 5\n\nNow we take the sum \n9x9x8x7 9x9x8 + 9x9 + 9 + \n2x8x7x6 + 3x7x6 + 4x6 + 5 + 1 (to include n=13579) = 6102\nWe return 13579 - 6102 = 7477 which is the ans\n \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nI believe it is $$O(log_{10}n)$$ as we are counting the number of digits\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nI think it is $$O(log_{10}n)$$ as well? as we only store the number of digits in both seen and numList\n# Code\n```\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n temp = n\n numList = []\n while temp > 0:\n numList.insert(0, temp%10)\n temp //=10\n digits = len(numList)\n totalNum = 0\n res = 0\n # less than K digits\n for j in range(digits-1, 0, -1):\n res = 9\n for k in range(9, 9-j+1,-1):\n res *= k\n totalNum += res\n #K digits\n seen = {}\n for i in range(0,digits):\n leadingDigit = numList[i]\n remainingDigits = len(numList) - i - 1\n for j in range(1 if i==0 else 0, leadingDigit):\n if j in seen:\n continue\n res = 1\n for k in range(9-i, 9-i-remainingDigits,-1):\n res *= k\n totalNum += res\n if leadingDigit in seen:\n break\n seen[leadingDigit] = 1\n seen = {}\n for num in numList:\n if num in seen:\n return n-totalNum\n seen[num] = 1\n return n-totalNum - 1\n``` | 5 | 0 | ['Python3'] | 1 |
numbers-with-repeated-digits | C++ | DIGIT-DP | BIT-MASKING | c-digit-dp-bit-masking-by-chikzz-ymh4 | PLEASE UPVOTE IF U FIND MY SOLUTION HELPFUL :)\n\n\nclass Solution\n{\n int dp[1<<10][10][2][2];\n int helper(string &s,int i,int mask,int lz,int bound)\n | chikzz | NORMAL | 2022-06-27T15:04:18.579035+00:00 | 2022-06-27T15:04:18.579078+00:00 | 837 | false | **PLEASE UPVOTE IF U FIND MY SOLUTION HELPFUL :)**\n\n```\nclass Solution\n{\n int dp[1<<10][10][2][2];\n int helper(string &s,int i,int mask,int lz,int bound)\n {\n if(i==s.length())return 1;\n \n if(dp[mask][i][lz][bound]!=-1)\n return dp[mask][i][lz][bound];\n \n int maxx=bound?s[i]-\'0\':9;\n \n int tot=0;\n \n for(int j=0;j<=maxx;j++)\n {\n if((mask&(1<<j))&&lz==0)continue;\n mask|=(1<<j);\n tot+=helper(s,i+1,mask,lz&(j==0),bound&(j==maxx));\n mask^=(1<<j);\n }\n \n return dp[mask][i][lz][bound]=tot;\n }\n public:\n int numDupDigitsAtMostN(int n)\n {\n string s=to_string(n);\n memset(dp,-1,sizeof(dp));\n int mask=0;\n int res=(n+1)-helper(s,0,mask,1,1);\n return res;\n }\n};\n``` | 5 | 0 | ['Bitmask'] | 4 |
numbers-with-repeated-digits | C# Study code from ranking No. 1 in weekly contest 128 | c-study-code-from-ranking-no-1-in-weekly-34k3 | March 21, 2019\nIt is one of weekly contest 128 algorithms. What I like to do is to learn ranking No. 1\'s code, and then I add some comment to explain the idea | jianminchen | NORMAL | 2019-03-21T18:26:25.160119+00:00 | 2019-10-10T04:31:02.004789+00:00 | 901 | false | March 21, 2019\nIt is one of weekly contest 128 algorithms. What I like to do is to learn ranking No. 1\'s code, and then I add some comment to explain the idea to make it easy to follow. The player finished the algorithm using 7 minutes 5 seconds. \n\n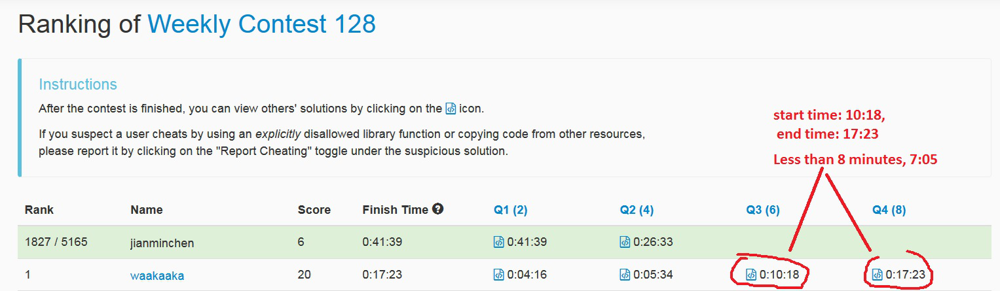\n\n\nHere are a few tips:\n1. using one binary number to store all unique digits in the number; mapping is described in the comment\n2. using & operator to avoid any duplicated digit\n3. using or to include current digit into the binary number\n\n**More detail**\nEvery number from 0 to 9 can be represented using one bit in a binary number. So all digits in any integer number can be recorded using one binary number including 10 bits at most. \n\n0 is expressed in 0, in binary format, 1 << 0\n1 is expressed in 10, in binary format, 1 << 1\n2 is expressed in 100\n3 is expressed in 1000\n4 is expressed in 10000\n5 is expressed in 100000\n6 is expressed in 1000000\n7 is expressed in 10000000\n8 is expressed in 100000000\n9 is expressed in 1000000000, in binary format, 1 << 9\n\n**How to determine current digit is not duplicated**\n\nUsing one binary number to express all unique digits in the number, and then using **and &** operator to check uniqueness, and **or | operator** to include current digits. \n\nLet us work on one example in the following. \nChoose a number with unique digits, for example, 123 or 321 or 213. All digits in the number can be expressed using one binary number 1110, so next digit should avoid duplication of those three digits. \n\nIf current digit is 4, the exiting digits include {1, 2, 3}, then 1110 & (1 << 4) = 1110 & 10000 = 0, \nsince there is no duplication of digits. However, any digit from {1, 2, 3}, its binary format number & 1110 > 0.\n\nIt is the excellent practice to warm up bit manipulation and learn how to write a solution in less than 10 minutes. Othewise, it is better to use standard depth first search, and use an array instead of a binary number to mark the digit used. I also posted the solution on that: https://leetcode.com/problems/numbers-with-repeated-digits/discuss/259737/C-standard-depth-first-search-with-back-tracking\n\nHere is my C# code based on code study. \n\t\t\t\t\n```\nusing System;\nusing System.Collections.Generic;\nusing System.Linq;\nusing System.Text;\nusing System.Threading.Tasks;\n\nnamespace _1015_number_with_repeated_digits_1\n{\n class Program\n {\n static void Main(string[] args)\n {\n var result = NumDupDigitsAtMostN(20);\n }\n\n public static int n;\n public static int uniqueDigitis;\n\n /// <summary>\n /// study code on weekly contest 128 rank No. 1 waakaaka\n /// https://leetcode.com/contest/weekly-contest-128/ranking\n /// </summary>\n /// <param name="N"></param>\n /// <returns></returns>\n public static int NumDupDigitsAtMostN(int N)\n {\n uniqueDigitis = 0;\n n = N;\n runDepthFirstSearchLeftToRight(0,0);\n return N + 1 - uniqueDigitis; \n }\n\n /// <summary>\n /// code review March 21, 2019\n /// Here are a few tips:\n /// 1. using one binary number to store all unique digits in the number; mapping is described in the comment\n /// 2. using & operator to avoid any duplicated digit\n /// 3. using or to include current digit into the binary number\n /// </summary>\n /// <param name="value"></param>\n /// <param name="binaryShift"></param>\n private static void runDepthFirstSearchLeftToRight(long value, int binaryShift)\n {\n if (value <= n)\n {\n uniqueDigitis++;\n }\n\n if (value * 10 > n)\n {\n return;\n }\n\n for (int digit = 0; digit <= 9; digit++)\n {\n // no 0 for first digit\n if (binaryShift == 0 && digit == 0)\n {\n continue;\n }\n\n // every number from 0 to 9 is represented using binary number\n // 0 is expressed in 0\n // 1 is expressed in 10\n // 2 is expressed in 100\n // 3 is expressed in 1000\n // 4 is expressed in 10000\n // 5 is expressed in 100000\n // 6 is expressed in 1000000\n // 7 is expressed in 10000000\n // 8 is expressed in 100000000\n // 9 is expressed in 1000000000\n var currentDigitExpression = 1 << digit; \n \n // number with unique digits, for example, 123 or 321 or 213. \n // all digits in the number can be expressed using one binary number 1110\n // so next digit should avoid duplication of those three digits\n // if current digit is 4, the exiting digits include {1, 2, 3}, then 1110 & (1 << 4) = 1110 & 10000 = 0, \n // since there is no duplication of digits \n // any digit from {1, 2, 3} & 1110 > 0 \n if ((binaryShift & currentDigitExpression) > 0)\n {\n continue; \n }\n\n // using | to include current digit\n var nextBinary = binaryShift | currentDigitExpression;\n runDepthFirstSearchLeftToRight(value * 10 + digit, nextBinary); \n }\n }\n }\n}\n``` | 5 | 0 | [] | 2 |
numbers-with-repeated-digits | [Python3] Digit DP + BIT Mask - Simple + Detail Explanation - Easy To Understand | python3-digit-dp-bit-mask-simple-detail-nuc2r | Intuition\nFind total of numbers in range with specific condition => digit DP\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. In | dolong2110 | NORMAL | 2024-01-13T14:35:51.968473+00:00 | 2024-01-13T14:35:51.968557+00:00 | 405 | false | # Intuition\nFind total of numbers in range with specific condition => digit DP\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialization\n- The input number `n` is converted to a list of digits (`digits`).\n2. Dynamic Programming Function\n- The function `dp` is a recursive dynamic programming function that calculates the count of numbers with repeated digits.\n- Parameters:\n - `pos`: The current position (digit position).\n - `mask`: A bitmask representing the used digits.\n - `is_smaller`: A boolean indicating whether the current number is smaller than `n`.\n- Base Case:\n - If `pos` reaches the length of `digits`, return 1, indicating a valid number with repeated digits.\n- Recursive Case:\n - Iterate over the possible digits (`d`) from 0 to the upper limit based on `is_smaller`.\n - Check if the digit `d` is already used (`mask & (1 << d)`). If used, skip to the next digit.\n - Update `new_is_smaller` based on whether the current digit is smaller than the upper limit.\n - Update `new_mask` to include the current digit (`d`) in the bitmask.\n - Recursively call `dp` for the next position (`pos + 1`) with the updated parameters.\n - Accumulate the total count of valid numbers.\n3. Main Fuanction\n\n- Call the `dp` function with initial parameters (`pos=0, mask=0, is_smaller=True`).\n- Subtract 1 from the result to exclude the number `0`.\n- Return the result as the count of numbers with repeated digits up to `n`.\n\n4. Note\nThe solution employs dynamic programming to count the numbers with repeated digits by recursively considering each digit\'s possibilities. The cache decorator is used for memoization, which helps avoid redundant calculations and improves the efficiency of the solution. Finally, the main function returns the total count of such numbers in the given range.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n digits = list(map(int, str(n)))\n \n @cache\n def dp(pos: int, mask: int, is_smaller: bool = True) -> int:\n if pos == len(digits): return 1\n\n total = 0\n upper_limit = digits[pos] if is_smaller else 9\n for d in range(upper_limit + 1):\n if mask & (1 << d): continue\n new_is_smaller = is_smaller and d == upper_limit\n new_mask = mask if mask == 0 and d == 0 else mask | (1 << d)\n total += dp(pos + 1, new_mask, new_is_smaller)\n\n return total\n\n return n - (dp(0, 0) - 1)\n``` | 4 | 0 | ['Dynamic Programming', 'Bitmask', 'Python3'] | 0 |
numbers-with-repeated-digits | [C++] Let Backtracking do it's work , clean and crisp code | c-let-backtracking-do-its-work-clean-and-0z1y | \nclass Solution {\npublic:\n int dfs(long curr, int mask, int n) {\n if(curr > n) return 0;\n int ans=1; //since n < 123456789 and all its per | P3rf3ct0 | NORMAL | 2022-08-15T11:00:56.633229+00:00 | 2022-08-15T11:03:36.433876+00:00 | 450 | false | ```\nclass Solution {\npublic:\n int dfs(long curr, int mask, int n) {\n if(curr > n) return 0;\n int ans=1; //since n < 123456789 and all its permutations therefore 1 number always exists\n for(int i=0; i<10; i++) {\n if(!mask and !i) continue; //leading 0 not allowed\n if(mask & (1<<i)) continue; //repetition not allowed\n ans+=dfs(curr*10+i,mask+(1<<i),n);\n }\n return ans;\n }\n \n int numDupDigitsAtMostN(int n) {\n return n+1-dfs(0,0,n);\n }\n};\n``` | 4 | 0 | ['Backtracking', 'Depth-First Search', 'C', 'Bitmask', 'C++'] | 0 |
numbers-with-repeated-digits | Digit DP | digit-dp-by-ayushman_123-v0ku | I didn\'t get any soln in discuss that contains digit dp in python so I did this In this soln, to see whether any digit repeated or not, i take a memo , i guess | Ayushman_123 | NORMAL | 2022-07-02T08:15:55.697843+00:00 | 2024-06-23T12:47:58.827279+00:00 | 1,012 | false | I didn\'t get any soln in discuss that contains digit dp in python so I did this In this soln, to see whether any digit repeated or not, i take a memo , i guess you have used it before if not then see following problem it just contain 1 for integer if it\'s already taken otherwise 0 and put it in binary form . Ya it\'s 5 order dp so don\'t be confused i just used it for memoization. if you don\'t know more about digit dp, I will highly recommend you to see kartik arora\'s digit dp video on youtube.\n\n```\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n dp=[[[[[-1 for tight in range(2)] for i in range(2)] for i in range(2)] for i in range(2**10)] for i in range(10)]\n len1 = len(str(n))\n def fun(i,check,tight,memo,leading_zero):\n if i==len1:\n if check==1:\n return 1\n return 0\n end = 9\n if dp[i][memo][check][leading_zero][tight]!=-1:\n return dp[i][memo][check][leading_zero][tight]\n if tight==1:\n end = int(str(n)[i])\n res = 0\n for j in range(end+1):\n if j==0 and leading_zero==1:\n res+=fun(i+1,0,tight&(j==end),memo,1)\n continue\n if check==1:\n res+=fun(i+1,1,tight&(j==end),memo|(1<<j),0)\n continue\n if memo&(1<<j):\n res+=fun(i+1,1,tight&(j==end),memo,0)\n else:\n res+=fun(i+1,0,tight&(j==end),memo|(1<<j),0)\n dp[i][memo][check][leading_zero][tight] = res\n return res\n return fun(0,0,1,0,1) | 4 | 0 | ['Python'] | 0 |
numbers-with-repeated-digits | C++ digit dp with backtracking | c-digit-dp-with-backtracking-by-sai_pras-5qst | \nclass Solution {\npublic:\n \n int anotherdp[15][2];\n \n int total(string x,int n,bool tight,set<int> &s){\n if(n==0){\n return | sai_prasad_07 | NORMAL | 2021-01-21T06:58:00.571786+00:00 | 2021-01-21T06:58:00.571819+00:00 | 643 | false | ```\nclass Solution {\npublic:\n \n int anotherdp[15][2];\n \n int total(string x,int n,bool tight,set<int> &s){\n if(n==0){\n return 1;\n }\n if(anotherdp[n][tight]!=-1){\n return anotherdp[n][tight];\n }\n int ub = (tight==1) ? x[x.length()-n]-\'0\' : 9;\n int res=0;\n for(int i=0;i<=ub;i++){\n if(s.empty() && i==0) continue;\n else if(s.find(i)==s.end()){\n s.insert(i);\n res+=total(x,n-1,(tight & (i==ub)),s);\n s.erase(s.find(i));\n }\n }\n return (anotherdp[n][tight]=res);\n }\n \n int numDupDigitsAtMostN(int N) {\n if(N<=10){\n return 0;\n }\n int n = log10(N);\n int dp[n+1];\n memset(dp,0,sizeof(dp));\n dp[1] = 9;\n int x=9;\n int y=9;\n for(int i=2;i<=n;i++){\n x*=y;\n y--;\n dp[i] = x;\n dp[i]+=dp[i-1];\n }\n set<int> s;\n s.clear(); \n string xx = to_string(N);\n memset(anotherdp,-1,sizeof(anotherdp));\n int temp = total(xx,xx.length(),1,s);\n return N-(dp[n]+temp);\n }\n};\n``` | 4 | 0 | [] | 0 |
numbers-with-repeated-digits | C++ Solution || Digit DP || Clean and Concise || Bitmask | c-solution-digit-dp-clean-and-concise-bi-6jbh | Code\n\nclass Solution {\npublic:\n\n int dp[10][2][1025][2]; //2^10 = 1024 for bitmask\n\n int count(int idx,bool tight,int bitmask,bool isrepeated,strin | Harsh_0903 | NORMAL | 2023-06-05T09:28:59.456414+00:00 | 2023-06-05T09:28:59.456455+00:00 | 637 | false | # Code\n```\nclass Solution {\npublic:\n\n int dp[10][2][1025][2]; //2^10 = 1024 for bitmask\n\n int count(int idx,bool tight,int bitmask,bool isrepeated,string& num){\n if(idx==num.size()){\n return (isrepeated&&bitmask)?1:0;\n }\n if(dp[idx][tight][bitmask][isrepeated]!=-1) return dp[idx][tight][bitmask][isrepeated];\n int lo = 0;\n int hi = tight?(num[idx]-\'0\'):9;\n int cnt = 0;\n if(!bitmask){\n cnt += count(idx+1,false,bitmask,isrepeated,num);\n }\n for(int i = lo;i<=hi;i++){\n if(!bitmask && i==0) continue;\n int repeated = bitmask & (1<<i);\n if(repeated){\n cnt += count(idx+1,tight&&(i==hi),bitmask,true,num);\n }\n else{\n cnt += count(idx+1,tight&&(i==hi),bitmask|(1<<i),isrepeated,num);\n }\n }\n return dp[idx][tight][bitmask][isrepeated] = cnt;\n }\n\n int numDupDigitsAtMostN(int n) {\n memset(dp,-1,sizeof(dp));\n string num = to_string(n);\n return count(0,true,0,false,num);\n }\n};\n``` | 3 | 1 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Bitmask', 'C++'] | 0 |
numbers-with-repeated-digits | [C++] Permutation with explaination | c-permutation-with-explaination-by-kamin-l34e | \nclass Solution {\npublic:\n int permutation(int m, int n) {\n // m number with len n\n // m * (m - 1) * (m - 2) .. * (m - n + 1) \n in | kaminyou | NORMAL | 2022-05-06T15:58:34.101755+00:00 | 2022-05-06T15:58:34.101810+00:00 | 565 | false | ```\nclass Solution {\npublic:\n int permutation(int m, int n) {\n // m number with len n\n // m * (m - 1) * (m - 2) .. * (m - n + 1) \n int res = 1;\n while (n) {\n res *= m;\n m--;\n n--;\n }\n return res;\n }\n int numDupDigitsAtMostN(int n) {\n vector<int> digits; // to store each digit\n for (int x = n + 1; x > 0; x /= 10) {\n digits.push_back(x % 10);\n }\n // make it from high to low\n // e.g., n=137 => [7, 1, 3] => [1, 3, 7]\n reverse(digits.begin(), digits.end());\n \n // get the # of digits\n int size = digits.size();\n \n // to count the number without duplicates\n int res = 0;\n \n // one digit to (size - 1) digits\n // e.g, n=8759 (4 digits), ignore leading 8 here\n // so the last 3 digits have 9 * (9 * 8) permutations\n // the last 2 digits have 9 * (9) permutations\n // the last 1 digits have 9 permutations\n for (int i = 1; i < size; i++) {\n res += 9 * permutation(9, i - 1);\n }\n \n // consider the leading digit\n unordered_set<int> st; // to store the leading fixed one\n // for each digit\n for (int i = 0; i < size; i++) {\n // i = 0 (first digit) e.g., n=8759 | the free will be\n // 1xxx, 2xxx, ..., 7xxx\n // i > 0 e.g., n=8759 | the free will be\n // 80xx, 81xx, ...86xx\n for (int j = i > 0 ? 0 : 1; j < digits[i];j++) {\n // the current digit should not duplicated with the fixed one\n if (st.find(j) != st.end()) continue;\n res += permutation(9 - i, size - i - 1);\n }\n // if the current leading digit duplicate with previous ones => break\n if (st.find(digits[i]) != st.end()) break;\n // insert the current leading digit to the hash table\n st.insert(digits[i]);\n }\n return n - res;\n }\n};\n``` | 3 | 0 | ['C'] | 1 |
numbers-with-repeated-digits | [Python] Well commented solution with easy to follow recursion | python-well-commented-solution-with-easy-qzif | \nclass Solution(object):\n def numDupDigitsAtMostN(self, N):\n """\n :type N: int\n :rtype: int\n """\n memo = {}\n | algomelon | NORMAL | 2020-04-23T03:09:09.882541+00:00 | 2020-04-23T03:13:35.345699+00:00 | 842 | false | ```\nclass Solution(object):\n def numDupDigitsAtMostN(self, N):\n """\n :type N: int\n :rtype: int\n """\n memo = {}\n def f(digits_of_N, i, digits_used, any_digit):\n if i == k:\n return 1\n \n key = (i, digits_used, any_digit)\n if key in memo:\n return memo[key]\n \n # For each digit position, we iterate through all possible choices\n cnt = 0\n # If it\'s the leading digit, at position 0, we cannot pick 0 as a choice\n min_digit = 1 if i == 0 else 0\n # We can pick up to and including the digit at the i-th position of N so\n # the number stays <= N. However if we\'ve picked some previous digit less\n # than that in N at the same position, then we can pick any digit we want.\n # Why? Because if the more significant digit has a smaller number, it doesn\'t\n # matter what number we pick for less sigificant digit positions.\n max_digit = 9 if any_digit else digits_of_N[i]\n for d in range(min_digit, max_digit + 1):\n # Use a bitmask to record if we\'ve already used a digit. Since we only want\n # integers with unique digits, once a digit is used, it cannot be picked again.\n if digits_used & (1 << d) != 0:\n continue\n # If we picked some digit less than the i-th digit of N, then for the\n # digit positions after i we can pick whatever we want, as long as\n # the digit picked is unique, and it will be less than N. \n cnt += f(digits_of_N, i + 1, digits_used | (1 << d), any_digit or (d < digits_of_N[i]))\n \n memo[key] = cnt\n return cnt\n \n # Life is easier without having to deal with the single-digit case.\n # It\'s only interesting when we have at least 2 digits.\n if N <= 9:\n return 0\n \n # Let k be the number of digits in N\n k = len(str(N))\n # We break the set of positive integers <= N with at least one duplicate digit into \n # two disjoint sets A and B, where:\n # - A is the set of positive integers with k - 1 or less number of digits, with at least 1\n\t\t# duplicate digit\n # - B is the set of positive integers <= N with exactly k number of digits, with at least 1\n\t\t# duplicate digit\n \n # Let\'s first count the size A.\n # Given i in [1.. k - 1], the set of positive integers with i digits and at least 1 duplicate digit\n\t\t# must be:\n # The set of positive integers with i digits - positive integers with only unique digits.\n # Well positive integers with i digits is just 9 * 10^(i - 1) -- we have {1, 2 .. 9} as \n # possible choices for the leading digit and then {0..9} as possible choices for each of the \n # remaining digits. \n # And positive integers with i digits and only unique digits must be:\n # 9 * 9 * 8 * 7 ... up to i terms\n # We have {1..9} as possible choices for the leading digit and then 10 - 1 possible choices\n # for the second digit -- whatever leading digit we picked we cannot select that again.\n # And having made a choice for the second digit, we\'d then only have 8 possible choices \n # for the 3rd digit and so on, until we have only 1 possible digit choice left.\n cnt = 0\n for i in range(1, k):\n all_possible_ints = 9 * 10**(i-1)\n ints_with_unique_digits = 9\n nb_choices = 9\n for j in range(1, i):\n ints_with_unique_digits *= nb_choices\n nb_choices -= 1\n cnt += all_possible_ints - ints_with_unique_digits\n \n # Let\'s then count the size of B. Again it\'s similar to A.\n # For positive integers with exactly k digits <= N. e.g. if N = 12483, then \n # we have 12483 - 9999 possible integers with 5 digits. (9999 or below are all\n # numbers with less than 5 digits)\n all_ints_with_k_digits = N - int(\'9\'*(k-1))\n # To count the number of positive integers <= N with exactly k unique digits,\n # we\'ll need a bit of recursion. See comments in f()\n digits_of_N = [int(d) for d in str(N)]\n ints_with_unique_k_digits = f(digits_of_N, 0, 0, False)\n cnt += all_ints_with_k_digits - ints_with_unique_k_digits\n \n return cnt\n``` | 3 | 0 | [] | 0 |
numbers-with-repeated-digits | Python Digit DP (Pattern For Similar Questions) | python-digit-dp-pattern-for-similar-ques-uua7 | Theory: https://codeforces.com/blog/entry/53960\n\nMore of the same approach:\n902. Numbers At Most N Given Digit Set\n788. Rotated Digits\n1397. Find All Good | migfulcrum | NORMAL | 2020-04-02T11:12:50.697802+00:00 | 2020-04-17T21:36:27.947204+00:00 | 1,957 | false | Theory: https://codeforces.com/blog/entry/53960\n\nMore of the same approach:\n[902. Numbers At Most N Given Digit Set](https://leetcode.com/problems/numbers-at-most-n-given-digit-set/discuss/559624/python-digit-dp)\n[788. Rotated Digits](https://leetcode.com/problems/rotated-digits/discuss/560601/python-digit-dp)\n[1397. Find All Good Strings](https://leetcode.com/problems/find-all-good-strings/discuss/560841/Python-Digit-DP)\n[233. Number of Digit One](https://leetcode.com/problems/number-of-digit-one/discuss/560876/Python-Digit-DP)\n[357. Count Numbers with Unique Digits](https://leetcode.com/problems/count-numbers-with-unique-digits/discuss/560898/Python-Digit-DP)\n[600. Non-negative Integers without Consecutive Ones](https://leetcode.com/problems/non-negative-integers-without-consecutive-ones/discuss/584350/Python-Digit-DP-(Pattern-For-Similar-Questions))\n\nAt each recursive call (adding digit to less significant position) compute:\n- isPrefix - if the new number is the prefix of N\n- isBigger - if the new number will be bigger than N when we reach final position\n- digits - current digits of the new number\n- repeated - if there is already a repeated digit\nOptimization - if there is already a repeated number and the current number cannot be bigger than N when we reach the last position we can add 10 (for 10 digits) to the result and every subresult gets multiplied by 10.\n```\n def numDupDigitsAtMostN(self, N: int) -> int:\n N = list(map(int, str(N)))\n\n @functools.lru_cache(None)\n def dp(pos, isPrefix, isBigger, digits, repeated):\n if pos == len(N):\n return 0\n if repeated and not isPrefix and not isBigger:\n return 10 + 10 * dp(pos + 1, False, False, digits, True)\n result = 0\n for i in range(0 if pos > 0 else 1, 10):\n _isPrefix = isPrefix and i == N[pos]\n _isBigger = isBigger or (isPrefix and i > N[pos])\n _repeated = repeated\n if (digits >> i) & 1 == 1:\n _repeated = True\n if _repeated and not (pos == len(N) - 1 and _isBigger):\n result += 1\n _digits = digits | (1 << i)\n result += dp(pos + 1, _isPrefix, _isBigger, _digits, _repeated)\n return result\n return dp(0, True, False, 0, False)\n\t``` | 3 | 0 | [] | 0 |
numbers-with-repeated-digits | Correct Solution but Exceeded Time Limit | correct-solution-but-exceeded-time-limit-tjrp | This solution will give correct answer but will exceed time limit:\n```\nclass Solution:\n def numDupDigitsAtMostN(self, N: int) -> int:\n countRepeat | andrewlang | NORMAL | 2019-12-24T01:34:36.254772+00:00 | 2019-12-24T01:34:36.254824+00:00 | 744 | false | This solution will give correct answer but will exceed time limit:\n```\nclass Solution:\n def numDupDigitsAtMostN(self, N: int) -> int:\n countRepeat = 0\n for x in range(1, N+1):\n intList = [char for char in str(x)]\n if len(str(x)) != len(list(set(intList))):\n countRepeat += 1\n return countRepeat | 3 | 0 | ['Python', 'Python3'] | 1 |
numbers-with-repeated-digits | Solution in Python 3 (beats ~99%) | solution-in-python-3-beats-99-by-junaidm-x7ef | ```\nclass Solution:\n def numDupDigitsAtMostN(self, N: int) -> int:\n \tT = [9,261,4725,67509,831429,9287109,97654149,994388229]\n \tt = [99,999,9999, | junaidmansuri | NORMAL | 2019-07-11T10:26:09.874910+00:00 | 2019-07-11T10:36:10.138106+00:00 | 1,588 | false | ```\nclass Solution:\n def numDupDigitsAtMostN(self, N: int) -> int:\n \tT = [9,261,4725,67509,831429,9287109,97654149,994388229]\n \tt = [99,999,9999,99999,999999,9999999,99999999,999999999]\n \tif N < 10:\n \t\treturn 0\n \tL = len(str(N))\n \tm, n = [1], []\n \tg = 11-L\n \tfor i in range(L):\n \t\tn.append(int(str(N)[i]))\n \t\tm.append(g)\n \t\tg = g*(12-L+i)\n \tS = 0\n \tfor i in range(L):\n \t\tif len(set(n[:L-i-1])) != len(n)-i-1:\n \t\t\tcontinue\n \t\tk = 0\n \t\tfor j in range(10):\n \t\t\tif j not in n[:L-i-1] and j > n[L-i-1]:\n \t\t\t\tk += 1\n \t\tS += k*m[i]\n \treturn(T[L-2]-(t[L-2]-N-S))\n\t\n- Python 3\n- Junaid Mansuri | 3 | 1 | ['Python', 'Python3'] | 1 |
numbers-with-repeated-digits | C++/Python, digit dp solution with explanation | cpython-digit-dp-solution-with-explanati-ahfo | find how many number without repeated digits\nfill a number digit by digit.\ni means we are filling i-th digit.\nmask is number we used in the number, it is a b | shun6096tw | NORMAL | 2023-08-21T10:19:50.047881+00:00 | 2023-08-21T10:19:50.047900+00:00 | 135 | false | ### find how many number without repeated digits\nfill a number digit by digit.\ni means we are filling i-th digit.\nmask is number we used in the number, it is a bitmask, means which number we have used in [0,9].\nis_limit means the current number is on the upper bound, e.g., n = 234, and digit is 23, we are filling last number -> 23[4].\nhas_leading0s means digits are all 0s, e.g., 000, and we can fill a valid digit or skip it (fill a 0).\n\nfor i-th digit,\nif has_leading0s is true, we can skip i-th digit, keep has_leading0s\nor fill a digit in [1,9],\nif has_leading0s is true, digit can not be 0\nif is_limit is true, digit is at most int(s[i]).\n\neumerate digit from low to high,\nif this digit is not repeated, we can fill next digit.\n\n\n### python\n```python\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n s = str(n)\n @cache\n def dfs(i, mask, is_limit, has_leading0s):\n if i == len(s): return int(not has_leading0s)\n sub = 0\n if has_leading0s:\n sub = dfs(i+1, mask, False, True)\n low = 1 if has_leading0s else 0\n high = int(s[i]) if is_limit else 9\n for d in range(low, high+1):\n if mask >> d & 1 == 0:\n sub += dfs(i+1, mask | (1 << d), is_limit and d == high, False)\n return sub\n \n return n - dfs(0, 0, True, True)\n```\n\n### c++\n```cpp\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int n) {\n string s = to_string(n);\n vector<vector<int>> dp (s.size(), vector<int>(1<<10, -1));\n function<int(int, int, bool, bool)> dfs = [&] (int i, int mask, bool is_limit, bool leading0s) {\n if (i == s.size()) return (int)!leading0s;\n if (!is_limit && !leading0s && dp[i][mask] != -1) return dp[i][mask];\n int sub = 0;\n if (leading0s) sub = dfs(i+1, mask, false, true);\n int low = leading0s? 1:0, high = is_limit? s[i]-\'0\': 9;\n for (int d = low; d <= high; d+=1) {\n if ((mask >> d & 1) == 0) {\n sub += dfs(i+1, mask | (1<<d), is_limit && d == high, false);\n }\n }\n if (!is_limit && !leading0s) dp[i][mask] = sub;\n return sub;\n };\n return n - dfs(0, 0, true, true);\n }\n};\n```\n\n### find how many number at least one repeated digit\n\nfill a number digit by digit.\n\nhas_repeated means digits we filled has at least one repeated digit.\n\n\n\n### python\n```python\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n s = str(n)\n @cache\n def dfs(i, mask, is_limit, leading0s, has_repeated):\n if i == len(s): return int(has_repeated)\n sub = 0\n if leading0s: sub = dfs(i+1, mask, False, True, False)\n low = 1 if leading0s else 0\n high = int(s[i]) if is_limit else 9\n for d in range(low, high+1):\n sub += dfs(i+1, mask | (1 << d), is_limit and d == high, False, has_repeated or mask >> d & 1 == 1)\n return sub\n return dfs(0, 0, True, True, False)\n```\n\n### c++\n```cpp\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int n) {\n string s = to_string(n);\n vector<vector<vector<int>>> dp (s.size(), vector<vector<int>>(1<<10, vector<int>(2, -1)));\n function<int(int, int, bool, bool, bool)> dfs = [&] (int i, int mask, bool is_limit, bool leading0s, bool has_repeated) {\n if (i == s.size()) return (int) has_repeated;\n if (!is_limit && !leading0s && dp[i][mask][(int) has_repeated] != -1) return dp[i][mask][(int) has_repeated];\n int sub = 0;\n if (leading0s) sub = dfs(i+1, mask, false, true, false);\n int low = leading0s? 1:0, high = is_limit? s[i] - \'0\': 9;\n for (int d = low; d <= high; d+=1)\n sub += dfs(i+1, mask | (1 << d), is_limit && d == high, false, has_repeated || mask >> d & 1);\n if (!is_limit && !leading0s) dp[i][mask][(int) has_repeated] = sub;\n return sub;\n };\n return dfs(0, 0, true, true, false);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'C', 'Python'] | 0 |
numbers-with-repeated-digits | Easy Bitmask DP Solution | easy-bitmask-dp-solution-by-abhi-1301-b2nh | \n\n# Code\n\nint dp[10][1<<10][2][10];//index digit_set flag length\n\nstring s;\n\nint solve(int ind,int mask,bool f,int len)\n{\n if(ind>=len)\n re | Abhi-1301 | NORMAL | 2023-02-17T10:01:37.172272+00:00 | 2023-02-17T10:08:16.134538+00:00 | 1,495 | false | \n\n# Code\n```\nint dp[10][1<<10][2][10];//index digit_set flag length\n\nstring s;\n\nint solve(int ind,int mask,bool f,int len)\n{\n if(ind>=len)\n return 1;\n \n auto &p=dp[ind][mask][f][len];\n\n if(p!=-1)\n return p;\n \n p=0;\n\n int maxi=9;\n\n if(f&&len==s.size())\n maxi=s[ind]-\'0\';\n \n for(int i=0;i<=maxi;++i)\n {\n if((mask&(1<<i)))\n continue;\n if(f)\n {\n bool c=(i==maxi);\n p+=solve(ind+1,mask^(1<<i),c,len);\n continue;\n }\n p+=solve(ind+1,mask^(1<<i),false,len);\n }\n return p;\n\n}\n\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int n) {\n s=to_string(n);\n memset(dp,-1,sizeof(dp));\n int ans=0;\n\n for(int len=1;len<=s.size();++len)\n {\n int maxi=9;\n if(len==s.size())\n {\n maxi=s[0]-\'0\';\n for(int i=1;i<=maxi;++i)\n {\n bool f=(i==maxi);\n ans+=solve(1,1<<i,f,len);\n }\n }\n else\n {\n for(int i=1;i<10;++i)\n {\n ans+=solve(1,1<<i,false,len);\n }\n }\n }\n ans=n-ans;\n return ans;\n\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Bitmask', 'C++'] | 0 |
numbers-with-repeated-digits | 0ms C++ SOLUTION | 0ms-c-solution-by-obose-1kfd | Intuition\n Describe your first thoughts on how to solve this problem. \nThe idea of this solution is to count the number of integers with unique digits from 0 | Obose | NORMAL | 2023-01-18T03:47:55.106084+00:00 | 2023-01-18T03:47:55.106120+00:00 | 1,113 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea of this solution is to count the number of integers with unique digits from 0 to N, which can be done by considering the different cases for each digit. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe start by looping through the digits of N, starting from the least significant digit. For each digit, we first calculate the number of integers with unique digits that are smaller than N and have the same number of digits as N. For this, we use a helper function `A(m, n)` which calculates the number of numbers with digits 1, 2, ..., m, where each digit can appear at most once and the total number of digits is n. \n\nThen, for the current digit, we loop through all possible digits (skipping 0 if the current digit is the most significant digit) and check if it has already been seen. If yes, we break, as it means that all the remaining digits should be the same as the current digit. Otherwise, we increment the count by the number of integers with unique digits that are smaller than N and have the same number of digits as N. \n\nFinally, we subtract the count from N to get the result.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int n) {\n vector<int> digits;\n for (int x = n + 1; x > 0; x /= 10) {\n digits.push_back(x % 10);\n }\n reverse(digits.begin(), digits.end());\n int ans = 0, k = digits.size();\n for (int i = 1; i < k; ++i) {\n ans += 9 * A(9, i - 1);\n }\n set<int> seen;\n for (int i = 0; i < k; ++i) {\n for (int j = i > 0 ? 0 : 1; j < digits[i]; ++j) {\n if (!seen.count(j)) {\n ans += A(9 - i, k - i - 1);\n }\n }\n if (seen.count(digits[i])) {\n break;\n }\n seen.insert(digits[i]);\n }\n return n - ans;\n }\n int A(int m, int n) {\n return n == 0 ? 1 : A(m, n - 1) * (m - n + 1);\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
numbers-with-repeated-digits | C++ | Standard Digit DP | c-standard-digit-dp-by-baihuaxie-48hz | This is a standard digit DP problem.\n\nA few words on digit DP for those who are not so familiar with the concept. The basic idea here is to group the sequence | baihuaxie | NORMAL | 2022-08-31T01:48:25.478167+00:00 | 2022-08-31T01:59:43.848292+00:00 | 113 | false | This is a standard digit DP problem.\n\nA few words on digit DP for those who are not so familiar with the concept. The basic idea here is to group the sequences into subsets or sub-problems, then apply regular top-down DP on each sub-problem. Here by "sequences" I just mean any integer within the range `[1,n]` , so there are `n` such sequences. They all have length (in terms of number of digits) equal to number of digits in `n`, b/c we will be including leading zeros.\n\nObviously in brute-force we can enumerate each sequence and check if it meets the condition, but this will explode in time complexity since `n` is very large. Instead we divide them into subsets. How? A very natural way is to group sequences sharing the same prefix into the same set. For instance, the two sequences `1123` and `1145` can be thought of as belonging to the same subset, since they both starts w/t the prefix `11`. Now the prefix can have different lengths, so we start with the left-most bit i.e. the most significant bit, we use a parameter `pos` to represent the current bit we are at, so `pos` equals to the length of the prefix that we have built so far. In the previous example, we can say the prefix `11` is at position `pos=2`.\n\nAn additional variable `tight`, which is boolean, is used to make it more convenient to expand the prefix; when `tight=1` it means the prefix so far exactly matchs the prefix part in `n`, therefore at `pos+1` the digit we can choose are limited to the corresponding digit in `n`. For instance if `n=12345` and we are currently at `pos=3` with `tight=1`, this would indicate the prefix we have built so far is `123`, for the next position, we cannot choose any digit larger than `4`, because if we choose say `1235` then it would have already be out-of-bounds. When `tight=0` we can choose any digit from 0 to 9. \n\nThese two variables `pos` and `tight` are standard for any digit DP solution, please refer to better tutorials e.g. [this one](https://codeforces.com/blog/entry/53960) for more detailed explanations. With `pos` and `tight` we are able to build the complete search tree from left to right in a very standard DFS framework e.g.:\n\n```\nint dfs (int pos, int tight, ...) {\n\t// return leaf node\n\t// memoization\n\t\n\tint res = 0;\n\tint limit = tight==1 ? nums[pos] : 9;\n\tfor (int i = 0; i <= limit; ++i) {\n\t\t// do sth.\n\t\tres += dfs(pos+1, newTight, ...);\n\t}\n\t\n\treturn dp[pos][tight][...] = res;\n}\n```\n\nHere for each node at position = `pos`, we just enumerate all possible digits from 0~9 or from 0 ~ `limit` depending on the `tight` condition. The digit `i` is put into position `pos+1` to expand the prefix and it is hence a child node of the current node. To return the solution of the sub-problem associated with the current node, we just accumulate from the solutions over all of its child sub-trees. This is therefore very standard top-down DP approach.\n\nA node in the tree is therefore identifiable by its prefix sequence. But in this way each node is distinct, and there are way too many nodes for memoization to work properly. Therefore we need to apply a further grouping on the prefixes. We define a mapping function `f(p)->state` where `p` is a prefix and `state` is an integer value of limited range. For instance, for LC#233 counting the digit 1 in integers, we can let `state` = number of 1\'s in the prefix.\n\nHere for this problem, notice that if we have two prefixes e.g. `22345***` and `23524***`, they are similar in the sense that they both contain two 2\'s i.e. they both have repeated digits; moreover, they both have used the same digits `2,3,4,5`, although in different ordering. So these two prefixes (and all the descendant full sequences containing these prefixes) should be grouped into the same sub-problem.\n\nConcretely, we actually need to use a 2d state variable, `(rep, mask)`. Here `rep` is a boolean value indicating whether there has already been at least one repeated digit in the prefix built so far, and `mask` is a bit-mask indicating which digits have been used in the prefix. For the previous example the state for the two prefixes should be `rep=1` and `mask=0000111100` indicating the usage of digits `2,3,4,5`. Thefore, the mapping function from prefixes to states are many-to-one, each state now identifies a sub-problem containing many sequences which share similar prefixes. It should be noted that the mapping must be chosen in such a way as to ensure the sub-problems won\'t overlap. Now we apply memoization on these sub-problems, since the number of these states will be limited, and these values will be shared and re-used throughout the DFS on the search tree.\n\nIn summary, the sub-problem (i.e. a specific subset of sequences grouped together) in digit DP is indexed by a set of variables `(pos, tight, state)`. The `dp[pos][tight][state]` value function therefore stores the solution to the corresponding sub-problem, i.e. the original problem but on the sub-set of sequences. When considering the state transitions, since `pos` and `tight` are used just for building the search tree, their transitions are always the same for different problems; in particular:\n```\nint new_pos = pos+1;\nint new_tight = (tight == 1 && i == limit ) ? 1 : 0;\n```\nHere we always transition into the child nodes by `pos+1` and compute the correct `tight` variable. The problem-specific aspect lies with the `state` variable and its transitions. Here in this problem, using `(rep, mask)` as the state, the digit DP solution is as follows in C++:\n\n```\nclass Solution {\n vector<int> nums;\n int s;\n // dp[pos][tight][rep][mask]\n\t// if rep=1 means the prefix sequence contains at least one repeated digit\n int dp[10][2][2][1024];\npublic:\n int dfs(int pos, int tight, int rep, int mask) {\n\t\t// at leaf node exclude the cases where mask==0 i.e. leading zeros\n\t\t// if rep=1 means a sequence with at least one repeated digit has been found, so return 1;\n if (pos == s)\n return ( mask != 0 && rep ) ? 1 : 0;\n \n\t\t// memoization\n if (dp[pos][tight][rep][mask] != -1)\n return dp[pos][tight][rep][mask];\n \n int limit = tight == 1 ? nums[pos] : 9;\n int res = 0;\n for (int i = 0; i <= limit; ++i) {\n int newTight = (tight == 1 && i == limit) ? 1 : 0;\n\t\t\t\n\t\t\t// if mask==0 means it\'s all leading zeros, so when i=0 it\'s still leading zero, not counted;\n\t\t\t// otherwise set the corresponding bit of i to 1 in newMask\n int newMask = (mask == 0 && i == 0) ? mask : mask | 1 << i;\n\t\t\t\n\t\t\t// exclude cases of leading zero here as well\n\t\t\t// for other cases, if rep==1 means there has already been repeated digits, so newRep = 1 also\n\t\t\t// otherwise, check if i has been set in `mask` by the bitwise AND operation; if so, newRep = 1;\n int newRep = (mask == 0 && i == 0) ? 0 : rep | bool(mask & 1 << i);\n \n res += dfs(pos+1, newTight, newRep, newMask);\n }\n \n return dp[pos][tight][rep][mask] = res;\n }\n \n int numDupDigitsAtMostN(int n) {\n while (n > 0) {\n nums.push_back(n % 10);\n n = n / 10;\n }\n s = nums.size();\n reverse(nums.begin(), nums.end());\n memset(dp, -1, sizeof(dp));\n\t\t\n\t\t// the original full problem is represented by an empty prefix\n\t\t// so pos=0\n\t\t// tight=1 b/c the first digit we place in the prefix must be bounded by nums[0] i.e. the msb in n, so it\'s tight condition is set.\n\t\t// rep=0 and mask=0 b/c in empty prefix there is no repetion, no digit used\n return dfs(0, 1, 0, 0);\n }\n};\n``` | 2 | 0 | [] | 0 |
numbers-with-repeated-digits | [C++] || Digit DP || Total - NonRepeating | c-digit-dp-total-nonrepeating-by-rahul92-yknl | bound variable ensures that we dont overshoot the given n value at any time.\n\n mask check which digits are taken and which are yet to be taken.\n\n pos tracks | rahul921 | NORMAL | 2022-08-26T01:41:51.310315+00:00 | 2022-08-26T01:48:14.490520+00:00 | 340 | false | * `bound` variable ensures that we dont overshoot the given `n` value at any time.\n\n* `mask` check which digits are taken and which are yet to be taken.\n\n* `pos` tracks the length of orignal number.\n\n```\nclass Solution {\npublic:\n int dp[11][1025][2] ;\n string ref ;\n int solve(int pos, int mask , int bound){\n if(pos >= ref.size()) return (mask != 0) ;\n if(dp[pos][mask][bound] != -1) return dp[pos][mask][bound] ;\n \n int res = 0 , maxi = bound ? (ref[pos]-\'0\') : 9 ;\n for(int i = 0 ; i <= maxi ; ++i ){\n if(mask & (1 << i)) continue ;\n int newMask = (!i and !mask) ? mask : mask | (1 << i) ; // dont put leading zeros\n \n if(bound) res += solve(pos + 1 , newMask , (ref[pos]-\'0\') == i) ;\n else res += solve(pos + 1 , newMask , 0) ;\n }\n \n return dp[pos][mask][bound] = res ;\n }\n \n int numDupDigitsAtMostN(int n) {\n memset(dp,-1,sizeof(dp)) ;\n //answer will be total positive integers - the ones where no repetition is allowed \n ref = to_string(n);\n int nonRepeating = solve(0,0,1) ;\n return n - nonRepeating ;\n }\n};\n```\n\n\n* [Refer This Video For Digit Dp Intro](https://www.youtube.com/watch?v=wWfGCIL0AfU) | 2 | 0 | ['C'] | 1 |
numbers-with-repeated-digits | C++ | digit dp | c-digit-dp-by-deepanshu_johar-j3ik | \nclass Solution {\npublic:\n string num;\n int len;\n int setKthBit(int n, int k)\n {\n return ((1 << (k)) | n);\n }\n bool isKthBitSe | deepanshu_johar | NORMAL | 2021-12-15T20:06:28.544780+00:00 | 2021-12-15T20:06:28.544808+00:00 | 418 | false | ```\nclass Solution {\npublic:\n string num;\n int len;\n int setKthBit(int n, int k)\n {\n return ((1 << (k)) | n);\n }\n bool isKthBitSet(int n, int k)\n {\n return ( n & (1 << k) );\n }\n\n // mask reprsents the set of numbers already in the number //\n // like for 1,2,4 maks = 00000001011 // \n // we can also use an explicit set but that will be difficult to cache and as we can have only 10 numbers that are 0-9 therefore only 2^11 will be used 2048 \n int memo[12][2][5000][2];\n // to find the count of numbers with unique digits //\n int dp(int n, bool tight, int mask, bool leadingzero){\n \n // base case //\n if(n==0){\n int base = 0;\n int ub = tight ? num[len-1-n]-\'0\' : 9;\n for(int i=0; i<=ub; ++i){\n if(!isKthBitSet(mask, i))\n base += 1;\n } \n return base;\n }\n \n if(memo[n][tight][mask][leadingzero]!=-1)\n return memo[n][tight][mask][leadingzero];\n \n // recc //\n int res = 0;\n int ub = tight ? num[len-1-n]-\'0\' : 9;\n \n \n for(int i=0; i<=ub; ++i){\n if(i==0){// for leading zero we wont set it in the mask // eg 00035 is actually unique but as there are 3 zeros leading it wont be unique therfore to handle these type of cases//\n if(leadingzero)\n res += dp(n-1, tight && i==ub, mask, leadingzero);\n else{\n if(!isKthBitSet(mask, i))\n res += dp(n-1, tight && i==ub, setKthBit(mask, i), leadingzero);\n } \n \n }\n else{\n if(!isKthBitSet(mask, i)){\n res += dp(n-1, tight && i==ub, setKthBit(mask, i), false);\n } \n }\n }\n return memo[n][tight][mask][leadingzero] = res;\n }\n \n int numDupDigitsAtMostN(int n) {\n \n memset(memo, -1, sizeof memo);\n \n num = to_string(n);\n len = num.length();\n \n int ans = dp(len-1, true, 0, true);\n \n ans = n+1 - ans ; \n \n return ans;\n }\n};\n``` | 2 | 0 | ['Dynamic Programming'] | 0 |
numbers-with-repeated-digits | python easy follow | python-easy-follow-by-xjsun-430k | the basic idea here is computing the non-repeat numbers first and then use N minus the non-repeat numbers.\nsuppose N is abcde, compute non- repeat numbers smal | xjsun | NORMAL | 2021-01-15T19:49:22.838227+00:00 | 2021-01-15T19:49:22.838279+00:00 | 489 | false | the basic idea here is computing the non-repeat numbers first and then use N minus the non-repeat numbers.\nsuppose N is abcde, compute non- repeat numbers smaller than a0000. then compute non-repeat number between a0000 and ab000, and so on.\n\n\'\'\'\n\n\tdef numDupDigitsAtMostN(self, N: int) -> int:\n def helper(s):\n non_repeat = 0\n carry = set()\n for i in range(len(s)-1):\n if s[i] in carry:\n return non_repeat\n carry.add(s[i])\n tem = int(s[i+1])\n for _ in range(int(s[i+1])):\n if str(_) in carry:\n tem -= 1\n tem = max(tem, 0)\n for j in range(i+2, len(s)):\n tem *= (10-j)\n non_repeat += tem\n return non_repeat + (s[-1] not in carry)\n num = str(N)\n non_repeat = 0\n\t\t# compute non- repeat numbers smaller than a0000\n for l in range(1, len(num) + 1):\n if l == len(num):\n pre, i = int(num[0]) -1, 1\n else:\n pre, i = 9, 1\n while i < l:\n pre *= (10 - i)\n i += 1\n non_repeat += pre \n return N - non_repeat - helper(num)\n\'\'\' | 2 | 0 | [] | 0 |
numbers-with-repeated-digits | Python. Easy. | python-easy-by-nag007-hlib | \ndef f(n,s,e,ci,di,v):\n if n==ci:\n return 1\n a=0\n if (e,ci,v) in di:\n return di[e,ci,v]\n for i in range(10):\n if e= | nag007 | NORMAL | 2020-07-10T15:59:59.376953+00:00 | 2020-07-10T15:59:59.376988+00:00 | 694 | false | ```\ndef f(n,s,e,ci,di,v):\n if n==ci:\n return 1\n a=0\n if (e,ci,v) in di:\n return di[e,ci,v]\n for i in range(10):\n if e==0:\n if not v>>i&1:\n eee=v|(1<<i)\n a+=f(n,s,0,ci+1,di,eee)\n else:\n if i>int(s[ci]):\n break\n if int(s[ci])==i:\n if not v>>i&1:\n eee=v|(1<<i)\n a+=f(n,s,1,ci+1,di,eee)\n break\n if not v>>i&1:\n eee=v|(1<<i)\n a+=f(n,s,0,ci+1,di,eee)\n di[e,ci,v]=a\n return a\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n if n<=10:\n return 0\n s=str(n)\n l=len(s)\n ans=10\n prev=9\n for i in range(9,9-l+2,-1):\n ans+= prev*i\n prev=prev*i\n a=0\n di={}\n v=0\n for i in range(1,10):\n if i>int(s[0]):\n break\n if i==int(s[0]):\n e=1<<i\n a+=f(l,s,1,1,di,e)\n break\n e=1<<i\n a+=f(l,s,0,1,di,e)\n return n-a-ans+1\n``` | 2 | 4 | [] | 0 |
numbers-with-repeated-digits | Simple & Efficient C++ Digit DP solution with comments | simple-efficient-c-digit-dp-solution-wit-9gpg | Top Down multi-dimensional DP approach\n\n\n#define ll long long\n\nclass Solution {\npublic:\n string s;\n int dp[10][2][2][2][1<<10];\n\n ll ff(int p | abhisharma404 | NORMAL | 2020-01-23T19:37:41.065685+00:00 | 2020-01-23T19:38:07.025602+00:00 | 667 | false | **Top Down multi-dimensional DP approach**\n\n```\n#define ll long long\n\nclass Solution {\npublic:\n string s;\n int dp[10][2][2][2][1<<10];\n\n ll ff(int pos, bool tight, bool st, bool cnt, int mask) {\n // If index reaches the length of the string return whether\n // any repetition till now has been found or not?\n if (pos == s.size()) return cnt ? 1 : 0;\n \n // Look in the DP table\n if (dp[pos][tight][st][cnt][mask] != -1)\n return dp[pos][tight][st][cnt][mask];\n\n ll res = 0;\n ll en = tight ? s[pos]-\'0\':9;\n\n if (!st) {\n // Place 0s, go to the rightmost\n res = ff(pos+1, tight&s[pos]==\'0\', st, cnt, mask);\n for (ll i=1; i<=en; i++) {\n // Start the number, st = true\n res += ff(pos+1, tight&(i==en), st|(i > 0), cnt, mask|1<<i);\n }\n }else {\n // Number has started\n for (ll i=0; i<=en; i++) {\n // If number is found repeated, check using bitmask (mask & (1 << i))\n // Make the cnt = true, i.e. cnt | mask&(1<<i)\n res += ff(pos+1, tight&(i==en), st, cnt|(mask&(1<<i)), mask|1<<i);\n }\n }\n\n return dp[pos][tight][st][cnt][mask] = res;\n }\n\n int numDupDigitsAtMostN(int N) {\n s = to_string(N);\n memset(dp, -1, sizeof dp);\n return ff(0, true, false, false, 0);\n }\n};\n```\n\nRead more about **Digit DP:**\nhttps://codeforces.com/blog/entry/53960 | 2 | 1 | [] | 6 |
numbers-with-repeated-digits | [C++] Share my DP solution (count the numbers without repeated digits) | c-share-my-dp-solution-count-the-numbers-9zhx | \n// DP State is current digit index, visited bitmask,\n// comparison of current number to N, left digits.\nint dp[11][2048][3][11];\n\nint sgn(int val) {\n | todor91 | NORMAL | 2019-04-25T06:59:51.677143+00:00 | 2019-04-25T06:59:51.677189+00:00 | 846 | false | ```\n// DP State is current digit index, visited bitmask,\n// comparison of current number to N, left digits.\nint dp[11][2048][3][11];\n\nint sgn(int val) {\n return (0 < val) - (val < 0);\n}\n\nclass Solution {\npublic:\n\n vector<int> N;\n \n int genAll(int curDigitIndex, int vis, int cmpN, int len) {\n if (len == 0) {\n return cmpN <= 0;\n }\n int &res = dp[curDigitIndex][vis][cmpN + 1][len];\n if (res != -1) return res;\n res = 0;\n for (int i = 0; i <= 9; ++i) {\n if (curDigitIndex == 0 && i == 0) continue;\n if (vis & (1 << i)) continue;\n \n int nCmpN = cmpN \n ? cmpN \n : sgn(i - N[curDigitIndex]);\n \n res += genAll(\n curDigitIndex + 1,\n vis | (1 << i),\n nCmpN,\n len - 1);\n }\n return res;\n }\n\n int numDupDigitsAtMostN(int n) {\n memset(dp, -1, sizeof(dp));\n int nn = n;\n while (nn) {\n N.push_back(nn % 10);\n nn /= 10;\n }\n reverse(N.begin(), N.end());\n\n int allNonRep = 0;\n for (int i = 1; i <= N.size(); ++i) {\n int cmpN = i < N.size() ? -1 : 0;\n\t\t // generate all numbers with non repeating\n\t\t // digits with \'i\' length\n allNonRep += genAll(0, 0, cmpN, i);\n }\n return n - allNonRep;\n }\n};\n``` | 2 | 0 | [] | 1 |
numbers-with-repeated-digits | Java 0ms solution with explanations | java-0ms-solution-with-explanations-by-k-39ld | The idea is simple. Count all numbers that do not have repeating digits and less than or equal to N. Substract the count from N and return. My initial idea was | karayv | NORMAL | 2019-03-18T00:06:09.687562+00:00 | 2019-03-18T00:06:09.687603+00:00 | 1,012 | false | The idea is simple. Count all numbers that do not have repeating digits and less than or equal to `N`. Substract the count from `N` and return. My initial idea was to permutate 10 digits in [1..`digsCount`] slots (`digsCount` is a number of digits in `N`) and take into account those results of permutation that are <= `N` only. And this worked, but the submition time was ~1400ms.\n\nAn alternative approach uses similar idea but instead of generating permutations we can count them using \'number of permutations of n objects taken r at a time\' formula *P(n,r)=n!/(n\u2212r)!*. \nBecause digit 0 cannot be a highest digit (number \'010\' does not make sence, there is number \'10\' instead), we need to adjust the formula *P\'(n,r) = (n-1) * P(n - 1,r - 1)=(n-1)(n-1)!/(n\u2212r)!* In this case *n* equals to 10, *r* is in [1..`digsCount`). *P\'(r)=9 9! / (10 \u2212 r)!*\n\nLet\'s consider number 112.\n`digsCount` = `getDigits(N, digits)` = 3\n`digits` = [2, 1, 1]\n`uniq` = `initPermCount(digsCount)` = *P\'(1) + P\'(2)* = 9 * 9! / (10 - 1)! + 9 * 9! / (10 - 2)! = 9 + 9 * 9 = 90\n\nNow, for every `i` in (`digsCount`..0] we get all the digits `j` smaller than `digits[i]` and that are not used in the higher digits of `N`. We calculate P(10 - `digsCount` + `i`, `i`). Zero cannot be highest digit, so we skip it (`j = (i == digsCount - 1) ? 1 : 0`). If `digits[i]` was used before it means the original number `N` is not composed of unique digits only, and at this point we stop calculations.\n\n`i` = 2, `digits[i]` = 1, `j` = 1, `used` = [] (skip since `j` is not < `digits[i]`)\n\n`i` = 1, `digits[i]` = 1, `j` = 0, `used` = [1]\nSince two digits are used (0 and 1) we calculate permutation using 10 - 2 digits:\n`uniq` = `uniq` + P(10 - `digsCount` + `i`, `i`) = 90 + P(10-3+1, 1) = 90 + 8 = 98\n\n`i` = 1, `digits[i]` = 1, `j` = 1, `used` = [1] (skip since `j` is not < `digits[i]`)\n\nFinish calculations since `digits[i]` is in `used`. Since `digits` contains duplicates we do not increment `uniq`;\n\nReturn `N` - `uniq` = 112 - 98 = 14\n\n```java\n public int numDupDigitsAtMostN(int N) {\n int[] digits = new int[10];\n int digsCount = getDigits(N, digits);\n\n boolean[] used = new boolean[10];\n boolean numUniq = true;\n int uniq = initPermCount(digsCount);\n for (int i = digsCount - 1; i >= 0; i--) {\n for (int j = (i == digsCount - 1) ? 1 : 0; j < digits[i]; j++) {\n if (!used[j]) {\n uniq += permCount(digsCount, digsCount - i);\n }\n }\n if (used[digits[i]]) {\n numUniq = false;\n break;\n }\n used[digits[i]] = true;\n }\n if (numUniq) {\n uniq++;\n }\n return N - uniq;\n }\n\n private int getDigits(int num, int[] digits) {\n int i = 0;\n while (num > 0) {\n digits[i] = num % 10;\n num /= 10;\n i++;\n }\n return i;\n }\n\n private int initPermCount(int digsCount) {\n int sum = 0;\n for (int i = 1; i < digsCount; i++) {\n sum += 9 * permCount(i, 1);\n }\n return sum;\n }\n\n private int permCount(int n, int reserved) {\n int hi = 10 - reserved, lo = hi - (n - reserved);\n int res = 1;\n while (hi > lo) {\n res *= hi--;\n }\n return res;\n }\n``` | 2 | 0 | [] | 1 |
numbers-with-repeated-digits | Math,O(logN) | mathologn-by-maxatom-jy3b | Count the number without repeated digit.\nwe start with the highest bit of N, if N is 1000, the highest bit must less than 1, so we start with 0,\nthe biggest | maxatom | NORMAL | 2019-03-17T10:43:25.196324+00:00 | 2019-03-17T10:43:25.196391+00:00 | 644 | false | Count the number without repeated digit.\nwe start with the highest bit of N, if N is 1000, the highest bit must less than 1, so we start with 0,\nthe biggest number without repeated dight is 999, the leghth is 3.\nthe highest bit can be 1~9 ( we count numbers start with 0 later) , the second bit can be 0~9, excluding that is the same with the previous bits... and so on.\nthe total number is 9*(10-1)*(10-2)+count(2,9) ( if the second bit is 0, we consider it as a new number whose lenght is 2)\n\n```\npublic int numDupDigitsAtMostN(int N) {\n int n=N;\n int count=0;\n int[] arr=new int[11];\n while (n>0) {\n arr[++count]=n%10;\n n/=10;\n }\n int res=count(count, arr[count]-1);\n Set<Integer> set=new HashSet<>(10);\n set.add(arr[count]);\n for (int i = count-1; i >0; i--) {\n int maxcur=arr[i], rems=0;\n while (maxcur>=0 && set.contains(maxcur))\n maxcur--;\n if(maxcur<0) break;\n set.add(maxcur);\n int bit=maxcur-1;\n while (bit>=0){\n if(!set.contains(bit)) rems++;\n bit--;\n }\n if(maxcur<arr[i]) rems++;\n int cnt=rems;\n for (int j = 1; j < i; j++) {\n cnt*=(10-(count-i)-j);\n }\n res+=cnt;\n if(maxcur<arr[i]) {\n set.remove(maxcur);\n break;\n }\n arr[i]=maxcur;\n }\n if(set.size()==count) res+=1;\n return N-res;\n }\n\t//count the number without repeated digit and the highest less than num, the lenght is n\n public int count(int n, int num){\n if(n<1) return 0;\n if(n==1) return num;\n int count=0, N=n;\n\t\t//the highest bit isn\'t 0\n if(num>0) {\n count=num;\n while (--n > 0) {\n count *= (10 - n);\n }\n }\n\t\t//if the highest bit is 0\n count+=count(N-1, 9);\n return count;\n }\n``` | 2 | 1 | [] | 0 |
numbers-with-repeated-digits | Beats 100% | detailed solution | Python3 | beats-100-detailed-solution-python3-by-a-rkob | Please UpvoteCode | Alpha2404 | NORMAL | 2025-04-03T17:31:44.398135+00:00 | 2025-04-03T17:31:44.398135+00:00 | 40 | false | # Please Upvote
# Code
```python3 []
class Solution:
def numDupDigitsAtMostN(self, N: int) -> int:
def permutation(m, k):
# Computes the number of ways to arrange k numbers out of m possibilities.
result = 1
for i in range(k):
result *= (m - i)
return result
s = str(N)
n = len(s)
# Count unique-digit numbers with fewer digits than N.
unique_count = 0
for i in range(1, n):
unique_count += 9 * permutation(9, i - 1)
# Count unique-digit numbers with the same number of digits as N.
seen = set()
for i, char in enumerate(s):
digit = int(char)
# For each digit position, consider smaller digits not used so far.
for j in range(0 if i > 0 else 1, digit):
if j in seen:
continue
unique_count += permutation(10 - i - 1, n - i - 1)
# If the current digit is already used, break out.
if digit in seen:
break
seen.add(digit)
else:
# If loop completes without break, include N itself.
unique_count += 1
# Total numbers (0 to N) minus unique-digit numbers gives the duplicate-digit count.
return N - unique_count
``` | 1 | 0 | ['Math', 'Python3'] | 0 |
numbers-with-repeated-digits | One of the Best Digit DP + Bitmask question solution(c++ solution) | one-of-the-best-digit-dp-bitmask-questio-5e2i | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | jishudip389 | NORMAL | 2023-09-06T11:51:38.908634+00:00 | 2023-09-06T11:51:38.908656+00:00 | 121 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n int dp[70][2][1025][2][2];\n int f(int i,int t,int flag,int flag2,int flag3,string &s){\n\n if(i == s.size() && flag2 == true)return 1;\n else if(i == s.size())return 0;\n \n if(dp[i][t][flag][flag2][flag3]!=-1)return dp[i][t][flag][flag2][flag3];\n\n int ans = 0;\n int high = t ? s[i]-\'0\' : 9;\n int low = 0;\n for(int k=low;k<=high;k++){\n if(flag3 == false){//we have not yet started \n if(k == 0)ans+=f(i+1,t && high == k,flag,flag2,0,s);\n else ans+= f(i+1,t && high == k,flag|(1<<k),0,1,s);\n }\n else if((flag&(1<<k))){//this digit is already taken previously\n ans+= f(i+1,t && high == k,flag|(1<<k),1,1,s);//i have taken repeated digit\n }\n else ans+=f(i+1,t && high == k,flag|(1<<k),flag2,1,s);\n }\n return dp[i][t][flag][flag2][flag3] = ans;\n }\npublic:\n int numDupDigitsAtMostN(int n) {\n \n string res = "";\n while(n>0){\n res.push_back(n%10+\'0\');\n n = n/10;\n }\n reverse(res.begin(),res.end());\n memset(dp,-1,sizeof(dp));\n return f(0,1,0,0,0,res);\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
numbers-with-repeated-digits | Java easy to understand(Digit Dp + Bit Manipulation) | java-easy-to-understanddigit-dp-bit-mani-j73l | \nclass Solution {\n Integer[][][][] dp;\n private int solve(char[] num, int curDig, boolean isStrict, int bit, boolean repeated) {\n if(curDig == | manmohansaraswat15 | NORMAL | 2023-06-06T05:18:35.843623+00:00 | 2023-06-06T05:18:35.843659+00:00 | 529 | false | ```\nclass Solution {\n Integer[][][][] dp;\n private int solve(char[] num, int curDig, boolean isStrict, int bit, boolean repeated) {\n if(curDig == num.length) return repeated ? 1 : 0;\n if(dp[curDig][isStrict ? 1 : 0][bit][repeated ? 1 : 0] != null) return dp[curDig][isStrict ? 1 : 0][bit][repeated ? 1 : 0];\n int end = isStrict ? num[curDig] - \'0\' : 9;\n int res = 0;\n for(int i = 0; i <= end; i++) {\n if(bit == 0 && i == 0) \n res += solve(num, curDig + 1, isStrict && i == end, bit, repeated);\n else\n res += solve(num, curDig + 1, isStrict && i == end, bit | (1 << i), repeated | (bit & (1 << i)) != 0);\n }\n return dp[curDig][isStrict ? 1 : 0][bit][repeated ? 1 : 0] = res;\n }\n public int numDupDigitsAtMostN(int n) {\n char[] num = String.valueOf(n).toCharArray();\n dp = new Integer[10][2][1025][2];\n return solve(num, 0, true, 0, false);\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Bit Manipulation', 'Recursion', 'Bitmask', 'Java'] | 0 |
numbers-with-repeated-digits | 100% Faster Solution using Math and Recursion TC : O(1) || C++ Explained | 100-faster-solution-using-math-and-recur-tkax | Please upvote if you like my solution .\n\nclass Solution {\npublic:\n // to return factorial starting at st and multiplying till t no of times\n int fac( | rkkumar421 | NORMAL | 2022-10-30T16:59:02.160104+00:00 | 2022-10-30T17:00:36.312812+00:00 | 135 | false | **Please upvote if you like my solution .**\n```\nclass Solution {\npublic:\n // to return factorial starting at st and multiplying till t no of times\n int fac(int st,int t){\n int ans = 1;\n while(t){\n ans *= st;\n st--;\n t--;\n }\n return ans;\n }\n // mask will create mask over digits fixed\n vector<bool> mask;\n // we are counting numbers with 0 duplicate digits\n int solve(vector<int> &dig, int ind, int st){\n if(ind == dig.size()) return 1;\n int ans = 0;\n if(ind == 0){\n // 0 cannot be used\n for(int i=1;i<dig[ind];i++){\n if(i < dig[ind]){\n ans += fac(st,dig.size()-1);\n }\n }\n // here we are fixing digit equal to dig[ind] and masking it to use in future\n mask[dig[ind]] = 1;\n // now calling solve for next index\n ans += solve(dig,ind + 1, st);\n return ans;\n }\n // if we are not at first index means we can use 0 now\n for(int i=0;i<dig[ind];i++){\n if(mask[i]) continue; // see if we have used this digit before than we cannot indclude its contribution\n if(i < dig[ind]){\n ans += fac(st-1,dig.size()-ind-1);\n }\n }\n // if we have used dig[ind] before than return ans no need to solve for next index \n if(mask[dig[ind]]) return ans;\n mask[dig[ind]] = 1;\n ans += solve(dig,ind + 1,st-1);\n return ans;\n }\n \n int numDupDigitsAtMostN(int n) {\n // here we can use 10 digits including 0 but must not start with zero\n if(n<=10) return 0;\n int nc = n;\n vector<int> dig;\n while(nc){\n dig.push_back(nc%10);\n nc /= 10;\n }\n reverse(dig.begin(), dig.end());\n // now we have digits\n mask.resize(10,0);\n // till number of n digits\n vector<int> v(10,0); // this contains numbers that have unique digits in ith digit number\n long int a = 9;\n for(int i=1;i<10;i++){\n v[i] = a;\n a = a*(10-i);\n }\n // Now till we try n digits number \n int ans = 0;\n for(int i=1;i<dig.size();i++){\n ans += v[i];\n }\n // Now for dig.size digit number we can\n ans += solve(dig,0,9);\n return n-ans;\n }\n};\n```\n\n | 1 | 0 | ['Math', 'Recursion', 'C'] | 0 |
numbers-with-repeated-digits | C++ Solution || Digit DP Solution | c-solution-digit-dp-solution-by-shubham_-dezm | cpp\nclass Solution {\npublic:\n int dp[10][1<<10][2][2];\n int solve(string &nums,int i=0,int mask=0,bool rep=0,int tight=1){\n if(i>=nums.size()) | shubham_lohan | NORMAL | 2022-08-19T12:53:09.877537+00:00 | 2022-08-19T12:53:09.877569+00:00 | 108 | false | ```cpp\nclass Solution {\npublic:\n int dp[10][1<<10][2][2];\n int solve(string &nums,int i=0,int mask=0,bool rep=0,int tight=1){\n if(i>=nums.size())\n return rep and mask!=0;\n if(dp[i][mask][rep][tight]!=-1)\n return dp[i][mask][rep][tight];\n int ub=tight?(nums[i]-\'0\'):9;\n int ans=0;\n for(int j=0;j<=ub;j++){\n if(mask==0 and j==0 )\n ans+=solve(nums,i+1,mask,rep,tight&(j==ub));\n else if(mask&(1<<j))\n ans+=solve(nums,i+1,mask,true,tight&(j==ub));\n else\n ans+=solve(nums,i+1,mask|(1<<j),rep,tight&(j==ub));\n }\n return dp[i][mask][rep][tight]=ans;\n }\n int numDupDigitsAtMostN(int n) {\n string nums=to_string(n);\n memset(dp,-1,sizeof(dp));\n return solve(nums);\n }\n};\n``` | 1 | 0 | [] | 1 |
numbers-with-repeated-digits | C++ | Greedy | c-greedy-by-tangerrine2112-f3gi | \nclass Solution {\npublic:\n int numDupDigitsAtMostN(int n) {\n vector<int> V;\n int n2 = n;\n while(n2){\n V.emplace_back(n | tangerrine2112 | NORMAL | 2022-08-14T05:38:51.102389+00:00 | 2022-08-14T05:38:51.102442+00:00 | 402 | false | ```\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int n) {\n vector<int> V;\n int n2 = n;\n while(n2){\n V.emplace_back(n2%10);\n n2/=10;\n }\n int len = V.size();\n \n int sum = 0;\n for(int i = 0; i < len-1; i++){\n sum += 9*A(9,i);\n }\n \n vector<int> dig_visited(10,0);\n for(int i = len-1; i >= 0; i--){\n int dig = V[i];\n int count = 0;\n for(int j = 0; j < dig; j++){\n if(dig_visited[j]){continue;}\n count++;\n }\n if(i == len-1){count--;}\n sum += count*A(10-(len-i), i);\n if(dig_visited[dig]){break;}\n if(i == 0 && dig_visited[dig] == 0){sum++;}\n dig_visited[dig] = 1;\n }\n \n return n - sum;\n }\n \n int A(int num, int len){\n int tmp = 1;\n for(int i = 0; i < len; i++){tmp *= (num-i);}\n return tmp;\n }\n};\n``` | 1 | 0 | [] | 0 |
numbers-with-repeated-digits | Am I the only one who misunderstand the question? | am-i-the-only-one-who-misunderstand-the-z5g61 | I spent over 1 hr debugging couldn\'t figure out why my answer is wrong for some large numbers. \n\nThe question states that have at least one repeated digit. I | Student2091 | NORMAL | 2022-07-21T02:16:44.730412+00:00 | 2022-07-21T02:19:15.406031+00:00 | 561 | false | I spent over 1 hr debugging couldn\'t figure out why my answer is wrong for some large numbers. \n\nThe question states that have at least one repeated digit. I took that to mean "101" is NOT OK because both "1" are not glued together, and "11" is OK because they are together.\n\nI eventually gave up and checked the solution and realized "101" is actually OK because "1" appears twice. Am I the only person who didn\'t understand the question? \n\nIt is really frustrating.\n\n```Java\nclass Solution {\n public int numDupDigitsAtMostN(int n) {\n // 983582\n // 108318\n int ttl = n++;\n int ans = 0;\n List<Integer> list = new ArrayList<>();\n while(n>0){\n list.add(n%10);\n n/=10;\n }\n for (int i = 1; i < list.size(); i++){\n ans+=9*find(i-1, 9);\n }\n boolean[] seen = new boolean[10];\n for (int i = list.size(), d = 9; i > 0; --i, d--){\n int count = i == list.size()? list.get(i-1)-1: list.get(i-1);\n for (int j = 0; j < list.get(i-1); j++){\n if (seen[j]){\n count--;\n }\n }\n ans += count*find(i-1, d);\n if (seen[list.get(i-1)]){\n break;\n }\n seen[list.get(i-1)]=true;\n }\n return ttl-ans;\n }\n\n private int find(int n, int d){\n // dCn*n!\n // d!/(d-n)/(d-n).../1\n int ans = 1;\n for (int i = 1; i <= d; i++){\n ans *= i;\n }\n for (int i = n+1; i <= d; i++){\n ans /= (i-n);\n }\n return ans;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
numbers-with-repeated-digits | [Python] Permutation rule + Find the numbers without repeted digits | python-permutation-rule-find-the-numbers-973p | \n\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n \n nums = [int(i) for i in str(n+1)] # digits in n+1\n d = len(num | haydarevren | NORMAL | 2022-07-13T15:44:43.082039+00:00 | 2022-07-13T15:46:21.797476+00:00 | 651 | false | \n```\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n \n nums = [int(i) for i in str(n+1)] # digits in n+1\n d = len(nums) # number of digits in n+1\n res = 0 # number of no duplicates\n \n # count no duplicates for numbers with <d digits\n for i in range(1,d):\n res += 9 * math.perm(9,i-1)\n \n\t\t# count no duplicates for numbers with d digits and smaller than n\n for i, x in enumerate(nums):\n if i == 0:\n digit_range = range(1,x) # first digit can not be 0\n else:\n digit_range = range(x)\n \n for y in digit_range:\n if y not in nums[:i]:\n res += math.perm(9-i,d-1-i)\n if x in nums[:i]: break\n \n return n - res\n```\n \n\t\t | 1 | 0 | ['Combinatorics', 'Python'] | 0 |
numbers-with-repeated-digits | [JAVA] For if else lovers | java-for-if-else-lovers-by-_rodeo-tr05 | Strategy\nWe\'re taking the problem, slice it into smaller bites, solve for the smaller bites, and\nadd up what we calculate in each slice. \n\nSolution\nImagin | _rodeo_ | NORMAL | 2021-11-02T23:51:37.616118+00:00 | 2021-11-02T23:51:37.616150+00:00 | 721 | false | **Strategy**\nWe\'re taking the problem, slice it into smaller bites, solve for the smaller bites, and\nadd up what we calculate in each slice. \n\n**Solution**\nImagine we have three digits, x, y, and z. There are multiple ways to have a permutation\nof these digits such that at least one of the digits is repeated. Let\'s not solve for that.\nInstead we solve for permutations w/o repeated digits. The idea is for index 0 we have\nthree digits to choose from, x, y, and z. For index 1 we only have two choices left since\none choice has already been exhausted when we picked a digit for index 0. It doesn\'t\nmatter which digit we choose at what index. What matters is the number of choices we\nhave at each index.\n\n**Example 1**\nLet\'s say we\'re calculating the number of permutations w/o repeated digits and lower\nthan 1000. Let\'s slice our problem into smaller problems. We don\'t care about the\nvalue of 1000 at this point. We say 1000 is consisting of four digits. We solve the\noriginal problem for numbers lower than 9 (one 9), lower than 99 (two 9\'s), and lower\nthan 999 (three 9\'s). We know that not all four digit numbers are lower than 1000 so\nwe won\'t solve for numbers lower than 9999 (four 9\'s). We\'ll take care of four digits\nnumbers later. Solving for numbers consisting of 9\'s is easy. Let\'s explain what happens\nnext in Example 2.\n\n**Example 2**\nLet\'s say we\'re solving for 1,534,634. Plan is to slice it into smaller problems. Let\'s\nsay we already solved for numbers up to 999,999 like what we explained in Example 1.\nFor 1,000,000 to 1,534,634 our smaller problems are solving for 1,499,999 plus solving\nfor 1,500,000 all the way to 1,534,634. The latter piece will be sliced into smaller \nproblems as well. Smaller problems from 1,500,000 to 1,534,634 are solving for the \nfollowings,\nsolving for 1,529,999 plus\nsolving for 1,533,999 plus\nsolving for 1,534,599 plus\nsolving for 1,534,629 plus\nsolving for 1,534,634.\nIn each iteration we keep track of a pointer which is a pivot pointer. All digits \nbefore pivot represent themselves, so the possibilities for each is always one.\nThe pivot digit can take any digit up to the value of the pivot digit minus all \npossibilities that we\'ve already exhausted.\nLet\'s say we\'re dealing w/ 1,529,999 and pivot is at index 2 meaning starting from\nleft first digit is 1 and represents itself b/c it\'s before pivot. Second digit is\n5 and represents itself for the same reason. Now digit 2 is our pivot digit. We say\nour possibilities are 0, 1, and 2 so three possibilities but we have already exhausted\none of our possibilities which is 1 at index 0. So we\'re left w/ only two possibilities\nand again 1 and 5 represent themselves and 2 is lower than 5 so the only exhausted\npossibility is 1. For all those 9\'s after pivot we say possibilities are 0 to 9 which\nis 10 possibilities minus the count of exhausted possibilities, so in this case for\nthe first 9 we have 10-3=7 possibilities, for the second 9 we have 6 possibilities and \nso on.\nAdd up all counts from each iteration and we have all permutations w/o repeated digits.\nSubtract the total count from the original input number and we have all permutations\nw/ at least one repeated digit.\n```\nimport java.util.HashSet;\n\nclass Solution {\n\tint noRepeatCount = 0;\n\n\tpublic int numDupDigitsAtMostN(int n) {\n\t\tint nStrLength = String.valueOf(n).length();\n\t\tint allNineLength = 0;\n\n\t\t// Edge cases out of the way.\n\t\tif (n < 0 || nStrLength < 2)\n\t\t\treturn 0;\n\t\t\n\t\t// If n is all 9\'s like 99999.\n\t\telse if (Math.pow(10, nStrLength) - 1 == n)\n\t\t\tallNineLength = nStrLength;\n\t\t\n\t\t// If n is not all 9\'s we calculate the largest number lower than n consisting of all 9\'s.\n\t\telse\n\t\t\tallNineLength = nStrLength - 1;\n\n\t\t// Calculating all 9\'s e.g. for 10^6 we calculate for six 9\'s which is 999,999.\n\t\tfor (int numberOfDigits = 1; numberOfDigits <= allNineLength; numberOfDigits++) {\n\t\t\tnoRepeatCount += calcNumberOfNoRepeat(numberOfDigits);\n\t\t}\n\n\t\t// Calculating from all 9\'s to n e.g. for 10^6 we already calculated up to 999,999 and\n\t\t// we just need to calculate for the rest.\n\t\tif (Math.pow(10, nStrLength) - 1 > n) {\n\t\t\t\n\t\t\t// Count of all possible values 0 to 9.\n\t\t\tint mutations = 10;\n\t\t\t\n\t\t\t// HashSet is used only in part of the code. Worst case size() is the number of\n\t\t\t// mutations. contains() is called nStrLength times worst case in each iteration\n\t\t\t// w/ no more than nStrLength iterations.\n\t\t\tHashSet<Integer> hs = new HashSet<>();\n\t\t\t\n\t\t\t// We have two pointers each nStrLength hops to travel.\n\t\t\t// index1 is the pivot index and index2 keeps track of the current digit in n.\n\t\t\t// Based on index1 we decide what to do w/ digit at index2.\n\t\t\tfor (int index1 = 0; index1 < nStrLength; index1++) {\n\t\t\t\t\n\t\t\t\t// In each iteration we count noRepeat numbers. At the end of the iteration\n\t\t\t\t// we add local noRepeat count to the total noRepeat count.\n\t\t\t\tint noRepeatCountLocal = 0;\n\t\t\t\t\n\t\t\t\t// Digits visited in each iteration have nothing to do w/ other iterations\n\t\t\t\t// so we clear the HashSet before start of each inner iteration.\n\t\t\t\ths.clear();\n\t\t\t\tfor (int index2 = 0; index2 < nStrLength; index2++) {\n\t\t\t\t\t// Extracting digit at index2.\n\t\t\t\t\tint index2Digit = (int) (n / Math.pow(10, String.valueOf(n).length() - (index2 + 1)) % 10);\n\t\t\t\t\t// index1 is the pivot. Anything before index1 is already taken care of.\n\t\t\t\t\t// This means digits before index1 can only represent themselves, which\n\t\t\t\t\t// means if we see duplicate digits before index1 noRepeatCountLocal\n\t\t\t\t\t// for that entire iteration becomes zero. Remember we\'re counting numbers\n\t\t\t\t\t// w/o repeated digits.\n\t\t\t\t\tif (index2 < index1) {\n\t\t\t\t\t\t// This is where we use HashSet. If digit at index2 is already in the\n\t\t\t\t\t\t// HashSet that means we\'re dealing w/ a duplicate so noRepeatCountLocal\n\t\t\t\t\t\t// is set to zero and we\'re done w/ the iteration.\n\t\t\t\t\t\tif (hs.contains(index2Digit)) {\n\t\t\t\t\t\t\tnoRepeatCountLocal = 0;\n\t\t\t\t\t\t\tbreak;\n\t\t\t\t\t\t} else\n\t\t\t\t\t\t\t// If digit at index2 is not part of the HashSet add it to the HashSet.\n\t\t\t\t\t\t\ths.add(index2Digit);\n\t\t\t\t\t// index2 is meeting the pivot digit. The idea is to subtract 1 from the pivot\n\t\t\t\t\t// digit and make a possible big jump depending on the position of index1.\n\t\t\t\t\t// Imagine we\'re dealing w/ 15,564,465. The idea is to count for 14,xxx,xxx. \n\t\t\t\t\t// We\'ll replace those x\'s w/ 9\'s later in the code. So basically we skip over\n\t\t\t\t\t// 10^7-1 to 1.5*10^7-1.\n\t\t\t\t\t} else if (index2 == index1) {\n\t\t\t\t\t\t// Special case when both pointers are at index 0 meaning we\'re dealing w/\n\t\t\t\t\t\t// the first digit of n, which can\'t be 0.\n\t\t\t\t\t\tif (index2 == 0) {\n\t\t\t\t\t\t\tnoRepeatCountLocal = index2Digit - 1;\n\t\t\t\t\t\t} else {\n\t\t\t\t\t\t\tint inIndex2Range = 0;\n\t\t\t\t\t\t\t// Any digit before digit at index2 and larger than digit at index2\n\t\t\t\t\t\t\t// has no effect on digit at index2. Imagine digit at index2 is 5 \n\t\t\t\t\t\t\t// and digits before that are 8 and 9. Plan is to subtract 1 from 5 and\n\t\t\t\t\t\t\t// pad w/ 9\'s, which gives us 8949999... Knowing that pivot is at 4 and\n\t\t\t\t\t\t\t// 8 and 9 represent themselves, digit at index2 can potentially be any\n\t\t\t\t\t\t\t// value from 0 to 4, which are all less than 8 and 9. As a result 8 \n\t\t\t\t\t\t\t// and 9 have no effect on possible digits at index2. Now if we had 1 \n\t\t\t\t\t\t\t// and 2 instead of 8 and 9 then the possible values for digit at index2\n\t\t\t\t\t\t\t// would be 0, 3, and 4 since 1 and 2 are already used before index2.\n\t\t\t\t\t\t\t// There\'s a special case though when index2 points to the last digit,\n\t\t\t\t\t\t\t// in which we don\'t subtract 1 and we don\'t pad with 9\'s.\n\t\t\t\t\t\t\t// After the first if statement we have a count of all exhausted possible\n\t\t\t\t\t\t\t// values to subtract from all possible values for digit at index2.\n\t\t\t\t\t\t\tfor (int j : hs) {\n\t\t\t\t\t\t\t\tif ((index2 < nStrLength - 1 && j <= index2Digit - 1)\n\t\t\t\t\t\t\t\t\t\t|| (index2 == nStrLength - 1 && j <= index2Digit))\n\t\t\t\t\t\t\t\t\tinIndex2Range++;\n\t\t\t\t\t\t\t}\n\t\t\t\t\t\t\tif (index2 == nStrLength - 1)\n\t\t\t\t\t\t\t\tnoRepeatCountLocal = index2Digit + 1 - inIndex2Range;\n\t\t\t\t\t\t\telse\n\t\t\t\t\t\t\t\tnoRepeatCountLocal = index2Digit - inIndex2Range;\n\t\t\t\t\t\t}\n\t\t\t\t\t// Working on 9\'s like in 123,999,999. Possible values for each 9 is 10\n\t\t\t\t\t// for 0 to 9. Actual possible values however are possible values at each\n\t\t\t\t\t// index minus exhausted possible values at that index.\n\t\t\t\t\t} else {\n\t\t\t\t\t\tnoRepeatCountLocal *= mutations - index2;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\t// Inner for is done. Adding whatever we\'ve calculated to the total count.\n\t\t\t\tif (noRepeatCountLocal > 0)\n\t\t\t\t\tnoRepeatCount += noRepeatCountLocal;\n\t\t\t}\n\t\t}\n\t\t// Now we have count of permutations w/o repeated digits. Subtracting from n gives\n\t\t// count of permutations <= n w/ at least one repeated digit.\n\t\treturn n - noRepeatCount;\n\t}\n\n\t// Helper function to calculate count of permutations w/o repeated digits. Input is the\n\t// number of 9\'s to be accounted for. \n\tpublic int calcNumberOfNoRepeat(int numberOfDigits) {\n\t\tint noRepeatCount = 0;\n\t\tint mutations = 9;\n\t\tfor (int i = 0; i < numberOfDigits; i++) {\n\t\t\tif (i == 0)\n\t\t\t\tnoRepeatCount = mutations;\n\t\t\telse {\n\t\t\t\tnoRepeatCount *= mutations--;\n\t\t\t}\n\t\t}\n\t\treturn noRepeatCount;\n\t}\n}\n``` | 1 | 0 | ['Probability and Statistics', 'Java'] | 0 |
numbers-with-repeated-digits | Python O(1) time | python-o1-time-by-decomplexifier-n2j8 | The idea is to first count the numbers that have distinct digits. There are two cases. (1) Without the limitation of being at most n, there are 9*9*8*...(9-k+2) | decomplexifier | NORMAL | 2021-08-16T06:16:37.565979+00:00 | 2021-08-16T06:19:03.197777+00:00 | 487 | false | The idea is to first count the numbers that have distinct digits. There are two cases. (1) Without the limitation of being at most `n`, there are `9*9*8*...(9-k+2)` such numbers with `k` digits. (2) With the limitation `n`, we can count such numbers in ranges. For example, for `n = 3579`, we count the numbers with distinct digits as follows:\n[1, 10): 1 digit without limitation\n[10, 100): 2 digits without limitation\n[100, 1000): 3 digits without limitation\n[1000, 3000): 4 digits of the form {1,2}???\n[3000, 3500): 4 digits of the form 3{0,1,2,4}??\n[3500, 3570): 4 digits of the form 35{0,1,2,4,6}?\n[3570, 3579): 4 digits of the form 357{0,1,2,3,4,6,8}\n{3579}: 4 digits of the form 3579\n\nSince the complexity is linear in the number of digits of `n`, it is O(1).\n\n```\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n \n print = lambda *args: None\n \n n2 = min(n, 10**10-1)\n m = len(str(n2))\n print(f\'up to {n2} ({m} digits)\')\n \n @lru_cache\n def num_perms(start:int, count:int) -> int:\n if count <= 0:\n return 1\n elif count == 1:\n return start\n return start * num_perms(start-1, count-1)\n \n no_repeats = 0\n for k in range(1, m):\n no_repeats += 9 * num_perms(9, k-1)\n print(f\'up to length {m-1} no repeat: {no_repeats}\')\n \n digits = []\n n3 = n2\n while n3 > 0:\n digits.append(n3 % 10)\n n3 //= 10\n digits = digits[::-1]\n nd = len(digits)\n print(digits, nd)\n fixed_digits = set()\n for i, d in enumerate(digits):\n below = range(1,d) if i==0 else range(d)\n cand = set(below) - fixed_digits\n nc = len(cand)\n if i == 0:\n no_repeats_i = nc * num_perms(9, nd-i-1)\n else:\n no_repeats_i = nc * num_perms(10-i-1, nd-i-1)\n print(f\'no repeats fixing {digits[:i]}: {no_repeats_i}, cand={cand}\')\n no_repeats += no_repeats_i\n \n if d in fixed_digits:\n break\n fixed_digits.add(d)\n if len(fixed_digits) == nd:\n no_repeats += 1\n print(f\'total no repeat: {no_repeats}\')\n return n - no_repeats\n``` | 1 | 0 | [] | 0 |
numbers-with-repeated-digits | [Java] dfs+memo+bit | java-dfsmemobit-by-66brother-seyk | \nclass Solution {\n int dp[][][];\n public int numDupDigitsAtMostN(int N) {\n //at least 1 repeat digit\n if(N<=10)return 0;\n Strin | 66brother | NORMAL | 2020-09-09T00:59:28.028809+00:00 | 2020-09-09T01:04:25.858482+00:00 | 371 | false | ```\nclass Solution {\n int dp[][][];\n public int numDupDigitsAtMostN(int N) {\n //at least 1 repeat digit\n if(N<=10)return 0;\n String s=N+"";\n int cnt=0;\n int first=s.charAt(0)-\'0\';\n dp=new int[s.length()][1<<10][2];\n \n for(int i=0;i<dp.length;i++){\n for(int j=0;j<dp[0].length;j++){\n Arrays.fill(dp[i][j],-1);\n }\n }\n \n for(int i=1;i<=first;i++){\n if(i==first){\n cnt+=dfs(s,1,1<<i,1);\n }else{\n cnt+=dfs(s,1,1<<i,0);\n }\n }\n cnt+=dfs(s,1,0,0);//0 \n return N-cnt;\n }\n \n public int dfs(String s,int index,int bit,int state){\n if(index>=s.length())return 1;\n if(dp[index][bit][state]!=-1)return dp[index][bit][state];\n int digit=s.charAt(index)-\'0\';\n int res=0;\n if(state==1){//smae prefix\n for(int i=0;i<=digit;i++){\n if((bit&(1<<i))!=0)continue;\n if(i==digit){\n res+=dfs(s,index+1,(bit|(1<<i)),1);\n }else{\n res+=dfs(s,index+1,(bit|(1<<i)),0);\n }\n }\n \n }else{\n for(int i=0;i<10;i++){\n if((bit&(1<<i))!=0)continue;\n if(i==0&&bit==0&&index==s.length()-1)continue;\n if(i==0&&bit==0)res+=dfs(s,index+1,0,0);\n else res+=dfs(s,index+1,(bit|(1<<i)),0);\n }\n \n }\n dp[index][bit][state]=res;\n return res;\n }\n\n}\n\n``` | 1 | 0 | [] | 1 |
numbers-with-repeated-digits | constant time combinatorial counting | constant-time-combinatorial-counting-by-jgs3x | (A similar problem: https://leetcode.com/problems/ones-and-zeroes/)\n\nIf you studied probability, it is well known that considering the complement problem: \'t | vvave | NORMAL | 2019-09-29T18:27:51.877585+00:00 | 2019-09-29T18:33:05.110333+00:00 | 246 | false | (A similar problem: https://leetcode.com/problems/ones-and-zeroes/)\n\nIf you studied probability, it is well known that considering the complement problem: \'the count of number WITHOUT repeating digit that\'s less than N\' is easier to solve. And then we get the answer by subtracting this cnt from N.\n\nSo numbers M without repeating digits that\'s less than N has three types:\n1. M has the same prefix as N.\n2. M has the same length but the leading digit is non-zero and strictly less than leaading digit as N.\n3. M has strictly less digits than N.\n\nWe can count type (1)-(2) together, and (3) later.\ntype 1 and 2 requires us to remember the number of digit that\'s not used in the prefix but strictly less than the current digit. Let\'s see an example.\nSuppose N = 453232\n\ntype (1) are of the form 3xxxxx, 2xxxxx, 1xxxxx, the leading digit has 4-1 = 3 choices. Then the xxx part we can use whatever number, but not the choice of our leading digit, so that\'s 9\\*8\\*7\\*6\\*5, which we call perm(9,5).\ntype (2) are of the form 4yxxxx, 45yxxx, 453yxx, 4532yx, but we can\'t consider 45323x(?) because we see a repeating digit. so starting from the MSD we\'ll just count up to the first time we see a repeating digit in N. Notices that I put \'y\' instead of \'x\' for the first digit after the prefix. For 4yxxxx, since N = 453232, we can\'t use y to be greater than 5. so we use 3, 2, or 1, or 0. Notice that we can\'t use 4, because 4 has appeaered in the prefix. Anyhow, we use an array to store the number of digits available at i-th index that\'s strictly less than the ith-indes of N and hasn\'t been used in the prefix so far.\n\nFor type (3), we always have 9 choice for MSD, 9 choice for 2nd digit, 8 choice for 3rd digit. Using N=543232 as same exmaple, type (3) would cover 1000-9999, 100-999, 10-99, 0-9. Simple counting problem.\n\nNow subtract type (1) +(2)+(3) from N, that\'s the answer we have. \n\n```\nclass Solution {\n public int numDupDigitsAtMostN(int N) {\n int ans = 0;\n\n String num = Integer.toString(N);\n //Convert N to an array of digits for easy proccessing. A[0] stores the most sigifinicant digit.\n int[] A = new int[num.length()];\n for(int i = 0;i<A.length; i++){\n A[i] = num.charAt(i)-\'0\';\n }\n //cnt array stores the number of digit strictly smaller than A[i] and hasn\'t been used in the prefix. \n int[] cnt = new int[A.length];\n boolean[] used = new boolean[10];\n used[A[0]] = true;\n //we require the most significant digit to be non-zero.\n cnt[0] = A[0]-1;\n //rpt: The first repeating idx, after this idx, no number with the same prefix as N and is smaller than N has no repeating digit. So stop counting.\n int rpt = A.length;\n \n for(int i=1;i<A.length; i++){\n for(int j = 0;j<A[i];j++){\n if(!used[j]) cnt[i]++;\n }\n if(used[A[i]]){\n rpt=i;\n break;\n }\n used[A[i]] = true;\n }\n \n //count from most significant digit, the number of no repeating number with same prefix and has same length with N. \n \n for(int i = 0;i<rpt; i++){\n int c = cnt[i];\n c*=perm(9-i,A.length-i-1);\n ans+=c;\n }\n //if there\'s repeating idx, count that in.\n if(rpt!=A.length) ans+= cnt[rpt]*perm(9-rpt, A.length-rpt-1);\n \n //Now count the numbers which has length strictly less than N.\n for(int i = 1;i<A.length;i++){\n ans+= 9*perm(9,A.length-i-1);\n }\n if(rpt==A.length) ans++;\n return N-ans;\n }\n \n public int perm(int n, int k){\n int a= 1;\n for(int i = 0;i<k;i++){\n a*=(n-i);\n }\n return a;\n }\n \n}\n``` | 1 | 0 | [] | 0 |
numbers-with-repeated-digits | Java Digital DP | java-digital-dp-by-pokehunter-j191 | java\nclass Solution {\n public int numDupDigitsAtMostN(int N) {\n int[] digits = new int[10];\n int pos = 0, temp = N;\n while (N > 0) | pokehunter | NORMAL | 2019-09-21T08:03:16.167059+00:00 | 2019-09-21T08:03:16.167103+00:00 | 631 | false | ```java\nclass Solution {\n public int numDupDigitsAtMostN(int N) {\n int[] digits = new int[10];\n int pos = 0, temp = N;\n while (N > 0) {\n digits[pos++] = N % 10;\n N /= 10;\n }\n return temp - dfs(digits, pos - 1, 0, new int[10][1 << 10], true) + 1;\n }\n \n public int dfs(int[] digits, int pos, int pre, int[][] dp, boolean limit) {\n if (pos == -1) return 1;\n if (!limit && dp[pos][pre] != 0) return dp[pos][pre];\n int up = limit ? digits[pos] : 9;\n int ans = 0;\n for (int i = 0; i <= up; i++) {\n if ((pre & (1 << i)) != 0 && (pre != 0 || i != 0)) continue;\n if (pre == 0 && i == 0) {\n ans += dfs(digits, pos - 1, pre, dp, limit && i == up);\n } else {\n ans += dfs(digits, pos - 1, pre ^ (1 << i), dp, limit && i == up);\n }\n }\n if (!limit) dp[pos][pre] = ans;\n return ans;\n }\n}\n``` | 1 | 0 | [] | 2 |
numbers-with-repeated-digits | C++ Divide-and-conquer | c-divide-and-conquer-by-sanzenin_aria-b5jd | I guess no one want to read this long solution. So I am lazy to add comment\n```\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int N) {\n vector v | sanzenin_aria | NORMAL | 2019-06-19T01:29:23.037689+00:00 | 2019-06-19T01:37:38.834697+00:00 | 412 | false | I guess no one want to read this long solution. So I am lazy to add comment\n```\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int N) {\n vector<int> v = toVec(N);\n int n1 = numNoRepeat1(v, {}, 0);\n int n2 = numNoRepeat2(v.size() - 1);\n cout << N << " " << n1 << " " << n2 << endl;\n return N - n1 - n2;\n }\n\n // from 10^pow to N \n int numNoRepeat1(vector<int> & v, set<int> used, int i) {\n if (i == v.size()) return 1;\n int res = 0;\n int nCanbeUse = v[i]; // 0,1,2,3,4,...v[0]-1\n if (i == 0) nCanbeUse--; //leading digit cannot be 0\n for (auto x : used) if (x < v[i]) nCanbeUse--;\n res += nCanbeUse * permutation(10 - used.size() - 1, v.size() - i - 1);\n\n //repeated, early return\n if(used.count(v[i])) return res;\n\n used.insert(v[i]);\n res += numNoRepeat1(v, used, i + 1);\n return res;\n }\n\n int permutation(int num, int k) {\n int prod = 1;\n while (k--) prod *= num--;\n return prod;\n }\n\n // from 0 to 10^pow10 \n int numNoRepeat2(int pow10) {\n int sum = 0;\n while (pow10) {\n sum += 9 * permutation(9, pow10 - 1);\n pow10--;\n }\n return sum;\n }\n\n vector<int> toVec(int N) {\n auto s = to_string(N);\n vector<int> v;\n for (auto c : s) v.push_back(c - \'0\');\n return v;\n }\n}; | 1 | 0 | [] | 0 |
numbers-with-repeated-digits | C# standard depth first search with back tracking | c-standard-depth-first-search-with-back-m5cxu | March 21, 2019\nIt is the hard level algorithm. I like to share the standard depth first search using back tracking technique to solve the problem. What I did i | jianminchen | NORMAL | 2019-03-21T21:13:51.933991+00:00 | 2019-10-10T04:31:32.855618+00:00 | 433 | false | March 21, 2019\nIt is the hard level algorithm. I like to share the standard depth first search using back tracking technique to solve the problem. What I did is to study weekly contest 128 ranking 13 player\'s code, and then I wrote one based on my understanding. \n\nHere are steps to follow:\n1. Brute force solution, from rightmost digit, enumerate all the possible digit; \n2. Go to next digit by moving to left side, skip those used digits. Use one array with size 10 to record used digit from 0 to 9. \n3. Combine step 1 and step2, the brute force solution time complexity O(10!)\n4. Do not forget to back tracking\n```\nusing System;\nusing System.Collections.Generic;\nusing System.Diagnostics;\nusing System.Linq;\nusing System.Text;\nusing System.Threading.Tasks;\n\nnamespace _1015_number_with_repeated_digits_13\n{\n class Program\n {\n static void Main(string[] args)\n {\n NumDupDigitsAtMostN(872427638);\n Debug.Assert(value == 10); \n }\n\n public static int value = 0; \n public static bool[] taken = new bool[10];\n\n /// <summary>\n /// March 20, 2019\n /// study code based on ranking No. 13, VladaMG98\n /// https://leetcode.com/contest/weekly-contest-128/ranking/\n /// </summary>\n /// <param name="N"></param>\n /// <returns></returns>\n public static int NumDupDigitsAtMostN(int N)\n { \n return N - getAllDifferent(N) + 1; \n }\n\n private static int getAllDifferent(int N)\n {\n value = 0;\n for (int i = 0; i < taken.Length; i++)\n {\n taken[i] = false; \n }\n\n recursive(0, 0, N);\n return value; \n }\n\n /// <summary>\n /// Brute force solution\n /// Make sure that all numbers in the integer are distinct, less than and equal N.\n /// Problem statement:\n /// Given a positive integer N, return the number of positive integers less than or \n /// equal to N that have at least 1 repeated digit.\n /// Start from rightmost digit. \n /// </summary>\n /// <param name="number"></param>\n /// <param name="digit"></param>\n /// <param name="N"></param>\n private static void recursive(double number, int digit, int N)\n {\n if (number > N)\n {\n return; \n }\n\n // current number with value number is the one. \n value += 1;\n\n // Fix timeout bug\n if (number * 10 > N)\n {\n return;\n }\n\n for (int x = 0; x < 10; x++)\n {\n if (taken[x])\n {\n continue; \n }\n\n // make sure that the number is positive number\n var numberIsZero = digit == 0 && x == 0;\n if (numberIsZero)\n {\n continue;\n }\n\n taken[x] = true;\n recursive(number * 10 + x, digit + 1, N);\n \n // backtracking\n taken[x] = false; \n }\n }\n }\n}\n``` | 1 | 0 | [] | 1 |
numbers-with-repeated-digits | C++ method using permutation | c-method-using-permutation-by-lingtengqi-v1tg | \nauto __ =[]()\n{\n std::ios::sync_with_stdio(false);\n cin.tie(nullptr);\n return nullptr;\n}();\nclass Solution {\npublic:\n int numDupDigitsAtMo | lingtengqiu | NORMAL | 2019-03-18T06:49:11.037706+00:00 | 2019-03-18T06:49:11.037748+00:00 | 461 | false | ```\nauto __ =[]()\n{\n std::ios::sync_with_stdio(false);\n cin.tie(nullptr);\n return nullptr;\n}();\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int N) {\n //\u65E2\u7136\u8BA1\u7B97\u7684\u662F\u91CD\u590D\u7684\u4E2A\u6570\u6211\u4EEC\u53EF\u4EE5\u8BA1\u7B97\u4E0D\u91CD\u590D\u7684\u4E2A\u6570\uFF0C\u8FD9\u5C31\u662F\u4E2A\u6392\u5217\u7EC4\u5408\u7684\u95EE\u9898\n //\u5BF9\u4E8E\u8FD9\u4E2A\u95EE\u9898\u6211\u4EEC\u8981\u5148\u5199\u51FA\u6392\u5217\u7EC4\u5408\u7684\u7B97\u6CD5\u3002\n // second we must define our method upper boader.\n // such that 8999-->(9,0,0,0) \n // \n int retv = 0;\n vector<int> remain;\n for(int n = N+1;n>0;n/=10)\n {\n remain.insert(remain.begin(),n%10);\n }\n for(int i =1;i<remain.size();i++)\n {\n retv+=9*A(9,i-1);\n }\n // condition ,if this \u548C\u524D\u9762\u7684\u4E00\u6837\u5219\u8DF3\u8FC7\uFF0C\u56E0\u4E3A\u4E0D\u80FD\u6709\u91CD\u590D\u7684\uFF0C\u5982\u679C\u5B58\u5728\u4E24\u4E2A\u4E0A\u754C\u4E00\u6837beak \u6389\uFF0C\u56E0\u4E3A\u4E0D\u53EF\u80FD\u5728\u4ECE\u8FD9\u91CC\u51FA\u73B0\u4E24\u4E2A\u5B8C\u5168\u4E0D\u4E00\u6837\u7684\n unordered_set<int> sets;\n for(int i = 0;i<remain.size();i++)\n {\n for(int j = i==0?1:0;j<remain[i];j++)\n {\n if(!sets.count(j))\n {\n retv += A(9-i,remain.size()-1-i);\n }\n }\n if(sets.count(remain[i]))\n break;\n else\n {\n sets.insert(remain[i]);\n }\n }\n return N-retv;\n \n }\n int A(int n,int m)\n {\n //means C{n,m}\n //How can we deal with this problem, Can you give me a method to do ?\n //in this time, wo di it, such that.\n //A(n,m) = n*n-1*n-2*..n-m+1 = (n-m+1)*A(n,m-1)\n return m == 0?1:(n-m+1)*A(n,m-1);\n }\n};\n``` | 1 | 0 | [] | 0 |
numbers-with-repeated-digits | golang dp | golang-dp-by-lddlinan-0x9x | \ncount(0, dn...d1) = count(0, 9...9) + count(10...0, dn...d1)\ncount(10...0, dn...d1) = count(10...0, dn0...0-1) + count(dn0...0, dn...d1)\n\ndefine dp(s, n), | lddlinan | NORMAL | 2019-03-17T06:41:05.449380+00:00 | 2019-03-17T06:41:05.449410+00:00 | 256 | false | \ncount(0, dn...d1) = count(0, 9...9) + count(10...0, dn...d1)\ncount(10...0, dn...d1) = count(10...0, dn0...0-1) + count(dn0...0, dn...d1)\n\ndefine dp(s, n), the count for numbers who has n-digits not determined yet and s is its 0-9 indicator for its known digits. (do not care whether its known digits are all 0s)\ndp(s, n) = sum(s&(1<<i)? 10...0: dp(s|1<<i, n-1) for i in 0...9 )\n\nhence:\ncount(0, 9...9) = sum(countd(n) for n in {1..dn}) and countd(n) = sum(dfs(1<<i, n-1) for i in {1..9})\ncount(dn0...0, dn...d1) = sum(count(dni0...0, dn(i+1)0...0-1) for i in {0...d(n-1)-1})\nkeep track of the 0-9 mask for the processed digits, and if 0-9 mask already 1, then count all the possibles , otherwise solve sub problem.\n\nMaybe this is way too unnecessarily complex...... sadly this is how my brain wired....\n```\nvar dp map[int]int\nvar cs = []int{1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000}\n/* s is a 10-bit map indicating whether 0-9 digits already exist\ndp[s][n] yield a count for numbers which have at least n digits number, and some prefix map s\n*/\nfunc dfs(s, n int) int {\n if n<=0 { return 0; }\n k := (s<<4)|n;\n if v, ok := dp[k]; ok {\n return v\n }\n c := 0\n var i uint\n for i=0; i<10; i++ {\n if (s&(1<<i)) != 0 {\n c += cs[n-1]\n } else {\n c += dfs(s|(1<<i), n-1)\n }\n }\n dp[k] = c\n return c\n}\n\n/* count n digit numbers, between 10...0 to 99...9 */\nfunc count(n int) int {\n if n<=1 { return 0 }\n c := 0\n var i uint\n for i=1; i<10; i++ {\n c += dfs(1<<i, n-1)\n }\n return c\n}\n\nfunc numDupDigitsAtMostN(N int) int {\n if dp==nil { dp = make(map[int]int) }\n rem := make([]int, 10)\n for i:=0; i<10; i++ { rem[i] = N % cs[i] }\n d, ds := 0, make([]uint, 16)\n for {\n ds[d] = uint(N % 10)\n d += 1\n N /= 10\n if N==0 { break }\n }\n c, s := 0, 0\n /* accumulate counts from 0 to 9...9, where 9...9 < N */\n for i:=1; i<d; i++ { c += count(i) }\n /* from higher digit down, accumulate d(i+1)0..0 to d(i+1)d(i)0..0-1 */\n for i:=d-1; i>=0; i-- {\n var j uint\n if i==d-1 {j=1}\n for ; j<ds[i]; j++ {\n if ((s&(1<<j)) != 0) {\n c += cs[i]\n } else {\n c += dfs(s|(1<<j), i);\n }\n }\n if (s&(1<<ds[i])) != 0 {\n /* all the remaining numbers should be counted */\n c += (rem[i]+1)\n break\n }\n s |= (1<<ds[i])\n }\n return c\n}\n``` | 1 | 0 | [] | 0 |
numbers-with-repeated-digits | Digit Dp Soln | digit-dp-soln-by-ptfan-d64o | class Solution {\npublic:\n string num;\n int l ;\n int dp[11][2][2][1030];\n \n int d(int N)\n {\n int c = 0;\n while(N)\n | ptfan | NORMAL | 2019-03-17T06:17:32.181529+00:00 | 2019-03-17T06:17:32.181598+00:00 | 794 | false | class Solution {\npublic:\n string num;\n int l ;\n int dp[11][2][2][1030];\n \n int d(int N)\n {\n int c = 0;\n while(N)\n {\n c++;\n N /= 10;\n }\n return c;\n }\n \n int solve(int bit, int tight, int nonz, int mask)\n {\n if(dp[bit][tight][nonz][mask] != -1)\n return dp[bit][tight][nonz][mask];\n \n if(bit == l)\n {\n if(nonz)\n return dp[bit][tight][nonz][mask] = 1;\n else\n return dp[bit][tight][nonz][mask] = 0;\n }\n \n int v = num[bit] - \'0\';\n //cout << v << \'\\n\';\n int cans = 0;\n if(tight)\n {\n for(int i = 0; i <= v; i++)\n {\n int new_mask = mask;\n int new_tight = 0;\n int c_bit = ((mask >> i) & 1);\n if(nonz || (i != 0))\n new_mask |= (1 << i);\n if(i == v)\n new_tight = 1;\n if(c_bit == 0)\n cans += solve(bit + 1, new_tight, nonz || (i != 0),new_mask);\n }\n }\n else\n {\n for(int i = 0; i <= 9; i++)\n {\n int new_mask = mask;\n int c_bit = ((mask >> i) & 1);\n if(nonz || (i != 0))\n new_mask |= (1 << i);\n if(c_bit == 0)\n cans += solve(bit + 1, 0, nonz || (i != 0), new_mask);\n }\n }\n return dp[bit][tight][nonz][mask] = cans;\n }\n int numDupDigitsAtMostN(int N) {\n int dig = d(N);\n num = to_string(N);\n l = num.size();\n memset(dp, -1, sizeof dp);\n return (N - solve(0,1,0,0));\n }\n}; | 1 | 0 | [] | 1 |
numbers-with-repeated-digits | Simple || Digit DP || Bitmasking | simple-digit-dp-bitmasking-by-_phoenix_1-mb2d | IntuitionApproachComplexity
Time complexity:
O(k∗2∗1024∗2) where k represent the number of Digit in n
Space complexity:
O(k∗2∗1024∗2) where k represent t | _Phoenix_14 | NORMAL | 2025-04-10T10:54:39.989917+00:00 | 2025-04-10T10:54:39.989917+00:00 | 10 | false | # Intuition
Modified the standard Digit DP approach
# Approach
Started masking digits after occurance of a non zero digit
i.e. skipping leading zeros as they can repeat multiple times
# Complexity
- Time complexity:
O(k∗2∗1024∗2) where k represent the number of Digit in n
- Space complexity:
O(k∗2∗1024∗2) where k represent the number of Digit in n
# Code
```cpp []
class Solution {
public:
int dp[11][2][1024][2];
int f(string& num, int n, bool tight, int mask, bool started) { //started rep leading zeroes over or not
if (n == 0) return 1;
if (dp[n][tight][mask][started] != -1) return dp[n][tight][mask][started];
int ub = tight ? (num[num.size() - n] - '0') : 9;
int ans = 0;
for (int dig = 0; dig <= ub; dig++){
bool newStrt=started|(dig!=0); //check did first non 0 come?
int masked=mask;
if(newStrt){ //newStrt becomes 1 then we can start masking
if (mask & (1<<dig)) continue; //digit used earlier
masked|=(1<<dig);
}
ans+=f(num,n-1,tight&(dig==ub),masked,newStrt);
}
return dp[n][tight][mask][started] = ans;
}
int numDupDigitsAtMostN(int n) {
memset(dp,-1,sizeof dp);
string num = to_string(n);
return n - f(num,num.length(),1,0,0) +1;
}
};
``` | 0 | 0 | ['Math', 'Dynamic Programming', 'C++'] | 0 |
numbers-with-repeated-digits | Numbers With Repeated Digits | numbers-with-repeated-digits-by-ujju27-1owc | IntuitionInstead of counting numbers with repeated digits directly, we use a complement approach:
Count numbers that only have unique digits (easier to compute) | UjjU27 | NORMAL | 2025-03-03T21:10:42.548260+00:00 | 2025-03-03T21:10:42.548260+00:00 | 16 | false | # Intuition
Instead of counting numbers with repeated digits directly, we use a complement approach:
Count numbers that only have unique digits (easier to compute).
Subtract from n to get the count of numbers with at least one repeated digit.
Example
For n = 100, we count:
Unique digit numbers (1-100): {1, 2, 3, ..., 9, 10, 12, ..., 98}
Numbers with repeated digits: {11, 22, ..., 99, 100}
Answer: n - unique_count = 100 - 90 = 10
# Approach
Convert n to a digit array:
Example: 1000 → [1,0,0,0]
Count numbers with all unique digits:
For numbers with fewer digits (1 to d-1 digits):
Use permutations to count numbers with unique digits.
For numbers with the same length as n:
Use backtracking with a set to ensure uniqueness.
Compute the result using the complement principle:
Numbers with repeated digits
=
𝑛
−
Numbers with unique digits
Numbers with repeated digits=n−Numbers with unique digits
# Complexity
- Time complexity:O(logn) (as d ≤ 10 for n ≤ 10^9)
- Space complexity:O(1), since only a few variables are used
# Code
```java []
import java.util.*;
class Solution {
public int numDupDigitsAtMostN(int n) {
List<Integer> digits = new ArrayList<>();
int temp = n + 1; // To include 'n' in the calculation
while (temp > 0) {
digits.add(temp % 10);
temp /= 10;
}
Collections.reverse(digits);
int numDigits = digits.size();
int uniqueCount = 0;
// Count numbers with fewer digits
for (int i = 1; i < numDigits; i++) {
uniqueCount += countUniqueNumbersWithLength(i);
}
// Count numbers with the same length as 'n' but smaller
Set<Integer> seen = new HashSet<>();
for (int i = 0; i < numDigits; i++) {
int digit = digits.get(i);
for (int d = (i == 0) ? 1 : 0; d < digit; d++) {
if (!seen.contains(d)) {
uniqueCount += countPermutations(9 - i, numDigits - i - 1);
}
}
if (seen.contains(digit)) break;
seen.add(digit);
}
return n - uniqueCount;
}
// Count numbers with unique digits for lengths < numDigits
private int countUniqueNumbersWithLength(int length) {
if (length == 1) return 9; // 1-9
int count = 9, available = 9;
for (int i = 1; i < length; i++) {
count *= available;
available--;
}
return count;
}
// Count valid numbers with unique digits using permutation formula
private int countPermutations(int available, int length) {
int count = 1;
for (int i = 0; i < length; i++) {
count *= available;
available--;
}
return count;
}
public static void main(String[] args) {
Solution sol = new Solution();
System.out.println(sol.numDupDigitsAtMostN(20)); // Output: 1
System.out.println(sol.numDupDigitsAtMostN(100)); // Output: 10
System.out.println(sol.numDupDigitsAtMostN(1000)); // Output: 262
}
}
``` | 0 | 0 | ['Java'] | 0 |
numbers-with-repeated-digits | 🧮 Digit DP with Bitmask 🔢 | Time: O(10 × 2^10 × log n) | Space: O(10 × 2^10) | digit-dp-with-bitmask-time-o10-x-210-x-l-hv0e | IntuitionThis problem asks to find the number of positive integers less than or equal to n that have at least one repeated digit. A direct approach would be ine | holdmypotion | NORMAL | 2025-02-26T19:09:39.928306+00:00 | 2025-02-26T19:09:39.928306+00:00 | 6 | false | # Intuition
This problem asks to find the number of positive integers less than or equal to `n` that have at least one repeated digit. A direct approach would be inefficient, requiring checking each number from 1 to n. Instead, the solution uses a complementary counting technique: find all numbers with no repeated digits and subtract from n.
The key insight is to use digit-based dynamic programming (Digit DP) with a bitmask to track which digits have already been used, ensuring uniqueness.
# Approach
The solution employs a top-down dynamic programming approach with memoization:
1. Convert the number `n` to a string to process each digit individually
2. Define a recursive function `dp(pos, tight, used, started)` with parameters:
- `pos`: Current position in the number
- `tight`: Boolean indicating if current digit is constrained by the original number
- `used`: Bitmask representing which digits have been used
- `started`: Boolean indicating if we've started placing non-zero digits
3. Base case: If all positions are filled and we've placed at least one digit, return 1
4. For each position, there are two scenarios:
- Skip the current position if we haven't started placing digits yet
- Try placing each valid digit (0-9) if it hasn't been used before
5. Track state using the bitmask `used`, where the i-th bit represents whether digit i has been used
6. Use the `tight` flag to ensure we don't exceed the original number
7. Finally, subtract the count of numbers with unique digits from `n` to get the answer
The memoization table stores results for each state combination, avoiding redundant calculations.
# Complexity
- Time complexity: **O(10 × 2^10 × log n)**
- Number of digits in n is proportional to log n
- For each position, we have at most 10 digit choices
- Bitmask for used digits has 2^10 possible states
- Each state combination is computed once due to memoization
- Space complexity: **O(10 × 2^10 × log n)**
- The memoization table stores results for each state: position (log n) × tight (2) × used (2^10) × started (2)
- This can be simplified to O(10 × 2^10) since the other factors are small constants
# Code
```python3
class Solution:
def numDupDigitsAtMostN(self, n: int) -> int:
s = str(n)
memo = {}
def dp(pos, tight, used, started):
if pos >= len(s):
return 1 if started else 0
key = (pos, tight, used, started)
if key in memo:
return memo[key]
res = 0
if not started:
res += dp(pos + 1, False, used, False)
start = 0 if started else 1
limit = int(s[pos]) if tight else 9
for digit in range(start, limit+1):
if (used >> digit) & 1:
continue
new_mask = used | (1 << digit)
new_tight = tight and (digit == limit)
res += dp(pos + 1, new_tight, new_mask, True)
memo[key] = res
return res
return n-dp(0, True, 0, False)
```
# Detailed Explanation
The solution leverages Digit DP, a powerful technique for solving problems involving digit constraints:
1. **State Definition**:
- `pos`: Current position in the number (0-indexed from left)
- `tight`: Restricts digit choices if we're following n's prefix
- `used`: Bitmask where the i-th bit is 1 if digit i has been used
- `started`: Indicates if we've started placing non-zero digits
2. **Bit Manipulation**:
- `(used >> digit) & 1`: Checks if digit is already used
- `used | (1 << digit)`: Marks digit as used in the bitmask
3. **Decision Logic**:
- If `not started`, we can skip the current position (leading zeros are ignored)
- For valid digits, we update `new_tight` based on whether the current digit matches the limit
- The starting digit range is adjusted to avoid leading zeros in numbers
4. **Final Calculation**:
- `dp(0, True, 0, False)` counts numbers with no repeated digits
- Subtracting from `n` gives the count of numbers with at least one repeated digit
This approach efficiently handles the counting without explicitly checking each number, making it suitable for large values of n.
---
If you find this editorial helpful, please consider upvoting! ⬆️ | 0 | 0 | ['Dynamic Programming', 'Python3'] | 0 |
numbers-with-repeated-digits | easy solution but throwing tle ( | easy-solution-but-throwing-tle-by-lovell-5xlp | Code | lovell3232 | NORMAL | 2025-01-30T11:17:53.177427+00:00 | 2025-01-30T11:17:53.177427+00:00 | 7 | false | # Code
```python3 []
class Solution:
def numDupDigitsAtMostN(self, n: int) -> int:
c = 0
for y in range(0, n+1):
if len(set(str(y))) != len(str(y)):
c += 1
return c
``` | 0 | 0 | ['Python3'] | 0 |
numbers-with-repeated-digits | Python Hard Digit DP + Bitmask | python-hard-digit-dp-bitmask-by-lucassch-kwj1 | null | lucasschnee | NORMAL | 2025-01-07T16:18:40.432693+00:00 | 2025-01-07T16:18:40.432693+00:00 | 8 | false | ```python3 []
class Solution:
def numDupDigitsAtMostN(self, n: int) -> int:
'''
all - none
digit dp free and constrained
'''
s = str(n)
N = len(s)
@cache
def free(index, used):
if index == N:
return 1
t = 0
for i in range(10):
if not (1 << i) & used:
t += free(index + 1, used | (1 << i))
return t
@cache
def need_zero(index):
if index == N:
return 0
t = need_zero(index + 1)
for i in range(1, 10):
t += free(index + 1, 1 << i)
return t
@cache
def constrained(index, used):
if index == N:
return 1
best = 0
for i in range(int(s[index])):
if not (1 << i) & used:
best += free(index + 1, (1 << i) | used)
if not (1 << int(s[index])) & used:
best += constrained(index + 1, (1 << int(s[index])) | used)
return best
# total numbers
total = n
# numbers with no reps
no_rep = 0
for i in range(1, int(s[0])):
no_rep += free(1, (1 << i))
no_rep += need_zero(1)
no_rep += constrained(1, (1 << int(s[0])))
# print(total, no_rep)
return total - no_rep
``` | 0 | 0 | ['Python3'] | 0 |
numbers-with-repeated-digits | 1012. Numbers With Repeated Digits | 1012-numbers-with-repeated-digits-by-g8x-636c | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-01T12:50:08.734222+00:00 | 2025-01-01T12:50:08.734222+00:00 | 8 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numDupDigitsAtMostN(int n) {
vector<int> digits;
int temp = n + 1;
while (temp) {
digits.push_back(temp % 10);
temp /= 10;
}
int res = 0, len = digits.size(), mult = 9;
for (int i = 0; i < len - 1; i++) {
res += mult;
mult *= 9 - i;
}
mult /= 9;
vector<bool> used(10, false);
for (int i = 0; i < len; i++) {
int d = digits[len - i - 1];
for (int j = i == 0 ? 1 : 0; j < d; j++) if (!used[j]) res += mult;
mult /= 9 - i;
if (used[d]) break;
used[d] = true;
}
return n - res;
}
};
``` | 0 | 0 | ['C++'] | 0 |
numbers-with-repeated-digits | O(1) / O(1) via precomputation | o1-o1-via-precomputation-by-adam-hoelsch-q975 | IntuitionThere are far more numbers that have repeated digits than those that don't. If we can efficiently enumerate all the numbers that do not have repeated d | adam-hoelscher | NORMAL | 2024-12-25T08:34:29.731091+00:00 | 2025-01-06T17:51:51.174837+00:00 | 10 | false | # Intuition
There are far more numbers that have repeated digits than those that don't. If we can efficiently enumerate all the numbers that do not have repeated digits into a sorted array, then we can use a binary search to efficiently count the number that are less than `n+1`. Subtracting that from `n` will give us the count of numbers that do have repeated digits.
# Approach
Precompute all numbers that have no repeated digits and sort them when the program starts. Run a binary search for each individual query.
To save time we can do a couple simple things:
1. Precompute the values in order, so they don't have to be sorted.
2. Preallocate the array, since the number of elements is fixed at 8,877,690.
Also to save time, we want to already know which digits are unused in each value when we reach it. This allows us to save time by iterating over just the unused digits instead of over all 10 digits. Attempting to use a second array for this will run us out of memory, so we get a bit clever.
1. When we first add a value to the array we left shift it by 10 bits and also store a bit set representing the digits that are not part of that number.
2. Later when when we reach each value, we first extract the set of unused digits and then right shift the element to restore the original value.
This is not a fantastically intuitive approach, but it cuts the precomputation time significantly. In Go, this allows the entire bad array to be created in less than 50 milliseconds.
# Complexity
- Time complexity: $$O(1)$$
Binary search runs in $$O(log(len(array)))$$. The array's size is fixed, regardless of the value of `n`.
Since the base is fixed to 10, precomputation of the array is also $$O(1)$$.
If the base, `b`, were not fixed, the precomputation time would be dominated by the permuation of all `b` digits, which would take $$O(b!)$$ time.
- Space complexity: $$O(1)$$
Precomputation creates an array of fixed size for a fixed base. Therefore space is $$O(1)$$.
If the base, `b`, were not fixed, the precomputed array's contents would be dominated by the permuation of all `b` digits, which would take $$O(b!)$$ space.
# Code
```golang []
// Preallocating space drops the time for init() significantly
var bad = make([]int, 0, 8_877_690)
func init() {
// Bit set of all 10 digits
var full int = 1 << 10 - 1
for i := 1; i < 10; i++ {
// Make bit set of digits other than i
mask := full &^ (1 << i)
// Add both the value and the bit set to the array
bad = append(bad, i << 10 | mask)
}
for i := 0; i < len(bad); i++ {
// Extract the set of unused digits
open := bad[i] & full
// Make the element just the value
bad[i] >>= 10
for curr, b := open, 0; curr > 0; curr ^= b {
// Get the LSB from those remaining
b = curr & -curr
// Convert that bit to the digit it represents
d := bits.Len(uint(b)) - 1
// Get the correct mask for the next value
mask := open ^ (1 << d)
// Add the next value and its mask to the array
bad = append(bad, (10*bad[i]+d) << 10 | mask)
}
}
}
func numDupDigitsAtMostN(n int) int {
// Binary search for n+1 in case n is in the array
return n - sort.SearchInts(bad, n+1)
}
``` | 0 | 0 | ['Go'] | 0 |
numbers-with-repeated-digits | Track repeat using bit mask then digit dp | track-repeat-using-bit-mask-then-digit-d-g4tw | Intuition\n Describe your first thoughts on how to solve this problem. \nWe can keep a track of digits used so far using a bit mask and if digit we are trying t | el-profesor | NORMAL | 2024-11-03T12:37:39.947681+00:00 | 2024-11-03T12:37:39.947705+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can keep a track of digits used so far using a bit mask and if digit we are trying to use now is already set in the bit mask then set the \'repeat\' variable to 1 (or true)\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDigit dp with mask. We also need a nz (non-zero) tracker, as for the leading 0s we should not set the bit mask to 1.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(1024 x logn) # base 10\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1024 x logn) # base 10\n\n# Code\n```python3 []\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n @cache \n def dp(i, num, less, mask, rep, nz):\n if i==len(num):\n if rep and mask!=1: return 1\n return 0\n res = 0\n for j in range(10):\n new_mask = mask\n if not (nz==0 and j==0):\n new_mask = mask|(1<<j)\n new_rep = rep\n if mask&(1<<j):\n new_rep = 1\n\n if j<int(num[i]):\n res+=dp(i+1, num, 1, new_mask, new_rep, nz|(j!=0))\n elif j==int(num[i]):\n res+=dp(i+1, num, less, new_mask, new_rep, nz|(j!=0))\n elif less:\n res+=dp(i+1, num, 1, new_mask, new_rep, nz|(j!=0))\n return res\n return dp(0, str(n), 0, 0, 0, 0)\n``` | 0 | 0 | ['Python3'] | 0 |
numbers-with-repeated-digits | Solution using Digit DP by Top-down and Bottom-up | solution-using-digit-dp-by-top-down-and-mn4fb | Code\n\n### Top-down approach\npython3 []\nclass Solution:\n def convert(self, digit):\n return ord(digit) - ord(\'0\')\n\n # f1 bool: has smaller | trieutrng | NORMAL | 2024-10-05T08:40:27.549965+00:00 | 2024-10-05T08:40:27.549986+00:00 | 15 | false | # Code\n\n### Top-down approach\n```python3 []\nclass Solution:\n def convert(self, digit):\n return ord(digit) - ord(\'0\')\n\n # f1 bool: has smaller digit appeared?\n # f2 int: bitmask for tracking appeared digits\n # f3 bool: leading zeros?\n def digitDP(self, i, f1, f2, f3, s, dp):\n if i>=len(s):\n return 1\n if dp[i][f1][f2][f3] != None:\n return dp[i][f1][f2][f3]\n bound = 10\n if not f1:\n bound = self.convert(s[i]) + 1\n cnt = 0\n # digit 0 -> 9 at i\n for digit in range(bound):\n # if not leading zeros and current digit is 0 but exists in f2\n if not f3 and digit==0 and f2&1 == 1:\n continue\n\n # if digit is chosen\n if f2 & (1<<digit) != 0:\n continue\n \n newF1 = f1 or (digit<self.convert(s[i]))\n newF2 = f2\n\n # if leading zeros and digit is 0, keep leading zeros\n newF3 = f3 and digit==0\n # if not leading zeros, add digit to appeared set (include 0)\n if not newF3:\n newF2 ^= (1<<digit)\n \n cnt += self.digitDP(i+1, newF1, newF2, newF3, s, dp)\n\n dp[i][f1][f2][f3] = cnt\n\n return dp[i][f1][f2][f3]\n\n def topDown(self, n):\n # because find numers with condition at least one tougher than condition no repeated digits\n # therefore, I will find all the number without repeated digits and then get the required number by all number - no repeated\n s = str(n)\n l = len(s)\n dp = [[ [ [ None for _ in range(2) ] for _ in range(1<<11) ] for _ in range(2) ] for _ in range(l)]\n return n - self.digitDP(0, 0, 0, 1, s, dp) + 1 \n\n def numDupDigitsAtMostN(self, n: int) -> int:\n return self.topDown(n)\n```\n\n### Bottom-up approach\n```python3 []\nclass Solution:\n def convert(self, digit):\n return ord(digit) - ord(\'0\')\n\n def bottomUp(self, n):\n s = str(n)\n l = len(s)\n\n # dp[i][f1][f2][f3]\n # the ith digit from left\n # f1 bool: has smaller digit appeared?\n # f2 int: bitmask for tracking appeared digits\n # f3 bool: leading zeros?\n dp = [[ [ [ 0 for _ in range(2) ] for _ in range(1<<11) ] for _ in range(2) ] for _ in range(l+1)]\n\n # base case: all the zero length will be treated as successful\n for f1 in range(2):\n for f2 in range(1<<11):\n for f3 in range(2):\n dp[l][f1][f2][f3] = 1\n\n for i in range(l-1, -1, -1):\n for f1 in range(2):\n for f2 in range(1<<11):\n for f3 in range(2):\n bound = 10\n if f1==0:\n bound = self.convert(s[i]) + 1\n\n # digit 0 -> 9 at i\n for digit in range(bound):\n # if not leading zeros and current digit is 0 but exists in f2\n if f3==0 and digit==0 and f2&1 == 1:\n continue\n # if digit is chosen\n if f2 & (1<<digit) != 0:\n continue\n\n newF1 = f1==1 or (digit<self.convert(s[i]))\n newF2 = f2\n\n # if leading zeros and digit is 0, keep leading zeros\n newF3 = f3==1 and digit==0\n # if not leading zeros, add digit to appeared set (include 0)\n if not newF3:\n newF2 ^= (1<<digit)\n \n dp[i][f1][f2][f3] += dp[i+1][newF1][newF2][newF3]\n\n return n - dp[0][0][0][1] + 1\n\n def numDupDigitsAtMostN(self, n: int) -> int:\n return self.bottomUp(n)\n``` | 0 | 0 | ['Dynamic Programming', 'Bitmask', 'Python3'] | 0 |
numbers-with-repeated-digits | 4 dimensions Digit DP - Top-Down approach | 4-dimensions-digit-dp-top-down-approach-c94qc | Code\npython3 []\nclass Solution:\n def convert(self, digit):\n return ord(digit) - ord(\'0\')\n\n # f1 bool: has smaller digit appeared?\n # f2 | trieutrng | NORMAL | 2024-10-05T03:43:55.099296+00:00 | 2024-10-05T08:00:35.675299+00:00 | 13 | false | # Code\n```python3 []\nclass Solution:\n def convert(self, digit):\n return ord(digit) - ord(\'0\')\n\n # f1 bool: has smaller digit appeared?\n # f2 int: bitmask for tracking appeared digits\n # f3 bool: leading zeros?\n def digitDP(self, i, f1, f2, f3, s, dp):\n if i>=len(s):\n return 1\n if dp[i][f1][f2][f3] != None:\n return dp[i][f1][f2][f3]\n bound = 10\n if not f1:\n bound = self.convert(s[i]) + 1\n cnt = 0\n # digit 0 -> 9 at i\n for digit in range(bound):\n # if not leading zeros and current digit is 0 but exists in f2\n if not f3 and digit==0 and f2&1 == 1:\n continue\n\n # if digit is chosen\n if f2 & (1<<digit) != 0:\n continue\n \n newF1 = f1 or (digit<self.convert(s[i]))\n newF2 = f2\n\n # if leading zeros and digit is 0, keep leading zeros\n newF3 = f3 and digit==0\n # if not leading zeros, add digit to appeared set (include 0)\n if not newF3:\n newF2 ^= (1<<digit)\n \n cnt += self.digitDP(i+1, newF1, newF2, newF3, s, dp)\n\n dp[i][f1][f2][f3] = cnt\n\n return dp[i][f1][f2][f3]\n\n def numDupDigitsAtMostN(self, n: int) -> int:\n # because find numers with condition at least one tougher than condition no repeated digits\n # therefore, I will find all the number without repeated digits and then get the required number by all number - no repeated\n s = str(n)\n l = len(s)\n dp = [[ [ [ None for _ in range(2) ] for _ in range(1<<10) ] for _ in range(2) ] for _ in range(l)]\n return n - self.digitDP(0, 0, 0, 1, s, dp) + 1 \n``` | 0 | 0 | ['Dynamic Programming', 'Bitmask', 'Python3'] | 0 |
numbers-with-repeated-digits | Bitmask DP + Digit DP | C++ 17ms Solution | bitmask-dp-digit-dp-c-17ms-solution-by-n-fw8k | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | noobita_07 | NORMAL | 2024-09-30T12:03:02.631882+00:00 | 2024-09-30T12:03:02.631917+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\n int dp[(1<<10)+1][10][2][2][2];\npublic:\n int solve(string &str, int i, bool tight, bool ok, bool is, int mask,\n int dp[(1<<10)+1][10][2][2][2]){\n if(i == str.size()) return ok;\n if(dp[mask][i][tight][ok][is] != -1) return dp[mask][i][tight][ok][is];\n int ans = 0;\n if(tight){\n for(char ch=\'0\';ch<=str[i];ch++){\n if(!is && (ch == \'0\')){\n ans += solve(str,i+1,(ch==str[i]),0, 0, 0,dp);\n }\n else {\n int z = ch-\'0\';\n ans += solve(str, i+1,(ch==str[i]), (ok | (mask&(1<<z))), 1, mask | (1<<z),dp);\n }\n }\n }\n else{\n for(char ch=\'0\';ch<=\'9\';ch++){\n if(!is && (ch == \'0\')){\n ans += solve(str, i+1,0, 0, 0, 0, dp);\n }\n else {\n int z = ch-\'0\';\n ans += solve(str, i+1, 0, (ok | mask&(1<<z)), 1, mask | (1<<z), dp);\n }\n }\n }\n return dp[mask][i][tight][ok][is] = ans;\n }\n int numDupDigitsAtMostN(int n) {\n string str = to_string(n);\n memset(dp, -1, sizeof(dp));\n return solve(str, 0, 1, 0, 0, 0, dp);\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'C++'] | 0 |
numbers-with-repeated-digits | [c++] dp bitmask | c-dp-bitmask-by-vl4deee11-a9o5 | \n#include <iostream>\n#include <queue>\n#include <vector>\n#include <cmath>\n#include <string>\n#include <sstream>\n#include <cstring>\n#include <algorithm>\n# | vl4deee11 | NORMAL | 2024-09-27T14:33:55.334113+00:00 | 2024-09-27T14:33:55.334150+00:00 | 0 | false | ```\n#include <iostream>\n#include <queue>\n#include <vector>\n#include <cmath>\n#include <string>\n#include <sstream>\n#include <cstring>\n#include <algorithm>\n#include <climits>\n#include <stack>\n#include <set>\n#include <map>\n#include <list>\n#include <cassert>\n#include <unordered_map>\n#include <numeric>\n#include <iomanip>\n#include <iostream>\n#include <cstdio>\n#include <algorithm>\n#include <queue>\n#include <cstdlib>\n#include <cstring>\n\nusing namespace std;\n#pragma GCC optimize("O3,unroll-loops")\n#pragma GCC target("avx2,bmi,bmi2,lzcnt,popcnt")\n\n/* TYPES */\n#define xf first\n#define xs second\n#define ll long long int\n#define lli int64_t\n#define ulli uint64_t\n#define dbl double\n#define ldbl long double\n#define str string\n#define pii pair<int, int>\n#define pll pair<ll,ll>\n#define vi vector<int>\n#define vs vector<string>\n#define vll vector<long long>\n#define mii map<int, int>\n#define si set<int>\n#define sc set<char>\n\n/* FUNCTIONS */\n#define mid(l, r) \t ((l + r) >> 1)\n#define all(a) a.begin(),a.end()\n#define v(t) vector<t>\n#define st(t) stack<t>\n#define ar(t,sz) array<t,sz>\n#define s(t) set<t>\n#define ss(a) sort(a.begin(),a.end())\n#define ms(t) multiset<t>\n#define mipq(t) priority_queue<t>\n#define mapq(t) priority_queue<t,v(t),less<t>>\n#define trpl(a,b,c) tuple<a,b,c>\n#define m(t, t2) map<t, t2>\n#define um(t, t2) unordered_map<t, t2>\n#define p(t, t2) pair<t, t2>\n#define f(i, s, e) for(long long int i=s;i<e;i++)\n#define fc(i, s, e, c) for(long long int i=s;i<e;i+=c)\n#define fa(k,in) for(auto k:in)\n#define fm(i, s, e) for(long long int i=s;i!=e;i++)\n#define cf(i, s, e) for(long long int i=s;i<=e;i++)\n#define rf(i, e, s) for(long long int i=e-1;i>=s;i--)\n#define wl(c) while(c)\n#define pb push_back\n#define mpp make_pair\n#define cl clear\n#define eb emplace_back\n\nint mem[10][2][2][2][1024];\nstr fs;\nclass Solution {\npublic:\n int dp(int i,bool f,bool f2,int c,int bm){\n if(i<0)return(!f&&c!=0&&f2)?1:0;\n if(mem[i][f][f2][c][bm]!=-1)return mem[i][f][f2][c][bm];\n int z=fs[i]-\'0\';\n int a=0;\n f(nk,0,10){\n ll k=(1<<nk);\n bool nf2=f2;\n if((bm&k)!=0){nf2|=1;}\n a+=dp(i-1,nk<z?0:(nk==z?f:1),nf2,nk!=0,bm|k);\n }\n return mem[i][f][f2][c][bm]=a+(c!=0&&f2);\n }\n\n int numDupDigitsAtMostN(int n) {\n if(n<=10){return 0;}\n memset(mem,-1,sizeof(mem));\n fs=to_string(n);\n return dp(fs.size()-1,0,0,0,0);\n }\n};\n``` | 0 | 0 | [] | 0 |
numbers-with-repeated-digits | Digit DP with Bitmasking | digit-dp-with-bitmasking-by-anshab45-kfqy | Intuition\nThe goal is to count how many numbers up to a given number n have repeated digits. To solve this, we use digit DP. \n\nThe idea is to break down the | ANSHAB45 | NORMAL | 2024-09-12T09:00:10.731675+00:00 | 2024-09-12T09:00:10.731740+00:00 | 11 | false | # Intuition\nThe goal is to count how many numbers up to a given number `n` have repeated digits. To solve this, we use **digit DP**. \n\nThe idea is to break down the problem digit by digit and track the state of the number being formed.\n\nWe use a bitmask to keep track of which digits have been used so far.\n\n# Approach\nWe define a recursive function `solve()` that explores each digit of the number `n`:\n\n1. **State Variables**:\n - `pos`: The current index of digit we are processing.\n - `tight`: Whether we are still bound by the digits of `n` (true if the current prefix of the number is still less than or equal to the corresponding prefix of `n`).\n - `mask`: A bitmask to track which digits have been used so far (each bit in the mask corresponds to a digit).\n - `repeated`: A boolean that tracks if any digit has been repeated in the current number.\n\n2. **Recursive Case**:\n - For each digit in the range of possible digits (`0-9` or `0-upper_bound` based on the `tight` constraint), we either set a digit for the current position or skip to the next state.\n - If the digit `i` has already been used (tracked using the mask), we set `repeated = true`.\n - If `i` is a new digit, we mark it in the mask by toggling its corresponding bit.\n - Leading zeros are handled separately to avoid marking them in the mask.\n\n3. **Base Case**:\n - When we reach the end of the number (i.e., `pos == str.size()`), we return whether a repeated digit has been found for this number.\n\n4. **DP Memoization**:\n - We use a 4D DP array `dp[pos][tight][mask][repeated]` to store the results of previously computed states, which avoids redundant calculations.\n\n\n# Complexity\n- **Time complexity**: \n The time complexity is determined by the number of digits in `n`, which is at most `log10(n)`. For each position (digit), there are at most `2` possible values for `tight` and `repeated`, and `1024` possible bitmasks (since we are using a 10-bit mask for the digits). Hence, the time complexity is approximately $$O(\\log_{10}(n) \\times 2 \\times 1024 \\times 2)$$, which simplifies to $$O(\\log_{10}(n)*(2^n))$$ in practical terms.\n\n- **Space complexity**: \n The space complexity is determined by the size of the DP table, which has dimensions `log10(n) \xD7 2 \xD7 1024 \xD7 2`, and the recursive stack. Hence, the space complexity is $$O(\\log_{10}(n) \\times 2 \\times 1024 \\times 2)$$, which also simplifies to $$O(\\log_{10}(n)*(2^n))$$.\n\n# Code\n```cpp\nclass Solution {\npublic:\nstring s;\nint sz;\nint dp[10][1<<10][2][2];\n int dfs(int ind, int mask, bool tight, bool repeated)\n {\n if(ind == sz) return repeated;\n int ub = tight ? s[ind] - \'0\' : 9;\n if(dp[ind][mask][tight][repeated]!=-1) return dp[ind][mask][tight][repeated];\n int res = 0;\n for(int i = 0;i<=ub;i++)\n {\n int newMask = mask;\n if(i != 0 || mask != 0)\n {\n newMask = mask | (1<<i);\n }\n res += dfs(ind+1,newMask,tight & (i == ub), repeated | (mask&(1<<i)));\n }\n return dp[ind][mask][tight][repeated] = res;\n }\n int numDupDigitsAtMostN(int n) {\n int mask = 0;\n memset(dp,-1,sizeof(dp));\n bool repeated = false;\n bool tight = true;\n s = to_string(n);\n sz = s.size();\n return dfs(0,mask,tight,repeated);\n }\n}; | 0 | 0 | ['Recursion', 'Memoization', 'C++'] | 0 |
numbers-with-repeated-digits | Numbers With Repeated Digits || DP || C++ | numbers-with-repeated-digits-dp-c-by-dna-ypgb | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | dnanper | NORMAL | 2024-09-09T09:42:53.477058+00:00 | 2024-09-09T09:42:53.477087+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int n) \n {\n string digit = to_string(n+1);\n int m = digit.size();\n int res = 0;\n for (int i = 1; i < m; i++)\n res += 9*A(9, i-1);\n vector<int> seen(10, 0);\n for (int i = 0; i < m; i++)\n {\n int cur = digit[i] - \'0\';\n for (int k = (i>0) ? 0 : 1; k < cur; k++)\n if (!seen[k]) res += A(10-(i+1), m-(i+1));\n if (seen[cur]) break;\n seen[cur] = 1;\n }\n return n-res;\n }\nprivate:\n int A(int a, int b)\n {\n if (b==0) return 1;\n return (a-b+1)*A(a, b-1); // A(9,3) -> 7*8*9\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
numbers-with-repeated-digits | 1012. Numbers With Repeated Digits.cpp | 1012-numbers-with-repeated-digitscpp-by-teqmm | Code\n\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int n) {\n vector<int> V;\n int n2 = n;\n while(n2){\n V.emplace_ | 202021ganesh | NORMAL | 2024-08-31T10:18:38.056627+00:00 | 2024-08-31T10:18:38.056645+00:00 | 1 | false | **Code**\n```\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int n) {\n vector<int> V;\n int n2 = n;\n while(n2){\n V.emplace_back(n2%10);\n n2/=10;\n }\n int len = V.size(); \n int sum = 0;\n for(int i = 0; i < len-1; i++){\n sum += 9*A(9,i);\n } \n vector<int> dig_visited(10,0);\n for(int i = len-1; i >= 0; i--){\n int dig = V[i];\n int count = 0;\n for(int j = 0; j < dig; j++){\n if(dig_visited[j]){continue;}\n count++;\n }\n if(i == len-1){count--;}\n sum += count*A(10-(len-i), i);\n if(dig_visited[dig]){break;}\n if(i == 0 && dig_visited[dig] == 0){sum++;}\n dig_visited[dig] = 1;\n } \n return n - sum;\n } \n int A(int num, int len){\n int tmp = 1;\n for(int i = 0; i < len; i++){tmp *= (num-i);}\n return tmp;\n }\n};\n``` | 0 | 0 | ['C'] | 0 |
numbers-with-repeated-digits | Numbers With Repeated Digits | numbers-with-repeated-digits-by-shaludro-g6hg | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Shaludroid | NORMAL | 2024-08-19T19:35:01.373993+00:00 | 2024-08-19T19:35:01.374026+00:00 | 21 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int numDupDigitsAtMostN(int n) {\n // Convert n + 1 to a character array to handle it digit by digit\n String numStr = Integer.toString(n + 1);\n int len = numStr.length();\n \n // Step 1: Count numbers without repeated digits less than the length of numStr\n int countNoRepeat = 0;\n for (int i = 1; i < len; i++) {\n countNoRepeat += 9 * A(9, i - 1);\n }\n \n // Step 2: Count numbers without repeated digits with exactly \'len\' digits\n boolean[] used = new boolean[10];\n for (int i = 0; i < len; i++) {\n int digit = numStr.charAt(i) - \'0\';\n for (int j = i == 0 ? 1 : 0; j < digit; j++) {\n if (!used[j]) {\n countNoRepeat += A(9 - i, len - i - 1);\n }\n }\n if (used[digit]) break;\n used[digit] = true;\n }\n \n // Step 3: The result is n - count of numbers without repeated digits\n return n - countNoRepeat;\n }\n\n // Helper function: P(m, n) = m * (m-1) * ... * (m-n+1)\n private int A(int m, int n) {\n return n == 0 ? 1 : A(m, n - 1) * (m - n + 1);\n }\n\n public static void main(String[] args) {\n Solution solution = new Solution();\n System.out.println(solution.numDupDigitsAtMostN(20)); // Output: 1\n System.out.println(solution.numDupDigitsAtMostN(100)); // Output: 10\n System.out.println(solution.numDupDigitsAtMostN(1000)); // Output: 262\n }\n}\n\n``` | 0 | 0 | ['Java'] | 0 |
numbers-with-repeated-digits | Beats 100% (0ms) | Java | Combinatorial solution and explanation without digit dp/recursion | beats-100-0ms-java-combinatorial-solutio-cph4 | Intuition\nRather than computing how many numbers in a range have a repeated digit, it may be easired to compute how many numbers have no repeated digits and t | TheBFL | NORMAL | 2024-07-23T05:12:59.148499+00:00 | 2024-07-23T15:23:54.215564+00:00 | 108 | false | # Intuition\nRather than computing how many numbers in a range have a repeated digit, it may be easired to compute how many numbers have no repeated digits and then subtract that from the total number of numbers in the range. \nThe problem then is reduced to finding a fast way to enumerate non-repeating numbers in a range. \n\n# Approach\nWe are given a number $n$. If it is no more than $10$, there are obviously no numbers with repeating digits less than or equal to it, so we return zero. Otherwise, we extract the digits, and proceed from there. Suppose that $n$ is represented by digits $d_kd_{k-1}\\dots d_1d_0$. \n\nNow, read from left to right along a number. Replace $d_i$ with the count of numbers in the range $[0, d_i]$ that have not already occured. (If a number occurs twice, then we set every digit to the right of it to zero). Call this new sequence of adjusted digits $a_i$. \n\nWe then calculate the following values ($E$ and $F$ are the variables `partial` and `full`)\n$$\n\\begin{align}\nE & = 9P(9,0) + 9P(9,1) + \\cdots+ 9P(9,k-1)\\\\\nF & = (a_k - 1)P(9,k) + a_{k-1}P(8,k-1) + \\cdots + a_1P(9-k+1,1)+a_0P(9-k,0)\n\\end{align}\n$$\nWhere $P(n,k) = \\frac{n!}{(n-k)!}$. \n\n$E$ is the number of non-repeating positive integers that have fewer digits than $n$, while $F$ is the number of non-repeating positive integers that have the same number of digits as $n$, but are less than $n$. Together $E + F$ give the number of positive integers without repeating digits that are less than $n$. So, depending on if $n$ itself repeats, the number of positive integers with repeating digits in the range $1$ through $n$ is either $n - (E + F)$ or $n - (E + F + 1)$. \nThis is what the final for-loop calculates, except that we take advantage of the fact that $P(n + 1,k +1) = (n+1)P(n,k)$ to reduce the need to calculate all of the factorials. \n\nThe formula for $E$ comes from considering how many ways a non-repeating number can be made out of a given number of digits. There are 9 non-repeating 1-digit numbers, 81 2-digit, 648 3-digit amd so on. The pattern is that, in general, there are $9$ options for the first digit, being 1-9. Then, 9 options for the second digit, because while the first may not be used again, it is possible to use zero. There are 8 options for the third (to avoid reusing the digit from the first or second space), then 7,6,5 etc. Each term of $E$ corresponds to a different number of digits.\n\nThe formula for $F$ is a bit less obvious. Each term gives the number of non-repeating numbers which differ from $n$ in a given digit. The $a_0$ term gives those which agree in all places except the very right digit, while the $a_k$ term counts up how many ways a non-repeating number can be made whose first digit range from $1$ to 1 less than the starting digit of $n$, and those in between count how the in-between digits may be varied.\n\n \n\n# Code\n```\nclass Solution {\n public int numDupDigitsAtMostN(int n) {\n if (n < 11)\n {\n return 0;\n }\n\n //extract the digits\n int digits[] = new int[10];\n int tempN = n; \n int digitCount = 0;\n while (tempN > 0)\n {\n digits[digitCount] = tempN % 10;\n tempN /= 10;\n digitCount++;\n }\n\n //Using those digits, calculate the adjusted digits: suppose the prefix is maximized, how many \n //digits may fill this \'slot\'\n boolean occ[] = new boolean[10];\n boolean zeroRest = false;\n for (int i = digitCount-1; i >= 0; i--)\n {\n if (zeroRest)\n {\n digits[i] = 0;\n continue;\n }\n\n int digit = digits[i];\n int adjusted = digit;\n for (int j = 0; j < digit; j++)\n {\n if (occ[j])\n {\n adjusted -= 1;\n }\n }\n \n //if this is a repeat\n if (occ[digit])\n {\n zeroRest = true;\n }\n\n digits[i] = adjusted;\n occ[digit] = true; \n }\n\n if (!zeroRest)\n {\n digits[0]++;\n }\n\n\n int full = 0; \n int partial = 0;\n\n int suffixCount = 1;\n int partialSuffixCount = 1;\n for (int i = 0; i < digitCount - 1; i++)\n {\n full += digits[i] * suffixCount;\n suffixCount *= (11 - digitCount + i);\n\n partial += 9 * partialSuffixCount;\n partialSuffixCount *= (9 - i);\n\n }\n full += (digits[digitCount-1]-1)*suffixCount;\n\n return n - full - partial;\n\n }\n}\n```\n\n\n\n\n | 0 | 0 | ['Math', 'Combinatorics', 'Java'] | 0 |
numbers-with-repeated-digits | 100 % runtime 0ms Easy and intuitive | 100-runtime-0ms-easy-and-intuitive-by-aa-gg0i | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nSimply find the count o | Aaditya_26 | NORMAL | 2024-07-21T18:12:06.933422+00:00 | 2024-07-21T18:12:06.933450+00:00 | 11 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSimply find the count of all number that have all digits unique and then eventually subtract from given n . \n\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(10)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(10)\n\n# Code\n```\nclass Solution {\npublic:\n int ans = 0 ; \n\n bool check(string &temp){\n if(temp=="")return false;\n vector<int> v(14);\n\n for(auto i:temp){ v[i-\'0\']++; }\n return *max_element(v.begin(),v.end())>1 ;\n }\n\n bool check2(string &temp , int index){\n for(int i=0;i<temp.size() ;i++){\n if(temp[i]==index)return true;\n }\n return false;\n }\n\n\n void func(string &temp , string &s , int index){\n if(check(temp))return;\n if(index>= s.size()){\n ans++;\n return;\n }\n\n for(int i=\'0\';i<s[index] ; i++){\n if(index==0 && i==\'0\')continue;\n if(check2(temp,i))continue;\n\n int n = 10-index-1;\n int k = 1;\n for(int i=index+1;i<s.size();i++){\n k = k*n;\n n--;\n }\n // cout<<k<<" ";\n ans+= k ;\n }\n\n temp.push_back(s[index]);\n func(temp,s,index+1);\n }\n\n int numDupDigitsAtMostN(int n) {\n // n - no. of unique digits \n string s = to_string(n);\n int len = s.size(); \n\n vector<int> dp(13);\n dp[1]=9;\n dp[2]=81;\n dp[3]=dp[2]*8;\n dp[4]=dp[3]*7;\n dp[5]=dp[4]*6;\n dp[6]=dp[5]*5;\n dp[7]=dp[6]*4;\n dp[8]=dp[7]*3;\n dp[9]=dp[8]*2;\n dp[10]=dp[9]*1;\n\n for(int i=1;i<=len-1;i++){\n ans+= dp[i];\n }\n\n // cout<<ans<<endl;\n\n string temp = "";\n func(temp , s , 0 );\n\n // cout<<ans<<endl;\n\n return n-ans; \n\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
numbers-with-repeated-digits | Numbers With Repeated Digits | numbers-with-repeated-digits-by-sam_neam-lif3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Sam_Neamah | NORMAL | 2024-07-03T14:07:22.455729+00:00 | 2024-07-03T14:07:22.455760+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number} n\n * @return {number}\n */\nvar numDupDigitsAtMostN = function(n) {\n const digits = String(n).split(\'\').map(Number);\n const len = digits.length;\n \n const dp = Array.from({ length: len }, () => Array(1 << 10).fill(-1));\n \n const countUnique = (pos, mask, isTight, hasLeadingZero) => {\n if (pos === len) return hasLeadingZero ? 0 : 1;\n if (!isTight && dp[pos][mask] !== -1) return dp[pos][mask];\n \n let limit = isTight ? digits[pos] : 9;\n let result = 0;\n \n for (let digit = 0; digit <= limit; digit++) {\n if (hasLeadingZero && digit === 0) {\n result += countUnique(pos + 1, mask, isTight && (digit === limit), true);\n } else if ((mask & (1 << digit)) === 0) {\n result += countUnique(pos + 1, mask | (1 << digit), isTight && (digit === limit), false);\n }\n }\n \n if (!isTight) dp[pos][mask] = result;\n return result;\n };\n \n const totalUnique = countUnique(0, 0, true, true);\n \n return n - totalUnique;\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
numbers-with-repeated-digits | Python (Simple Digit DP) | python-simple-digit-dp-by-rnotappl-3ash | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rnotappl | NORMAL | 2024-06-20T15:46:21.466097+00:00 | 2024-06-20T15:46:21.466132+00:00 | 59 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numDupDigitsAtMostN(self, n):\n ans = [int(i) for i in str(n)]\n m = len(ans)\n\n @lru_cache(None)\n def function(pos,tight,mask):\n if pos == m:\n return 1 \n\n total = 0 \n\n upperlimit = ans[pos] if tight else 9 \n\n for d in range(upperlimit+1):\n if mask&(1<<d) == 0:\n new_tight = tight and d == upperlimit \n new_mask = mask if mask == 0 and d == 0 else mask|(1<<d)\n total += function(pos+1,new_tight,new_mask)\n\n return total \n\n return n-(function(0,True,0)-1)\n``` | 0 | 0 | ['Python3'] | 0 |
numbers-with-repeated-digits | Swift | Recursive, *non* DP solution | swift-recursive-non-dp-solution-by-pagaf-knkh | The idea is to generate all numbers <= n that have unique digits and subtract the count from n.\n\nFinding the numbers with no repeated digits is very much liki | pagafan7as | NORMAL | 2024-06-14T23:45:29.152700+00:00 | 2024-06-14T23:45:29.152717+00:00 | 12 | false | The idea is to generate all numbers <= n that have unique digits and subtract the count from n.\n\nFinding the numbers with no repeated digits is very much liking generating all the permutations of 0123456789, so it\'s a well known problem.\n\nBecause there are not that many such numbers (say less than a few million), this can be done on time with the problem constraints.\n\n\n\n# Code\n```\nclass Solution {\n func numDupDigitsAtMostN(_ n: Int) -> Int {\n func countUnique(_ prefix: Int, _ seen: inout [Bool], _ uniqueCount: inout Int) {\n if prefix > n { return }\n if prefix > 0 { uniqueCount += 1 }\n for i in 0...9 where !seen[i] {\n if prefix == 0 && i == 0 { continue }\n seen[i] = true\n countUnique(prefix * 10 + i, &seen, &uniqueCount)\n seen[i] = false\n }\n }\n\n var seen = Array(repeating: false, count: 10)\n var uniqueCount = 0\n countUnique(0, &seen, &uniqueCount)\n\n return n - uniqueCount\n }\n}\n``` | 0 | 0 | ['Swift'] | 0 |
numbers-with-repeated-digits | 94% Running Time Faster, yet simple python solution | 94-running-time-faster-yet-simple-python-3cts | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | runorz | NORMAL | 2024-06-01T12:43:24.269837+00:00 | 2024-06-01T12:43:24.269869+00:00 | 43 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport math\n\nFACT9 = math.factorial(9)\n\ndef getCountByNumber(n):\n if n < 2:\n return 0\n return int(9*(10**(n-1)) - 9*(FACT9/math.factorial(9-n+1)))\n\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n len_n = len(str(n))\n list_n = list(str(n))\n res = 0\n for i in range(2,len_n):\n res += getCountByNumber(i)\n\n s = 1\n for i in range(len_n-1, -1, -1):\n if i > 0:\n s += (int(list_n[i]) * (10**(len_n-i-1)))\n else:\n s += ((int(list_n[i])-1) * (10**(len_n-i-1)))\n u = 1 if len(set(list_n)) == len_n else 0\n for i in range(len_n-1, -1, -1):\n if len(set(list_n[:i])) < i:\n continue\n else:\n if i > 0:\n cur = int(list_n[i])\n for e in list_n[:i]:\n if int(e) < int(list_n[i]):\n cur -= 1\n tmp = 1\n for j in range(len_n-i-1):\n tmp *= (9-i-j)\n u += (cur * tmp)\n else:\n cur = int(list_n[i])-1\n tmp = 1\n for j in range(len_n-i-1):\n tmp *= (9-i-j)\n u += (cur * tmp)\n res += (s-u)\n return res\n``` | 0 | 0 | ['Python3'] | 0 |
numbers-with-repeated-digits | Short and concise C++ solution | Digit DP | short-and-concise-c-solution-digit-dp-by-6ulq | Intuition\nSimple digit dp problem , check if current constructed number is less than the given number and choose digits accordingly.\nTo check if a digit is re | ratuldawar11 | NORMAL | 2024-05-29T03:39:31.262896+00:00 | 2024-05-29T03:39:31.262923+00:00 | 16 | false | # Intuition\nSimple digit dp problem , check if current constructed number is less than the given number and choose digits accordingly.\nTo check if a digit is repeated or not use a 0-9 digit bit mask.\n\n\n# Code\n```\nclass Solution {\npublic:\n int dp[10][2][2][1<<10];\n int recur(int curr,int isLess, bool isRepeated, int mask,vector<int> &digits){\n int n = digits.size();\n if(curr >= n)return isRepeated;\n if(dp[curr][isLess][isRepeated][mask] != - 1)return dp[curr][isLess][isRepeated][mask];\n int ans = 0;\n for(int i = 0;i <= (isLess ? 9 : digits[curr]);i++){\n ans += recur(curr + 1,isLess | (i < digits[curr]), isRepeated | ((mask&(1<<i)) != 0), i != 0 ? (mask | (1<<i)) : (mask | (mask != 0)) ,digits);\n }\n return dp[curr][isLess][isRepeated][mask] = ans;\n }\n int numDupDigitsAtMostN(int n) {\n vector<int> digitVector;\n while(n > 0){\n digitVector.push_back(n%10);\n n = n/10;\n }\n reverse(digitVector.begin(),digitVector.end());\n memset(dp,-1,sizeof(dp));\n return recur(0,0,0,0,digitVector);\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
numbers-with-repeated-digits | c++ sol | c-sol-by-aaditi01-3fou | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Aaditi01 | NORMAL | 2024-03-29T14:13:04.027219+00:00 | 2024-03-29T14:13:04.027269+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numDupDigitsAtMostN(int n) {\n // we take n+1 number to make n inclusive in our algo\n // in the algo we find number with non repeated digits and to calculate number with repeated digits we subtract it from n \n int temp = n+1;\n vector<int> digits ; // store the digits;\n while(temp>0)\n {\n int digit = temp % 10;\n digits.push_back(digit);\n temp/=10;\n }\n int countnonrepeatedno=0;\n int countways= 9; // initally for most significan digit count will be 9 (exclude 0)\n for(int i =0;i< digits.size()-1; i++)\n {\n countnonrepeatedno += countways;\n countways=countways*(9-i);\n }\n int m = digits.size();\n //for further possible ways remove the previous counts \n countways/= 9;\n // for second part \n vector<int>fixed(10, 0); // [0-9] digits so size =10 , we have taken this so that same element not processed again\n for(int i = m-1; i>=0; i--)\n { int x= digits[i];\n int j ;\n if(i==m-1)\n j=1;\n else\n j =0;\n \n while(j<x)\n {\n if(fixed[j]==0)\n {\n countnonrepeatedno+= countways ;\n\n }\n j++;\n }\n countways/=(9-(m-i-1));\n if(fixed[x]!=0)\n break;\n fixed[x]=1;\n\n }\n return n - countnonrepeatedno;\n \n\n\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
numbers-with-repeated-digits | C++ | Digit Dp | Video Solution | 77% faster than others! | c-digit-dp-video-solution-77-faster-than-984a | Digit Dp\n\n# Video Solution\n\nhttps://youtu.be/IKQSexsR7eE?si=5Mnk7J7MYc2YycON\n\n# Code\n\nclass Solution {\npublic:\n int dp[11][2][1<<10][2];\n int f | mj_08 | NORMAL | 2024-03-28T08:53:28.590083+00:00 | 2024-03-28T08:55:55.464579+00:00 | 5 | false | # Digit Dp\n\n# Video Solution\n\n[https://youtu.be/IKQSexsR7eE?si=5Mnk7J7MYc2YycON]()\n\n# Code\n```\nclass Solution {\npublic:\n int dp[11][2][1<<10][2];\n int f(int i,string& s,int lz,int mask,int ise){\n if(i==s.size()) return 1;\n if(dp[i][lz][mask][ise]!=-1) return dp[i][lz][mask][ise];\n int mxx=(ise)?(s[i]-\'0\'):9,ans=0;\n for(int j=0;j<=mxx;j++){\n if(lz==0 && (mask&(1<<j))) continue;\n mask|=(1<<j);\n ans+=f(i+1,s,lz&(j==0),mask,ise&(j==mxx));\n mask^=(1<<j);\n }\n return dp[i][lz][mask][ise]=ans;\n }\n int numDupDigitsAtMostN(int n) {\n string s=to_string(n);\n memset(dp,-1,sizeof(dp));\n int ans=n+1-f(0,s,1,0,1);\n return ans;\n }\n};\n``` | 0 | 0 | ['Math', 'Dynamic Programming', 'Brainteaser', 'Memoization', 'Bitmask', 'C++'] | 0 |
numbers-with-repeated-digits | BitMask DP || C++ | bitmask-dp-c-by-bhanunegi420-qvxp | Intuition\nFinding numbers with at least one repeated digits means finding numbers with all unique digits and subtracting it from n this will give us the digits | bhanunegi420 | NORMAL | 2024-03-25T17:14:37.853933+00:00 | 2024-03-25T17:16:31.272372+00:00 | 18 | false | # Intuition\nFinding numbers with at least one repeated digits means finding numbers with all unique digits and subtracting it from $$n$$ this will give us the digits with at least one repeated digit in it.\nNow we Divide the problem into two parts in the first part we will calculate number of unique numbers in the range \n0-9 (1 digit)\n10-99 (2 digits)\n100-999 (3 digits)\n....... (number of digits in $$n$$ -1)\n(1 - x) in total\n\nThen in the second half we will find number of unique numbers in the range (x+1 to n).\n \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nFor the first half just make use of simple permutaion. Compute for every number of digits.\nIn the second half make use of BitMask.\nMake a dp array that will store the position we are currently in, is our current position/digit our max value i.e. we can go higher than it? and a mask that will store wether the number has been added or not. \n\n\nI\'m open to discussion of my code if you are stuck anywhere.\nJust leave a comment and I will reply within 1 hour max.\nPlease upvote if you find it useful. \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(11 * 2 * 1024)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(11 * 2 * 1024)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nint dp[11][2][1024];\nclass Solution {\npublic:\n\n int f(int position,bool isprefix,int mask,int n,string num){\n\n if(position >= n) return 1;\n if(dp[position][isprefix][mask] != -1) return dp[position][isprefix][mask];\n\n int start = (position == 0)? 1 : 0;\n int limit = isprefix ? (num[position] - \'0\') : 9;\n int ans = 0;\n for(int i = start; i <= limit; i++){\n if(mask&(1<<i)) continue;\n bool newprefix = isprefix ? (i == limit) : false;\n ans += f(position+1,newprefix,mask | (1<<i),n,num);\n }\n\n return dp[position][isprefix][mask] = ans;\n }\n\n int permute(int n){\n if(n == 1) return 9;\n int fac = 362880;\n int r = 9-n+1;\n\n int num = 1;\n for(int i=1; i <=r; i++){\n num *= i;\n }\n\n return 9*fac/num;\n }\n\n int numDupDigitsAtMostN(int n) {\n\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n cout.tie(NULL);\n\n string s = to_string(n);\n int ans = 0;\n // First Half\n for(int i=1; i < s.length(); i++){\n ans += permute(i);\n }\n\n //Second Half\n memset(dp,-1,sizeof(dp));\n ans += f(0,1,0,s.length(),s);\n return n-ans;\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Bit Manipulation', 'Bitmask', 'C++'] | 0 |
numbers-with-repeated-digits | use bitmask dp | use-bitmask-dp-by-priyanshu_gupta_9620-aba8 | Code\n\nclass Solution {\npublic:\n int rec(int ind,int mask,int f,int limit,vector<vector<vector<vector<int>>>>&dp,string &s){\n if(ind==s.size()){\n | Priyanshu_gupta_9620 | NORMAL | 2024-03-14T16:51:34.473367+00:00 | 2024-03-14T16:51:34.473405+00:00 | 5 | false | # Code\n```\nclass Solution {\npublic:\n int rec(int ind,int mask,int f,int limit,vector<vector<vector<vector<int>>>>&dp,string &s){\n if(ind==s.size()){\n if(!f){\n return 0;\n }\n return 1;\n }\n else if(dp[ind][mask][f][limit]!=-1){\n return dp[ind][mask][f][limit];\n }\n else{\n int upper=s[ind]-\'0\';\n int ans=0;\n if(limit==1){\n for(int i=0;i<=upper;i++){\n int lastm=mask;\n int lastf=f;\n if(i==0){\n if(f==1){\n if((mask&(1<<i))==0){\n mask=(mask|(1<<i));\n }\n else{\n continue;\n }\n }\n }\n else{\n f=1;\n if((mask&(1<<i))==0){\n mask=(mask|(1<<i));\n }\n else{\n continue;\n }\n }\n if(i==upper){\n ans+=(rec(ind+1,mask,f,1,dp,s));\n }\n else{\n ans+=(rec(ind+1,mask,f,0,dp,s));\n }\n mask=lastm;\n f=lastf;\n }\n }\n else{\n for(int i=0;i<=9;i++){\n int lastm=mask;\n int lastf=f;\n if(i==0){\n if(f==1){\n if((mask&(1<<i))==0){\n mask=(mask|(1<<i));\n }\n else{\n continue;\n }\n }\n }\n else{\n f=1;\n if((mask&(1<<i))==0){\n mask=(mask|(1<<i));\n }\n else{\n continue;\n }\n }\n ans+=(rec(ind+1,mask,f,0,dp,s));\n mask=lastm;\n f=lastf;\n }\n\n }\n return dp[ind][mask][f][limit]=ans;\n }\n }\n int numDupDigitsAtMostN(int n) {\n string s="";\n int n1=n;\n while(n!=0){\n int a=n%10;\n s+=(\'0\'+a);\n n/=10;\n }\n reverse(s.begin(),s.end());\n vector<vector<vector<vector<int>>>> dp(10,vector<vector<vector<int>>>(1025,vector<vector<int>>(2,vector<int>(2,-1))));\n int ans=rec(0,0,0,1,dp,s);\n return n1-ans;\n \n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
numbers-with-repeated-digits | Digit DP and Bitmasking Solution | digit-dp-and-bitmasking-solution-by-josh-i0y9 | \n\n# Code\n\nclass Solution {\npublic:\n int digits[10];\n int dp[10][2][2][2][1024];\n\n int solve(int pos, int tight, int repeated, int zero, int ma | Joshiiii | NORMAL | 2024-03-12T11:59:48.735903+00:00 | 2024-03-12T11:59:48.735927+00:00 | 10 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int digits[10];\n int dp[10][2][2][2][1024];\n\n int solve(int pos, int tight, int repeated, int zero, int mask, string &s) {\n if (pos == s.length())\n return !zero && repeated;\n\n if (dp[pos][tight][repeated][zero][mask] != -1)\n return dp[pos][tight][repeated][zero][mask];\n\n int ans = 0;\n int limit = tight ? (s[pos] - \'0\') : 9;\n\n for (int i = 0; i <= limit; i++) {\n if (!zero || i > 0){\n digits[i]++;\n ans += solve(pos + 1, tight && (i == limit), repeated || digits[i] >= 2, zero && (i == 0), mask|(1<<i), s);\n digits[i]--;\n }\n else{\n ans += solve(pos + 1, tight && (i == limit), repeated || digits[i] >= 2, zero && (i == 0), mask, s);\n }\n }\n\n return dp[pos][tight][repeated][zero][mask] = ans;\n }\n\n int numDupDigitsAtMostN(int n) {\n string s = to_string(n);\n memset(digits, 0, sizeof(digits));\n memset(dp, -1, sizeof(dp));\n return solve(0, 1, 0, 1, 0, s);\n }\n};\n\n\n``` | 0 | 0 | ['Dynamic Programming', 'Bitmask', 'C++'] | 0 |
numbers-with-repeated-digits | Python Solution Using Combinatorics and beats 94% of submissions | python-solution-using-combinatorics-and-duki8 | Code\n\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n strn = str(n)\n length = len(strn)\n low = 0\n for i in | hassan_abioye | NORMAL | 2024-02-15T02:14:14.148976+00:00 | 2024-02-15T02:14:14.149021+00:00 | 68 | false | # Code\n```\nclass Solution:\n def numDupDigitsAtMostN(self, n: int) -> int:\n strn = str(n)\n length = len(strn)\n low = 0\n for i in range(1,length):\n low+=(9*(math.factorial(9)//math.factorial(9-i+1)))\n topval = int(strn[0])\n diff = topval-1\n mid=diff*(math.factorial(9)//math.factorial(9-length+1))\n left = 9\n pos = 1\n seen = set([topval])\n def trav(pos,left,seen):\n nonlocal strn, length\n if pos == length:\n return 1\n current = int(strn[pos])\n sub = 0\n for item in seen:\n if item < current:\n sub+=1\n add = (current-sub)*(math.factorial(left-1)//math.factorial(10-length))\n if current in seen:\n return add\n else:\n seen.add(current)\n add+=trav(pos+1,left-1,seen)\n return add\n top=trav(pos,left,seen)\n return n-(low+mid+top)\n``` | 0 | 0 | ['Python3'] | 0 |
numbers-with-repeated-digits | TS Solution | ts-solution-by-gennadysx-whi5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | GennadySX | NORMAL | 2024-02-09T06:53:50.415281+00:00 | 2024-02-09T06:53:50.415308+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunction numDupDigitsAtMostN(n: number): number {\n const s = n.toString();\n const dp = Array.from({length: s.length}, () => Array(1<<10).fill(-1));\n const dfs = (i: number, mask: number, is_limit: boolean, leading0s: boolean): number => {\n if (i === s.length) return leading0s? 0: 1;\n if (!is_limit && !leading0s && dp[i][mask] !== -1) return dp[i][mask];\n let sub = 0;\n if (leading0s) sub = dfs(i+1, mask, false, true);\n const low = leading0s? 1:0, high = is_limit? +s[i]: 9;\n for (let d = low; d <= high; d+=1) {\n if ((mask >> d & 1) === 0) {\n sub += dfs(i+1, mask | (1<<d), is_limit && d === high, false);\n }\n }\n if (!is_limit && !leading0s) dp[i][mask] = sub;\n return sub;\n };\n return n - dfs(0, 0, true, true);\n}\n``` | 0 | 0 | ['TypeScript'] | 0 |
numbers-with-repeated-digits | Simple Approach using digit DP | simple-approach-using-digit-dp-by-pythag-4p6n | Code\n\nclass Solution {\npublic:\n int dp[12][1<<10][2][2];\n int func(string &num, int n, int vis, bool tight, bool zer){\n if(n==0){\n | Pythagoras235 | NORMAL | 2024-02-07T16:26:03.849995+00:00 | 2024-02-07T16:26:03.850022+00:00 | 16 | false | # Code\n```\nclass Solution {\npublic:\n int dp[12][1<<10][2][2];\n int func(string &num, int n, int vis, bool tight, bool zer){\n if(n==0){\n return 1;\n }\n if(dp[n][vis][tight][zer]!=-1) return dp[n][vis][tight][zer];\n int ans = 0;\n int ub = tight ? (num[num.length()-n]-\'0\') : 9;\n for(int dig = 0; dig <= ub; dig++){\n if(zer==1 && dig==0){\n ans+=func(num,n-1,vis,tight&(dig==ub),zer);\n }\n else if((vis&(1<<dig))==0){\n ans+=func(num,n-1,(vis|(1<<dig)),tight&(dig==ub),zer&0);\n }\n }\n return dp[n][vis][tight][zer] = ans;\n }\n int numDupDigitsAtMostN(int n) {\n string s = to_string(n);\n int len = s.size();\n memset(dp,-1,sizeof(dp));\n int ans = func(s,len,0,1,1);\n return n+1-ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
numbers-with-repeated-digits | Digit DP || Short & Simple Code || Explained | digit-dp-short-simple-code-explained-by-vmmhl | Intuition\n\nNo. having at least = Total - No. having only\n 1 repeating digit Numbers unique digits\n\n=> Ans = n+1 - | coder_rastogi_21 | NORMAL | 2024-02-07T13:33:03.403559+00:00 | 2024-02-07T13:33:03.403583+00:00 | 34 | false | # Intuition\n```\nNo. having at least = Total - No. having only\n 1 repeating digit Numbers unique digits\n\n=> Ans = n+1 - solve(.........)\n```\n# Complexity\n- Time complexity: $$O(11*2*2*1024)$$ \n\n- Space complexity: $$O(11*2*2*1024)$$ \n\n# Code\n```\n\'int dp[11][2][2][1<<10];\nclass Solution {\n int solve(int i, int bound, int zero, int mask, int len, string s)\n {\n if(i == len) //base case\n return 1;\n\n if(dp[i][bound][zero][mask] != -1) //memoization step\n return dp[i][bound][zero][mask];\n\n int curr = 0, maxDigit = bound ? (s[i]-\'0\') : 9;\n for(int j=0; j<=maxDigit; j++)\n {\n if(mask == 0 && j == 0) //in case of leading 0\n curr += solve(i+1,bound & (j==(s[i]-\'0\')),zero,mask,len,s);\n else if((mask & (1<<j)) == 0 || zero) //check that digit j should not have repeated \n curr += solve(i+1,bound & (j==(s[i]-\'0\')),zero&(j==0),mask|(1<<j),len,s);\n }\n return dp[i][bound][zero][mask] = curr;\n }\npublic:\n int numDupDigitsAtMostN(int n) {\n memset(dp,-1,sizeof(dp)); //initializing dp with -1\n string s = to_string(n);\n int len = s.length();\n return n+1 - solve(0,1,1,0,len,s);\n } \n \n};\n``` | 0 | 0 | ['Dynamic Programming', 'C++'] | 0 |
numbers-with-repeated-digits | Solution | solution-by-penrosecat-2lzi | Intuition\n Describe your first thoughts on how to solve this problem. \n\nDigit dp. Try to find the numbers without repeated digits from 1 to N. Then subtract | penrosecat | NORMAL | 2024-01-26T15:53:45.205343+00:00 | 2024-01-26T15:53:45.205367+00:00 | 14 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nDigit dp. Try to find the numbers without repeated digits from 1 to N. Then subtract this from N.\n\n1. DP form: knapsack. We pick from what digit we want at what position. We decide the num1 and num2 between which we calculate beforehand.\n2. DP meaning: dp(i, state, tight1, tight2) = number of numbers without repeated digits from i..n given state is the bitmask where set bit means the digit has already been used and tight1, tight2 are bools which indicate whether the digits so far are exactly those used in num1 and num2 respectively.\n3. DP transition: dp(i, state, tight1, tight2) -> dp(i+1, (1<<d)|state, tight1&&(d==num1[i]), tight2&&(d==num2[i])). For handling leading zeros we can have an extra boolean in the recurrence so that we don\'t set any bit 0 till we actually use 0 inside a number and not as a leading zero.\n4. TC: O(log(n)) as we depend on the number of digits in n\n5. Set the inital values of num1 and num2 to 00..001 and num2 = n respectively such that both have the same length. We can generalize this to any n1 and n2 as well.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int dp[10][1024][2][2];\n int n;\n string num1;\n string num2;\n\n\n int rec(int i, int state, bool tight1, bool tight2, bool leading_zeros)\n {\n if(i == n)\n {\n return 1;\n }\n\n if(dp[i][state][tight1][tight2] != -1)\n {\n return dp[i][state][tight1][tight2];\n }\n\n int ans = 0;\n\n int lower_bound = tight1 ? (num1[i] - \'0\') : 0;\n int upper_bound = tight2 ? (num2[i] - \'0\') : 9;\n\n for(int d = lower_bound; d<=upper_bound; d++)\n {\n\n if(d == 0 && leading_zeros)\n {\n ans = (ans + rec(i+1, state, tight1 && (d == lower_bound), tight2 && (d == upper_bound), leading_zeros));\n }\n else\n {\n int bit = (1 << d);\n\n if((bit & state) == 0)\n {\n ans = (ans + rec(i+1, bit|state, tight1 && (d == lower_bound), tight2 && (d == upper_bound), false));\n }\n }\n }\n\n return dp[i][state][tight1][tight2] = ans;\n }\n\n int numDupDigitsAtMostN(int n) {\n memset(dp, -1, sizeof(dp));\n this->num2 = to_string(n);\n this->num1 = string((this->num2).size() - 1, \'0\') + "1";\n this->n = (this->num2).size();\n rec(0, 0, true, true, true);\n return n - dp[0][0][1][1]; // replace this line with n2 - n1 + 1 - dp[0][0][1][1] for general n1, n2\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
numbers-with-repeated-digits | very simple digit DP even beginners can understand | very-simple-digit-dp-even-beginners-can-g66vo | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem seems to involve counting the number of unique digits in numbers up to a gi | MohdShahjahan | NORMAL | 2024-01-08T10:35:26.492453+00:00 | 2024-01-08T10:35:26.492494+00:00 | 45 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem seems to involve counting the number of unique digits in numbers up to a given value n. The use of dynamic programming suggests that there might be overlapping subproblems that can be optimized.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAnswer can be **total numbers - numbers with only unique digits**\n\nFirst understand the bitmask , dont worry it is easy ,lemme tell you how\n \nMaximum number of digits are (0-9) is 10. So, think like in bits we use 0th bit for 0 digits and so on . So, for 10 total digits we can use :-\n9 8 7 6 5 4 3 2 1 0\n**1 1 1 1 1 1 1 1 1 1** -->(1023 in bits)\nif we use any digit we can set the digit bit to off. What I mean to say is if we use 5 digit in the answer then the bit representation of mask will 1 1 1 1 0 1 1 1 1 1 which represent we use 5 th digit so infuture for ongoing recursion call we cant have 5 in the digit. You can look at the code if you know xor properties to turn off bit at a specific position or you can google that it is very simple. \n\nThere is one more concept of leading zeroes and we have to keep the track of it why? because 00003 is a number and 3 is also a number\nbut in 00003 zero is repeated and in 3 no zero is repeated, this means till 0000 number is not stared and from 3 number is started if number is not started then we dont need to add that in ans i used z for leading zeroes 1 for yes and 0 for no.\n\nTightness implies that a digit at a particular position cannot exceed a certain limit to maintain the given condition.\nif my max number is 545454\nthen first digit i can\'t use more than 5, if use anything less then there will be no tightness. This will tell if the current digits range is restricted or not. If the current digit\u2019s \nrange is not restricted then it will span from 0 to 9 (inclusively) else it will span \nfrom 0 to digit[idx] (inclusively).\nExample: consider our limiting integer to be 3245 and we need to calculate G(3245) \nindex : 4 3 2 1 \ndigits : 3 2 4 5 \n \nUnrestricted range: \nNow suppose the integer generated till now is : 3 1 * * ( * is empty place, where digits are to be inserted to form the integer). \n\n index : 4 3 2 1 \n digits : 3 2 4 5\n generated integer: 3 1 _ _ \nhere, we see that index 2 has unrestricted range. Now index 2 can have digits from range 0 to 9(inclusively). \nFor unrestricted range tight = 0\nRestricted range: \nNow suppose the integer generated till now is : 3 2 * * ( \u2018*\u2019 is an empty place, where digits are to be inserted to form the integer). \n\n index : 4 3 2 1 \n digits : 3 2 4 5\n generated integer: 3 2 _ _ \nhere, we see that index 2 has a restricted range. Now index 2 can only have digits from range 0 to 4 (inclusively) \nFor restricted range tight = 1\n\nNow you can understand the problem and able to understand the code you do it without dp as the constraint are small Trust me with only recursion TC-> logn.\n\nThe code utilizes a dynamic programming approach to **count the number of unique digits**. The function dfs recursively explores different digit combinations while considering constraints like tightness and a bitmask to track used digits. The dynamic programming array dp is used to memoize results and avoid redundant calculations.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nnear about **O(1)** because of constant time\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nnear about **O(1)** because of constant space\n\n# Code\n```\nclass Solution {\n int dp[12][2][1024];\n int dfs(string &s, int i, int z, int tight , int mask){\n if(i==s.length()){\n if(!z)return 1;\n return 0;\n }\n if(dp[i][tight][mask]!=-1)return dp[i][tight][mask];\n int limit = tight == 1? s[i]-\'0\':9;\n int ans = 0;\n for(int j=0;j<=limit;j++){\n int t = tight&(j==limit);\n int nz = z & (j==0);\n if(nz){\n ans+= dfs(s,i+1,nz,t,mask);\n }\n else{\n if(mask>>j & 1){\n int nm = mask ^ (1<<j);\n ans += dfs(s,i+1,nz,t,nm);\n }\n }\n }\n return dp[i][tight][mask] = ans;\n }\npublic:\n int numDupDigitsAtMostN(int n) {\n string s = to_string(n);\n memset(dp,-1,sizeof(dp));\n return n - dfs(s,0,1,1,1023);\n }\n};\n```\n\n**SORRY FOR MY ENGLISH **\n\n\n | 0 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 0 |
numbers-with-repeated-digits | Java | java-by-ogyrchik14479-a5gs | \n# Code\n\nclass Solution {\n public int numDupDigitsAtMostN(int N) {\n // \u041F\u0440\u0435\u043E\u0431\u0440\u0430\u0437\u0443\u0435\u043C N + 1 \ | Ogyrchik14479 | NORMAL | 2023-12-16T21:31:49.662344+00:00 | 2023-12-16T21:33:43.296941+00:00 | 31 | false | \n# Code\n```\nclass Solution {\n public int numDupDigitsAtMostN(int N) {\n // \u041F\u0440\u0435\u043E\u0431\u0440\u0430\u0437\u0443\u0435\u043C N + 1 \u0432 \u0441\u0442\u0440\u043E\u043A\u0443, \u0442\u0430\u043A \u043A\u0430\u043A \u043D\u0430\u043C \u043D\u0443\u0436\u043D\u043E \u0432\u043A\u043B\u044E\u0447\u0438\u0442\u044C N\n char[] nums = String.valueOf(N + 1).toCharArray();\n int len = nums.length;\n\n // \u041F\u043E\u0434\u0441\u0447\u0435\u0442 \u043A\u043E\u043B\u0438\u0447\u0435\u0441\u0442\u0432\u0430 \u0443\u043D\u0438\u043A\u0430\u043B\u044C\u043D\u044B\u0445 \u043F\u0435\u0440\u0435\u0441\u0442\u0430\u043D\u043E\u0432\u043E\u043A \u0434\u043B\u044F \u043A\u0430\u0436\u0434\u043E\u0433\u043E \u043C\u0435\u0441\u0442\u0430\n int result = 0;\n for (int i = 1; i < len; i++) {\n result += 9 * permutation(9, i - 1);\n }\n\n // \u041F\u043E\u0434\u0441\u0447\u0435\u0442 \u0443\u043D\u0438\u043A\u0430\u043B\u044C\u043D\u044B\u0445 \u043F\u0435\u0440\u0435\u0441\u0442\u0430\u043D\u043E\u0432\u043E\u043A \u0434\u043B\u044F \u043E\u0441\u0442\u0430\u0432\u0448\u0438\u0445\u0441\u044F \u0446\u0438\u0444\u0440\n Set<Character> seen = new HashSet<>();\n for (int i = 0; i < len; i++) {\n for (char digit = i == 0 ? \'1\' : \'0\'; digit < nums[i]; digit++) {\n if (!seen.contains(digit)) {\n result += permutation(9 - i, len - i - 1);\n }\n }\n\n if (!seen.add(nums[i])) {\n break;\n }\n }\n\n return N - result;\n }\n\n // \u0424\u0443\u043D\u043A\u0446\u0438\u044F \u0434\u043B\u044F \u043F\u043E\u0434\u0441\u0447\u0435\u0442\u0430 \u043F\u0435\u0440\u0435\u0441\u0442\u0430\u043D\u043E\u0432\u043E\u043A\n private int permutation(int n, int k) {\n int result = 1;\n for (int i = 0; i < k; i++) {\n result *= n - i;\n }\n return result;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
numbers-with-repeated-digits | Digit DP | digit-dp-by-deleted_user-qm2c | Code\n\nclass Solution {\npublic:\n int dp[10][2][1025][10];\n int solve(int index, int tight, int mask, int zeroCount, string &s) {\n if(index == | deleted_user | NORMAL | 2023-12-15T20:19:56.929188+00:00 | 2023-12-15T20:19:56.929228+00:00 | 8 | false | # Code\n```\nclass Solution {\npublic:\n int dp[10][2][1025][10];\n int solve(int index, int tight, int mask, int zeroCount, string &s) {\n if(index == s.length()) {\n return 1;\n }\n if(dp[index][tight][mask][zeroCount] != -1) {\n return dp[index][tight][mask][zeroCount];\n }\n int ub = tight ? s[index] - \'0\' : 9;\n int ans = 0;\n for(int i = 0; i <= ub; i++) {\n int newZeroCount = zeroCount;\n if(i == 0) {\n if(mask > 0) {\n newZeroCount++;\n } else {\n if(newZeroCount >= 1) newZeroCount++;\n }\n if(newZeroCount <= 1) ans = ans + solve(index + 1, (tight && i == ub), mask, newZeroCount, s);\n } else {\n if((mask & (1 << i)) == 0) {\n ans = ans + solve(index + 1, (tight && i == ub), (mask | (1 << i)), zeroCount, s);\n }\n }\n }\n return dp[index][tight][mask][zeroCount] = ans;\n }\n int numDupDigitsAtMostN(int n) {\n memset(dp, -1 ,sizeof(dp));\n string s = to_string(n);\n int ans = n - (solve(0, 1, 0, 0, s) - 1);\n return ans;\n\n }\n};\n \n``` | 0 | 0 | ['C++'] | 0 |
numbers-with-repeated-digits | JAVA || Digit DP | java-digit-dp-by-vsai5120-9i5t | Complexity\n- Time complexity: O(num.length() * 2 * 2^10)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(num.length() * 2 * 2^10)\n Add yo | vsai5120 | NORMAL | 2023-11-08T19:11:59.944000+00:00 | 2023-11-08T19:11:59.944020+00:00 | 73 | false | # Complexity\n- Time complexity: O(num.length() * 2 * 2^10)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(num.length() * 2 * 2^10)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numDupDigitsAtMostN(int n) {\n String num = Integer.toString(n);\n int[][][] dp = new int[num.length()][2][1 << 10];\n for (int[][] a : dp) {\n for (int[] b : a) Arrays.fill(b, -1);\n }\n return n - findNoDup(num, num.length(), 0, 0, 0, dp);\n }\n\n private int findNoDup(String num, int n, int index, int decider, int mask, int[][][] dp) {\n if (index == n) return mask == 0 ? 0 : 1;\n if (dp[index][decider][mask] != -1) return dp[index][decider][mask];\n int res = 0;\n int limit = decider == 1 ? 9 : num.charAt(index) - \'0\';\n\n for (int i = 0; i <= limit; i++) {\n if ((mask & (1 << i)) != 0) continue;\n int newDecider = i < limit ? 1 : decider;\n int newMask = i == 0 && mask == 0 ? mask : mask | (1 << i);\n res += findNoDup(num, n, index + 1, newDecider, newMask, dp);\n }\n\n return dp[index][decider][mask] = res;\n }\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Memoization', 'Java'] | 0 |
numbers-with-repeated-digits | Digit DP C++ | digit-dp-c-by-aglakshya02-jxag | Code\n\nclass Solution {\npublic:\n\n // Digit DP with bitmask\n\n string s;\n int n;\n\n int dp[10][2][1<<10][2][2];\n\n int f(int i, int tight, | aglakshya02 | NORMAL | 2023-10-14T06:00:42.937094+00:00 | 2023-10-14T06:00:42.937119+00:00 | 21 | false | # Code\n```\nclass Solution {\npublic:\n\n // Digit DP with bitmask\n\n string s;\n int n;\n\n int dp[10][2][1<<10][2][2];\n\n int f(int i, int tight, int mask, int repeat, int allzeros){\n if(i==n)return repeat==1 && allzeros == 1;\n\n if(dp[i][tight][mask][repeat][allzeros] != -1) return dp[i][tight][mask][repeat][allzeros];\n\n int ub = tight ? s[i]-\'0\' : 9;\n\n int ans=0;\n\n for(int j=0;j<=ub;j++){\n int newtight = (tight && j==ub);\n int newallzeros = (allzeros || (j!=0));\n\n int newmask=mask;\n if(newallzeros != 0) newmask = (mask | (1<<j));\n\n int newrepeat = 0;\n // leading zeros might be repeating\n if(newallzeros != 0) newrepeat = (repeat || (mask & (1<<j))); \n\n ans+= f(i+1, newtight, newmask, newrepeat, newallzeros);\n \n }\n\n return dp[i][tight][mask][repeat][allzeros] = ans;\n }\n\n int numDupDigitsAtMostN(int N) {\n s=to_string(N);\n n=s.size();\n memset(dp,-1,sizeof(dp));\n return f(0,1,0,0,0);\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
numbers-with-repeated-digits | Digit DP + Bitmask | digit-dp-bitmask-by-nuagen-45cv | Code\n\nclass Solution {\npublic:\n\n int dp[10][2][2][2][1024];\n\n int okay(string s, int i, bool tight, bool lead, bool dup, int mask)\n {\n | Nuagen | NORMAL | 2023-10-05T11:54:32.475737+00:00 | 2023-10-05T11:54:32.475765+00:00 | 22 | false | # Code\n```\nclass Solution {\npublic:\n\n int dp[10][2][2][2][1024];\n\n int okay(string s, int i, bool tight, bool lead, bool dup, int mask)\n {\n if(i == s.size())\n {\n return dup;\n }\n\n if(dp[i][tight][lead][dup][mask] != -1)\n {\n return dp[i][tight][lead][dup][mask];\n }\n\n int x = (tight)? s[i]-\'0\': 9;\n int cnt = 0;\n\n for(int j = 0; j <= x; j++)\n {\n if(j!= 0 || (j == 0 && lead == 0))\n {\n if(((1<<j)&mask))\n { \n cnt+=okay(s,i+1,(tight&(j==x)),0,1,(mask|(1<<j)));\n }\n else\n {\n cnt+=okay(s,i+1,(tight&(j==x)),0,dup,(mask|(1<<j)));\n }\n }\n else\n {\n if(lead)\n {\n cnt+=okay(s,i+1,0,1,0,mask);\n }\n }\n }\n\n return dp[i][tight][lead][dup][mask] = cnt;\n }\n\n int numDupDigitsAtMostN(int n) {\n \n string s = to_string(n);\n memset(dp,-1, sizeof(dp));\n return okay(s,0,1,1,0,0);\n }\n};\n``` | 0 | 0 | ['Math', 'Dynamic Programming', 'Bitmask', 'C++'] | 0 |
numbers-with-repeated-digits | Digit DP + Bitmask | digit-dp-bitmask-by-nuagen-fixf | Code\n\nclass Solution {\npublic:\n\n int dp[10][2][2][2][1024];\n\n int okay(string s, int i, bool tight, bool lead, bool dup, int mask)\n {\n | Nuagen | NORMAL | 2023-10-05T11:53:45.243748+00:00 | 2023-10-05T11:53:45.243773+00:00 | 10 | false | # Code\n```\nclass Solution {\npublic:\n\n int dp[10][2][2][2][1024];\n\n int okay(string s, int i, bool tight, bool lead, bool dup, int mask)\n {\n if(i == s.size())\n {\n return dup;\n }\n\n if(dp[i][tight][lead][dup][mask] != -1)\n {\n return dp[i][tight][lead][dup][mask];\n }\n\n int x = (tight)? s[i]-\'0\': 9;\n int cnt = 0;\n\n for(int j = 0; j <= x; j++)\n {\n if(j!= 0 || (j == 0 && lead == 0))\n {\n if(((1<<j)&mask))\n { \n cnt+=okay(s,i+1,(tight&(j==x)),0,1,(mask|(1<<j)));\n }\n else\n {\n cnt+=okay(s,i+1,(tight&(j==x)),0,dup,(mask|(1<<j)));\n }\n }\n else\n {\n if(lead)\n {\n cnt+=okay(s,i+1,0,1,0,mask);\n }\n }\n }\n\n return dp[i][tight][lead][dup][mask] = cnt;\n }\n\n int numDupDigitsAtMostN(int n) {\n \n string s = to_string(n);\n memset(dp,-1, sizeof(dp));\n return okay(s,0,1,1,0,0);\n }\n};\n``` | 0 | 0 | ['Math', 'Dynamic Programming', 'Bitmask', 'C++'] | 0 |
numbers-with-repeated-digits | Digit DP + Bitmask | digit-dp-bitmask-by-nuagen-3zqv | Code\n\nclass Solution {\npublic:\n\n int dp[10][2][2][2][1024];\n\n int okay(string s, int i, bool tight, bool lead, bool dup, int mask)\n {\n | Nuagen | NORMAL | 2023-10-05T11:53:05.586324+00:00 | 2023-10-05T11:53:05.586347+00:00 | 5 | false | # Code\n```\nclass Solution {\npublic:\n\n int dp[10][2][2][2][1024];\n\n int okay(string s, int i, bool tight, bool lead, bool dup, int mask)\n {\n if(i == s.size())\n {\n return dup;\n }\n\n if(dp[i][tight][lead][dup][mask] != -1)\n {\n return dp[i][tight][lead][dup][mask];\n }\n\n int x = (tight)? s[i]-\'0\': 9;\n int cnt = 0;\n\n for(int j = 0; j <= x; j++)\n {\n if(j!= 0 || (j == 0 && lead == 0))\n {\n if(((1<<j)&mask))\n { \n cnt+=okay(s,i+1,(tight&(j==x)),0,1,(mask|(1<<j)));\n }\n else\n {\n cnt+=okay(s,i+1,(tight&(j==x)),0,dup,(mask|(1<<j)));\n }\n }\n else\n {\n if(lead)\n {\n cnt+=okay(s,i+1,0,1,0,mask);\n }\n }\n }\n\n return dp[i][tight][lead][dup][mask] = cnt;\n }\n\n int numDupDigitsAtMostN(int n) {\n \n string s = to_string(n);\n memset(dp,-1, sizeof(dp));\n return okay(s,0,1,1,0,0);\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
number-of-subsequences-that-satisfy-the-given-sum-condition | [Java/C++/Python] Two Sum | javacpython-two-sum-by-lee215-cgha | Intuition\nAlmost same as problem two sum.\nIf we want to know the count of subarray in sorted array A,\nthen it\'s exactly the same.\nMake sure you can do two | lee215 | NORMAL | 2020-06-28T05:10:46.101498+00:00 | 2020-09-17T08:14:12.961139+00:00 | 51,617 | false | # **Intuition**\nAlmost same as problem two sum.\nIf we want to know the count of subarray in sorted array `A`,\nthen it\'s exactly the same.\nMake sure you can do two sum before continue.\n<br>\n\n# **Explanation**\nSort input `A` first,\nFor each `A[i]`, find out the maximum `A[j]`\nthat `A[i] + A[j] <= target`.\n\nFor each elements in the subarray `A[i+1] ~ A[j]`,\nwe can pick or not pick,\nso there are `2 ^ (j - i)` subsequences in total.\nSo we can update `res = (res + 2 ^ (j - i)) % mod`.\n\nWe don\'t care the original elements order,\nwe only want to know the count of sub sequence.\nSo we can sort the original `A`, and the result won\'t change.\n<br>\n\n# **Complexity**\nTime `O(NlogN)`\nSpace `O(1)` for python\n(`O(N)` space for java and c++ can be save anyway)\n<br>\n\n**Java**\n```java\n public int numSubseq(int[] A, int target) {\n Arrays.sort(A);\n int res = 0, n = A.length, l = 0, r = n - 1, mod = (int)1e9 + 7;\n int[] pows = new int[n];\n pows[0] = 1;\n for (int i = 1 ; i < n ; ++i)\n pows[i] = pows[i - 1] * 2 % mod;\n while (l <= r) {\n if (A[l] + A[r] > target) {\n r--;\n } else {\n res = (res + pows[r - l++]) % mod;\n }\n }\n return res;\n }\n```\n**C++**\n```cpp\n int numSubseq(vector<int>& A, int target) {\n sort(A.begin(), A.end());\n int res = 0, n = A.size(), l = 0, r = n - 1, mod = 1e9 + 7;\n vector<int> pows(n, 1);\n for (int i = 1 ; i < n ; ++i)\n pows[i] = pows[i - 1] * 2 % mod;\n while (l <= r) {\n if (A[l] + A[r] > target) {\n r--;\n } else {\n res = (res + pows[r - l++]) % mod;\n }\n }\n return res;\n }\n```\n**Python:**\n```py\n def numSubseq(self, A, target):\n A.sort()\n l, r = 0, len(A) - 1\n res = 0\n mod = 10**9 + 7\n while l <= r:\n if A[l] + A[r] > target:\n r -= 1\n else:\n res += pow(2, r - l, mod)\n l += 1\n return res % mod\n```\n<br>\n | 564 | 3 | [] | 79 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.