question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
sum-of-prefix-scores-of-strings | Solution By Dare2Solve | Detailed Explanation | Clean Code | solution-by-dare2solve-detailed-explanat-gxhd | Exlanation []\nauthorslog.com/blog/FxtvdgRwjW\n\n# Code\n\ncpp []\nclass TrieNode {\npublic:\n unordered_map<char, TrieNode*> children;\n int prefixCount; | Dare2Solve | NORMAL | 2024-09-25T06:51:42.615867+00:00 | 2024-09-25T06:51:42.615900+00:00 | 787 | false | ```Exlanation []\nauthorslog.com/blog/FxtvdgRwjW\n```\n# Code\n\n```cpp []\nclass TrieNode {\npublic:\n unordered_map<char, TrieNode*> children;\n int prefixCount;\n \n TrieNode() {\n prefixCount = 0;\n }\n};\n\nclass Trie {\npublic:\n TrieNode* root;\n \n Trie() {\n root = new TrieNode();\n }\n \n void insert(const string& word) {\n TrieNode* node = root;\n for (char c : word) {\n if (node->children.find(c) == node->children.end()) {\n node->children[c] = new TrieNode();\n }\n node = node->children[c];\n node->prefixCount++;\n }\n }\n \n int getPrefixScore(const string& word) {\n TrieNode* node = root;\n int score = 0;\n for (char c : word) {\n node = node->children[c];\n score += node->prefixCount;\n }\n return score;\n }\n};\n\nclass Solution {\npublic:\n vector<int> sumPrefixScores(vector<string>& words) {\n Trie trie;\n vector<int> result;\n \n // Insert all words into the trie\n for (const string& word : words) {\n trie.insert(word);\n }\n \n // Get the prefix score for each word\n for (const string& word : words) {\n result.push_back(trie.getPrefixScore(word));\n }\n \n return result;\n }\n};\n```\n\n```python []\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.prefixCount = 0\n\nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n\n def insert(self, word):\n node = self.root\n for char in word:\n if char not in node.children:\n node.children[char] = TrieNode()\n node = node.children[char]\n node.prefixCount += 1\n\n def getPrefixScore(self, word):\n node = self.root\n score = 0\n for char in word:\n node = node.children[char]\n score += node.prefixCount\n return score\n\nclass Solution:\n def sumPrefixScores(self, words):\n trie = Trie()\n result = []\n for word in words:\n trie.insert(word)\n for word in words:\n result.append(trie.getPrefixScore(word))\n return result\n```\n\n```java []\nclass TrieNode {\n Map<Character, TrieNode> children = new HashMap<>();\n int prefixCount = 0;\n}\n\nclass Trie {\n TrieNode root;\n\n public Trie() {\n root = new TrieNode();\n }\n\n public void insert(String word) {\n TrieNode node = root;\n for (char ch : word.toCharArray()) {\n node.children.putIfAbsent(ch, new TrieNode());\n node = node.children.get(ch);\n node.prefixCount++;\n }\n }\n\n public int getPrefixScore(String word) {\n TrieNode node = root;\n int score = 0;\n for (char ch : word.toCharArray()) {\n node = node.children.get(ch);\n score += node.prefixCount;\n }\n return score;\n }\n}\n\npublic class Solution {\n public int[] sumPrefixScores(String[] words) {\n Trie trie = new Trie();\n int[] result = new int[words.length];\n for (String word : words) {\n trie.insert(word);\n }\n for (int i = 0; i < words.length; i++) {\n result[i] = trie.getPrefixScore(words[i]);\n }\n return result;\n }\n}\n\n```\n\n```javascript []\n/**\n * @param {string[]} words\n * @return {number[]}\n */\nclass TrieNode {\n constructor() {\n this.children = {}; //a trie\n this.prefixCount = 0; \n }\n}\nclass Trie {\n constructor() {\n this.root = new TrieNode();\n }\n insert(word) {\n let node = this.root;\n for (const char of word) {\n if (!node.children[char]) { //Create a Trie if not exists\n node.children[char] = new TrieNode();\n }\n node = node.children[char]; //add element to the Trie\n node.prefixCount++;\n }\n }\n\n getPrefixScore(word) {\n let node = this.root;\n let score = 0;\n for (const char of word) {\n node = node.children[char];\n score += node.prefixCount;\n }\n return score;\n }\n}\nvar sumPrefixScores = function(words) {\n const trie = new Trie();\n for (const word of words) {\n trie.insert(word);\n }\n const result = words.map(word => trie.getPrefixScore(word));\n \n return result;\n};\n``` | 4 | 0 | ['String', 'Trie', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
sum-of-prefix-scores-of-strings | C++ || Easy Tries Implementation ✅✅ || Beats 82.29% | c-easy-tries-implementation-beats-8229-b-67ym | Intuition\nThe problem requires calculating prefix scores for a list of words. The prefix score of a word is defined as the sum of the counts of occurrences of | arunk_leetcode | NORMAL | 2024-09-25T05:52:44.613774+00:00 | 2024-09-25T05:52:44.613804+00:00 | 288 | false | # Intuition\nThe problem requires calculating prefix scores for a list of words. The prefix score of a word is defined as the sum of the counts of occurrences of all its prefixes in a trie structure. The trie allows efficient insertion and retrieval of prefix counts, making it a suitable data structure for this task.\n\n# Approach\n1. **Trie Structure**: Create a `Trie` class with a nested `node` class. Each node will store:\n - `ew`: The count of words that end at that node.\n - `cp`: The count of prefixes that pass through that node.\n - An array of pointers to the next nodes corresponding to each character.\n\n2. **Insert Method**: For each word, iterate through its characters:\n - If the corresponding child node doesn\'t exist, create it.\n - Move to the child node and update the `cp` count to reflect the number of prefixes that pass through that node.\n - After processing the word, increment the `ew` count for the last node.\n\n3. **Prefix Count Method**: For each word, calculate the prefix score by iterating through its characters and summing the `cp` counts of the nodes corresponding to each prefix.\n\n4. **Main Function**: For the given list of words, first insert all words into the trie, then calculate the prefix scores for each word and store them in a result vector.\n\n# Complexity\n- **Time complexity**: *O(m.n)*.\n \n- **Space complexity**: *O(m.n).*\n\n# Code\n```cpp\n#include <string>\n#include <vector>\n\nclass Solution {\n class Trie {\n class node {\n public:\n int ew, cp;\n node* next[26];\n node() {\n ew = 0;\n cp = 0;\n for (int i = 0; i < 26; i++) {\n next[i] = nullptr;\n }\n }\n };\n\n node *trie;\n\n public:\n Trie() {\n trie = new node();\n }\n\n void insert(const string& word) {\n node *it = trie;\n for (char ch : word) {\n if (it->next[ch - \'a\'] == nullptr) {\n it->next[ch - \'a\'] = new node();\n }\n it = it->next[ch - \'a\'];\n it->cp++;\n }\n it->ew++;\n }\n\n int getPrefCount(const string& word) {\n node *it = trie;\n int cnt = 0;\n for (char ch : word) {\n if (it->next[ch - \'a\'] == nullptr) {\n return 0;\n }\n it = it->next[ch - \'a\'];\n cnt += it->cp;\n }\n return cnt;\n }\n };\n\npublic:\n vector<int> sumPrefixScores(vector<string>& words) {\n Trie t;\n for (const auto& word : words) {\n t.insert(word);\n }\n vector<int> ans(words.size(), 0);\n for (int i = 0; i < words.size(); i++) {\n ans[i] = t.getPrefCount(words[i]);\n }\n return ans;\n }\n};\n | 4 | 0 | ['String', 'Trie', 'C++'] | 0 |
sum-of-prefix-scores-of-strings | simple and easy Python solution || Trie | simple-and-easy-python-solution-trie-by-ypbpa | if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n###### Let\'s Connect on LinkedIn: www.linkedin.com/in/shishirrsiam\n###### Let\'s Connect on Facebook: ww | shishirRsiam | NORMAL | 2024-09-25T05:05:59.695746+00:00 | 2024-09-25T05:05:59.695776+00:00 | 368 | false | # if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n###### Let\'s Connect on LinkedIn: www.linkedin.com/in/shishirrsiam\n###### Let\'s Connect on Facebook: www.fb.com/shishirrsiam\n\n\n\n# Complexity\n- Time complexity: O(n * l)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```python3 []\nclass TrieNode:\n def __init__(self):\n self.count = 0\n self.children = [None] * 26\n\nclass Solution:\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n root = TrieNode()\n\n for w in words:\n node = root\n for ch in w:\n index = ord(ch) - ord(\'a\')\n if not node.children[index]:\n node.children[index] = TrieNode()\n node = node.children[index]\n node.count += 1\n\n ans = []\n for w in words:\n sum = 0\n node = root\n for ch in w:\n index = ord(ch) - ord(\'a\')\n node = node.children[index]\n sum += node.count\n ans.append(sum)\n return ans\n``` | 4 | 0 | ['Array', 'String', 'Trie', 'Counting', 'Python', 'Python3'] | 7 |
sum-of-prefix-scores-of-strings | Simple Solution Using Trie Data Structure | Java | simple-solution-using-trie-data-structur-rj75 | \n# Code\njava []\nclass Trie {\n Trie[] arr = new Trie[26];\n int count = 0;\n}\nclass Solution {\n\n Trie root = new Trie();\n\n void add_word(Str | eshwaraprasad | NORMAL | 2024-09-25T04:59:02.526614+00:00 | 2024-09-25T04:59:02.526647+00:00 | 247 | false | \n# Code\n```java []\nclass Trie {\n Trie[] arr = new Trie[26];\n int count = 0;\n}\nclass Solution {\n\n Trie root = new Trie();\n\n void add_word(String str) {\n Trie curr = root;\n int ind;\n for(char ch : str.toCharArray()) {\n ind = ch - \'a\';\n if(curr.arr[ind] == null) curr.arr[ind] = new Trie();\n curr = curr.arr[ind];\n curr.count++;\n }\n }\n int get_value(String str) {\n Trie curr = root;\n int ind;\n int count = 0;\n for(char ch : str.toCharArray()) {\n ind = ch - \'a\';\n if(curr.arr[ind] == null) return count;\n curr = curr.arr[ind];\n count += curr.count;\n }\n return count;\n }\n public int[] sumPrefixScores(String[] words) {\n for(String str : words) {\n add_word(str);\n }\n int result[] = new int[words.length];\n int ind = 0;\n for(String str : words) {\n result[ind++] = get_value(str);\n }\n return result;\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
sum-of-prefix-scores-of-strings | simple and easy C++ solution || Trie | simple-and-easy-c-solution-trie-by-shish-dfqt | \n# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n###### Let\'s Connect on LinkedIn: www.linkedin.com/in/shishirrsiam\n###### Let\'s Connect on Facebook | shishirRsiam | NORMAL | 2024-09-25T04:54:03.126625+00:00 | 2024-09-25T04:54:03.126665+00:00 | 514 | false | \n# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n###### Let\'s Connect on LinkedIn: www.linkedin.com/in/shishirrsiam\n###### Let\'s Connect on Facebook: www.fb.com/shishirrsiam\n\n# Complexity\n- Time complexity: O(n * l)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass TrieNode {\n public:\n int count;\n TrieNode* children[26];\n TrieNode() : count(0), children{NULL} {}\n};\nclass Solution {\npublic:\n vector<int> sumPrefixScores(vector<string>& words) \n {\n auto *root = new TrieNode();\n\n for(auto w : words)\n {\n auto *node = root;\n for(auto ch : w)\n {\n int assci = ch - \'a\';\n if(not node->children[assci])\n node->children[assci] = new TrieNode();\n node = node->children[assci];\n node->count += 1;\n }\n }\n\n vector<int>ans;\n for(auto w : words)\n {\n auto sum = 0;\n auto *node = root;\n for(auto ch : w)\n {\n int assci = ch - \'a\';\n node = node->children[assci];\n sum += node->count;\n }\n ans.push_back(sum);\n }\n\n return ans;\n }\n};\n``` | 4 | 0 | ['Array', 'String', 'Trie', 'Counting', 'C++'] | 6 |
sum-of-prefix-scores-of-strings | 2 Approaches || Trie & Hashing | 2-approaches-trie-hashing-by-imdotrahul-z4up | Intuition\n Describe your first thoughts on how to solve this problem. \nTrie:\nTrie approach leverages the tree structure to store and count the frequency of e | imdotrahul | NORMAL | 2024-09-25T03:35:42.553575+00:00 | 2024-09-25T03:35:42.553617+00:00 | 393 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Trie:**\nTrie approach leverages the tree structure to store and count the frequency of each prefix. Each node in the Trie represents a prefix formed by the characters from the root to that node. As words are inserted into the Trie, we track how many times each prefix has been encountered. This allows us to quickly compute the sum of prefix scores for any word by traversing its corresponding path in the Trie and summing the counts stored in the nodes. The Trie structure is ideal for efficiently handling problems related to prefixes in multiple strings.\n\n**Hashing:**\nHashing approach calculates a unique hash value for each prefix of a word and uses an unordered map to store the frequency of each prefix across all words. As we iterate through each string, we update the hash and check the map to count how many times each prefix has appeared. After processing the strings, we calculate the prefix score for each word by summing the frequencies of its prefixes stored in the map. This method is faster for lookups and requires less memory in comparison to a Trie but lacks the structural benefits of the Trie.\n\n---\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Trie Approach:**\n- Initialize a Trie where each node represents a character from \'a\' to \'z\'.\n- For each word, traverse its characters and insert them into the Trie.\n- As you insert a character, update the x value (prefix count) in the corresponding Trie node.\n- Ensure that new nodes are created for characters not already present in the current path.\n- Repeat the process for all words to fully construct the Trie with prefix counts.\n- To compute the prefix score for a word, traverse its characters in the Trie.\n- Sum the x values (prefix counts) encountered along the path of the word.\n- Store the prefix sum for each word in a result array.\n\n\n**Hashing Approach:**\n- Initialize an unordered map to track the frequency of each prefix\u2019s hash.\n- For each word, iterate through its characters, calculating a rolling hash for each prefix.\n- For each calculated hash, increment its count in the map to track the prefix\u2019s occurrences.\n- Repeat the process for all words, updating the prefix counts in the map.\n- To compute the prefix score for a word, iterate through its characters and recalculate the prefix hashes.\n- For each prefix hash of a word, sum the frequency stored in the map.\n- Repeat this for all words, summing the counts of their respective prefixes.\n- Store the prefix sum for each word in a result array.\n\n\n---\n\n\n\n## For better understanding and detailed explanation see inline comments \n\n---\n\n\n\n# Complexity\n- Time complexity: O(N.M)-> Both Approaches\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N.M)-> Both Approaches\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n{:style=\'width:250px\'}\n\n# Code\n**Trie:**\n```cpp []\n// Trie Node definition\nclass trie {\n public:\n int x; // To store how many times the prefix ending at this node has been seen.\n trie *v[26]; // Array of pointers to children nodes for each character \'a\' to \'z\'.\n};\n\n// Function to insert a string into the Trie and update prefix counts\nvoid maketrie(string str, trie* node) {\n for (auto &i: str) { // Traverse each character in the string\n // If the node for this character doesn\'t exist, create it\n if (node->v[i - \'a\'] == NULL) {\n node->v[i - \'a\'] = new trie(); // Create a new Trie node\n node = node->v[i - \'a\']; // Move to the newly created node\n node->x = node->x + 1; // Increment the count for this prefix\n } else {\n node = node->v[i - \'a\']; // Move to the existing node\n node->x = node->x + 1; // Increment the count for this prefix\n }\n }\n}\n\n// Function to calculate the sum of prefix scores for a given string\nvoid solve(string str, trie* node, int &x) {\n trie* p = node; // Pointer to traverse the Trie\n for (auto &i: str) { // Traverse each character in the string\n p = p->v[i - \'a\']; // Move to the next node in the Trie\n x += p->x; // Add the count of this prefix to the total score\n }\n}\n\n// Main solution class\nclass Solution {\npublic:\n // Function to calculate sum of prefix scores for all words\n vector<int> sumPrefixScores(vector<string>& words) {\n trie *node = new trie(); // Create the root node of the Trie\n \n // Step 1: Insert each word into the Trie and build the prefix tree\n for (auto &i: words) {\n maketrie(i, node); // Insert word into the Trie\n }\n \n vector<int> ans; // Vector to store the final prefix scores\n int x = 0; // Variable to store the current score for a word\n \n // Step 2: Calculate the prefix score for each word\n for (auto &i: words) {\n x = 0; // Reset the score for the new word\n solve(i, node, x); // Calculate the prefix score for the current word\n ans.push_back(x); // Store the score in the answer vector\n }\n \n return ans; // Return the final list of prefix scores\n }\n};\n\n```\n**Hashing:**\n```cpp []\nclass Solution {\npublic:\n vector<int> sumPrefixScores(vector<string>& nums) {\n int n = nums.size(); // Get the number of strings in the input.\n unordered_map<long long, int> mp; // Hash map to store the count of each unique prefix hash.\n long long mod = 1e15 + 7; // A large prime number used as a modulus to avoid overflow in hash computation.\n \n // Step 1: Calculate and store the hash of each prefix for all strings.\n for (int i = 0; i < n; i++) {\n long long hash = 0; // Initialize hash for the current string.\n for (auto &ch : nums[i]) { // For each character in the current string:\n hash = (hash * 97 + (ch)) % mod; // Update the hash using the current character.\n mp[hash]++; // Increment the count of this particular prefix hash in the map.\n }\n }\n\n // Step 2: Calculate the prefix score for each string.\n vector<int> ans(n, 0); // Initialize the result vector to store prefix scores for each string.\n for (int i = 0; i < n; i++) {\n int count = 0; // To store the sum of prefix scores for the current string.\n long long hash = 0; // Initialize hash for the current string.\n for (auto &ch : nums[i]) { // For each character in the current string:\n hash = (hash * 97 + (ch)) % mod; // Recalculate the hash for each prefix.\n count += mp[hash]; // Add the count of this prefix from the hash map to the score.\n }\n ans[i] = count; // Store the total prefix score for this string.\n }\n\n return ans; // Return the vector of prefix scores.\n }\n};\n``` | 4 | 0 | ['Array', 'Hash Table', 'String', 'Trie', 'Counting', 'C++'] | 0 |
sum-of-prefix-scores-of-strings | All solutions | all-solutions-by-dixon_n-t85c | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Dixon_N | NORMAL | 2024-09-25T03:01:15.368206+00:00 | 2024-09-25T03:11:57.990356+00:00 | 28 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\n\nclass Solution {\n public int[] sumPrefixScores(String[] words) {\n int n = words.length;\n int[] answer = new int[n];\n \n for (int i = 0; i < n; i++) {\n String word = words[i];\n for (int j = 1; j <= word.length(); j++) {\n String prefix = word.substring(0, j);\n for (String w : words) {\n if (w.startsWith(prefix)) {\n answer[i]++;\n }\n }\n }\n }\n \n return answer;\n }\n}\n```\n```java []\nclass Solution {\n public int[] sumPrefixScores(String[] words) {\n TreeMap<String, Integer> prefixCount = new TreeMap<>();\n \n // Count all prefixes\n for (String word : words) {\n for (int i = 1; i <= word.length(); i++) {\n String prefix = word.substring(0, i);\n prefixCount.put(prefix, prefixCount.getOrDefault(prefix, 0) + 1);\n }\n }\n \n // Calculate scores\n int[] answer = new int[words.length];\n for (int i = 0; i < words.length; i++) {\n String word = words[i];\n int score = 0;\n for (int j = 1; j <= word.length(); j++) {\n String prefix = word.substring(0, j);\n score += prefixCount.get(prefix);\n }\n answer[i] = score;\n }\n \n return answer;\n }\n}\n```\n```java []\nclass Solution {\n class TrieNode {\n TrieNode[] children;\n int count;\n\n TrieNode() {\n children = new TrieNode[26];\n count = 0;\n }\n }\n\n public int[] sumPrefixScores(String[] words) {\n TrieNode root = new TrieNode();\n int n = words.length;\n\n // Build the Trie\n for (String word : words) {\n TrieNode node = root;\n for (char c : word.toCharArray()) {\n int index = c - \'a\';\n if (node.children[index] == null) {\n node.children[index] = new TrieNode();\n }\n node = node.children[index];\n node.count++;\n }\n }\n\n // Calculate prefix scores\n int[] answer = new int[n];\n for (int i = 0; i < n; i++) {\n TrieNode node = root;\n for (char c : words[i].toCharArray()) {\n node = node.children[c - \'a\'];\n answer[i] += node.count;\n }\n }\n\n return answer;\n }\n}\n```\n\n| Solution | Time Complexity | Space Complexity |\n|------------|---------------------------|-------------------|\n| Brute Force| O(n * m^2) | O(1) |\n| Trie | O(N * L) | O(N) |\n| TreeMap | O(N * L * log(N * L)) | O(N * L) |\n\nWhere:\n- n = number of words\n- m = length of the longest word\n- N = total number of characters across all words\n- L = average length of words\n\nDetailed Explanation:\n\n1. Brute Force Solution:\n - Time: O(n * m^2)\n - We iterate through each word (n)\n - For each word, we generate all prefixes (up to m)\n - For each prefix, we check against all words (n)\n - Space: O(1)\n - We only use a fixed-size array to store the results\n\n2. Trie-based Solution:\n - Time: O(N * L)\n - We iterate through all characters of all words once to build the Trie\n - We iterate through all characters again to calculate scores\n - Space: O(N)\n - In the worst case (no common prefixes), we store all characters in the Trie\n\n3. TreeMap-based Solution:\n - Time: O(N * L * log(N * L))\n - We generate all prefixes (N * L operations)\n - Each TreeMap operation (put/get) takes log(N * L) time\n - Space: O(N * L)\n - We store all prefixes as strings in the TreeMap\n\n\n### Hashmap solution\n\n```java []\n\n/* TLE same as TreeMap.\n\nTime Complexity: O(N * L^2)\n\nN is the number of words\nL is the average length of the words\n\n\nCounting prefixes:\n\nWe iterate through each word: O(N)\nFor each word, we generate all prefixes: O(L)\nSubstring operation and HashMap put: O(L)\nTotal: O(N * L^2)\n\n\nCalculating scores:\n\nWe iterate through each word again: O(N)\nFor each word, we generate all prefixes: O(L)\nHashMap get and sum: O(1)\nTotal: O(N * L^2)\n*/\n\nclass Solution {\n public int[] sumPrefixScores(String[] words) {\n List<Integer> res = new ArrayList<>();\n Map<String, Integer> count = new HashMap<>();\n \n // Count prefixes\n for (String w : words) {\n for (int i = 1; i <= w.length(); i++) {\n String prefix = w.substring(0, i);\n count.put(prefix, count.getOrDefault(prefix, 0) + 1);\n }\n }\n \n // Calculate scores\n for (String w : words) {\n int score = 0;\n for (int i = 1; i <= w.length(); i++) {\n score += count.get(w.substring(0, i));\n }\n res.add(score);\n }\n \n // Convert List<Integer> to int[] without streams\n int[] resultArray = new int[res.size()];\n for (int i = 0; i < res.size(); i++) {\n resultArray[i] = res.get(i);\n }\n \n return resultArray;\n }\n}\n\n\n``` | 4 | 0 | ['Java'] | 4 |
sum-of-prefix-scores-of-strings | Sum of Prefix Scores of Strings || DCC 25/09/24 || Trie Solution ✅✅ | sum-of-prefix-scores-of-strings-dcc-2509-d1sz | Intuition\nThe problem revolves around finding the sum of scores for all prefixes of each word in the list. A Trie (prefix tree) is particularly suited for this | Ayush_Singh2004 | NORMAL | 2024-09-25T02:36:02.165959+00:00 | 2024-09-25T02:36:02.165991+00:00 | 161 | false | # Intuition\nThe problem revolves around finding the sum of scores for all prefixes of each word in the list. A Trie (prefix tree) is particularly suited for this task, as it efficiently stores and retrieves prefixes of words. By traversing the Trie, we can track how many times each prefix appears, which allows us to compute the score for each word\'s prefixes.\n\n# Approach\n**Trie Construction:**\n- We use a Trie where each node corresponds to a character, and cnt at each node stores the number of words that pass through that node (i.e., the number of words with a given prefix).\nInsert each word into the Trie. For every character of the word, we traverse the Trie, creating nodes as necessary and incrementing the cnt at each node to keep track of how many words have that prefix.\n\n**Score Calculation:**\n- For each word, we calculate the sum of scores of all its prefixes by traversing the Trie from the root for each prefix. At each node corresponding to a character, we add the cnt value (indicating how many words share this prefix) to the total score for that word.\n\n**Efficiency:**\n- The Trie allows us to efficiently find the score for each word\'s prefixes in linear time relative to the length of the word.\n\n**Code Explanation:**\n- The Trie class manages the Trie structure. It has methods:\n->insert: To add a word to the Trie.\n->search: To retrieve the count of words sharing a given prefix.\n- The sumPrefixScores function first inserts all the words into the Trie. Then for each word, it computes the total score by summing up the counts for each prefix in the Trie.\n\n# Complexity\n**Time complexity:**\n- Insertion: Inserting a word into the Trie takes $$O(L)$$ time where L is the length of the word. For n words with average length L, it takes $$O(n * L)$$ to insert all words.\n- Score Calculation: For each word, calculating the score involves traversing its prefixes, which also takes $$O(L)$$. For n words, this takes $$O(n * L)$$.\n- Overall time complexity is O(n * L), where n is the number of words, and L is the average length of the words.\n\n**Space complexity:**\n- The space complexity is $$O(n * L)$$ due to the Trie structure, which can have at most `n * L` nodes in the worst case (if all words are unique and share no common prefixes).\n\n# Code\n```cpp []\nclass Solution {\npublic:\n class Trie {\n public:\n Trie() {\n cnt = 0;\n for(int i=0;i<26;i++){\n this->next[i] = NULL;\n }\n }\n void insert(string word, Trie* root) {\n Trie* node = root;\n int i = 0;\n for (char ch : word) {\n ch -= \'a\';\n if (!node->next[ch]) { node->next[ch] = new Trie(); }\n node->next[ch]->cnt++;\n node = node->next[ch];\n i++;\n }\n }\n\n int search(char ch, Trie* node) {\n return node->next[ch-\'a\']->cnt;\n }\n\n Trie* next[26] = {};\n int cnt;\n };\n vector<int> sumPrefixScores(vector<string>& words) {\n Trie t;\n Trie *root = new Trie();\n int n = words.size();\n for(int i=0;i<n;i++){\n t.insert(words[i], root);\n }\n vector<int> ans;\n for(int i=0;i<n;i++){\n string cur = "";\n int c = 0;\n Trie *node = root;\n for(int j=0;j<words[i].length();j++){\n c += t.search(words[i][j], node);;\n if(node->next[words[i][j]-\'a\'] == NULL) break;\n node = node->next[words[i][j]-\'a\'];\n }\n ans.push_back(c);\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Array', 'Trie', 'C++'] | 0 |
sum-of-prefix-scores-of-strings | Trie, just 3 steps | trie-just-3-steps-by-raviteja_29-v20w | Intuition\n Describe your first thoughts on how to solve this problem. \nTo solve this problem, you need to efficiently calculate the number of times each prefi | raviteja_29 | NORMAL | 2024-07-24T17:12:09.056160+00:00 | 2024-07-24T17:12:09.056191+00:00 | 176 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this problem, you need to efficiently calculate the number of times each prefix of a given string appears in the list of words. A direct approach could involve checking each prefix of each string against all words, but this would be too slow. Instead, using a Trie (prefix tree) is a more efficient way to keep track of prefix frequencies.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Trie Construction:\n\n* Use a Trie data structure to store all words. In this Trie, each node represents a character in the words, and we will maintain a count of how many times each prefix is encountered.\n2. Inserting Words into Trie:\n\n* For each word, insert it into the Trie. During insertion, for each character in the word, increment the char_count at the corresponding Trie node. This count will help us determine how many words share that prefix.\n3. Calculate Prefix Scores:\n\n* For each word in the list, traverse the Trie to calculate the sum of the scores for all non-empty prefixes of the word. This can be done by accumulating the counts of each prefix as you traverse the Trie.\n\n# Complexity\n- Time complexity: O(nxm)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.is_end_of_word = False\n self.char_count = 0\n\nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n \n def insert(self, word):\n node = self.root\n for char in word:\n if char not in node.children:\n node.children[char] = TrieNode()\n node = node.children[char]\n node.char_count += 1\n node.is_end_of_word = True\n\n def search(self, word):\n node = self.root\n ans = 0\n for char in word:\n node = node.children[char]\n ans += node.char_count\n return ans\n\n\nclass Solution:\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n trie = Trie()\n for x in words:\n trie.insert(x)\n l = []\n for x in words:\n l.append(trie.search(x))\n return l\n\n``` | 4 | 0 | ['Python3'] | 2 |
sum-of-prefix-scores-of-strings | c++ two solution trie || hashing | c-two-solution-trie-hashing-by-dilipsuth-ylai | \nclass Solution\n{\n public:\n struct node\n {\n node *child[26] = { NULL\n };\n int count = 0;\n };\n | dilipsuthar17 | NORMAL | 2022-09-18T04:01:48.861504+00:00 | 2022-09-18T07:00:46.630347+00:00 | 361 | false | ```\nclass Solution\n{\n public:\n struct node\n {\n node *child[26] = { NULL\n };\n int count = 0;\n };\n node *root = new node();\n void insert(string & s)\n {\n int n = s.size();\n node *curr = root;\n for (int i = 0; i < n; i++)\n {\n int index = s[i] - \'a\';\n if (curr->child[index] == NULL)\n {\n curr->child[index] = new node();\n }\n curr = curr->child[index];\n curr->count++;\n }\n }\n int find(node *curr, string &s)\n {\n int ans = 0;\n for (char &ch: s)\n {\n if (curr->child[ch - \'a\'] != NULL)\n {\n curr = curr->child[ch - \'a\'];\n ans += curr->count;\n }\n }\n return ans;\n }\n vector<int> sumPrefixScores(vector<string> &nums)\n {\n int n = nums.size();\n for (int i = 0; i < n; i++)\n {\n insert(nums[i]);\n }\n vector<int> ans;\n for (int i = 0; i < n; i++)\n {\n node *curr = root;\n int value = find(curr, nums[i]);\n ans.push_back(value);\n }\n return ans;\n }\n};\n```\n\n```\nclass Solution {\npublic:\n vector<int> sumPrefixScores(vector<string>&nums) \n {\n int n=nums.size();\n unordered_map<long long,int>mp;\n long long mod=1e15+7;\n for(int i=0;i<n;i++)\n {\n long long hash=0;\n for(auto &ch:nums[i])\n {\n hash=(hash*97+(ch))%mod;\n mp[hash]++;\n }\n }\n vector<int>ans(n,0);\n for(int i=0;i<n;i++)\n {\n int count=0;\n long long hash=0;\n for(auto &ch:nums[i])\n {\n hash=(hash*97+(ch))%mod;\n count+=mp[hash];\n }\n ans[i]=count;\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Trie', 'C', 'C++'] | 0 |
sum-of-prefix-scores-of-strings | Trie || striver Templete | trie-striver-templete-by-mayank670-hene | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Mayank670 | NORMAL | 2024-09-25T13:25:25.359060+00:00 | 2024-09-25T13:25:25.359082+00:00 | 22 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nstruct Node{\n Node* links[26];\n int cnt = 0; \n bool flag = false; \n\n bool isPresent(char ch){\n return links[ch - \'a\'] != NULL; \n }\n\n void put(char ch, Node* node){\n links[ch - \'a\'] = node;\n }\n\n Node* get(char ch){\n return links[ch - \'a\']; \n }\n\n void increaseCount() {\n cnt++;\n }\n\n int getCount() {\n return cnt;\n }\n\n void setEnd(){\n flag = true; \n }\n\n bool isEnd(){\n return flag; \n }\n};\n\nclass Solution {\n private: \n Node* root; \n public:\n Solution(){\n root = new Node(); \n }\n\n void insert(string word){\n Node* node = root; \n for(int i = 0; i < word.size(); i++){\n if(!node->isPresent(word[i])){\n node->put(word[i], new Node()); \n }\n node = node->get(word[i]); \n node->increaseCount(); \n }\n node->setEnd(); \n }\n\n int search(string word){\n Node* node = root; \n int score = 0; \n for(int i = 0; i < word.size(); i++){\n if(!node->isPresent(word[i])) return score; \n node = node->get(word[i]); \n score += node->getCount(); \n }\n return score; \n }\n\n vector<int> sumPrefixScores(vector<string>& words) {\n for(auto &word : words){\n this->insert(word); \n }\n \n vector<int> result; \n for(auto &word : words){\n result.push_back(this->search(word)); \n }\n return result; \n }\n};\n\n``` | 3 | 0 | ['String', 'Trie', 'C++'] | 0 |
sum-of-prefix-scores-of-strings | JAVA | Trie Data Structure | java-trie-data-structure-by-sudhikshagha-q9dl | Code\njava []\nclass TrieNode {\n TrieNode [] children = new TrieNode[26];\n int count = 0;\n}\nclass Solution {\n TrieNode root = new TrieNode();\n | SudhikshaGhanathe | NORMAL | 2024-09-25T12:57:31.022161+00:00 | 2024-09-25T12:57:31.022197+00:00 | 24 | false | # Code\n```java []\nclass TrieNode {\n TrieNode [] children = new TrieNode[26];\n int count = 0;\n}\nclass Solution {\n TrieNode root = new TrieNode();\n public void add(String word) {\n TrieNode curr = root;\n for (char c : word.toCharArray()) {\n int idx = c - \'a\';\n if (curr.children[idx] == null)\n curr.children[idx] = new TrieNode();\n curr = curr.children[idx];\n curr.count += 1;\n }\n }\n public int sum(String word) {\n TrieNode curr = root;\n int res = 0;\n for (char c : word.toCharArray()) {\n int idx = c - \'a\';\n curr = curr.children[idx];\n res += curr.count;\n }\n return res;\n }\n public int[] sumPrefixScores(String[] words) {\n int [] res = new int[words.length];\n for (String word : words) add(word);\n for (int i = 0 ; i < words.length ; i++)\n res[i] = sum(words[i]);\n return res;\n }\n}\n``` | 3 | 0 | ['Trie', 'Counting', 'Java'] | 0 |
sum-of-prefix-scores-of-strings | [EASY] Simplified explantion of logic (using Trie Data Structure): | easy-simplified-explantion-of-logic-usin-h15g | Intuition\nThe problem asks us to compute the sum of prefix scores for each word in the given list. A prefix score is the total number of words in the list that | rinsane | NORMAL | 2024-09-25T11:25:27.674667+00:00 | 2024-09-25T11:25:27.674700+00:00 | 40 | false | # Intuition\nThe problem asks us to compute the sum of prefix scores for each word in the given list. A prefix score is the total number of words in the list that share the same prefix, up to every letter in the word.\n\nTo efficiently solve this problem, we can leverage a **Trie** (prefix tree). Tries are well-suited for problems involving prefixes, as they allow us to store and count the occurrence of prefixes across multiple words.\n\nThe key insight is to insert each word into the Trie while counting how many words pass through each node (which corresponds to a character in a prefix). Once all words are inserted, we can compute the prefix score for each word by summing the counts of nodes visited while traversing the Trie.\n\n# Approach\n1. **Trie Construction**:\n - First, we define a `Node` class to represent each node in the Trie. Each node stores an array for child nodes (`self.char`), one for each letter of the alphabet, and a counter (`self.count`) to track how many words pass through this node.\n - In the `Solution` class, we initialize the Trie by creating the root node.\n\n2. **Insert Function**:\n - For each word, we traverse the Trie, creating new nodes as necessary for each character. While traversing, we increment the `count` of each node to record how many words share the prefix leading to that node.\n\n3. **Calculate Prefix Scores**:\n - After building the Trie, for each word, we again traverse the Trie and sum the `count` values of the nodes along the path defined by the word\u2019s characters. This sum gives us the total prefix score for the word.\n\n4. **Result**:\n - We repeat the above for each word and store the results in a list to be returned.\n\n# Complexity\n- **Time Complexity**: \n The time complexity is $$O(n \\cdot m)$$, where `n` is the number of words, and `m` is the maximum length of a word. Each insertion and traversal through the Trie takes $$O(m)$$, and we do this for each word.\n \n- **Space Complexity**: \n The space complexity is also $$O(n \\cdot m)$$, as the Trie may contain up to `n * m` nodes in the worst case, where `n` is the number of words and `m` is the average word length.\n\n# Code\n```python3\n# Node class representing a single character in the Trie\nclass Node:\n def __init__(self):\n # Each node has 26 possible children (for \'a\' to \'z\')\n self.char = [None] * 26\n # Count keeps track of how many words have passed through this node\n self.count = 0\n\n# Solution class that uses the Trie to solve the problem\nclass Solution:\n def __init__(self):\n # Root of the Trie is an empty node\n self.root = Node()\n \n # Inserts a word into the Trie and updates the count of each node\n def insert(self, word):\n curr = self.root\n for c in word:\n # Calculate index of the character (0 for \'a\', 25 for \'z\')\n idx = ord(c) - ord(\'a\')\n # If no node exists for this character, create one\n if curr.char[idx] is None:\n curr.char[idx] = Node()\n # Move to the next node in the Trie\n curr = curr.char[idx]\n # Increment the count for the current node (since a word passes through it)\n curr.count += 1\n\n # Computes the prefix scores for each word in the input list\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n # First, insert all words into the Trie\n for word in words:\n self.insert(word)\n\n ans = []\n # For each word, calculate the prefix score\n for word in words:\n curr = self.root\n currans = 0\n # Traverse the Trie and sum the counts along the path of the word\n for c in word:\n idx = ord(c) - ord(\'a\')\n curr = curr.char[idx]\n # Add the count of the current node to the result\n currans += curr.count\n # Append the total prefix score for the current word\n ans.append(currans)\n \n return ans | 3 | 0 | ['Trie', 'Python3'] | 1 |
sum-of-prefix-scores-of-strings | Sum of Prefix Scores of Strings | sum-of-prefix-scores-of-strings-by-pushp-viai | \n# Approach\n Describe your approach to solving the problem. \nHashMap and Trie\n\n\n\n# Time complexity:\n Add your time complexity here, e.g. O(n) \n- Hashma | Pushparaj_Shetty | NORMAL | 2024-09-25T05:41:08.626147+00:00 | 2024-09-25T05:41:08.626186+00:00 | 89 | false | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n**HashMap** and **Trie**\n\n\n\n# Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- **Hashmap**: O(n * k\xB2)\n \n\n- **Trie**: O(n * k)\n\n\n\n# Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- **Hashmap**: O(n * k)\n\n- **Trie**: O(n * k)\n\n\nFor anyone wondering why it\'s O(n * k\xB2) for the hashmap, it\'s because for each of the n words, generating all k prefixes requires slicing the string, which takes O(k) time per slice, leading to O(k\xB2) operations for each word\n\n# Code\n```python3 []\nfrom collections import defaultdict\n\n# TrieNode class that defines the structure of each node in the Trie.\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.counter = 0\n\nclass Solution:\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n # Method 1: Using HashMap \n # This approach uses a hash map to store the count of each prefix.\n # It\'s simple but inefficient in terms of memory and time due to repeated prefix calculations.\n # Time complexity: O(n * k^2)\n # Space complexity: O(n * k)\n # h = defaultdict(int)\n # for word in words:\n # for j in range(1, len(word) + 1):\n # h[word[:j]] += 1\n \n # # Calculate the prefix scores by summing the counts of all prefixes for each word.\n # res = []\n # for word in words:\n # total = 0\n # for j in range(1, len(word) + 1):\n # total += h[word[:j]]\n # res.append(total)\n \n # return res\n\n # Method 2: Using Trie (optimized approach)\n # This approach uses a Trie data structure to store prefixes and calculate their frequency efficiently.\n # Time complexity: O(n * k)\n # Space complexity: O(n * k)\n trie = TrieNode() \n\n # Step 1: Build the Trie and count how many words pass through each prefix.\n for word in words:\n cur = trie \n for char in word:\n if char not in cur.children:\n cur.children[char] = TrieNode() \n cur = cur.children[char] \n cur.counter += 1 \n\n # Step 2: Calculate the prefix score for each word by summing up the counters of its prefixes.\n res = []\n for word in words:\n cur = trie \n total = 0 \n for char in word:\n cur = cur.children[char] \n total += cur.counter \n res.append(total) \n\n return res\n\n``` | 3 | 0 | ['Trie', 'Counting', 'Python3'] | 1 |
sum-of-prefix-scores-of-strings | Easy Solution | Explained with Example & Visual Walkthrough | Beginner Friendly | | easy-solution-explained-with-example-vis-iw3s | Approach\nBuilding the Trie:\nEvery time a letter is inserted into the Trie, we update the count for that letter\u2019s node. This count keeps track of how many | Guna01 | NORMAL | 2024-09-25T01:56:07.257494+00:00 | 2024-09-25T01:57:35.709746+00:00 | 93 | false | # Approach\nBuilding the Trie:\nEvery time a letter is inserted into the Trie, we update the count for that letter\u2019s node. This count keeps track of how many words pass through that node.\n\nExample Words: ["abc", "ab", "bc", "b"]\n\nInsert "abc":\n\'a\' goes into the Trie (count is now 1).\n\'b\' goes into the Trie (count is now 1).\n\'c\' goes into the Trie (count is now 1).\n\n`root -> a(1) -> b(1) -> c(1)`\n\nInsert "ab":\n\'a\' already exists, so just increase the count (now 2).\n\'b\' already exists, so just increase the count (now 2).\n\n`root -> a(2) -> b(2) -> c(1)`\n\nInsert "bc":\n\'b\' doesn\'t exist directly to the root, so we create it (count is 1).\n\'c\' follows \'b\' (count is 1)\n\n```\nroot -> a(2) -> b(2) -> c(1)\n \\\n b(1) -> c(1)\n\n```\nInsert "b":\n\'b\' already exists under the root, so we just increase its count (now 2).\n```\nroot -> a(2) -> b(2) -> c(1)\n \\\n b(2) -> c(1)\n\n```\n\nCalculating Prefix Scores:\nFor each word, we traverse the Trie and sum up the counts of the nodes we visit.\n\nWord "abc":\nFrom the root and go through \'a\' (count = 2), \'b\' (count = 2), and \'c\' (count = 1).\nPrefix score = 2 + 2 + 1 = 5.\n\nWord "ab":\nFrom the root and go through \'a\' (count = 2) and \'b\' (count = 2).\nPrefix score = 2 + 2 = 4.\n\nWord "bc":\nFrom the root and go through \'b\' (count = 2) and \'c\' (count = 1).\nPrefix score = 2 + 1 = 3.\n\nWord "b":\nFrom the root and go through \'b\' (count = 2).\nPrefix score = 2 = 2.\n\n\nThe array of prefix scores will be: [5, 4, 3, 2]\n\n\nFinal Trie will be:\n```\n (root)\n / \\\n a(2) b(2)\n | |\n b(2) c(1)\n |\n c(1)\n\n```\n\n#### Upvote if this solution is good \u2B06\uFE0F\n\n\n\n# Code\n```java []\nclass Solution {\n class Trie{\n Trie children[] =new Trie [26];\n int count = 0;\n }\n public int[] sumPrefixScores(String[] words) {\n Trie root = new Trie();\n for(String s : words){\n Trie curr = root;\n for(char ch:s.toCharArray()){\n if(curr.children[ch-\'a\']==null){\n curr.children[ch-\'a\']=new Trie();\n }\n curr = curr.children[ch-\'a\'];\n curr.count++;\n }\n } \n int n = words.length;\n int ans[] = new int[n];\n int i =0;\n for(String s:words){\n Trie curr = root;\n int sum = 0;\n for(char ch:s.toCharArray()){\n curr = curr.children[ch-\'a\'];\n sum+=curr.count;\n }\n ans[i]=sum;\n i++;\n }\n return ans;\n }\n}\n``` | 3 | 0 | ['Array', 'String', 'Trie', 'Counting', 'Java'] | 0 |
sum-of-prefix-scores-of-strings | Rust Solution | rust-solution-by-evanchun-txf6 | Intuition\n\n# Approach\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n\n#[derive(Default)]\nstruct Trie {\n cnt: usize,\n | evanchun | NORMAL | 2024-06-05T06:39:39.949211+00:00 | 2024-06-05T06:39:39.949240+00:00 | 47 | false | # Intuition\n\n# Approach\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\n#[derive(Default)]\nstruct Trie {\n cnt: usize,\n children: [Option<Box<Trie>>; 27],\n}\n\nimpl Solution {\n pub fn sum_prefix_scores(words: Vec<String>) -> Vec<i32> {\n let mut root = Trie::default();\n\n for word in words.iter() {\n let mut curr = &mut root;\n \n for c in word.chars().map(|x| x as usize - \'a\' as usize) {\n curr = curr.children[c].get_or_insert_with(Default::default);\n curr.cnt += 1;\n }\n }\n\n let mut res = vec![0; words.len()];\n\n for (i, word) in words.into_iter().enumerate() {\n let mut cnt = 0;\n let mut curr = &root;\n\n for c in word.chars().map(|x| x as usize - \'a\' as usize) {\n curr = curr.children[c].as_ref().unwrap();\n cnt += curr.cnt;\n }\n\n res[i] = cnt as _;\n }\n\n res\n }\n}\n``` | 3 | 0 | ['Rust'] | 0 |
sum-of-prefix-scores-of-strings | [Python3] Trie - Simple Solution + Detailed Explanation | python3-trie-simple-solution-detailed-ex-rylt | Intuition\n Describe your first thoughts on how to solve this problem. \n- Check for Common Prefix for string -> Trie\n\n# Approach\n Describe your approach to | dolong2110 | NORMAL | 2024-02-18T10:37:47.966641+00:00 | 2024-09-25T07:24:31.004457+00:00 | 143 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Check for Common Prefix for string -> Trie\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n**1. Node Class:**\n\n- Represents a node in the Trie data structure.\n- `cnt_prf` stores the count of prefixes that end at this node.\n- `children` is a dictionary to store child nodes for each character.\n\n**2. Trie Class:**\n\n- Represents the Trie data structure.\n- `root` is the root node of the Trie.\n- `insert(word)` function:\n - Inserts the given word into the Trie.\n - Starts from the root node.\n - Iterates over each character in the word.\n - Creates a child node if it doesn\'t exist and moves to the child node.\n - Increments the `cnt_prf` of the current node to indicate that a new prefix ends at this node.\n- `get_sum_prf(word)` function:\n - Calculates the sum of prefix scores for the given word.\n - Starts from the root node.\n - Initializes a counter `cnt` to 0.\n - Iterates over each character in the word.\n - If the current character is not found as a child of the current node, breaks the loop (no further prefix exists).\n - Moves to the child node and adds the `cnt_prf` of the child node to `cnt`.\n - Returns the final `cnt`, which represents the sum of prefix scores for the word.\n\n**3. Solution Class:**\n\n- `sumPrefixScores(words)` function:\n - Creates a `Trie` object.\n - Inserts each word in the given list into the Trie.\n - Creates a list to store the sum of prefix scores for each word.\n - Iterates over each word in the list.\n - Calls `trie.get_sum_prf(word)` to calculate the sum of prefix scores for the current word.\n - Appends the calculated sum to the result list.\n - Returns the final list containing the sum of prefix scores for each word.\n\n**Overall Functionality:**\n\nThe Trie is used to efficiently store and retrieve prefixes of the words. By inserting each word into the Trie, the `cnt_prf` values at each node represent the number of words that have the corresponding prefix. The `get_sum_prf` function traverses the Trie for a given word, accumulating the `cnt_prf` values along the path to calculate the total number of prefixes.\n\n# Complexity\n- Time complexity: $$O(N * S)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(26^S)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nWith `N` is length of `words` and `S` is length of a `word` in `words`\n\n# Code\n```\nclass Node:\n\n def __init__(self):\n self.cnt_prf = 0\n self.children = collections.defaultdict(Node)\n\n\nclass Trie:\n\n def __init__(self):\n self.root = Node()\n\n def insert(self, word: str) -> None:\n node = self.root\n for c in word:\n node = node.children[c]\n node.cnt_prf += 1\n\n def get_sum_prf(self, word: str) -> int:\n node = self.root\n cnt = 0\n for c in word:\n if c not in node.children:break\n node = node.children[c]\n cnt += node.cnt_prf\n\n return cnt\n\n\nclass Solution:\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n trie = Trie()\n for word in words: trie.insert(word)\n return [trie.get_sum_prf(word) for word in words]\n``` | 3 | 0 | ['String', 'Trie', 'Counting', 'Python3'] | 0 |
sum-of-prefix-scores-of-strings | C++ || EASY || TRIE | c-easy-trie-by-ganeshkumawat8740-em2l | Code\n\nclass trie{\n public:\n int x;\n trie *v[26];\n};\nvoid maketrie(string str,trie* node){\n for(auto &i: str){\n if(node->v[i- | ganeshkumawat8740 | NORMAL | 2023-05-26T09:10:27.874682+00:00 | 2023-05-26T09:10:27.874711+00:00 | 1,373 | false | # Code\n```\nclass trie{\n public:\n int x;\n trie *v[26];\n};\nvoid maketrie(string str,trie* node){\n for(auto &i: str){\n if(node->v[i-\'a\'] == NULL){\n node->v[i-\'a\'] = new trie();\n node = node->v[i-\'a\'];\n node->x = node->x +1 ;\n }else{\n node = node->v[i-\'a\'];\n node->x = node->x +1 ;\n }\n }\n}\nvoid solve(string str,trie* node,int &x){\n trie* p = node;\n for(auto &i: str){\n p = p->v[i-\'a\'];\n x += p->x;\n }\n}\nclass Solution {\npublic:\n vector<int> sumPrefixScores(vector<string>& words) {\n trie *node = new trie();\n for(auto &i: words){\n maketrie(i,node);\n }\n int x = 0;\n vector<int> ans;\n for(auto &i: words){\n x = 0;\n solve(i,node,x);\n ans.push_back(x);\n } \n return ans;\n }\n};\n``` | 3 | 0 | ['Array', 'String', 'Trie', 'Counting', 'C++'] | 0 |
sum-of-prefix-scores-of-strings | C++ || TRIE || EASY TO UNDERSTAND || SHORT & SWEET CODE | c-trie-easy-to-understand-short-sweet-co-35ai | \nclass trie{//make trie class\n public:\n int cnt;\n trie* v[26];\n trie(){\n cnt = 0;//no of common prefix\n for | yash___sharma_ | NORMAL | 2023-04-12T12:57:32.046538+00:00 | 2023-04-12T12:59:16.023159+00:00 | 205 | false | ````\nclass trie{//make trie class\n public:\n int cnt;\n trie* v[26];\n trie(){\n cnt = 0;//no of common prefix\n for(int i = 0; i < 26; i++){\n v[i] = NULL;\n }\n }\n};\nclass Solution {\npublic:\n vector<int> sumPrefixScores(vector<string>& words) {\n trie *node = new trie(),*tmp;//inittilize trie root node\n for(auto &i: words){\n tmp = node;\n for(auto &j: i){\n if(tmp->v[j-\'a\']==NULL){//if node not found make node\n tmp->v[j-\'a\'] = new trie();\n tmp = tmp->v[j-\'a\'];\n tmp->cnt++;\n }else{//if node found\n tmp = tmp->v[j-\'a\'];\n tmp->cnt++;//increment prefix count by one\n }\n }\n }\n int sum = 0;\n vector<int> ans;\n for(auto &i: words){\n sum = 0;// for string i ans = 0\n tmp = node;\n for(auto &j: i){\n sum += (tmp->v[j-\'a\'])->cnt;//add no of common prefix\n tmp = tmp->v[j-\'a\'];\n }\n ans.push_back(sum);\n }\n return ans;\n }\n};\n```` | 3 | 0 | ['Trie', 'C', 'C++'] | 0 |
sum-of-prefix-scores-of-strings | C++ Fully optimized Trie 99% faster 87% less memory | c-fully-optimized-trie-99-faster-87-less-3ykr | This is based on the Trie approach but with significantly less memory usage.\nMy original Trie was 779 ms\t700.9 MB\nThis one is 353 ms\t186.5 MB\nhttps://leetc | flowac | NORMAL | 2022-10-17T07:10:06.129557+00:00 | 2022-10-17T07:10:06.129592+00:00 | 369 | false | This is based on the Trie approach but with significantly less memory usage.\nMy original Trie was 779 ms\t700.9 MB\nThis one is 353 ms\t186.5 MB\nhttps://leetcode.com/submissions/detail/824255922/\n\nI don\'t remember what this method is called. Please comment if you know the name.\n\nTake "abcd", "abef" for example:\n1. "abcd": I will first create the "a" node in Trie, then put "abcd" into str field of the "a" node and stop.\n2a. "abef": I see that "a" node exists, and the str field is not empty. Thus I need to move the "abcd".\n2b. For the original "abcd", "b" node is created. I then check if b also exists in "abef" in the same position.\n2c. I continue to go thru the first string until either my current index exceeds the length of either string, or if the character at the current position in both strings no longer matches.\n2d. Finally, for "abcd", I create the "c" node, and copy "cd" into it.\n2e. For "abef", I create the "e" node, and copy "ef" into it.\n2f. I clean up the "abcd" in the "a" node because it has been moevd.\n\n```\nclass Solution {\npublic:\n typedef struct Trie {\n struct Trie *data[26]{};\n char *str{};\n int vis{}, slen{};\n } Trie;\n\n vector<int> sumPrefixScores(vector<string>& words) {\n vector<int> ret;\n Trie *root = (Trie *) calloc(1, sizeof(Trie)), *tmp, *tmp2;\n int sum, depth;\n\n for (string &x : words)\n {\n tmp = root;\n for (int i = 0, ilen = x.size(); i < ilen; ++i)\n {\n char y = x[i] - \'a\';\n if (!tmp->data[y])\n {\n // If the node does not exist, create node, copy the entire substring into "str" field and stop\n tmp->data[y] = (Trie *) calloc(1, sizeof(Trie));\n tmp = tmp->data[y];\n tmp->vis = 1;\n tmp->slen = ilen - i;\n tmp->str = (char *) calloc(1, tmp->slen + 1);\n memcpy(tmp->str, x.data() + i, tmp->slen);\n break;\n }\n\n tmp = tmp->data[y];\n ++tmp->vis;\n // If the node exists and "str" field is empty, continue\n if (tmp->slen == 0) continue;\n\n int j, jlen = tmp->slen;\n char *&ts = tmp->str;\n int &tslen = tmp->slen;\n // Find the index where the two strings are no longer the same\n for (j = 1; j < jlen && j + i < ilen && x[j + i] == ts[j]; ++j)\n {\n y = ts[j] - \'a\';\n tmp->data[y] = (Trie *) calloc(1, sizeof(Trie));\n tmp = tmp->data[y];\n tmp->vis = 2;\n }\n\n // Create new nodes and copy substrings for the two strings, if applicable\n tmp2 = tmp;\n if (j < jlen)\n {\n y = ts[j] - \'a\';\n tmp->data[y] = (Trie *) calloc(1, sizeof(Trie));\n tmp = tmp->data[y];\n tmp->vis = 1;\n tmp->slen = jlen - j;\n tmp->str = (char *) calloc(1, tmp->slen + 1);\n memcpy(tmp->str, ts + j, tmp->slen);\n }\n j += i;\n if (j < ilen)\n {\n tmp = tmp2;\n y = x[j] - \'a\';\n tmp->data[y] = (Trie *) calloc(1, sizeof(Trie));\n tmp = tmp->data[y];\n tmp->vis = 1;\n tmp->slen = ilen - j;\n tmp->str = (char *) calloc(1, tmp->slen + 1);\n memcpy(tmp->str, x.data() + j, tmp->slen);\n }\n free(ts);\n ts = NULL;\n tslen = 0;\n break;\n }\n }\n\n // Tally results\n for (string &x : words)\n {\n tmp = root;\n sum = depth = 0;\n for (char y : x)\n {\n y -= \'a\';\n tmp = tmp->data[y];\n if (tmp->vis == 1)\n {\n sum += x.size() - depth;\n break;\n }\n sum += tmp->vis;\n ++depth;\n }\n ret.push_back(sum);\n }\n\n return ret;\n }\n};\n``` | 3 | 0 | ['C', 'C++'] | 1 |
sum-of-prefix-scores-of-strings | [Javascript] get rid of memory allocation problem | javascript-get-rid-of-memory-allocation-36ybg | I found that in javascript, you will face memory problem in some testcase\nSo i\'m posting my solution here\n\nyou have to know that words with different inital | haocherhong | NORMAL | 2022-09-19T16:13:03.051066+00:00 | 2022-09-19T16:13:03.051115+00:00 | 154 | false | I found that in javascript, you will face memory problem in some testcase\nSo i\'m posting my solution here\n\nyou have to know that words with different inital characters wont affect each others\' score\nfor example, `abcd, aaab, acab` wont affect the scores of `cbcd, bacd, bbab, ccccd`.\nKnowing the fact, you know you only need to build a trie for same initial chacaters in order to solve the score of the groups instead of build a huge trie for all words together.\nThis allows system to do gc between each group solving their score.\n\n```\n/**\n * @param {string[]} words\n * @return {number[]}\n */\nvar sumPrefixScores = function(words) {\n const scores = {};\n const groups = words.reduce((groups, word) => {\n if (!groups[word[0]]) {\n groups[word[0]] = [];\n }\n groups[word[0]].push(word);\n return groups;\n }, {});\n \n for (const group of Object.values(groups)) {\n const root = createNode();\n for (let i = 0; i < group.length; i++) {\n const word = group[i];\n insert(root, word);\n }\n for (let i = 0; i < group.length; i++) {\n const word = group[i];\n scores[word] = getScore(root, word, 0);\n }\n }\n\t\n return words.map(word => scores[word]);\n};\n\nconst getScore = (node, word, i) => {\n if (i === word.length) {\n return 0;\n }\n const charCode = word.charCodeAt(i) - 97;\n const next = node.children[charCode];\n const score = next.count;\n return score + getScore(next, word, i + 1);\n}\n\nconst insert = (node, word, i = 0) => {\n node.count++;\n if (i === word.length) {\n return;\n }\n const charCode = word.charCodeAt(i) - 97;\n if (!node.children[charCode]) {\n node.children[charCode] = createNode();\n }\n insert(node.children[charCode], word, i+ 1);\n}\n\nconst createNode = () => {\n return {\n count: 0,\n children: new Array(26),\n };\n}\n``` | 3 | 0 | [] | 2 |
sum-of-prefix-scores-of-strings | C++ Rabin Karp Algorithm || Easy Implementation | c-rabin-karp-algorithm-easy-implementati-e443 | \ntypedef long long ll;\nclass Solution {\npublic:\n ll mod = 100000000007;\n ll dp[1005],pa[1005];\n void preProcess(string s){\n ll p = 29; / | manavmajithia6 | NORMAL | 2022-09-19T03:18:40.755823+00:00 | 2022-09-19T03:18:40.755956+00:00 | 98 | false | ```\ntypedef long long ll;\nclass Solution {\npublic:\n ll mod = 100000000007;\n ll dp[1005],pa[1005];\n void preProcess(string s){\n ll p = 29; // any prime no.\n ll pow = p;\n\n dp[0] = s[0] - \'a\' + 1;\n pa[0] = 1;\n for(ll i = 1;i < s.length();i++){\n dp[i] = (dp[i-1] + (s[i] - \'a\' + 1) * pow) % mod;\n pa[i] = pow;\n pow *= p;\n pow %= mod;\n }\n }\n \n ll hashQuery(ll l, ll r){\n ll ans = dp[r];\n if(l > 0)\n ans = (ans - dp[l - 1] + mod) % mod;\n return ans;\n }\n vector<int> sumPrefixScores(vector<string>& words) {\n map<ll, int> m;\n int n = words.size();\n for(int i = 0;i < n;i++){\n string s = words[i];\n memset(dp, 0, sizeof(dp));\n memset(pa, 0, sizeof(pa));\n preProcess(s);\n ll sum1 = 0;\n \n for(int j = 0;j < s.length();j++){\n ll pref = hashQuery(0, j);\n m[pref]++;\n }\n }\n vector<int> ans(n);\n for(int i = 0;i < n;i++){\n string s = words[i];\n ll sum1 = 0,sum2 = 0;\n memset(dp, 0, sizeof(dp));\n memset(pa, 0, sizeof(pa));\n preProcess(s);\n for(int j = 0;j < s.length();j++){\n ll pref = hashQuery(0, j);\n sum2 += m[pref];\n }\n ans[i] = sum2;\n }\n \n return ans;\n }\n};\n``` | 3 | 0 | ['Dynamic Programming', 'C'] | 0 |
sum-of-prefix-scores-of-strings | Easy with Trie | easy-with-trie-by-deleted_user-m2h4 | \nclass TrieNode{\n constructor(){\n this.ch = {};\n this.score = 0;\n }\n}\n\nclass Trie{\n constructor(){\n this.root = new TrieNode();\n }\n ad | deleted_user | NORMAL | 2022-09-18T16:46:30.724748+00:00 | 2022-09-18T16:46:30.724794+00:00 | 166 | false | ```\nclass TrieNode{\n constructor(){\n this.ch = {};\n this.score = 0;\n }\n}\n\nclass Trie{\n constructor(){\n this.root = new TrieNode();\n }\n add(word){\n let cur = this.root;\n for(let c of word){\n if (!cur.ch.hasOwnProperty(c)){\n cur.ch[c] = new TrieNode();\n }\n cur = cur.ch[c];\n cur.score += 1;\n }\n }\n get_score(word){\n let cur = this.root;\n let tot = 0;\n for(let c of word){\n if (!cur.ch.hasOwnProperty(c)){\n break;\n }\n cur = cur.ch[c];\n tot += cur.score;\n }\n return tot;\n }\n}\n\nvar sumPrefixScores = function(words) {\n\n let s = words;\n let tree = new Trie();\n let ans = [];\n for(let w of s){\n tree.add(w)\n }\n for(let w of words){\n ans.push(tree.get_score(w));\n }\n return ans;\n};\n```\n# PlEASE UPVOTE! | 3 | 0 | ['Trie', 'JavaScript'] | 1 |
sum-of-prefix-scores-of-strings | ✅✅Faster || Easy To Understand || C++ Code | faster-easy-to-understand-c-code-by-__kr-ycjg | Trie\n\n Time Complexity :- O(N * M)\n\n Space Complexity :- O(N)\n\n\nclass Solution {\npublic:\n \n // structure for TrieNode\n \n struct TrieNode | __KR_SHANU_IITG | NORMAL | 2022-09-18T05:38:48.648195+00:00 | 2022-09-18T05:38:48.648232+00:00 | 289 | false | * ***Trie***\n\n* ***Time Complexity :- O(N * M)***\n\n* ***Space Complexity :- O(N)***\n\n```\nclass Solution {\npublic:\n \n // structure for TrieNode\n \n struct TrieNode\n {\n TrieNode* child[26];\n \n int count;\n \n TrieNode()\n {\n count = 0;\n \n for(int i = 0; i < 26; i++)\n {\n child[i] = NULL;\n }\n }\n };\n \n // declare a global root\n \n TrieNode* root = new TrieNode();\n \n // function for insert\n \n void insert(string str)\n {\n int n = str.size();\n \n TrieNode* curr = root;\n \n for(int i = 0; i < n; i++)\n {\n int idx = str[i] - \'a\';\n \n // insert a new node\n \n if(curr -> child[idx] == NULL)\n {\n curr -> child[idx] = new TrieNode(); \n }\n \n // increment the count of prefix\n \n curr -> child[idx] -> count++;\n \n // move curr pointer\n \n curr = curr -> child[idx];\n }\n }\n \n // function for get_sum\n \n int get_sum(string str)\n {\n int n = str.size();\n \n int sum = 0;\n \n TrieNode* curr = root;\n \n for(int i = 0; i < n; i++)\n {\n int idx = str[i] - \'a\';\n \n sum += curr -> child[idx] -> count;\n \n curr = curr -> child[idx];\n }\n \n return sum;\n }\n \n vector<int> sumPrefixScores(vector<string>& words) {\n \n int n = words.size();\n \n // insert all the words into trie\n \n for(int i = 0; i < n; i++)\n {\n insert(words[i]);\n }\n \n vector<int> res(n, 0);\n \n // find sum for every word\n \n for(int i = 0; i < n; i++)\n {\n int sum = get_sum(words[i]);\n \n res[i] = sum;\n }\n \n return res;\n }\n};\n``` | 3 | 0 | ['Trie', 'C', 'C++'] | 0 |
sum-of-prefix-scores-of-strings | Easy peasy || Trie | easy-peasy-trie-by-kageyama09-21o4 | Using normal trie implementation with a branch property which at any node wil tell us the total number of branches that are merged with the current path i.e, th | kageyama09 | NORMAL | 2022-09-18T04:10:15.945624+00:00 | 2022-09-18T04:10:15.945650+00:00 | 115 | false | Using normal trie implementation with a **branch** property which at any node wil tell us the total number of branches that are merged with the current path i.e, the total number of prefixes ending at the current node.\nImplementing this and storing all the string in that trie will be a key to that answer, because after than you just have to traverse the path of your given string adding up all the branches count you see.\n\n```\nclass Solution {\n class Node{\n char ch;\n Node[] links;\n boolean isEnd;\n int branch;\n Node(char ch){\n this.ch=ch;\n links=new Node[26];\n branch=1;\n }\n }\n Node root;\n public Solution() {\n this.root=new Node(\'*\');\n }\n \n public void insert(String word) {\n Node curr=this.root;\n for(int i=0;i<word.length();i++){\n char ch=word.charAt(i);\n if(curr.links[ch-\'a\']!=null){\n curr.links[ch-\'a\'].branch++;\n curr=curr.links[ch-\'a\'];\n }\n else{\n curr.links[ch-\'a\']=new Node(ch);\n curr=curr.links[ch-\'a\'];\n }\n }\n curr.isEnd=true;\n }\n \n public int startsWith(String prefix) {\n Node curr=this.root;\n int res=0;\n for(int i=0;i<prefix.length();i++){\n char ch=prefix.charAt(i);\n if(curr.links[ch-\'a\']!=null){\n res+=curr.links[ch-\'a\'].branch;\n curr=curr.links[ch-\'a\'];\n }\n else{\n return res;\n }\n }\n return res;\n }\n \n public int[] sumPrefixScores(String[] words) {\n int n=words.length;\n int[] ans=new int[n];\n \n for(int i=0;i<n;i++){\n insert(words[i]);\n }\n \n for(int i=0;i<n;i++){\n ans[i]=startsWith(words[i]);\n }\n return ans;\n }\n}\n```\n\nBtw this is my first time solving all for questions ;)\nThanks | 3 | 0 | ['Trie'] | 0 |
sum-of-prefix-scores-of-strings | Trie [Count and fetch] | C++ | trie-count-and-fetch-c-by-xxvvpp-k098 | C++\n struct trie {\n trie *child[26] = {};\n int count=0;\n }; \n \n vector sumPrefixScores(vector& A) {\n trie td;\n \n | xxvvpp | NORMAL | 2022-09-18T04:02:12.182150+00:00 | 2022-09-18T04:18:59.036580+00:00 | 143 | false | # C++\n struct trie {\n trie *child[26] = {};\n int count=0;\n }; \n \n vector<int> sumPrefixScores(vector<string>& A) {\n trie td;\n \n //put all words\n for(auto w:A){\n //insert word in trie\n auto root= &td;\n for(auto j:w){\n if(!root->child[j-\'a\']) root->child[j-\'a\']= new trie();\n root= root->child[j-\'a\'];\n root->count++;\n }\n }\n \n vector<int> ans; ans.reserve(A.size());\n \n for(auto w:A){\n auto root= &td;\n int n=0;\n for(auto j:w){\n root= root->child[j-\'a\'];\n //get count of prefix stored\n n+= root->count;\n }\n ans.push_back(n);\n }\n \n return ans;\n } | 3 | 0 | ['Trie', 'C'] | 0 |
sum-of-prefix-scores-of-strings | trie| c++ 🔥 the very fundamental of trie data structure Easy & Intutive | trie-c-the-very-fundamental-of-trie-data-b4kc | first of all how we can identify that this problem is related to trie data structure?\n\n\ntime complexcity total: Sum (size of each words)<=10^6\nspace complex | demon_code | NORMAL | 2024-09-25T17:37:19.233104+00:00 | 2024-09-26T17:11:54.734508+00:00 | 7 | false | first of all how we can identify that this problem is related to trie data structure?\n\n```\ntime complexcity total: Sum (size of each words)<=10^6\nspace complexcity total : Sum (size of each words) <=10^6\n```\n\nfirst when we see what they are asking is calculate sum of ( frequencies of prefixes (prifix which is genrated by given string) ) in entire set of string\nthis can be very ambigeous to think but let me clear it :\n```\nlet\'s say we have two string only for simplicity : "abc", "ab"\n```\n\n```\nso count of prifix:\n"a" = 2 one a is genrated by abc and other is genrated by ab\n"ab" = 2 one ab is genrated by abc and other is genrated by ab\n"abc" = 1 abc can be genrated by abc only\n```\n\n```\nso now when we take abc :\nwe have 3 possible prifixes: {"a", "ab", "abc"}\n```\n```\nnow we look into our globle frequency list and sum it which will be the answer for abc:\n2 a + 2 ab + 1 abc= 5\nsimilarly for ab\n2 a + 2 ab = 4\n```\n\nso what we are summing here?\nbasically the count of common path followed by each string, path mean common prifixes which are present in each string\n\n\nremeber how we store each string in trie?\nfor each character we create a node thus it form a tree and we can say that a word follows the path of it\'s char\'s node to the end \nbut on key thing to notice here is we want to calculate the frequency of each prefixes so we don\'t need to mark end of the word but here strating from first char where ever u stop that\'s one of your prefixes so here we will keep count at nodes how many words have passed this node \n\nand once we created the entire tree we will just collect all sum by traversing from root for each word\n\n```\n\nclass Solution {\npublic:\n \n class trie\n {\n public:\n trie* next[26];\n int end;\n\n trie()\n {\n for(int i=0; i<26; i++)\n next[i]=NULL;\n end=0;\n }\n\n };\n\t\n\t//build the tree\n trie* maketree(vector<string> &s)\n {\n trie* root=new trie();\n for(int i=0; i<s.size(); i++)\n {\n trie* curr=root;\n for(int j=0; j<s[i].size(); j++)\n {\n if(curr->next[s[i][j]-\'a\']==NULL)\n {\n curr->next[s[i][j]-\'a\']=new trie();\n \n }\n curr=curr->next[s[i][j]-\'a\'];\n curr->end+=1; // increment by one when ever any word passes this node\n \n }\n \n }\n \n return root;\n \n \n }\n \n \n int sum(string &s, trie* &root)\n {\n trie* curr= root;\n int ans=0;\n int n=s.size();\n for(int i=0; i<n; i++)\n {\n curr= curr->next[s[i]-\'a\'];\n ans+= curr->end; // accumulate all the sum while moving down with each word\n }\n return ans;\n \n }\n \n vector<int> sumPrefixScores(vector<string>& words) \n {\n trie* root= maketree(words);\n vector<int> ans;\n for(auto i: words)\n {\n ans.push_back(sum(i,root));\n }\n return ans;\n }\n};\n\n\n\n```\n\n\n\n\n\n | 2 | 0 | ['Trie', 'C'] | 0 |
sum-of-prefix-scores-of-strings | Fastest Solution in Java with Explanation | fastest-solution-in-java-with-explanatio-w1qu | Intuition\n Describe your first thoughts on how to solve this problem. \nThe goal of this problem is to calculate a score for each word, where the score is the | heyysankalp | NORMAL | 2024-09-25T16:30:23.839791+00:00 | 2024-09-28T12:16:21.388542+00:00 | 40 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal of this problem is to calculate a score for each word, where the score is the sum of lengths of common prefixes between the word and every other word in the input array. To efficiently compute this, sorting the words and processing them in a way that allows us to compare neighboring words for common prefixes is a good approach. By using sorted indices, we can minimize comparisons and efficiently accumulate the prefix scores for each word.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the words by lexicographical order: This ensures that words with imilar prefixes are next to each other, allowing for easier comparison.\n\n2. Calculate the lengths of common prefixes: For each adjacent pair of sorted words, compute the length of their common prefix. Store these lengths for further use.\n\n3. Compute prefix scores:\n- For each word, add its full length to its score.\n- Then, for each word, compare it with subsequent words, using the precomputed common prefix lengths to avoid unnecessary recomputations. Add these common prefix lengths to the score for both words involved.\n4. Return the result: After computing the prefix scores for all words, return the result array.\n# Complexity\n- Time complexity:O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] sumPrefixScores(String[] words) {\n int wordCount = words.length;\n Integer[] sortedIndices = new Integer[wordCount];\n for (int i = 0; i < wordCount; i++) {\n sortedIndices[i] = i;\n }\n Arrays.sort(sortedIndices, (a, b) -> words[a].compareTo(words[b]));\n \n int[] commonPrefixLengths = calculateCommonPrefixLengths(words, sortedIndices);\n int[] scores = calculateScores(words, sortedIndices, commonPrefixLengths);\n return scores;\n }\n\n private int[] calculateCommonPrefixLengths(String[] words, Integer[] sortedIndices) {\n int[] commonPrefixLengths = new int[words.length];\n for (int i = 1; i < words.length; i++) {\n String prevWord = words[sortedIndices[i - 1]];\n String currWord = words[sortedIndices[i]];\n int commonLength = 0;\n while (commonLength < prevWord.length() && \n commonLength < currWord.length() && \n prevWord.charAt(commonLength) == currWord.charAt(commonLength)) {\n commonLength++;\n }\n commonPrefixLengths[i] = commonLength;\n }\n return commonPrefixLengths;\n }\n\n private int[] calculateScores(String[] words, Integer[] sortedIndices, int[] commonPrefixLengths) {\n int[] scores = new int[words.length];\n for (int i = 0; i < sortedIndices.length; i++) {\n int wordIndex = sortedIndices[i];\n int wordLength = words[wordIndex].length();\n scores[wordIndex] += wordLength;\n int j = i + 1;\n int commonLength = wordLength;\n while (j < words.length) {\n commonLength = Math.min(commonLength, commonPrefixLengths[j]);\n if (commonLength == 0) {\n break;\n }\n scores[wordIndex] += commonLength;\n scores[sortedIndices[j]] += commonLength;\n j++;\n }\n }\n return scores;\n }\n}\n``` | 2 | 0 | ['Array', 'String', 'Trie', 'Counting', 'Java'] | 1 |
sum-of-prefix-scores-of-strings | EASY AND BEGINNER FRIENDLY PYTHON SOLUTION🔥🔥🔥 | easy-and-beginner-friendly-python-soluti-1xld | Intuition\nThe problem requires calculating the prefix score of each word, which depends on how many other words share the same prefix at each step. A Trie (pre | FAHAD_26 | NORMAL | 2024-09-25T14:28:10.271245+00:00 | 2024-09-25T14:28:10.271287+00:00 | 10 | false | # Intuition\nThe problem requires calculating the prefix score of each word, which depends on how many other words share the same prefix at each step. A Trie (prefix tree) is ideal for such tasks because it allows efficient prefix matching. By building a Trie with all the words and keeping track of how many words pass through each node (each character in the Trie), we can easily determine how many words share a particular prefix. The goal is to calculate the prefix score by summing the number of words that share the same prefix for each character in the word.\n\n# Approach\n1. Trie Construction: First, we build a Trie where each node represents a character. As we insert a word character by character, we traverse the Trie, and for each node we visit, we increment a (prefix_count) to track how many words share the prefix that leads to that node. This allows us to later know how many words share the same prefix up to any point in the word.\n\n2. Insert Words into Trie: For each word in the list, we insert it into the Trie. Each time we encounter a character that hasn\'t been added yet, we create a new node. As we traverse the word, we increment the (prefix_count) of each node along the way, reflecting the number of words that have passed through that node.\n\n3. Calculate Prefix Scores: After building the Trie, for each word, we traverse it again from the root of the Trie. For each character, we sum the (prefix_count) at the corresponding node, which gives us the number of words that share the prefix up to that point. This sum is the prefix score for the word.\n\n4. Return Results: We repeat the prefix score calculation for every word in the list and store the results in a list, which is returned as the final output.\n\n# Complexity\n- Time complexity: \uD835\uDC42(\uD835\uDC41\xD7\uD835\uDC3F)\n\n- Space complexity: \uD835\uDC42(\uD835\uDC41\xD7\uD835\uDC3F)\n\n# Code\n```python []\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.prefix_count = 0\n\nclass Solution(object):\n\n def __init__(self):\n self.root = TrieNode()\n\n def insert(self, word):\n node = self.root\n for char in word:\n if char not in node.children:\n node.children[char] = TrieNode()\n node = node.children[char]\n node.prefix_count += 1\n\n def sumPrefixScores(self, words):\n \n for word in words:\n self.insert(word)\n\n scores = []\n\n for word in words:\n score = 0\n node = self.root\n\n for char in word:\n if char in node.children:\n node = node.children[char]\n score += node.prefix_count\n scores.append(score)\n \n return scores\n\n``` | 2 | 0 | ['Python'] | 0 |
sum-of-prefix-scores-of-strings | Concise and beautiful Trie | Cracking Hard into Easy | concise-and-beautiful-trie-cracking-hard-tyvz | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nJust use a custom Trie, | sulerhy | NORMAL | 2024-09-25T12:02:45.722178+00:00 | 2024-09-25T12:02:45.722218+00:00 | 23 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nJust use a custom Trie, with infomation of `count` as the number of words in `words` which also has this character\n\n# Complexity\n- Time complexity: O(n * k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n * k)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Node:\n def __init__(self):\n self.children = {}\n self.count = 0\nclass Trie:\n def __init__(self):\n self.root = Node()\n \n def add_word(self, word):\n cur = self.root\n for c in word:\n if c not in cur.children:\n cur.children[c] = Node()\n cur = cur.children[c]\n cur.count += 1\n \n def get_sum_score(self, word):\n cur = self.root\n total = 0\n for c in word:\n if c not in cur.children:\n return total\n cur = cur.children[c]\n total += cur.count\n return total\n \nclass Solution:\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n trie = Trie()\n for word in words:\n trie.add_word(word)\n res = []\n for word in words:\n res.append(trie.get_sum_score(word))\n return res\n``` | 2 | 0 | ['String', 'Trie', 'Python3'] | 0 |
sum-of-prefix-scores-of-strings | Small & Simple Graph Count Traversal in Kotlin (Beats 100%) | small-simple-graph-count-traversal-in-ko-jmml | \n\n# Intuition\nThe question that was asked; to sum up all the prefixes and occurences for every seperate word, can be achieved by simply counting how many tim | mdekaste | NORMAL | 2024-09-25T11:08:19.176137+00:00 | 2024-09-25T11:14:18.498386+00:00 | 36 | false | \n\n# Intuition\nThe question that was asked; to sum up all the prefixes and occurences for every seperate word, can be achieved by simply counting how many times a character reaches a node in a graph.\n\n# Approach\nBy letting every word traverse character for character from the same root, and keeping track of its traversal order, you could simply sum up the counts per node.\n\n\n```\ninput = ["abc", "abd"]\n"abc" = 0 + 2 + 2 + 1 = 5\n"abd" = 0 + 2 + 2 + 1 = 5\nresult = [5, 5]\n```\n\n- Create a root Node that every word will use as a start.\n- Traverse and build from the root, character per character\n - Keep track of traversed nodes per word\n - Increment a nodecounter every time it is visited by the algorithm\n- Afterwards, for every word, count up the nodecounters\n\n\n# Complexity\n- Time complexity:\n - Building the graph: O(wordsCount * maxLengthOfWord) = O(n * m)\n - Traversing the graph: O(wordsCount * maxLengtOfWord) = O(n * m)\n\n- Space complexity:\n - Root node graph: O(wordscount * maxLengthOfWord) = O(n * m)\n - Traversal List: O(wordscount * maxLengthOfWord) = O(n * m)\n\n\n# Code\n```kotlin []\nclass Solution {\n fun sumPrefixScores(words: Array<String>): IntArray {\n val root = Node()\n fun traversal(word: String) = word.runningFold(root, Node::traverse)\n return words\n .map(::traversal)\n .map { node -> node.sumOf(Node::count) }\n .toIntArray()\n }\n\n private class Node {\n val next = mutableMapOf<Char, Node>()\n var count = 0\n fun traverse(char: Char): Node = next.getOrPut(char, ::Node).apply { count++ }\n }\n}\n``` | 2 | 0 | ['Trie', 'Kotlin'] | 1 |
sum-of-prefix-scores-of-strings | JAVA EASY SOLUTION | java-easy-solution-by-007harsh-qc0o | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires counting how many strings in the given list start with each prefix | 007Harsh- | NORMAL | 2024-09-25T09:37:22.152039+00:00 | 2024-09-25T09:37:22.152073+00:00 | 16 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires counting how many strings in the given list start with each prefix of every word. A naive approach would be to check each prefix of every word against all other words, but this would be inefficient. Using a Trie `(Prefix Tree)` can help us efficiently track and count how many words share each prefix as we process the input list.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Trie Construction: We construct a Trie where each node represents a character and holds the count of how many words pass through that node. This allows us to keep track of how many words have a certain prefix.\n\n2. Insertion: We insert each word into the Trie, updating the count at each node (representing a prefix).\n\n3. Prefix Score Calculation: For each word, we traverse through the Trie and accumulate the scores of its prefixes by summing the counts stored at each node corresponding to the word\'s prefixes.\n\n4. Efficiency: By using a Trie, we ensure that the prefix counts are shared across different words, making the solution more efficient than comparing each prefix to every word individually.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is \n\uD835\uDC42(\uD835\uDC5B*\uD835\uDC3F)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\uD835\uDC42(\uD835\uDC5B*\uD835\uDC3F)\n# Code\n```java []\nclass TrieNode {\n Map<Character, TrieNode> children;\n int count;\n\n public TrieNode() {\n children = new HashMap<>();\n count = 0;\n }\n}\nclass Trie {\n private TrieNode root;\n\n public Trie() {\n root = new TrieNode();\n }\n public void insert(String word) {\n TrieNode node = root;\n for (char c : word.toCharArray()) {\n if (!node.children.containsKey(c)) {\n node.children.put(c, new TrieNode());\n }\n node = node.children.get(c);\n node.count++;\n }\n }\n public int getScore(String word) {\n TrieNode node = root;\n int score = 0;\n for (char c : word.toCharArray()) {\n node = node.children.get(c);\n score += node.count;\n }\n return score;\n }\n}\nclass Solution {\n public int[] sumPrefixScores(String[] words) {\n Trie trie = new Trie();\n \n for (String word : words) {\n trie.insert(word);\n }\n\n \n int[] result = new int[words.length];\n for (int i = 0; i < words.length; i++) {\n result[i] = trie.getScore(words[i]);\n }\n\n return result;\n }\n}\n``` | 2 | 0 | ['Trie', 'Prefix Sum', 'Java'] | 0 |
sum-of-prefix-scores-of-strings | Easy Solution || C++ || Tries || TC- O(N*L) | easy-solution-c-tries-tc-onl-by-manavtor-ke9p | Intuition\nWhen solving this problem, the main challenge is calculating the prefix scores efficiently for multiple words. A brute force approach of calculating | manavtore | NORMAL | 2024-09-25T08:40:31.502404+00:00 | 2024-09-25T08:40:31.502460+00:00 | 52 | false | # Intuition\nWhen solving this problem, the main challenge is calculating the prefix scores efficiently for multiple words. A brute force approach of calculating prefix scores individually for each word would be inefficient, especially with longer word lists. The Trie (prefix tree) data structure is well-suited for problems involving prefixes, as it allows us to store common prefixes and retrieve them efficiently\uD83D\uDE0E.\n\n# Approach\n1. Trie Construction:\n\n - We construct a Trie where each node represents a character in the word.\n - As we insert words into the Trie, we maintain a count for each node, which keeps track of how many words pass through this node (or how many words have this character as part of their prefix). This is crucial for computing the prefix score later.\n\n2. Prefix Score Calculation:\n\n - Once the Trie is constructed, we can calculate the prefix score of each word.\n - For each word, we traverse the Trie and accumulate the count values for each character in the word. The sum of these counts gives us the prefix score for that word.\nEfficiency:\n\nUsing a Trie ensures that common prefixes are only processed once, making the solution more efficient than processing each word from scratch.\n\n# Complexity\n**- *Time complexity: O(n * L)***\n\n**- *Space complexity: O(n)***\n\n# Code\n```cpp []\nclass TrieNode{\n public:\n TrieNode* children[26] = {0};\n int count = 0;\n};\n\nclass Trie{\n public:\n TrieNode* root;\n \n Trie() {\n root = new TrieNode();\n }\n\n void insert(const string& word){\n TrieNode* node = root;\n for(char c:word){\n int idx = c - \'a\';\n if(!node->children[idx]){\n node->children[idx]=new TrieNode;\n }\n node = node->children[idx];\n node->count++;\n }\n }\n\n int getPrefixScore(const string& word){\n TrieNode* node = root;\n int score = 0;\n for(char c:word){\n int idx = c - \'a\';\n if(node ->children[idx]){\n node = node->children[idx];\n score += node->count;\n }\n }\n return score;\n }\n};\n\nclass Solution {\n public:\n vector<int> sumPrefixScores(vector<string>& words) {\n Trie trie;\n\n for(const string& word:words){\n trie.insert(word);\n }\n vector<int> result;\n\n for(const string& word:words){\n int score = trie.getPrefixScore(word);\n result.push_back(score);\n }\n return result;\n }\n};\n``` | 2 | 0 | ['Array', 'String', 'Trie', 'Counting', 'C++'] | 1 |
sum-of-prefix-scores-of-strings | C++ Simple Trie / Prefix Tree implementation | c-simple-trie-prefix-tree-implementation-5ibo | Intuition\n- In this problem we need to find the number of strings that has a prefix in the current string.\n- Thus when it comes to counting prefixes of string | Codesmith28 | NORMAL | 2024-09-25T06:47:41.969002+00:00 | 2024-09-25T12:50:45.244243+00:00 | 23 | false | # Intuition\n- In this problem we need to find the number of strings that has a prefix in the current string.\n- Thus when it comes to counting prefixes of strings and counting occurrences, we can rely on Trie / prefix tree data structure to efficiently store the strings and traverse through them.\n# What is Trie ?\n- A data structure that efficiently stores strings by sharing common prefixes. \n- Each node represents a character, and branches are created at points where strings diverge, allowing for quick retrieval and prefix-based searching.\n# Approach\n- We can store all the strings in a Trie using the `insert` function, which handles the following:\n\t- For each character in the string, we traverse down the Trie, creating new nodes as necessary.\n\t- Each node contains a `count` variable that keeps track of how many strings share the prefix up to that node, making it easy to find out how many strings have the same prefix.\n- Then we can iterate through all the strings in the array, and count for the number of strings has a prefix in the current string.\n\t- We do this by traversing in Trie and increment our score based on the `count` of the current node.\n# Code\n```cpp []\nstruct TrieNode {\n TrieNode *child[26];\n bool isEnd;\n int count = 0;\n TrieNode() {\n isEnd = false;\n count = 0;\n for (int i = 0; i < 26; i++) child[i] = NULL;\n }\n};\n\nvoid insert(TrieNode *root, string key) {\n TrieNode *node = root;\n for (char c : key) {\n int idx = c - \'a\';\n if (!node->child[idx]) node->child[idx] = new TrieNode();\n node = node->child[idx];\n node->count++;\n }\n node->isEnd = true;\n}\n\nint startWith(TrieNode *root, string pref) {\n int score = 0;\n TrieNode *node = root;\n for (char c : pref) {\n int idx = c - \'a\';\n if (!node->child[idx]) break;\n node = node->child[idx];\n score += node->count;\n }\n return score;\n}\n\nclass Solution {\n public:\n vector<int> sumPrefixScores(vector<string> &words) {\n TrieNode *root = new TrieNode();\n for (auto it : words) insert(root, it);\n\n vector<int> res;\n for (auto it : words) res.push_back(startWith(root, it));\n return res;\n }\n};\n``` | 2 | 0 | ['String', 'Trie', 'Counting', 'C++'] | 0 |
sum-of-prefix-scores-of-strings | C++ Solution || Trie | c-solution-trie-by-rohit_raj01-t8z9 | Intuition\nThe problem is about calculating a score for each word based on how many times its prefixes appear across all the words in the input list. A Trie (pr | Rohit_Raj01 | NORMAL | 2024-09-25T06:33:47.863491+00:00 | 2024-09-25T06:33:47.863522+00:00 | 47 | false | # Intuition\nThe problem is about calculating a score for each word based on how many times its prefixes appear across all the words in the input list. A Trie (prefix tree) is an efficient data structure for handling prefix-based problems because it allows for fast insertion and traversal of strings. By storing prefix frequencies in the Trie, we can quickly calculate the prefix score for each word.\n\n# Approach\n1. Use a Trie data structure where each node represents a character and contains a `countP` value, which keeps track of how many times this character (or its associated prefix) has been encountered.\n2. Insert each word into the Trie, incrementing the `countP` value at each character node as you traverse through the word.\n3. For each word, traverse the Trie and accumulate the `countP` values to calculate the prefix score.\n4. Return a list of prefix scores, where each score corresponds to a word in the input list.\n\n# Complexity\n- Time complexity: $$O(n*w)$$\n\n- Space complexity: $$O(n*w)$$\n\n# Code\n```cpp []\nstruct trie {\n int countP = 0;\n trie* children[26];\n};\n\nclass Solution {\npublic:\n trie* getTrieNode() {\n trie* newNode = new trie();\n for (int i = 0; i < 26; i++) {\n newNode->children[i] = NULL;\n }\n newNode->countP = 0;\n return newNode;\n }\n\n void insert(string& word, trie* root) {\n trie* node = root;\n for (auto ch : word) {\n int ind = ch - \'a\';\n\n if (node->children[ind] == NULL) {\n node->children[ind] = getTrieNode();\n }\n node->children[ind]->countP += 1;\n node = node->children[ind];\n }\n }\n\n int getScore(string& word, trie* root) {\n trie* node = root;\n int score = 0;\n for (auto ch : word) {\n int ind = ch - \'a\';\n score += node->children[ind]->countP;\n node = node->children[ind];\n }\n return score;\n }\n\n vector<int> sumPrefixScores(vector<string>& words) {\n int n = words.size();\n trie* root = getTrieNode();\n for (auto& word : words) {\n insert(word, root);\n }\n\n vector<int> res(n); \n\n for (int i = 0; i < n; i++) {\n res[i] = getScore(words[i], root);\n }\n\n return res;\n }\n};\n\n```\n> *In coding, as in life, it\u2019s all about the connections\u2014Tries are just really good at finding the right ones!*\n\n\n\n | 2 | 0 | ['String', 'Trie', 'C++'] | 0 |
sum-of-prefix-scores-of-strings | Simple C++ solution | TRIE | simple-c-solution-trie-by-saurabhdamle11-p6qt | Intuition\nFor every word, we need to find all the prefixes and get the count of all such prefixes which will be the score of that word.\n\nSince we need to fin | saurabhdamle11 | NORMAL | 2024-09-25T05:26:22.391583+00:00 | 2024-09-25T05:26:22.391620+00:00 | 71 | false | # Intuition\nFor every word, we need to find all the prefixes and get the count of all such prefixes which will be the score of that word.\n\nSince we need to find and store all the prefixes, a Trie will be the best Data Structure to use here.\n\n# Approach\n1. Initialize a trie and insert all the words into the trie.\n2. For every letter in the word, increment the prefixCount of prefix ending at that letter by 1.\n3. Again iterate over over the words array.\n4. For every word, get all of its prefixes and add the respective prefixCount to score. \n\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(n * m)\nn=size of vector\nm=size of word\n\n# Code\n```cpp []\nstruct Node{\n Node* links[26];\n int prefixCount=0;\n\n bool containsKey(char c){\n return (links[c-\'a\']!=NULL);\n }\n\n void put(char c,Node* node){\n links[c-\'a\']=node;\n }\n\n Node* get(char c){\n return links[c-\'a\'];\n }\n\n void increasePrefixCount(){\n prefixCount++;\n }\n\n};\n\n\nclass Solution {\n\nprivate:\n\n Node* root = new Node();\n\n void insert(string &word){\n Node* node = root;\n for(char &c:word){\n if(!node->containsKey(c)){\n node->put(c,new Node());\n }\n node=node->get(c);\n node->increasePrefixCount();\n }\n }\n\n int getScore(string&word){\n Node* node=root;\n int score=0;\n for(char &c:word){\n node=node->get(c);\n score+=node->prefixCount;\n }\n return score;\n }\n\npublic:\n vector<int> sumPrefixScores(vector<string>& words) {\n for(string &word:words){\n insert(word);\n }\n vector<int>ans;\n for(string &word:words){\n ans.push_back(getScore(word));\n }\n return ans;\n }\n};\n```\n\nPlease upvote if you found it useful!! | 2 | 0 | ['Array', 'String', 'Trie', 'Counting', 'C++'] | 2 |
sum-of-prefix-scores-of-strings | [C++] ✅|| 2 Approach | HashMap & Trie | Easy to understand 🚀 | c-2-approach-hashmap-trie-easy-to-unders-3941 | Approach - 1: (Using Hashmap) \n\nclass Solution {\npublic:\n vector<int> sumPrefixScores(vector<string>& words) \n {\n unordered_map<string, int>m | RIOLOG | NORMAL | 2024-09-25T05:06:59.978248+00:00 | 2024-09-25T05:07:35.685520+00:00 | 27 | false | Approach - 1: (Using Hashmap) \n```\nclass Solution {\npublic:\n vector<int> sumPrefixScores(vector<string>& words) \n {\n unordered_map<string, int>mp;\n for (int i=0;i<words.size();i++)\n {\n string temp = "";\n string curr = words[i];\n \n for (int j=0;j<curr.size();j++)\n {\n temp += curr[j];\n mp[temp] += 1;\n }\n }\n \n vector<int>ans;\n for (int i=0;i<words.size();i++)\n {\n string temp = "";\n string curr = words[i];\n int count = 0;\n \n for (int j=0;j<curr.size();j++)\n {\n temp += curr[j];\n if (mp.find(temp) != mp.end()) count += mp[temp];\n }\n ans.push_back(count);\n }\n \n return ans;\n }\n};\n```\n\nApproach - 2: (Using Trie)\n```\nstruct Node {\n Node* link[26];\n bool flag = false;\n int prefixCount = 0;\n\n void put(char ch, Node* node) {\n link[ch - \'a\'] = node;\n }\n \n bool containsKey(char ch) {\n return (link[ch - \'a\'] != NULL);\n }\n \n Node* get (char ch) {\n return link[ch - \'a\'];\n }\n \n bool isEnd() {\n return flag;\n }\n \n void setEnd() {\n flag = true;\n }\n \n void increasePrefixCount () {\n prefixCount += 1;\n }\n \n int getPrefixCount() {\n return prefixCount;\n }\n};\n\nclass Solution {\nprivate:\n Node* root;\npublic:\n Solution () \n {\n root = new Node();\n }\n \n vector<int> sumPrefixScores(vector<string>& words) \n {\n for (int i=0;i<words.size();i++)\n {\n string word = words[i];\n Node* node = root;\n \n for (int j=0;j<word.size();j++)\n {\n if (!node -> containsKey(word[j])) \n {\n node->put(word[j], new Node());\n }\n node = node -> get(word[j]);\n node -> increasePrefixCount();\n }\n \n node -> setEnd();\n }\n \n vector<int>ans;\n for (int i=0;i<words.size();i++)\n {\n string word = words[i];\n Node* node = root;\n int count = 0;\n \n for (int j=0;j<word.size();j++)\n {\n if (node -> containsKey(word[j]))\n {\n // count += node -> getPrefixCount();\n node = node -> get(word[j]);\n count += node -> getPrefixCount();\n }\n }\n ans.push_back(count);\n }\n \n return ans;\n \n }\n};\n```\n\n | 2 | 0 | ['Trie', 'C'] | 0 |
sum-of-prefix-scores-of-strings | HashMap Solution | hashmap-solution-by-jastegsingh007-y1ql | Soch\nFollowing up for yesterday\'s POTD, store all subsets with there subset and count and just add them\n\n# Code\npython3 []\nclass Solution:\n def sumPre | jastegsingh007 | NORMAL | 2024-09-25T04:20:33.876354+00:00 | 2024-09-25T04:20:33.876403+00:00 | 243 | false | # Soch\nFollowing up for yesterday\'s POTD, store all subsets with there subset and count and just add them\n\n# Code\n```python3 []\nclass Solution:\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n k=defaultdict(int)\n ans=[]\n for i in words:\n for j in range(len(i)):\n k[i[0:j+1]]+=1\n #print(k)\n for i in words:\n temp=0\n for j in range(len(i)):\n temp+=k[i[0:j+1]]\n ans.append(temp)\n return ans\n \n``` | 2 | 0 | ['Python3'] | 2 |
sum-of-prefix-scores-of-strings | Java: Trie solution with comments and explanation. Easy to understand. | java-trie-solution-with-comments-and-exp-jmlc | Intuition\nWe are given a array of words. For each word, we need to compute prefix score. Any word of length n has n prefixes. For example, word abcd has prefix | cg7293 | NORMAL | 2024-09-25T04:09:51.117128+00:00 | 2024-09-25T04:09:51.117192+00:00 | 65 | false | # Intuition\nWe are given a array of words. For each word, we need to compute $$prefix score.$$ Any word of length `n` has `n` prefixes. For example, word `abcd` has prefixes `a`, `ab`, `abc` and `abcd`. For each prefix we need to find number of times it occurs in the words array.\n\n# Approach\nFor each word, we add the word to the trie. Each node in the trie has a count field which indicates how many times the prefix has occurred. \n\nConsider the following array `[abcd, ab, acf, bad, bat, dog, dad]`\n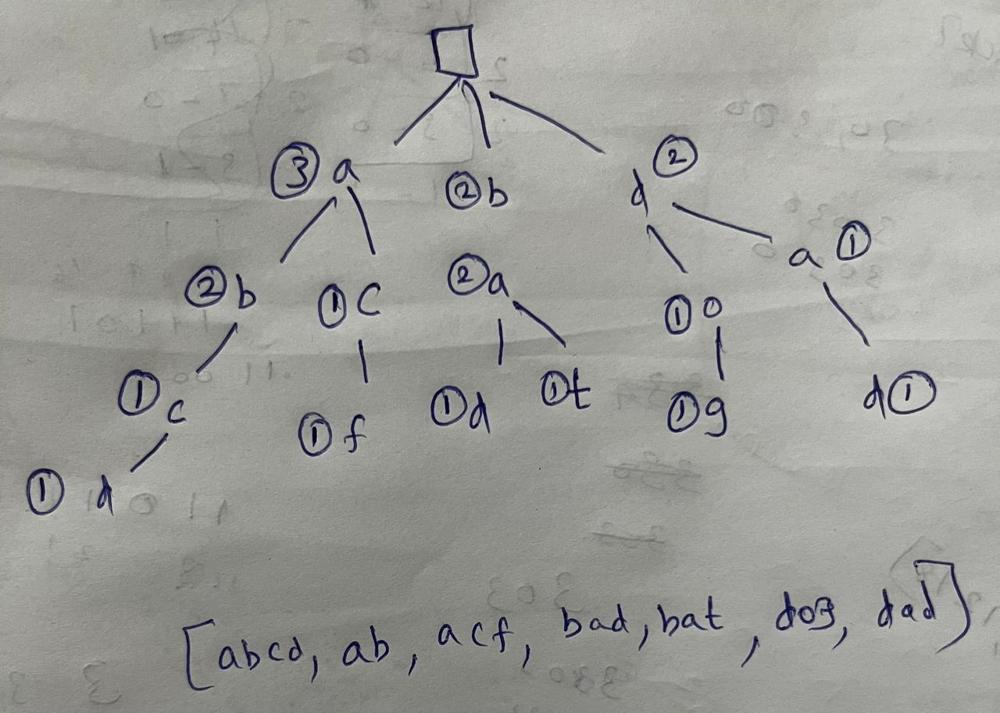\n\nIn the above diagarm, you could see the count for each prefix in the trie node.\n\n# Complexity\n- Time complexity: $\\sum_{i = 1}^{n} (NumChars(Word_i))$\n\n- Space complexity: $\\sum_{i = 1}^{n} (NumChars(Word_i))$\n\n# Code\n```java []\nclass Solution {\n public int[] sumPrefixScores(String[] words) {\n TrieNode trie = new TrieNode();\n for (String word : words)\n insert(word, trie);\n \n int[] resArr = new int[words.length];\n int resIdx = 0;\n for (String word : words)\n resArr[resIdx++] = findCount(word, trie);\n \n return resArr;\n }\n\n /**\n Function to find overall prefix count of word.\n We traverse each character in the trie and collect the counts for each prefix as we traverse the tree.\n **/\n private int findCount(String word, TrieNode trie) {\n TrieNode curNode = trie;\n int res = 0;\n for (int i = 0; i < word.length(); i++) {\n int nodeId = word.charAt(i) - \'a\';\n curNode = curNode.charNodes[nodeId];\n if (curNode == null)\n break; // This should be unreachable since we should have all nodes once we insert the word.\n res += curNode.count;\n }\n\n return res;\n }\n\n // Function to insert word into Trie.\n private void insert(String word, TrieNode trie) {\n TrieNode curNode = trie;\n\n for (int i = 0; i < word.length(); i++) {\n int nodeId = word.charAt(i) - \'a\';\n if (curNode.charNodes[nodeId] == null)\n curNode.charNodes[nodeId] = new TrieNode();\n curNode = curNode.charNodes[nodeId];\n curNode.count++;\n }\n }\n\n class TrieNode {\n public TrieNode[] charNodes;\n public int count;\n\n public TrieNode() {\n charNodes = new TrieNode[26];\n count = 0;\n }\n }\n}\n``` | 2 | 0 | ['Trie', 'Java'] | 0 |
sum-of-prefix-scores-of-strings | Simple trie | simple-trie-by-vortexz-sf3i | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vortexz | NORMAL | 2024-09-25T03:10:53.576254+00:00 | 2024-09-25T03:10:53.576302+00:00 | 39 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c []\n// Trie node structure\nstruct TrieNode {\n struct TrieNode* child[26];\n int freq;\n};\n\n// Function to create a new Trie node\nstruct TrieNode* getNode() {\n struct TrieNode* node = malloc(sizeof(struct TrieNode));\n node->freq = 0;\n for (int i = 0; i < 26; i++) {\n node->child[i] = NULL;\n }\n return node;\n}\n\n// Function to insert a key into the Trie\nvoid insert(struct TrieNode* root, const char* key) {\n struct TrieNode* curr = root;\n while (*key) {\n int index = *key - 97;\n if (!curr->child[index]) {\n curr->child[index] = getNode();\n }\n curr->child[index]->freq++;\n curr = curr->child[index];\n key++;\n }\n}\n\nint freq(struct TrieNode* root, const char* key) {\n struct TrieNode* curr = root;\n int count=0;\n while (*key) {\n int index = *key - 97;\n if (!curr->child[index]) {\n return false;\n }\n count+= curr->child[index]->freq;\n curr = curr->child[index];\n key++;\n }\n return count;\n}\n\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint* sumPrefixScores(char** words, int wordsSize, int* returnSize) {\n *returnSize=wordsSize;\n int *res=malloc(wordsSize*sizeof(int));\n struct TrieNode* root = getNode();\n //generate the trie\n for (int i = 0; i < wordsSize; i++) {\n insert(root, words[i]);\n }\n //count the frequency of letter from each words\n for (int i=0;i < wordsSize;i++) {\n res[i]= freq(root,words[i]);\n }\n \n return res;\n}\n``` | 2 | 0 | ['Trie', 'C'] | 0 |
sum-of-prefix-scores-of-strings | Python 3 solution - clean use of trie data structure and hash map soluton. | python-3-solution-clean-use-of-trie-data-xn6b | Code\npython [Prefix Trie]\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.count = 0\n\nclass Trie:\n def __init__(self): | iloabachie | NORMAL | 2024-09-25T01:51:51.114003+00:00 | 2024-09-25T03:00:15.836290+00:00 | 231 | false | # Code\n```python [Prefix Trie]\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.count = 0\n\nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n \n def insert(self, words: List[str]) -> None:\n for word in words:\n current = self.root\n for letter in word:\n if letter not in current.children:\n current.children[letter] = TrieNode()\n current = current.children[letter]\n current.count += 1\n \n def sum_prefix(self, word: str) -> int:\n current = self.root\n count = 0\n for letter in word: \n current = current.children[letter]\n count += current.count\n return count\n\nclass Solution:\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n prefix_trie = Trie()\n prefix_trie.insert(words) \n return [prefix_trie.sum_prefix(word) for word in words]\n \n```\n```python [Hash map]\nclass Solution:\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n hash_map = defaultdict(int)\n for word in words:\n for i in range(1, len(word) + 1):\n hash_map[word[:i]] += 1\n result = []\n for word in words:\n result.append(0)\n for i in range(1, len(word) + 1):\n result[-1] += hash_map[word[:i]]\n return result\n\n``` | 2 | 0 | ['Python3'] | 0 |
sum-of-prefix-scores-of-strings | TRIE makes it easy !! | trie-makes-it-easy-by-saurav_1928-qz1w | \n# Code\ncpp []\nclass Node {\npublic:\n unordered_map<char, pair<Node*, int>> arr;\n bool isEnd = false;\n};\n\nvoid insert(Node* root, string& word) {\ | saurav_1928 | NORMAL | 2024-09-25T01:18:51.249115+00:00 | 2024-09-25T01:18:51.249195+00:00 | 61 | false | \n# Code\n```cpp []\nclass Node {\npublic:\n unordered_map<char, pair<Node*, int>> arr;\n bool isEnd = false;\n};\n\nvoid insert(Node* root, string& word) {\n Node* curr = root;\n for (auto ch : word) {\n if (curr->arr.find(ch) == curr->arr.end()) {\n curr->arr[ch] = {new Node(), 0};\n }\n curr->arr[ch].second++;\n curr = curr->arr[ch].first;\n }\n curr->isEnd = true;\n}\n\nint solve(Node* root, string& word) {\n int cnt = 0;\n Node* curr = root;\n for (char ch : word) {\n if (curr->arr.find(ch) == curr->arr.end()) {\n break;\n }\n cnt += curr->arr[ch].second;\n curr = curr->arr[ch].first;\n }\n return cnt;\n}\n\nclass Solution {\npublic:\n vector<int> sumPrefixScores(vector<string>& words) {\n Node* root = new Node();\n for (auto& word : words) {\n insert(root, word);\n }\n vector<int> ans;\n for (auto& word : words)\n ans.push_back(solve(root, word));\n return ans;\n }\n};\n\n``` | 2 | 0 | ['Array', 'String', 'Trie', 'Counting', 'C++'] | 1 |
sum-of-prefix-scores-of-strings | Easy, well explained Javascript and Trie solution | easy-well-explained-javascript-and-trie-oheti | Intuition\nThe task is to compute the prefix score for each word by summing how many words share each prefix. It\'s possible to solve it using a HashMap, but it | balfin | NORMAL | 2024-09-25T00:40:20.205023+00:00 | 2024-09-25T00:41:56.490448+00:00 | 157 | false | # Intuition\nThe task is to compute the prefix score for each word by summing how many words share each prefix. It\'s possible to solve it using a HashMap, but it will fail by time limit on the last casess, so more efficient data structure is needed. Using a Trie allows us to efficiently store and count shared prefixes while avoiding redundant calculations.\n\n# Approach\n- Build the Trie: Insert each word into a Trie, tracking how many words pass through each prefix.\n- Calculate Prefix Scores: For each word, traverse its characters in the Trie, summing the counts of how many words share that prefix.\n\n# Complexity\n- Time complexity:\n$$O(N\xD7L)$$ where N is the number of words and L is the average word length.\n\n- Space complexity:\n$$O(N\xD7L)$$ - to store the same data assuming minimal to NO amount of intersections\n\n# Code\n```javascript []\n/**\n * @param {string[]} words\n * @return {number[]}\n */\nclass TrieNode {\n constructor() {\n this.children = {}; //a trie\n this.prefixCount = 0; \n }\n}\n\nclass Trie {\n constructor() {\n this.root = new TrieNode();\n }\n\n insert(word) {\n let node = this.root;\n for (const char of word) {\n if (!node.children[char]) { //Create a Trie if not exists\n node.children[char] = new TrieNode();\n }\n node = node.children[char]; //add element to the Trie\n node.prefixCount++; //Adjust counter\n }\n }\n\n getPrefixScore(word) {\n let node = this.root;\n let score = 0;\n for (const char of word) {\n node = node.children[char];\n score += node.prefixCount;\n }\n return score;\n }\n}\n\nvar sumPrefixScores = function(words) {\n const trie = new Trie();\n\n //Add words to Trie\n for (const word of words) {\n trie.insert(word);\n }\n\n //Map words and counts\n const result = words.map(word => trie.getPrefixScore(word));\n \n return result;\n};\n\n``` | 2 | 0 | ['Trie', 'JavaScript'] | 0 |
sum-of-prefix-scores-of-strings | brain dead solution in python | brain-dead-solution-in-python-by-mostkno-veeq | Intuition\nUses the idea of tries but no tries hehe\n\nHonestly, just build the prefix of a word as you go.\n\n# Approach\nFor each word, I create a buffer and | mostknownunknown | NORMAL | 2023-02-06T02:09:20.985569+00:00 | 2023-02-06T02:09:20.985614+00:00 | 263 | false | # Intuition\nUses the idea of tries but no tries hehe\n\nHonestly, just build the prefix of a word as you go.\n\n# Approach\nFor each word, I create a `buffer` and build a prefix for each character of the word.\n\nSo I continuously build a `buffer` character at a time without doing some weird indexing calculation.\n\nOnce the buffer has an appended character I check if that character is in `ws`. If not, add an entry to `ws` for buffer to zero, if so just increment by one.\n\nSo that is the first pass.\n\n2nd pass,\n\nSame thing as the first, building the prefix for each word,\nbut here I am checking the overall count that the current buffer appears and summing it into its respective index with the variable `counts`.\n\nand yeah just return counts yeet\n\n# Complexity\n- Time complexity:\nthe yung O(N * M) where N is the number of words and M is thee max size of word.\n\n- Space complexity:\nO(N * M) + O(N) = O(N * M)\n\ngg bois\n# Code\n```\nclass Solution:\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n\n\n ws = dict()\n\n for word in words:\n buffer = ""\n for c in word:\n buffer += c\n if buffer not in ws:\n ws[buffer] = 0\n ws[buffer] += 1\n\n counts = [0] * len(words)\n for i, word in enumerate(words):\n buffer = ""\n for c in word:\n buffer += c\n if buffer in ws:\n counts[i] += ws[buffer]\n return counts\n\n``` | 2 | 0 | ['Python3'] | 0 |
sum-of-prefix-scores-of-strings | Count all Prefixes in a Hash Map | count-all-prefixes-in-a-hash-map-by-jana-zbky | Intuition\nIterate over all the workds x prefixes and create a hashmap of all prefix counts. Then just use that to count the score\n\n# Approach\niterate over a | janakagoon | NORMAL | 2023-01-15T05:09:12.802485+00:00 | 2023-01-15T05:09:12.802533+00:00 | 57 | false | # Intuition\nIterate over all the workds x prefixes and create a hashmap of all prefix counts. Then just use that to count the score\n\n# Approach\niterate over all the workds x prefixes and create a hashmap of all prefix counts. Then just use that to count the score\n\n# Complexity\n- Time complexity:\nO(W x L)\n\nW: number of words\nL: Max length of words\n\n- Space complexity:\nO(W x L)\n\nW: number of words\nL: Max length of words\n\n# Code\n```\nfunc sumPrefixScores(words []string) []int {\n prefixCounts := make(map[string]int)\n\n for _, w := range words {\n for i := 1; i <= len(w); i ++ {\n prefixCounts[w[:i]]++\n }\n }\n\n res := make([]int, len(words))\n\n for i, w := range words {\n for j := 1; j <= len(w); j ++ {\n res[i] += prefixCounts[w[:j]]\n }\n }\n\n return res\n}\n``` | 2 | 0 | ['Go'] | 0 |
sum-of-prefix-scores-of-strings | C++ | Trie + search Prefixes | c-trie-search-prefixes-by-ajay_5097-i7zi | cpp\nclass TrieNode {\npublic:\n vector<TrieNode*> child;\n int availablePrefix;\n};\n\nconst int CHILD_COUNT = 26;\nconst int nax = 1e7 + 9;\nTrieNode po | ajay_5097 | NORMAL | 2022-11-21T11:08:02.135159+00:00 | 2022-11-21T11:08:02.135206+00:00 | 1,085 | false | ```cpp\nclass TrieNode {\npublic:\n vector<TrieNode*> child;\n int availablePrefix;\n};\n\nconst int CHILD_COUNT = 26;\nconst int nax = 1e7 + 9;\nTrieNode pool[nax];\nint cnt;\nTrieNode *getNode() {\n auto t = &pool[cnt++];\n t->child.resize(CHILD_COUNT);\n for (int i = 0; i < CHILD_COUNT; ++i) {\n t->child[i] = nullptr;\n }\n t->availablePrefix = 0;\n return t;\n}\n\nclass Solution {\npublic:\n TrieNode *root;\n //this would insert all the prefixes of the current string\n //in to the TRIE\n void insert(const string &word) {\n auto ptr = root;\n for (char ch: word) {\n int idx = ch - \'a\';\n if (!ptr->child[idx]) {\n ptr->child[idx] = getNode();\n }\n ptr = ptr->child[idx];\n ptr->availablePrefix += 1;\n }\n }\n \n //This searches a string in TRIE and counts \n //all the prefixes along the path\n int search (const string &word) {\n auto ptr = root;\n int prefixCount = 0;\n for (char ch: word) {\n int idx = ch - \'a\';\n if (!ptr->child[idx]) {\n return prefixCount;\n }\n ptr = ptr->child[idx];\n prefixCount += ptr->availablePrefix;\n }\n return prefixCount;\n }\n vector<int> sumPrefixScores(vector<string>& words) {\n cnt = 0;\n root = getNode();\n for (const string &s: words) {\n insert(s);\n }\n vector<int> result;\n for (const string &s: words) {\n result.push_back(search(s));\n }\n return result;\n }\n};\n``` | 2 | 0 | [] | 0 |
sum-of-prefix-scores-of-strings | [Javascript] Simple Trie implementation | javascript-simple-trie-implementation-by-mkk3 | It\'s a pretty simple and understandable solution, written in Javascript\n\n```\nvar sumPrefixScores = function(words) {\n const n = words.length;\n const | vik_13 | NORMAL | 2022-11-17T10:25:56.537869+00:00 | 2022-11-18T23:30:52.905921+00:00 | 152 | false | It\'s a pretty simple and understandable solution, written in Javascript\n\n```\nvar sumPrefixScores = function(words) {\n const n = words.length;\n const trie = {_count: 0};\n const result = [];\n \n\t// Create our own custom trie with _count property.\n // We are storing how many time we passed current node.\n for (let i = 0; i < n; i++) {\n const word = words[i];\n \n let node = trie;\n for (let j = 0; j < word.length; j++) {\n if (!node[word[j]]) node[word[j]] = {};\n node = node[word[j]];\n node._count = (node._count || 0) + 1;\n }\n }\n \n\t// Collect all _count values together as a result\n for (let i = 0; i < n; i++) {\n const word = words[i];\n let count = 0;\n \n let node = trie;\n for (let j = 0; j < word.length; j++) {\n node = node[word[j]];\n count += (node._count || 0);\n }\n \n result[i] = count;\n }\n \n return result;\n}; | 2 | 0 | ['Trie', 'JavaScript'] | 0 |
sum-of-prefix-scores-of-strings | Python | Trie | Modular clean code | python-trie-modular-clean-code-by-jnaik-3b4l | Standard Trie implmentation, which I follow to solve all the Trie problems with just slight variation in search and insert method as per problem statement. Maki | jnaik | NORMAL | 2022-10-21T17:17:45.347485+00:00 | 2022-10-21T17:31:55.054512+00:00 | 121 | false | Standard Trie implmentation, which I follow to solve all the Trie problems with just slight variation in search and insert method as per problem statement. Making a habit to follow a template makes you fast and well organized and it leaves the best impression on interviewer.\n\nSolution inspired from: https://leetcode.com/problems/sum-of-prefix-scores-of-strings/discuss/2590701/Concise-Python-Tire-Implementation\n\nIntuition: While inserting words in Trie, maintain a count of all the prefixes and just sum them up while performing search for each word and each prefix. We can also add a memo dict to keep count of already explored prefixes that will help reduce time complexity but will increase space complexity. A trade-off to choose from but a must to mention during interviews.\n\nn = len(words)\nm = len(max(words))\n\nTime Complexity:\nInsert: O(mn) \nSearch: O(mn), traversing all the nodes of tree\n\nSC: O(mn), from storing it in trie\n\n```\nclass Node:\n def __init__(self):\n self.children = {}\n self.isWord = False\n self.count = 0\n\nclass Trie:\n def __init__(self):\n self.root = Node()\n \n def insert(self, word):\n node = self.root\n \n for ch in word:\n if ch not in node.children:\n node.children[ch] = Node()\n\t\t\t# Increment occurrence of the current prefix in Trie\n node.children[ch].count += 1\n node = node.children[ch]\n \n node.isWord = True\n \n def search(self, word) -> int :\n score = 0\n node = self.root\n \n for ch in word:\n\t\t\t# Add count for current prefix \n score += node.count\n node = node.children[ch]\n\t\t\t\n # Add count for current word \n score += node.count\n \n return score\n\nclass Solution:\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n \n trie = Trie()\n \n # Insert word in to trie\n for word in words:\n trie.insert(word)\n \n scores =[]\n # Search words for all prefixes of current word\n for word in words:\n scores.append(trie.search(word))\n \n return scores\n \n``` | 2 | 0 | ['String', 'Trie', 'Python', 'Python3'] | 0 |
sum-of-prefix-scores-of-strings | Java | Trie | Detailed Explanation and Comments | java-trie-detailed-explanation-and-comme-7t41 | Here I will explain the super detailed thought process to solve this problem. For a concise explanation, only read section Problem Approach and Final Approach I | zheng_four_oranges | NORMAL | 2022-09-24T02:53:05.425818+00:00 | 2022-09-24T02:58:20.659346+00:00 | 291 | false | Here I will explain the super detailed thought process to solve this problem. For a concise explanation, only read section **Problem Approach** and **Final Approach Implementation**.\n\n**Problem Approach:**\nFor each String **S** in words, for all **S\'s prefixes Sj** (**j denoting the length of Sj**), we essentially want to **sum up** the **number of strings in words that start with Sj**.\n\n**First Thought:**\n\n***Brute force***\nRecord Sjn for any String S in words. Say words = ["abc", "ab", "b", "bc", "ccc"], we record Sjn for "a" (2), "ab" (2), "abc" (1), "b" (2), "bc" (1), "c" (1), "cc" (1), "ccc" (1). \n\n***Implementation***\nFor each S, we increment each Sjn by 1. Then for each S, the answer is the sum of Sjn.\n\n***Issue: O(n ^ 3) TLE***\n**Say there are 1000 strings, each with 1000 characters, and the first 3 characters of each S are distinct** (say if one String starts with "abc", others cannot. It\'s possible since there are 26^3 > 1000 combinations of the first 3 characters), note that any prefix Sj for any S s.t. j >= 3 are distinct (for 2 prefixes P1 and P2 that belong to the same S, they are different, otherwise, they differ by the first 3 characters, thus P1 and P2 must also be different), resulting in the number of characters for all distinct Sj to be the magnitude of **1000 (distinct S) * ((3 + 1000) * 998 / 2) (number of characters in all Sj for S) = O(n ^ 3)** where n = 1000, resulting in TLE (usually the most you can get to pass is 10^7).\n\n***Solution***\nWe notice there are many overlaps between prefixes of the same S, say S999 and S1000, the first 999 characters are the same. So instead of making each Sj separate strings, we might be able to compact the representing of Sj into something that has O(n) space / time complexity. We use Trie to achieve this.\n\nIf you don\'t know Trie, here\'s a 5-min tutorial.\nhttps://www.youtube.com/watch?v=zIjfhVPRZCg\n\n**Final Approach:**\nUse Trie, each S is a path in the Trie from the root of Trie. Think of the path for S as a linked-list of Trie nodes with head = root, where the i-th node in the list stores Sin. Say S = "abc" = \'a\'->\'b\'->\'c\' in list form, with node \'a\' storing S1n (number of strings that start with "a"), \'b\' storing S2n (number of strings that start with "ab", essentially serving the same function as creating a String "ab" and setting its score). Essentially each node we create (O(1)), we save time / space by refraining from recreating all characters leading up to this node / storing them separately.\n\nFor a complete view of the Trie, say words = ["ab", "ad"], then the node representing "a" would have two children representing "ab" and "ad" respectively (corresponding to \'b\' and \'d\', and at index \'b\' - \'a\' and \'d\' - \'a\' of the node\'s children array, respectively). "a".sz = 2, "ab".sz = 1, "ad".sz = 1.\n\n**Final Approach Implementation**\nEach node N represents the prefix Sj resulted from concatenating all characters from root to N. N.sz = Sjn.\n***Step 1***: Compute all Sjn: For all S, for each prefix Sj, go 1 level deeper into Trie to find the node that represents Sj and increment Sj.sz by 1.\n***Step 2*** : Summing Sjn to get answer : Compute the sum of Sj for each S by dfs on Trie (answer for S = sum of sz for all nodes in the path from root to the end of S, say S = "abc", then answer for S = S1n + S2n + S3n = "a".sz + "ab".sz + "abc".sz, which can be done by dfs in O(n^2) (number of characters in words)). \n\n**Final Complexity:**\nO(# of characters in words) (step 1) + O(# of characters in words) (step 2) = O(n ^ 2) (n = 1000)\n\n**Conclusion:**\nWhen to use Trie? When you want to save repeated computation / string construction for prefixes or suffixes of S. It\'s essentially a compact representation of all prefixes for all S in words. To have a compact representation of all suffixes, simply add each S from back to front to the Trie.\n```\nclass Solution {\n public class Trie{\n //number of words that have prefix = the path represented by this Trie node\n int sz;\n //children array, ch[i] not null if there is a string with char(i + \'a\') as the next character\n Trie[] ch;\n //str is not null if the path represented by this Trie is a String in words, utilized by HashMap below\n String str;\n public Trie(){\n sz = 0;\n ch = new Trie[26];\n str = null;\n }\n }\n \n //computes the answers to the problem by summing sz along the path representing each String in words\n public void dfs(Trie node, int sum){\n //sum represents the sum of all sz in the path from root to node\n sum += node.sz;\n \n //put the answer to the string represented by node to map to save repeated computation\n if(node.str != null){\n map.put(node.str, sum);\n }\n \n //dfs all non-null children\n for(Trie child : node.ch){\n if(child != null){\n dfs(child, sum);\n }\n }\n }\n HashMap<String, Integer> map;\n public int[] sumPrefixScores(String[] words) {\n map = new HashMap<>();\n //root, stores no character, root[i] is not null if some string in words starts with char(i + \'a\'), easier to do dfs with this design (can just start at root instead of 26 potential Tries).\n Trie root = new Trie();\n \n //step 1: add each String to Trie iteratively\n for(String S : words){\n char[] s = S.toCharArray();\n Trie cur = root;\n for(char b : s){\n int ind = b - \'a\';\n \n //make new Trie if no previous string has b as the next character\n if(cur.ch[ind] == null){\n cur.ch[ind] = new Trie();\n }\n cur = cur.ch[ind];\n ++cur.sz;\n }\n cur.str = S;\n }\n \n\t\t//step 2\n dfs(root, 0);\n int[] res = new int[words.length];\n for(int i = 0; i < words.length; ++i){\n res[i] = map.get(words[i]);\n }\n return res;\n }\n}\n```\n | 2 | 0 | ['Depth-First Search', 'Trie', 'Java'] | 1 |
sum-of-prefix-scores-of-strings | Beginner Friendly Trie Implementation | C++ Solution | beginner-friendly-trie-implementation-c-t5xko | In addition to the general implementation of Trie, Storing an extra information how many prefixes end with a specific character in each node.\n\nstruct node{\n | wa_survivor | NORMAL | 2022-09-18T17:27:59.676905+00:00 | 2022-09-18T17:28:28.550459+00:00 | 211 | false | In addition to the general implementation of Trie, Storing an extra information how many prefixes end with a specific character in each node.\n```\nstruct node{\n node* mp[26];\n int cnt[26];\n bool isPresent(char c){\n if(mp[c-\'a\']==NULL) return false;\n return true;\n }\n node* getKey(char c){\n return mp[c-\'a\'];\n }\n void addKey(char c,node* temp){\n mp[c-\'a\']=temp;\n }\n void increment(char c){\n cnt[c-\'a\']++;\n }\n};\nclass Solution {\npublic:\n vector<int> sumPrefixScores(vector<string>& words) {\n node *root=new node();\n for(auto word:words){\n node* temp=root;\n for(int i=0;i<word.size();i++){\n if(!temp->isPresent(word[i])){\n temp->addKey(word[i],new node());\n }\n temp->increment(word[i]);\n temp=temp->getKey(word[i]);\n }\n }\n vector<int> ans(words.size());\n int k=0;\n for(auto word:words){\n int c=0;\n node* temp=root;\n for(int i=0;i<word.size();i++){\n c+=temp->cnt[word[i]-\'a\'];\n temp=temp->getKey(word[i]);\n }\n ans[k]=c;\n k++;\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Trie', 'C', 'C++'] | 0 |
sum-of-prefix-scores-of-strings | Trie Java Solution. | trie-java-solution-by-harshraj9988-jh3j | \nclass Solution {\n\tclass TrieNode {\n TrieNode[] next;\n int[] cnt;\n\n public TrieNode() {\n next = new TrieNode[26];\n | HarshRaj9988 | NORMAL | 2022-09-18T05:40:03.269899+00:00 | 2022-09-18T05:40:03.269946+00:00 | 39 | false | ```\nclass Solution {\n\tclass TrieNode {\n TrieNode[] next;\n int[] cnt;\n\n public TrieNode() {\n next = new TrieNode[26];\n cnt = new int[26];\n }\n\n \n }\n\n public void insert(String word, TrieNode root) {\n TrieNode curr = root;\n for (int i = 0; i < word.length(); i++) {\n int c = word.charAt(i)-\'a\';\n if (curr.next[c]==null) {\n curr.next[c] = new TrieNode();\n curr.cnt[c] = 1;\n } else {\n curr.cnt[c]++;\n }\n curr = curr.next[c];\n }\n }\n\n private int getNode(String word, TrieNode root) {\n TrieNode curr = root;\n int sum = 0;\n for (int i = 0; i < word.length(); i++) {\n int c = word.charAt(i)-\'a\';\n\n if (curr.next[c]==null) {\n return 0;\n }\n sum+=curr.cnt[c];\n curr = curr.next[c];\n }\n return sum;\n }\n\n\n public int[] sumPrefixScores(String[] words) {\n TrieNode root = new TrieNode();\n for(String str: words) {\n insert(str, root);\n }\n int n = words.length;\n int[] ans = new int[n];\n for(int i=0; i<n; i++) {\n ans[i] = getNode(words[i], root);\n }\n return ans;\n }\n}\n``` | 2 | 0 | ['Depth-First Search', 'Trie'] | 0 |
sum-of-prefix-scores-of-strings | C++ Easy Solution | Trie | c-easy-solution-trie-by-b_rabbit007-slnc | I have created Trie data structure with array of pointers next to point all alphabets and wordCount which will store number of words having prefix string ending | B_Rabbit007 | NORMAL | 2022-09-18T05:06:07.081209+00:00 | 2022-09-23T01:45:51.031904+00:00 | 53 | false | I have created `Trie` data structure with array of pointers `next` to point all alphabets and `wordCount` which will store number of words having prefix string ending at current node.\n\nFor example - consider array of strings `["abc", "ab", "b"]`\nTrie will be like -\n```\n\t\t\t\t\t\t\t Root\n\t\t\t\t\t\t wordCount = 0\n\t\t\t\t\t\t/ \\\n\t\t\t\t \'a\' \'b\'\n\t\t \twordCount = 2 wordCount = 1\n\t\t /\n\t\t \'b\'\n\t\t wordCount = 2\n\t\t\t/\n\t\t\'c\'\n wordCount = 1\n\n```\n\nThen for each word i have traversed the trie data structure and added `wordCount` for each character.\n\n```\nclass trie {\n public:\n trie* next[26] = {};\n int wordCount;\n trie(){\n wordCount = 0;\n }\n};\n\nclass Solution {\npublic:\n vector<int> sumPrefixScores(vector<string>& words) {\n trie* root = new trie();\n int n = words.size();\n \n\t\t// constructing trie data structure\n for (int i = 0; i < n; i++) {\n auto cur = root;\n for (char c : words[i]) {\n if (!cur -> next[c - \'a\'])\n cur -> next[c - \'a\'] = new trie();\n cur = cur -> next[c - \'a\'];\n cur -> wordCount++;\n }\n }\n \n\t\t// calculating ans for each word\n vector<int> ans(n);\n for (int i = 0; i < n; i++) {\n auto cur = root;\n for (int j = 0; j < words[i].size(); j++) {\n cur = cur -> next[words[i][j] - \'a\'];\n ans[i] += cur -> wordCount;\n }\n }\n \n return ans;\n }\n};\n```\nHope it helps and feel free to ask if you have any doubts :) | 2 | 0 | ['Trie', 'C'] | 0 |
sum-of-prefix-scores-of-strings | Python3 ✅ || Simple Trie | python3-simple-trie-by-husharbabu-dqbu | `.\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.word = False\n self.count = 1\n \nclass | HusharBabu | NORMAL | 2022-09-18T04:42:08.785353+00:00 | 2022-09-18T04:42:08.785391+00:00 | 32 | false | ```.\nclass TrieNode:\n def __init__(self):\n self.children = {}\n self.word = False\n self.count = 1\n \nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n\n def insert(self, word):\n trav = self.root\n for c in word:\n if c in trav.children:\n trav.children[c].count += 1\n trav = trav.children[c]\n else:\n trav.children[c] = TrieNode()\n trav = trav.children[c]\n trav.word = True\n\nclass Solution:\n \n \n def sumPrefixScores(self, words: List[str]) -> List[int]:\n \n trie = Trie()\n \n for word in words:\n trie.insert(word)\n \n ans = []\n for word in words:\n count = 0\n trav = trie.root\n for c in word:\n if c in trav.children:\n count += trav.children[c].count\n trav = trav.children[c]\n ans.append(count)\n \n return ans\n \xA0 \xA0 `` | 2 | 0 | [] | 0 |
sum-of-prefix-scores-of-strings | Java | Roling Hash | java-roling-hash-by-aaveshk-dhk1 | \nclass Solution\n{\n final int m = 1023;\n public int[] sumPrefixScores(String[] words)\n {\n HashMap<Long,Integer> map = new HashMap<>();\n | aaveshk | NORMAL | 2022-09-18T04:22:19.628297+00:00 | 2022-09-18T04:22:30.890943+00:00 | 243 | false | ```\nclass Solution\n{\n final int m = 1023;\n public int[] sumPrefixScores(String[] words)\n {\n HashMap<Long,Integer> map = new HashMap<>();\n for(String S : words)\n {\n char[] s = S.toCharArray();\n long hash_so_far = 0L;\n int n = s.length;\n for (int i = 0; i < n; i++)\n {\n hash_so_far = hash_so_far*m+s[i];\n map.put(hash_so_far,map.getOrDefault(hash_so_far,0)+1);\n }\n }\n int cur = 0;\n int[] ret = new int[words.length];\n for(String S : words)\n {\n char[] s = S.toCharArray();\n long hash_so_far = 0L;\n int n = s.length;\n for (int i = 0; i < n; i++)\n {\n hash_so_far = hash_so_far*m+s[i];\n ret[cur] += map.get(hash_so_far);\n }\n cur++;\n }\n return ret;\n }\n}\n``` | 2 | 0 | ['Rolling Hash', 'Java'] | 2 |
sum-of-prefix-scores-of-strings | SIMPLE TRIE | C++ | BRUTE FORCE | simple-trie-c-brute-force-by-deepanshu_d-icx7 | TRIE PRACTICE PROBLEMS \n\n1. Implement Trie (Prefix Tree)\n2. Maximum XOR of Two Numbers in an Array\n3. Search Suggestions System\n\n// trie node \nstruct no | Deepanshu_Dhakate | NORMAL | 2022-09-18T04:19:23.567619+00:00 | 2022-09-18T04:19:23.567664+00:00 | 73 | false | **TRIE PRACTICE PROBLEMS **\n\n[1. Implement Trie (Prefix Tree)](https://leetcode.com/problems/implement-trie-prefix-tree/)\n[2. Maximum XOR of Two Numbers in an Array](https://leetcode.com/problems/maximum-xor-of-two-numbers-in-an-array/)\n[3. Search Suggestions System](https://leetcode.com/problems/search-suggestions-system/)\n```\n// trie node \nstruct node{\n int count;\n node* child[26];\n node(){\n for(int i=0;i<26;i++){\n child[i]=NULL;\n }\n count=0;\n }\n};\n\nclass Solution{\npublic:\n vector<int> sumPrefixScores(vector<string>& words){\n vector<int> ans;\n node* root=new node();\n \n //inserting words in trie \n for(auto s:words){\n int n=s.length();\n node* temp=root;\n for(int i=0;i<n;i++){\n if(temp->child[s[i]-\'a\']==NULL){\n temp->child[s[i]-\'a\']=new node();\n }\n temp=temp->child[s[i]-\'a\'];\n \n //updating count of that prefix \n temp->count++;\n }\n }\n \n //traversing to each words \n for(auto s:words){\n int n=s.length();\n int curr=0;\n node* temp=root;\n //suming up value of each prefix \n for(int i=0;i<n;i++){\n temp = temp->child[s[i]-\'a\'];\n curr += temp->count;\n }\n //updating ans to that word \n ans.push_back(curr);\n }\n \n return ans;\n }\n};\n\n\n\n\n\n\n\n``` | 2 | 1 | ['Depth-First Search', 'Trie', 'C'] | 0 |
sum-of-prefix-scores-of-strings | C++ | Trie Solution | c-trie-solution-by-travanj05-hxai | cpp\nclass Node {\npublic:\n char ch;\n Node* children[26] = {nullptr};\n int prefix_cnt;\n};\n\nclass Solution {\nprivate:\n Node* root = new Node; | travanj05 | NORMAL | 2022-09-18T04:14:11.844955+00:00 | 2022-09-18T04:14:11.844986+00:00 | 43 | false | ```cpp\nclass Node {\npublic:\n char ch;\n Node* children[26] = {nullptr};\n int prefix_cnt;\n};\n\nclass Solution {\nprivate:\n Node* root = new Node;\n int prefixCount(string &prefix) {\n Node* tmp = root;\n int cnt = 0;\n for (char &ch : prefix) {\n int index = ch - \'a\';\n if (tmp->children[index] == nullptr) break;\n tmp = tmp->children[index];\n cnt += tmp->prefix_cnt;\n }\n return cnt;\n }\n void insertWord(string &word) {\n Node* ptr = root;\n for (char &ch : word) {\n if (ptr->children[ch - \'a\'] == nullptr)\n ptr->children[ch - \'a\'] = new Node();\n ptr = ptr->children[ch - \'a\'];\n ptr->prefix_cnt++;\n }\n }\npublic:\n vector<int> sumPrefixScores(vector<string>& words) {\n vector<int> res;\n for (string &word : words) insertWord(word);\n for (string &word : words) {\n int r = prefixCount(word);\n res.push_back(r);\n }\n return res;\n }\n};\n``` | 2 | 0 | ['Trie', 'C', 'C++'] | 0 |
sum-of-prefix-scores-of-strings | [Java] Trie | O(NM) Time | Easy to Understand | java-trie-onm-time-easy-to-understand-by-17es | java\nclass Solution {\n public int[] sumPrefixScores(String[] words) {\n if (words.length == 1) {\n return new int[] { words[0].length() } | jjeeffff | NORMAL | 2022-09-18T04:12:10.387993+00:00 | 2022-09-21T08:09:55.883935+00:00 | 227 | false | ``` java\nclass Solution {\n public int[] sumPrefixScores(String[] words) {\n if (words.length == 1) {\n return new int[] { words[0].length() };\n }\n \n Trie trie = new Trie();\n for (String word : words) {\n trie.addWord(word);\n }\n int[] ans = new int[words.length];\n for (int i = 0; i < words.length; i++) {\n ans[i] = trie.getPrefixCount(words[i]);\n }\n return ans;\n }\n}\n\nclass Trie {\n TrieNode root;\n \n Trie() {\n root = new TrieNode();\n }\n \n void addWord(String word) {\n TrieNode current = root;\n for (char c : word.toCharArray()) {\n int index = c - \'a\';\n if (current.children[index] == null) {\n current.children[index] = new TrieNode();\n }\n current.children[index].prefixCount++;\n current = current.children[index];\n }\n }\n \n int getPrefixCount(String word) {\n int sum = 0;\n TrieNode current = root;\n for (char c : word.toCharArray()) {\n int index = c - \'a\';\n if (current.children[index] == null) {\n return sum;\n }\n current = current.children[index];\n sum += current.prefixCount;\n }\n return sum;\n }\n}\n\nclass TrieNode {\n final static int R = 26;\n \n int prefixCount;\n TrieNode[] children;\n \n TrieNode() {\n prefixCount = 0;\n children = new TrieNode[R];\n }\n}\n``` | 2 | 0 | ['Trie', 'Java'] | 0 |
sum-of-prefix-scores-of-strings | Java || Trie Solution | java-trie-solution-by-yog_esh-361o | \nclass Solution {\n public int[] sumPrefixScores(String[] words) {\n \n Tries trie=new Tries();\n \n \n \n for(Str | yog_esh | NORMAL | 2022-09-18T04:07:00.240820+00:00 | 2022-09-18T04:07:00.240846+00:00 | 397 | false | ```\nclass Solution {\n public int[] sumPrefixScores(String[] words) {\n \n Tries trie=new Tries();\n \n \n \n for(String word:words){\n \n add(word,trie);\n }\n \n int[] res=new int[words.length];\n \n \n for(int i=0;i<words.length;i++){\n \n Tries temp=trie;\n res[i]=count(temp,words[i],0);\n }\n return res;\n }\n \n public int count(Tries temp,String word,int in){\n \n \n if(in==word.length()) return 0;\n char ch=word.charAt(in);\n \n int ans=0;\n if(temp.map.containsKey(ch)){\n // System.out.println(ch+" -->"+temp.count);\n ans+=temp.map.get(ch).count+count(temp.map.get(ch),word,in+1); \n \n }\n return ans;\n }\n \n public void add(String str,Tries trie){\n \n Tries temp=trie;\n for(int i=0;i<str.length();i++){\n \n char ch=str.charAt(i);\n \n if(!temp.map.containsKey(ch)){\n temp.map.put(ch,new Tries());\n }\n \n \n temp=temp.map.get(ch);\n temp.count+=1;\n }\n }\n public class Tries{\n \n HashMap<Character,Tries> map=new HashMap<>();\n int count=0;\n }\n}\n``` | 2 | 0 | ['Trie', 'Java'] | 1 |
sum-of-prefix-scores-of-strings | Very simple Python trie code | very-simple-python-trie-code-by-rjmcmc-xked | ```\nclass Solution:\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n trie = {}\n \n for word in words:\n t = tr | rjmcmc | NORMAL | 2022-09-18T04:03:19.731203+00:00 | 2022-09-18T04:03:19.731241+00:00 | 67 | false | ```\nclass Solution:\n def sumPrefixScores(self, words: List[str]) -> List[int]:\n trie = {}\n \n for word in words:\n t = trie\n for char in word:\n if char not in t:\n t[char] = {}\n t = t[char]\n if \'$\' not in t:\n t[\'$\'] = 0\n t[\'$\'] += 1\n \n ans = []\n \n for word in words:\n t = trie\n temp_ans = 0\n for char in word:\n t = t[char]\n temp_ans += t[\'$\']\n ans.append(temp_ans)\n return ans \n | 2 | 0 | [] | 0 |
sum-of-prefix-scores-of-strings | Simple Solution Using Trie Tree | simple-solution-using-trie-tree-by-pbara-ycv3 | The question gives Intution of Trie tree as storing all the prefixes will cause TLE\n\nWith the standard implementation of trie tree we can keep a array of coun | pbarak6 | NORMAL | 2022-09-18T04:02:07.624350+00:00 | 2022-09-18T04:02:07.624389+00:00 | 124 | false | The question gives Intution of Trie tree as storing all the prefixes will cause TLE\n\nWith the standard implementation of trie tree we can keep a array of count that will count the frequency of that charcater\n\n=>> Below is the simple CPP implementation\n\n```\nstruct Node{\n bool flag=false;\n int count[26] = {0};\n Node* links[26];\n\t// Increment count while getting the next node\n Node* get(char ch){\n count[ch-\'a\']++;\n return links[ch-\'a\'];\n }\n\t// As we need not to increment count when we are getting to build ans\n Node* get2(char ch){\n // count[ch-\'a\']++;\n return links[ch-\'a\'];\n }\n int getCount(char ch){\n return count[ch-\'a\'];\n }\n\t// Adding next character to trie\n void put(char ch,Node* temp){\n // count[ch-\'a\']++;\n links[ch-\'a\']=temp;\n }\n bool containsKey(char ch){\n return links[ch-\'a\']!=NULL;\n }\n};\n\nclass Trie {\npublic:\n Node *root;\n Trie() {\n root = new Node();\n }\n void insert(string s){\n Node* temp=root;\n for(int i=0;i<s.size();i++){\n if(!temp->containsKey(s[i]))\n temp->put(s[i],new Node());\n temp=temp->get(s[i]);\n }\n temp->flag=true;\n }\n \n int getAns(string s) {\n Node* temp = root;\n int ans = 0;\n for(int i=0;i<s.size();i++) {\n ans += temp->getCount(s[i]);\n temp = temp->get2(s[i]);\n }\n return ans;\n }\n};\n\n\nclass Solution {\npublic:\n vector<int> sumPrefixScores(vector<string>& words) {\n int n = words.size();\n Trie trie;\n for(string s:words) trie.insert(s);\n vector<int> ans(n,0);\n for(int i=0;i<n;i++) {\n ans[i] = trie.getAns(words[i]);\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Tree', 'Trie', 'C++'] | 1 |
sum-of-prefix-scores-of-strings | [JavaScript] Trie | javascript-trie-by-jialihan-cv7c | \nclass TrieNode {\n constructor() {\n this.children = {};\n this.cnt = 0;\n }\n}\n\n\nvar sumPrefixScores = function(words) {\n const ro | jialihan | NORMAL | 2022-09-18T04:01:40.170494+00:00 | 2022-09-18T04:01:40.170546+00:00 | 97 | false | ```\nclass TrieNode {\n constructor() {\n this.children = {};\n this.cnt = 0;\n }\n}\n\n\nvar sumPrefixScores = function(words) {\n const root = new TrieNode();\n function add(w) {\n let cur = root;\n for(let i = 0; i<w.length; i++){\n const c = w[i];\n if(!cur.children[c]) {\n cur.children[c] = new TrieNode();\n }\n cur = cur.children[c];\n cur.cnt++;\n } \n }\n function find(w) {\n let total = 0;\n let cur = root;\n for(let i = 0; i<w.length; i++){\n const c = w[i];\n if(!cur.children[c]) {\n break;\n }\n cur = cur.children[c];\n total += cur.cnt;\n } \n return total;\n }\n for(const word of words) {\n add(word);\n }\n const ans = [];\n for(const word of words) {\n ans.push(find(word));\n }\n return ans; \n};\n``` | 2 | 1 | ['Trie', 'JavaScript'] | 0 |
sum-of-prefix-scores-of-strings | trie cpp | trie-cpp-by-sreyash_11-1hc5 | space complexity here, e.g. O(n) -->Code | sreyash_11 | NORMAL | 2025-03-17T06:50:17.580238+00:00 | 2025-03-17T06:50:17.580238+00:00 | 7 | false | space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
struct Node {
Node *links[26];
int precnt = 0;
Node() {
for (int i = 0; i < 26; i++) links[i] = nullptr;
}
bool containsKey(char ch) {
return links[ch - 'a'] != nullptr;
}
Node* get(char ch) {
return links[ch - 'a'];
}
void put(char ch, Node* node) {
links[ch - 'a'] = node;
}
void setpre() {
precnt++;
}
int getpre() {
return precnt;
}
};
class Trie {
public:
Node* root;
Trie() {
root = new Node();
}
void insert(string word) {
Node *node = root;
for (char ch : word) {
if (!node->containsKey(ch)) {
node->put(ch, new Node());
}
node = node->get(ch);
node->setpre();
}
}
int searchPrefixScore(string word) {
Node *node = root;
int ans = 0;
for (char ch : word) {
node = node->get(ch);
if (!node) break;
ans += node->getpre();
}
return ans;
}
};
class Solution {
public:
vector<int> sumPrefixScores(vector<string>& words) {
Trie t;
for (auto &word : words) {
t.insert(word);
}
vector<int> ans(words.size());
for (int i = 0; i < words.size(); i++) {
ans[i] = t.searchPrefixScore(words[i]);
}
return ans;
}
};
``` | 1 | 0 | ['String', 'Trie', 'String Matching', 'C++'] | 0 |
type-of-triangle | ✅THE BEST EXPLANATION||Beats 100% Users | the-best-explanationbeats-100-users-by-h-00os | ---\n# PLEASE UPVOTE IF YOU LIKE IT \u2705\n---\n\n\n---\n# Intuition\n Describe your first thoughts on how to solve this problem. \n\nThe goal is to determine | harshal2024 | NORMAL | 2024-02-03T16:16:02.600254+00:00 | 2024-02-03T16:16:02.600277+00:00 | 1,830 | false | ---\n# PLEASE UPVOTE IF YOU LIKE IT \u2705\n---\n\n\n---\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThe goal is to determine the type of triangle that can be formed based on the given array of three sides. We need to check if the sides satisfy the conditions for forming a triangle and then identify whether it\'s equilateral, isosceles, scalene, or none.\n\n---\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Triangle Inequality Condition Check:**\n\nThe code starts by checking the triangle inequality condition. This condition ensures that the sum of any two sides of a triangle must be greater than the length of the third side.\nIf this condition is not met for the given sides, it means a triangle cannot be formed, and the function returns "none."\n\n**Identifying Triangle Types:**\n\nIf the triangle inequality condition is satisfied, the code proceeds to check the type of triangle.\nFor an equilateral triangle, all sides must be of equal length. This is checked by comparing each side with the other two sides using equality.\nFor a scalene triangle, all sides must be of different lengths. This is checked by ensuring that no two sides are equal.\nIf the triangle is not equilateral or scalene, it is considered isosceles.\n\n**Returning the Result:**\n\nFinally, the function returns the type of triangle identified based on the conditions.\nIf the sides do not form a triangle, it returns "none."\nIf all sides are equal, it returns "equilateral."\nIf all sides are different, it returns "scalene."\nOtherwise, it returns "isosceles."\n\n**In Summary:**\n\nThe code checks if the given sides can form a triangle using the triangle inequality condition. If they can, it further determines the type of triangle (equilateral, isosceles, scalene) based on the lengths of the sides and returns the result. If the sides cannot form a triangle, it returns "none."\n\n---\n\n# Complexity\n- Time complexity: O(1) \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n \n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n\n\n\n---\n\n# Code\nC++\n```\nclass Solution {\npublic:\n // Function to determine the type of triangle based on given sides\n string triangleType(vector<int>& nums) {\n // Step 1: Check the triangle inequality condition\n if (!((nums[0] + nums[1] > nums[2]) && (nums[0] + nums[2] > nums[1]) && (nums[2] + nums[1] > nums[0])))\n return "none"; // If the sides do not satisfy the triangle inequality, return "none"\n\n // Step 2: Check if all sides are equal (equilateral)\n if (nums[0] == nums[1] && nums[1] == nums[2])\n return "equilateral"; // If all sides are equal, return "equilateral"\n else if (nums[0] != nums[1] && nums[0] != nums[2] && nums[1] != nums[2])\n return "scalene"; // If no two sides are equal, return "scalene"\n\n // Step 3: If not equilateral or scalene, it is isosceles\n return "isosceles"; // Return "isosceles" as the default option\n }\n};\n\n```\n\n---\nPython3\n```\nclass Solution:\n # Function to determine the type of triangle based on given sides\n def triangleType(self, nums: List[int]) -> str:\n # Step 1: Check the triangle inequality condition\n if not (nums[0] + nums[1] > nums[2] and nums[0] + nums[2] > nums[1] and nums[2] + nums[1] > nums[0]):\n return "none" # If the sides do not satisfy the triangle inequality, return "none"\n\n # Step 2: Check if all sides are equal (equilateral)\n if nums[0] == nums[1] == nums[2]:\n return "equilateral" # If all sides are equal, return "equilateral"\n elif nums[0] != nums[1] and nums[0] != nums[2] and nums[1] != nums[2]:\n return "scalene" # If no two sides are equal, return "scalene"\n\n # Step 3: If not equilateral or scalene, it is isosceles\n return "isosceles" # Return "isosceles" as the default option\n\n```\n\n---\nJava\n```\npublic class Solution {\n // Function to determine the type of triangle based on given sides\n public String triangleType(int[] nums) {\n // Step 1: Check the triangle inequality condition\n if (!(nums[0] + nums[1] > nums[2] && nums[0] + nums[2] > nums[1] && nums[2] + nums[1] > nums[0]))\n return "none"; // If the sides do not satisfy the triangle inequality, return "none"\n\n // Step 2: Check if all sides are equal (equilateral)\n if (nums[0] == nums[1] && nums[1] == nums[2])\n return "equilateral"; // If all sides are equal, return "equilateral"\n else if (nums[0] != nums[1] && nums[0] != nums[2] && nums[1] != nums[2])\n return "scalene"; // If no two sides are equal, return "scalene"\n\n // Step 3: If not equilateral or scalene, it is isosceles\n return "isosceles"; // Return "isosceles" as the default option\n }\n} \n```\n | 13 | 0 | ['Python', 'C++', 'Java', 'Python3'] | 1 |
type-of-triangle | Sort | sort-by-votrubac-q5jc | We sort the sides first to simplify the logic.\n\nC++\ncpp\nstring triangleType(vector<int>& n) {\n sort(begin(n), end(n));\n if (n[2] >= n[0] + n[1])\n | votrubac | NORMAL | 2024-02-03T16:04:32.494865+00:00 | 2024-02-03T16:04:32.494895+00:00 | 1,259 | false | We sort the sides first to simplify the logic.\n\n**C++**\n```cpp\nstring triangleType(vector<int>& n) {\n sort(begin(n), end(n));\n if (n[2] >= n[0] + n[1])\n return "none";\n return n[0] == n[2] ? "equilateral" : n[0] == n[1] || n[1] == n[2] ? "isosceles" : "scalene";\n}\n``` | 13 | 1 | ['C'] | 5 |
type-of-triangle | Simple java solution | simple-java-solution-by-siddhant_1602-0hto | Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(1)\n\n# Code\n\nclass Solution {\n public String triangleType(int[] nums) {\n if(nums[0]+ | Siddhant_1602 | NORMAL | 2024-02-03T16:01:16.030489+00:00 | 2024-02-03T16:06:45.022384+00:00 | 783 | false | # Complexity\n- Time complexity: $$O(1)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution {\n public String triangleType(int[] nums) {\n if(nums[0]+nums[1]>nums[2] && nums[1]+nums[2]>nums[0] && nums[2]+nums[0]>nums[1])\n {\n if(nums[0]==nums[1] && nums[1]==nums[2])\n {\n return "equilateral";\n }\n else if(nums[0]!=nums[1] && nums[1]!=nums[2] && nums[0]!=nums[2] )\n {\n return "scalene";\n }\n else if(nums[0]==nums[1] || nums[0]==nums[2] || nums[1]==nums[2])\n {\n return "isosceles";\n }\n }\n return "none";\n }\n}\n``` | 12 | 0 | ['Java'] | 0 |
type-of-triangle | Without if-else spaghetti | without-if-else-spaghetti-by-almostmonda-teqg | Intuition\n Describe your first thoughts on how to solve this problem. \nThe \space Triangle \space Inequality \space Theorem says:\n> The sum of two sides of a | almostmonday | NORMAL | 2024-02-03T20:53:35.920274+00:00 | 2024-02-03T21:37:46.827111+00:00 | 379 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n$$The \\space Triangle \\space Inequality \\space Theorem$$ says:\n> The sum of two sides of a triangle must be greater than the third side.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFind the right type of a triangle.\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n---\n* You could find some other extraordinary solutions in my [profile](https://leetcode.com/almostmonday/) on the Solutions tab (I don\'t post obvious or not interesting solutions at all.)\n* If this was helpful, please upvote so that others can see this solution too.\n---\n\n\n# Code\n```\nclass Solution:\n def triangleType(self, nums: List[int]) -> str:\n res = ["none", "equilateral", "isosceles", "scalene"]\n nums.sort()\n\n return res[len(set(nums)) * (nums[2] < nums[0] + nums[1])]\n``` | 8 | 1 | ['Geometry', 'Python', 'Python3'] | 3 |
type-of-triangle | Sort & 3 conditions | sort-3-conditions-by-kreakemp-frlb | \n# C++\n\nstring triangleType(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n if(nums[0] + nums[1] <= nums[2]) return "none";\n if(nums[0] == | kreakEmp | NORMAL | 2024-02-03T16:42:41.170212+00:00 | 2024-02-03T16:42:50.220112+00:00 | 2,567 | false | \n# C++\n```\nstring triangleType(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n if(nums[0] + nums[1] <= nums[2]) return "none";\n if(nums[0] == nums[1] && nums[1] == nums[2]) return "equilateral";\n if(nums[0] == nums[1] || nums[1] == nums[2]) return "isosceles";\n return "scalene";\n}\n```\n\n# Java\n```\npublic String triangleType(int[] nums) {\n Arrays.sort(nums);\n if(nums[0] + nums[1] <= nums[2]) return "none";\n if(nums[0] == nums[1] && nums[1] == nums[2]) return "equilateral";\n if(nums[0] == nums[1] || nums[1] == nums[2]) return "isosceles";\n return "scalene";\n}\n\n``` | 7 | 1 | ['C++', 'Java'] | 4 |
type-of-triangle | Type of Triangle📐🔍: Simple if-else ✨|| 0ms⏰ ||Beats 100%✅ || JAVA ☕️ | type-of-triangle-simple-if-else-0ms-beat-myd9 | \n# Intuition\nYou\'re checking the type of triangle based on its side lengths, following these rules:\n\n- If any side length is greater than or equal to the s | Megha_Mathur18 | NORMAL | 2024-06-23T14:16:52.692709+00:00 | 2024-06-23T14:18:41.489093+00:00 | 117 | false | \n# Intuition\nYou\'re checking the type of triangle based on its side lengths, following these rules:\n\n- If any side length is greater than or equal to the sum of the other two sides, it\'s not a valid triangle ("none").\n- If all three sides are equal, it\'s an "Equilateral triangle".\n- If exactly two sides are equal, it\'s an "Isosceles triangle".\n- If all sides are different, it\'s a "Scalene triangle".\n\n# Approach\n1. **Input Handling:** You are given nums contains exactly three integers representing the side lengths of a triangle (Check Constraints).\n2. **Triangle Validity Check:** You first check if the given sides can form a triangle using the triangle inequality theorem.\n3. **Triangle Type Determination:** Based on the side lengths:\n- If all sides are equal, return "equilateral".\n- If exactly two sides are equal, return "isosceles".\n- Otherwise, return "scalene".\n\n# Complexity\n- **Time complexity:**\nThe time complexity is **O(1)** since the operations involve a fixed number of comparisons (specifically, 3 comparisons and potentially a few arithmetic operations for checking triangle inequality).\n\n- **Space complexity:**\nThe space complexity is also **O(1)** because you are using a fixed amount of extra space regardless of the input size.\n\n\n# Code\n```\nclass Solution {\n public String triangleType(int[] nums) {\n int a = nums[0];\n int b = nums[1];\n int c = nums[2];\n\n if (a+b <= c || b+c <= a || a+c <= b)\n return "none";\n\n else if (a == b && b == c)\n return "equilateral";\n\n else if (a == b || b == c || a == c)\n return "isosceles";\n\n else\n return "scalene";\n }\n}\n```\n---\n\n | 6 | 0 | ['Java'] | 0 |
type-of-triangle | [Java] ✅ ⬆️ | Simple 🔥🔥 | Clean | Self Explanatory | java-simple-clean-self-explanatory-by-sa-2nep | Complexity\nTime complexity: O(1)\nSpace complexity: O(1)\n\npublic String triangleType(int[] nums) {\n int a = nums[0];\n int b = nums[1];\n | sandeepk97 | NORMAL | 2024-02-03T16:35:16.785226+00:00 | 2024-02-03T16:37:54.391528+00:00 | 248 | false | **Complexity**\nTime complexity: O(1)\nSpace complexity: O(1)\n```\npublic String triangleType(int[] nums) {\n int a = nums[0];\n int b = nums[1];\n int c = nums[2];\n\n if (isValidTriangle(a, b, c)) {\n if (a == b && b == c) {\n return "equilateral";\n } else if (a == b || b == c || a == c) {\n return "isosceles";\n } else {\n return "scalene";\n }\n } else {\n return "none";\n }\n }\n\n private boolean isValidTriangle(int a, int b, int c) {\n return a + b > c && a + c > b && b + c > a;\n }\n``` | 5 | 0 | ['Java'] | 1 |
type-of-triangle | 🔥BEATS 💯 % 🎯 |✨SUPER EASY FOR BEGINNERS 👏 | beats-super-easy-for-beginners-by-vignes-f5u7 | Code | vigneshvaran0101 | NORMAL | 2025-02-25T17:00:14.251211+00:00 | 2025-02-25T17:00:14.251211+00:00 | 136 | false | 
# Code
```python3 []
class Solution:
def triangleType(self, nums: List[int]) -> str:
if nums[0] >= nums[1] + nums[2] or nums[1] >= nums[0] + nums[2] or nums[2] >= nums[0] + nums[1]:
return "none"
if len(set(nums)) == len(nums):
return "scalene"
elif len(set(nums)) == len(nums)-1:
return "isosceles"
else:
return "equilateral"
``` | 3 | 0 | ['Python3'] | 0 |
type-of-triangle | Java Check None first | java-check-none-first-by-hobiter-u869 | See code. \n# Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \nO(1)\n- Space complexity:\n Add your space complexity here, e.g. O(n) | hobiter | NORMAL | 2024-02-04T21:57:58.178602+00:00 | 2024-02-04T21:57:58.178620+00:00 | 871 | false | See code. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(1)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\n final String EQ = "equilateral";\n final String ISO = "isosceles";\n final String SCA = "scalene";\n final String NONC = "none";\n public String triangleType(int[] nums) {\n int a = nums[0], b = nums[1], c = nums[2];\n if (a + b <= c || b +c <= a || a + c <= b) return NONC;\n if (a == b && b == c) return EQ;\n if (a == b || b == c || a == c) return ISO;\n return SCA;\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
type-of-triangle | ✅Beats 100% || Classifying triangles in Java, Python & C++ | beats-100-classifying-triangles-in-java-xl2tw | Intuition\nThe code checks the validity of a triangle based on its side lengths and classifies it as equilateral, isosceles, scalene, or none.\n\n# Approach\nTh | Mohit-P | NORMAL | 2024-02-03T16:32:57.937652+00:00 | 2024-02-03T16:32:57.937675+00:00 | 203 | false | # Intuition\nThe code checks the validity of a triangle based on its side lengths and classifies it as equilateral, isosceles, scalene, or none.\n\n# Approach\nThe approach involves using conditional statements to check the triangle\'s validity and then determining its type based on the side lengths.\n\n# Complexity\n- Time complexity:\nThe time complexity of this solution is O(1) since the code involves a fixed number of comparisons and conditions\n\n- Space complexity:\nThe space complexity is O(1) as there is no additional space used that scales with the input size. \n\n```Java []\nclass Solution {\n public String triangleType(int[] nums) {\n \n if(nums[0]+nums[1]<=nums[2] || nums[1]+nums[2]<=nums[0] || nums[0]+nums[2]<=nums[1])\n return "none";\n else if (nums[0] == nums[1] && nums[1] == nums[2])\n return "equilateral";\n else if(nums[0]==nums[1] || nums[1]==nums[2] || nums[2]==nums[0])\n return "isosceles";\n else \n return "scalene";\n\n }\n}\n```\n```python []\nclass Solution:\n def triangleType(self, nums: List[int]) -> str:\n if nums[0] + nums[1] <= nums[2] or nums[1] + nums[2] <= nums[0] or nums[0] + nums[2] <= nums[1]:\n return "none"\n elif nums[0] == nums[1] == nums[2]:\n return "equilateral"\n elif nums[0] == nums[1] or nums[1] == nums[2] or nums[2] == nums[0]:\n return "isosceles"\n else:\n return "scalene"\n\n```\n```C++ []\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n if (nums[0] + nums[1] <= nums[2] || nums[1] + nums[2] <= nums[0] || nums[0] + nums[2] <= nums[1])\n return "none";\n else if (nums[0] == nums[1] && nums[1] == nums[2])\n return "equilateral";\n else if (nums[0] == nums[1] || nums[1] == nums[2] || nums[2] == nums[0])\n return "isosceles";\n else\n return "scalene";\n }\n};\n```\n\nIf you found this content helpful, consider giving it an **upvote** and share your thoughts in the comments.\n | 3 | 0 | ['Python', 'C++', 'Java'] | 1 |
type-of-triangle | Easy to Understand | Beats 100% | O(1) | 0ms Runtime🔥🧯🦹🏻♀️ | easy-to-understand-beats-100-o1-0ms-runt-7ata | Intuition : FOR THE LACKWITS!!
equilateral if it has all sides of equal length.
isosceles if it has exactly two sides of equal length.
scalene if all its sides | tyagideepti9 | NORMAL | 2025-01-30T17:10:42.700338+00:00 | 2025-01-30T17:13:28.103898+00:00 | 373 | false | # Intuition : FOR THE LACKWITS!!
- equilateral if it has all sides of equal length.
- isosceles if it has exactly two sides of equal length.
- scalene if all its sides are of different lengths.
- sum of two sides is not greater than third one, then not a valid triangle
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
Check for all the above conditions!
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public string TriangleType(int[] nums) {
if(nums[0]+nums[1] <= nums[2] || nums[1]+nums[2] <= nums[0] || nums[2]+nums[0] <= nums[1]){
return "none";
}
else if(nums[0]==nums[1] && nums[1]==nums[2]){
return "equilateral";
}
else if(nums[0]==nums[1] || nums[0]==nums[2] || nums[1]==nums[2]){
return "isosceles";
}
return "scalene";
}
}
``` | 2 | 0 | ['Array', 'Math', 'Sorting', 'Java', 'C#', 'MS SQL Server'] | 1 |
type-of-triangle | Easy To Understand | Beats 100% | O(1) | 0ms runtime 🔥🧯 | easy-to-understand-beats-100-o1-0ms-runt-kmnp | Intuition - FOR THE LACKWITS!!Two Side Sum < Third Side - Not a Triangle
All Sides Equal - Equilateral
Two Sides Equal - Isosceles
No Side Equal - ScaleneApproa | aman-sagar | NORMAL | 2025-01-30T17:09:46.780862+00:00 | 2025-01-30T17:10:34.887117+00:00 | 252 | false | # Intuition - FOR THE LACKWITS!!
<!-- Describe your first thoughts on how to solve this problem. -->
Two Side Sum < Third Side - Not a Triangle
All Sides Equal - Equilateral
Two Sides Equal - Isosceles
No Side Equal - Scalene
# Approach
<!-- Describe your approach to solving the problem. -->
If if elif elif else else
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def triangleType(self, nums: List[int]) -> str:
x, y, z = nums
if x+y>z and y+z>x and z+x>y:
if x == y == z:
return "equilateral"
elif x == y or y == z or z == x:
return "isosceles"
else:
return "scalene"
else:
return "none"
``` | 2 | 0 | ['Array', 'Math', 'Sorting', 'C++', 'Python3', 'MySQL'] | 1 |
type-of-triangle | easy answer for the questions beats 100% | easy-answer-for-the-questions-beats-100-pzum5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | wfjvxY4Pch | NORMAL | 2024-08-26T17:02:14.322395+00:00 | 2024-08-26T17:02:14.322422+00:00 | 79 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public String triangleType(int[] nums) {\n Arrays.sort(nums);\n int a = nums[0], b = nums[1], c = nums[2];\n if(a+b > c)\n {\n if(a==b)\n {\n if(b==c)\n return "equilateral";\n return "isosceles";\n }\n else if(b==c)\n return "isosceles";\n return "scalene";\n }\n return "none"; \n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
type-of-triangle | Easy Java Solution || Beginner Friendly | easy-java-solution-beginner-friendly-by-jq0ex | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | anikets101 | NORMAL | 2024-04-20T13:53:49.037239+00:00 | 2024-04-20T13:53:49.037288+00:00 | 33 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n private boolean check(int[] nums){\n Arrays.sort(nums);\n return ((nums[0]+nums[1])>nums[2]);\n }\n \n public String triangleType(int[] nums) {\n \n if(check(nums)){\n if(nums[0]==nums[1] && nums[1]==nums[2]){\n return "equilateral";\n } else if((nums[0]==nums[1] && nums[1]!=nums[2]) || (nums[0]==nums[2] && nums[1]!=nums[0]) || (nums[1]==nums[2] && nums[1]!=nums[0])){\n return "isosceles";\n } else{\n return "scalene";\n }\n }\n return "none";\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
type-of-triangle | THE EASIEST SOLUTION FOR YOU | Type of Triangle | 3024 | the-easiest-solution-for-you-type-of-tri-dbkp | \n# Code\n\nclass Solution:\n def triangleType(self, nums: List[int]) -> str:\n ns = set(nums)\n l = len(ns)\n a, b, c = nums[0], nums[1 | JustChis100 | NORMAL | 2024-03-22T13:17:09.579457+00:00 | 2024-03-22T13:17:09.579489+00:00 | 172 | false | \n# Code\n```\nclass Solution:\n def triangleType(self, nums: List[int]) -> str:\n ns = set(nums)\n l = len(ns)\n a, b, c = nums[0], nums[1], nums[2]\n if not (a < b + c and b < a + c and c < b + a) :\n return "none"\n if l == 2 :\n return "isosceles"\n if l == 1 :\n return "equilateral"\n return "scalene"\n```\n## PLS BRO>> | 2 | 0 | ['Array', 'Math', 'Python', 'Python3'] | 1 |
type-of-triangle | MATH || Solution of type of triangle problem | math-solution-of-type-of-triangle-proble-5y7c | Approach\n- Triangle Properties - The sum of the length of the two sides of a triangle is greater than the length of the third side.\n\n# Complexity\n- Time com | tiwafuj | NORMAL | 2024-03-19T15:26:42.387639+00:00 | 2024-04-06T08:53:15.214650+00:00 | 98 | false | # Approach\n- Triangle Properties - The sum of the length of the two sides of a triangle is greater than the length of the third side.\n\n# Complexity\n- Time complexity: O(1) - as all algorithms require constant time \n\n- Space complexity: O(1) - as no extra space is requried\n\n# Code\n```\nclass Solution:\n def triangleType(self, nums: List[int]) -> str:\n nums.sort()\n answer = ["equilateral", "isosceles", "scalene"]\n if nums[2] < nums[0] + nums[1]:\n return answer[len(set(nums)) - 1]\n else:\n return "none"\n``` | 2 | 0 | ['Array', 'Math', 'Sorting', 'Python3'] | 0 |
type-of-triangle | Simple If-else solution | Beginners Friendly | 💯% user's beat | simple-if-else-solution-beginners-friend-p76d | \n\n\n# Approach\nif nums[0]==nums[1]==nums[2]:\nThis line checks if all three sides of the triangle are equal, which would indicate an equilateral triangle.\nr | Pankaj_Tyagi | NORMAL | 2024-02-04T11:38:50.175149+00:00 | 2024-02-05T09:49:36.409483+00:00 | 225 | false | \n\n\n# Approach\nif nums[0]==nums[1]==nums[2]:\nThis line checks if all three sides of the triangle are equal, which would indicate an equilateral triangle.\nreturn "equilateral"\n\nIf the condition in line 1 is true, the function returns "equilateral" because all sides are equal.\nelif (nums[0]+nums[2] > nums[1]) and (nums[0]+nums[1] > nums[2]) and (nums[1]+nums[2] > nums[0]):\n\nThis line checks the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. If this condition is met, it proceeds to the next block.\nif nums[0]==nums[1] or nums[0]==nums[2] or nums[1]==nums[2]:\n\nWithin the valid triangle condition, this line checks if at least two sides are equal, which would indicate an isosceles triangle.\nreturn "isosceles"\n\nIf the condition in line 4 is true, the function returns "isosceles" because at least two sides are equal.\nelse:\n\nIf the condition in line 4 is false (i.e., the triangle has passed the triangle inequality theorem check but doesn\'t have two equal sides), it means the triangle is scalene.\nreturn "scalene"\n\nIf the condition in line 4 is false, the function returns "scalene" because all three sides are different.\nelse:\n\nIf the condition in line 3 is false (i.e., the triangle inequality theorem check fails), the function returns "none" because the sides provided cannot form a valid triangle.\n\n\n# Code\n```\nclass Solution:\n def triangleType(self, nums: List[int]) -> str:\n if nums[0]==nums[1]==nums[2]:\n return "equilateral"\n elif (nums[0]+nums[1] > nums[2]) and (nums[0]+nums[2] > nums[1]) and (nums[1]+nums[2] > nums[0]):\n if nums[0]==nums[1] or nums[0]==nums[2] or nums[1]==nums[2]:\n return "isosceles"\n else:\n return "scalene"\n else:\n return "none"\n``` | 2 | 0 | ['Python', 'Python3'] | 1 |
type-of-triangle | ✅✔️Simple Solution using Triangle Property ✈️✈️✈️ | simple-solution-using-triangle-property-wztql | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ajay_1134 | NORMAL | 2024-02-03T16:08:44.896827+00:00 | 2024-02-03T16:08:44.896922+00:00 | 61 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n \n string triangleType(vector<int>& nums) {\n if(!(nums[0] + nums[1] > nums[2] && nums[1] + nums[2] > nums[0] && nums[0] + nums[2] > nums[1])) return "none";\n if(nums[0] == nums[1] && nums[0] == nums[2]) return "equilateral";\n if(nums[0] == nums[1] || nums[1] == nums[2] || nums[0] == nums[2]) return "isosceles";\n return "scalene";\n }\n};\n``` | 2 | 0 | ['Math', 'C++'] | 0 |
type-of-triangle | a few solutions | a-few-solutions-by-claytonjwong-h416 | Game Plan\n\n\uD83D\uDEAB We cannot form a triangle if the sum of the minimum two side lengths is less-than-or-equal-to the maximum side length.\n \'none\'\n\n\ | claytonjwong | NORMAL | 2024-02-03T16:02:04.901408+00:00 | 2024-02-03T16:56:01.381456+00:00 | 520 | false | # Game Plan\n\n\uD83D\uDEAB We cannot form a triangle if the sum of the minimum two side lengths is less-than-or-equal-to the maximum side length.\n* `\'none\'`\n\n\u2705 Otherwise we return the type of triangle based on the **cardinality of the set of side lengths:**\n\n1. `\'equilateral\'`\n2. `\'isosceles\'`\n3. `\'scalene\'`\n\n---\n\n*Kotlin*\n```\nclass Solution {\n var triangleType = { A: IntArray -> if (A.sorted().slice(0..1).sum() <= A.max()!!) "none" else if (1 == A.toSet().size) "equilateral" else if (2 == A.toSet().size) "isosceles" else "scalene" }\n}\n```\n\n*Javascript*\n```\nlet triangleType = A => _.sum(A.sort((a, b) => a - b).slice(0, 2)) <= Math.max(...A) ? \'none\' : 1 == new Set(A).size ? \'equilateral\' : 2 == new Set(A).size ? \'isosceles\' : \'scalene\';\n```\n\n*Python3*\n```\nclass Solution:\n triangleType = lambda self, A: \'none\' if sum(sorted(A)[:2]) <= max(A) else "equilateral" if len(set(A)) == 1 else "isosceles" if len(set(A)) == 2 else "scalene"\n```\n\n*Rust*\n```\nuse std::collections::HashSet;\nimpl Solution {\n pub fn triangle_type(mut A: Vec<i32>) -> String {\n let f = (|s| String::from(s));\n A.sort();\n let (lo, hi) = (A[0] + A[1], A[2]);\n if lo <= hi {\n return f("none");\n }\n let S: HashSet<i32> = A.drain(..).collect();\n let N = S.len();\n if N == 1 { f("equilateral") } else if N == 2 { f("isosceles") } else { f("scalene") }\n }\n}\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using Set = unordered_set<int>;\n string triangleType(VI& A) {\n sort(A.begin(), A.end());\n auto [lo, hi] = make_pair(A[0] + A[1], A[2]);\n if (lo <= hi)\n return "none";\n auto N = Set{ A.begin(), A.end() }.size();\n return N == 1 ? "equilateral" : N == 2 ? "isosceles" : "scalene";\n }\n};\n```\n\n---\n\n# Supplemental\n\n\uD83D\uDE35 I totally bombed today\'s contest \uD83D\uDC7B\n\n\n\n\uD83E\uDD2A After TLE via Hidden TC for [Q3](https://leetcode.com/problems/maximum-good-subarray-sum/description/), I went back to [Q2](https://leetcode.com/contest/biweekly-contest-123/problems/find-the-number-of-ways-to-place-people-i/) and ran out of time \u231B\uFE0F\n\n\n## Q3: [3026. Maximum Good Subarray Sum](https://leetcode.com/problems/maximum-good-subarray-sum/description/)\n```\n# track previously seen i-th value and index\n\n# then for each current j-th value index, lookup A[j] - K <=== was that previously seen? if so, then consider prefix sums from i..j inclusive for best solution\n\n# class Solution:\n# def maximumSubarraySum(self, A: List[int], K: int, INF = int(1e123)) -> int:\n# best = INF\n# N = len(A)\n# S = [0] * (N + 1)\n# for i in reversed(range(N)):\n# S[i] = S[i + 1] + A[i]\n# m = defaultdict(set)\n# for j in range(N):\n# T = A[j] - K\n# if T in m:\n# for i in m[T]:\n# cand = S[j + 1] - S[i]\n# best = max(best, cand)\n# m[A[j]].add(j)\n# return best if best < INF else 0\n\n# 7:45am - debug code\n\n# [-1,-2,-3,-4], k = 2\n\n# [-10, -9, -7, -4, 0]\n# target: -3\n# not found in m\n# target: -4\n# not found in m\n# target: -5\n# not found in m\n# target: -6\n# not found in m\n# defaultdict(<class \'set\'>, {-1: {0}, -2: {1}, -3: {2}, -4: {3}})\n\n# [-1,3,2,4,5], k = 3\n\n# [13, 14, 11, 9, 5, 0]\n# target: 2\n# not found in m\n# target: 6\n# not found in m\n# target: 5\n# not found in m\n# target: 7\n# not found in m\n# target: 8\n# not found in m\n# defaultdict(<class \'set\'>, {-1: {0}, 3: {1}, 2: {2}, 4: {3}, 5: {4}})\n\n# class Solution:\n# def maximumSubarraySum(self, A: List[int], K: int, INF = -int(1e123)) -> int:\n# best = INF\n# N = len(A)\n# S = [0] * (N + 1)\n# for i in reversed(range(N)):\n# S[i] = S[i + 1] + A[i]\n# print(S)\n# m = defaultdict(set)\n# for j in range(N):\n# T = A[j] + (-K if 0 <= A[j] else K)\n# print(f\'target: {T}\')\n# if T in m:\n# print(\'found in m ok\')\n# for i in m[T]:\n# cand = S[i] - S[j + 1]\n# print(f\'cand: {cand} best: {best}\')\n# best = max(best, cand)\n# else:\n# print(\'not found in m\')\n# m[A[j]].add(j)\n# print(m)\n# print()\n# print()\n# return best if best != INF else 0\n\n# Submission Result: Wrong Answer \n# Input:\n# [1,4,3]\n# 1\n# Output:\n# 0\n# Expected:\n# 7\n\n# [1,4,3]\n# 1\n# Your stdout\n# [8, 7, 3, 0]\n# target: 0\n# not found in m\n# target: 3\n# not found in m\n# target: 2\n# not found in m\n# defaultdict(<class \'set\'>, {1: {0}, 4: {1}, 3: {2}})\n\n# Submission Result: Time Limit Exceeded \n# Last executed input:\n# Hidden for this testcase during contest.\n\n# class Solution:\n# def maximumSubarraySum(self, A: List[int], K: int, INF = -int(1e123)) -> int:\n# best = INF\n# N = len(A)\n# S = [0] * (N + 1)\n# for i in reversed(range(N)):\n# S[i] = S[i + 1] + A[i]\n# m = defaultdict(set)\n# for j in range(N):\n# for offset in [-K, K]:\n# T = A[j] + offset\n# if T in m:\n# for i in m[T]:\n# cand = S[i] - S[j + 1]\n# best = max(best, cand)\n# m[A[j]].add(j)\n# return best if best != INF else 0\n \n# Submission Result: Time Limit Exceeded \n# Last executed input:\n# Hidden for this testcase during contest.\n\n# class Solution:\n# def maximumSubarraySum(self, A: List[int], K: int, INF = -int(1e123)) -> int:\n# best = INF\n# N = len(A)\n# S = [0] * (N + 1)\n# for i in reversed(range(N)):\n# S[i] = S[i + 1] + A[i]\n# m = defaultdict(set)\n# for j in range(N):\n# for offset in [-K, K]:\n# T = A[j] + offset\n# if T in m:\n# for i in m[T]:\n# cand = S[i] - S[j + 1]\n# best = max(best, cand)\n# m[A[j]].add(j)\n# return best if best != INF else 0\n```\n\n## Q2: [3025. Find the Number of Ways to Place People I](https://leetcode.com/problems/find-the-number-of-ways-to-place-people-i/description/)\n```\n# just a linear scan of sorted values?\n\n# so we can have "buckets" per x-coordinate which have sorted y-coordinate\n\n# use rule-of-product? we just need counts per bucket\n\n# Submission Result: Wrong Answer \n# Input:\n# [[0,0],[0,3]]\n# Output:\n# 0\n# Expected:\n# 1\n\n# we are looking for all current x bucket values which are less-than-or-equal-to the lowest previoux x bucket value\n\n# [[1,1],[2,2],[3,3]]\n# pre: -1 last: 1234567890\n# y: 1 in cur: 1\n# pre: 1 last: 1\n# y: 2 in cur: 2\n# last: 1 <= y: 2\n# pre: 2 last: 2\n# y: 3 in cur: 3\n# last: 2 <= y: 3\n\n\n# [[6,2],[4,4],[2,6]]\n\n# 2,6\n# 4,4\n\n# pre: -1 last: 1234567890\n# y: 6 in cur: 2\n# pre: 2 last: 6\n# y: 4 in cur: 4\n# pre: 4 last: 4\n# y: 2 in cur: 6\n\n# from sortedcontainers import SortedList\n# class Solution:\n# def numberOfPairs(self, A: List[List[int]], t = 0, pre = -1) -> int:\n# m = defaultdict(SortedList)\n# for x, y in A:\n# m[x].add(y)\n# for cur in sorted(m.keys()):\n# same = len(m[cur])\n# t += same - 1 # corner case for same bucket\n# last = m[pre][-1] if pre in m else -1234567890\n# print(f\'pre: {pre} last: {last}\')\n# for y in m[cur]:\n# print(f\'y: {y} in cur: {cur}\')\n# if y <= last:\n# print(f\'y: {y} <= last: {last}\')\n# t += 1\n# pre = cur\n# print()\n# print()\n# print()\n# return t\n\n# Submission Result: Wrong Answer \n# Input:\n# [[0,1],[1,3],[6,1]]\n# Output:\n# 1\n# Expected:\n# 2\n\n# from sortedcontainers import SortedList\n# class Solution:\n# def numberOfPairs(self, A: List[List[int]], t = 0, pre = -1) -> int:\n# m = defaultdict(SortedList)\n# for x, y in A:\n# m[x].add(y)\n# for cur in sorted(m.keys()):\n# same = len(m[cur])\n# t += same - 1 # corner case for same bucket\n# last = m[pre][-1] if pre in m else -1234567890\n# for y in m[cur]:\n# if y <= last:\n# t += 1\n# pre = cur\n# return t\n\n# Submission Result: Wrong Answer \n# Input:\n# [[0,5],[4,4],[1,6]]\n# Output:\n# 1\n# Expected:\n# 2\n\n# from sortedcontainers import SortedList\n# class Solution:\n# def numberOfPairs(self, A: List[List[int]], t = 0, pre = -1) -> int:\n# m = defaultdict(SortedList)\n# rows = Counter()\n# for x, y in A:\n# m[x].add(y)\n# rows[y] += 1\n# for cur in sorted(m.keys()):\n# same = len(m[cur])\n# t += same - 1 # corner case for same bucket\n# last = m[pre][0] if pre in m else -1234567890\n# for y in m[cur]:\n# if y < last:\n# t += 1\n# pre = cur\n# for cnt in rows.values():\n# t += cnt - 1\n# return t\n\n# count of bottom-most previous-bucket values above top-most current-bucket values (inclusive)\n\n# [[6,2],[4,4],[2,6]]\n\nfrom sortedcontainers import SortedList\nclass Solution:\n def numberOfPairs(self, A: List[List[int]], t = 0, pre = -1, INF = 1234567890) -> int:\n m = defaultdict(SortedList)\n for x, y in A:\n m[x].add(y)\n seen = []\n for cur in sorted(m.keys()):\n if pre in m:\n bottom = m[pre][0]\n top = m[cur][-1]\n print(f\'bottom: {bottom} top: {top}\')\n i = bisect_left(seen, top)\n print(f\'seen: {seen} t: {t} += len(seen): {len(seen)} - i: {i} = {len(seen) - i}\')\n print()\n t += len(seen) - i\n seen.append(m[cur][0]) # bottom of current\n pre = cur\n return t\n\n# class Solution:\n# def numberOfPairs(self, A: List[List[int]], t = 0, pre = -1) -> int:\n# m = defaultdict(list)\n# for x, y in A:\n# m[x].append(y)\n# for x in m.keys():\n# m[x].sort()\n# for cur in sorted(m.keys()):\n# last = m[pre][-1]\n# for x in m[cur]:\n# if last <= x:\n# t += 1\n# pre = cur\n# return t\n``` | 2 | 0 | ['C++', 'Python3', 'Rust', 'Kotlin', 'JavaScript'] | 2 |
type-of-triangle | Easy Java Solution | easy-java-solution-by-krishn13-fu9z | IntuitionSchool Level Mathematics., if sum of any two sides is greater than the third one, then it is a valid triangle.Approach
nums contains 3 values, denoting | krishn13 | NORMAL | 2025-03-16T07:36:45.644402+00:00 | 2025-03-16T07:36:45.644402+00:00 | 137 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
School Level Mathematics., if sum of any two sides is greater than the third one, then it is a valid triangle.
# Approach
<!-- Describe your approach to solving the problem. -->
1. `nums` contains 3 values, denoting sides of the triangle., so we stored that into three variables, named `a`,`b`and `c`.
2. If all the three sides are equal., its `equilateral`.
3. If all the three sides are different., its `scalene`.
4. Rest, its `isosceles`.
5. If the condition -> sum of any two sides is greater than the third one., becomes false., return `none`.
---
**UPVOTE PLEASE**
---------
---
# Complexity
- Time complexity: $$O(1)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
int a = nums[0], b = nums[1], c = nums[2];
if(a + b > c && b + c > a && c + a > b)
{
if(a==b && b==c && c==a) return "equilateral";
if(a!=b && b!=c && c!=a) return "scalene";
return "isosceles";
}
return "none";
}
}
``` | 1 | 0 | ['Java'] | 0 |
type-of-triangle | Java, Beats 100% | java-beats-100-by-sarn1-4igd | Code | Sarn1 | NORMAL | 2025-03-13T15:49:36.827493+00:00 | 2025-03-13T15:49:36.827493+00:00 | 32 | false |
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
if (nums[0] + nums[1] <= nums[2] || nums[0] + nums[2] <= nums[1] || nums[1] + nums[2] <= nums[0]) return "none";
else if (nums[0] == nums[1] && nums[0] == nums[2]) return "equilateral";
else if (nums[0] == nums[1] || nums[1] == nums[2] || nums[0] == nums[2]) return "isosceles";
else if (nums[0] != nums[1] && nums[1] != nums[2] && nums[0] != nums[2]) return "scalene";
return "none";
}
}
``` | 1 | 0 | ['Java'] | 0 |
type-of-triangle | Mastering Triangle Classification with C++ || Beats 100% || O(1) || Easy for beginners to understand | mastering-triangle-classification-with-c-3clb | IntuitionThe problem requires us to determine the type of triangle that can be formed from three given side lengths. The key conditions to check are:Triangle Va | GeekyRahul04 | NORMAL | 2025-02-26T15:09:05.910744+00:00 | 2025-02-26T15:09:05.910744+00:00 | 103 | false | # Intuition
The problem requires us to determine the type of triangle that can be formed from three given side lengths. The key conditions to check are:
Triangle Validity:
A triangle is only valid if the sum of any two sides is greater than the third side.
This ensures the given lengths satisfy the Triangle Inequality Theorem.
Classifying Triangle Types:
If all three sides are equal → "equilateral".
If only two sides are equal → "isosceles".
If all three sides are different → "scalene".
If the given sides do not form a valid triangle → "none".
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
Step 1: Check Triangle Validity
A valid triangle must satisfy:
nums[0]+nums[1]>nums[2]
nums[1]+nums[2]>nums[0]
nums[0]+nums[2]>nums[1]
If this condition is not met, return "none" immediately.
Step 2: Sort the Array
Sorting ensures a consistent way to compare the sides.
The smallest side is at nums[0], the middle at nums[1], and the largest at nums[2].
Step 3: Classify the Triangle
Equilateral Triangle:
If all three sides are equal (nums[0] == nums[1] == nums[2]), return "equilateral".
Isosceles Triangle:
If any two sides are equal but not all three, return "isosceles".
Scalene Triangle:
If all three sides are different, return "scalene".
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
string triangleType(vector<int>& nums) {
if (nums[0] + nums[1] > nums[2] && nums[1] + nums[2] > nums[0] && nums[0] + nums[2] > nums[1]) {
sort(nums.begin(),nums.end());
if(nums[0]!=nums[1] && nums[1]!=nums[2]) return "scalene";
else if(nums[0] == nums[1] && nums[0] != nums[2] || nums[0] != nums[1] && nums[1] == nums[2] || nums[0] == nums[2] && nums[1] != nums[2]) return "isosceles";
else return "equilateral";
}
else{
return "none";
}
return "none";
}
};
``` | 1 | 0 | ['Array', 'Math', 'Sorting', 'C++'] | 0 |
type-of-triangle | O(1) 🔥 c++ | o1-c-by-varuntyagig-yxu5 | Complexity
Time complexity:
O(1)
Space complexity:
O(1)
Code | varuntyagig | NORMAL | 2025-02-21T06:01:01.781593+00:00 | 2025-02-21T06:01:01.781593+00:00 | 93 | false | # Complexity
- Time complexity:
$$O(1)$$
- Space complexity:
$$O(1)$$
# Code
```cpp []
class Solution {
public:
string triangleType(vector<int>& nums) {
if (nums[0] + nums[1] <= nums[2])
return "none";
if (nums[0] + nums[2] <= nums[1])
return "none";
if (nums[1] + nums[2] <= nums[0])
return "none";
unordered_set<int> store;
for (int i = 0; i < nums.size(); i++) {
store.insert(nums[i]);
}
if (store.size() == 1) {
return "equilateral";
} else if (store.size() == 2) {
return "isosceles";
}
return "scalene";
}
};
``` | 1 | 0 | ['Ordered Set', 'C++'] | 0 |
type-of-triangle | Python soln with thorough explanation | python-soln-with-thorough-explaination-b-vint | IntuitionAfter reading the problem and to solve it efficiently. We can proceed with hashset.ApproachUpon deciding, We chose hashsets as they dont repeat the sam | 9chaitanya11 | NORMAL | 2025-02-06T08:26:04.311667+00:00 | 2025-02-06T08:47:28.489430+00:00 | 69 | false | # Intuition
After reading the problem and to solve it efficiently. We can proceed with hashset.
# Approach
Upon deciding, We chose hashsets as they dont repeat the same value again. So, if a triangle has all three sides as {3,3,3}, the hashset will only store one 3. By which, we can conclude that the given triangle is equilateral.
Same goes for the other two. If the triangle has 2 same sides and one differen (3,3,4).The hashset will store only 2 values which tell us that it's an isosceles. And if the triangle has three different sides {3,4,5}, The hashset will store all three different values which tell us that this triangle is scalene.
We also have to look for a fact that the one side of the triangle is not greater or equal to the other two sides. If it is, we can't called it a triangle. So, we make a hashset name tri. Loop it and get the elmts. After that, we get its length which in turn, solves the problem.
# Complexity
- Time complexity:
O(1) is constant because we are only looping through the nums which is 3 times.
- Space complexity:
O(1) is constant because we are using a hashset whose value will not exceed 3.
# Code
```python3 []
class Solution:
def triangleType(self, nums: List[int]) -> str:
if nums[0] >= nums[1] + nums[2] or nums[1] >= nums[0] + nums[2] or nums[2] >= nums[0] + nums[1]:
return "none"
tri = set()
for i in nums:
tri.add(i)
length = len(tri)
if length == 1:
return "equilateral"
elif length == 2:
return "isosceles"
else:
return "scalene"
``` | 1 | 0 | ['Python3'] | 0 |
type-of-triangle | 3 LINES JAVA CODE BEATING 100% | 3-lines-java-code-beating-100-by-arshi_b-zc23 | Complexity
Time complexity: O(1)
Space complexity: O(1)
Code | arshi_bansal | NORMAL | 2025-01-09T07:54:04.905663+00:00 | 2025-01-09T07:54:04.905663+00:00 | 208 | false | # Complexity
- Time complexity: O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution{
public String triangleType(int[] nums){
if(nums[0]+nums[1]<=nums[2]||nums[1]+nums[2]<=nums[0]||nums[0]+nums[2]<=nums[1]){
return "none";
}
if(nums[0]==nums[1]&&nums[1]==nums[2]){
return "equilateral";
}
if(nums[0]==nums[1]||nums[1]==nums[2]||nums[0]==nums[2]){
return "isosceles";
}
return "scalene";
}
}
``` | 1 | 0 | ['Java'] | 0 |
type-of-triangle | O(1) Python Solution Using Sets | o1-python-solution-using-sets-by-odysseu-7foa | IntuitionA set is list of distinct objects. So that can help observe how many sides are the same since a repeated side will be deleted and that could be observe | Odysseus_v01 | NORMAL | 2024-12-28T03:26:18.645132+00:00 | 2024-12-28T03:26:18.645132+00:00 | 116 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
A set is list of distinct objects. So that can help observe how many sides are the same since a repeated side will be deleted and that could be observed in the length of the set.
# Approach
<!-- Describe your approach to solving the problem. -->
The the list of lengths is made into a set. Then first if statement is there so that it is possible the triangle can exist using the triangle inequality theorem. If the length of the set is 1 that means all the lengths are the same. That means the triangle is equilateral. If the lengths are two, then two sides are the same. That means the triangle is an isosceles. Lastly if the length is 3 all the sides are distinct. That means the triangle is scalene.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(1)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(1)$$
# Code
```python3 [Code]
class Solution:
def triangleType(self, nums: List[int]) -> str:
nums1 = set(nums)
if (nums[0] + nums[1] <= nums[2]) or (nums[2] + nums[1] <= nums[0]) or (nums[0] + nums[2] <= nums[1]):
return "none"
else:
if len(nums1) == 1:
return "equilateral"
elif len(nums1) == 2:
return "isosceles"
else:
return "scalene"
``` | 1 | 0 | ['Python3'] | 1 |
type-of-triangle | 0 ms || BEATS 100% | 0-ms-beats-100-by-deepakk2510-zxtc | Code | deepakk2510 | NORMAL | 2024-12-16T09:28:10.780815+00:00 | 2024-12-16T09:28:10.780815+00:00 | 197 | false | \n# Code\n```cpp []\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n if((nums[0]==nums[1]) && (nums[1]==nums[2])) return "equilateral";\n sort(nums.begin(),nums.end()); \n if((nums[0]+nums[1])>nums[2]){\n if((nums[0]==nums[1]) || (nums[1]==nums[2]) || (nums[0]==nums[2])) return "isosceles";\n else\n return "scalene";\n }\n return "none";\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
type-of-triangle | 0ms very easy java code | 0ms-very-easy-java-code-by-galani_jenis-zr9x | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Galani_jenis | NORMAL | 2024-12-15T04:06:36.552956+00:00 | 2024-12-15T04:06:36.552956+00:00 | 165 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public String triangleType(int[] nums) {\n if ( nums[0] + nums[1] <= nums[2] || nums[0] + nums[2] <= nums[1] || nums[2] + nums[1] <= nums[0]) { return "none";}\n else if (nums[0] == nums[1] && nums[1] == nums[2]) { return "equilateral"; }\n else if (nums[0] == nums[1] || nums[1] == nums[2] || nums[0] == nums[2]) { return "isosceles";}\n return "scalene";\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
type-of-triangle | Very easy code 0ms 100% beat java code | very-easy-code-0ms-100-beat-java-code-by-ci2d | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Galani_jenis | NORMAL | 2024-12-15T04:05:20.493141+00:00 | 2024-12-15T04:05:20.493141+00:00 | 88 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public String triangleType(int[] nums) {\n if ( nums[0] + nums[1] <= nums[2] || nums[0] + nums[2] <= nums[1] || nums[2] + nums[1] <= nums[0]) {\n return "none";\n }\n else if (nums[0] == nums[1] && nums[1] == nums[2]) { return "equilateral";\n }\n else if (nums[0] == nums[1] || nums[1] == nums[2] || nums[0] == nums[2]) {\n return "isosceles";\n }\n return "scalene";\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
type-of-triangle | C++ Simple 4-line Solution | c-simple-4-line-solution-by-yehudisk-cw9a | Intuition\nSimply check all conditions.\n\n# Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(1)\n\n# Code\ncpp []\nclass Solution {\npublic:\n s | yehudisk | NORMAL | 2024-11-26T13:40:42.698245+00:00 | 2024-11-26T13:40:42.698328+00:00 | 70 | false | # Intuition\nSimply check all conditions.\n\n# Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(1)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n if ((nums[0] + nums[1] <= nums[2]) || (nums[0] + nums[2] <= nums[1]) || (nums[1] + nums[2] <= nums[0])) return "none";\n if (nums[0] == nums[1] && nums[1] == nums[2]) return "equilateral";\n if (nums[0] == nums[1] || nums[1] == nums[2] || nums[0] == nums[2]) return "isosceles";\n return "scalene";\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
type-of-triangle | Easy solution | 100% beats | easy-solution-100-beats-by-ravindran_s-t48c | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | RAVINDRAN_S | NORMAL | 2024-11-11T05:17:27.144598+00:00 | 2024-11-11T05:17:27.144637+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n bool check(vector<int>& nums){\n if (nums[0]+nums[1]>nums[2] && nums[0]+nums[2]>nums[1] && nums[1]+nums[2]>nums[0]){\n return true;\n }\n return false;\n \n }\n string triangleType(vector<int>& nums) {\n if (nums[0]==nums[1] && nums[1]==nums[2]){\n return "equilateral";\n } if (check(nums)){\n if (nums[0]!=nums[1] && nums[1]!=nums[2] && nums[0]!=nums[2]){\n return "scalene";\n } else if (nums[0]==nums[1]!=nums[2]|| nums[1]==nums[2]!=nums[0]|| nums[0]==nums[2]!=nums[1]){\n return "isosceles";\n }\n }\n return "none";\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
type-of-triangle | Type of Triangle | type-of-triangle-by-tejdekiwadiya-sr9b | Intuition\nThe problem requires determining the type of a triangle based on the lengths of its sides. A triangle can be categorized as:\n- Equilateral: All thre | tejdekiwadiya | NORMAL | 2024-10-21T16:25:42.577915+00:00 | 2024-10-21T16:25:42.577940+00:00 | 74 | false | # Intuition\nThe problem requires determining the type of a triangle based on the lengths of its sides. A triangle can be categorized as:\n- **Equilateral**: All three sides are equal.\n- **Isosceles**: Two sides are equal.\n- **Scalene**: All sides are different.\n- **None**: If the sides don\'t form a valid triangle.\n\nMy first thought is to use the triangle inequality theorem, which ensures that the sum of the lengths of any two sides must be greater than the length of the third side. Sorting the array of side lengths simplifies the logic for checking this condition and for comparing the sides.\n\n# Approach\n1. **Sort the Array**: First, sort the array to easily apply the triangle inequality theorem (`nums[0] + nums[1] > nums[2]`).\n \n2. **Check Validity**: After sorting, check whether the sides form a valid triangle by verifying that the sum of the two smaller sides is greater than the third side.\n\n3. **Classify the Triangle**: \n - If all sides are equal, it\'s an **equilateral** triangle.\n - If two sides are equal, it\'s an **isosceles** triangle.\n - If all sides are different, it\'s a **scalene** triangle.\n\n4. **Return Result**: If the triangle doesn\'t meet the validity condition, return `"none"`. Otherwise, classify it based on the side lengths.\n\n# Complexity\n- **Time complexity**: \n - Sorting the array takes (O(log n)) for (n = 3), but this simplifies to constant time, (O(1)), for a fixed-size array of 3 elements.\n - The triangle classification itself is constant time, so overall complexity is **(O(1))**.\n \n- **Space complexity**: \n - Sorting is in-place, so the only space used is constant, (O(1)).\n\n# Code\n```java []\nclass Solution {\n public String triangleType(int[] nums) {\n // Sort the array to make the logic clearer\n Arrays.sort(nums);\n\n // Check for a valid triangle first (triangle inequality)\n if (nums[0] + nums[1] <= nums[2]) {\n return "none";\n }\n\n // Check for equilateral\n if (nums[0] == nums[1] && nums[1] == nums[2]) {\n return "equilateral";\n }\n\n // Check for isosceles\n if (nums[0] == nums[1] || nums[1] == nums[2] || nums[0] == nums[2]) {\n return "isosceles";\n }\n\n // If it\'s not equilateral or isosceles, it must be scalene\n return "scalene";\n }\n}\n``` | 1 | 0 | ['Array', 'Math', 'Sorting', 'Java'] | 0 |
type-of-triangle | Simplest logic!! 0ms runtime :) | simplest-logic-0ms-runtime-by-raana_01-2yzt | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Raana_01 | NORMAL | 2024-10-20T07:09:49.882534+00:00 | 2024-10-20T07:09:49.882560+00:00 | 98 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def triangleType(self, nums: List[int]) -> str:\n if not (nums[0] + nums[1] > nums[2] and nums[1] + nums[2] > nums[0] and nums[0] + nums[2] >nums[1]) :\n return "none"\n if nums[0] == nums[1] == nums[2] :\n return "equilateral"\n elif nums[0] != nums[1] and nums[1] != nums[2] and nums[2] != nums[0] :\n return "scalene"\n else:\n return "isosceles"\n``` | 1 | 0 | ['Python3'] | 0 |
type-of-triangle | Easy Solution | easy-solution-by-shamnad_skr-x3i1 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shamnad_skr | NORMAL | 2024-09-18T11:43:10.966855+00:00 | 2024-09-18T11:43:10.966884+00:00 | 51 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```typescript []\nfunction triangleType(nums: number[]): string {\n\n const [a, b, c] = nums; //here i assigned values to this variables to easy calculation\n\n \n if (a + b <= c || a + c <= b || b + c <= a) {\n return "none"; // Not a valid triangle\n }\n\n // Classify the triangle\n if (a === b && b === c) {\n return "equilateral"; // All sides are equal\n } \n if (a === b || b === c || a === c) {\n return "isosceles"; // Two sides are equal\n }\n \n return "scalene"; // All sides are different\n \n};\n``` | 1 | 0 | ['TypeScript', 'JavaScript'] | 0 |
type-of-triangle | PYTHON | python-by-kanvapuri_sai_praneetha-8tsx | Code\n\nclass Solution:\n def triangleType(self, nums: List[int]) -> str:\n if len(nums)==3 and nums[0]<nums[1]+nums[2] and nums[1]<nums[0]+nums[2] an | kanvapuri_sai_praneetha | NORMAL | 2024-08-05T18:51:05.716653+00:00 | 2024-08-05T18:51:05.716689+00:00 | 64 | false | # Code\n```\nclass Solution:\n def triangleType(self, nums: List[int]) -> str:\n if len(nums)==3 and nums[0]<nums[1]+nums[2] and nums[1]<nums[0]+nums[2] and nums[2]<nums[1]+nums[0]:\n if len(set(nums))==1:\n return "equilateral"\n elif len(set(nums))==2:\n return "isosceles"\n else:\n return "scalene"\n return "none" \n \n``` | 1 | 0 | ['Python3'] | 1 |
type-of-triangle | Python solution in easy steps | python-solution-in-easy-steps-by-shubhas-v07l | \n\nclass Solution:\n def triangleType(self, nums: List[int]) -> str:\n \n if nums[0] + nums[1] > nums[2] and nums[0] + nums[2] > nums[1] and n | Shubhash_Singh | NORMAL | 2024-08-04T11:56:50.357419+00:00 | 2024-08-04T11:56:50.357453+00:00 | 14 | false | \n```\nclass Solution:\n def triangleType(self, nums: List[int]) -> str:\n \n if nums[0] + nums[1] > nums[2] and nums[0] + nums[2] > nums[1] and nums[1] + nums[2] > nums[0]:\n if nums[0]==nums[1] and nums[1] == nums[2]:\n return "equilateral"\n elif nums[0] != nums[1] and nums[0] != nums[2] and nums[1] != nums[2]:\n return "scalene"\n else:\n return "isosceles"\n else:\n return "none"\n``` | 1 | 0 | ['Python3'] | 0 |
type-of-triangle | Easy Java / C++ Solution (😍100% Beats Runtime in Java) 😎😎 -> 😮😮 | easy-java-c-solution-100-beats-runtime-i-629p | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n1. For "equilateral" tr | jeeleej | NORMAL | 2024-07-26T18:30:04.573702+00:00 | 2024-07-26T18:30:04.573740+00:00 | 30 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. For `"equilateral"` triangle all size of triangle is same so **num[0]==nums[1]==nums[2]** is the condition for that.\n2. For `"isosceles"` triangle any two side of the triangle would be same and triangle\'s any two side\'s sum is always greater then remaining third side is the condition for it.\n3. For `"scalene"` triangle only condition is that triangle\'s any two side\'s sum is always greater then remaining third side.\n4. If none of the above condition is true then the given three side doesn\'t make triangle so in that case return `"none"`.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code for Java\n```\nclass Solution {\n public String triangleType(int[] nums) {\n \n if(nums[0]==nums[1] && nums[1]==nums[2])\n return ("equilateral");\n\n else if(\n (nums[0]==nums[1] || nums[0]==nums[2] || nums[1]==nums[2])\n && nums[0]+nums[1]>nums[2] && nums[0]+nums[2]>nums[1]\n && nums[2]+nums[1]>nums[0])\n return ("isosceles");\n\n else if(nums[0]+nums[1]>nums[2] && nums[0]+nums[2]>nums[1]\n && nums[2]+nums[1]>nums[0])\n return ("scalene");\n\n else\n return ("none");\n }\n}\n```\n\n# Code for C++\n```\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n \n if(nums[0]==nums[1] && nums[1]==nums[2])\n return ("equilateral");\n\n else if(\n (nums[0]==nums[1] || nums[0]==nums[2] || nums[1]==nums[2])\n && nums[0]+nums[1]>nums[2] && nums[0]+nums[2]>nums[1]\n && nums[2]+nums[1]>nums[0])\n return ("isosceles");\n\n else if(nums[0]+nums[1]>nums[2] && nums[0]+nums[2]>nums[1]\n && nums[2]+nums[1]>nums[0])\n return ("scalene");\n\n else\n return ("none");\n }\n};\n```\n | 1 | 0 | ['Array', 'C++', 'Java'] | 0 |
type-of-triangle | Simple Easy to Understand Java Code | simple-easy-to-understand-java-code-by-s-8mz1 | Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(1)\n# Code\n\nclass Solution {\n public String triangleType(int[] nums) {\n if(nums[0] == | Saurabh_Mishra06 | NORMAL | 2024-06-24T12:53:33.379685+00:00 | 2024-06-24T12:53:33.379719+00:00 | 136 | false | # Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(1)\n# Code\n```\nclass Solution {\n public String triangleType(int[] nums) {\n if(nums[0] == nums[1] && nums[1] == nums[2]){\n return "equilateral";\n }\n if(nums[0] + nums[1] <= nums[2] || nums[1] + nums[2] <= nums[0] || nums[0] + nums[2] <= nums[1]){\n return "none";\n }\n if(nums[0] == nums[1] || nums[1] == nums[2] || nums[0] == nums[2]){\n return "isosceles";\n }\n return "scalene";\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.