question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
type-of-triangle | Best Java Submission for Logic ✅️🍀 | best-java-submission-for-logic-by-atharv-ddqf | Best Java Solution using If Else only\n\n\n**** | AtharvaKote81 | NORMAL | 2024-05-14T08:58:48.005224+00:00 | 2024-05-14T08:58:48.005260+00:00 | 29 | false | Best Java Solution using If Else only\n\n\n**** | 1 | 0 | [] | 0 |
type-of-triangle | Array destructure | array-destructure-by-phyapanchakpram-ovf7 | \nvar triangleType = function(nums) {\n [a,b,c]= nums;\n if((a+b)<=c || (b+c) <= a || (c+a) <= b) return \'none\'\n else if(a===b && b===c && c===a) re | phyapanchakpram | NORMAL | 2024-05-07T12:01:35.249763+00:00 | 2024-05-07T12:01:35.249796+00:00 | 10 | false | ```\nvar triangleType = function(nums) {\n [a,b,c]= nums;\n if((a+b)<=c || (b+c) <= a || (c+a) <= b) return \'none\'\n else if(a===b && b===c && c===a) return \'equilateral\'\n else if(a !== b && b !== c && c !== a) return \'scalene\'\n else return \'isosceles\'\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
type-of-triangle | image solution provide || 5++ language||c||java||javascript||c++||array|| | image-solution-provide-5-languagecjavaja-dgag | Approach\n Describe your approach to solving the problem. \n1. we sort the array then we check nums[0]+nums[1]>nums[2]if this condition is satisfy then we check | ANKITBI1713 | NORMAL | 2024-03-10T04:44:51.528527+00:00 | 2024-03-10T04:44:51.528549+00:00 | 616 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n1. we sort the array then we check nums[0]+nums[1]>nums[2]if this condition is satisfy then we check which type of triangle is given\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# using java \n# Code\n```\nclass Solution {\n public String triangleType(int[] nums) {\n Arrays.sort(nums);\n if (nums[0]+nums[1]>nums[2]){\n if (nums[0]==nums[1]&&nums[1]==nums[2]){\n return "equilateral";\n } \n else if (nums[0]==nums[1]||nums[1]==nums[2]||nums[0]==nums[2]){\n return "isosceles";\n } \n else{\n return "scalene";\n }\n } \n return "none";\n }\n}\n```\n# using c \n# Code\n```\n char* triangleType(int* nums, int numsSize) {\n int compare(const void* a, const void* b) \n {\n return (*(int*)a - *(int*)b);\n }\n qsort(nums, numsSize, sizeof(int), compare);\n if (nums[0]+nums[1]>nums[2]){\n if (nums[0]==nums[1]&&nums[1]==nums[2]){\n return "equilateral";\n } \n else if (nums[0]==nums[1]||nums[1]==nums[2]||nums[0]==nums[2]){\n return "isosceles";\n } \n else{\n return "scalene";\n }\n } \n return "none";\n}\n``` | 1 | 0 | ['Array', 'Math', 'C', 'Python', 'C++', 'Java'] | 1 |
type-of-triangle | [TypeScript] Sort solution. No If-Then. | typescript-sort-solution-no-if-then-by-b-6dri | Complexity\nBiggest side must be strictly less then sum of two other.\n\n# Code\n\nconst triangleType = (nums: number[]): string => {\n const triangles = [\' | badnewz | NORMAL | 2024-03-08T17:46:05.735348+00:00 | 2024-03-08T17:46:05.735395+00:00 | 5 | false | # Complexity\nBiggest side must be *strictly* less then sum of two other.\n\n# Code\n```\nconst triangleType = (nums: number[]): string => {\n const triangles = [\'none\', \'equilateral\', \'isosceles\', \'scalene\'];\n nums.sort((a, b) => b - a);\n return triangles[nums[0] < nums[1] + nums[2] ? (new Set(nums)).size : 0];\n};\n``` | 1 | 0 | ['Math', 'TypeScript'] | 0 |
type-of-triangle | Concise Kotlin solution | concise-kotlin-solution-by-yuanruqian-rxcl | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | yuanruqian | NORMAL | 2024-02-27T21:49:15.529871+00:00 | 2024-02-27T21:49:15.529903+00:00 | 13 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n fun triangleType(nums: IntArray): String {\n nums.sort()\n \n if(nums[0] + nums[1] <= nums[2]) {\n return "none"\n }\n \n val counterMap = nums.toTypedArray().groupingBy { it }.eachCount()\n\n return when (counterMap.size) {\n 1 -> "equilateral"\n 2 -> "isosceles"\n else -> "scalene"\n }\n }\n}\n``` | 1 | 0 | ['Kotlin'] | 0 |
type-of-triangle | Easy C // C++ // Java Solution Beats 100% | easy-c-c-java-solution-beats-100-by-edwa-y9aq | Intuition\n\nJava []\nclass Solution {\n public String triangleType(int[] nums) {\n int a = nums[0];\n int b = nums[1];\n int c = nums[2 | Edwards310 | NORMAL | 2024-02-10T13:31:28.281976+00:00 | 2024-02-10T13:31:28.282015+00:00 | 65 | false | # Intuition\n\n```Java []\nclass Solution {\n public String triangleType(int[] nums) {\n int a = nums[0];\n int b = nums[1];\n int c = nums[2];\n\n if (a == b && b == c)\n return "equilateral";\n if ((a == b && a + b > c) || (b == c && b + c > a) || (a == c && a + c > b))\n return "isosceles";\n if (a + b > c && b + c > a && a + c > b)\n return "scalene";\n\n return "none";\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n if (nums[2] >= nums[0] + nums[1])\n return "none";\n \n return nums[0] == nums[2] ? "equilateral": nums[0] == nums[1] || nums[1] == nums[2] ? "isosceles" : "scalene";\n }\n};\n```\n```C []\nchar* triangleType(int* nums, int numsSize) {\n int a = nums[0];\n int b = nums[1];\n int c = nums[2];\n\n if (a == b && b == c)\n return "equilateral";\n if ((a == b && a + b > c) || (b == c && b + c > a) || (a == c && a + c > b))\n return "isosceles";\n if (a + b > c && b + c > a && a + c > b)\n return "scalene";\n\n return "none";\n}\n```\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\nclass Solution {\n public String triangleType(int[] nums) {\n int a = nums[0];\n int b = nums[1];\n int c = nums[2];\n\n if (a == b && b == c)\n return "equilateral";\n if ((a == b && a + b > c) || (b == c && b + c > a) || (a == c && a + c > b))\n return "isosceles";\n if (a + b > c && b + c > a && a + c > b)\n return "scalene";\n\n return "none";\n }\n}\n```\n# Please upvote if it\'s helpful... | 1 | 0 | ['C', 'C++', 'Java'] | 0 |
type-of-triangle | Type Of Triangle 2 | type-of-triangle-2-by-suyog_30-hzhz | Intuition\n Describe your first thoughts on how to solve this problem. \nThe code checks whether the given lengths of sides form a valid triangle or not by veri | suyog_30 | NORMAL | 2024-02-08T18:13:39.739903+00:00 | 2024-02-08T18:13:39.739935+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code checks whether the given lengths of sides form a valid triangle or not by verifying the triangle inequality theorem. Then, it further checks for the type of triangle based on the equality of sides.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe code first checks if the given lengths can form a triangle or not. If they do, it proceeds to check the type of triangle based on the lengths of its sides. It considers three cases: scalene (no sides are equal), equilateral (all sides are equal), and isosceles (two sides are equal).\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this code is O(1) because it performs a constant number of comparisons and operations regardless of the size of the input array (which is always of size 3).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this code is also O(1) because it uses a constant amount of extra space. The space used does not grow with the size of the input array.\n# Code\n```\nclass Solution {\n public String triangleType(int[] nums) {\n if(nums[0] + nums[1] > nums[2] && nums[1] + nums[2] > nums[0] && nums[2] + nums[0] > nums[1]){\n if (nums[0]!=nums[1] && nums[1]!=nums[2] && nums[0]!=nums[2]){\n return "scalene";\n }else if(nums[0]==nums[1] && nums[1] == nums[2]){ \n return "equilateral";\n }else{\n return "isosceles";\n }\n }else{\n return "none";\n }\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
type-of-triangle | Easy C++ Solution || Beats 100% ✅✅ | easy-c-solution-beats-100-by-abhi242-4vnv | Code\n\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n if(nums[0]>=(nums[1]+nums[2]) || nums[1]>=(nums[0]+ nums[2]) || nums[2] | Abhi242 | NORMAL | 2024-02-07T20:18:39.331283+00:00 | 2024-02-07T20:18:39.331306+00:00 | 16 | false | # Code\n```\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n if(nums[0]>=(nums[1]+nums[2]) || nums[1]>=(nums[0]+ nums[2]) || nums[2]>=(nums[0]+nums[1])){\n return "none";\n }\n if(nums[0]==nums[1] && nums[1]==nums[2]){\n return "equilateral";\n }\n if(nums[0]==nums[1] || nums[1]==nums[2] || nums[0]==nums[2]){\n return "isosceles";\n }\n return "scalene";\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
type-of-triangle | ✅Beats 100.00% of users || Best Method🔥 || C# || Easy Explanation || Beginner Friendly🔥🔥🔥 | beats-10000-of-users-best-method-c-easy-c6cmy | Intuition\n- Problem: Determine the type of triangle that can be formed from three given side lengths.\n- Approach: Sort the lengths, check triangle inequality | Sayan98 | NORMAL | 2024-02-04T11:40:56.619509+00:00 | 2024-02-04T11:40:56.619535+00:00 | 87 | false | # Intuition\n- **Problem**: Determine the type of triangle that can be formed from three given side lengths.\n- **Approach**: Sort the lengths, check triangle inequality and side equality conditions to classify the triangle.\n\n\n\n\n# Approach\n- Sort the lengths: Ensure smallest to largest order for easier comparisons.\n- Check triangle inequality: If the sum of the two shortest sides is less than or equal to the longest side, no triangle can be formed ("**none**").\n- Check for equilateral: If all three sides are equal, it\'s an equilateral triangle ("**equilateral**").\n- Check for isosceles: If any two sides are equal, it\'s an isosceles triangle ("**isosceles**").\n- Otherwise, it\'s a scalene triangle: All sides have different lengths ("**scalene**").\n\n# Complexity\n- Time complexity:\n - O(N log N), dominated by the sorting algorithm (Array.Sort()).\n - The remaining comparisons and logic take constant time.\n\n- Space complexity:\n - O(1), constant space.\n\n# Code\n```\npublic class Solution {\n public string TriangleType(int[] nums) {\n \n Array.Sort(nums);\n \n if( nums[0] + nums[1] <= nums[2]) return "none";\n else if(nums[0] == nums[1] && nums[0] == nums[2]) return "equilateral";\n else if(nums[0] == nums[1] || nums[1] == nums[2]) return "isosceles";\n else return "scalene";\n }\n}\n``` | 1 | 0 | ['Sorting', 'C#'] | 0 |
type-of-triangle | Easy Solution - no Sorting | easy-solution-no-sorting-by-shivamtiwari-m77v | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ShivamTiwari214 | NORMAL | 2024-02-04T09:32:14.716349+00:00 | 2024-02-04T09:32:14.716375+00:00 | 355 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n\n // To check if the tirangle is valid of not \n if(nums[0] + nums[1] <= nums[2] || nums[1] + nums[2] <= nums[0] || nums[0] + nums[2] <= nums[1]) return "none" ;\n \n // To check if the tirangle is Equilateral or not \n else if ( nums[0]==nums[1]&& nums[1]==nums[2] ) return "equilateral" ;\n\n // To check if the triangle is Isosceles or not \n else if ( nums[0] == nums[1] || nums[1]== nums[2] || nums[0] == nums[2]) return "isosceles" ;\n\n // If the triangle is neither isosceles nor Equilateral and is a valid triangle then it is Scalene \n return "scalene";\n }\n};\n``` | 1 | 0 | ['Array', 'Math', 'C++'] | 0 |
type-of-triangle | Simple with java using HashMap(100% Faster Solution). | simple-with-java-using-hashmap100-faster-jkmu | Intuition\n- When I understand this problem,Then firstly HashMap Data Structure was come to mind and then I started work with HashMap and I got better result;\ | shubh_hacker_01 | NORMAL | 2024-02-04T06:53:13.151874+00:00 | 2024-02-04T06:53:53.597310+00:00 | 15 | false | # Intuition\n- When I understand this problem,Then firstly HashMap Data Structure was come to mind and then I started work with HashMap and I got better result;\n\n# Approach\n- Take a HashMap and put all the possible sum of array with condition(as you are see in code).\n- Then check simply if map size is 1 then simply return "equilateral" else if map size is 2 then return "isosceles" else simply return "scalene";\n\n# Complexity\n- Time complexity:\n O(1);\n\n- Space complexity:\n- o(3);\n\n# Code\n```\nclass Solution {\n public String triangleType(int[] nums) {\n \n HashMap<Integer,Integer>map=new HashMap<>();\n\n int x=nums[0]+nums[1];\n int y=nums[0]+nums[2];\n int z=nums[1]+nums[2];\n if(x>nums[2]) \n map.put(x,1);\n else\n return "none";\n if(y>nums[1])\n map.put(y,1);\n else \n return "none";\n if(z>nums[0])\n map.put(z,1);\n else\n return "none";\n if(map.size()==1)\n return "equilateral";\n else if(map.size()==2)\n return "isosceles";\n return "scalene";\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
type-of-triangle | C++ easy solution using hash table 🔥 | c-easy-solution-using-hash-table-by-hk34-tooc | Intuition\n Describe your first thoughts on how to solve this problem. \nwe have to check for properties -\n-> if equilateral triangle, all sides equal\n-> if i | hk342064 | NORMAL | 2024-02-04T06:51:09.042453+00:00 | 2024-02-04T06:51:09.042481+00:00 | 156 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe have to check for properties -\n-> if equilateral triangle, all sides equal\n-> if isosceles triangle, two sides equal and sum of two sides are greater than third side\n-> if scalene triangle, none of the sides are equal and sum of two sides are greater than third side\n\nSo , we can store the sides of triangle in a map DS to check-\n\n \n# Approach\n<!-- Describe your approach to solving the problem. -->\ncreate a unordered map to store the values then check for these value.\n map size=1 means all sides are equal\n eg - [3,3,3] map stores -[3->3] so map size is one when all sides are equal\n map size=2 means two sides are equal \n eq - [5,4,4] map stores -[5->1,4->2] so map size is two when two sides are equal\n else all sides are not equal\n\nIn scalene and isosceles , we have to check for one more condition that sum of the two sides is greater than the third side.\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n unordered_map<int,int> mpp;\n \n mpp[nums[0]]++;\n mpp[nums[1]]++;\n mpp[nums[2]]++;\n \n if(mpp.size()==1){\n return "equilateral";\n }\n else if(mpp.size()==2){\n if(nums[0]+nums[1]>nums[2] && nums[0]+nums[2]>nums[1] && nums[2]+nums[1]>nums[0]){\n return "isosceles";\n }\n }\n else{\n if(nums[0]+nums[1]>nums[2] && nums[0]+nums[2]>nums[1] && nums[2]+nums[1]>nums[0]){\n return "scalene";\n }\n }\n return "none";\n }\n};\n``` | 1 | 0 | ['Hash Table', 'C++'] | 0 |
type-of-triangle | [JavaScript] - easy solution | javascript-easy-solution-by-qusinn-q3em | Complexity\n- Time complexity: O(1)\n- Space complexity: O(1)\n\n# Code\n\n/**\n * @param {number[]} nums\n * @return {string}\n */\nvar triangleType = function | qusinn | NORMAL | 2024-02-03T16:59:46.289374+00:00 | 2024-02-03T17:18:11.098379+00:00 | 107 | false | # Complexity\n- Time complexity: $$O(1)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\n/**\n * @param {number[]} nums\n * @return {string}\n */\nvar triangleType = function(nums) {\n nums.sort((a, b) => a - b);\n if (nums[0] + nums[1] <= nums[2]) {\n return \'none\';\n }\n if (nums[0] === nums[1] && nums[1] === nums[2]) {\n return \'equilateral\';\n }\n if (nums[0] === nums[1] || nums[1] === nums[2]) {\n return \'isosceles\';\n }\n return \'scalene\';\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
type-of-triangle | Sort & Conditions!! | sort-conditions-by-hustle_code-3vlq | \nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n\n if (nums[0] + nums[1] > nums[2]) {\n | hustle_code | NORMAL | 2024-02-03T16:54:12.500500+00:00 | 2024-02-03T16:54:12.500520+00:00 | 105 | false | ```\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n\n if (nums[0] + nums[1] > nums[2]) {\n if (nums[0] == nums[1] && nums[1] == nums[2]) {\n return "equilateral";\n } else if (nums[0] == nums[1] || nums[1] == nums[2]) {\n return "isosceles";\n } else {\n return "scalene";\n }\n } else {\n return "none";\n }\n }\n};\n``` | 1 | 0 | ['C', 'Sorting'] | 0 |
type-of-triangle | Clean✓ Java Solution🔥||🔥LeetCode BiWeekly Challenges🔥 | clean-java-solutionleetcode-biweekly-cha-f460 | Complexity\n- Time complexity:O(sorting)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(1)\n Add your space complexity here, e.g. O(n) \n\n | Shree_Govind_Jee | NORMAL | 2024-02-03T16:43:23.807319+00:00 | 2024-02-03T16:43:23.807345+00:00 | 126 | false | # Complexity\n- Time complexity:$$O(sorting)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n private boolean check(int[] nums){\n Arrays.sort(nums);\n return ((nums[0]+nums[1])>nums[2]);\n }\n \n public String triangleType(int[] nums) {\n \n if(check(nums)){\n if(nums[0]==nums[1] && nums[1]==nums[2]){\n return "equilateral";\n } else if((nums[0]==nums[1] && nums[1]!=nums[2]) || (nums[0]==nums[2] && nums[1]!=nums[0]) || (nums[1]==nums[2] && nums[1]!=nums[0])){\n return "isosceles";\n } else{\n return "scalene";\n }\n }\n return "none";\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
type-of-triangle | Short Code || HashSet || 1ms 🔥🔥|| Please upvote | short-code-hashset-1ms-please-upvote-by-gvq6f | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem appears to involve determining the type of triangle based on its side lengt | Satyam_Mishra_1 | NORMAL | 2024-02-03T16:43:22.239625+00:00 | 2024-02-03T16:43:22.239648+00:00 | 86 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem appears to involve determining the type of triangle based on its side lengths. The code seems to check the validity of a triangle using the triangle inequality theorem and then identifies the type (equilateral, isosceles, or scalene) based on the count of unique side lengths.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTriangle Inequality Check: The code checks whether the given side lengths satisfy the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.\n\nType Identification: After the triangle inequality check, the code uses a HashSet to count the unique side lengths. Based on the count, it identifies whether the triangle is equilateral, isosceles, or scalene.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution {\n public String triangleType(int[] nums) {\n int a=nums[0];\n int b=nums[1];\n int c=nums[2];\n // checking validity of Triangle\n if(a + b <= c || b + c <= a || a + c <= b){\n return "none";\n }\n\n // Checking Type of Triangle\n HashSet<Integer> num = new HashSet<>();\n for (int n: nums) num.add(n);\n if(num.size()==1) return "equilateral";\n else if (num.size()==2) return "isosceles";\n else return "scalene";\n }\n}\n``` | 1 | 0 | ['Hash Table', 'Java'] | 0 |
type-of-triangle | ✅✅Easy to understand|| c++|| sorting | easy-to-understand-c-sorting-by-techsidh-m067 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | techsidh | NORMAL | 2024-02-03T16:27:00.355313+00:00 | 2024-02-03T16:27:00.355342+00:00 | 90 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n int n=nums.size();\n sort(nums.begin(),nums.end());\n if(nums[0]+nums[1]<=nums[2]){\n return "none";\n }\n if(nums[0]+nums[1]==2*nums[2]){\n return "equilateral";\n }\n if(nums[1]==nums[2] || nums[0]==nums[1]){\n return "isosceles";\n }\n return "scalene";\n }\n};\n``` | 1 | 0 | ['Sorting', 'C++'] | 0 |
type-of-triangle | easy solution | beats 100% | easy-solution-beats-100-by-leet1101-j0jy | Code\n\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n if (nums[0] == nums[1] && nums[0] == nums[2]){\n return "equ | leet1101 | NORMAL | 2024-02-03T16:18:18.193161+00:00 | 2024-02-03T16:18:18.193196+00:00 | 28 | false | # Code\n```\nclass Solution {\npublic:\n string triangleType(vector<int>& nums) {\n if (nums[0] == nums[1] && nums[0] == nums[2]){\n return "equilateral" ;\n }\n else {\n if ((nums[0]+nums[1]>nums[2]) && (nums[1]+nums[2]>nums[0]) && (nums[0]+nums[2]>nums[1])){\n if(nums[0]==nums[1] || nums[0]==nums[2] || nums[1]==nums[2]){\n return "isosceles" ;\n }\n else return "scalene" ;\n }\n }\n return "none" ;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
type-of-triangle | Check Triangle Properties | C++ | check-triangle-properties-c-by-jay_1410-4wp6 | Code\n\nclass Solution {\npublic:\n string triangleType(vector<int>& nums){\n sort(nums.begin(),nums.end());\n if(nums[0] + nums[1] > nums[2]){ | Jay_1410 | NORMAL | 2024-02-03T16:12:30.602335+00:00 | 2024-02-03T16:12:30.602364+00:00 | 71 | false | # Code\n```\nclass Solution {\npublic:\n string triangleType(vector<int>& nums){\n sort(nums.begin(),nums.end());\n if(nums[0] + nums[1] > nums[2]){\n if(nums[0] == nums[1] && nums[1] == nums[2]) return "equilateral";\n if(nums[0] == nums[1] || nums[1] == nums[2]) return "isosceles";\n if(nums[0] != nums[1] && nums[1] != nums[2]) return "scalene";\n }\n return "none";\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
type-of-triangle | JS || Solution by Bharadwaj | js-solution-by-bharadwaj-by-manu-bharadw-t2ab | Code\n\nvar triangleType = function (nums) {\n nums.sort((a, b) => a - b);\n if (nums[0] + nums[1] > nums[2]) {\n if (nums[0] === nums[1] && nums[1 | Manu-Bharadwaj-BN | NORMAL | 2024-02-03T16:09:31.379299+00:00 | 2024-02-03T16:09:31.379333+00:00 | 173 | false | # Code\n```\nvar triangleType = function (nums) {\n nums.sort((a, b) => a - b);\n if (nums[0] + nums[1] > nums[2]) {\n if (nums[0] === nums[1] && nums[1] === nums[2]) {\n return "equilateral";\n }\n else if (nums[0] === nums[1] || nums[1] === nums[2]) {\n return "isosceles";\n }\n else {\n return "scalene";\n }\n } else {\n return "none";\n }\n};\n``` | 1 | 0 | ['JavaScript'] | 2 |
type-of-triangle | Simple java code 0 ms beats 100 % | simple-java-code-0-ms-beats-100-by-arobh-y30i | Complexity\n\n\n# Code\n\nclass Solution {\n public String triangleType(int[] nums) {\n if(nums[0]+nums[1]<=nums[2]||nums[0]+nums[2]<=nums[1]||nums[1] | Arobh | NORMAL | 2024-02-03T16:07:55.352236+00:00 | 2024-02-03T16:07:55.352277+00:00 | 4 | false | # Complexity\n\n\n# Code\n```\nclass Solution {\n public String triangleType(int[] nums) {\n if(nums[0]+nums[1]<=nums[2]||nums[0]+nums[2]<=nums[1]||nums[1]+nums[2]<=nums[0]){\n return "none";\n }\n else if(nums[0]==nums[1]&&nums[1]==nums[2]){\n return "equilateral";\n }\n else if(nums[0]==nums[1]||nums[0]==nums[2]||nums[1]==nums[2]){\n return "isosceles";\n }\n else{\n return "scalene";\n }\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
type-of-triangle | Easy Solution in Java . | easy-solution-in-java-by-prajesh07-j4a2 | IntuitionApproachComplexity
Time complexity: O(1) .
Space complexity: O(1) .
Code | prajesh07 | NORMAL | 2025-04-07T17:36:29.652542+00:00 | 2025-04-07T17:36:29.652542+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(1) .
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1) .
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public String triangleType(int[] arr) {
if ((arr[0] == arr[1]) && (arr[1] == arr[2])) {
return "equilateral";
}
else if (arr[0] + arr[1] > arr[2] && arr[1] + arr[2] > arr[0] &&
arr[0] + arr[2] > arr[1]) {
if (arr[0] == arr[1] || arr[1] == arr[2] || arr[0] == arr[2]) {
return "isosceles";
}
else if (arr[0] != arr[1] && arr[1] != arr[2] && arr[0] != arr[2]) {
return "scalene";
}
}
return "none";
}
}
``` | 0 | 0 | ['Java'] | 0 |
type-of-triangle | Easy Solution in C++ . | easy-solution-in-c-by-prajesh07-95qn | IntuitionApproachComplexity
Time complexity: O(1) .
Space complexity: O(1) .
Code | prajesh07 | NORMAL | 2025-04-07T17:34:39.211071+00:00 | 2025-04-07T17:34:39.211071+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(1) .
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1) .
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
string triangleType(vector<int>&arr) {
if ((arr[0] == arr[1]) && (arr[1] == arr[2])) {
return "equilateral";
}
else if (arr[0] + arr[1] > arr[2] && arr[1] + arr[2] > arr[0] &&
arr[0] + arr[2] > arr[1]) {
if (arr[0] == arr[1] || arr[1] == arr[2] || arr[0] == arr[2]) {
return "isosceles";
}
else if (arr[0] != arr[1] && arr[1] != arr[2] &&
arr[0] != arr[2]) {
return "scalene";
}
}
return "none";
}
};
``` | 0 | 0 | ['C++'] | 0 |
type-of-triangle | Easy Solution in C . | easy-solution-in-c-by-prajesh07-oz1b | IntuitionApproachComplexity
Time complexity: O(1) .
Space complexity: O(1) .
Code | prajesh07 | NORMAL | 2025-04-07T17:32:20.484511+00:00 | 2025-04-07T17:32:20.484511+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(1) .
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1) .
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```c []
char* triangleType(int* arr, int arrsize) {
if ((arr[0] == arr[1]) && (arr[1] == arr[2])) {
return "equilateral";
}
else if (arr[0] + arr[1] > arr[2] && arr[1] + arr[2] > arr[0] &&
arr[0] + arr[2] > arr[1]) {
if (arr[0] == arr[1] || arr[1] == arr[2] || arr[0] == arr[2]) {
return "isosceles";
}
else if (arr[0] != arr[1] && arr[1] != arr[2] && arr[0] != arr[2]) {
return "scalene";
}
}
return "none";
}
``` | 0 | 0 | ['C'] | 0 |
type-of-triangle | very simple c code | very-simple-c-code-by-sanjaykumar_chittu-sdzc | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | sanjaykumar_chitturi | NORMAL | 2025-04-05T06:37:36.509807+00:00 | 2025-04-05T06:37:36.509807+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```c []
#define equilateral "equilateral"
#define isosceles "isosceles"
#define scalene "scalene"
#define none "none"
char* triangleType(int* nums, int numsSize) {
if ((nums[0]+nums[1]<=nums[2])||(nums[0]+nums[2]<=nums[1])||(nums[1]+nums[2]<=nums[0])) return none;
if (nums[0]==nums[1]&&nums[1]==nums[2])
{
return equilateral;
}
else if ((nums[0]==nums[1])||(nums[0]==nums[2])||(nums[1]==nums[2])) return isosceles;
else return scalene;
}
``` | 0 | 0 | ['C'] | 0 |
type-of-triangle | Beats 100% | Using Triangle Inequality Theorem | beats-100-using-triangle-inequality-theo-afuc | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | katedel28 | NORMAL | 2025-04-01T16:14:30.975186+00:00 | 2025-04-01T16:14:30.975186+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {number[]} nums
* @return {string}
*/
var triangleType = function(nums) {
let a = nums[0], b = nums[1], c = nums[2];
// Check for valid triangle using triangle inequality theorem
if (a + b > c && a + c > b && b + c > a) {
// Check if all sides are equal
if (a === b && b === c) {
return "equilateral"; // All sides are equal
}
// Check if two sides are equal
else if (a === b || b === c || a === c) {
return "isosceles"; // Two sides are equal
}
// If no sides are equal
else {
return "scalene"; // All sides are different
}
}
// If triangle inequality is not satisfied
return "none"; // Not a valid triangle
};
``` | 0 | 0 | ['JavaScript'] | 0 |
type-of-triangle | One more task | one-more-task-by-pasha_iden-sguy | in two ways.Code | pasha_iden | NORMAL | 2025-03-31T16:22:43.155430+00:00 | 2025-03-31T16:22:43.155430+00:00 | 1 | false | in two ways.
# Code
```python []
class Solution(object):
def triangleType(self, nums):
if nums[0] == nums[1] == nums[2]:
return "equilateral"
else:
mi = min(nums)
nums.remove(mi)
av = min(nums)
nums.remove(av)
ma = nums[0]
if mi + av <= ma:
return "none"
elif mi == av or av == ma:
return "isosceles"
else:
return "scalene"
# class Solution(object):
# def triangleType(self, nums):
# if nums[0] == nums[1] == nums[2]:
# return "equilateral"
# else:
# nums.sort()
# if nums[0] + nums[1] <= nums[2]:
# return "none"
# elif nums[0] == nums[1] or nums[1] == nums[2]:
# return "isosceles"
# else:
# return "scalene"
``` | 0 | 0 | ['Python'] | 0 |
type-of-triangle | Python | BEATS 100% | Simple If-else | python-beats-100-simple-if-else-by-saran-lrq7 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | sarangrakhecha | NORMAL | 2025-03-29T05:05:38.322485+00:00 | 2025-03-29T05:05:38.322485+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def triangleType(self, nums: List[int]) -> str:
if nums[0] + nums[1] <= nums[2] or nums[0] + nums[2] <= nums[1] or nums[1] + nums[2] <= nums[0]:
return "none"
else:
if nums[0] == nums[1] == nums[2]:
return "equilateral"
if nums[0] == nums[1] or nums[1] == nums[2] or nums[0] == nums[2]:
return "isosceles"
else:
return "scalene"
``` | 0 | 0 | ['Python3'] | 0 |
type-of-triangle | 100% working | 100-working-by-vishnukiran24-crcb | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | vishnukiran24 | NORMAL | 2025-03-28T16:20:02.646011+00:00 | 2025-03-28T16:20:02.646011+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```c []
char* triangleType(int* nums, int numsSize) {
static char str[12];
if(nums[0]+nums[1]<=nums[2]||nums[0]+nums[2]<=nums[1]||nums[1]+nums[2]<=nums[0])
strcpy(str, "none");
else if(nums[0]==nums[1]&&nums[1]==nums[2])
strcpy(str, "equilateral");
else if(nums[0]==nums[1]||nums[0]==nums[2]||nums[1]==nums[2])
strcpy(str, "isosceles");
else
strcpy(str, "scalene");
return str;
}
``` | 0 | 0 | ['C'] | 0 |
type-of-triangle | Easy To Understand | Beats 100% | O(1) | 0ms runtime | determine-triangle-type-equilateral-isos-r09r | IntuitionThe problem asks to determine the type of triangle (equilateral, isosceles, scalene) or check if a triangle is valid based on given side lengths.Approa | Srinivasanb07 | NORMAL | 2025-03-28T04:58:21.343279+00:00 | 2025-03-28T05:00:56.032905+00:00 | 3 | false | # Intuition
The problem asks to determine the type of triangle (equilateral, isosceles, scalene) or check if a triangle is valid based on given side lengths.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
Sorting
Triangle Validity Check
Frequency Count:
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n log n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def triangleType(self, nums: List[int]) -> str:
nums.sort()
b=[]
for i in nums:
b.append(i*i)
if (b[0]+b[1])*0.5==b[2] or nums[0]+nums[1]>nums[2]:
a=Counter(nums)
if len(a)==1:
return "equilateral"
if len(a)==2:
return "isosceles"
else:
return "scalene"
return "none"
``` | 0 | 0 | ['Python3'] | 0 |
type-of-triangle | Easy Approach || Beginner's Code || O(1) | easy-approach-beginners-code-o1-by-prave-nzz7 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Praveen__Kumar__ | NORMAL | 2025-03-27T04:10:21.789503+00:00 | 2025-03-27T04:10:21.789503+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
int s1 = nums[0];
int s2 = nums[1];
int s3 = nums[2];
if(s1 == s2 && s2==s3) return "equilateral";
if(s1+s2 > s3 && s2+s3 > s1 && s1+s3 > s2){
if(s1==s2 || s2 == s3 || s1==s3 ) return "isosceles";
else return "scalene";
}
return "none";
}
}
``` | 0 | 0 | ['Math', 'Geometry', 'Java'] | 0 |
type-of-triangle | Readable Solution With Explanation | readable-solution-with-explanation-by-v1-bm1i | Sort nums to find longest side and return "none" if the values can not make a triangle (sum of smaller sides is <= greater side).
Count equal sides using for l | V1Nut | NORMAL | 2025-03-24T18:15:55.281044+00:00 | 2025-03-24T18:15:55.281044+00:00 | 1 | false | 1. Sort nums to find longest side and return "none" if the values can not make a triangle (sum of smaller sides is <= greater side).
2. Count equal sides using for loop with modulus to make it circular.
3. Return string based on how many sides are equivalent.
# Code
```kotlin []
class Solution {
fun triangleType(nums: IntArray): String {
nums.sort()
if (nums[0] + nums[1] <= nums[2]) return "none"
var count = 0
for (i in 0..2) {
if (nums[i] == nums[(i + 1) % 3]) count++
}
return when {
count == 0 -> "scalene"
count == 1 -> "isosceles"
else -> "equilateral"
}
}
}
``` | 0 | 0 | ['Array', 'Math', 'Sorting', 'Kotlin'] | 0 |
type-of-triangle | ✅ Easy to understand || ✅0ms || 100% beats🔥|| Php | easy-to-understand-0ms-100-beats-php-by-mjbf6 | IntuitionThe problem requires identifying the type of triangle based on the given side lengths.
First, we need to check if the sides can form a valid triangle u | djupraity | NORMAL | 2025-03-24T17:45:44.018645+00:00 | 2025-03-24T17:45:44.018645+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem requires identifying the type of triangle based on the given side lengths.
First, we need to check if the sides can form a valid triangle using the **triangle inequality theorem**:
- `side1 + side2 > side3`
- `side1 + side3 > side2`
- `side2 + side3 > side1`
If the sides form a valid triangle, we classify it into one of the following types:
- **Equilateral**: All sides are equal.
- **Isosceles**: Two sides are equal.
- **Scalene**: All sides are different.
If the sides do not satisfy the triangle inequality, it is labeled as **"none"**.
# Approach
<!-- Describe your approach to solving the problem. -->
1. **Sort the array** → Sorting makes it easier to check the inequality condition with the largest side at the end.
2. **Triangle inequality check** → If the sum of the two smaller sides is less than or equal to the largest side, it cannot form a triangle, so return **"none"**.
3. **Triangle type check**:
- If all sides are equal → Return **"equilateral"**.
- If two sides are equal → Return **"isosceles"**.
- If all sides are different → Return **"scalene"**.
# Complexity
- **Time complexity:**
- $$O(n \log n)$$ → Due to sorting the sides.
- **Space complexity:**
- $$O(1)$$ → No extra space is used, only variables for the sides.
# Code
```php
class Solution {
/**
* @param Integer[] $nums
* @return String
*/
function triangleType($nums) {
sort($nums);
// Triangle inequality check
if ($nums[0] + $nums[1] <= $nums[2])
return "none";
// Check triangle type
if ($nums[0] == $nums[1] && $nums[1] == $nums[2])
return "equilateral";
elseif ($nums[0] == $nums[1] || $nums[1] == $nums[2] || $nums[0] == $nums[2])
return "isosceles";
else
return "scalene";
}
}
```
| 0 | 0 | ['PHP'] | 0 |
type-of-triangle | 100% beats easy c solution | 100-beats-easy-c-solution-by-kunsh2301-uok6 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | kunsh2301 | NORMAL | 2025-03-24T14:22:49.209279+00:00 | 2025-03-24T14:22:49.209279+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```c []
char* triangleType(int* nums, int numsSize) {
int a=nums[0];
int b=nums[1];
int c=nums[2];
if(a==b&&b==c) return "equilateral";
if((a==b&&a+b>c)||(b==c&&b+c>a)||(a==c&&a+c>b)) return "isosceles";
if(a+b>c&&b+c>a&&c+a>b) return "scalene";
return "none";
}
``` | 0 | 0 | ['C'] | 0 |
type-of-triangle | JAVA || Beginner Friendly || Easy to Understand || IF-ELSE Approach | java-beginner-friendly-easy-to-understan-l518 | ApproachCheck if the Given Sides Form a Valid Triangle (isTri function):
A valid triangle must satisfy the Triangle Inequality Theorem, which states that the s | hpathak875 | NORMAL | 2025-03-24T13:34:30.329661+00:00 | 2025-03-24T13:34:30.329661+00:00 | 2 | false |
# Approach
Check if the Given Sides Form a Valid Triangle (isTri function):
- A valid triangle must satisfy the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides must be greater than the length of the third side.
- The method isTri(int[] arr) verifies this condition by checking:
𝑎 + 𝑏 > 𝑐, 𝑏 + 𝑐 > 𝑎, and 𝑎 + 𝑐 > 𝑏
- If all these conditions hold, the method returns true; otherwise, it returns false, meaning the given sides do not form a valid triangle.
Determine the Triangle Type (triangleType function):
- If isTri(nums) returns false, it means the given sides cannot form a triangle, and the function returns "none".
- If it is a valid triangle, the function classifies it into one of three categories:
- Equilateral: All three sides are equal. (nums[0] == nums[1] == nums[2])
- Isosceles: Exactly two sides are equal. (nums[0] == nums[1] OR nums[1] == nums[2] OR nums[0] == nums[2])
- Scalene: All sides have different lengths.
# Complexity
- Time complexity: $$ O(1)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$ O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
if(!isTri(nums)){
return "none";
}
else{
if(nums[0]==nums[1] && nums[1]==nums[2]){
return "equilateral";
}
else if((nums[0]==nums[1]) || (nums[1]==nums[2]) ||(nums[0]==nums[2])){
return "isosceles";
}
else{
return "scalene";
}
}
}
public boolean isTri(int[] arr){
int side1=arr[0]+arr[1];
int side2=arr[1]+arr[2];
int side3=arr[0]+arr[2];
if((side1>arr[2]) && (side2>arr[0]) && (side3>arr[1])){
return true;
}
else{
return false;
}
}
}
``` | 0 | 0 | ['Array', 'Math', 'Sorting', 'Java'] | 0 |
type-of-triangle | Types Of Triangle | types-of-triangle-by-jishabpatel-jyze | Code | Jishabpatel | NORMAL | 2025-03-23T16:51:17.770161+00:00 | 2025-03-23T16:51:17.770161+00:00 | 2 | false |
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
int a = nums[0];
int b = nums[1];
int c = nums[2];
if(a+b>c && b+c>a && c+a>b){
if(a==b && b==c && c==a) return "equilateral";
if(a!=b && b!=c && c!=a) return "scalene";
return "isosceles";
}
return "none";
}
}
``` | 0 | 0 | ['Java'] | 0 |
type-of-triangle | Self Generated Solution | self-generated-solution-by-pranaykadu59-t3mu | IntuitionWe are given three side lengths and need to determine what type of triangle they form. A valid triangle must satisfy the triangle inequality rule (sum | pranaykadu59 | NORMAL | 2025-03-21T21:22:20.263959+00:00 | 2025-03-21T21:22:20.263959+00:00 | 2 | false | # Intuition
We are given three side lengths and need to determine what type of triangle they form. A valid triangle must satisfy the **triangle inequality rule** (sum of two smaller sides must be greater than the largest side). Based on side lengths, a triangle can be:
- **Equilateral** → All three sides are the same.
- **Isosceles** → Exactly two sides are the same.
- **Scalene** → All sides are different.
- **None** → If it doesn’t satisfy the triangle inequality, it’s not a triangle.
# Approach
1. **Sort** the sides to make comparisons easier.
2. **Check for an equilateral triangle** (all sides are equal).
3. **Verify if it forms a valid triangle** using the triangle inequality rule. If not, return `"none"`.
4. **Check for isosceles** (at least two sides are the same).
5. **If none of the above, it must be scalene** (all sides different and valid).
# Complexity
- Time complexity:
- Sorting a 3-element array takes **O(1)** (constant time).
- Comparisons are **O(1)**.
- **Total: O(1) (constant time).**
- Space complexity:
- Only a few extra variables are used.
- **Total: O(1) (constant space).**
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
Arrays.sort(nums);
if(nums[0]==nums[1] && nums[1]==nums[2]){
return "equilateral";
}
else if(nums[0]+nums[1]<=nums[2]){
return "none";
}
else if(nums[0]==nums[1] || nums[1]==nums[2] || nums[2]==nums[0]){
return "isosceles";
}
else if(nums[0] != nums[1] && nums[1] != nums[2] && (nums[0] + nums[1] > nums[2]) ){
return "scalene";
}
else{
return "none";
}
}
}
// class Solution {
// public String triangleType(int[] nums) {
// // sort(nums.begin(), nums.end());
// Arrays.sort(nums);
// if(nums[0] + nums[1] <= nums[2]){
// return "none";
// }
// else if(nums[0]==nums[2]){ // all elements are sorted first==third
// return "equilateral";
// }
// else if(nums[0]==nums[1] || nums[1]==nums[2]){ // all elements are sorted either=> first==second or second==third
// return "isosceles";
// }
// else{
// return "scalene";
// }
// }
// }
// Aryan Mittal
// Time Complexity Analysis
// The algorithm first sorts the array using Arrays.sort(nums), which has a worst-case time complexity of O(n log n).
// After sorting, it performs a few conditional checks, all of which are O(1) operations.
// Therefore, the overall time complexity is O(n log n) due to the sorting step.
// Space Complexity Analysis
// The algorithm sorts the array in place, meaning no extra space is required for sorting.
// It only uses a few extra variables for comparisons and returning results, all of which take O(1) space.
// Therefore, the overall space complexity is O(1).
``` | 0 | 0 | ['Java'] | 0 |
type-of-triangle | 0ms || JAVA || MOST BASIC CODE || SIMPLE TO UNDERSTAND..!!! | 0ms-java-most-basic-code-simple-to-under-8qji | IntuitionApproachComplexity
Time complexity:O(1)
Space complexity:
Code | Devesh_Agrawal | NORMAL | 2025-03-19T14:15:38.877558+00:00 | 2025-03-19T14:15:38.877558+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
int a = nums[0];
int b = nums[1];
int c = nums[2];
if(a==b && a==c)
{
return "equilateral";
}
if(a+b>c && a+c>b && b+c>a)
{
if(a==b || a==c || b==c)
{
return "isosceles";
}
else
{
return "scalene";
}
}
return "none";
}
}
``` | 0 | 0 | ['Java'] | 0 |
type-of-triangle | Simple solution in Java. Beats 100 % | simple-solution-in-java-beats-100-by-kha-jza7 | Complexity
Time complexity:
O(1)
Space complexity:
O(1)
Code | Khamdam | NORMAL | 2025-03-16T04:49:53.806525+00:00 | 2025-03-16T04:49:53.806525+00:00 | 2 | false | # Complexity
- Time complexity:
O(1)
- Space complexity:
O(1)
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
int a = nums[0];
int b = nums[1];
int c = nums[2];
if (a + b <= c || a + c <= b || c + b <= a) {
return "none";
} else {
if (a == b && a == c) {
return "equilateral";
} else if (a == b || a == c || b == c) {
return "isosceles";
} else {
return "scalene";
}
}
}
}
``` | 0 | 0 | ['Array', 'Java'] | 0 |
type-of-triangle | Using JAVA Beats 100% | using-java-beats-100-by-namannirwal0401-cig2 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | namannirwal0401 | NORMAL | 2025-03-08T14:29:34.856969+00:00 | 2025-03-08T14:29:34.856969+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution
{
public String triangleType(int[] nums)
{
//condition for not forming a triangle
if( nums[0]+nums[1]<=nums[2] )
return "none";
else if( nums[0]+nums[2]<=nums[1] )
return "none";
if( nums[1]+nums[2]<=nums[0] )
return "none";
//now if execution is at this line --> this means a triangle is formed
if( (nums[0]==nums[1] && nums[1]==nums[2]) && (nums[0]==nums[2]) )
return "equilateral";
else if( (nums[0]!=nums[1] && nums[1]!=nums[2]) && (nums[0]!=nums[2]) )
return "scalene";
return "isosceles";
}
}
``` | 0 | 0 | ['Java'] | 0 |
type-of-triangle | Easy code for beginners 100% beats | easy-code-for-beginners-100-beats-by-kri-1oi5 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | kritee_2307 | NORMAL | 2025-03-06T10:23:25.393204+00:00 | 2025-03-06T10:23:25.393204+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```c []
const char* triangleType(int* nums, int numsSize) {
if (nums[0] == nums[1] && nums[1] == nums[2]) {
return "equilateral";
} else if ((nums[0] == nums[1] || nums[1] == nums[2] || nums[0] == nums[2]) &&
(nums[0] + nums[1] > nums[2] && nums[0] + nums[2] > nums[1] && nums[1] + nums[2] > nums[0])) {
return "isosceles";
} else if (nums[0] != nums[1] && nums[1] != nums[2] && nums[0] != nums[2] &&
(nums[0] + nums[1] > nums[2] && nums[0] + nums[2] > nums[1] && nums[1] + nums[2] > nums[0])) {
return "scalene";
} else {
return "none";
}
return "none";
}
``` | 0 | 0 | ['Array', 'Math', 'C'] | 0 |
type-of-triangle | No if-else spaghetti and actually readable? | no-if-else-spaghetti-and-actually-readab-xeoj | IntuitionKeep count of which number appears most. Then use that count to determine the type of triangle.ApproachStore each number as a key in a map and assign t | nate-osterfeld | NORMAL | 2025-03-02T20:52:05.529660+00:00 | 2025-03-02T20:52:05.529660+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Keep count of which number appears most. Then use that count to determine the type of triangle.
# Approach
<!-- Describe your approach to solving the problem. -->
Store each number as a key in a map and assign the number of times it appears to that key's value. If the value surpasses the current `count`, then we assign a new `count` using that value; giving us the max count.
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {number[]} nums
* @return {string}
*/
var triangleType = function(nums) {
if (!isValid(nums)) return 'none'
const map = {}
let count = 0
for (let num of nums) {
map[num] = (map[num] || 0) + 1
count = Math.max(count, map[num])
}
switch (count) {
case 1: return 'scalene'
case 2: return 'isosceles'
case 3: return 'equilateral'
}
};
var isValid = function(nums) {
if (nums[0] + nums[1] <= nums[2]) return false
if (nums[0] + nums[2] <= nums[1]) return false
if (nums[1] + nums[2] <= nums[0]) return false
return true
}
``` | 0 | 0 | ['JavaScript'] | 0 |
type-of-triangle | JS solution with bubbleSort implementation | js-solution-with-bubblesort-implementati-ldcr | IntuitionApproachComplexity
Time complexity: O(n2)
Space complexity: O(1)
Code | bwnQYni8bB | NORMAL | 2025-02-28T11:41:12.090870+00:00 | 2025-02-28T11:41:12.090870+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: $$O(n^2)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
function triangleType(nums) {
bblSort(nums);
if (nums[0] + nums[1] <= nums[2]) {
return 'none';
}
if (nums[0] === nums[1] && nums[1] === nums[2]) {
return 'equilateral';
}
if (nums[0] === nums[1] || nums[1] === nums[2]) {
return 'isosceles';
}
return 'scalene';
};
function bblSort(nums) {
for (let i = 0; i < nums.length; i++) {
for (let j = 0; j < nums.length; j++) {
if (nums[j] > nums[j + 1]) {
let temp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = temp;
}
}
}
return nums;
}
``` | 0 | 0 | ['JavaScript'] | 0 |
type-of-triangle | IF | if-by-marcelo_kobayashi-ao8r | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Marcelo_Kobayashi | NORMAL | 2025-02-26T20:05:41.167825+00:00 | 2025-02-26T20:05:41.167825+00:00 | 0 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python []
class Solution(object):
def triangleType(self, nums):
"""
:type nums: List[int]
:rtype: str
"""
um = nums[0]
dois = nums[1]
tres = nums[2]
if um == dois and dois == tres:
return "equilateral"
if (um + dois) > tres and (um + tres) > dois and (dois + tres) > um:
if (um == dois) or (um == tres) or (dois == tres):
return "isosceles"
else:
return "scalene"
else:
return "none"
``` | 0 | 0 | ['Python'] | 0 |
type-of-triangle | 1. Easy to understand | 1-easy-to-understand-by-sonhandsome06-0yq2 | Approach
If it is triangle when 2 sides > remaining side.
I use for to update to Set. if size = 1: equilateral , size = 2: isosceles, size = 3: scalene
Complexi | sonhandsome06 | NORMAL | 2025-02-26T14:40:30.691252+00:00 | 2025-02-26T14:40:30.691252+00:00 | 3 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
1. If it is triangle when 2 sides > remaining side.
2. I use for to update to Set. if size = 1: equilateral , size = 2: isosceles, size = 3: scalene
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(1)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
int A = nums[0];
int B = nums[1];
int C = nums[2];
boolean isTriangle = (A+B) > C && (A + C) > B && (B + C) > A;
if (isTriangle) {
Set<Integer> sides = new HashSet<>();
for (int i = 0; i < nums.length; i++) {
sides.add(nums[i]);
}
if (sides.size() == 3) {
return "scalene";
} else if(sides.size() == 2) {
return "isosceles";
} else {
return "equilateral";
}
} else
return "none";
}
}
``` | 0 | 0 | ['Java'] | 0 |
type-of-triangle | C# | c-by-sahooalok-ljqr | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | sahooalok | NORMAL | 2025-02-21T03:07:17.557096+00:00 | 2025-02-21T03:07:17.557096+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public string TriangleType(int[] nums) {
int x = nums[0]; int y = nums[1]; int z = nums[2];
if(x+y>z && y+z>x && x+z>y)
{
if(x == y & y == z)
{
return "equilateral";
}
else if(x==y || y == z || z == x)
{
return "isosceles";
}
else
{
return "scalene";
}
}
return "none";
}
}
``` | 0 | 0 | ['C#'] | 0 |
type-of-triangle | EASY TO UNDERSTAND SOLUTION IN C++ | easy-to-understand-solution-in-c-by-le2j-oxdx | IntuitionApproach:The only properties you need to remember:
A Triangle can only be formed if some of ANY two sides is GREATER then the third side.
Equilateral T | Yadav_Tarun | NORMAL | 2025-02-20T17:20:56.629628+00:00 | 2025-02-20T17:20:56.629628+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach:
The only properties you need to remember:
1. A Triangle can only be formed if some of ANY two sides is GREATER then the third side.
2. Equilateral Triangle: triangle having all 3 sides Equal.
3. Isoceles Triangle: Triangle having exactly 2 sides equal.
4. Scalene Triangle: Triangle with all the 3 sides of unequal lengths
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
string triangleType(vector<int>& nums) {
if(nums[0]+nums[1] > nums[2] && nums[0]+nums[2] > nums[1] && nums[1]+nums[2] > nums[0]){
if(nums[0] == nums[1] && nums[0] == nums[2]){
return "equilateral";
}else if(nums[0] == nums[1] || nums[0] == nums[2] || nums[1] == nums[2] )
{
return "isosceles";
}else
{
return "scalene";
}
}else{
return "none";
}
}
};
``` | 0 | 0 | ['C++'] | 0 |
type-of-triangle | Solved with O(1) time & space complexity beats 100%. | solved-with-o1-time-space-complexity-bea-939e | ScreenShotApproach
used else if ladder and check in in if condition check if any two sides sum is greater than 3 side then return "none".
in else if condition c | Vedant_Bachhav | NORMAL | 2025-02-18T13:59:34.944386+00:00 | 2025-02-18T13:59:34.944386+00:00 | 2 | false | # ScreenShot
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
1. used else if ladder and check in in if condition check if any two sides sum is greater than 3 side then return "none".
2. in else if condition check all three sides are equl if they are equal then return "equilateral".
3. in another else if check two sides are equal if two sides are equal then return "isosceles".
4. in else condition return "scalene".
# Complexity
- Time complexity:O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
if(nums[0]+nums[1]<=nums[2] || nums[1]+nums[2]<=nums[0] || nums[0]+nums[2]<=nums[1]){
return "none";
}
else if(nums[0]==nums[1] && nums[1]==nums[2]){
return "equilateral";
}
else if(nums[0]==nums[1] || nums[1]==nums[2] || nums[0]==nums[2] ){
return "isosceles";
}
else{
return "scalene";
}
}
}
``` | 0 | 0 | ['Array', 'Math', 'Java'] | 0 |
type-of-triangle | Simple Maths | simple-maths-by-user3660l-mjxl | IntuitionApproachComplexity
Time complexity:
O(1)
Space complexity:
O(1)
Code | user3660L | NORMAL | 2025-02-14T10:50:25.151318+00:00 | 2025-02-14T10:50:25.151318+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(1)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
string triangleType(vector<int>& nums) {
if(nums[0]+nums[1]<=nums[2]) return "none";
if(nums[1]+nums[2]<=nums[0]) return "none";
if(nums[0]+nums[2]<=nums[1]) return "none";
if(nums[0]==nums[1]&& nums[0]==nums[2]) return "equilateral";
int x = nums[0]==nums[1];int y = nums[2]==nums[1];int z = nums[0]==nums[2];
if(x+y+z == 1) return "isosceles";
return "scalene" ;
}
};
``` | 0 | 0 | ['C++'] | 0 |
type-of-triangle | VERY EASY SOLUTION IN C++ | very-easy-solution-in-c-by-cmacxssxua-htkf | IntuitionUSING SIMPLE MATHMATICAL LOGIC THE PROBLEM IS DONE.
FOR EQUILATERAL:ALL SIDES MUST BE OF SAME LENGTH
FOR SCALENE:ALL SIDES MUST BE OF DIFFERENT LENGTH | CmAcXSsxUa | NORMAL | 2025-02-12T16:29:08.380013+00:00 | 2025-02-12T16:31:59.501717+00:00 | 3 | false | # Intuition
USING SIMPLE MATHMATICAL LOGIC THE PROBLEM IS DONE.
FOR EQUILATERAL:ALL SIDES MUST BE OF SAME LENGTH
FOR SCALENE:ALL SIDES MUST BE OF DIFFERENT LENGTH
NOW IF ABOVE TWO CONDITIONS FAILED TO MEET THEN IT IS NOTHING BUT ISOSCELES.
NOTE:TO FORM A TRIANGLE WITH GIVEN LENGHT OF SIDES THE MAIN CRITERIA IS THAT "THE SUM OF ANY TWO SIDES OF A TRIANGLE MUST BE STRICTLY GREATER THAN THE THIRD SIDE".SO IF THIS CONDITON FAILS THEN WE CAN'T FORM ANY TRIANGLE WITH THE GIVEN LENGTHS....
# Approach
APPROACH IS VERY SIMPLE.FROM THE ABOVE MENTIONED INTUITION WE HAVE JUST APPLIED THEM WITH CONDITIONAL OPERATORS AND SOLVED THE PROBLEM....
# Complexity
- Time complexity:
O(1)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
string triangleType(vector<int>& nums) {
if(nums[0]>=nums[1]+nums[2]||nums[1]>=nums[2]+nums[0]||nums[2]>=nums[0]+nums[1]){
return "none";
}
if(nums[0]==nums[1]&&nums[1]==nums[2]&&nums[2]==nums[0]){
return "equilateral" ;
}
if(nums[0]!=nums[1]&&nums[1]!=nums[2]&&nums[2]!=nums[0]){
return "scalene";
}
return "isosceles";
}
};
``` | 0 | 0 | ['Math', 'C++'] | 0 |
type-of-triangle | Long but simple | Beats 100% | long-but-simple-by-stenpenny-3gdz | ApproachNot the best approach I am sure but it works!Code | stenpenny | NORMAL | 2025-02-11T21:37:14.128528+00:00 | 2025-02-11T21:37:45.960820+00:00 | 5 | false | # Approach
Not the best approach I am sure but it works!
# Code
```python3 []
class Solution:
def triangleType(self, nums: List[int]) -> str:
if nums[0] == nums[1] and nums[0] == nums[2]:
return "equilateral"
elif nums[0] == nums[1] and nums[0] + nums[1] > nums[2]:
return "isosceles"
elif nums [0] == nums[2] and nums[0] + nums[2] > nums[1]:
return "isosceles"
elif nums[1] == nums[2] and nums[1] + nums[2] > nums[0]:
return "isosceles"
elif nums[0] + nums[1] > nums[2] and nums[0] + nums[2] > nums[1] and nums[1] + nums[2] > nums[0]:
return "scalene"
else:
return "none"
``` | 0 | 0 | ['Python3'] | 0 |
type-of-triangle | PYTHON3 SOLUTION | python3-solution-by-saikaushik07-bm5d | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Saikaushik07 | NORMAL | 2025-02-08T08:25:52.319330+00:00 | 2025-02-08T08:25:52.319330+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def triangleType(self, nums: List[int]) -> str:
nums.sort()
if nums[0] + nums[1] <= nums[2]:
return "none"
if nums[0] == nums[2]:
return "equilateral"
if nums[0] == nums[1] or nums[1] == nums[2]:
return "isosceles"
return "scalene"
``` | 0 | 0 | ['Python3'] | 0 |
type-of-triangle | 0 ms Beats 100.00% In JavaScript | 0-ms-beats-10000-in-javascript-by-agzam0-22oh | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | agzam06 | NORMAL | 2025-02-01T12:49:03.826794+00:00 | 2025-02-01T12:49:03.826794+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {number[]} nums
* @return {string}
*/
var triangleType = function (n) {
if (
n[0] + n[1] <= n[2] ||
n[0] + n[2] <= n[1] ||
n[1] + n[2] <= n[0]
) {
return "none";
}
if (n[0] === n[1] && n[1] === n[2]) return "equilateral";
else if (n[0] === n[1] || n[0] === n[2] || n[1] === n[2]) return "isosceles";
else return "scalene";
};
``` | 0 | 0 | ['JavaScript'] | 0 |
type-of-triangle | JS Solution | Beats 100% | js-solution-beats-100-by-soumyakhanda-nf04 | Code | SoumyaKhanda | NORMAL | 2025-01-30T19:16:17.869919+00:00 | 2025-01-30T19:16:17.869919+00:00 | 7 | false | # Code
```javascript []
function triangleType(nums) {
const s1 = nums[0] + nums[1];
const s2 = nums[0] + nums[2];
const s3 = nums[1] + nums[2];
return isTriangle(nums[0], nums[1], nums[2]) ? getTriangleType(s1, s2, s3) : 'none';
};
function getTriangleType(s1, s2, s3) {
if (s1 === s2 && s2 === s3)
return 'equilateral';
else if (s1 !== s2 && s2 !== s3 && s1 !== s3)
return 'scalene';
return 'isosceles';
}
function isTriangle(n1, n2, n3) {
return n1 + n2 > n3 && n1 + n3 > n2 && n2 + n3 > n1;
}
``` | 0 | 0 | ['JavaScript'] | 0 |
type-of-triangle | Python Approach | python-approach-by-nirmal1234-9er0 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Nirmal_Manoj | NORMAL | 2025-01-30T17:16:19.860153+00:00 | 2025-01-30T17:16:19.860153+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def triangleType(self, nums: List[int]) -> str:
if nums[0]+nums[1]>nums[2] and nums[0]+nums[2]>nums[1] and nums[1]+nums[2]>nums[0]:
if len(set(nums)) ==1:
return "equilateral"
elif len(set(nums)) ==2:
return "isosceles"
else:
return "scalene"
return "none"
``` | 0 | 0 | ['Python3'] | 0 |
type-of-triangle | Easy solution 🧠 | easy-solution-by-ilhbqgglvs-82d0 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | iLhbQGglVs | NORMAL | 2025-01-30T17:03:55.758562+00:00 | 2025-01-30T17:03:55.758562+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
int a=nums[0];
int b=nums[1];
int c=nums[2];
// condition to form a Triangle
if(a+b<=c ||b+c<=a || c+a<=b) return "none";
if(a==b && b==c) return "equilateral";
if(a==b || b==c || c==a) return "isosceles";
return "scalene";
}
}
``` | 0 | 0 | ['Java'] | 0 |
type-of-triangle | ✅✅Simple and 🚀Easy 💯💯 in JAVA | simple-and-easy-in-java-by-bojaadarsh-8648 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | BojaAdarsh | NORMAL | 2025-01-30T16:58:20.637179+00:00 | 2025-01-30T16:58:20.637179+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution{
public String triangleType(int[] nums){
if(nums[0]+nums[1]<=nums[2]||nums[1]+nums[2]<=nums[0]||nums[0]+nums[2]<=nums[1]){
return "none";
}
if(nums[0]==nums[1]&&nums[1]==nums[2]){
return "equilateral";
}
if(nums[0]==nums[1]||nums[1]==nums[2]||nums[0]==nums[2]){
return "isosceles";
}
return "scalene";
}
}
``` | 0 | 0 | ['Java'] | 0 |
type-of-triangle | Java O(1) solution with detailed explanation | java-o1-solution-with-detailed-explanati-czr2 | IntuitionWe need to check if a triangle exists and count amount of distinct sides.ApproachFirstly, we check if a triangle exist. We know that a triangle can not | had0uken | NORMAL | 2025-01-27T13:24:11.104243+00:00 | 2025-01-27T13:24:11.104243+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We need to check if a triangle exists and count amount of distinct sides.
# Approach
<!-- Describe your approach to solving the problem. -->
Firstly, we check if a triangle exist. We know that a triangle can not exit if sum of his any two sides equals or bigger that the thirds side. To check it we sort the input array. We are aware that a length of the input array is three, so we can use sort method with O(1) complexity. After sorting, we know that the last element of the array is the biggest side, so we can check if the triangle exist. Then, we have to define the type of the triangle. To do it, we have to count distinct sides. It`s convenient to do that is using switch-case construction.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(1)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
Arrays.sort(nums);
if (nums[0] + nums[1] <= nums[2]) return "none";
return switch ((int)(Arrays.stream(nums).distinct().count())){
case 1 -> "equilateral";
case 2 -> "isosceles";
default -> "scalene";
};
}
}
``` | 0 | 0 | ['Java'] | 0 |
type-of-triangle | 3024. Type of Triangle | 3024-type-of-triangle-by-sohailtech-t5md | IntuitionWhen you want to determine the type of triangle from three given side lengths, the first thing is to check if the sides can even form a triangle. If th | SohailTech | NORMAL | 2025-01-27T11:07:22.175474+00:00 | 2025-01-27T11:07:22.175474+00:00 | 7 | false | # Intuition
When you want to determine the type of triangle from three given side lengths, the first thing is to check if the sides can even form a triangle. If they can, the type of triangle (equilateral, isosceles, or scalene) depends on whether the side lengths are equal or not.
# Approach
Validation:
To form a valid triangle, the sum of any two sides must be greater than the third side. This is checked using the validateTriangle function.
Triangle Type:
If all three sides are equal, it's an equilateral triangle.
If two sides are equal, it's an isosceles triangle.
If all three sides are different, it's a scalene triangle.
Invalid Case:
If the sides don’t satisfy the triangle condition, return "none".
# Complexity
- Time complexity:
Since the code only performs a few simple comparisons, the time complexity is
𝑂(1)
- Space complexity:
𝑂(1)
# Code
```cpp []
class Solution {
bool validateTriangle(vector<int>& nums){
int count = 0;
if(nums[0] + nums[1] > nums[2]){
count++;
}
if(nums[1] + nums[2] > nums[0]){
count++;
}
if(nums[2] + nums[0] > nums[1]){
count++;
}
if(count == 3) return true;
return false;
}
public:
string triangleType(vector<int>& nums) {
bool answer = validateTriangle(nums);
if(answer == true){
if(nums[0] == nums[1] && nums[0] == nums[2]) return "equilateral";
else if(nums[0] == nums[1] || nums[0] == nums[2] || nums[1] == nums[2]){
return "isosceles";
}
else if(nums[0] != nums[1] && nums[0] != nums[2] && nums[1] != nums[2]){
} return "scalene";
}
return "none";
}
};
``` | 0 | 0 | ['C++'] | 0 |
type-of-triangle | PHP | php-by-shamilgadzhiev-74bi | Code | shamilGadzhiev | NORMAL | 2025-01-25T10:45:24.615405+00:00 | 2025-01-25T10:45:24.615405+00:00 | 2 | false | # Code
```php []
class Solution {
/**
* @param Integer[] $nums
* @return String
*/
function triangleType($nums) {
if (max($nums) >= array_sum($nums) - max($nums)){
return "none";
}
if ($nums[0] === $nums[1] && $nums[1] === $nums[2]){
return "equilateral";
}
if ($nums[0] === $nums[1] || $nums[1] === $nums[2] || $nums[2] === $nums[0]){
return "isosceles";
}
return "scalene";
}
}
``` | 0 | 0 | ['PHP'] | 0 |
type-of-triangle | Easy c++ code | easy-c-code-by-ashutosh_soni14-9src | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Ashutosh_soni14 | NORMAL | 2025-01-19T19:16:52.173518+00:00 | 2025-01-19T19:16:52.173518+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool isTriangle(vector<int>nums){
int s1,s2,s3;
s1 = nums[0]+nums[1];
s2 = nums[1]+nums[2];
s3 = nums[0]+nums[2];
if(s1>nums[2] && s2>nums[0] && s3>nums[1]){
return true;
}
return false;
}
string triangleType(vector<int>& nums) {
string s = "none";
if(nums[0] == nums[1]&& nums[1] == nums[2]){
s = "equilateral";
return s;
}
if(nums[0]!=nums[1]&&nums[1]!=nums[2] && nums[0]!=nums[2]){
if(isTriangle(nums)){
s = "scalene";
return s;
}
}
if(nums[0]==nums[1]||nums[1]==nums[2]||nums[0]==nums[2]){
if(isTriangle(nums)){
s = "isosceles";
return s;
}
}
return s;
}
};
``` | 0 | 0 | ['C++'] | 0 |
type-of-triangle | clean n structured solution !!! beats 100% user | clean-n-structured-solution-beats-100-us-n420 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | deepesh_25 | NORMAL | 2025-01-15T07:45:48.724433+00:00 | 2025-01-15T07:45:48.724433+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public String triangleType(int[] nums) {
if(nums[0]+nums[1]>nums[2] && nums[1]+nums[2]>nums[0] && nums[2]+nums[0]>nums[1]){
if(nums[0]==nums[1] && nums[1]==nums[2]){
return "equilateral";
}
else if(nums[0]!=nums[1] && nums[1]!=nums[2] && nums[0]!=nums[2]){
return "scalene";
}
else{
return "isosceles";
}
}
else{
return "none";
}
}
}
``` | 0 | 0 | ['Java'] | 0 |
count-anagrams | C++ Solution, Math with Explanation [Each step in detail] | c-solution-math-with-explanation-each-st-b023 | Explanation\n1. The basic idea is to multiply the number of ways to write each word.\n2. The number of ways to write a word of size n is n factorial i.e\xA0n!.\ | devanshu171 | NORMAL | 2022-12-24T19:16:35.379126+00:00 | 2022-12-26T11:06:31.179116+00:00 | 7,230 | false | # Explanation\n1. The basic idea is to multiply the number of ways to write each word.\n2. The number of ways to write a word of size n is `n factorial` i.e\xA0`n!`.\n3. For example *"abc" ->"abc","acb","bac","bca","cab","cba".* total 6 ways = 3!.\n3. Here we want total ***unique count***, so words like "aa" can be written in only `1` way. So we divide our ways by the factorial of all repeating characters\' frequencies.\n4. So we create a frequency array of word freq[].\n4. Now our formula is as follows:` ways = n! / ( freq[i]! * freq[i+1]! *...freq[n-1]! )`.\n5. So our overall answer is `ways[i] * ways[i+1] *...ways[n]`.\n6. But the problem here is that our answer can be a large number, so we have to return `modulo 1e9+7`.\n7. Well, that\'s not a big problem as we can just use `cnt % mod` for our answer, but here we have to use modulo for every computation as numbers can be very large. In our formula:` a= n!`, `b = (freq[i]! * freq[i+1]!... freq[n-1]!` is `(a / b)%mod`.\n8. But ` (a / b) % mod != (a% mod) / (b% mod)`. So here we use `Modular Multiplicative Inverse`,\xA0i.e `(A / B) % mod =\xA0A * ( B ^ -1 ) % mod`. Now `( B ^ -1 ) % mod` we can get by\xA0`Fermat\'s little theorem`, whose end conclusion is\xA0`(b ^ -1) % mod = b ^ (mod -2)`\xA0if mod is `prime`.\n9. now mod is 1e9+7. We can\'t get` b ^ (mod -2)` using for loop which is `O(n)`. for this we can use ***Binary Exponentiation*** which allows us to calculate \u200A`a ^ n` in `O(log(n))`.\n\n\n### Read about [*Modular Multiplicative Inverse*](https://cp-algorithms.com/algebra/module-inverse.html) and [*Binary Exponentiation*](https://cp-algorithms.com/algebra/binary-exp.html)\n\n\n# *C++ Code*\n```\nclass Solution {\npublic:\nint mod=1e9+7;\nint fact[100002];\n\nint modmul(int a,int b){\n return((long long)(a%mod)*(b%mod))%mod;\n}\n\nint binExpo(int a,int b){\n if(!b)return 1;\n int res=binExpo(a,b/2);\n if(b&1){\n return modmul(a,modmul(res,res));\n }else{\n return modmul(res,res);\n }\n}\n\nint modmulinv(int a){\n return binExpo(a,mod-2);\n}\n\nvoid getfact() {\n fact[0]=1;\n for(int i=1;i<=100001;i++){\n fact[i]=modmul(fact[i-1],i);\n }\n}\n\nint ways(string str) {\n int freq[26] = {0};\n for(int i = 0; i<str.size(); i++) {\n freq[str[i] - \'a\']++;\n }\n int totalWays = fact[str.size()];\n int factR=1; \n for(int i = 0; i<26; i++) {\n factR=modmul(factR,fact[freq[i]]);\n }\n return modmul(totalWays,modmulinv(factR));\n}\n \n int countAnagrams(string s) {\n getfact();\n istringstream ss(s);\n string word; \n int ans=1;\n while (ss >> word)\n {\n ans=modmul(ans,ways(word));\n }\n return ans;\n }\n \n};\n``` | 63 | 1 | ['Math', 'C++'] | 8 |
count-anagrams | Multiply Permutations | multiply-permutations-by-votrubac-v5x8 | We count permutations of each word, and multiply those permutatons.\n\nThe number of permutations with repetitions is a factorial of word lenght, divided by fac | votrubac | NORMAL | 2022-12-24T22:42:12.491924+00:00 | 2022-12-24T23:18:36.468881+00:00 | 3,829 | false | We count permutations of each word, and multiply those permutatons.\n\nThe number of permutations with repetitions is a factorial of word lenght, divided by factorial of count of each character.\n\n**Python 3**\nPython developers are in luck due to `factorial` and large integer support.\n\n```python\nclass Solution:\n def countAnagrams(self, s: str) -> int:\n res = 1\n for w in s.split(" "):\n cnt, prem = Counter(w), factorial(len(w))\n for rep in cnt.values():\n prem = prem // factorial(rep)\n res = res * prem % 1000000007\n return res\n```\n**C++**\nNeed to pre-compute factorials and inverse modulos (to simulate divisions).\n\n```cpp\nint fact[100001] = {1, 1}, inv_fact[100001] = {1, 1}, mod = 1000000007;\nclass Solution {\npublic: \nint countAnagrams(string s) {\n if (fact[2] == 0) {\n vector<int> inv(100001, 1);\n for (long long i = 2; i < sizeof(fact) / sizeof(fact[0]); ++i) {\n fact[i] = i * fact[i - 1] % mod;\n inv[i] = mod - mod / i * inv[mod % i] % mod;\n inv_fact[i] = 1LL * inv_fact[i - 1] * inv[i] % mod; \n }\n }\n int res = 1;\n for (int i = 0, j = 0; i <= s.size(); ++i)\n if (i == s.size() || s[i] == \' \') {\n long long cnt[26] = {}, prem = fact[i - j];\n for (int k = j; k < i; ++k)\n ++cnt[s[k] - \'a\'];\n for (int rep : cnt)\n prem = prem * inv_fact[rep] % mod;\n res = res * prem % mod;\n j = i + 1;\n }\n return res;\n}\n};\n``` | 22 | 0 | ['C', 'Python'] | 4 |
count-anagrams | [Python] simple math | python-simple-math-by-pbelskiy-wb7t | Just use formula from school to get permutation number of each part.\nhttps://en.wikipedia.org/wiki/Permutation#k-permutations_of_n\n\npython\nclass Solution:\n | pbelskiy | NORMAL | 2022-12-24T16:48:30.879387+00:00 | 2023-01-03T10:35:49.002270+00:00 | 2,584 | false | Just use formula from school to get permutation number of each part.\nhttps://en.wikipedia.org/wiki/Permutation#k-permutations_of_n\n\n```python\nclass Solution:\n def countAnagrams(self, s: str) -> int:\n\n def get(word):\n n = math.factorial(len(word))\n\n for v in Counter(word).values():\n n //= math.factorial(v)\n\n return int(n) % (10**9 + 7)\n\n total = 1 \n for word in s.split():\n total *= get(word)\n\n return total % (10**9 + 7)\n```\n\n\n**Please vote up if you like my solution** \uD83D\uDE4F | 17 | 5 | ['Math', 'Python', 'Python3'] | 4 |
count-anagrams | Python 3 || 11 lines, w/ explanation || T/S: 96 % / 99% | python-3-11-lines-w-explanation-ts-96-99-ksuh | The problem reduces to finding the multinomial coefficient for each word and then returning their product as the answer. (The binomial coeficient is a particula | Spaulding_ | NORMAL | 2023-07-11T07:35:31.513149+00:00 | 2024-06-17T02:56:49.998502+00:00 | 681 | false | - The problem reduces to finding the *multinomial coefficient* for each word and then returning their product as the answer. (The *binomial coeficient* is a particular case of the multinomial coefficient.)\n\n- Unfortunately, computing each of these multinomial coefficients, because by definition they require factorial computations, cost significant time and space.\n- Fortunately, binomial coefficients can be computed very efficiently (*O*(*n*) by a recurrence relation, which is used in the `math.comb` method.\n- And more fortunately, there\'s another recurrence relation that permits multinomial coefficients to be computed much more efficiently from binomial coeficients. \n\n(The interested reader may wish to do the research on these mathematical references.)\n___\nHere\'s the code:\n```\nclass Solution:\n def countAnagrams(self, s: str, ans = 1) -> int:\n\n prod = lambda x, y: x*y %1_000_000_007\n\n def count(vals):\n res, sm = 1, sum(vals)\n for r in vals:\n res = prod(res, comb(sm,r))\n sm -= r\n return res\n\n \n for word in s.split():\n vals = Counter(word).values()\n ans = prod(ans, count(vals))\n\n return ans\n\n```\n[https://leetcode.com/problems/count-anagrams/submissions/1290637367/](https://leetcode.com/problems/count-anagrams/submissions/1290637367/)\n\n\nI could be wrong, but I think that time is *O*(*MN*) and space is *O*(*M*), in which, *N* ~ `len(s)` and *M* ~ *maxLength*(*words*) | 14 | 0 | ['Python3'] | 0 |
count-anagrams | Easy to Understand Java Solution Permutations and Inverse Factorial | easy-to-understand-java-solution-permuta-7pdy | Intuition\n Describe your first thoughts on how to solve this problem. \nThe idea is how to calcuate number of permutations with duplicates.\n\n# Approach\n Des | jimkirk | NORMAL | 2022-12-24T18:19:48.281646+00:00 | 2023-04-16T19:44:34.112645+00:00 | 2,215 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea is how to calcuate number of permutations with duplicates.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor string such as "AAABBCCD", the length of string is 8, and has 3 \'A\'s, 2 \'B\'s, 2 \'C\'s, and 1 \'D\'.\n\nPermutations of duplicates only contribute to one of unique permutation, therefore, number of permuations of the entire string needs to be divided by number of permuations of each duplicate.\n\nThus, the the number of permutations of string "AAABBCCD" is 8!/(3!*2!*2!*1!).\n\nThe next question is how to calcuate inverse of factorials when number is large.\n\nLet A * A\' = 1 and MOD = 1000000007, then (A * A\') = 1 (mod MOD), we need to calculate (A * A\') = 1 (mod MOD). Then \n\n```\n(A ^ (MOD - 2) * A) % MOD = A ^ (MOD - 1) % MOD = 1 % MOD\n```\n\nWe used [Fermat\'s little theorem](https://en.wikipedia.org/wiki/Fermat%27s_little_theorem), let P be a prime number, then\n\n```\nA ^ P = A (mod P)\n```\n\nThus, if we want to calculate A\', we just calculate\n\n```\nA ^ (MOD - 2)\n\n```\nBecause MOD = 1000000007 and 1000000007 is a prime number.\n\n# Complexity\nLet maximum length of individual string is m and number of strings be n, then time complexity is O(m) for calculating factorial, O(n * log(MOD)) for calculating inverse factorial ~ O(n).\nIf there are n individual strings, the time to calculate number of permutations is O(m * constant).\n\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(m + n).\n\nWe need to store information of factorial and inverse factorial array, space complexity of this part is O(m). Because the auxiliary array of `String[] strs`, space complexity of this part is O(m * n).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m * n).\n\n# Code\n```\nclass Solution {\n private static final int MOD = 1000000007;\n public int countAnagrams(String s) {\n String[] strs = s.split(" ");\n long result = 1;\n int maxLen = 0;\n for (String str : strs) { \n maxLen = Math.max(maxLen, str.length());\n }\n int[] factorial = getFactorial(maxLen);\n int[] invFactorial = getInverseFactorial(maxLen, factorial);\n int[] count = new int[26];\n int len = 0;\n long numOfPermutations = 0;\n for (String str : strs) {\n Arrays.fill(count, 0);\n len = str.length();\n for (int i = 0; i < len; i++) {\n count[str.charAt(i) - \'a\']++;\n }\n numOfPermutations = factorial[len];\n for (int i = 0; i < 26; i++) {\n if (count[i] > 0) {\n numOfPermutations = (numOfPermutations * invFactorial[count[i]]) % MOD;\n }\n }\n result = (result * numOfPermutations) % MOD;\n }\n return (int) result;\n }\n private int[] getFactorial(int num) {\n int[] factorial = new int[num + 1];\n factorial[0] = 1;\n for (int i = 1; i <= num; i++) {\n factorial[i] = (int) ((1L * factorial[i - 1] * i) % MOD);\n }\n return factorial;\n }\n private int[] getInverseFactorial(int num, int[] factorial) {\n int[] invFactorial = new int[num + 1];\n for (int i = 1; i <= num; i++) {\n invFactorial[i] = (int) powMod(factorial[i], MOD - 2) % MOD;\n }\n return invFactorial;\n }\n private long powMod(long num, int pow) {\n long result = 1;\n while (pow >= 1) {\n if (pow % 2 == 1) {\n result = (result * num) % MOD;\n }\n pow /= 2;\n num = (num * num) % MOD;\n }\n return result;\n }\n}\n\n``` | 10 | 0 | ['Combinatorics', 'Java'] | 2 |
count-anagrams | C++ Solution | c-solution-by-pranto1209-ni6a | Intuition\n Describe your first thoughts on how to solve this problem. \n Calculate the number of permutations of each word,\n Formula is: N! / (Ma! * Mb! | pranto1209 | NORMAL | 2022-12-24T17:28:46.580815+00:00 | 2023-03-14T08:13:39.187103+00:00 | 1,843 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n Calculate the number of permutations of each word,\n Formula is: N! / (Ma! * Mb! * ... * Mz!)\n where N is the amount of letters in the word, and \n Ma, Mb, ..., Mz are the occurrences of repeated letters in the word. \n Each M equals the amount of times the letter appears in the word.\n \n Multiply number of permutations of each word.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(Nlog(mod))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n# Code\n```\n#define ll long long\n#define mod 1000000007\nclass Solution {\npublic:\n ll fact[100005];\n\n void factorial(ll n) {\n fact[0] = 1;\n for(ll i=1; i<=n; i++) fact[i] = i * fact[i-1] % mod;\n }\n\n ll powmod(ll a, ll b) {\n ll ans = 1;\n while(b > 0) {\n if(b & 1) ans = ans * a % mod;\n a = a * a % mod;\n b >>= 1;\n }\n return ans;\n }\n\n ll inv(ll x) {\n return powmod(x, mod-2);\n }\n \n int countAnagrams(string s) {\n ll n = s.size();\n factorial(n);\n s.push_back(\' \');\n unordered_map<char, ll> mp;\n ll ans = 1, cnt = 0;\n for(auto c: s) {\n if(c == \' \') {\n ll up = fact[cnt];\n for(auto x: mp) {\n ll down = fact[x.second];\n up = up * inv(down) % mod;\n }\n ans = ans * up % mod;\n mp.clear();\n cnt = 0;\n }\n else {\n mp[c]++;\n cnt++;\n }\n }\n return ans;\n }\n};\n``` | 9 | 0 | ['C++'] | 3 |
count-anagrams | C++ Euclidean algorithm modular Inverse& Factorials||12ms beats 100% | c-euclidean-algorithm-modular-inverse-fa-dzgz | Intuition\n Describe your first thoughts on how to solve this problem. \nReal math solution is solved by Number theoretical trick, Modular Inverse.\nLet $w$ den | anwendeng | NORMAL | 2024-02-06T07:02:43.411925+00:00 | 2024-02-06T09:42:26.853422+00:00 | 357 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nReal math solution is solved by Number theoretical trick, Modular Inverse.\nLet $w$ denote a word in the string `s` with length $len(w)$ & frequency table\nfreq(w)=$(w_{0}, w_1\\cdots w_{25})$\nThen the answer is\n$$\nans=\\Pi_{w\\in s}\\frac{len(w)!}{w_0!w_1!\\cdots w_{25}!}\\pmod{ p=10^9+7}\n$$\nwhere $x!$ ($x\\in N$) denotes the factorial, i.e. $x=x(x-1)\\cdots(2)1.$ & $0!=1$.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWhy this formula works? The valid anagram, say $\\sigma : s\\to t$ will keep the restriction $\\sigma|_w$ being also an anagram for each word $w$ in `s`.\n\nThe number of anagrams for the word $w$ is the total number of permutaions on $w$ (considering total $len(w)$ letters with $w_0$ a, $w_1$ b$\\cdots w_{25}$ z)which is \n$$\nn(w)=\\frac{len(w)!}{w_0!w_1!\\cdots w_{25}!}.\n$$\nAccording to the multiplicative principle for counting (combinatorics), the total number of valid anagrams is the product.\n\nThe factorial $x=w_i!$ in the denominator is not computed by the usual division, but by computing its modular Inverse $x^{-1}$ ($x\\times x^{-1}\\equiv 1\\pmod{p}$) by the Euclidean algorithm, for that the existence of the modular Inverse is quaranteed by the number $p=10^9+7$ being a prime.\n\nThe idea of applying Euclidean algorithm for finding the modular Inverse is also applied for other Leetcode problems:\n[2954. Count the Number of Infection Sequences](https://leetcode.com/problems/count-the-number-of-infection-sequences/solutions/4357894/c-extended-euclidean-algorithm-modular-power-combinatorics/)\n[2400. Number of Ways to Reach a Position After Exactly k Steps](https://leetcode.com/problems/number-of-ways-to-reach-a-position-after-exactly-k-steps/solutions/4263879/c-extended-euclidean-algorthm-for-modinverse0ms-beats-100/)\n[2906. Construct Product Matrix](https://leetcode.com/problems/construct-product-matrix/solutions/4170288/cmodular-inverse-modpow-vs-prefix-product-suffix-product/)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# C++ Code 12ms beats 100%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nstatic int mod=1e9+7;\nclass Solution {\npublic:\n vector<long long> fact;\n void factorialMod(int n){\n fact.assign(n+1, 1);\n for(int i=2; i<=n; i++){\n fact[i]=fact[i-1]*i%mod;\n }\n }\n // Find x, y, d such that ax + by = d where d = gcd(a, b)\n int modInverse(int a, int b=mod) {//mod is prime d=1\n int x0 = 1, x1 = 0;\n int r0 = a, r1 = b;\n while (r1 != 0) {\n int q = r0/r1, rr = r1, xx = x1;\n r1 = r0-q * r1;\n x1 = x0-q * x1;\n r0 = rr;\n x0 = xx;\n }\n if (x0 < 0) x0+= b;\n return x0;\n }\n long long computePerm(array<int, 26>& freq, int wlen){\n long long ans=fact[wlen];\n for(int f: freq){\n if (f!=0){\n ans=(ans*modInverse(fact[f]))%mod;\n }\n }\n return ans%mod;\n }\n int countAnagrams(string& s) {\n int n=s.size();\n factorialMod(n);\n long long ans=1;\n array<int, 26> freq={0};\n int wlen=0;\n for (int i=0; i<n; i++){\n while(i<n && s[i]!=\' \'){\n freq[s[i]-\'a\']++;\n wlen++;\n i++;\n }\n ans=(ans*computePerm(freq, wlen))%mod;\n if (i<n){\n freq.fill(0);\n wlen=0;\n }\n }\n return ans%mod;\n }\n};\n\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n``` | 6 | 0 | ['Math', 'Combinatorics', 'Counting', 'Number Theory', 'C++'] | 0 |
count-anagrams | [Java] multiply Anagrams of every strings | java-multiply-anagrams-of-every-strings-qjdjy | Code\njava\nclass Solution {\n long mod = (long) 1e9+7;\n public int countAnagrams(String s) {\n int n = s.length();\n long[] fact = new lon | virendra115 | NORMAL | 2022-12-24T18:02:39.074506+00:00 | 2022-12-24T18:15:03.514572+00:00 | 1,863 | false | # Code\n```java\nclass Solution {\n long mod = (long) 1e9+7;\n public int countAnagrams(String s) {\n int n = s.length();\n long[] fact = new long[n+1];\n fact[0] = 1L;\n for(int i=1;i<=n;i++){\n fact[i] = fact[i-1]*i%mod;\n }\n String[] str = s.split(" ");\n long ans = 1;\n for(String t:str){\n int[] ch = new int[26];\n for(char c:t.toCharArray()){\n ch[c-\'a\']++;\n }\n long cur = 1;\n for(int a:ch){\n cur = cur *fact[a]%mod;\n }\n long cur = fact[t.length()] * binpow(cur,mod-2) % mod;\n ans = ans * cur % mod;\n }\n return (int) ans;\n }\n long binpow(long a, long b) {\n if (b == 0)\n return 1;\n long res = binpow(a, b / 2);\n res = res * res % mod;\n if (b % 2==1)\n return res * a % mod;\n else\n return res;\n }\n}\n``` | 6 | 0 | ['Java'] | 2 |
count-anagrams | c++ solution | c-solution-by-dilipsuthar60-oalm | \nclass Solution {\npublic:\n using ll =long long;\n ll mod=1e9+7;\n ll fact[100005];\n ll power(ll a,ll b)\n {\n ll res=1;\n while | dilipsuthar17 | NORMAL | 2022-12-24T17:04:17.453465+00:00 | 2022-12-24T17:04:17.453528+00:00 | 1,600 | false | ```\nclass Solution {\npublic:\n using ll =long long;\n ll mod=1e9+7;\n ll fact[100005];\n ll power(ll a,ll b)\n {\n ll res=1;\n while(b)\n {\n if(b&1)\n {\n res=(res*a)%mod;\n }\n a=(a*a)%mod;\n b/=2;\n }\n return res;\n }\n ll cal(vector<int>&dp)\n {\n ll sum=0;\n for(int i=0;i<26;i++)\n {\n sum+=dp[i];\n }\n ll ans=fact[sum]; // total permutation \n for(int i=0;i<26;i++)\n {\n ans*=(power(fact[dp[i]],mod-2)); // remove duplicate\n ans%=mod;\n }\n /*\n formula\n n!/(a!* b! * c! )\n where a b c are freq of char\n */\n return ans;\n }\n int countAnagrams(string s) \n {\n fact[0]=1;\n for(int i=1;i<100005;i++)\n {\n fact[i]=(i*fact[i-1])%mod;\n }\n int n=s.size();\n vector<int>dp(26,0);\n ll ans=1;\n for(int i=0;i<n;i++)\n {\n if(s[i]==\' \')\n {\n ll value=cal(dp);\n ans*=value;\n ans%=mod;\n dp=vector<int>(26,0);\n }\n else\n {\n dp[s[i]-\'a\']++;\n }\n }\n ll value=cal(dp);\n ans*=value;\n ans%=mod;\n return (int)ans;\n }\n};\n``` | 6 | 0 | ['Math', 'C', 'C++'] | 1 |
count-anagrams | [C++|Java|Python3] multinomial coefficients | cjavapython3-multinomial-coefficients-by-ggo3 | Please pull this commit for solutions of biweekly 94. \n\nIntuition\nOn the math level, this is basically a test of multinomial coeffcients. The tricky part lie | ye15 | NORMAL | 2022-12-24T16:59:04.818730+00:00 | 2022-12-24T18:29:33.133224+00:00 | 2,746 | false | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/3ffc910c12ff8c84890fb15351216a0fa85dc3ac) for solutions of biweekly 94. \n\n**Intuition**\nOn the math level, this is basically a test of multinomial coeffcients. The tricky part lies in the implementation. \n**C++**\n```\nclass Solution {\npublic: \n int countAnagrams(string s) {\n const int mod = 1\'000\'000\'007; \n int n = s.size(); \n vector<long> fact(n+1, 1), ifact(n+1, 1), inv(n+1, 1); \n for (int x = 1; x <= n; ++x) {\n if (x >= 2) inv[x] = mod - mod/x * inv[mod%x] % mod; \n fact[x] = fact[x-1] * x % mod; \n ifact[x] = ifact[x-1] * inv[x] % mod; \n }\n long ans = 1; \n istringstream iss(s); \n string buff; \n while (iss >> buff) {\n ans = ans * fact[buff.size()] % mod; \n vector<int> freq(26); \n for (auto& ch : buff) ++freq[ch-\'a\']; \n for (auto& x : freq) ans = ans * ifact[x] % mod; \n }\n return ans; \n }\n}; \n```\n**Java**\n```\nclass Solution {\n\tpublic int countAnagrams(String s) {\n\t\tfinal int mod = 1_000_000_007; \n\t\tint n = s.length(); \n\t\tlong[] fact = new long[n+1], ifact = new long[n+1], inv = new long[n+1]; \n\t\tfact[0] = ifact[0] = inv[0] = inv[1] = 1; \n\t\tfor (int x = 1; x <= n; ++x) {\n\t\t\tif (x >= 2) inv[x] = mod - mod/x * inv[mod%x] % mod; \n\t\t\tfact[x] = fact[x-1] * x % mod; \n\t\t\tifact[x] = ifact[x-1] * inv[x] % mod; \n\t\t}\n\t\tlong ans = 1; \n\t\tfor (var buff : s.split(" ")) {\n\t\t\tans = ans * fact[buff.length()] % mod; \n\t\t\tint[] freq = new int[26]; \n\t\t\tfor (var ch : buff.toCharArray()) ++freq[ch-\'a\']; \n\t\t\tfor (var x : freq) ans = ans * ifact[x] % mod; \n\t\t}\n\t\treturn (int) ans; \n\t}\n}\n```\n**Python3**\n```\nclass Solution: \n def countAnagrams(self, s: str) -> int:\n n = len(s)\n mod = 1_000_000_007\n inv = [1]*(n+1)\n fact = [1]*(n+1)\n ifact = [1]*(n+1)\n for x in range(1, n+1): \n if x >= 2: inv[x] = mod - mod//x * inv[mod % x] % mod \n fact[x] = fact[x-1] * x % mod \n ifact[x] = ifact[x-1] * inv[x] % mod \n ans = 1\n for word in s.split(): \n ans *= fact[len(word)]\n for x in Counter(word).values(): ans *= ifact[x]\n ans %= mod \n return ans \n``` | 6 | 0 | ['C', 'Java', 'Python3'] | 3 |
count-anagrams | C++ || FACTORIAL AND THEIR INVERSE (Mathematics) (Easy to Understand) | c-factorial-and-their-inverse-mathematic-v5cd | Explanation:\nAns is multiplication of nos of different permutations of all words in the given string\n\nExample:\n\nsuppose the given string is "abc bcd ffa"\n | amitkumaredu | NORMAL | 2022-12-24T16:50:56.811139+00:00 | 2022-12-24T17:27:47.651890+00:00 | 1,726 | false | Explanation:\nAns is multiplication of nos of different permutations of all words in the given string\n\nExample:\n\nsuppose the given string is "abc bcd ffa"\nwe can write abc in 6 ways\nbcd in 6 ways\nsimilarly ffa in 3 ways (ffa,faf,aff)\ntotal no of different strings that can be produced\nwe have 3 positions\n"___ ___ ___"\nTotal 6 * 6 * 3 ways (Fundamental Principle of Counting) or can say observation.\n\nTo find individual way of writing a word we can do\nFactorial of length of that word divide by\n(Multiplication of factorial of count of [\'a\',\'z\'] in that word).\n\nBut here factorials value are large so we can\'t perform divide instead we can multiply with their inverse.\n\nHope You understand the solutoin.\nFor clarification comment down.\n\n**Complexity**\n\n**Time complexity:** O(logn+n+(no of words*(length of word + 26)) )\n**Space complexity:** O(n)\n\n**Code**\n```\n\n\n\nclass Solution\n{\npublic:\n#define ll long long\n const int mod = 1e9 + 7;\n\n vector<ll> fact, invfact;\n\n ll binpow(ll a, ll b, ll p)\n {\n ll res = 1;\n a %= p;\n while (b)\n {\n if (b & 1)\n res = (res * a) % p;\n a = (a * a) % p;\n b >>= 1;\n }\n return res;\n }\n\n void precompute()\n {\n ll n = 100000;\n\n fact.resize(n + 1);\n invfact.resize(n + 1);\n\n fact[0] = 1;\n for (int i = 1; i <= n; ++i)\n fact[i] = (fact[i - 1] * i) % mod;\n\n invfact[n] = binpow(fact[n], mod - 2, mod);\n for (int i = n - 1; i >= 0; --i)\n invfact[i] = (invfact[i + 1] * (i + 1)) % mod; // computing all factorial inverses in O(N)\n }\n\n int countAnagrams(string s)\n {\n precompute();\n vector<string> S;\n stringstream ss(s);\n string SS;\n while (ss >> SS)\n S.push_back(SS); // Getting all words from the main string ( we can do normal for loop also)\n int ans = 1;\n for (auto x : S)\n {\n ans = (ans * fact[x.size()]) % mod;\n map<char, int> mp;\n for (auto y : x)\n mp[y]++;\n for (auto counts : mp)\n ans = (ans * invfact[counts.second]) % mod;\n\n }\n\n return ans;\n }\n};\n``` | 5 | 1 | ['Math', 'String', 'Combinatorics'] | 2 |
count-anagrams | Best Solution for Arrays, DP, String 🚀 in C++, Python and Java || 100% working | best-solution-for-arrays-dp-string-in-c-x87fw | 💡 IntuitionFor each word, count the permutations by dividing the factorial of its length by the factorials of the frequencies of its characters. Use modular ari | BladeRunner150 | NORMAL | 2025-01-10T06:46:59.554924+00:00 | 2025-01-10T06:46:59.554924+00:00 | 367 | false | # 💡 Intuition
For each word, count the permutations by dividing the factorial of its length by the factorials of the frequencies of its characters. Use modular arithmetic to handle large numbers. 🚀
# 🔮 Approach
1. Put all numbers in a HashSet (removes duplicates automatically)
2. Loop from 1 to n
3. If number isn't in set, it's missing! ✨
# ⏳ Complexity
- Time: $$O(n)$$ for creating set and checking numbers
- Space: $$O(n)$$ for storing set
# 💻 Code
```cpp []
Code
class Solution {
public:
int countAnagrams(string s) {
long long MOD = 1e9 + 7;
vector<long long> fact(101, 1);
for (int i = 2; i <= 100; i++) {
fact[i] = fact[i - 1] * i % MOD;
}
long long ans = 1;
stringstream ss(s);
string word;
while (ss >> word) {
vector<int> freq(26, 0);
for (char c : word) freq[c - 'a']++;
long long count = fact[word.size()];
for (int f : freq) {
if (f > 1) count = count * pow(fact[f], MOD - 2, MOD) % MOD;
}
ans = ans * count % MOD;
}
return ans;
}
};
```
```python []
Code
class Solution(object):
def countAnagrams(self, s):
MOD = 10**9 + 7
def mod_inv(x, mod=MOD):
return pow(x, mod - 2, mod)
arr = s.split()
max_len = max(len(word) for word in arr)
fact = [1] * (max_len + 1)
for i in range(2, max_len + 1):
fact[i] = fact[i - 1] * i % MOD
ans = 1
for word in arr:
count = fact[len(word)]
freq = {}
for char in word:
freq[char] = freq.get(char, 0) + 1
for v in freq.values():
count = count * mod_inv(fact[v]) % MOD
ans = ans * count % MOD
return ans
```
```java []
Code
class Solution {
public int countAnagrams(String s) {
long MOD = 1_000_000_007;
String[] words = s.split(" ");
int maxLen = 0;
for (String word : words) {
maxLen = Math.max(maxLen, word.length());
}
long[] fact = new long[maxLen + 1];
fact[0] = 1;
for (int i = 1; i <= maxLen; i++) {
fact[i] = fact[i - 1] * i % MOD;
}
long ans = 1;
for (String word : words) {
long count = fact[word.length()];
int[] freq = new int[26];
for (char c : word.toCharArray()) {
freq[c - 'a']++;
}
for (int f : freq) {
if (f > 1) count = count * modInverse(fact[f], MOD) % MOD;
}
ans = ans * count % MOD;
}
return (int) ans;
}
private long modInverse(long x, long mod) {
long res = 1, pow = mod - 2;
while (pow > 0) {
if ((pow & 1) == 1) res = res * x % mod;
x = x * x % mod;
pow >>= 1;
}
return res;
}
}
``` | 4 | 0 | ['Hash Table', 'Math', 'String', 'Combinatorics', 'Counting', 'Python', 'C++', 'Java', 'Python3'] | 1 |
count-anagrams | Math + combinatorics [EXPLAINED] | math-combinatorics-explained-by-r9n-78yt | IntuitionI noticed that the problem is about finding how many ways we can rearrange the letters of each word while keeping the words in their original positions | r9n | NORMAL | 2024-12-27T03:57:11.220880+00:00 | 2024-12-27T03:57:11.220880+00:00 | 63 | false | # Intuition
I noticed that the problem is about finding how many ways we can rearrange the letters of each word while keeping the words in their original positions. Since we only care about permutations of the letters in each word, I focused on counting all unique arrangements for every word separately.
# Approach
Break the sentence into individual words, compute how many unique ways each word's letters can be rearranged by using the counts of each letter to adjust the total number of possibilities, and then combine the results for all the words while keeping everything within a set mathematical limit to handle large results.
# Complexity
- Time complexity:
O(n + m) where n is the length of the string for splitting and m is for precomputing factorials.
- Space complexity:
O(m) for storing factorials and character counts.
# Code
```rust []
impl Solution {
pub fn count_anagrams(s: String) -> i32 {
const MOD: i64 = 1_000_000_007;
// Helper function to compute factorial modulo MOD
fn factorial_mod(n: usize, mod_val: i64) -> Vec<i64> {
let mut fact = vec![1; n + 1];
for i in 2..=n {
fact[i] = fact[i - 1] * i as i64 % mod_val;
}
fact
}
// Helper function to compute modular multiplicative inverse
fn mod_inverse(x: i64, mod_val: i64) -> i64 {
let mut base = x;
let mut exp = mod_val - 2;
let mut result = 1;
while exp > 0 {
if exp % 2 == 1 {
result = result * base % mod_val;
}
base = base * base % mod_val;
exp /= 2;
}
result
}
// Precompute factorials and modular inverses up to the max possible length
let max_len = 100_000;
let fact = factorial_mod(max_len, MOD);
s.split_whitespace()
.map(|word| {
let mut freq = vec![0; 26];
for &b in word.as_bytes() {
freq[(b - b'a') as usize] += 1;
}
let mut result = fact[word.len()];
for &count in &freq {
if count > 1 {
result = result * mod_inverse(fact[count], MOD) % MOD;
}
}
result
})
.fold(1, |acc, x| acc * x % MOD) as i32
}
}
``` | 4 | 0 | ['Hash Table', 'Math', 'String', 'Combinatorics', 'Counting', 'Rust'] | 0 |
count-anagrams | Super short simple Python Solution || Dictionaries and Math.factorial | super-short-simple-python-solution-dicti-fk1o | Intuition\n Describe your first thoughts on how to solve this problem. \nThe idea is very simple. Total count of anagrams for each word is\n(factorial of length | u-day | NORMAL | 2023-02-01T05:33:22.721355+00:00 | 2023-02-01T05:33:22.721410+00:00 | 294 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea is very simple. Total count of anagrams for each word is\n(factorial of length of word) divided by factorial of duplicates.\n\nEg : aabbc - 5!/(2! * 2!)\n\n# Code\n```\nmod = 10**9+7\n\nclass Solution:\n def countAnagrams(self, s: str) -> int:\n\n l = s.split()\n ans = 1\n\n for i in l:\n d = {}\n # counting frequencies of word i in dictionary d\n for j in i:\n if(d.get(j)):\n d[j] += 1\n else:\n d[j] = 1 \n \n duplicates = 1\n for j in d.values():\n duplicates *= math.factorial(j)\n curr = math.factorial(len(i))//duplicates\n\n ans *= curr\n ans = ans%mod\n\n return ans \n \n \n``` | 4 | 0 | ['Python3'] | 0 |
count-anagrams | Java build-in method to calc mod inverse | java-build-in-method-to-calc-mod-inverse-kpud | Intuition\nAssuming you have already known that a / b != (a % mod) / (b % mod)\n(Division is not allowed as a modular arithmetic operation.) \nOne of the approc | Vegetablebirds | NORMAL | 2022-12-26T16:52:08.561666+00:00 | 2022-12-26T16:52:08.561708+00:00 | 1,192 | false | # Intuition\nAssuming you have already known that a / b != (a % mod) / (b % mod)\n(Division is not allowed as a modular arithmetic operation.) \nOne of the approches to handle this problme is using inverse multiplication.)\n\nkudos to this post: https://leetcode.cn/problems/count-anagrams/solution/java-cheng-fa-ni-yuan-nei-zhi-han-shu-by-02y7/\n\nThere is an Java build-in method:\n` public BigInteger modInverse(BigInteger m)` to calc mod inverse\uFF08a BigInteger whose value is this ^ -1 mod m)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nlong inv = BigInteger.valueOf(fac[v]).modInverse(BigInteger.valueOf(mod)).longValue();\n\n# Complexity\n- Time complexity:\nN/A\n\n- Space complexity:\nN/A\n\n# Code\n```\nimport java.math.BigInteger;\nclass Solution {\n long mod = (long) (1e9 + 7);\n long[] fac;\n public int countAnagrams(String s) {\n\n fac = new long[s.length() + 1];\n fac[1] = 1;\n for (int i = 2; i <= s.length(); i++) {\n fac[i] = (fac[i - 1] * i) % mod;\n }\n String[] ws = s.split(" ");\n long ans = 1;\n for (String w : ws) {\n ans = (ans * calc(w)) % mod;\n }\n return (int)ans;\n }\n private long calc(String w) {\n Map<Character, Integer> m = new HashMap<>();\n for (char ch : w.toCharArray()) {\n m.put(ch, m.getOrDefault(ch, 0) + 1);\n }\n long all = fac[w.length()];\n for (int v : m.values()) {\n long inv = BigInteger.valueOf(fac[v]).modInverse(BigInteger.valueOf(mod)).longValue();\n all = all * inv % mod;\n }\n return all;\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
count-anagrams | [Python3] Math (combinatorics) | python3-math-combinatorics-by-xil899-45tq | Code\n\nclass Solution:\n def countAnagrams(self, s: str) -> int:\n MOD = 10 ** 9 + 7\n ans = 1\n for word in s.split():\n an | xil899 | NORMAL | 2022-12-24T21:47:04.857870+00:00 | 2022-12-24T21:47:20.841189+00:00 | 471 | false | # Code\n```\nclass Solution:\n def countAnagrams(self, s: str) -> int:\n MOD = 10 ** 9 + 7\n ans = 1\n for word in s.split():\n ans = (ans * self.count(word)) % MOD\n return ans\n \n def count(self, word):\n n = len(word)\n ans = 1\n for f in Counter(word).values():\n ans *= math.comb(n, f)\n n -= f\n return ans\n \n``` | 4 | 0 | ['Math', 'Combinatorics', 'Python3'] | 2 |
count-anagrams | C++ || FACTORIAL | c-factorial-by-ganeshkumawat8740-382i | calculate no of possible combinarion of each word and than multiplay each calculated ans of each word.\n# Code\n\nclass Solution {\npublic:\n int modin(int x | ganeshkumawat8740 | NORMAL | 2023-05-25T10:51:30.065956+00:00 | 2023-05-25T10:51:30.066002+00:00 | 2,359 | false | calculate no of possible combinarion of each word and than multiplay each calculated ans of each word.\n# Code\n```\nclass Solution {\npublic:\n int modin(int x){\n int k = 1e9+5, mod = 1e9+7,ans = 1;\n while(k){\n if(k&1){\n ans = (ans*1LL*x)%mod;\n }\n x = (x*1LL*x)%mod;\n k >>= 1;\n }\n return ans;\n }\n int countAnagrams(string s) {\n int ans = 1, mod = 1e9+7,k;\n int n = s.length(),i;\n vector<int> dp(n+1,1);\n for(i = 2; i <= n; i++){\n dp[i] = (i*1LL*dp[i-1])%mod;\n }\n vector<int> v(26,0);\n int x = 0;\n for(auto &i: s){\n if(i==\' \'){\n k = dp[x];\n for(auto &j: v){\n if(j>1)\n k = (k*1LL*modin(dp[j]))%mod;\n }\n ans = (ans*1LL*k)%mod;\n // cout<<ans<< " ";\n fill(v.begin(),v.end(),0);\n x = 0;\n }else{\n x++;\n v[i-\'a\']++;\n }\n }\n // cout<<"#";\n k = dp[x];\n for(auto &j: v){\n if(j>1)\n k = (k*1LL*modin(dp[j]))%mod;\n }\n ans = (ans*1LL*k)%mod;\n // cout<<ans;\n \n return ans;\n }\n};\n``` | 3 | 0 | ['Hash Table', 'Math', 'String', 'Combinatorics', 'C++'] | 0 |
count-anagrams | Fast C++ soln | Maths explained | O(n) TC | fast-c-soln-maths-explained-on-tc-by-arj-f9ld | Intuition\nFor a given string, the answer can be found separately for each word in the string and multiplying over all words (from fundamental counting principl | arjunp0710 | NORMAL | 2022-12-25T03:56:51.729919+00:00 | 2022-12-25T03:56:51.729946+00:00 | 638 | false | # Intuition\nFor a given string, the answer can be found separately for each word in the string and multiplying over all words (from fundamental counting principle)\n\nFor each word, again use the counting principle. For ex: given a word `abbccd`\nthe number of anagrams is the number of permutations of this string -\n$ n= 6 \\ \\ \\textrm{(length of the string)}$\n$freq(a) = 1 \\\\ \n freq(b) = 2 \\\\\n freq(c) = 2 \\\\\n freq(d) = 1\n$\n$ count = \\frac{6!}{1! \\times 2! \\times 2! \\times 1!}\n$\n\n# Approach\n\n\n1. split the given string into words. I have done this using [`std::stringstream`](https://cplusplus.com/reference/sstream/stringstream/stringstream/).\n2. For each word calculate the number of anagrams as follows -\n\n 1. find the frequency of each character in the word. Let it be denoted by $count(i)$ where $i$ is a character in the word\n 2. let $n$ be the length of this word\n 3. now the answer is \n $$ans= \\frac{n!}{\\prod count(i)!}$$\n3. multiply the answer across all words.\n\nI have precalculated the factorial and its inverse using the following formulae -\n\n$ f(i) =f(i-1) \\times i$\n\nthe inverse is a direct result of [Fermat\'s Little Theorem](https://en.wikipedia.org/wiki/Fermat%27s_little_theorem)\n\n$$ x^{-1} \\equiv x^{m-2}\\ \\textrm{mod}\\ m $$\n\nFurther-\n\n$f(i)^{-1} = (i \\times f(i-1))^{-1}$\n$ \\implies f(i)^{-1} =i^{-1} \\times f(i-1)^{-1} $\n$\\implies f(i-1)^{-1}=f(i)^{-1} \\times i $\n\n\n\n\n# Code\n```\nconst long long mod=1e9+7;\nusing ll=long long;\n\n// binary exponentiation\nll binpow(ll a, ll b, ll m)\n{\n\ta %= m;\n\tll res = 1;\n\twhile (b > 0)\n\t{\n\t\tif (b & 1) res = res * a % m;\n\t\ta = a * a % m;\n\t\tb >>= 1;\n\t}\n\treturn res;\n}\n// find modular multiplicative inverse \n// using fermat\'s little theorem\nll inv(ll a, ll m = mod) { return binpow(a, m - 2, m); }\n\nconst int N=(int)1e5;\nll fact[N+1];\nll inv_fact[N+1];\nvoid precalc()\n{\n fact[0]=1;\n for(int i=1;i<=N;i++)\n fact[i]=(fact[i-1]*i)%mod;\n inv_fact[N]=inv(fact[N]);\n for(int i=N-1;i>=0;i--)\n inv_fact[i]=(inv_fact[i+1]*(i+1))%mod;\n}\nclass Solution {\npublic:\n Solution()\n {\n // call precalc only once across all testcases\n precalc();\n }\n // get the answer for each word\n int calc_for_word(const string&s)\n {\n // frequency array for each character \n ll a[26]{};\n for(auto &ch:s)\n {\n a[ch-\'a\']++;\n }\n ll ans=fact[s.size()];\n for(int i=0;i<26;i++)\n {\n ans*=inv_fact[a[i]];\n ans%=mod;\n }\n return ans; \n }\n int countAnagrams(string str) {\n std::stringstream ss(str);\n string temp;\n ll ans=1;\n while(ss>>temp){\n ans*=calc_for_word(temp);\n ans%=mod;\n }\n return ans;\n }\n};\n\n```\n\n# Complexity\n- Time complexity:\n 1. `precalc` - $O(n)$\n 2. `countAnagrams` - $O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n | 3 | 0 | ['Math', 'Memoization', 'C++'] | 1 |
count-anagrams | C++ Solution✅ | Detailed Explanation ⭐️ | c-solution-detailed-explanation-by-f_in_-77gp | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problems essentially asks us to find the number of distinct permutations for the en | f_in_the_chat | NORMAL | 2022-12-24T17:15:35.467141+00:00 | 2022-12-24T17:15:35.467198+00:00 | 573 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problems essentially asks us to find the number of distinct permutations for the entire string. \n\nThis boils down to finding the number of distinct permuations of each word in the string and multiplying them to get total number of permuations. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor every word, we get it\'s length. We also keep track of the occurrence of every character in that word. \n\nAfter this let\'s find the number of distinct permuations for this word.\nIt\'s going to be $$({n!}/{(x! * y! * ... z!)})$$, here n is the length of the word, and x, y, z are characters that have repeated x, y, z times.\n\nNow, we just multiply this with our answer and reset all the variables and keep doing this for all the words. \n\nFor calculating the factorials we can precompute all factorials till 1e5.\n\nSince, there is division taking place under modulo, we need to find the modulo multiplicative inverse of $${(x! * y! * ... z!)}$$ with respect to our modulo (1e9+7).\n\nModulo Multiplicative Inverse for a number N, when the modulo is prime is given by : $$(N^{MOD-2})$$ with respect to modulo $${MOD}$$\n\nWe can use binary exponentiation to calculate $$(a^b)$$ in $$log(b)$$ time.\nAlso, keep in mind to use modular multiplication everywhere.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nlogn)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\nclass Solution {\nprivate:\n const int mod=1e9+7;\n long long fact[100001];\n \n int modMul(int a,int b,int mod){\n return ((long long)(a%mod)*(b%mod))%mod;\n }\n \n int binpow(int a,int b,int mod){\n if(b==0)return 1;\n long long res=binpow(a,b/2,mod);\n res=modMul(res,res,mod);\n if(b & 1){\n res=modMul(res,a,mod);\n }\n return res;\n }\n \n void computeFactorial(){\n fact[0]=1;\n for(int i=1;i<100001;i++){\n fact[i]=modMul(fact[i-1],i,mod);\n }\n } \n \n int modInv(int a,int mod){\n return binpow(a,mod-2,mod);\n }\npublic:\n // For a given word of len(n) the number of permutations are: \n // n!/(x1!*x2!*..xk!),\n // where x1,x2,.. are repeating letters.\n int countAnagrams(string s) {\n computeFactorial();\n \n map<char,int>characterOccurrence;\n string cur="";\n int curLen=0;\n int rep=0;\n int ans=1;\n int n=(int)s.size(); \n \n for(int i=0;i<n;i++){\n if(s[i]==\' \'){\n int currentLenFact=fact[curLen]; \n int repFact=1;\n for(auto character:characterOccurrence){\n repFact=modMul(repFact,fact[character.second],mod); \n } \n ans=modMul(ans,modMul(currentLenFact,modInv(repFact,mod),mod),mod);\n curLen=0,rep=0;\n characterOccurrence.clear();\n }\n else{\n characterOccurrence[s[i]]++;\n curLen++;\n }\n }\n int currentLenFact=fact[curLen];\n int repFact=1;\n for(auto character:characterOccurrence){\n repFact=modMul(repFact,fact[character.second],mod); \n }\n ans=modMul(ans,modMul(currentLenFact,modInv(repFact,mod),mod),mod);\n return ans;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
count-anagrams | C++ || Math || Modulo Multiplicative Inverse || Permutations | c-math-modulo-multiplicative-inverse-per-z3rn | Here, for all words we can find distinct permutations and than for distinct permutations for whole string we have to multiply all distinct permutations that can | krunal_078 | NORMAL | 2022-12-24T16:52:35.341643+00:00 | 2022-12-24T17:39:31.365011+00:00 | 2,057 | false | * Here, for all words we can find distinct permutations and than for distinct permutations for whole string we have to multiply all distinct permutations that can be made from each words.\n* For `too` there are three possible permutations `1.too 2. oot 3. oto` .\n* For finding distinct permutations ,` n! / r1! * r2! ... rn! `, where n is the size of the string and r1 to rn is frequency of the repetitive characters.\n* ` s = "too hot"` i.e for `too = 3! / 2! = 3`, `hot = 3! = 6`, so answer is 3 * 6 = 18.\n* For dividing by factorial we can use modulo multiplicative inverse.\n\n```\nclass Solution {\npublic:\n const static int mod = 1e9+7,N = 1e5+10;\n long long fact[N];\n long long power(long long x,int y,int mod){\n long long ans = 1;\n x = x%mod;\n while(y >0){\n if(y&1){\n ans = (ans*x)%mod;\n }\n y>>=1;\n x = (x*x)%mod;\n }\n return ans;\n }\n long long modInverse(long long n,int mod){\n return power(n,mod-2,mod);\n }\n void init(){\n fact[0] = 1;\n for(int i=1;i<N;i++){\n fact[i] = (fact[i-1]*i)%mod;\n }\n }\n int countAnagrams(string s){\n init();\n int n = s.size();\n vector<string> tmp;\n string val = "";\n for(int i=0;i<n;i++){\n if(s[i]==\' \'){\n if(val!="") tmp.push_back(val);\n val = "";\n }\n else{\n val.push_back(s[i]);\n }\n }\n if(val!="") tmp.push_back(val);\n long long ans = 1;\n for(auto &ele:tmp){\n cout<<ele<<" ";\n unordered_map<char,int> mp;\n for(int i=0;i<ele.size();i++){\n mp[ele[i]]++;\n }\n ans = (ans*fact[(int)ele.size()])%mod;\n for(auto &pr:mp){\n long long inv = modInverse(fact[pr.second],mod)%mod;\n ans = (ans*inv)%mod;\n }\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['Math', 'C'] | 3 |
count-anagrams | PYTHON || FACTORIAL|| SIMPLE SOLUTION USING HASHMAP | python-factorial-simple-solution-using-h-y491 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Panda_606 | NORMAL | 2023-11-22T08:59:51.510627+00:00 | 2023-11-22T08:59:51.510656+00:00 | 583 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countAnagrams(self, s: str) -> int:\n def display(word):\n fact=math.factorial(len(word))\n hashmap={}\n for w in word:\n hashmap[w]=hashmap.get(w,0)+1\n \n for val in hashmap.values():\n fact//=math.factorial(val)\n \n return fact\n ways=1\n for word in s.split():\n ways*=display(word)\n return ways%((10**9)+ 7)\n \n``` | 2 | 0 | ['Python3'] | 1 |
count-anagrams | Simple python3 Solution || Explained code | simple-python3-solution-explained-code-b-x85m | Intuition\nCode explained in comments.\n\n# Code\n\n#from itertools import permutations\nclass Solution:\n def countAnagrams(self, s: str) -> int:\n m | Priyanka0505 | NORMAL | 2023-06-15T21:27:54.494813+00:00 | 2023-06-15T21:27:54.494844+00:00 | 224 | false | # Intuition\nCode explained in comments.\n\n# Code\n```\n#from itertools import permutations\nclass Solution:\n def countAnagrams(self, s: str) -> int:\n mod= 10**9 + 7\n #splitting the words of string s in list w\n w=s.split(" ")\n a=[]\n #then iterating the words in list and appending the permutation of the word to list a\n for i in w:\n a.append(Solution.perm(i))\n #multiplying the elements of list to return the total count of Anagrams\n result = 1\n for num in a:\n result *= num\n return result % mod\n\n #function to calculate the permutation of a given string \n def perm(inputt):\n char_counts = Counter(inputt)\n total_permutations = factorial(len(inputt))\n denominator = 1\n for i in char_counts.values():\n denominator *= factorial(i)\n return total_permutations // denominator\n``` | 2 | 0 | ['Python3'] | 0 |
count-anagrams | easy solution with modular inverse, stringstream | easy-solution-with-modular-inverse-strin-s2k4 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | minuszk4 | NORMAL | 2023-06-10T11:21:02.597250+00:00 | 2023-06-10T11:21:02.597282+00:00 | 178 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n \nconst int MOD = 1e9+7;\nint modInverse(int a, int m) {\n int m0 = m;\n int y = 0, x = 1;\n\n if (m == 1)\n return 0;\n\n while (a > 1) {\n int q = a / m;\n int t = m;\n\n m = a % m;\n a = t;\n t = y;\n\n y = x - q * y;\n x = t;\n }\n\n if (x < 0)\n x += m0;\n\n return x;\n}\n\nint countAnagrams(string s) {\n stringstream ss(s);\n string temp;\n long long ans = 1;\n vector<int> fac(s.size()+10,1);\n for (int i = 2; i <= s.size()+8; i++) {\n fac[i] = (i * 1LL * fac[i - 1]) % MOD;\n }\n\n while (ss >> temp) {\n int tem = fac[temp.size()];\n map<char, int> mp;\n\n for (int i = 0; i < temp.size(); i++) {\n mp[temp[i]]++;\n }\n\n for (auto m : mp) {\n int inverse = modInverse(fac[m.second], MOD);\n tem = (tem * 1LL * inverse) % MOD;\n }\n\n\n ans = (ans *1LL* tem) % MOD;\n }\n\n return ans;\n}\n};\n``` | 2 | 0 | ['Hash Table'] | 1 |
count-anagrams | Modular Arithmetic | Inverse Modulo | Explanation with comments | modular-arithmetic-inverse-modulo-explan-iee2 | \nclass Solution\n{\n\tlong long binExpo(long long a, long long b, long long m)\n\t{\n\t\tif (b == 0)\n\t\t{\n\t\t\treturn 1;\n\t\t}\n\t\tlong long ans = binExp | aksh_mangal | NORMAL | 2023-04-23T18:19:42.654830+00:00 | 2023-04-23T18:20:10.617052+00:00 | 527 | false | ```\nclass Solution\n{\n\tlong long binExpo(long long a, long long b, long long m)\n\t{\n\t\tif (b == 0)\n\t\t{\n\t\t\treturn 1;\n\t\t}\n\t\tlong long ans = binExpo(a, b / 2, m);\n\t\tans = (ans * ans) % m;\n\t\tif (b & 1)\n\t\t{\n\t\t\tans = (ans * a) % m;\n\t\t}\n\t\treturn ans;\n\t}\n\npublic:\n\tint countAnagrams(string s)\n\t{\n\t\t// conversion of string of words into vector of words for simplicity\n\t\tstringstream ss(s);\n\t\tvector<string> words;\n\t\tstring str = "";\n\t\tint maxi = -1; // storing maximum length of word in s\n\n\t\twhile (ss >> str)\n\t\t{\n\t\t\twords.push_back(str);\n\t\t\tint len = str.size();\n\t\t\tmaxi = max(maxi, len); // calculating the maximum length of word for precomputation\n\t\t}\n\n\t\tlong long fact[maxi + 1];\n\t\tfact[0] = 1;\n\t\tlong long mod = 1e9 + 7;\n\t\tfor (int i = 1; i <= maxi; i++)\n\t\t{\n\t\t\tfact[i] = (fact[i - 1] * i) % mod;\n\t\t}\n\t\tunordered_map<char, int> freq; // used to store freq of each of each character\n\t\tint res = 1;\t\t\t\t // final result\n\n\t\tfor (auto &curr : words)\n\t\t{\n\t\t\tfor (auto &j : curr)\n\t\t\t{ // calculating the freq of each char of curr word\n\t\t\t\tfreq[j]++;\n\t\t\t}\n\t\t\tlong ans = fact[curr.size()];\n\t\t\tfor (auto j : freq)\n\t\t\t{\n\t\t\t\tans = (ans * binExpo(fact[j.second], mod - 2, mod)) % mod; // inverse modulo\n\t\t\t}\n\t\t\tres = ((res % mod) * (ans % mod)) % mod;\n\t\t\tfreq.clear();\n\t\t}\n\t\treturn res;\n\t}\n};\n``` | 2 | 0 | ['Math', 'String', 'Combinatorics', 'Counting', 'C++'] | 0 |
count-anagrams | C++ || TIME O(n),SPACE(n) || MULTIPLY PERMUTATION || SHORT & SWEET CODE | c-time-onspacen-multiply-permutation-sho-r07n | /\nlets a substring is aaabbbcc\nso ans for this \n 8!/(3!3!2!)\n/\n\nclass Solution {\npublic:\n int getinverse(long long int a,int b,int c){\n | yash___sharma_ | NORMAL | 2023-04-13T10:12:18.099211+00:00 | 2023-04-13T10:12:35.258205+00:00 | 1,423 | false | /*\nlets a substring is aaabbbcc\nso ans for this \n 8!/(3!*3!*2!)\n*/\n````\nclass Solution {\npublic:\n int getinverse(long long int a,int b,int c){\n long long int ans = 1;\n while(b){\n if(b&1){\n ans = (ans*a)%c;\n }\n a = (a*a)%c;\n b >>= 1;\n }\n return ans;\n }\n int countAnagrams(string s) {\n int mod = 1e9+7;\n int n = s.length(),i;\n vector<int> fact(n+10,1);\n for(i = 2; i <= n+8; i++){\n fact[i] = (fact[i-1]*1LL*i)%mod;//get factorial till s.length\n }\n long long int ans = 1,tmp;\n vector<int> factinv(n+10,0);\n for(int i = 0; i <= n+8; i++){\n factinv[i] = getinverse(fact[i],mod-2,mod);//factorial inverse of eash number\n }\n vector<int> dp(26,0);\n int k = 0;//k = length of substring\n for(auto &i: s){\n if(i==\' \'){//perform above mentioned approach\n tmp = fact[k];//\n for(auto &j: dp){\n tmp = (tmp*1LL*factinv[j])%mod;\n }\n ans = (ans*tmp)%mod;\n fill(dp.begin(),dp.end(),0);\n k = 0;\n }else{\n dp[i-\'a\']++;\n k++;\n }\n }\n\t\t//for last substring\n tmp = fact[k];\n for(auto &j: dp){\n tmp = (tmp*1LL*factinv[j])%mod;\n }\n ans = (ans*tmp)%mod;\n return ans;\n }\n};\n```` | 2 | 0 | ['Math', 'String', 'C', 'C++'] | 1 |
count-anagrams | [scala] - modulo arithmetic step by step guide | scala-modulo-arithmetic-step-by-step-gui-p239 | Intuition\nIn order to count anagrams we should count permutations of letters for each word and multiply them. Permutations are computed with factorial. The sim | nikiforo | NORMAL | 2023-01-18T17:16:15.876715+00:00 | 2023-01-18T17:16:15.876762+00:00 | 48 | false | # Intuition\nIn order to count anagrams we should count permutations of letters for each word and multiply them. Permutations are computed with factorial. The simplest solution looks like this:\n\n```scala\nval m = 1000000007\n\ndef countAnagrams(s: String): Int = {\n val wordCounts = s.split(\' \').map { word =>\n val charCounts = word.groupBy(identity).map(pair => factorial(pair._2.length()))\n factorial(word.length()) / charCounts.reduce(_ * _)\n }\n wordCounts.reduce(_ * _).mod(m).toInt\n}\n\ndef factorial(n: Int): BigInt = BigInt(2.to(n).foldLeft(1)((acc, el) => acc * el % m))\n```\nHowever, the solution fails the performance test case. To count it effectively we should switch to modulo arithmetics.\nNotice, that we require only four operations in our algebra:\n```scala\ntrait Arithmetic[T] {\n def factorial(n: Int): T\n def multiply(a: T, b: T): T\n def division(a: T, b: T): T\n def toInt(n: T): Int\n}\n```\n\nThe original solution can be rewritten in terms of this trait:\n```scala\ndef doCount[T](s: String, ar: Arithmetic[T]): Int = {\n val wordCounts = s.split(\' \').toList.map { word =>\n val charCounts = word.groupBy(identity).map(pair => ar.factorial(pair._2.length))\n ar.division(ar.factorial(word.length()), charCounts.reduce(ar.multiply))\n }\n ar.toInt(wordCounts.reduce(ar.multiply))\n}\n```\nwith the corresponding arithemtic:\n```scala\nfinal class BigIntModuloArithmetic(m: Int) extends Arithmetic[BigInt] {\n def factorial(n: Int): BigInt = 2.to(n).foldLeft(BigInt(1))((acc, el) => acc * el)\n def multiply(a: BigInt, b: BigInt): BigInt = a * b\n def division(a: BigInt, b: BigInt): BigInt = a / b\n def toInt(n: BigInt): Int = (n % m).toInt\n}\n```\nWe can verify that this code works the same as the original solution using\n```scala\ndef countAnagrams(s: String): Int =\n doCount(s, new BigIntModuloArithmetic(1000000007))\n```\n\nLastly, we need to implement modulo arithmetic. `factorial`, `multiply` and `toInt` are trivial, whereas `division` is not.\n```scala\nfinal class IntModuloArithmetic(mInt: Int) extends Arithmetic[Int] {\n private val m = BigInt(mInt)\n def factorial(n: Int): Int = 2.to(n).foldLeft(1)((acc, el) => multiply(acc, el))\n def multiply(a: Int, b: Int): Int = (BigInt(a) * BigInt(b)).mod(m).toInt\n def division(a: Int, b: Int): Int = (BigInt(b).modInverse(m) * a).mod(m).toInt\n def toInt(n: Int): Int = n\n}\n```\nTo verify the implementation we need to change the implementation of `countAnagram` \n```scala\ndef countAnagrams(s: String): Int =\n doCount(s, new IntModuloArithmetic(1000000007))\n``` | 2 | 0 | ['Scala'] | 0 |
count-anagrams | easy python solution | easy-python-solution-by-ashok0888-gtmy | \ndef countAnagrams(self, s: str) -> int:\n res=1\n for i in s.split():\n a=Counter(i)\n l=factorial(len(i))\n \n | ashok0888 | NORMAL | 2023-01-09T14:39:48.371075+00:00 | 2023-01-09T14:39:48.371117+00:00 | 415 | false | ```\ndef countAnagrams(self, s: str) -> int:\n res=1\n for i in s.split():\n a=Counter(i)\n l=factorial(len(i))\n \n for k,v in a.items():\n l=l//factorial(v)\n res=(res*l)\n return res%((10**9)+7)\n``` | 2 | 0 | [] | 0 |
count-anagrams | Python Elegant & Short | One line) | python-elegant-short-one-line-by-kyrylo-kun0r | If you like this solution remember toupvote itto let me know. | Kyrylo-Ktl | NORMAL | 2023-01-04T17:41:21.431301+00:00 | 2025-02-18T10:56:48.978810+00:00 | 491 | false | ```python []
from collections import Counter
from math import perm, prod
class Solution:
def countAnagrams(self, string: str) -> int:
count = 1
for word in string.split():
count *= perm(len(word)) // prod(map(perm, Counter(word).values()))
count %= 1_000_000_007
return count
```
If you like this solution remember to **upvote it** to let me know. | 2 | 0 | ['Combinatorics', 'Python', 'Python3'] | 0 |
count-anagrams | modulo multiplicative inverse using binary exponentiation easy c++ solution | modulo-multiplicative-inverse-using-bina-kati | \n// modulo multiplicative inverse using binary exponentiation for better understanding\n//https://youtu.be/Gd9w8m-klho\n# Code\n\nusing ll=long long;\nclass So | aashi__70 | NORMAL | 2022-12-26T10:20:33.064480+00:00 | 2023-01-29T10:36:01.350206+00:00 | 273 | false | \n// modulo multiplicative inverse using binary exponentiation for better understanding\n//https://youtu.be/Gd9w8m-klho\n# Code\n```\nusing ll=long long;\nclass Solution {\npublic:\nconst int N=1e5+1;\n ll mod=1e9+7;\n vector<ll> precompute;\n ll temp=1;\n void fun(){\n for(int i=1;i<N;i++){\n temp=((temp%mod)*i)%mod;\n precompute.push_back(temp);\n }\n }\n ll binaryexp(int a,int b,int m){\n ll res=1;\n while(b>0){\n if(b%2==1){\n res=((1ll)*res*a)%m;\n }\n a=((1ll)*a*a)%mod;\n b=b>>1;\n }\n return res;\n }\n\n int countAnagrams(string s) {\n int n=s.size();\n stringstream s1(s);\n precompute.push_back(1);\n string word;\n fun();\n vector<ll> sum;\n ll ans=1;\n while(s1>>word){\n unordered_map<char,ll> m;\n for(auto &j:word){\n m[j]++;\n }\n int n1=word.size();\n long long temp1=precompute[n1];\n ll temp2=1;\n for(auto &j1:m){\n if(j1.second>1){\n ll k=j1.second;\n temp2=((temp2%mod)*precompute[k])%mod;\n \n }\n }\n \n ll den=binaryexp(temp2,mod-2,mod); //denominator\n \n ll proeach=((temp1%mod)*den)%mod;\n ans=((ans%mod)*proeach)%mod;\n // cout<<temp2<<" "<<den<<" "<<proeach<<" "<<ans<<endl;\n \n }\n \n return ans%mod;\n \n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
count-anagrams | [C++] Division with prime modulo 10^9+7 Solution Explained. | c-division-with-prime-modulo-1097-soluti-hi73 | Formula for factorial\n4! = 1 x 2 x 3 x 4\n\nFormula for permutations.\nFor permutations of "cccbhbq", "c" is repeated 3 times and "b" is repeated 2 times. Ther | pr0d1g4ls0n | NORMAL | 2022-12-24T17:09:06.409543+00:00 | 2022-12-24T18:23:20.724609+00:00 | 549 | false | **Formula for factorial**\n4! = `1 x 2 x 3 x 4`\n\n**Formula for permutations.**\nFor permutations of "cccbhbq", "c" is repeated 3 times and "b" is repeated 2 times. There are 7 total characters. Therefore, calculation for the permutations is `7! / (3! * 2!)`.\n\n**For dividing with prime modulo:**\n`a / b` == `a * b^(-1)`\n`b^(-1) mod m` == `b^(modulo - 2)` \n\n**Time complexity**\nO(N log N). Loop through each character in the string thus `O(N)`. For every word, there is a `O(log N)` calculation of denominator to the power of `mod-2`.\n```\nclass Solution {\npublic:\n int mod = 1000000007;\n int countAnagrams(string s) {\n\t\t// preprocess factorial calculations\n\t\tvector<long> factorial {1};\n for (int i = 1; i <100004; ++i) {\n long curr = (factorial[factorial.size()-1] * i);\n curr %= mod;\n factorial.push_back(curr);\n }\n\t\t\n vector<int> freq(26); \n int prev = 0;\n long permutations = 1;\n for (int i = 0; i <= s.size(); ++i) {\n if (i != s.size() && s[i] != \' \') {\n freq[s[i]-\'a\']++;\n } else {\n\t\t\t\t// calculate according to permutation formula\n long num = factorial[i-prev];\n long denom = 1;\n for (long val : freq) { // multiply factorial of repeated characters to denominator\n if (val <= 1) continue;\n denom *= factorial[val];\n denom %= mod;\n }\n permutations *= (num * (fastpow(denom, mod-2) % mod)) % mod;\n permutations %= mod;\n \n\t\t\t\t// reset hash map and previous index\n freq.assign(26, 0);\n prev = i+1;\n }\n }\n \n return permutations;\n }\n \n\t// fast pow function i found online o(logn)\n long long fastpow(long long b, long long ex){\n if (b==1)return 1;\n long long r = 1;\n while (ex ){\n if (ex&1)r=(r * b)%mod;\n ex = ex >> 1;\n b = (b * b)%mod;}\n return r;\n }\n};\n``` | 2 | 0 | [] | 1 |
count-anagrams | Python3 counting & functional programming | python3-counting-functional-programming-tnb67 | Approach
For each word, count arrangements of all letters.
Also count arrangements of each repeated letter.
Divide (1) by the product of (2) to drop all non-uni | mattbain | NORMAL | 2025-02-19T18:46:39.493384+00:00 | 2025-02-21T04:56:15.013892+00:00 | 81 | false | Approach
--------
1. For each word, count arrangements of all letters.
2. Also count arrangements of each repeated letter.
3. Divide (1) by the product of (2) to drop all non-unique options.
4. Return the product of unique arrangements across words.
# Code
```python3 []
from operator import mul
from math import factorial
from collections import Counter
class Solution:
def countAnagrams(self, s: str) -> int:
MOD = 10 ** 9 + 7
def count_unique_perms(word: str) -> int:
counts = Counter(word).values()
n_perms = factorial(len(word))
n_duplicates = reduce(mul, map(factorial, counts))
return (n_perms // n_duplicates) % MOD
n_unique_perms = map(count_unique_perms, s.split(' '))
return reduce(mul, n_unique_perms, 1) % MOD
``` | 1 | 0 | ['Python3'] | 0 |
count-anagrams | ✅☑️ Java Solution || Count-anagrams || Using Fermat's Little Theorem | java-solution-count-anagrams-using-ferma-taup | mul(long a, long b): Performs multiplication (a * b) % mod in a way that handles large numbers by taking the modulo at each step.\n\nbinaryExpo(long a, long n): | sajal_pandey | NORMAL | 2024-04-11T09:09:34.034476+00:00 | 2024-04-11T09:09:34.034511+00:00 | 101 | false | **mul(long a, long b):** Performs multiplication (a * b) % mod in a way that handles large numbers by taking the modulo at each step.\n\n**binaryExpo(long a, long n):** Implements binary exponentiation to efficiently calculate a^n % mod. This method reduces the computational complexity by halving n at each recursive step.\n\n**countAnagrams(String s):** Main method to calculate the product of the number of anagrams that can be formed from each word in the input string s.\n\n**Fermat\'s little theorm for Modulo inverse:**\nhttps://en.wikipedia.org/wiki/Fermat%27s_little_theorem#:~:text=Pierre%20de%20Fermat%20first%20stated,1%20is%20divisible%20by%20p. \n\nTime Complexity : \nIf we consider L as the total length of the input string and W as the number of words, the overall time complexity can be approximated as\nO(n)+O(L)+W.O(logn), simplifying to \n\n**O(n+L+Wlogn)**\n\nPlease upvote if you like\n\n# Code\n```\nclass Solution {\n int mod = (int) (Math.pow(10, 9) + 7);\n\n public int [] calculateFactorial(int n) {\n int [] fact = new int[n+1];\n fact[0] = fact[1] = 1;\n for(int i=2; i<=n; i++)\n fact[i] = (int)mul(i , fact[i-1] );\n return fact;\n }\n\n public long mul(long a, long b) {\n return ((a%mod) * (b%mod))%mod;\n }\n public long binaryExpo(long a, long n) {\n if(n == 0)\n return 1;\n long partialAns = binaryExpo(a, n/2);\n partialAns = mul(partialAns, partialAns);\n if(n%2==0)\n return partialAns;\n return mul(partialAns, a);\n }\n public int countAnagrams(String s) {\n int n = s.length();\n int[] fact = calculateFactorial(n);\n long result = 1;\n String [] strArr = s.split(" ");\n for(String str : strArr) {\n int [] freq = new int[26];\n for(char ch : str.toCharArray())\n freq[ch - \'a\']++;\n \n //anagrams of current word will\n //n! / !freq[char...to ...length]\n long curr = 1;\n for(int fr : freq)\n curr = mul(curr , fact[fr]);\n\n curr = mul(fact[str.length()] , binaryExpo(curr, mod - 2));\n\n result = mul(result, curr);\n }\n return (int)result;\n }\n}\n```\n | 1 | 0 | ['Number Theory', 'Java'] | 0 |
count-anagrams | Beats 100% in time and memory, the fastest solution | beats-100-in-time-and-memory-the-fastest-01di | Approach\nTo get the number of anagrams of the entire string, we need to calculate the number of anagrams of each word and multiply them.\nTo calculate the numb | andigntv | NORMAL | 2024-02-12T23:14:54.425620+00:00 | 2024-02-12T23:19:06.349414+00:00 | 38 | false | # Approach\nTo get the number of anagrams of the entire string, we need to calculate the number of anagrams of each word and multiply them.\nTo calculate the number of anagrams of one particular word, we can use the multinomial coefficient:\n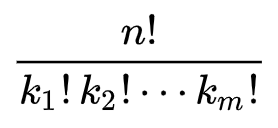\nwhere $$n$$ - length of the word and $$k_i$$ - number of times the i-th letter has occurred in a word.\nCalculating this value directly in Go is quite difficult (as in many other languages).\nKnowing that we need to give an answer modulo $$10^9+7$$ we can make some optimizations:\nWe can use this\n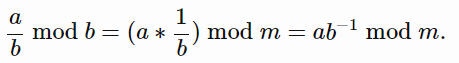\nand this\n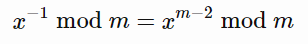\nwhere $$m$$ is a prime number, to translate the problem of multiplying large numbers to the problem of exponentiation, because $$10^9+7$$ is a prime number. \nAnd in order to quickly raise a number to a large power, we can use binary exponentiation\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n + w * log(10^9+7))$$, where $$w$$ - amount of words\nAs $$log(10^9+7)$$ is a constant and $$w < n$$, we can say that time complexity is $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunc countAnagrams(s string) int {\n\tvar mod int64 = 1e9 + 7\n\tfactorials := make([]int64, len(s) + 1)\n\tfactorials[0] = 1\n\tfor i := 1; i <= len(s); i++ {\n\t\tfactorials[i] = (factorials[i-1] * int64(i)) % mod\n\t}\n\tvar pow func(val, p int64) int64\n\tpow = func(val, p int64) int64 {\n\t\tif p == 1 {\n\t\t\treturn val\n\t\t}\n\t\tif p%2 == 0 {\n\t\t\ttemp := pow(val, p/2)\n\t\t\treturn (temp * temp) % mod\n\t\t} else {\n\t\t\treturn (pow(val, p-1) * val) % mod\n\t\t}\n\t}\n\tcountAnagramsForWord := func(word string) int64 {\n\t\tcount := [26]int{}\n\t\tfor _, c := range word {\n\t\t\tcount[c-\'a\']++\n\t\t}\n\t\tn := len(word)\n\t\tresult := factorials[n]\n\t\tfor _, c := range count {\n\t\t\tresult = (result * pow(factorials[c], mod-2)) % mod\n\t\t}\n\t\treturn result\n\t}\n\tvar result int64 = 1\n\twords := strings.Fields(s)\n\tfor _, word := range words {\n\t\tresult = (result * countAnagramsForWord(word)) % mod\n\t}\n\treturn int(result)\n}\n``` | 1 | 0 | ['Go'] | 0 |
count-anagrams | Python/C++ Beats 100% | pythonc-beats-100-by-ashwani2529-eqd8 | Code\nC++ []\nclass Solution {\npublic:\n long long mod = 1000000007;\n\n long long factorial(int n) {\n if (n == 0 || n == 1) {\n retur | Ashwani2529 | NORMAL | 2024-02-05T19:24:19.023177+00:00 | 2024-02-05T19:24:19.023211+00:00 | 301 | false | # Code\n```C++ []\nclass Solution {\npublic:\n long long mod = 1000000007;\n\n long long factorial(int n) {\n if (n == 0 || n == 1) {\n return 1;\n }\n long long result = 1;\n for (int num = 2; num <= n; num++) {\n result = (result * num) % mod;\n }\n return result;\n }\n\n long long count(string s) {\n unordered_map<char, int> h;\n for (char i : s) {\n h[i]++;\n }\n long long j = 1;\n for (auto i : h) {\n j = (j * factorial(i.second)) % mod;\n }\n return j;\n }\n\n long long power(long long x, long long y, long long m) {\n if (y == 0)\n return 1;\n long long p = power(x, y / 2, m) % m;\n p = (p * p) % m;\n return (y % 2 == 0) ? p : (x * p) % m;\n }\n\n long long modInverse(long long a, long long m) {\n return power(a, m - 2, m);\n }\n\n int countAnagrams(string s) {\n stringstream ss(s);\n string word;\n vector<string> x;\n while (ss >> word) {\n x.push_back(word);\n }\n long long ans = 1;\n for (string word : x) {\n ans = (ans * factorial(word.size())) % mod;\n ans = (ans * modInverse(count(word), mod)) % mod;\n }\n return ans % mod;\n }\n};\n```\n```python []\nclass Solution:\n def __init__(self):\n self.mod = 10**9 + 7\n\n def factorial(self, n):\n if n == 0 or n == 1:\n return 1\n result = 1\n for num in range(2, n + 1):\n result = (result * num) % self.mod\n return result\n\n def count(self, s):\n char_count = Counter(s)\n count_factorials = 1\n for count in char_count.values():\n count_factorials = (count_factorials * self.factorial(count)) % self.mod\n return count_factorials\n\n def power(self, x, y, m):\n if y == 0:\n return 1\n p = self.power(x, y // 2, m) % m\n p = (p * p) % m\n return p if y % 2 == 0 else (x * p) % m\n\n def modInverse(self, a, m):\n return self.power(a, m - 2, m)\n\n def countAnagrams(self, s):\n words = s.split()\n ans = 1\n for word in words:\n ans = (ans * self.factorial(len(word))) % self.mod\n ans = (ans * self.modInverse(self.count(word), self.mod)) % self.mod\n return ans % self.mod\n\n``` | 1 | 0 | ['Python', 'C++', 'Python3'] | 1 |
count-anagrams | JAVA Solve | java-solve-by-feedwastfeed-1tj5 | \n# Code\n\nclass Solution {\n private static final int MOD = 1000000007;\n public int countAnagrams(String s) {\n long res=1;\n String stri | Feedwastfeed | NORMAL | 2023-02-05T20:40:12.951690+00:00 | 2023-02-05T20:40:12.951759+00:00 | 187 | false | \n# Code\n```\nclass Solution {\n private static final int MOD = 1000000007;\n public int countAnagrams(String s) {\n long res=1;\n String stringList [] = s.split(" ");\n for(int i=0 ; i<stringList.length; i++){\n long x = countChar(stringList[i]);\n long y = p(stringList[i].length());\n res *= (y*pow(x,MOD-2))%MOD;\n res %=MOD;\n }\n return (int)res;\n }\n public long p(long x){\n long temp = 1;\n for(int i=1 ; i<=x; i++) {\n temp *= i;\n temp %= (MOD);\n }\n return temp;\n }\n public long countChar(String s){\n long sum = 1;\n int arr[] = new int[26];\n for(int i=0 ; i<s.length(); i++){\n arr[s.charAt(i) - \'a\']++;\n }\n for(int i=0; i<arr.length; i++){\n if(arr[i] != 0) {\n sum *= p(arr[i]);\n sum %= MOD;\n }\n }\n return sum;\n }\n public long pow(long a,long n) {\n long res = 1;\n while(n>0) {\n if(n%2 == 1) {\n res = (res * a) % MOD;\n n--;\n }\n else {\n a = (a * a) % MOD;\n n = n / 2;\n }\n }\n return res;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
count-anagrams | c++ solution by counting the prime numbers | c-solution-by-counting-the-prime-numbers-oplq | Intuition\n1. Given a number n, it is not very hard to calculate all the primes less than n and therefore, it is also easy to find out the power of a prime numb | gc2021 | NORMAL | 2023-01-15T04:27:49.324097+00:00 | 2023-01-15T04:27:49.324124+00:00 | 160 | false | # Intuition\n1. Given a number n, it is not very hard to calculate all the primes less than n and therefore, it is also easy to find out the power of a prime number for n!\n2. To calculate n!/k!, it is equal to caculate the difference of the power of prime numbers of n! and k!. \n\n# Approach\n1. For any given word, calculate its length n and all the duplicate characters c1, c2,...ck. Save n and c1, c2, ..ck into two different vectors\n2. For each word length n, and for each prime number p less than n, calculate the power of p in n!. Sum up the power of p for all the word length.\n3. Similarily, for a given duplicate c, calcualte the power of p in c! and reduce this power from the step 2.\n4. For all the prime numbers and corresponding power, calculate the answer with module of 1e9 + 7.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n int countAnagrams(string s) {\n long long ans = 1;\n vector<int> wLens;\n int nMaxLen = 0;\n vector<int> dupLens;\n for (int i = 0, idx = 0; i < s.size(); i = idx + 1)\n {\n idx = i;\n vector<int> cm(26, 0);\n for (; idx < s.size() && s[idx] != \' \'; idx++) cm[s[idx] - \'a\']++; \n wLens.push_back(idx - i);\n nMaxLen = max(nMaxLen, idx - i);\n for (int j = 0; j < 26; ++j)\n if (cm[j] > 1) dupLens.push_back(cm[j]);\n }\n\n map<int, int> m;\n vector<int> primes;\n generatePrimes(nMaxLen + 1, primes);\n for(int i = 0; i < wLens.size(); ++i) addPrimeFactors(wLens[i], m, 1, primes);\n for(int i = 0; i < dupLens.size(); ++i) addPrimeFactors(dupLens[i], m, -1, primes);\n for (auto itr = m.begin(); itr != m.end(); ++itr)\n {\n for(int i = 0; i < itr->second; ++i)\n {\n ans = (ans * itr->first) % 1000000007;\n }\n }\n\n return ans;\n }\n\n void addPrimeFactors(int n, map<int, int>& m, int w, vector<int>& primes)\n {\n vector<int> nums(n + 1, 0);\n for(int i = 0; i < primes.size() && primes[i] <= n; ++i)\n {\n int count = 0;\n for(long long num = primes[i]; num <= n; num = num * primes[i]) count += (n / num);\n m[primes[i]] = m[primes[i]] + w*count;\n }\n }\n\n void generatePrimes(int n, vector<int>& primes)\n {\n if (n <= 2) return;\n primes = {2};\n vector<int> nums(n, 0);\n for(int i = 3; i < n; i = i + 2)\n {\n if (nums[i] == 1) continue;\n primes.push_back(i);\n for(int m = 3*i; m < n; m += 2*i) nums[m] = 1;\n }\n }\n};\n``` | 1 | 0 | ['C++'] | 1 |
count-anagrams | [Javascript] modular multiplicative inverse | javascript-modular-multiplicative-invers-wvts | Using modular multiplicative inverse formula found on internet https://cp-algorithms.com/algebra/module-inverse.html\n\n\n/**\n * @param {string} s\n * @return | aexg | NORMAL | 2023-01-07T08:02:10.978867+00:00 | 2023-01-07T08:02:10.978917+00:00 | 249 | false | Using modular multiplicative inverse formula found on internet https://cp-algorithms.com/algebra/module-inverse.html\n\n```\n/**\n * @param {string} s\n * @return {number}\n */\nvar countAnagrams = function (s) {\n let result = 1n;\n const MODULO = 1000000007n;\n\n // precompute factorials\n const facts = new Array(1e5 + 10).fill(1n);\n for (let i = 1; i < facts.length; ++i) facts[i] = ((facts[i - 1] % MODULO) * (BigInt(i) % MODULO)) % MODULO;\n\n for (const w of s.split(\' \')) {\n const cnt = w.split(\'\').reduce((a, x) => (a.set(x, (a.get(x) || 0) + 1), a), new Map());\n let divisor = [...cnt.values()].reduce((a, x) => (a * facts[x]) % MODULO, 1n);\n let div_inv_mod = 1n;\n let power = MODULO - 2n;\n while (0n < power) {\n if (power & 1n) div_inv_mod = (div_inv_mod * divisor) % MODULO;\n divisor = (divisor * divisor) % MODULO;\n power >>= 1n;\n }\n result = ((result * (facts[w.length] * div_inv_mod)) % MODULO) % MODULO;\n }\n\n return Number(result);\n};\n\n``` | 1 | 0 | ['JavaScript'] | 0 |
count-anagrams | Swift version: modular inverse | swift-version-modular-inverse-by-tzef-rf5i | Intuition\n Describe your first thoughts on how to solve this problem. \nGreat explanation please refer\nhttps://leetcode.com/problems/count-anagrams/solutions/ | tzef | NORMAL | 2022-12-30T17:04:41.136048+00:00 | 2022-12-30T17:05:29.317215+00:00 | 62 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGreat explanation please refer\nhttps://leetcode.com/problems/count-anagrams/solutions/2947111/c-solution-math-with-explanation-each-step-in-detail/?orderBy=most_votes\n\nAdd on reference for Fermat\'s little theorem\nhttps://en.wikipedia.org/wiki/Fermat%27s_little_theorem\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. catch the factorial result for reuse\n2. combination formula all $$n!/a!*b!$$ when there are 0...a and 0...b same items\n2. modularMultiplication for handling multiply overflow product\n3. binaryExponentiation for quickly get power of number\n4. moduloInverse for deal with dividing the factorial for same items\n\n\n# Code\n```\nclass Solution {\n let mod = Int(1e9+7)\n func countAnagrams(_ s: String) -> Int {\n var anagrams = [String: [Character: Int]]()\n for word in s.split(separator: " ") {\n var anagram = [Character: Int]()\n word.forEach {\n anagram[$0, default: 0] += 1\n }\n anagrams[String(word)] = anagram\n }\n\n var result = 1\n for anagram in anagrams {\n var permutation = factorial(anagram.key.count)\n var devideFactorial = 1\n for value in anagram.value.values {\n guard value > 1 else {\n continue\n }\n // (a/b)%m != a%m / b%m -> use modular inverse for division\n permutation = modularMultiplication(permutation, moduloInverse(factorial(value)))\n }\n result = modularMultiplication(result, permutation)\n }\n return result\n }\n \n var factorials = [Int: Int]()\n func factorial(_ n: Int) -> Int {\n if let cache = factorials[n] {\n return cache\n }\n guard n > 1 else {\n return 1\n }\n let result = modularMultiplication(n, factorial(n-1))\n factorials[n] = result\n return result\n }\n \n // n^-1 % m\n func moduloInverse(_ n: Int) -> Int {\n binaryExponentiation(n, mod-2) % mod\n }\n \n // (a * b) % m\n func modularMultiplication(_ a: Int, _ b: Int) -> Int {\n (a % mod * b % mod) % mod\n }\n \n // pow(a, b)\n func binaryExponentiation(_ a: Int, _ b: Int) -> Int {\n if b == 0 {\n return 1\n }\n let result = binaryExponentiation(a, b/2)\n if b % 2 == 1 {\n return modularMultiplication(a, modularMultiplication(result, result))\n } else {\n return modularMultiplication(result, result)\n }\n }\n}\n``` | 1 | 0 | ['Swift'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.