question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
zero-array-transformation-iii
|
Simple one priority queue solution
|
simple-one-priority-queue-solution-by-pi-mrv6
| null |
piyush_krs
|
NORMAL
|
2024-12-12T18:57:32.023753+00:00
|
2024-12-12T18:57:32.023753+00:00
| 21 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCheck the code\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCheck the code\n\n# Complexity\n- Time complexity:O(nlog(m))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n + m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxRemoval(vector<int>& nums, vector<vector<int>>& queries) {\n sort(queries.begin(), queries.end());\n int n = nums.size(), m = queries.size();\n priority_queue<int> pq;\n vector<int> reduction(n + 1, 0);\n int k = 0, usedCnt = 0;\n for(int i = 0; i < n; i++) {\n if(i > 0) reduction[i] += reduction[i - 1];\n while(k < m && queries[k][0] <= i)\n pq.push(queries[k++][1]);\n while(nums[i] > reduction[i]) {\n if(pq.empty() || pq.top() < i)\n return -1;\n usedCnt++;\n int top = pq.top();\n pq.pop();\n reduction[i]++;\n reduction[top + 1]--;\n }\n }\n return m - usedCnt;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
zero-array-transformation-iii
|
Finding Redundant Queries using minHeap and maxHeap
|
finding-redundant-queries-using-minheap-vp91c
| null |
Arghya_0802
|
NORMAL
|
2024-12-09T17:34:11.446553+00:00
|
2024-12-09T17:34:11.446553+00:00
| 46 | false |
# Intuition\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(Q * LogQ + N)\nwhere Q = Count of Queries, N = Length of Nums\n- Space complexity:\nO(Q) where Q = Count of Queries\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxRemoval(vector<int>& nums, vector<vector<int>>& queries) \n {\n int n = nums.size(), qLen = queries.size() ;\n\n priority_queue<int> maxHeap ; // All valid candidates\n priority_queue<int, vector<int>, greater<int>> minHeap ; // All chosen candidates\n\n int cnt = 0 ; // Keeps track of all the queries used till date\n int j = 0 ; // Traversing over queries[]\n\n // We need to get the queries in sorted order based on startingIndex\n sort(queries.begin(), queries.end() ) ; \n\n for(int i = 0 ; i < n ; i++)\n {\n // 1. Choosing all the valid Queies for the currentIndex\n while(j < qLen && queries[j][0] == i)\n {\n maxHeap.push(queries[j][1]) ;\n j++ ;\n }\n\n // 2. Decrementing nums[i] by the no of queries still left to be processed\n nums[i] -= (int) minHeap.size() ; \n\n // 3. Pushing all the queries which are required to decrement nums[i] to 0\n while(!maxHeap.empty() && maxHeap.top() >= i && nums[i] > 0) \n {\n nums[i]-- ;\n minHeap.push(maxHeap.top() ) ;\n maxHeap.pop() ;\n cnt++ ;\n }\n\n // 4. If we cannot decrement nums[i], we return -1\n if(nums[i] > 0) return -1 ;\n\n // 5. We remove all such queries which cannot contribute going further\n while(!minHeap.empty() && minHeap.top() <= i) minHeap.pop() ;\n }\n\n return qLen - cnt ;\n }\n};\n```
| 0 | 0 |
['Greedy', 'Sorting', 'Heap (Priority Queue)', 'C++']
| 0 |
number-of-provinces
|
Neat DFS java solution
|
neat-dfs-java-solution-by-vinod23-y3fz
|
```\npublic class Solution {\n public void dfs(int[][] M, int[] visited, int i) {\n for (int j = 0; j < M.length; j++) {\n if (M[i][j] == 1
|
vinod23
|
NORMAL
|
2017-04-02T03:16:47.024000+00:00
|
2018-10-16T08:12:16.529206+00:00
| 87,004 | false |
```\npublic class Solution {\n public void dfs(int[][] M, int[] visited, int i) {\n for (int j = 0; j < M.length; j++) {\n if (M[i][j] == 1 && visited[j] == 0) {\n visited[j] = 1;\n dfs(M, visited, j);\n }\n }\n }\n public int findCircleNum(int[][] M) {\n int[] visited = new int[M.length];\n int count = 0;\n for (int i = 0; i < M.length; i++) {\n if (visited[i] == 0) {\n dfs(M, visited, i);\n count++;\n }\n }\n return count;\n }\n}
| 392 | 6 |
[]
| 60 |
number-of-provinces
|
Java solution, Union Find
|
java-solution-union-find-by-shawngao-p934
|
This is a typical Union Find problem. I abstracted it as a standalone class. Remember the template, you will be able to use it later.\n\npublic class Solution {
|
shawngao
|
NORMAL
|
2017-04-02T03:26:00.352000+00:00
|
2018-10-16T08:10:09.072493+00:00
| 67,330 | false |
This is a typical ```Union Find``` problem. I abstracted it as a standalone class. Remember the template, you will be able to use it later.\n```\npublic class Solution {\n class UnionFind {\n private int count = 0;\n private int[] parent, rank;\n \n public UnionFind(int n) {\n count = n;\n parent = new int[n];\n rank = new int[n];\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n }\n }\n \n public int find(int p) {\n \twhile (p != parent[p]) {\n parent[p] = parent[parent[p]]; // path compression by halving\n p = parent[p];\n }\n return p;\n }\n \n public void union(int p, int q) {\n int rootP = find(p);\n int rootQ = find(q);\n if (rootP == rootQ) return;\n if (rank[rootQ] > rank[rootP]) {\n parent[rootP] = rootQ;\n }\n else {\n parent[rootQ] = rootP;\n if (rank[rootP] == rank[rootQ]) {\n rank[rootP]++;\n }\n }\n count--;\n }\n \n public int count() {\n return count;\n }\n }\n \n public int findCircleNum(int[][] M) {\n int n = M.length;\n UnionFind uf = new UnionFind(n);\n for (int i = 0; i < n - 1; i++) {\n for (int j = i + 1; j < n; j++) {\n if (M[i][j] == 1) uf.union(i, j);\n }\n }\n return uf.count();\n }\n}\n```
| 343 | 4 |
[]
| 62 |
number-of-provinces
|
Python, Simple Explanation
|
python-simple-explanation-by-awice-8vka
|
From some source, we can visit every connected node to it with a simple DFS. As is the case with DFS's, seen will keep track of nodes that have been visited.
|
awice
|
NORMAL
|
2017-04-02T03:35:31.848000+00:00
|
2018-10-24T02:46:54.854164+00:00
| 44,969 | false |
From some source, we can visit every connected node to it with a simple DFS. As is the case with DFS's, **seen** will keep track of nodes that have been visited. \n\nFor every node, we can visit every node connected to it with this DFS, and increment our answer as that represents one friend circle (connected component.)\n\n```\ndef findCircleNum(self, A):\n N = len(A)\n seen = set()\n def dfs(node):\n for nei, adj in enumerate(A[node]):\n if adj and nei not in seen:\n seen.add(nei)\n dfs(nei)\n \n ans = 0\n for i in xrange(N):\n if i not in seen:\n dfs(i)\n ans += 1\n return ans\n```
| 220 | 3 |
[]
| 27 |
number-of-provinces
|
[C++] Clean Code - DFS|UnionFind
|
c-clean-code-dfsunionfind-by-alexander-bdbk
|
DFS\n\nclass Solution {\npublic:\n int findCircleNum(vector<vector<int>>& M) {\n if (M.empty()) return 0;\n int n = M.size();\n vector<b
|
alexander
|
NORMAL
|
2017-04-02T03:23:02.861000+00:00
|
2018-10-13T22:26:02.102431+00:00
| 39,552 | false |
**DFS**\n```\nclass Solution {\npublic:\n int findCircleNum(vector<vector<int>>& M) {\n if (M.empty()) return 0;\n int n = M.size();\n vector<bool> visited(n, false);\n int groups = 0;\n for (int i = 0; i < visited.size(); i++) {\n groups += !visited[i] ? dfs(i, M, visited), 1 : 0;\n }\n return groups;\n }\n\nprivate:\n void dfs(int i, vector<vector<int>>& M, vector<bool>& visited) {\n visited[i] = true;\n for (int j = 0; j < visited.size(); j++) {\n if (i != j && M[i][j] && !visited[j]) {\n dfs(j, M, visited);\n }\n }\n }\n};\n```\n**UnionFind**\n```\nclass Solution {\npublic:\n int findCircleNum(vector<vector<int>>& M) {\n if (M.empty()) return 0;\n int n = M.size();\n\n vector<int> leads(n, 0);\n for (int i = 0; i < n; i++) { leads[i] = i; } // initialize leads for every kid as themselves\n\n int groups = n;\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) { // avoid recalculate M[i][j], M[j][i]\n if (M[i][j]) {\n int lead1 = find(i, leads);\n int lead2 = find(j, leads);\n if (lead1 != lead2) { // if 2 group belongs 2 different leads, merge 2 group to 1\n leads[lead1] = lead2;\n groups--;\n }\n }\n }\n }\n return groups;\n }\n\nprivate:\n int find(int x, vector<int>& parents) {\n return parents[x] == x ? x : find(parents[x], parents);\n }\n};\n```
| 172 | 5 |
[]
| 26 |
number-of-provinces
|
Simple C++ Solution || Fully Explained at begineers level || Easy Understanding of UNION concept
|
simple-c-solution-fully-explained-at-beg-vrr1
|
TOPIC: UNION FIND\n NOT A BIG TASK :), JUST GO LINE BY LINE \n\n In union we just make any element leader of any group and make other elements as a grou
|
ajaykumar0
|
NORMAL
|
2020-10-01T14:55:06.563372+00:00
|
2021-07-03T10:50:46.045832+00:00
| 16,703 | false |
**TOPIC: UNION FIND\n NOT A BIG TASK :), JUST GO LINE BY LINE** \n\n In union we just make any element leader of any group and make other elements as a group member.\n\n**Let\'s say 1 and 2 are friend , and 2 and 3 are also friend \nThen indirectly 1 and 3 are also friends. We can say that 1,2,3 are in same group.**\n\nHow we will deal with it in UNION:\n\nWE have given **n * n matrix** , then **maximum number of group will be n**, if nobody is friend of none.\n\nLets Say n=5\nNow we mark all of them initially with -1, because at starting all are alone, all are self leader.\n**At the end we will find -1 for those index which will be leader of any group**\n\n _INDEX : **[ 1 , 2 ,3 ,4 , 5]**\nVALUES: **[-1,-1,-1,-1,-1]**\n\nNow **1 is friend of 2**, mark **2** as a leader , how can we do this, simple ,**point index 2 from 1**\n _INDEX : **[ 1 , 2 ,3 ,4 , 5]**\nVALUES: **[ 2,-1,-1,-1, -1]**\nHere how we will find leader ,start from index 1\n\n**1 is pointing 2 , 1->2\n2 is pointing -1, 2 is leader of group**\n\n\nNow **2 is friend of 3**, Now **point 2 at index 3**\n _INDEX : **[ 1 , 2 ,3 ,4 , 5]**\nVALUES: **[ 2 , 3,-1,-1, -1]**\n\n**1 is pointing 2 , 1->2\n2 is pointing 3 , 2->3\n3 is pointing -1 , 3 is leader of group**\n\n\nNow if we start finding **leader of 1 and 2** , then **3** is the leader (**COMMON LEADER: SAME GROUP**)\n\nNow **4 is friend of 5**, Now **point 4 at index 5**\n _INDEX : **[ 1 , 2 ,3 ,4 , 5]**\nVALUES: **[ 2 , 3,-1, 5, -1]**\n\nAt the end just count total number of parent nodes whose value is -1.\nNow we have **two** groups **{1,2,3}** and **{4,5}** , NOW go to solution line by line :)\n \n```\nclass Solution {\npublic:\n \n //It will be use to store groups\n vector<int> v;\n \n //Find the leader of any group in which x lies\n //if not lie in any group then it is self leader\n int parent(int x)\n {\n //self leader\n if(v[x]==-1) return x; \n //find the leader of self parent\n return v[x]=parent(v[x]);\n }\n \n //Adding 2 friends in a group\n void _union(int a,int b)\n {\n //find the leader of both a and b\n int p_a=parent(a),p_b=parent(b);\n \n //if already in same group, i.e leader of both of them are same then return\n if(p_a==p_b) return; \n /*\n if both of them are from different group then add both the groups \n and make a single common group\n We can do this by -> leader of 1st group is member of 2nd group \n and now main leader of whole group is leader of 2nd member\n */ \n v[p_a]=p_b; //v[p_a] will store the index of leader of whole group\n }\n \n int findCircleNum(vector<vector<int>>& M) { \n int n=M.size();\n v=vector<int> (n,-1);//there will be maximum n group, mark all as a leader\n \n //making group\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<n;j++)\n {\n if(M[i][j]) //if i is friend of j, add them in a group\n { \n //if i is in any group then add j in that group\n //or vice-versa\n _union(i,j); //Add them in a group\n }\n }\n }\n int c=0; \n \n //counting group\n for(int i=0;i<n;i++)\n {\n if(v[i]==-1) c++; //counting total number of parents\n }\n return c; \n }\n};\n```\n\n***Time Complexity: O(N * N * log(N))\nSpace Complexity: O(N)*** \n\n**We are traversing N * N size matrix and finding parent each time in vector of size N\nUsing a vector to store parent of size N**\n\n\n
| 111 | 0 |
['Union Find', 'C', 'C++']
| 8 |
number-of-provinces
|
Oneliners :-P
|
oneliners-p-by-stefanpochmann-f1xv
|
Solution 1, using a SciPy function:\n\nimport scipy.sparse\n\nclass Solution(object):\n def findCircleNum(self, M):\n return scipy.sparse.csgraph.conn
|
stefanpochmann
|
NORMAL
|
2017-04-02T16:36:54.839000+00:00
|
2018-10-22T13:57:54.839527+00:00
| 18,983 | false |
Solution 1, using a SciPy function:\n```\nimport scipy.sparse\n\nclass Solution(object):\n def findCircleNum(self, M):\n return scipy.sparse.csgraph.connected_components(M)[0]\n```\n\nSolution 2, compute the transitive closure of the (boolean) matrix and count the number of different rows:\n```\nimport numpy as np\n\nclass Solution(object):\n def findCircleNum(self, M):\n return len(set(map(tuple, (np.matrix(M, dtype='bool')**len(M)).A)))\n```
| 100 | 21 |
[]
| 26 |
number-of-provinces
|
python, union find, dfs, bfs
|
python-union-find-dfs-bfs-by-journeyboy-pppn
|
union find:\n\npy\nclass UnionFind(object):\n def __init__(self, n):\n self.u = list(range(n))\n \n def union(self, a, b):\n ra, rb =
|
journeyboy
|
NORMAL
|
2019-06-01T05:33:50.044320+00:00
|
2019-06-01T05:33:50.044350+00:00
| 13,401 | false |
union find:\n\n```py\nclass UnionFind(object):\n def __init__(self, n):\n self.u = list(range(n))\n \n def union(self, a, b):\n ra, rb = self.find(a), self.find(b)\n if ra != rb: self.u[ra] = rb\n \n def find(self, a):\n while self.u[a] != a: a = self.u[a]\n return a\n \nclass Solution(object):\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n \n if not M: return 0\n s = len(M)\n \n uf = UnionFind(s)\n for r in range(s):\n for c in range(r,s):\n if M[r][c] == 1: uf.union(r,c)\n \n return len(set([uf.find(i) for i in range(s)]))\n```\n\nDFS:\n\n```py\nclass Solution(object):\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n \n if not M: return 0\n s = len(M)\n seen = set()\n \n def dfs(p):\n for q, adj in enumerate(M[p]):\n if (adj == 1) and (q not in seen):\n seen.add(q)\n dfs(q)\n \n cnt = 0\n for i in range(s):\n if i not in seen: \n dfs(i)\n cnt += 1\n \n return cnt\n```\n\nBFS:\n\n```py\nclass Solution(object):\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n \n if not M: return 0\n s = len(M)\n seen = set()\n cnt = 0\n for i in range(s):\n if i not in seen:\n q = [i]\n while q:\n p = q.pop(0)\n if p not in seen:\n seen.add(p)\n q += [k for k,adj in enumerate(M[p]) if adj and (k not in seen)]\n cnt += 1\n \n return cnt\n```\n
| 68 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Union Find', 'Python']
| 9 |
number-of-provinces
|
C++ DFS solution with Easy Explanation (Beats 90% submissions in one go)
|
c-dfs-solution-with-easy-explanation-bea-e7ka
|
Connected Components in a bidirectional Graph\nAs given in the question, we have n nodes. So we will make a visited array for n nodes. then we will start with o
|
hiteshgupta
|
NORMAL
|
2020-08-09T10:00:03.921394+00:00
|
2020-08-09T10:00:03.921429+00:00
| 7,528 | false |
# Connected Components in a bidirectional Graph\nAs given in the question, we have ```n``` nodes. So we will make a visited array for `n` nodes. then we will start with one node, and mark all its connected nodes as `visited=true`. So we will count only how many times we have to start this process. that will be our answer.\n\n```\nint findCircleNum(vector<vector<int>>& M) {\n\tint n=M.size(),ans=0;\n\tif(n==0) return 0;\n\n\tvector<bool>vis(n,false);\n\n\tfor(int i=0;i<n;i++)\n\t{\n\t\tif(!vis[i])\n\t\t{\n\t\t\tans++;\n\t\t\tdfs(M,vis,i);\n\t\t}\n\t}\n\treturn ans;\n}\n\nvoid dfs(vector<vector<int>>& M, vector<bool>& vis, int i)\n{\n\tvis[i]=true;\n\tfor(int j=0;j<M.size();j++)\n\t\tif(M[i][j]==1 && !vis[j])\n\t\t\tdfs(M,vis,j);\n}\n```
| 57 | 2 |
['Depth-First Search', 'Graph', 'C']
| 5 |
number-of-provinces
|
Python DFS solution with explanation, beats 97%
|
python-dfs-solution-with-explanation-bea-zpj6
|
In this problem, I first construct a graph with each person as a node and build an edge between two nodes if those two people know each other (they are direct f
|
user8307e
|
NORMAL
|
2020-01-04T22:19:02.191852+00:00
|
2020-01-04T22:29:24.524269+00:00
| 14,666 | false |
In this problem, I first construct a graph with each person as a node and build an edge between two nodes if those two people know each other (they are direct friends). Since the matrix is symmetric, I do not have to read all the values in the matrix but only half of them.\n\n```\nclass Solution:\n def findCircleNum(self, M: List[List[int]]) -> int:\n \n graph = collections.defaultdict(list)\n \n if not M:\n return 0\n \n n = len(M)\n for i in range(n):\n for j in range(i+1,n):\n if M[i][j]==1:\n graph[i].append(j)\n graph[j].append(i)\n \n visit = [False]*n\n \n def dfs(u):\n for v in graph[u]:\n if visit[v] == False:\n visit[v] = True\n dfs(v)\n \n count = 0\n for i in range(n):\n if visit[i] == False:\n count += 1\n visit[i] = True\n dfs(i)\n \n return count\n```\nTime Complexity: O(n^2). O(n^2) to construct the graph and O(n) to run DFS, so the total is O(n^2).\nSpace Complexity: O(n^2) for the worst case. O(n^2) to store the graph dictionary, if all the nodes are connected, the space is O(n^2). O(n) to store visit list. The space complexity of DFS is the depth of the recursion which is no more than O(n).\n\nSimilar solution without constructing the graph:\n```\n# time: O(n^2)\n# space: O(n) to store visit list\n\nclass Solution:\n def findCircleNum(self, M: List[List[int]]) -> int:\n \n if not M:\n return 0\n \n n = len(M)\n visit = [False]*n\n \n def dfs(u):\n for v in range(n):\n if M[u][v] ==1 and visit[v] == False:\n visit[v] = True\n dfs(v)\n \n count = 0\n for i in range(n):\n if visit[i] == False:\n count += 1\n visit[i] = True\n dfs(i)\n \n return count\n```
| 50 | 2 |
['Depth-First Search', 'Python', 'Python3']
| 6 |
number-of-provinces
|
Python Union Find solution
|
python-union-find-solution-by-rasca0027-i43r
|
\nclass Solution:\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n def find(node):\n
|
rasca0027
|
NORMAL
|
2018-07-22T05:48:59.805916+00:00
|
2018-10-22T15:29:21.108719+00:00
| 10,235 | false |
```\nclass Solution:\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n def find(node):\n if circles[node] == node: return node\n root = find(circles[node])\n circles[node] = root\n return root\n \n n = len(M)\n circles = {x:x for x in range(n)}\n num = n\n for i in range(n):\n for j in range(i, n):\n if i != j and M[i][j] == 1 and find(i) != find(j):\n circles[find(i)] = find(j) \n \n return sum([1 for k, v in circles.items() if k == v])\n ```
| 43 | 1 |
[]
| 11 |
number-of-provinces
|
Easy C++ DFS Solution
|
easy-c-dfs-solution-by-himanshugupta14-y24z
|
\nvoid dfs(vector<vector<int>>&M,vector<vector<int>>& vis,int r,int c){\n\tif(r<0 || r> M.size() || c<0 || c> M.size()) return ;\n\tvis[r][c]=1;\n\tvis[c][r]=1;
|
himanshugupta14
|
NORMAL
|
2019-09-07T06:44:49.170411+00:00
|
2019-09-09T17:19:29.797748+00:00
| 6,011 | false |
```\nvoid dfs(vector<vector<int>>&M,vector<vector<int>>& vis,int r,int c){\n\tif(r<0 || r> M.size() || c<0 || c> M.size()) return ;\n\tvis[r][c]=1;\n\tvis[c][r]=1;\n\tfor(int i=0;i<M[0].size();i++){\n\t\tif(!vis[c][i] && M[c][i] == 1) dfs(M,vis,c,i);\n\t}\n\treturn ;\n}\nint findCircleNum(vector<vector<int>>& M) {\n\tint n=M.size();\n\tint ans=0;\n\tvector<vector<int>> vis(n,vector<int>(n,0));\n\tfor(int i=0;i<n;i++){\n\t\tfor(int j=0;j<n;j++){\n\t\t\tif(!vis[i][j] && M[i][j] == 1) {\n\t\t\t\tdfs(M,vis,i,j);\n\t\t\t\tans++;\n\t\t\t}\n\t\t}\n\t}\n\treturn ans;\n}\n```
| 42 | 1 |
[]
| 7 |
number-of-provinces
|
Python3 solution with detailed explanation
|
python3-solution-with-detailed-explanati-kzxe
|
First note: If you hear anything regarding relationship, circle, etc., you should think of a way to interpret it as a graph. \n\nAfter you read the problem stat
|
peyman_np
|
NORMAL
|
2020-07-09T23:16:38.496697+00:00
|
2020-07-10T01:02:07.623713+00:00
| 5,091 | false |
First note: If you hear anything regarding relationship, circle, etc., you should think of a way to interpret it as a graph. \n\nAfter you read the problem statement, try to visualize some examples as a graph on a piece of paper. For example, for `M = [[1,1,0], [1,1,0], [0,0,1]]`. If you draw three nodes `0, 1, 2`, and try to connect them in case `M_{ij}` is one, you would connect node `0` to node `1`, and node `2` would be left alon. How many connected pieces do you have? 2! right? So, there are two friend cycles. That\' the idea behind our solution here. You try to go over all vertices (we have `n` vertices, which is the `len(M`), starting from whatever node you want! Once you start from a vertex, Depth First Search (DFS) algorithm would try to visit every node that can be arrived at given a specific starting vertex. The algorithm only stops if it visits all the vertices in a connected graph. Makes sense? Good! I\'m following the solution of [user8307e](https://leetcode.com/problems/friend-circles/discuss/470456/Python-DFS-solution-with-explanation-beats-97)\n\n\n```\nclass Solution(object):\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n n = len(M) #1\n visited = [False]*n #2\n count = 0 #3\n \n if not M: #4\n return 0 #5\n \n def dfs(u): #6\n for v in range(n): #7\n if M[u][v] == 1 and visited[v] == False: #8\n visited[v] = True #9\n dfs(v) #10\n \n \n for idx in range(n): #11\n if visited[idx] == False: #12\n count += 1 #13\n visited[idx] == True #14\n dfs(idx) #15\n \n return count #16\n```\n\nThe first three lines are initializations. Note that the line `#2` includes a way of initialization an array without using `numpy` or `graph` or anything else. \n\nLine `#4`: If `M` is empty, then we don\'t have any friend cycle. \n\nLine `#8` and `#9`: It\'s part of the DFS algorithm where it gets a vertex as input (`u`), and checks it versus all other vertices (let\'s call it `v`). If there\'s a connection between `u` and `v`, and this edge has not been visited yet (line `#8`), then it adds `v` to the visited vertices (line `#9`). Finally, it goes one layer deeper (line `#10`), does the exact same thing for `v`. This is the main part of the solution. Note that it doesn\'t necessary need to be recursive but it\'s more convinient this way. \n\n\nThe rest is pretty simple. It\'s the main function. You go over all the nodes, check if it\'s been visited (line `#12`), update the counter (`count`) by one (we update the counter here since if it has not been visited yet, it means that it\'s part of a friend cycle that has not been counted yet). Update the `visited` list so that we know later on that we visited this node. \n\n\nFinally, we return the `count`. Is that clear? \n\n\n===============================================================\nFinal note: Please let me know if you see ant typo/error/ etc. I\'ll try to fix it.\n\nFinal note 2: I find explaining stuff in a simple for instructive for myself, that\'s why I\'m doing this. Thanks for reading.
| 34 | 0 |
['Depth-First Search', 'Python', 'Python3']
| 4 |
number-of-provinces
|
javascript dfs+map w/ comments
|
javascript-dfsmap-w-comments-by-carti-t0af
|
\nfunction findCircleNum(M) {\n // visited set\n const visited = new Set();\n // friend circles count\n let circles = 0;\n\t\n // iterate thru ma
|
carti
|
NORMAL
|
2020-04-28T06:45:48.095124+00:00
|
2020-04-28T06:45:48.095171+00:00
| 3,801 | false |
```\nfunction findCircleNum(M) {\n // visited set\n const visited = new Set();\n // friend circles count\n let circles = 0;\n\t\n // iterate thru matrix\n for (let i = 0; i < M.length; i++) {\n // check if this friend has been visited before\n if (!visited.has(i)) {\n // start dfs for this friend\n dfs(i);\n // this is another friend circle\n circles++;\n }\n }\n\t\n return circles;\n\t\n // helper method to do dfs traversal thru M\n function dfs(i) {\n // go thru this friend\'s friends\n for (let j = 0; j < M.length; j++) {\n // check if this is a friend, and not visited before\n if (M[i][j] === 1 && !visited.has(j)) {\n // add as visited\n visited.add(j);\n // call dfs\n dfs(j);\n }\n }\n }\n}\n```\n
| 30 | 0 |
['Depth-First Search', 'JavaScript']
| 7 |
number-of-provinces
|
Easy Java Union Find Solution
|
easy-java-union-find-solution-by-giridha-i7qz
|
\npublic class Solution {\n public int findCircleNum(int[][] M) {\n int count = M.length;\n int[] root = new int[M.length];\n for(int i=
|
giridhar_bhageshpur
|
NORMAL
|
2017-05-04T10:37:20.229000+00:00
|
2018-08-31T07:48:30.614741+00:00
| 5,507 | false |
```\npublic class Solution {\n public int findCircleNum(int[][] M) {\n int count = M.length;\n int[] root = new int[M.length];\n for(int i=0;i<M.length;i++){\n root[i] =i;\n }\n for(int i=0;i<M.length;i++){\n for(int j=0;j<M[0].length;j++){\n if(M[i][j]==1){\n int rooti = findRoot(root,i);\n int rootj = findRoot(root,j);\n if(rooti!=rootj){\n root[rooti] = rootj;\n count--;\n }\n }\n }\n }\n return count;\n }\n public int findRoot(int[] roots,int id){\n while(roots[id]!=id){\n roots[id] = roots[roots[id]];\n id = roots[id];\n }\n return id;\n }\n}\n```
| 28 | 1 |
[]
| 7 |
number-of-provinces
|
[C++] Disjoint Set Union with Path Compression Optimization
|
c-disjoint-set-union-with-path-compressi-22o3
|
\n\nclass Solution {\npublic:\n int parent[201];\n \n int findCircleNum(vector<vector<int>>& M) {\n int i, j, groups = 0, n = M.size();\n
|
jatinpandey77
|
NORMAL
|
2020-04-13T16:05:15.319518+00:00
|
2020-07-31T12:20:09.844169+00:00
| 3,040 | false |
\n```\nclass Solution {\npublic:\n int parent[201];\n \n int findCircleNum(vector<vector<int>>& M) {\n int i, j, groups = 0, n = M.size();\n make_set(n);\n \n for(i = 0; i < n; i++) {\n for(j = i + 1; j < n; j++) {\n if(M[i][j])\n union_sets(i, j);\n }\n }\n \n for(i = 0; i < n; i++) {\n if(i == parent[i])\n groups++;\n }\n \n return groups;\n }\n\nprivate:\n void make_set(int n) {\n for(int i = 0; i < n; i++) \n parent[i] = i;\n }\n \n int find_set(int v) {\n if (v == parent[v])\n return v;\n return parent[v] = find_set(parent[v]);\n }\n \n void union_sets(int a, int b) {\n a = find_set(a);\n b = find_set(b);\n if (a != b)\n parent[b] = a;\n }\n};\n```\n\nRefer to [this](https://cp-algorithms.com/data_structures/disjoint_set_union.html) article for more details on DSU.
| 27 | 0 |
['Union Find', 'C']
| 1 |
number-of-provinces
|
C++ | Easy Solution | BFS and DFS Code
|
c-easy-solution-bfs-and-dfs-code-by-deep-ecwr
|
Intuition\nBy seeing the question we can understand that we need to calculate number of components present in the graph. Thus the problem is number of connected
|
deepak1408
|
NORMAL
|
2023-06-04T04:16:15.482033+00:00
|
2023-06-04T04:16:15.482110+00:00
| 5,751 | false |
# Intuition\nBy seeing the question we can understand that we need to calculate number of components present in the graph. Thus the problem is number of connected components which can be solved by using DFS/BFS.\n\n# Approach\nFor example we have 3 connected componenets in the graph G i.e. G1,G2,G3. G1 , G2, G3 are not connected to any other components.\n\nLet a,b,c belongs to G1.\nLet d,e,f,g belongs to G2.\nLet h,i belongs to G3.\n\na,b,c are connected to each other directly or indirectly same for d,e,f,g and h,i.\n\nNow if we apply DFS/BFS for any one of the nodes from G1 all the nodes of G1 are marked as visited because all the nodes in G1 are connected directly or indirectly.\n\nLet us check whether a node is visited. If yes continue with next one else apply BFS/DFS on the node which marks visited for the following component.\n\nThe final Answer would be number of DFS/BFS applied on the graph G.\n\n# Complexity\n- Time complexity:\nDFS - O(N+M)\nBFS - O(N+M)\n\nN - Number of Vertices.\nM - Number of Edges.\n\n- Space complexity:\nDFS - O(H)\nBFS - O(W)\n\nH - Maximum Height of the Graph\nW - Maximum Width of the Graph\n\n# DFS Code\n```\nclass Solution {\npublic:\nvoid soln(vector<int>adj[],int node,vector<bool>&vis){\n vis[node] = 1;\n for(auto i:adj[node]){\n if(!vis[i]){\n soln(adj,i,vis);\n }\n }\n}\n int findCircleNum(vector<vector<int>>& isConnected) {\n int n = isConnected.size();\n vector<int>adj[n];\n for(int i = 0;i<n;i++){\n for(int j = 0;j<n;j++){\n if(isConnected[i][j]){\n adj[i].push_back(j);\n adj[j].push_back(i);\n }\n }\n }\n vector<bool>vis(n,0);\n int ans= 0;\n for(int i = 0;i<n;i++){\n if(!vis[i]){\n soln(adj,i,vis);\n ans++;\n }\n }\n return ans;\n }\n};\n```\n# BFS Code\n```\nclass Solution {\npublic:\n int findCircleNum(vector<vector<int>>& isConnected) {\n int n = isConnected.size();\n vector<int>adj[n];\n for(int i = 0;i<n;i++){\n for(int j = 0;j<n;j++){\n if(isConnected[i][j]){\n adj[i].push_back(j);\n adj[j].push_back(i);\n }\n }\n }\n vector<bool>vis(n,0);\n int ans= 0;\n for(int i = 0;i<n;i++){\n if(!vis[i]){\n ans++;\n queue<int>q;\n q.push(i);\n while(!q.empty()){\n int node = q.front();\n q.pop();\n vis[node] = 1;\n for(auto child:adj[node]){\n if(!vis[child]){\n q.push(child);\n }\n }\n }\n }\n }\n return ans;\n }\n};\n```
| 26 | 1 |
['Depth-First Search', 'Breadth-First Search', 'Graph', 'C++']
| 4 |
number-of-provinces
|
Java Solution | 100% faster | Connected Components
|
java-solution-100-faster-connected-compo-xrr6
|
A must watch video if you\'re not already familier with connected compoents in graph theory: \nhttps://www.youtube.com/watch?v=z49Ohr5Ypnw\n\nclass Solution {\n
|
jyotiprakashrout434
|
NORMAL
|
2020-07-10T21:31:38.016685+00:00
|
2020-07-10T21:31:38.016715+00:00
| 5,114 | false |
A must watch video if you\'re not already familier with connected compoents in graph theory: \nhttps://www.youtube.com/watch?v=z49Ohr5Ypnw\n```\nclass Solution {\n public int findCircleNum(int[][] M) {\n int N = M.length;\n boolean[]visited = new boolean[N];\n int count = 0;\n \n for(int i = 0; i < N ;i++){\n if(!visited[i]){\n count++;\n dfs(M,i,visited);\n }\n }\n return count; \n }\n \n \n private void dfs(int[][]M,int i,boolean[]visited){\n for(int j = 0 ; j < M[i].length ; j++){\n if(!visited[j] && M[i][j] != 0){\n visited[j] = true;\n dfs(M,j,visited);\n }\n }\n }\n \n}\n```
| 23 | 0 |
['Depth-First Search', 'Java']
| 2 |
number-of-provinces
|
One Line Linear Algebraic Solution
|
one-line-linear-algebraic-solution-by-aa-fi7d
|
The problem is equivalent to finding the number of connected components of the matrix M (with n rows/cols). Let D be the degree matrix aka the rowsums of M, an
|
aagrawal
|
NORMAL
|
2020-08-04T12:39:01.293818+00:00
|
2021-01-03T10:10:53.850818+00:00
| 1,379 | false |
The problem is equivalent to finding the number of connected components of the matrix M (with n rows/cols). Let D be the degree matrix aka the rowsums of M, and the laplacian matrix be L = D - M. Then the number of connected components of M is given by the dimension of the nullspace of L. By rank-nullity, this is equal to n - rank(L). This algorithm is GPU-friendly and admits efficient approximations. \n \n```\nimport numpy as np\n\nclass Solution:\n def findCircleNum(self, M: List[List[int]]) -> int:\n return len(M) - np.linalg.matrix_rank(np.diag(np.sum(M, axis=1)) - np.array(M))\n```\n\n
| 22 | 0 |
['Python', 'Python3']
| 3 |
number-of-provinces
|
Easy Python Union Find
|
easy-python-union-find-by-localhostghost-mvhk
|
\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n def find(x):\n if x != pa
|
localhostghost
|
NORMAL
|
2018-10-22T23:19:59.645631+00:00
|
2018-10-22T23:19:59.645698+00:00
| 3,320 | false |
```\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n def find(x):\n if x != parents[x]:\n parents[x] = find(parents[x])\n return parents[x] \n def union(x, y):\n parents[find(x)] = find(y)\n n = len(M)\n parents = list(range(n))\n for i in range(len(M)):\n for j in range(len(M[i])):\n if M[i][j]:\n union(i, j)\n circle = set(find(i) for i in range(n)) \n return len(circle) \n```
| 20 | 2 |
[]
| 4 |
number-of-provinces
|
Java BFS - Equivalent to Finding Connected Components in a Graph
|
java-bfs-equivalent-to-finding-connected-un25
|
\npublic int findCircleNum(int[][] M) {\n int count = 0;\n for (int i=0; i<M.length; i++)\n if (M[i][i] == 1) { count++; BFS(i, M); }\n return c
|
compton_scatter
|
NORMAL
|
2017-04-02T03:13:05.242000+00:00
|
2018-10-21T22:29:19.628297+00:00
| 7,514 | false |
```\npublic int findCircleNum(int[][] M) {\n int count = 0;\n for (int i=0; i<M.length; i++)\n if (M[i][i] == 1) { count++; BFS(i, M); }\n return count;\n}\n\npublic void BFS(int student, int[][] M) {\n Queue<Integer> queue = new LinkedList<>();\n queue.add(student);\n while (queue.size() > 0) {\n int queueSize = queue.size();\n for (int i=0;i<queueSize;i++) {\n int j = queue.poll();\n M[j][j] = 2; // marks as visited\n for (int k=0;k<M[0].length;k++) \n if (M[j][k] == 1 && M[k][k] == 1) queue.add(k);\n }\n }\n}\n```
| 20 | 1 |
[]
| 4 |
number-of-provinces
|
[C++] Striver Approach | Clean and Easy to understand
|
c-striver-approach-clean-and-easy-to-und-d1wr
|
```\n void dfs(int node,vector& visited,vector adjList[])\n {\n \n for(auto it: adjList[node])\n {\n if(!visited[it])\n
|
_swatantra_
|
NORMAL
|
2022-08-12T05:55:03.059819+00:00
|
2022-10-05T13:38:09.609076+00:00
| 1,455 | false |
```\n void dfs(int node,vector<int>& visited,vector<int> adjList[])\n {\n \n for(auto it: adjList[node])\n {\n if(!visited[it])\n {\n visited[it]=1;\n dfs(it,visited,adjList);\n }\n }\n }\n int findCircleNum(vector<vector<int>>& isConnected) \n {\n int v=isConnected.size();\n vector<int> visited(v,0);\n vector<int> adjList[v];\n\t\t\n ** // converting adjency matrix to list **\n\t\t\n for(int i=0;i<v;i++)\n {\n for(int j=0;j<v;j++)\n {\n if(isConnected[i][j]==1 and i!=j)\n {\n adjList[i].push_back(j);\n adjList[j].push_back(i);\n }\n }\n }\n int count=0;\n for(int i=0;i<v;i++)\n {\n if(!visited[i])\n {\n count++;\n dfs(i,visited,adjList);\n }\n }\n \n return count;\n }
| 18 | 0 |
['Depth-First Search', 'Graph', 'C']
| 3 |
number-of-provinces
|
[Union Find Tutorial] Number of Provinces
|
union-find-tutorial-number-of-provinces-47z3e
|
Topic : Union Find\nA data structure that stores non overlapping or disjoint subset of elements is called Disjoint Set or Union Find data structure. In the Uni
|
never_get_piped
|
NORMAL
|
2024-07-06T04:39:40.005881+00:00
|
2024-07-06T07:27:19.314199+00:00
| 2,204 | false |
**Topic** : Union Find\nA data structure that stores non overlapping or disjoint subset of elements is called **Disjoint Set** or **Union Find** data structure. In the Union-Find data structure, each connected component (disjoint subset) is represented as a forest (or collection) of trees where each tree is rooted and nodes point to their parent. **Note that in this structure, the root node of each tree points to itself**. The elements of each subset are the nodes within these trees. The Union-Find data structure supports following operations:\n* Merging disjoint sets to a single disjoint set using **Union** operation.\n* Finding representative of a disjoint set using **Find** operation.\n* Check if two sets are disjoint or not. \n\n<br/>\n\n**Implementation**:\n\nLet\'s use Java as the example code for the Union-Find template:\n```\nclass UF {\n int[] p;\n int[] height;\n\n UF(int n) {\n p = new int[n];\n height = new int[n];\n for (int i = 0; i < n; i++) {\n p[i] = i;\n height[i] = 1;\n }\n }\n\n int find(int u) {\n if (p[u] == u) return u;\n return find(p[u]);\n }\n\n void merge(int root1, int root2) {\n if (root1 == root2) return;\n if (height[root1] < height[root2]) {\n int temp = root1;\n root1 = root2;\n root2 = temp;\n }\n p[root2] = root1;\n height[root1] = Math.max(height[root1], 1 + height[root2]);\n }\n}\n```\n\n<br/><br/>\n\n* Initially, in the Union-Find data structure, each node is its own root, forming a singleton tree (disjoint subset) where the node\'s parent points to itself.\n\t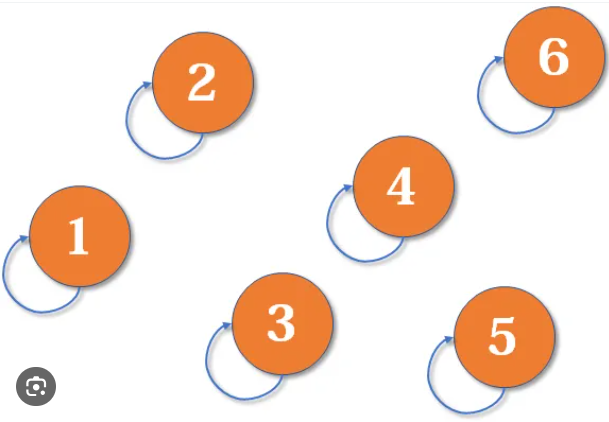\n\tThis initialization is done in the constructor of the UF data structure. We use `p[i]` to denote the parent of node i and `height[i]` to denote the height of the subtree with root node `i`. `p[i] = i` denotes that initially, each node is its own root.\n\t```\n\tUF(int n) {\n p = new int[n];\n height = new int[n];\n for (int i = 0; i < n; i++) {\n p[i] = i;\n height[i] = 1;\n }\n }\n\t```\n<br/><br/>\n\n* With the **find** operation, we traverse upwards to find the root of the current tree. This process stops when `p[u] = u`, indicating that `u` is the root node pointing to itself.\n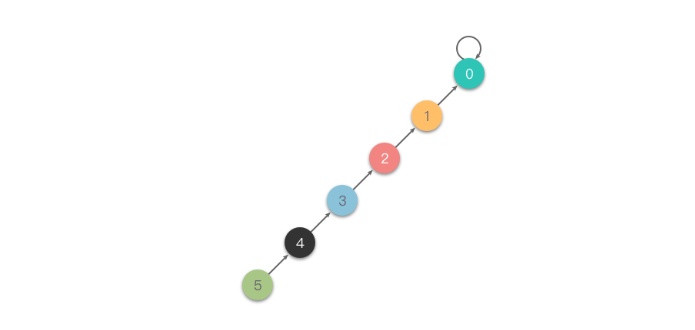\n\tThis is done via the `find` method:\n\t```\n\tint find(int u) {\n if (p[u] == u) return u;\n return find(p[u]);\n }\n\t```\n\t\n<br/><br/>\n* With the **Union** or **Merge** operation, we combine two trees (disjoint sets) into a single tree (disjoint set). In order to merge two trees, we simply set the root of one tree to point to the root of the other tree. **Note that before merging two roots, we must ensure they are not already in the same connected component**.\n\n\tTo optimize performance, we always merge the tree with smaller height to point to the root of the tree with greater height. \n\n\tThis is done via the `merge` method:\n\t```\n\tvoid merge(int root1, int root2) {\n if (root1 == root2) return;\n if (height[root1] < height[root2]) {\n int temp = root1;\n root1 = root2;\n root2 = temp;\n }\n p[root2] = root1;\n height[root1] = Math.max(height[root1], 1 + height[root2]);\n }\n\t```\n<br/><br/>\t\n* Time Complexity :\n\t* **Find** : `O(h)`, where `h` denotes the height of the tree. Given that we merge trees by always attaching the smaller tree under the root of the larger tree, the maximum height of any tree is `O(logn)` at most.\n\t* **Union** : `O(1)`.\n\t* **Constructor** : `O(n)`.\n* Space Complexity : `O(n)`\n___\n\n## Solution\nThe solution is straightforward: we use Union-Find to merge all connected nodes and then count the number of disjoint components at the end. \n\nAll nodes that are connected to each other can reach each other, so we place them within the same disjoint set to signify their mutual accessibility.\n\n<br/>\n\n```c++ []\nclass UF {\n public:\n vector<int> p; //parent\n vector<int> height; //size\n UF(int n) {\n for(int i = 0; i < n; i++) {\n p.push_back(i);\n height.push_back(1);\n }\n }\n\n int find(int u) {\n return p[u] == u ? u : find(p[u]);\n }\n\n void merge(int root1, int root2) {\n if(root1 == root2) {\n return;\n }\n if(height[root1] < height[root2]) {\n swap(root1, root2);\n }\n p[root1] = root2;\n height[root2] = max(height[root2], 1 + height[root1]);\n }\n};\n\nclass Solution {\npublic:\n int findCircleNum(vector<vector<int>>& isConnected) {\n int n = isConnected.size();\n UF uf(n);\n for(int i = 0; i < n; i++) {\n for(int j = i + 1; j < n; j++) {\n if(isConnected[i][j] == 1) {\n int root1 = uf.find(i);\n int root2 = uf.find(j);\n uf.merge(root1, root2);\n }\n }\n }\n \n set<int> components;\n for(int i = 0; i < n; i++) {\n components.insert(uf.find(i));\n }\n return components.size();\n }\n};\n```\n```java []\nclass UF {\n int[] p;\n int[] height;\n\n UF(int n) {\n p = new int[n];\n height = new int[n];\n for (int i = 0; i < n; i++) {\n p[i] = i;\n height[i] = 1;\n }\n }\n\n int find(int u) {\n if (p[u] == u) return u;\n return find(p[u]);\n }\n\n void merge(int root1, int root2) {\n if (root1 == root2) return;\n if (height[root1] < height[root2]) {\n int temp = root1;\n root1 = root2;\n root2 = temp;\n }\n p[root2] = root1;\n height[root1] = Math.max(height[root1], 1 + height[root2]);\n }\n}\n\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n int n = isConnected.length;\n UF uf = new UF(n);\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) {\n if (isConnected[i][j] == 1) {\n int root1 = uf.find(i);\n int root2 = uf.find(j);\n uf.merge(root1, root2);\n }\n }\n }\n \n Set<Integer> components = new HashSet<>();\n for (int i = 0; i < n; i++) {\n components.add(uf.find(i));\n }\n \n return components.size();\n }\n}\n```\n```python []\nclass UF:\n def __init__(self, n):\n self.p = list(range(n))\n self.height = [1] * n\n\n def find(self, u):\n if self.p[u] == u:\n return u\n return self.find(self.p[u])\n\n def merge(self, root1, root2):\n if root1 == root2:\n return\n if self.height[root1] < self.height[root2]:\n root1, root2 = root2, root1\n self.p[root2] = root1\n self.height[root1] = max(self.height[root1], 1 + self.height[root2])\n\nclass Solution:\n def findCircleNum(self, isConnected: List[List[int]]) -> int:\n n = len(isConnected)\n uf = UF(n)\n for i in range(n):\n for j in range(i + 1, n):\n if isConnected[i][j] == 1:\n root1 = uf.find(i)\n root2 = uf.find(j)\n uf.merge(root1, root2)\n \n components = set()\n for i in range(n):\n components.add(uf.find(i))\n \n return len(components) \n```\n```Go []\ntype UF struct {\n\tp []int\n\theight []int\n}\n\nfunc NewUF(n int) *UF {\n\tuf := UF{}\n\tuf.p = make([]int, n)\n\tuf.height = make([]int, n)\n\tfor i := 0; i < n; i++ {\n\t\tuf.p[i] = i\n\t\tuf.height[i] = 1\n\t}\n\treturn &uf\n}\n\nfunc (uf *UF) find(u int) int {\n\tif uf.p[u] == u {\n\t\treturn u\n\t}\n\treturn uf.find(uf.p[u])\n}\n\nfunc (uf *UF) merge(root1, root2 int) {\n\tif root1 == root2 {\n\t\treturn\n\t}\n\tif uf.height[root1] < uf.height[root2] {\n\t\troot1, root2 = root2, root1\n\t}\n\tuf.p[root2] = root1\n\tuf.height[root1] = max(uf.height[root1], 1+uf.height[root2])\n}\n\nfunc findCircleNum(isConnected [][]int) int {\n n := len(isConnected)\n\tuf := NewUF(n)\n\tfor i := 0; i < n; i++ {\n\t\tfor j := i + 1; j < n; j++ {\n\t\t\tif isConnected[i][j] == 1 {\n\t\t\t\troot1 := uf.find(i)\n\t\t\t\troot2 := uf.find(j)\n\t\t\t\tuf.merge(root1, root2)\n\t\t\t}\n\t\t}\n\t}\n\t\n\tcomponents := make(map[int]bool)\n\tfor i := 0; i < n; i++ {\n\t\tcomponents[uf.find(i)] = true\n\t}\n\t\n\treturn len(components)\n}\n```\n```PHP []\nclass UF {\n private $p;\n private $height;\n\n function __construct($n) {\n $this->p = range(0, $n - 1);\n $this->height = array_fill(0, $n, 1);\n }\n\n function find($u) {\n if ($this->p[$u] == $u) return $u;\n return $this->find($this->p[$u]);\n }\n\n function merge($root1, $root2) {\n if ($root1 == $root2) return;\n if ($this->height[$root1] < $this->height[$root2]) {\n list($root1, $root2) = array($root2, $root1);\n }\n $this->p[$root2] = $root1;\n $this->height[$root1] = max($this->height[$root1], 1 + $this->height[$root2]);\n }\n}\n\nclass Solution {\n\n /**\n * @param Integer[][] $isConnected\n * @return Integer\n */\n function findCircleNum($isConnected) {\n $n = count($isConnected);\n $uf = new UF($n);\n for ($i = 0; $i < $n; $i++) {\n for ($j = $i + 1; $j < $n; $j++) {\n if ($isConnected[$i][$j] == 1) {\n $root1 = $uf->find($i);\n $root2 = $uf->find($j);\n $uf->merge($root1, $root2);\n }\n }\n }\n \n $components = [];\n for ($i = 0; $i < $n; $i++) {\n $components[$uf->find($i)] = true;\n }\n \n return count($components);\n }\n}\n```\n```javascript []\n/**\n * @param {number[][]} isConnected\n * @return {number}\n */\n\nclass UF {\n constructor(n) {\n this.p = [...Array(n).keys()];\n this.height = Array(n).fill(1);\n }\n\n find(u) {\n if (this.p[u] === u) return u;\n return this.find(this.p[u]);\n }\n\n merge(root1, root2) {\n if (root1 === root2) return;\n if (this.height[root1] < this.height[root2]) {\n [root1, root2] = [root2, root1];\n }\n this.p[root2] = root1;\n this.height[root1] = Math.max(this.height[root1], 1 + this.height[root2]);\n }\n}\n\nvar findCircleNum = function(isConnected) {\n const n = isConnected.length;\n const uf = new UF(n);\n for (let i = 0; i < n; i++) {\n for (let j = i + 1; j < n; j++) {\n if (isConnected[i][j] === 1) {\n const root1 = uf.find(i);\n const root2 = uf.find(j);\n uf.merge(root1, root2);\n }\n }\n }\n \n const components = new Set();\n for (let i = 0; i < n; i++) {\n components.add(uf.find(i));\n }\n \n return components.size; \n};\n```\n\n**Complexity**:\n* Time Complexity : `O(n ^ 2 log(n))`\n* Space Complexity : `O(n)`\n\n<br/>\n\n**Homework**:\n* [Count Servers that Communicate](https://leetcode.com/problems/count-servers-that-communicate/)\n* [Satisfiability of Equality Equations](https://leetcode.com/problems/satisfiability-of-equality-equations/)\n* [Redundant Connection](https://leetcode.com/problems/redundant-connection/)\n* [Making A Large Island](https://leetcode.com/problems/making-a-large-island/)\n* [Smallest String With Swaps](https://leetcode.com/problems/smallest-string-with-swaps/)\n* [Largest Component Size by Common Factor](https://leetcode.com/problems/largest-component-size-by-common-factor/)\n\n\n**Feel free to leave a comment if something is confusing, or if you have any suggestions on how I can improve the post.**
| 16 | 0 |
['PHP', 'Python', 'Java', 'Go', 'JavaScript']
| 3 |
number-of-provinces
|
[Python] Union Find - Clean & Concise
|
python-union-find-clean-concise-by-hiepi-di58
|
\u2714\uFE0F Solution 1: Union Find (Naive)\npython\nclass UnionFind:\n def __init__(self, n):\n self.parent = [i for i in range(n)]\n \n de
|
hiepit
|
NORMAL
|
2021-09-13T16:26:58.104078+00:00
|
2022-05-01T22:50:33.579379+00:00
| 547 | false |
**\u2714\uFE0F Solution 1: Union Find (Naive)**\n```python\nclass UnionFind:\n def __init__(self, n):\n self.parent = [i for i in range(n)]\n \n def find(self, u):\n if u != self.parent[u]:\n u = self.find(self.parent[u])\n return u\n \n def union(self, u, v):\n pu, pv = self.find(u), self.find(v)\n if pu == pv: return False\n self.parent[pu] = pv\n return True\n\nclass Solution:\n def findCircleNum(self, isConnected: List[List[int]]) -> int:\n n = len(isConnected)\n \n component = n\n uf = UnionFind(n)\n for i in range(n):\n for j in range(i+1, n):\n if isConnected[i][j] == 1 and uf.union(i, j):\n component -= 1\n return component\n```\nComplexity:\n- Time: `O(N^3)`, where `N <= 200` is number of nodes\n- Space: `O(N)`\n\n---\n**\u2714\uFE0F Solution 2: Union Find (Path Compression)**\n```python\nclass UnionFind:\n def __init__(self, n):\n self.parent = [i for i in range(n)]\n \n def find(self, u):\n if u != self.parent[u]:\n self.parent[u] = self.find(self.parent[u]) # Path compression\n return self.parent[u]\n \n def union(self, u, v):\n pu, pv = self.find(u), self.find(v)\n if pu == pv: return False\n self.parent[pu] = pv\n return True\n\nclass Solution:\n def findCircleNum(self, isConnected: List[List[int]]) -> int:\n n = len(isConnected)\n \n component = n\n uf = UnionFind(n)\n for i in range(n):\n for j in range(i+1, n):\n if isConnected[i][j] == 1 and uf.union(i, j):\n component -= 1\n return component\n```\nComplexity:\n- Time: `O(N^2 * logN)`, where `N <= 200` is number of nodes\n- Space: `O(N)`\n\n---\n**\u2714\uFE0F Solution 3: Union Find (Union by Size & Path Compression)**\n```python\nclass UnionFind:\n def __init__(self, n):\n self.parent = [i for i in range(n)]\n self.size = [1] * n\n \n def find(self, u):\n if u != self.parent[u]:\n self.parent[u] = self.find(self.parent[u]) # Path compression\n return self.parent[u]\n \n def union(self, u, v):\n pu, pv = self.find(u), self.find(v)\n if pu == pv: return False\n if self.size[pu] < self.size[pv]: # Merge pu to pv\n self.size[pv] += self.size[pu]\n self.parent[pu] = pv\n else:\n self.size[pu] += self.size[pv]\n self.parent[pv] = pu\n return True\n\n\nclass Solution:\n def findCircleNum(self, isConnected: List[List[int]]) -> int:\n n = len(isConnected)\n \n component = n\n uf = UnionFind(n)\n for i in range(n):\n for j in range(i+1, n):\n if isConnected[i][j] == 1 and uf.union(i, j):\n component -= 1\n return component\n```\nComplexity:\n- Time: `O(N^2 * \u03B1(N))` ~ `O(N^2)`, where `N <= 200` is number of nodes\n Explanation: Using both **path compression** and **union by size** ensures that the **amortized time** per **UnionFind** operation is only `\u03B1(n)`, which is optimal, where `\u03B1(n)` is the inverse Ackermann function. This function has a value `\u03B1(n) < 5` for any value of n that can be written in this physical universe, so the disjoint-set operations take place in essentially constant time.\nReference: https://en.wikipedia.org/wiki/Disjoint-set_data_structure or https://www.slideshare.net/WeiLi73/time-complexity-of-union-find-55858534 for more information.\n- Space: `O(N)`
| 16 | 0 |
[]
| 2 |
number-of-provinces
|
python solution using union find
|
python-solution-using-union-find-by-alag-suq9
|
This question is similar to Number of Connected Components in an Undirected Graph\n\nsee this for union find explanation: https://youtu.be/ID00PMy0-vE\n\n\nclas
|
alagram
|
NORMAL
|
2017-04-02T03:13:55.123000+00:00
|
2018-09-11T02:22:25.889798+00:00
| 3,565 | false |
This question is similar to Number of Connected Components in an Undirected Graph\n\nsee this for union find explanation: https://youtu.be/ID00PMy0-vE\n\n```\nclass Solution(object):\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n ds = DisjointSet()\n\n for i in range(len(M)):\n ds.make_set(i)\n\n for i in range(len(M)):\n for j in range(len(M)):\n if M[i][j] == 1:\n ds.union(i, j)\n\n return ds.num_sets\n\nclass Node(object):\n def __init__(self, data, parent=None, rank=0):\n self.data = data\n self.parent = parent\n self.rank = rank\n\nclass DisjointSet(object):\n def __init__(self):\n self.map = {}\n self.num_sets = 0\n\n def make_set(self, data):\n node = Node(data)\n node.parent = node\n self.map[data] = node\n self.num_sets += 1\n\n def union(self, data1, data2):\n node1 = self.map[data1]\n node2 = self.map[data2]\n\n parent1 = self.find_set_util(node1)\n parent2 = self.find_set_util(node2)\n\n if parent1.data == parent2.data:\n return\n\n if parent1.rank >= parent2.rank:\n if parent1.rank == parent2.rank:\n parent1.rank += 1\n parent2.parent = parent1\n else:\n parent1.parent = parent2\n\n self.num_sets -= 1\n\n\n def find_set(self, data):\n return self.find_set_util(self.map[data])\n\n def find_set_util(self, node):\n parent = node.parent\n if parent == node:\n return parent\n\n node.parent = self.find_set_util(node.parent) # path compression\n return node.parent\n```
| 16 | 2 |
[]
| 1 |
number-of-provinces
|
[C++] Using bfs {beginners code}
|
c-using-bfs-beginners-code-by-shubhambha-0raa
|
Pls upvote if you find this helpful :)\n\nI\'m a beginner to graph theory and am finding it a bit difficult to grasp these concepts.Tried to learn union find b
|
shubhambhatt__
|
NORMAL
|
2020-05-29T15:46:13.366518+00:00
|
2020-05-29T15:46:13.366564+00:00
| 3,053 | false |
***Pls upvote if you find this helpful :)***\n\nI\'m a beginner to graph theory and am finding it a bit difficult to grasp these concepts.Tried to learn union find but couldn\'t understand it. It would be great if someone could help me understand it .Also if you have any other better method or can optimise this code then pls mention them in the comments.\n\nHere i have used the concept of bfs with a boolean visited array and a queue q1. I have tried to count the components of the given graph.\n```\nclass Solution {\npublic:\n int findCircleNum(vector<vector<int>>& M) {\n int n=M.size();\n if(n==0)return n;\n int circles=0;\n vector<bool> visited(n,false); \n for(int i=0;i<n;i++){\n if(visited[i])continue;\n queue<int> q1;\n q1.push(i);\n circles++;\n\n while(!q1.empty()){ \n int cur=q1.front();\n q1.pop();\n visited[cur]=true;\n for(int j=0;j<M[cur].size();j++){\n if(visited[j]==false&&M[cur][j]==1){\n q1.push(j);\n visited[j]=true;\n }\n }\n \n }\n \n \n }\n return circles;\n }\n};\n```
| 15 | 0 |
['Breadth-First Search', 'C', 'C++']
| 1 |
number-of-provinces
|
DFS | 93.33% Beats | 3ms | PHP
|
dfs-9333-beats-3ms-php-by-ma7med-ce54
|
Code
|
Ma7med
|
NORMAL
|
2025-01-09T11:55:34.475684+00:00
|
2025-01-15T08:42:10.659885+00:00
| 1,901 | false |
# Code
```php []
class Solution {
/**
* @param Integer[][] $isConnected
* @return Integer
*/
function findCircleNum($isConnected) {
$n = count($isConnected);
$visited = array_fill(0, $n, false); // To keep track of visited cities
$provinces = 0;
// Iterate through all cities
for ($i = 0; $i < $n; $i++) {
if (!$visited[$i]) {
$provinces++; // Found a new province
$this->dfs($i, $visited, $isConnected, $n);
}
}
return $provinces;
}
// Depth-First Search (DFS) helper function
private function dfs($node, &$visited, $isConnected, $n) {
$visited[$node] = true;
for ($neighbor = 0; $neighbor < $n; $neighbor++) {
if ($isConnected[$node][$neighbor] == 1 && !$visited[$neighbor]) {
$this->dfs($neighbor, $visited, $isConnected, $n);
}
}
}
}
```
| 14 | 0 |
['PHP']
| 0 |
number-of-provinces
|
Beginner Friendly - Using BFS and Adjacency list
|
beginner-friendly-using-bfs-and-adjacenc-avry
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires finding the number of connected components in an undirected graph.
|
VarmaNithin
|
NORMAL
|
2024-01-04T19:40:40.650492+00:00
|
2024-01-17T09:48:14.309370+00:00
| 1,752 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires finding the number of connected components in an undirected graph. Connected components are subsets of nodes in a graph where each node is reachable from any other node in the same subset.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**1.Adjacency List Creation:**\n\nThe code begins by converting the given adjacency matrix isConnected into an adjacency list l. This conversion makes it easier to traverse the graph using lists of connected nodes for each node.\n**2.Breadth-First Search (BFS):**\n\nThe main part of the code utilizes BFS to explore the graph and count the number of connected components.\nIt starts by iterating through each node.\nFor each unvisited node encountered, it initiates a BFS to explore all nodes connected to that node.\nIt keeps track of visited nodes using a HashSet (visited) to ensure nodes are not visited more than once.\nDuring BFS, it traverses the connected nodes of the current node and marks them as visited, ensuring all nodes in the same component are accounted for.\n**3.Counting Connected Components:**\n\nEach time BFS is initiated from an unvisited node, it identifies a new connected component and increments the count variable to keep track of the total count of connected components.\n**4.Returning the Count:**\n\nFinally, the code returns the total count of connected components found in the graph.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n\n int n = isConnected.length; \n // To create an adjacency list \'l\' \n List<List<Integer>> l = new ArrayList<>();\n\n // Creating adjacency list from the adjacency matrix\n for (int i = 0; i < n; i++) {\n l.add(new ArrayList<>());\n for (int j = 0; j < n; j++) {\n if (i != j && isConnected[i][j] == 1) {\n // Adding connected nodes to the adjacency list\n l.get(i).add(j);\n }\n }\n }\n\n Queue<Integer> q = new LinkedList<>();\n HashSet<Integer> visited = new HashSet<>();\n int count = 0; // Counter for connected components\n\n // Checking for each node whether it has any path or is part of a disjoint component\n for (int i = 0; i < n; i++) {\n if (!visited.contains(i)) {\n // Starting BFS from unvisited node\n q.add(i);\n visited.add(i);\n while (!q.isEmpty()) {\n int current = q.poll();\n for (int j : l.get(current)) {\n if (!visited.contains(j)) {\n q.add(j);\n visited.add(j);\n }\n }\n }\n count++; // Increment count for each connected component found\n }\n }\n return count; // Returning the total count of connected components\n }\n}\n\n```\n\n\n\n\n
| 14 | 0 |
['Breadth-First Search', 'Java']
| 2 |
number-of-provinces
|
JavaScript Clean Union Find
|
javascript-clean-union-find-by-control_t-fb4t
|
javascript\nvar findCircleNum = function(M) {\n \n class UnionFind {\n constructor(n) {\n this.graph = [...Array(n)].map((_, i) => i);\n
|
control_the_narrative
|
NORMAL
|
2020-07-23T17:04:12.983127+00:00
|
2020-07-23T17:04:12.983164+00:00
| 1,948 | false |
```javascript\nvar findCircleNum = function(M) {\n \n class UnionFind {\n constructor(n) {\n this.graph = [...Array(n)].map((_, i) => i);\n this.groups = n;\n }\n \n find(id) {\n if(this.graph[id] === id) return id;\n this.graph[id] = this.find(this.graph[id]);\n return this.graph[id];\n }\n \n union(x, y) {\n const rootX = this.find(x);\n const rootY = this.find(y);\n if(rootX !== rootY) {\n this.graph[rootY] = rootX;\n this.groups--;\n }\n }\n }\n\n const N = M.length, unionfind = new UnionFind(N);\n \n for(let r = 0; r < N; r++) {\n for(let c = 0; c < N; c++) {\n if(M[r][c]) unionfind.union(r, c);\n }\n }\n return unionfind.groups;\n};\n```
| 14 | 1 |
['Union Find', 'JavaScript']
| 2 |
number-of-provinces
|
🏆C++ || Easy DFS
|
c-easy-dfs-by-chiikuu-gb1a
|
Code\n\nclass Solution {\npublic:\n void dfs(vector<int>&vis,vector<int>ad[],int i){\n vis[i]=1;\n for(auto k:ad[i]){\n if(!vis[k]){
|
CHIIKUU
|
NORMAL
|
2023-06-04T04:47:02.887230+00:00
|
2023-06-04T04:47:02.887264+00:00
| 1,188 | false |
# Code\n```\nclass Solution {\npublic:\n void dfs(vector<int>&vis,vector<int>ad[],int i){\n vis[i]=1;\n for(auto k:ad[i]){\n if(!vis[k]){\n dfs(vis,ad,k);\n }\n }\n }\n int findCircleNum(vector<vector<int>>&g) {\n int n=g.size();\n vector<int>ad[n];\n for(int i=0;i<n;i++){\n for(int j=0;j<n;j++){\n if(g[i][j]){\n ad[i].push_back(j);\n ad[j].push_back(i);\n }\n }\n }\n int c=0;\n vector<int>vis(n,0);\n for(int i=0;i<n;i++){\n if(!vis[i]){\n c++;\n dfs(vis,ad,i);\n }\n }\n return c;\n }\n};\n```\n\n
| 13 | 0 |
['Depth-First Search', 'Graph', 'C++']
| 0 |
number-of-provinces
|
Union Find with union by ranks and path compression
|
union-find-with-union-by-ranks-and-path-3qpff
|
Time complexity: O(n2) because improved union find takes O(1) time and we traverse n * n grid, thus O(n * n * 1) = O(n2)\nSpace complexity: O(n) becuse UnionFin
|
polasprawka
|
NORMAL
|
2020-11-04T08:16:37.351086+00:00
|
2020-11-04T08:19:42.145578+00:00
| 2,200 | false |
Time complexity: O(n2) because improved union find takes O(1) time and we traverse n * n grid, thus O(n * n * 1) = O(n2)\nSpace complexity: O(n) becuse UnionFind allocates 2 arrays of n, thus O(n + n) = O(n)\n\n\tclass UnionFind:\n\t\tdef __init__(self, n):\n\t\t\tself.parents = [x for x in range(n)]\n\t\t\tself.count = [1 for _ in range(n)]\n\t\t\tself.groups = n\n\n\t\tdef find(self, a):\n\t\t\twhile a != self.parents[a]:\n\t\t\t\tself.parents[a] = self.parents[self.parents[a]]\n\t\t\t\ta = self.parents[a]\n\t\t\treturn a\n\n\t\tdef union(self, a, b):\n\t\t\ta_root, b_root = self.find(a), self.find(b)\n\n\t\t\tif a_root == b_root:\n\t\t\t\treturn True\n\n\t\t\tif self.count[a_root] > self.count[b_root]:\n\t\t\t\tself.parents[b_root] = a_root\n\t\t\t\tself.count[a_root] += self.count[b_root]\n\t\t\telse:\n\t\t\t\tself.parents[a_root] = b_root\n\t\t\t\tself.count[b_root] += self.count[a_root]\n\t\t\tself.groups -= 1\n\n\t\t\treturn False\n\n\tclass Solution:\n\t\tdef findCircleNum(self, grid: List[List[int]]) -> int:\n\t\t\tn = len(grid)\n\t\t\tif n < 1 or len(grid[0]) != n:\n\t\t\t\treturn 0\n\n\t\t\tunion = UnionFind(n)\n\n\t\t\tfor i in range(n):\n\t\t\t\tfor j in range(n):\n\t\t\t\t\tif grid[i][j] == 1:\n\t\t\t\t\t\tunion.union(i,j)\n\n\t\t\treturn union.groups
| 13 | 0 |
['Union Find', 'Python3']
| 2 |
number-of-provinces
|
Complete analysis and solutions for this question, DFS/BFS/UnionFind.
|
complete-analysis-and-solutions-for-this-a0w8
|
Solution1: DFS or BFS\n\nWe can reduce abstract this problem into finding connected groups in a undirected graph represented as an adjacency matrix. \n\nSince
|
YYY-YYY
|
NORMAL
|
2018-01-17T04:33:03.712000+00:00
|
2018-01-17T04:33:03.712000+00:00
| 885 | false |
# Solution1: DFS or BFS\n\nWe can reduce abstract this problem into finding __connected groups__ in a undirected graph represented as an __adjacency matrix__. \n\nSince we want to treat the input `M` as a adjacency matrix, we treate each row from `0` to `n - 1` as `n` nodes. Hence we use a `boolean[]` to store the visited status. \n\nTherefore, a normal graph traversal algorithms can be utilized to find the number of connected gropus in this undirected graph. \n\n## DFS solution:\n\nSince the input matrix `M` is `n*n` in size \nTime complexity: `O(n^2)` \n\nSpace complexity: `O(n)` \n\n```Java\nclass Solution {\n public int findCircleNum(int[][] M) {\n if (M == null || M.length == 0 || M[0].length == 0) return 0;\n boolean[] visited = new boolean[M.length];\n int count = 0;\n for (int i = 0; i < M.length; i++) {\n if (!visited[i]) {\n count++;\n dfs(M, i, visited);\n }\n }\n \n return count;\n }\n \n private void dfs(int[][] M, int i, boolean[] visited) {\n for (int j = 0; j < M[i].length; j++) {\n if (M[i][j] == 1 && !visited[j]) {\n visited[j] = true;\n dfs(M, j, visited);\n }\n }\n }\n}\n```\n\n## BFS solution: \n\nThe same idea, but used a `Queue` to perform the BFS process. \n\nTime complexity: `O(n^2)`\n\nSpace complexity: `O(n)`\n\n```Java\nclass Solution {\n public int findCircleNum(int[][] M) {\n if (M == null || M.length == 0 || M[0].length == 0) return 0;\n boolean[] visited = new boolean[M.length];\n int count = 0;\n for (int i = 0; i < M.length; i++) {\n if (!visited[i]) {\n bfs(M, i, visited);\n count++;\n }\n }\n \n return count;\n }\n \n private void bfs(int[][] M, int i, boolean[] visited) {\n Queue<Integer> queue = new LinkedList<>();\n queue.offer(i);\n visited[i] = true;\n while (!queue.isEmpty()) {\n int curr = queue.poll();\n for (int j = 0; j < M[curr].length; j++) {\n if (M[curr][j] == 1 && !visited[j]) {\n queue.offer(j);\n visited[j] = true;\n }\n }\n }\n }\n}\n```\n\n# Solution2: Union-find\n\nSince we've already reduced the question into a connectivity problem, __union-find__ algorithm seems to be appliable to this question, for it's suitable to be used for dynamic connectivity problem. \n\nFor this question, specifically, we still treat the input `M` as a __adjacency matrix__. And row index `0` to `n-1` as `n` nodes. We check each edge (`M[i][j]`) between each node pairs, and union `i` and `j`. After we `union`ed each edge, we check the number of roots, i.e. where `i == id[i]`, and return it as the number of connected components. \n\nNote that we have 2 optimization for the `union-find` algorithm: \n1. During the `union()` process, we check the size of each connected component and union the smaller one to the greater one. This is called __weighed union__ and can flatten the depth of the connected component and improve the efficiency of the `union-find` algorithm. \n2. During the `findRoot()` process, we used path compression to flatten the depth of the connected component, also improved the efficiency of the algorithm. \n\nBy utilizing this 2 improvements, the time complexity of calling `union()` for M times is `O(n + Mlg*n)`, which can be viewed as `O(n)`, because `lg*n` can be viewed as a constant. \n\n```Java\nclass Solution {\n // weighed quick union with path compression\n public int findCircleNum(int[][] M) {\n int[] size = new int[M.length];\n int[] id = new int[M.length];\n for (int i = 0; i < M.length; i++) {\n id[i] = i;\n size[i] = 1;\n }\n for (int i = 0; i < M.length; i++) {\n for (int j = 0; j < M[i].length; j++) {\n if (M[i][j] == 1) {\n union(id, size, i, j);\n }\n }\n }\n \n int count = 0;\n for (int i = 0; i < id.length; i++) {\n if (i == id[i]) {\n count++;\n }\n }\n \n return count;\n }\n \n private void union(int[] id, int[] size, int i, int j) {\n int rootI = findRoot(id, i);\n int rootJ = findRoot(id, j);\n \n // weighed quick union\n if (size[rootI] >= size[rootJ]) {\n id[rootJ] = rootI;\n size[rootI] += size[rootJ];\n } else {\n id[rootI] = rootJ;\n size[rootJ] += size[rootI];\n }\n }\n \n private int findRoot(int[] id, int curr) {\n while (curr != id[curr]) {\n // path compression\n id[curr] = id[id[curr]];\n curr = id[curr];\n }\n return curr;\n }\n}\n```
| 13 | 1 |
[]
| 1 |
number-of-provinces
|
Union by rank and path compression using C++ || easy to understand
|
union-by-rank-and-path-compression-using-613z
|
class Solution {\npublic:\n\n // function to find parent of the node\n int findPar(int node,vector&parent)\n {\n if(parent[node]==node)\n
|
dkshitij98
|
NORMAL
|
2021-05-18T06:38:20.557377+00:00
|
2021-05-18T06:41:08.567440+00:00
| 1,624 | false |
class Solution {\npublic:\n\n // function to find parent of the node\n int findPar(int node,vector<int>&parent)\n {\n if(parent[node]==node)\n {\n return node;\n }\n \n return parent[node]=findPar(parent[node],parent);//this line does path compression \n }\n //function to connect nodes on the basis of rank \n \n void unionn(int u,int v,vector<int>&parent,vector<int>&rank) \n {\n u=findPar(u,parent);\n v=findPar(v,parent);\n if(rank[u]>rank[v])\n {\n parent[v]=u;\n }\n else if(rank[u]<rank[v])\n {\n parent[u]=v;\n }\n else{\n parent[v]=u;\n rank[u]++;\n }\n }\n int findCircleNum(vector<vector<int>>& isConnected) {\n \n int n = isConnected.size();\n vector<int> parent(n);\n vector<int>rank(n,0);\n for(int i=0;i<n;i++)\n {\n parent[i]=i;\n }\n for(int i=0;i<n;i++)\n {\n for(int j=i;j<n;j++)\n {\n if(isConnected[i][j])\n {\n unionn(i,j,parent,rank);\n }\n }\n }\n \n map<int,int>mp;\n int count =0;\n for(int i=0;i<n;i++)\n {\n for(int j=i;j<n;j++)\n {\n if(isConnected[i][j])\n {\n //if nodes have same parent and not counted before then increase count and remember the parent\n if(findPar(i,parent)==findPar(j,parent) and mp.find(findPar(i,parent))==mp.end())\n {\n count++;\n mp[findPar(i,parent)]=1;\n }\n }\n }\n }\n return count;\n }\n};
| 12 | 1 |
['Union Find', 'C', 'C++']
| 7 |
number-of-provinces
|
[Java] UnionFind
|
java-unionfind-by-danny7226-k32k
|
\nclass UnionFind{\n int[] f;\n public UnionFind(int size){\n f = new int[size];\n for(int i = 0; i < size; i++){\n f[i] = i;\n
|
danny7226
|
NORMAL
|
2019-08-15T12:24:03.215108+00:00
|
2019-08-15T12:24:03.215141+00:00
| 2,660 | false |
```\nclass UnionFind{\n int[] f;\n public UnionFind(int size){\n f = new int[size];\n for(int i = 0; i < size; i++){\n f[i] = i;\n }\n }\n public int find(int x){\n if (f[x] != x){\n f[x] = find(f[x]);\n }\n return f[x];\n }\n public void unite(int x, int y){\n int fx = find(x);\n int fy = find(y);\n f[f[y]] = fx;\n } \n}\nclass Solution {\n public int findCircleNum(int[][] M) {\n if (M.length == 0 || M[0].length == 0) return 0;\n int row = M.length, column = M[0].length;\n UnionFind uf = new UnionFind(row);\n Set<Integer> set = new HashSet<Integer>();\n for (int i = 0; i < row; i++){\n for(int j = i + 1; j < column; j ++){\n if (M[i][j] == 1){\n uf.unite(i,j);\n }\n }\n }\n for(int i=0; i<row; i++){\n uf.f[i] = uf.find(i);\n set.add(uf.f[i]);\n }\n return set.size();\n \n }\n}\n```
| 12 | 0 |
['Union Find', 'Java']
| 3 |
number-of-provinces
|
DFS and BFS
|
dfs-and-bfs-by-dixon_n-xeh3
|
\nJust Started Graphs \uD83D\uDD25\n\nAdded More intuitive approaches!\n\n\n\n\n# Code\njava []\n// BFS\n\nclass Solution {\n public int findCircleNum(int[
|
Dixon_N
|
NORMAL
|
2024-06-15T20:44:58.102013+00:00
|
2024-07-22T08:57:24.291006+00:00
| 1,479 | false |
\nJust Started Graphs \uD83D\uDD25\n\nAdded More intuitive approaches!\n\n<br/>\n\n\n# Code\n```java []\n// BFS\n\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n int n = isConnected.length;\n boolean[] visited = new boolean[n];\n int provinces = 0;\n\n for (int i = 0; i < n; i++) {\n if (!visited[i]) {\n provinces++;\n bfs(isConnected, visited, i);\n }\n }\n\n return provinces;\n }\n\n private void bfs(int[][] isConnected, boolean[] visited, int city) {\n Queue<Integer> queue = new LinkedList<>();\n queue.add(city);\n visited[city] = true;\n\n while (!queue.isEmpty()) {\n int current = queue.poll();\n for (int neighbor = 0; neighbor < isConnected.length; neighbor++) {\n if (isConnected[current][neighbor] == 1 && !visited[neighbor]) {\n queue.add(neighbor);\n visited[neighbor] = true;\n }\n }\n }\n }\n}\n\n```\n```java []\n//DFS approach\n\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n int n = isConnected.length;\n boolean[] visited = new boolean[n];\n int provinces = 0;\n\n for (int i = 0; i < n; i++) {\n if (!visited[i]) {\n provinces++;\n dfs(isConnected, visited, i);\n }\n }\n\n return provinces;\n }\n\n private void dfs(int[][] isConnected, boolean[] visited, int city) {\n visited[city] = true;\n for (int neighbor = 0; neighbor < isConnected.length; neighbor++) {\n if (isConnected[city][neighbor] == 1 && !visited[neighbor]) {\n dfs(isConnected, visited, neighbor);\n }\n }\n }\n}\n\n```\n```java []\n//BFS approach\n\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n \n ArrayList<ArrayList<Integer>> adjLs = new ArrayList<ArrayList<Integer>>(); \n int V = isConnected.length;\n for(int i = 0;i<V;i++) {\n adjLs.add(new ArrayList<Integer>()); \n }\n \n // to change adjacency matrix to list \n for(int i = 0;i<V;i++) {\n for(int j = 0;j<V;j++) {\n // self nodes are not considered \n if(isConnected[i][j] == 1 && i != j) {\n adjLs.get(i).add(j); \n adjLs.get(j).add(i); \n }\n }\n }\n boolean vis[] = new boolean[V]; \n int cnt = 0; \n for(int i = 0;i<V;i++) {\n if(vis[i] ==false) {\n cnt++;\n bfs(i, adjLs, vis); \n }\n }\n return cnt; \n }\n\n private void bfs(int node, ArrayList<ArrayList<Integer>> adjLs, boolean [] vis) {\n \n Queue<Integer> q = new LinkedList<>();\n vis[node] = true;\n q.offer(node);\n while(!q.isEmpty()){\n int currentNode = q.poll();\n\n for(Integer it: adjLs.get(currentNode)){\n if(vis[it]==false){\n vis[it]=true;\n q.offer(it);\n }\n }\n }\n }\n}\n```\n```java []\n//DFS approach\n\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n \n ArrayList<ArrayList<Integer>> adjLs = new ArrayList<ArrayList<Integer>>(); \n int V = isConnected.length;\n for(int i = 0;i<V;i++) {\n adjLs.add(new ArrayList<Integer>()); \n }\n \n // to change adjacency matrix to list \n for(int i = 0;i<V;i++) {\n for(int j = 0;j<V;j++) {\n // self nodes are not considered \n if(isConnected[i][j] == 1 && i != j) {\n adjLs.get(i).add(j); \n adjLs.get(j).add(i); \n }\n }\n }\n boolean vis[] = new boolean[V]; \n int cnt = 0; \n for(int i = 0;i<V;i++) {\n if(vis[i] ==false) {\n cnt++;\n dfs(i, adjLs, vis); \n }\n }\n return cnt; \n }\n\n private void dfs(int node, ArrayList<ArrayList<Integer>> adjLs, boolean [] vis) {\n vis[node] = true;\n \n for(Integer it: adjLs.get(node)){\n if(vis[it]==false){\n vis[it]=true;\n dfs(it,adjLs,vis);\n }\n }\n }\n}\n```
| 11 | 0 |
['Java']
| 3 |
number-of-provinces
|
DFS - explanation & comments
|
python-dfs-explanation-comments-by-vikkt-5pnn
|
Approach: O(N^2) runtime, O(N) space for recursive stack - 176ms (97.57%), 15.3MB (10.18%)
DFS - easier to implement than Union Find, but slower big-O runtime (
|
vikktour
|
NORMAL
|
2021-03-30T21:16:11.383224+00:00
|
2024-12-27T18:35:49.734695+00:00
| 1,609 | false |
Approach: O(N^2) runtime, O(N) space for recursive stack - 176ms (97.57%), 15.3MB (10.18%)
DFS - easier to implement than Union Find, but slower big-O runtime (Union-Find method is O(NlogN))
Each row i indicates a connection from i to each item j in row i.
If item is 1, then there's a connection b/w i and j.
We can start with first item, and then recursively traverse that item's row, and continue down that path in DFS manner.
So we started off on row 0, but the nodes connected to i=0 will also be traversed down and we may end up clearing multiple rows just for the first iteration, which gives us one province. The nodes that we traverse will be stored in visited set() so we don't traverse them again. We continue to do it for other rows (new i), as long as it's not visited yet, which will help us find more provinces.
```py []
class Solution:
def findCircleNum(self, isConnected: List[List[int]]) -> int:
N = len(isConnected)
visited = set()
def dfs(cityI):
# cityIConnections is a row in isConnected, which contains the city i's connections
cityIConnections = isConnected[cityI]
visited.add(cityI) # Add cityI to seen, so we won't dfs it again (because we called it just now!)
# We want to take all 1's in cityIConnections to put together into a province
for cityJ in range(N):
# Check cityJ's connections first before finishing cityI's connections
if (cityJ not in visited) and (cityIConnections[cityJ] == 1) and (cityI != cityJ):
dfs(cityJ)
# We're done searching cityI's direct connections
return
numProvinces = 0
for cityI in range(N):
# Each entire dfs recursion set is going to be one province
if cityI not in visited:
dfs(cityI)
numProvinces += 1
return numProvinces
```
``` cpp []
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
int N = isConnected.size();
unordered_set<int> visited;
auto dfs = [&](int cityI, auto& dfs) -> void {
visited.insert(cityI); // Mark cityI as visited
for (int cityJ = 0; cityJ < N; ++cityJ) {
// If cityJ is not visited, there's a connection, and it's not itself
if (visited.find(cityJ) == visited.end() && isConnected[cityI][cityJ] == 1 && cityI != cityJ) {
dfs(cityJ, dfs);
}
}
};
int numProvinces = 0;
for (int cityI = 0; cityI < N; ++cityI) {
if (visited.find(cityI) == visited.end()) {
dfs(cityI, dfs);
++numProvinces;
}
}
return numProvinces;
}
};
```
``` java []
class Solution {
public int findCircleNum(int[][] isConnected) {
int N = isConnected.length;
Set<Integer> visited = new HashSet<>();
// Depth-first search function
void dfs(int cityI) {
visited.add(cityI); // Mark cityI as visited
for (int cityJ = 0; cityJ < N; cityJ++) {
// If cityJ is not visited, there's a connection, and it's not itself
if (!visited.contains(cityJ) && isConnected[cityI][cityJ] == 1 && cityI != cityJ) {
dfs(cityJ);
}
}
}
int numProvinces = 0;
for (int cityI = 0; cityI < N; cityI++) {
if (!visited.contains(cityI)) {
dfs(cityI);
numProvinces++;
}
}
return numProvinces;
}
}
```
| 11 | 0 |
['Depth-First Search', 'Python', 'C++', 'Java', 'Python3']
| 1 |
number-of-provinces
|
Video solution | Connected Components | Intuition explained in detail | C++ | Hindi
|
video-solution-connected-components-intu-6ysj
|
VideoHey everyone i have created a video solution for this problem (its in hindi), it involves intuitive explanation with code, this video is part of my playlis
|
_code_concepts_
|
NORMAL
|
2024-12-24T12:26:14.658940+00:00
|
2024-12-24T12:26:14.658940+00:00
| 1,177 | false |
# Video
Hey everyone i have created a video solution for this problem (its in hindi), it involves intuitive explanation with code, this video is part of my playlist "Master Graphs"
Video link : https://youtu.be/kktdI569gDo?si=TrjUUkBsQf2EL7oU
Playlist link: : https://www.youtube.com/playlist?list=PLICVjZ3X1AcZ5c2oXYABLHlswC_1LhelY
# Code
```cpp []
class Solution {
public:
void dfs(int i, vector<vector<int>>& isConnected, vector<bool>& visited) {
visited[i]=true;
for(int j=0;j<isConnected.size();j++){
if(i!=j && isConnected[i][j]==true && visited[j]==false){
dfs(j,isConnected,visited);
}
}
}
int findCircleNum(vector<vector<int>>& isConnected) {
int cities= isConnected.size();
vector<bool> visited(cities, false);
int provinces=0;
for(int i=0;i<cities;i++){
if(visited[i]==false){
dfs(i,isConnected,visited);
provinces++;
}
}
return provinces;
}
};
```
| 10 | 0 |
['C++']
| 1 |
number-of-provinces
|
Java | DFS | Beats > 98% | 13 lines | Clean code
|
java-dfs-beats-98-13-lines-clean-code-by-u9as
|
Complexity\n- Time complexity: O(n^2)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n) on the stack\n Add your space complexity here, e.g
|
judgementdey
|
NORMAL
|
2023-06-04T05:35:50.159266+00:00
|
2023-06-04T05:37:58.654876+00:00
| 2,277 | false |
# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ on the stack\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n private void dfs(int city, int[][] isConnected, boolean[] seen) {\n seen[city] = true;\n\n for (var i = 0; i < isConnected.length; i++)\n if (isConnected[city][i] == 1 && !seen[i])\n dfs(i, isConnected, seen);\n }\n\n public int findCircleNum(int[][] isConnected) {\n var n = isConnected.length;\n var seen = new boolean[n];\n var cnt = 0;\n\n for (var i=0; i<n; i++) {\n if (!seen[i]) {\n dfs(i, isConnected, seen);\n cnt++;\n }\n }\n return cnt;\n }\n}\n```\nIf you like my solution, please upvote it!
| 10 | 0 |
['Depth-First Search', 'Graph', 'Java']
| 0 |
number-of-provinces
|
C++ union find solution
|
c-union-find-solution-by-ag_piyush-wnxx
|
We will only traverse the following part of the grid for efficiency:\n| 0 | * | * | * | * |\n| 0 | 0 | * | * | * |\n| 0 | 0 | 0 | * | * |\n| 0 | 0 | 0 | 0 | * |
|
ag_piyush
|
NORMAL
|
2020-08-10T13:00:13.904644+00:00
|
2020-08-10T13:07:56.859125+00:00
| 975 | false |
We will only traverse the following part of the grid for efficiency:\n| 0 | * | * | * | * |\n| 0 | 0 | * | * | * |\n| 0 | 0 | 0 | * | * |\n| 0 | 0 | 0 | 0 | * |\n| 0 | 0 | 0 | 0 | 0 |\n\nThe diagonal elements are friends of themselves so we can ignore them, we are only concerned with distinct elements.\nAnd since M[i][j] = M[j][i] we don\'t need to traverse the other half.\n\nThen apply union and find operations sequentially on the desired part.\n\n```\nclass Solution {\npublic:\n vector<int> friends;\n \n int find_friend(int i) {\n if(friends[i] == i)\n return i;\n return friends[i] = find_friend(friends[i]);\n }\n \n void union_friends(int i, int j) {\n i = find_friend(i);\n j = find_friend(j);\n \n if(i!=j)\n friends[j] = i;\n }\n \n int findCircleNum(vector<vector<int>>& M) {\n int n = M.size();\n int groups=0;\n friends.resize(n);\n\n for(int i=0;i<n;i++)\n friends[i] = i;\n \n //Since each friend is initially friend to himself (M[i][i]),\n //We will traverse only in the top right half of grid\n //Since the bottom left half is the copy of it.\n \n for(int i=0;i<n;i++) {\n for(int j=i+1;j<n;j++) {\n if(M[i][j] == 1)\n union_friends(i,j);\n }\n }\n \n for(int i=0;i<n;i++) {\n if(friends[i] == i)\n groups++;\n }\n \n return groups;\n }\n};
| 10 | 0 |
['Union Find', 'C']
| 1 |
number-of-provinces
|
Python DFS solution (Explained in detail with analogy)
|
python-dfs-solution-explained-in-detail-xqozs
|
This is based on one of the approaches listed at: https://leetcode.com/problems/friend-circles/discuss/303150/python-union-find-dfs-bfs\n\nclass Solution:\n
|
xocolatyl
|
NORMAL
|
2019-07-06T16:34:43.960624+00:00
|
2019-07-06T16:34:43.960657+00:00
| 1,994 | false |
This is based on one of the approaches listed at: https://leetcode.com/problems/friend-circles/discuss/303150/python-union-find-dfs-bfs\n```\nclass Solution:\n def findCircleNum(self, M: List[List[int]]) -> int:\n #We\'re gonna imitate a DFS appraoch to this.\n #If we visit a row (person), look for every col index that\'s 1 and explore those partcular rows(people). The number of independent rows you need to search is the result. \n rows=len(M)\n seen=set()\n #dfs() enables the exploring\n def dfs(r):\n for c,val in enumerate(M[r]):\n if val==1 and c not in seen:\n seen.add(c)\n dfs(c)\n #Now start exploring\n count=0\n for i in range(rows):\n if i not in seen:\n dfs(i)\n count+=1\n return count\n \n```\n\nThe key here is to realize that the number of friend circles is the number of rows in the matrix(or groups of people in the school) that are distinct from other groups of people. \nTo do this, imagine a pen on a piece of paper. You\'ve heard of the challenge to not take off the pen from the sheet and yet trace a figure. \n\nIn our problem, this is like jumping from one row(person) to other rows(other people) based on which col indices are "1". Thus we dfs() from one row to another to another until no "1" references any other row that we have not yet "seen". Hence why we need the "seen" set- to make sure we dont infintely explore the same rows. \nEvery now and then we\'ll reach the end of a dfs traversal ansd still have rows we have not yet explored. \n\nThis why we need the for loop that goes through every row (with a check to see if we\'ve "seen" the row yet). This way, every row will be explored and the number of times we need to take the pen off the paper( or the num of times we need to let the for loop do a dfs() call) is the number of distinct friend groups. As usual, be sure to point out any errors in my analysis. \nVoila ;)
| 10 | 0 |
['Depth-First Search', 'Python']
| 1 |
number-of-provinces
|
Union Find
|
union-find-by-gracemeng-0rgd
|
If we regard a person as a node (or element), a friend circle as a connected component (or set), the problem becomes to find the total number of connected compo
|
gracemeng
|
NORMAL
|
2018-09-05T18:14:32.946499+00:00
|
2020-03-19T16:49:29.241653+00:00
| 1,677 | false |
If we regard a person as a `node` (or `element`), a friend circle as a `connected component` (or `set`), the problem becomes to find the total number of connected components in a graph.\n****\n```\nclass Solution {\n public int findCircleNum(int[][] M) {\n UF uf = new UF(M.length);\n \n for (int i = 0; i < M.length - 1; i++) {\n for (int j = i + 1; j < M.length; j++) {\n if (M[i][j] == 1) {\n uf.union(i, j);\n }\n }\n }\n \n return uf.count();\n }\n \n class UF{\n int[] parent;\n public UF(int n) {\n parent = new int[n];\n for (int i = 0; i < n; i++)\n parent[i] = i;\n }\n void union(int x, int y) {\n int rx = find(x);\n int ry = find(y);\n if (rx != ry) {\n parent[rx] = ry;\n }\n };\n int find(int x) {\n if (parent[x] == x) {\n return x;\n }\n return parent[x] = find(parent[x]); // path compression\n }\n int count() {\n // Count parent[x] = x\n int cnt = 0;\n for (int i = 0; i < parent.length; i++)\n if (parent[i] == i) {\n cnt++;\n }\n return cnt;\n }\n }\n}\n```\n
| 10 | 0 |
[]
| 2 |
number-of-provinces
|
Video Explanation | Union Find and DFS | Including Similar Problems
|
video-explanation-union-find-and-dfs-inc-z785
|
Approach\n\nhttps://youtu.be/76eTRuAszl0\n\n# Similar Problems\n- 463. Island Perimeter\n- 657. Robot Return to Origin\n- 200. Number of Islands\n- Number of Is
|
hridoy100
|
NORMAL
|
2023-08-15T14:14:54.427748+00:00
|
2023-08-15T14:14:54.427781+00:00
| 1,303 | false |
# Approach\n\nhttps://youtu.be/76eTRuAszl0\n\n# Similar Problems\n- [463. Island Perimeter](https://leetcode.com/problems/island-perimeter/)\n- [657. Robot Return to Origin](https://leetcode.com/problems/robot-return-to-origin/)\n- [200. Number of Islands](https://leetcode.com/problems/number-of-islands/)\n- [Number of Islands II](https://leetcode.com/problems/number-of-islands-ii/)\n- [2316. Count Unreachable Pairs of Nodes in an Undirected Graph](https://leetcode.com/problems/count-unreachable-pairs-of-nodes-in-an-undirected-graph/)\n- [Number of Distinct Islands](https://leetcode.com/problems/number-of-distinct-islands/)\n- [Number of Connected Components in an Undirected Graph](https://leetcode.com/problems/number-of-connected-components-in-an-undirected-graph/)\n- [130. Surrounded Regions](https://leetcode.com/problems/surrounded-regions/)\n- [2658. Maximum Number of Fish in a Grid](https://leetcode.com/problems/maximum-number-of-fish-in-a-grid/)\n- [994. Rotting Oranges](https://leetcode.com/problems/rotting-oranges/)\n- [695. Max Area of Island](https://leetcode.com/problems/max-area-of-island/)\n- [529. Minesweeper](https://leetcode.com/problems/minesweeper/)\n- [1376. Time Needed to Inform All Employees](https://leetcode.com/problems/time-needed-to-inform-all-employees/)\n- [2101. Detonate the Maximum Bombs](https://leetcode.com/problems/detonate-the-maximum-bombs/)\n\n# Union Find\n``` Java []\nclass Solution {\n int[] par;\n int[] rank;\n public int findCircleNum(int[][] isConnected) {\n int n = isConnected.length;\n par = new int[n];\n rank = new int[n];\n for(int i=0; i<n; i++){\n // make each node it\'s own parent..\n par[i] = i; \n // rank is the number of nodes it points to..\n rank[i] = 1;\n }\n int groups = n;\n for(int i=0; i<n; i++){\n for(int j=0; j<n; j++){\n if(isConnected[i][j]==1)\n // for each edge check if it is in a union\n // or add it to an existing union set\n // if added to an existing union set,\n // returns 1 which is decremented from res...\n // finally, the number of unions will be\n // res - the count of edges for which we added to previous union set.\n groups -= union_find(i, j);\n }\n }\n return groups;\n }\n \n int union_find(int n1, int n2){\n int p1 = find(n1);\n int p2 = find(n2);\n // the nodes that are already in a union set will have same parent\n if(p1==p2)\n return 0;\n \n // higher ranked node will be the parent of the lower rank node.. \n if(rank[p1]>rank[p2]){\n // change the parent of lower rank node\n par[p2] = p1;\n // increase the rank up to lower ranked node.. \n rank[p1] += rank[p2];\n }\n else{\n par[p1] = p2;\n rank[p2] += rank[p1];\n }\n return 1;\n }\n \n int find(int x){ \n // find the top most parent of the current node\n // top most parent will have itself as it\'s parent\n while(par[x]!=x){\n // basically it will be like a linkedlist..\n // optimization is to first check the grand parent of the node.\n par[x] = par[par[x]];\n x = par[x];\n }\n return x;\n }\n}\n```\n# Complexity\n- Time complexity: $$O(N^2)$$.\n - $$O(N^2)$$ time to iterate over all the values in **isConnected** matrix.\n - In worst case, the find operation takes $$O(N)$$ time. It takes $$O(1)$$ per operation and takes $$O(e)$$ time for all the $$e$$ edges.\n\n- Space complexity: $$O(N)$$.\nWe are using the parent and rank arrays, both of which require $$O(N)$$ space each.\n\n\n# DFS\n``` Java []\npublic class Solution {\n int n;\n public void dfs(int[][] isConnected, boolean[] visited, int i) {\n for (int j=0; j<n; j++) {\n if (isConnected[i][j] == 1 && !visited[j]) {\n visited[j] = true;\n dfs(isConnected, visited, j);\n }\n }\n }\n public int findCircleNum(int[][] isConnected) {\n n = isConnected.length;\n boolean[] visited = new boolean[n];\n int groups = 0;\n for (int i=0; i<n; i++) {\n if (!visited[i]) {\n dfs(isConnected, visited, i);\n groups++;\n }\n }\n return groups;\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n void dfs(int node, vector<vector<int>>& isConnected, vector<bool>& visited) {\n visited[node] = true;\n for (int i = 0; i < isConnected.size(); i++) {\n if (isConnected[node][i] && !visited[i]) {\n dfs(i, isConnected, visited);\n }\n }\n }\n\n int findCircleNum(vector<vector<int>>& isConnected) {\n int n = isConnected.size();\n int groups = 0;\n vector<bool> visited(n);\n\n for (int i = 0; i < n; i++) {\n if (!visited[i]) {\n groups++;\n dfs(i, isConnected, visited);\n }\n }\n\n return groups;\n }\n};\n```\n\n\n# Complexity\n- Time complexity: $$O(N^2)$$.\nIterating the matrix takes $$O(N^2)$$ time.\n\n- Space complexity: $$O(N)$$.\nThe **visited** array takes $$O(N)$$ space.\nThe recursion call stack used by dfs can have no more than $$n$$ elements in the worst-case scenario. It would take up $$O(N)$$ space in that case.\n
| 9 | 0 |
['Depth-First Search', 'Union Find', 'C++', 'Java']
| 0 |
number-of-provinces
|
547: Solution with step by step explanation
|
547-solution-with-step-by-step-explanati-bf8n
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. Initialize the variable visited to an empty set.\n2. Define a function
|
Marlen09
|
NORMAL
|
2023-03-14T05:23:51.438889+00:00
|
2023-03-14T05:23:51.438925+00:00
| 3,506 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize the variable visited to an empty set.\n2. Define a function called dfs that takes the input isConnected, visited, and i.\n3. Check if i is already in the visited set. If it is, return 0.\n4. Add i to the visited set.\n5. Loop through isConnected[i] to check if there are any direct connections between i and j.\n6. If there is a direct connection between i and j, call the dfs function recursively on j.\n7. Return 1 to represent the current province.\n8. Initialize the variable provinces to 0.\n9. Loop through the length of isConnected to check all the cities.\n10. For each city, call the dfs function on it and add the result to provinces.\n11. Return provinces as the total number of provinces.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findCircleNum(self, isConnected: List[List[int]]) -> int:\n visited = set() # Initialize visited set\n \n # Define depth-first search (dfs) function\n def dfs(isConnected, visited, i):\n if i in visited: # If already visited, return 0\n return 0\n visited.add(i) # Add i to visited set\n for j in range(len(isConnected[i])): # Check for direct connections\n if isConnected[i][j] == 1:\n dfs(isConnected, visited, j) # Recursively call dfs on j\n return 1 # Return 1 to represent current province\n \n provinces = 0 # Initialize provinces count\n for i in range(len(isConnected)): # Loop through all cities\n provinces += dfs(isConnected, visited, i) # Call dfs on city i and add result to provinces\n return provinces # Return total number of provinces\n\n```
| 9 | 2 |
['Depth-First Search', 'Breadth-First Search', 'Union Find', 'Python', 'Python3']
| 4 |
number-of-provinces
|
Neetcode's "Number of Connected Components in Graph" union find
|
neetcodes-number-of-connected-components-mfnh
|
\nclass Solution:\n def findCircleNum(self, isConnected: List[List[int]]) -> int:\n rows = len(isConnected)\n cols = len(isConnected[0])\n
|
slow-j1
|
NORMAL
|
2022-05-29T19:30:49.193121+00:00
|
2022-05-29T19:30:49.193168+00:00
| 737 | false |
```\nclass Solution:\n def findCircleNum(self, isConnected: List[List[int]]) -> int:\n rows = len(isConnected)\n cols = len(isConnected[0])\n \n amount = len(isConnected)\n \n parents = [i for i in range(amount)]\n rank = [1] * amount\n \n def find(n1):\n p = n1\n while p != parents[p]:\n parents[p] = parents[parents[p]]\n p = parents[p]\n return p\n \n def union(n1, n2):\n p1, p2 = find(n1), find(n2)\n if p1 == p2:\n return 0\n if rank[p1] >= rank[p2]:\n rank[p1] += rank[p2]\n parents[p2] = p1\n else:\n rank[p2] += rank[p1]\n parents[p1] = p2\n return 1\n \n for r in range(rows):\n for c in range(cols):\n if r != c and isConnected[r][c] == 1:\n amount -= union(r, c)\n isConnected[r][c] = 0\n isConnected[c][r] = 0\n \n return amount\n```
| 9 | 0 |
['Union Find', 'Python']
| 2 |
number-of-provinces
|
standard java dfs solution (easy to understand)
|
standard-java-dfs-solution-easy-to-under-mnia
|
\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n List<List<Integer>> adj = new ArrayList<>();\n int n = isConnected.lengt
|
rmanish0308
|
NORMAL
|
2021-07-28T12:14:38.207908+00:00
|
2021-07-28T12:14:38.207940+00:00
| 1,310 | false |
```\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n List<List<Integer>> adj = new ArrayList<>();\n int n = isConnected.length;\n for(int i=0;i<n;i++)\n adj.add(new ArrayList());\n \n for(int i=0;i<n;i++)\n {\n for(int j=0;j<n;j++)\n {\n if(i == j)\n continue;\n if(isConnected[i][j] == 1)\n adj.get(i).add(j);\n }\n }\n int ans = 0;\n boolean vis[] = new boolean[n];\n for(int i=0;i<n;i++)\n {\n if(vis[i] == false) \n {\n ans++;\n dfs(adj,i,vis);\n }\n }\n return ans;\n }\n void dfs(List<List<Integer>> adj,int src,boolean[] vis)\n {\n vis[src] = true;\n \n for(int nbr : adj.get(src))\n {\n if(vis[nbr] == false)\n dfs(adj,nbr,vis);\n }\n }\n}\n```\nPlease upvote if u find my code easy to understand
| 9 | 0 |
['Depth-First Search', 'Java']
| 1 |
number-of-provinces
|
JavaScript 3 Solutions: Union Find, DFS & BFS
|
javascript-3-solutions-union-find-dfs-bf-9fdn
|
Union Find:\n\nvar findCircleNum = function(M) {\n let res = 0;\n const dsu = new DSU(M.length);\n for(let row = 0; row < M.length; row++) {\n f
|
ChaoWan_2021
|
NORMAL
|
2020-04-22T01:13:21.626585+00:00
|
2020-04-22T01:13:21.626620+00:00
| 1,548 | false |
Union Find:\n```\nvar findCircleNum = function(M) {\n let res = 0;\n const dsu = new DSU(M.length);\n for(let row = 0; row < M.length; row++) {\n for(let col = 0; col < M[0].length; col++) {\n if(M[row][col] === 1) {\n dsu.union(row, col);\n }\n }\n }\n return new Set(M.map((m, i) => dsu.find(i))).size;\n};\n\nclass DSU {\n constructor(N) {\n this.parent = [...new Array(N).keys()];\n }\n find(x) {\n if(this.parent[x] !== x) this.parent[x] = this.find(this.parent[x]);\n return this.parent[x];\n }\n union(x, y) {\n this.parent[this.find(x)] = this.find(y);\n }\n}\n```\n\nDFS: \n```\nvar findCircleNum = function(M) {\n const seen = new Set();\n let res = 0;\n const dfs = (i) => {\n for(let j = 0; j < M[0].length; j++) {\n if(M[i][j] === 1 && !seen.has(j)) {\n seen.add(j);\n dfs(j);\n }\n }\n }\n for(let i = 0; i < M.length; i++) {\n if(!seen.has(i)) {\n dfs(i);\n res++;\n }\n }\n\n return res;\n};\n```\n\nBFS:\n```\nvar findCircleNum = function(M) {\n const seen = new Set();\n let res = 0;\n let stack = [];\n for(let i = 0; i < M.length; i++) {\n if(!seen.has(i)) {\n stack.push(i);\n while(stack.length) {\n const curr = stack.pop();\n seen.add(curr);\n for(let j = 0; j < M[0].length; j++) {\n if(M[curr][j] === 1 && !seen.has(j)) {\n stack.push(j);\n }\n }\n }\n res++;\n }\n }\n return res;\n};\n```
| 9 | 1 |
['Depth-First Search', 'Breadth-First Search', 'Union Find', 'JavaScript']
| 0 |
number-of-provinces
|
Intuitive Disjoint Set Union Find in [Java/Python3]
|
intuitive-disjoint-set-union-find-in-jav-9hpy
|
Java\n\nclass Solution {\n public int findCircleNum(int[][] M) {\n DSU dsu = new DSU(M.length);\n for (int i = 0; i < M.length; ++i) {\n
|
BryanBoCao
|
NORMAL
|
2020-01-13T20:41:08.116830+00:00
|
2020-06-13T20:54:49.819816+00:00
| 2,523 | false |
### Java\n```\nclass Solution {\n public int findCircleNum(int[][] M) {\n DSU dsu = new DSU(M.length);\n for (int i = 0; i < M.length; ++i) {\n for (int j = i; j < M[i].length; ++j)\n if (M[i][j] == 1) dsu.union(i, j);\n }\n return dsu.getNumFrdCir();\n }\n}\n\nclass DSU {\n private int[] par = null, rnk = null;\n private int numFrdCir = 0;\n\n public DSU(int len) {\n this.numFrdCir = len;\n this.par = new int[len];\n this.rnk = new int[len];\n for (int i = 0; i < len; ++i)\n\t\t\tthis.par[i] = i;\n }\n\n public int find(int x) {\n if (this.par[x] != x)\n\t\t\tthis.par[x] = this.find(this.par[x]);\n return this.par[x];\n }\n\n public void union(int x, int y) {\n int xr = this.find(x),\n yr = this.find(y);\n if (xr == yr)\n\t\t\treturn;\n else if (this.rnk[xr] < this.rnk[yr])\n\t\t\tthis.par[xr] = yr;\n else if (this.rnk[xr] > this.rnk[yr])\n\t\t\tthis.par[yr] = xr;\n else {\n this.par[yr] = xr;\n this.rnk[xr]++;\n }\n this.numFrdCir--;\n }\n \n public int getNumFrdCir() {\n return this.numFrdCir;\n }\n}\n```\n\nResults on Y2020M01D13Mon:\n```\nRuntime: 1 ms, faster than 100.00% of Java online submissions for Friend Circles.\nMemory Usage: 45 MB, less than 44.00% of Java online submissions for Friend Circles.\n```\n---\n### Python3\n```\nclass Solution:\n def findCircleNum(self, M: List[List[int]]) -> int:\n dsu = DSU(len(M))\n for i, r in enumerate(M):\n for j, v in enumerate(r):\n if j > i - 1: break\n if v == 1:\n dsu.union(i, j)\n return dsu.numFrdCir\n \nclass DSU:\n def __init__(self, num):\n self.numFrdCir = num\n self.par = list(range(num))\n self.rnk = [0] * num\n \n def find(self, x):\n if self.par[x] != x:\n self.par[x] = self.find(self.par[x])\n return self.par[x]\n \n def union(self, x, y):\n xr, yr = self.find(x), self.find(y)\n if xr == yr:\n\t\t\treturn\n elif self.rnk[xr] < self.rnk[yr]:\n self.par[xr] = yr\n elif self.rnk[xr] > self.rnk[yr]:\n self.par[yr] = xr\n else:\n self.par[yr] = xr\n self.rnk[xr] += 1\n self.numFrdCir -= 1\n```\nResults on Y2020M01D13Mon:\n```\nRuntime: 192 ms, faster than 90.01% of Python3 online submissions for Friend Circles.\nMemory Usage: 12.9 MB, less than 100.00% of Python3 online submissions for Friend Circles.\n```\n---\n### Analysis\nTime Complexity: O(N\u03B1(N))\u2248O(N), where N is the number of vertices (and also the number of edges) in the graph, and \u03B1 is the Inverse-Ackermann function.\nSpace Complexity: O(N). The current construction of the graph (embedded in our dsu structure) has at most N nodes.\n\nSince the matrix is symmetric with respect to the diagonal, we only need to iterate through either the left-bottom or the top-right triangle. For example, in this code, this can be done by ```j``` starting from ```i``` to ```M[i].length``` instead of ```0``` to ```M[i].length``` in ```Java```, or break the iteration ```for j, v in enumerate(r):``` when ```j > i - 1``` in ```Python3```.\n\n---\n\n### References\n\nIntuitive Explanation Video\nhttps://youtu.be/0jNmHPfA_yE\n\nhttps://leetcode.com/problems/redundant-connection/solution/\nhttps://leetcode.com/problems/friend-circles/discuss/247455/easy-to-understand-union-find-disjoint-set-union-in-java-following-q684s-solution-structure\nhttps://leetcode.com/problems/friend-circles/discuss/101336/Java-solution-Union-Find\n
| 9 | 0 |
['Union Find', 'Python', 'Java', 'Python3']
| 2 |
number-of-provinces
|
Simple DFS solution | C# | +95% efficient
|
simple-dfs-solution-c-95-efficient-by-ba-hvxi
|
Intuition\n Describe your first thoughts on how to solve this problem. \nApply DFS algorithm and keep track of the visited nodes. If all nodes are not covered i
|
Baymax_
|
NORMAL
|
2023-04-07T07:01:01.954363+00:00
|
2023-06-04T00:57:14.239065+00:00
| 685 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nApply DFS algorithm and keep track of the visited nodes. If all nodes are not covered in a single trace of DFS, it implies multiple components are present.\nThe number of such independent/dis-connected components is equals to the number of times we call the DFS from the top level (not including the recursive call, but the one we make at top level)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAs mentioned in the intuition, to find the number of disconnected components in graph check the number of times we need to make a DFS call explicity on the non-visited nodes.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) - as we need visit all nodes once\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) as we are using a hashset to keep track of visited nodes.\n\n# Code\n```\npublic class Solution {\n public int FindCircleNum(int[][] isConnected) {\n int count = 0;\n HashSet<int> h = new HashSet<int>();\n for (int i = 0; i < isConnected.Length; i++)\n {\n if (!h.Contains(i))\n {\n h.Add(i);\n DFS(isConnected, i, h);\n count++;\n }\n }\n \n return count;\n }\n \n private void DFS(int[][] graph, int i, HashSet<int> h)\n {\n for (int j = 0; j < graph[i].Length; j++)\n {\n if (i != j && graph[i][j] == 1 && !h.Contains(j))\n {\n h.Add(j);\n DFS(graph, j, h);\n }\n }\n }\n}\n```
| 8 | 0 |
['Depth-First Search', 'Graph', 'C#']
| 0 |
number-of-provinces
|
C++ || Easy Solution ✅ || DFS ✅ || Short Code 🔥
|
c-easy-solution-dfs-short-code-by-ujjwal-1mis
|
\nIf you learn/found something new please upvote \uD83D\uDC4D\n\n\nclass Solution {\n int n;\n void dfs(int i, vector<vector<int>>& isConnected, vector<in
|
UjjwalAgrawal
|
NORMAL
|
2022-10-11T16:41:39.772476+00:00
|
2022-11-04T13:56:35.018642+00:00
| 947 | false |
```\nIf you learn/found something new please upvote \uD83D\uDC4D\n```\n```\nclass Solution {\n int n;\n void dfs(int i, vector<vector<int>>& isConnected, vector<int> &vis){\n vis[i] = 1;\n \n for(int j = 0; j<n; j++){\n if(isConnected[i][j] == 1 && vis[j] == 0)\n dfs(j, isConnected, vis);\n }\n }\npublic:\n int findCircleNum(vector<vector<int>>& isConnected) {\n n = isConnected.size();\n \n int ans = 0;\n vector<int> vis(n, 0);\n for(int i = 0; i<n; i++){\n if(vis[i] == 0){\n dfs(i, isConnected, vis);\n ans++;\n }\n }\n \n return ans;\n }\n};\n```\n\n```\nIf you learn/found something new please upvote \uD83D\uDC4D\n```
| 8 | 0 |
['Depth-First Search', 'C']
| 1 |
number-of-provinces
|
Typescript | Javascript | DFS | With comments
|
typescript-javascript-dfs-with-comments-3czh0
|
\n// This question can be rephrased as:\n// How many connected graphs we have\nfunction findCircleNum(isConnected: number[][]): number {\n let numberOfProvince
|
OsidAbu-Alrub
|
NORMAL
|
2022-09-04T15:37:15.255090+00:00
|
2022-09-04T15:37:15.255130+00:00
| 553 | false |
```\n// This question can be rephrased as:\n// How many connected graphs we have\nfunction findCircleNum(isConnected: number[][]): number {\n let numberOfProvinces = 0;\n const visited = new Set<number>();\n for(let i = 0 ; i < isConnected.length ; i++){\n \n // if I find a node that I haven\'t visited before (new graph)\n // then visit all its neighbors (flood fill)\n if(!visited.has(i)){\n numberOfProvinces++;\n dfs(i, isConnected, visited);\n }\n }\n \n return numberOfProvinces;\n};\n\nfunction dfs(city: number, graph: number[][], visited: Set<number>){\n visited.add(city);\n for(let neighbor = 0 ; neighbor < graph[city].length ; neighbor++){\n if(graph[city][neighbor] === 1 && !visited.has(neighbor))\n dfs(neighbor, graph, visited);\n }\n}\n```
| 8 | 0 |
['Depth-First Search', 'TypeScript', 'JavaScript']
| 0 |
number-of-provinces
|
Easy and Simple || C++ Solution || DFS || Beginner friendly
|
easy-and-simple-c-solution-dfs-beginner-7qtre
|
the trick here is to convert the given n*n matrix into adjacent matrix and apply the dfs. \n\'\'\'\n\nclass Solution {\npublic:\n void dfs(vector<int>adj[]
|
Sahdeo
|
NORMAL
|
2021-09-25T13:11:43.993899+00:00
|
2021-09-25T13:11:43.993929+00:00
| 1,374 | false |
##### the trick here is to convert the given n*n matrix into adjacent matrix and apply the dfs. \n\'\'\'\n```\nclass Solution {\npublic:\n void dfs(vector<int>adj[],vector<bool>&vis,int src){\n vis[src]=1;\n for(auto x:adj[src]){\n if(vis[x]==0)\n dfs(adj,vis,x);\n }\n }\n int findCircleNum(vector<vector<int>>& v) {\n int n=v.size();\n vector<int>adj[n];\n vector<bool>visited(n,0);\n for(int i=0;i<n;i++){ // conversion into adjacent matrix\n for(int j=0;j<n;j++){\n if(v[i][j]==1)\n adj[i].push_back(j);\n }\n }\n int ans=0;\n for(int i=0;i<n;i++){\n if(visited[i]==0){\n ans++;\n dfs(adj,visited,i);\n }\n }\n return ans;\n }\n};\n```\nplz upvote if you find this helpful :)\n\'\'\'
| 8 | 0 |
['Depth-First Search', 'C', 'C++']
| 0 |
number-of-provinces
|
DFS Solution || JAVA
|
dfs-solution-java-by-sidsai-m5s1
|
Approach\nThe given code appears to be an implementation of finding the number of connected components in an undirected graph represented by an adjacency matrix
|
SidSai
|
NORMAL
|
2023-06-04T06:09:39.924407+00:00
|
2023-06-04T06:09:39.924433+00:00
| 463 | false |
# Approach\nThe given code appears to be an implementation of finding the number of connected components in an undirected graph represented by an adjacency matrix. The approach used is Depth-First Search (DFS). Here\'s a step-by-step breakdown of the approach:\n\n1. Create an `ArrayList` of `ArrayList<Integer>` named `adj` to represent the adjacency list of the graph.\n\n2. Iterate over each row in the given 2D array `v` (which represents the adjacency matrix of the graph).\n\n3. For each pair of vertices (i, j) where `v[i][j]` is 1 and `i` is not equal to `j`, it means there is an edge between vertex `i` and vertex `j`.\n\n4. Add `j` to the adjacency list of `i` and add `i` to the adjacency list of `j`. This step establishes the undirected nature of the graph.\n\n5. Create a boolean array `visit` of length `v.length` to keep track of visited vertices. Initially, all elements are set to `false`.\n\n6. Initialize a variable `count` to keep track of the number of connected components.\n\n7. Iterate over each vertex in the graph (from 0 to `v.length - 1`).\n\n8. If the current vertex `i` has not been visited (`!visit[i]`), it means it belongs to a new connected component. Increment `count` and call the `dfs` function with the current vertex, adjacency list (`adj`), and the `visit` array.\n\n9. The `dfs` function performs the depth-first search traversal. It marks the current vertex `v` as visited (`visit[v] = true`) and then recursively calls `dfs` on all adjacent vertices that have not been visited.\n\n10. Finally, return the value of `count`, which represents the number of connected components in the graph.\n\nThe overall approach uses DFS to explore the graph and find all connected components by traversing through adjacent vertices. The `adj` list is used to represent the graph efficiently, and the `visit` array helps keep track of visited vertices to avoid redundant exploration.\n\nPlease note that the code assumes that the input graph is represented as an adjacency matrix (`v`) and it starts the DFS traversal from vertex 0.\n\n# Complexity\n- Time complexity:\n - O(N^2)\n- Space complexity:\n - O(N^2)\n\n# Code\n```\nclass Solution {\n public int findCircleNum(int[][] v) {\n ArrayList<ArrayList<Integer>> adj=new ArrayList();\n for(int i=0;i<v.length;i++) adj.add(new ArrayList<>());\n for(int i=0;i<v.length;i++){\n for(int j=0;j<v.length;j++){\n if(v[i][j]==1 && i!=j){\n adj.get(i).add(j);\n adj.get(j).add(i);\n }\n }\n }\n boolean[] visit=new boolean[v.length];\n visit[0]=false;\n int count=0;\n for(int i=0;i<v.length;i++){\n if(!visit[i]){\n count++;\n dfs(i,adj,visit);\n }\n }\n\n return count;\n }\n static void dfs(int v,ArrayList<ArrayList<Integer>> adj,boolean[] visit){\n visit[v]=true;\n for(Integer i:adj.get(v)){\n if(!visit[i]){\n dfs(i,adj,visit);\n }\n }\n }\n}\n```
| 7 | 0 |
['Java']
| 0 |
number-of-provinces
|
C++ 🔥 || Beginner Friendly ⛳️ || DFS ⛳️ || 100% 🎯
|
c-beginner-friendly-dfs-100-by-rajharshi-94t9
|
\uD83D\uDD25 Donn Forget to Upvote if you liked the Approach. \uD83D\uDD25\n\n# Approach\nThe Problem is nothing but a variation to find no. of connected compon
|
singhdhroov
|
NORMAL
|
2023-06-04T04:51:30.135317+00:00
|
2023-06-04T04:51:30.135357+00:00
| 1,851 | false |
### \uD83D\uDD25 Donn Forget to Upvote if you liked the Approach. \uD83D\uDD25\n\n# Approach\n**The Problem is nothing but a variation to find no. of connected components of a graph.**\n\nApproach is quite simple we\'ll firstly structure the graph the apply DFS to all unvisited nodes while marking them 1.\n\nEach time when we\'ll call a unvisited node we\'ll increase our count by 1 and then we\'ll visit all the nodes connected with that node.\n\nIn the end we\'ll return the total count that will be our answer.\n\n\n\n# Code\n```\nclass Solution {\npublic:\n int visited[205];\n void check(vector<int> v[],int itr)\n {\n if(visited[itr]) \n return;\n// Visiting all the connected nodes with our called node.\n visited[itr]=1;\n for(int i=0;i<v[itr].size();i++)\n check(v,v[itr][i]);\n\n return;\n }\n\n\n int findCircleNum(vector<vector<int>>& isConnected) {\n int ans=0; // This is our count.\n vector<int> v[isConnected.size()];\n// Structuring the Graph.\n for(int i=0;i<isConnected.size();i++)\n for(int j=0;j<isConnected[i].size();j++)\n if(isConnected[i][j])v[i].push_back(j);\n// Calling the unvisited Nodes.\n for(int i=0;i<isConnected.size();i++)\n if(!visited[i])\n {\n check(v,i);\n ans++;\n }\n return ans;\n }\n};\n```
| 7 | 0 |
['Depth-First Search', 'Union Find', 'Graph', 'C++']
| 0 |
number-of-provinces
|
Golang | DFS
|
golang-dfs-by-pikachuu-q1th
|
Code\n\nfunc dfs(curr int, visited []bool, isConnected [][]int) {\n visited[curr] = true\n for next := 0; next < len(isConnected); next++ {\n if is
|
pikachuu
|
NORMAL
|
2023-06-04T04:26:22.256013+00:00
|
2023-06-04T04:26:22.256054+00:00
| 577 | false |
# Code\n```\nfunc dfs(curr int, visited []bool, isConnected [][]int) {\n visited[curr] = true\n for next := 0; next < len(isConnected); next++ {\n if isConnected[curr][next] == 0 {continue} \n if !visited[next] {\n dfs(next, visited, isConnected)\n }\n } \n}\n\nfunc findCircleNum(isConnected [][]int) int {\n var count int = 0\n visited := make([]bool, len(isConnected))\n for i := 0; i < len(isConnected); i++ {\n if !visited[i] {\n count++\n dfs(i, visited, isConnected)\n }\n }\n return count\n}\n```
| 7 | 0 |
['Depth-First Search', 'Graph', 'Go']
| 0 |
number-of-provinces
|
✅Checkout my Simple BFS solution
|
checkout-my-simple-bfs-solution-by-rahul-zquk
|
\nclass Solution {\n public int findCircleNum(int[][] pro) {\n \n boolean visited[]= new boolean[pro.length+1];\n int count = 0;\n
|
rahulb_001
|
NORMAL
|
2022-09-21T13:22:08.460346+00:00
|
2022-09-21T13:22:08.460426+00:00
| 930 | false |
```\nclass Solution {\n public int findCircleNum(int[][] pro) {\n \n boolean visited[]= new boolean[pro.length+1];\n int count = 0;\n for(int i=0;i < pro.length;++i){\n if(visited[i]== false){\n count++;\n Queue<Integer>q = new LinkedList<>();\n q.add(i);\n visited[i]= true; \n while(!q.isEmpty()){\n Integer vertex = q.poll(); \n for(int j=0;j<pro[0].length;++j){\n if(!visited[j] && pro[vertex][j]== 1){\n q.add(j);\n visited[j] = true;\n }\n }\n }\n }\n } \n return count;\n }\n}\n```
| 7 | 0 |
['Array', 'Breadth-First Search', 'Graph', 'Java']
| 0 |
number-of-provinces
|
Simple Java solution || beats 100%
|
simple-java-solution-beats-100-by-himans-4lyi
|
\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n boolean visited[] = new boolean[isConnected.length];\n int res = 0;\n
|
Himanshu_Goyal_517
|
NORMAL
|
2022-07-09T18:04:16.106282+00:00
|
2022-07-09T18:04:16.106318+00:00
| 812 | false |
```\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n boolean visited[] = new boolean[isConnected.length];\n int res = 0;\n for(int i = 0; i < visited.length; i++){\n if(visited[i] == false){\n dfs(isConnected,i, visited);\n res++;\n }\n }\n return res;\n }\n public void dfs(int[][] isConnected,int i, boolean[] visited){\n if(visited[i]) return ;\n visited[i] = true;\n for(int j = 0; j < isConnected.length; j++){\n if(isConnected[i][j] == 1 && j != i){\n dfs(isConnected,j,visited);\n }\n }\n }\n}\n```
| 7 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Graph', 'Java']
| 2 |
number-of-provinces
|
C++ | BFS Approach
|
c-bfs-approach-by-ama29n-8427
|
\n int findCircleNum(vector<vector<int>>& isConnected) {\n \n int n = isConnected.size(), provinces = 0;\n vector<int> adj[n + 1], vis(n
|
ama29n
|
NORMAL
|
2021-12-31T08:41:13.460824+00:00
|
2021-12-31T09:42:25.677041+00:00
| 199 | false |
```\n int findCircleNum(vector<vector<int>>& isConnected) {\n \n int n = isConnected.size(), provinces = 0;\n vector<int> adj[n + 1], vis(n + 1, 0);\n \n for(int i = 0; i < n; i++) \n for(int j = 0; j < n; j++)\n if(isConnected[i][j] == 1 && i != j) \n adj[i + 1].push_back(j + 1);\n \n for(int i = 1; i <= n; i++) {\n if(!vis[i]) {\n provinces++;\n queue<int> q;\n q.push(i);\n vis[i] = 1;\n while(q.size()) {\n int node = q.front();\n q.pop();\n for(auto it : adj[node]) if(!vis[it]) { q.push(it); vis[it] = 1; }\n }\n }\n }\n return provinces;\n }\n```
| 7 | 0 |
[]
| 1 |
number-of-provinces
|
C++ || DFS || Easy Solution || 88%
|
c-dfs-easy-solution-88-by-coolbangers143-6z3j
|
\'\'\'\nclass Solution {\npublic:\n \n void DFS(vector>& graph, vector &visited,int v)\n {\n visited[v] = true; //marking visited;\n \n
|
coolbangers1438
|
NORMAL
|
2021-07-22T11:16:56.672453+00:00
|
2021-07-22T11:16:56.672494+00:00
| 782 | false |
\'\'\'\nclass Solution {\npublic:\n \n void DFS(vector<vector<int>>& graph, vector<bool> &visited,int v)\n {\n visited[v] = true; //marking visited;\n \n //now check for its neighbors\n for(int i=0;i<graph[v].size();i++)\n {\n if(i == v)\n continue;\n \n if(graph[v][i] && !visited[i])\n DFS(graph,visited,i);\n }\n \n }\n \n int findCircleNum(vector<vector<int>>& graph) \n {\n int n = graph.size();\n \n vector<bool> visited(n,false);\n \n int ans = 0;\n for(int i=0;i<n;i++)\n {\n if(!visited[i])\n {\n DFS(graph,visited,i);\n ans++;\n }\n }\n return ans;\n \n \n }\n};\n\'\'\'\n
| 7 | 0 |
['Depth-First Search', 'Graph', 'C']
| 0 |
number-of-provinces
|
Python, Union-Find
|
python-union-find-by-warmr0bot-qqy5
|
\ndef findCircleNum(self, isConnected: List[List[int]]) -> int:\n\tn = len(isConnected)\n\troots = list(range(n))\n\tsizes = [1] * n\n\n\tdef find_parent(a):\n\
|
warmr0bot
|
NORMAL
|
2021-02-25T11:20:23.626855+00:00
|
2021-02-25T11:20:23.626884+00:00
| 1,171 | false |
```\ndef findCircleNum(self, isConnected: List[List[int]]) -> int:\n\tn = len(isConnected)\n\troots = list(range(n))\n\tsizes = [1] * n\n\n\tdef find_parent(a):\n\t\tif roots[a] != a:\n\t\t\troots[a] = find_parent(roots[a])\n\t\treturn roots[a]\n\n\tdef union(a, b):\n\t\tra = find_parent(a)\n\t\trb = find_parent(b)\n\n\t\tif ra == rb: return\n\t\trbig, rsmall = (ra, rb) if sizes[ra] > sizes[rb] else (rb, ra)\n\n\t\troots[rsmall] = rbig\n\t\tsizes[rbig] += sizes[rsmall]\n\n\tfor i in range(n):\n\t\tfor j in range(i+1, n):\n\t\t\tif isConnected[i][j]:\n\t\t\t\tunion(i, j)\n\n\treturn len(set(find_parent(i) for i in range(n)))\n```
| 7 | 0 |
['Union Find', 'Python', 'Python3']
| 0 |
number-of-provinces
|
C++: Union-Find with Rank, 97.19% time
|
c-union-find-with-rank-9719-time-by-tobi-8fmg
|
c++\nclass Solution {\npublic:\n // upper bound of N is 200\n \n // number of children\n int children[210];\n // index of parent\n int par[210
|
tobiaswahyudi
|
NORMAL
|
2019-11-22T03:20:47.572987+00:00
|
2019-11-22T03:20:47.573020+00:00
| 566 | false |
```c++\nclass Solution {\npublic:\n // upper bound of N is 200\n \n // number of children\n int children[210];\n // index of parent\n int par[210];\n \n // find parent operation = amortized O(log n)\n int findPar(int n){\n if(par[n] == n) return n;\n // move parent of every node along path to root\n // this amortizes the whole findPar operation to O(log n).\n // amortization is ONLY feasible if we unite by num of children\n return par[n] = findPar(par[n]);\n }\n \n //set union, considering rank\n void unite(int a, int b){\n // unite sets only if they are in different set.\n if(findPar(a) == findPar(b)) return;\n // make the smaller set be a subtree of the larger set.\n // this preserves the amortization, otherwise findPar\n // would run in worst-case O(N).\n if(children[findPar(a)] > children[findPar(b)]){\n children[findPar(a)] += children[findPar(b)];\n par[findPar(b)] = findPar(a);\n } else {\n children[findPar(b)] += children[findPar(a)];\n par[findPar(a)] = findPar(b);\n }\n }\n \n int findCircleNum(vector<vector<int>>& M) {\n // get N\n int n = M[0].size();\n \n for(int i = 0; i < n; ++i){\n //initialize each node to be in its own tree\n children[i] = 1;\n par[i] = i;\n }\n for(int i = 0; i < n; ++i){\n //ignore anything below and on diagonal\n for(int j = i+1; j < n; ++j){\n // unite if they are friends.\n if(M[i][j] == 1) unite(i,j);\n }\n }\n // the number of groups are the number of sets\n // equals the number of root nodes\n // equals the number of i where findPar(i) = i.\n int count = 0;\n for(int i = 0; i < n; ++i) if(findPar(i) == i) ++count;\n return count;\n \n // Total Complexity: (amortized) O(N log N)\n // 16 ms, faster than 97.19%\n // Memory usage: 10.8mb\n }\n};\n```\nhttps://leetcode.com/submissions/detail/280751633/\nIn my opinion, this algorithm is very useful and powerful. Look at how short and pretty the code is!\nTake the time to understand it - It\'s not a very complicated algorithm.\n\nGeeksForGeeks is a great resource to learn about this algo.\nhttps://www.geeksforgeeks.org/union-find/\nBest of luck :)
| 7 | 0 |
['Union Find', 'C']
| 1 |
number-of-provinces
|
Python DFS solution
|
python-dfs-solution-by-rogerfederer-kcob
|
\nclass Solution(object):\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n if not M:\n
|
rogerfederer
|
NORMAL
|
2018-07-17T12:33:58.237488+00:00
|
2018-07-17T12:33:58.237488+00:00
| 1,282 | false |
```\nclass Solution(object):\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n if not M:\n return 0\n\n visited = set()\n counter, n = 0, len(M)\n for i in xrange(n):\n if i not in visited:\n self.dfs(M, i, visited)\n counter += 1\n return counter\n\n def dfs(self, M, i, visited):\n visited.add(i)\n for idx, val in enumerate(M[i]):\n if val == 1 and idx not in visited:\n self.dfs(M, idx, visited)\n```
| 7 | 0 |
[]
| 0 |
number-of-provinces
|
C++ 100% Beats.
|
c-100-beats-by-ramudarsingh46-9ipf
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ramudarsingh46
|
NORMAL
|
2024-08-16T09:57:36.456458+00:00
|
2024-08-16T09:57:36.456490+00:00
| 515 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\nvoid dfs(int s, int n, vector<vector<int>>& isConnected, vector<bool>&visited){\n visited[s] = true;\n \n \n vector<int>adj;\n for(int i=0; i<n; i++ ){\n int x = isConnected[s][i]; // x = connection\n if(x == 1)\n adj.push_back(i);\n }\n \n for(auto x: adj){\n if(!visited[x]){\n dfs(x, n, isConnected, visited);\n }\n }\n \n } \n int findCircleNum(vector<vector<int>>& isConnected) {\n int n=isConnected.size();\n vector<bool> visited(n,0);\n int ans=0;\n\n for(int i=0;i<isConnected.size();i++){\n if(!visited[i]){\n ans++;\n dfs(i,n,isConnected,visited);\n }\n }\n \n return ans; \n }\n};\n```
| 6 | 0 |
['C++']
| 0 |
number-of-provinces
|
DFS Brute Force Java Solution
|
dfs-brute-force-java-solution-by-chaitan-hbsv
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem at hand is to find the number of connected components in a graph represente
|
Chaitanya_91
|
NORMAL
|
2024-07-15T11:01:45.406653+00:00
|
2024-07-15T11:01:45.406682+00:00
| 428 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem at hand is to find the number of connected components in a graph represented by an adjacency matrix isConnected. Each node represents a city, and an edge between two nodes (cities) means they are directly connected.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe initialize an array visited to keep track of visited cities.\nWe iterate through each city (node) using a loop. If a city hasn\'t been visited yet (visited[i] is false), it indicates the start of a new connected component.\nWe then perform DFS from this city to mark all cities reachable from it.\nEach time we initiate a DFS from an unvisited city, we increment our count of connected components.\n\n# Complexity\n- Time complexity: o(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n int n = isConnected.length;\n boolean[] visited = new boolean[n];\n int count = 0;\n\n for (int i = 0; i < n; i++) {\n if (!visited[i]) {\n dfs(isConnected, visited, i);\n count++;\n }\n }\n return count;\n }\n private void dfs(int[][] isConnected, boolean[] visited, int i) {\n visited[i] = true;\n for (int j = 0; j < isConnected.length; j++) {\n if (isConnected[i][j] == 1 && !visited[j]) {\n dfs(isConnected, visited, j);\n }\n }\n }\n}\n\n```
| 6 | 0 |
['Java']
| 0 |
number-of-provinces
|
Use scipy — it's great
|
use-scipy-its-great-by-burkh4rt-0uly
|
Code\n\nfrom scipy.sparse.csgraph import connected_components as cc\nfrom numpy import array as arr\n\n\nclass Solution:\n def findCircleNum(self, isConnecte
|
burkh4rt
|
NORMAL
|
2024-01-20T03:58:35.528670+00:00
|
2024-01-20T03:59:46.192498+00:00
| 967 | false |
# Code\n```\nfrom scipy.sparse.csgraph import connected_components as cc\nfrom numpy import array as arr\n\n\nclass Solution:\n def findCircleNum(self, isConnected: List[List[int]]) -> int:\n return cc(arr(isConnected))[0]\n```
| 6 | 1 |
['Python3']
| 1 |
number-of-provinces
|
JAVA FASTEST🚀 AND SIMPLEST CODE😉 || STEP BY STEP EXPLAINED😲
|
java-fastest-and-simplest-code-step-by-s-1rcd
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
abhiyadav05
|
NORMAL
|
2023-07-17T19:06:45.729585+00:00
|
2023-07-17T19:06:45.729610+00:00
| 521 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(N^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(N)\n\n\n\n# Code\n```\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n\n int numProvinces = isConnected.length; // Number of provinces\n boolean[] visited = new boolean[numProvinces]; // Array to track visited provinces\n int numCircles = 0; // Counter for the number of provinces in a circle\n \n for (int i = 0; i < numProvinces; i++) {\n if (!visited[i]) {\n numCircles++;\n dfs(isConnected, i, visited); // Perform DFS traversal to find provinces in the current circle\n }\n }\n \n return numCircles;\n }\n \n // Recursive function for DFS traversal to find provinces in a circle\n private void dfs(int[][] isConnected, int province, boolean[] visited) {\n \n visited[province] = true; // Mark the current province as visited\n \n // Iterate through the neighboring provinces of the current province\n for (int neighbor = 0; neighbor < isConnected[province].length; neighbor++) {\n // If the neighbor province is not visited and there is a connection, mark as visited and explore further\n if (!visited[neighbor] && isConnected[province][neighbor] == 1) {\n dfs(isConnected, neighbor, visited); // Recursive call for unvisited provinces in the current circle\n }\n }\n }\n}\n\n```
| 6 | 0 |
['Depth-First Search', 'Graph', 'Java']
| 0 |
number-of-provinces
|
BFS | DFS | C++ | Easy to understand code
|
bfs-dfs-c-easy-to-understand-code-by-war-2vff
|
Intuition\nWe have to find number of connected components in the graph.\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nNormal DFS/
|
warrior0331
|
NORMAL
|
2023-06-04T06:28:56.793049+00:00
|
2023-06-04T06:28:56.793085+00:00
| 725 | false |
# Intuition\nWe have to find number of connected components in the graph.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nNormal DFS/BFS traversals, number of times the traversal is done is the number of provinces.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```BFS []\nclass Solution {\npublic:\n\nvoid bfs(int node, vector<int> &vis, vector<int> adj[]){\n queue<int> q;\n q.push(node);\n vis[node]=1;\n while(!q.empty()){\n int node=q.front();\n q.pop();\n for(auto x:adj[node]){\n if(!vis[x]){\n vis[x]=1;\n q.push(x);\n }\n }\n }\n}\n\n int findCircleNum(vector<vector<int>>& isConnected) {\n int n=isConnected.size();\n vector<int> adj[n];\n for(int i=0;i<n;i++){\n for(int j=0;j<n;j++){\n if(i==j) continue;\n if(isConnected[i][j]==1){\n adj[i].push_back(j);\n adj[j].push_back(i);\n }\n }\n }\n int count=0;\n vector<int> vis(n,0);\n for(int i=0;i<n;i++){\n if(!vis[i]){\n bfs(i,vis,adj);\n count++;\n }\n }\n return count;\n }\n};\n```\n```DFS []\nclass Solution {\npublic:\n\nvoid dfs(int node, vector<int> &vis, vector<int> adj[]){\n vis[node]=1;\n for(auto x:adj[node]){\n if(!vis[x]) dfs(x,vis,adj);\n }\n}\n\n int findCircleNum(vector<vector<int>>& isConnected) {\n int n=isConnected.size();\n vector<int> adj[n];\n for(int i=0;i<n;i++){\n for(int j=0;j<n;j++){\n if(i==j) continue;\n if(isConnected[i][j]==1){\n adj[i].push_back(j);\n adj[j].push_back(i);\n }\n }\n }\n int count=0;\n vector<int> vis(n,0);\n for(int i=0;i<n;i++){\n if(!vis[i]){\n dfs(i,vis,adj);\n count++;\n }\n }\n return count;\n }\n};\n```\n# ***Upvote if it helped!***\n`
| 6 | 1 |
['C++']
| 0 |
number-of-provinces
|
Clean Code with easy explanation DFS/BFS code || C++ || DFS || BFS
|
clean-code-with-easy-explanation-dfsbfs-xnru1
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThis problem is asking for a province which is a group of directly or indirectly connec
|
sazzysaturn
|
NORMAL
|
2023-06-04T01:48:34.091050+00:00
|
2023-06-04T01:48:34.091080+00:00
| 963 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem is asking for a province which is a group of directly or indirectly connected cities, which is basically a connected component in a graph problem, that is we can achieve this easily with the help of Depth First Search and Breadth First Search\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nApproach is basically we would call DFS or BFS, 1 DFS/BFS call would visit 1 whole province(connected component) so by maintaining a visited array, the no. of calls to unvisited cities for dfs/bfs would be the no. of provinces\n\n# Complexity\n- Time complexity: O(n), Every city will be visited once only\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# DFS approach:\n```\nclass Solution {\npublic:\n void dfs(vector<vector<int>>& isConnected, int i, vector<int>& visited){\n int n = isConnected.size();\n if(visited[i]==1) return; //checking if already visited then return\n\n visited[i] = 1; //marking visited\n for(int j=0;j<n;j++){\n // calling to all cities connected to it through recursion\n if(isConnected[i][j]==1) dfs(isConnected,j,visited);\n }\n }\n\n int findCircleNum(vector<vector<int>>& isConnected) {\n //very simple dfs problem, classical \n int n = isConnected.size();\n vector<int> visited(n,0);\n int ans=0;\n for(int i=0;i<n;i++){\n if(visited[i]==0){ // calling only if not visited\n ans++;\n dfs(isConnected,i,visited);\n }\n }\n return ans;\n }\n};\n\n```\n# **BFS approach solution (done with queue):**\n```\nclass Solution {\npublic:\n void bfs(vector<vector<int>>& isConnected, int i, vector<int>& visited){\n int n = isConnected.size();\n\n queue<int> q;\n q.push(i);\n while(!q.empty()){\n int temp = q.front();\n q.pop();\n visited[temp]=1;\n for(int j=0;j<n;j++){\n if(isConnected[temp][j]==1 && visited[j]==0) q.push(j);\n }\n }\n }\n\n int findCircleNum(vector<vector<int>>& isConnected) {\n int n = isConnected.size();\n vector<int> visited(n,0);\n int ans=0;\n \n for(int i=0;i<n;i++){\n if(visited[i]==0){\n ans++;\n bfs(isConnected,i,visited);\n }\n }\n return ans;\n }\n};\n```
| 6 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Graph', 'C++']
| 1 |
number-of-provinces
|
Swift💯UnionFind
|
swiftunionfind-by-upvotethispls-xs8t
|
Union Find (accepted answer)\n\nclass Solution {\n func findCircleNum(_ isConnected: [[Int]]) -> Int {\n var groups = Array(isConnected.indices)\n
|
UpvoteThisPls
|
NORMAL
|
2023-06-04T00:16:55.547549+00:00
|
2024-10-29T23:29:49.360931+00:00
| 568 | false |
**Union Find (accepted answer)**\n```\nclass Solution {\n func findCircleNum(_ isConnected: [[Int]]) -> Int {\n var groups = Array(isConnected.indices)\n \n func find(_ x:Int) -> Int { groups[x]==x ? x : find(groups[x]) }\n \n for y in isConnected.indices {\n for x in y+1 ..< isConnected.count where isConnected[y][x] == 1 {\n groups[find(x)] = find(y) // form union between `x` and `y`\n }\n }\n\n return Set(groups.map(find)).count\n }\n}\n```
| 6 | 0 |
['Swift']
| 0 |
number-of-provinces
|
✅[Python] Simple and Clean, beats 99.95%✅
|
python-simple-and-clean-beats-9995-by-_t-5q7f
|
Please upvote if you find this helpful. \u270C\n\n\nThis is an NFT\n\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem c
|
_Tanmay
|
NORMAL
|
2023-05-23T20:21:25.284597+00:00
|
2023-05-23T20:21:25.284641+00:00
| 2,273 | false |
### Please upvote if you find this helpful. \u270C\n<img src="https://assets.leetcode.com/users/images/b8e25620-d320-420a-ae09-94c7453bd033_1678818986.7001078.jpeg" alt="Cute Robot - Stable diffusion" width="200"/>\n\n*This is an NFT*\n\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem can be thought of as finding the number of connected components in an undirected graph. Each city represents a node in the graph and an edge exists between two nodes if the cities are directly connected. A province is equivalent to a connected component in the graph.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a disjoint set data structure with each city as a separate set.\n1. Iterate over the adjacency matrix and for each pair of cities that are directly connected, merge their sets using the `union` operation.\n1. The number of provinces is equal to the number of disjoint sets at the end.\n\nThe code uses a disjoint set data structure with path compression and `union` by rank to keep track of the connected components. The `find` function finds the representative element of the set containing `x` and the `union` function merges two sets if their representative elements are different.\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findCircleNum(self, AMat: List[List[int]]) -> int:\n n = len(AMat)\n parent = [i for i in range(n)]\n rank = [1]*(n)\n # find function with path compression\n def find(x):\n p = parent[x]\n while p!=parent[p]:\n parent[p] = parent[parent[p]]\n p = parent[p]\n parent[x] = p\n return p\n\n # union function with union by rank\n def union(x1,x2):\n p1, p2 = find(x1), find(x2)\n if p1==p2:\n return False\n if rank[p1]>=rank[p2]:\n rank[p1]+=rank[p2]\n parent[p2] = p1\n else:\n rank[p2]+=rank[p1]\n parent[p1] = p2\n return True\n # iterate over adjacency matrix and merge sets\n for i in range(n):\n for j in range(i+1, n):\n if AMat[i][j] == 1:\n union(i, j)\n # count number of disjoint sets\n provinces = [find(x) for x in parent]\n return len(set(provinces))\n\n```
| 6 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Union Find', 'Graph', 'Python3']
| 0 |
number-of-provinces
|
Easy & Clear Solution Python3
|
easy-clear-solution-python3-by-moazmar-ojzr
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
moazmar
|
NORMAL
|
2023-03-30T01:13:47.182273+00:00
|
2023-03-30T01:13:47.182306+00:00
| 1,615 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findCircleNum(self, cnx: List[List[int]]) -> int:\n res=0\n n=len(cnx)\n def dfs(i):\n cnx[i][i]=2\n for j in range(0,n):\n if cnx[i][j]==1:\n cnx[i][j]=2\n dfs(j)\n for i in range(0,n):\n if cnx[i][i]==1:\n res+=1\n dfs(i)\n return res\n\n```
| 6 | 0 |
['Depth-First Search', 'Python3']
| 0 |
number-of-provinces
|
BFS ,DFS and disjoint union solution
|
bfs-dfs-and-disjoint-union-solution-by-p-iw92
|
BFS SOLUTION : \n \n\t void bfs(vector> &graph,vector &visited,int src){\n \n queue qu;\n qu.push(src);\n\n while(qu.empty()==fals
|
phoenix2000
|
NORMAL
|
2022-02-12T12:39:33.539738+00:00
|
2022-02-12T12:43:42.068299+00:00
| 610 | false |
**BFS SOLUTION :** \n \n\t void bfs(vector<vector<int>> &graph,vector<bool> &visited,int src){\n \n queue<int> qu;\n qu.push(src);\n\n while(qu.empty()==false){\n int p = qu.front();\n qu.pop();\n\n if(visited[p]==true){\n continue;\n }\n\n visited[p] = true;\n\n for(int i = 0; i<graph.size() ;i++){\n if(visited[i]==false and graph[p][i]==1){\n qu.push(i);\n }\n }\n\n }\n }\n int findCircleNum(vector<vector<int>>& isConnected) {\n \n int cntr = 0;\n vector<bool> visited(isConnected.size() , false);\n\n for(int i = 0; i<isConnected.size();i++){\n if(visited[i]==false){\n bfs(isConnected,visited,i);\n cntr++;\n }\n }\n\n return cntr;\n }\n\t\n**DFS SOLUTION**\n\n\n\t void dfs(vector<vector<int>> &isConnected,int i){\n\t\t\tisConnected[i][i] = 0;\n\t\t\tfor(int j = 0; j<isConnected[i].size() ; j++){\n\t\t\t\tif(isConnected[i][j]==1){\n\t\t\t\t\tisConnected[i][j] = 0; // mark as visited;\n\t\t\t\t\tif(isConnected[j][j]==1){\n\t\t\t\t\t\tdfs(isConnected,j); \n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\tint findCircleNum(vector<vector<int>>& isConnected) {\n\t\t\tint provinces = 0;\n\t\t\tfor(int i = 0; i<isConnected.size() ; i++){\n\t\t\t\tif(isConnected[i][i]==1){\n\t\t\t\t\tprovinces++;\n\t\t\t\t\tdfs(isConnected,i);\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn provinces;\n\t\t}\n\n**UNION BY RANK `&` PATH COMPRESSION**\n\n\t struct UnionFind{\n\t\t\tint *root;\n\t\t\tint *rank;\n\t\t\tint size;\n\n\t\t\tpublic:\n\t\t\t\tUnionFind(int size){\n\t\t\t\t\tthis->size = size;\n\t\t\t\t\troot = new int[size];\n\t\t\t\t\trank = new int[size];\n\n\t\t\t\t\tfor(int i = 0; i<size;i++){\n\t\t\t\t\t\troot[i] = i;\n\t\t\t\t\t\trank[i] = 1;\n\t\t\t\t\t}\n\t\t\t\t}\n\t// work in <O(log n)=> compression\n\t\t\t int find(int x){\n\t\t\t\t if(x==root[x]){\n\t\t\t\t\t return x;\n\t\t\t\t }\n\n\t\t\t\t int p = find(root[x]);\n\n\t\t\t\t root[x] = p;\n\t\t\t\t return p;\n\t\t\t } \n\n\t\t\t\tvoid Union(int x,int y){\n\t\t\t\t\tint rootX = find(x);\n\t\t\t\t\tint rootY = find(y);\n\n\t\t\t\t\tif(rootX==rootY)return;\n\n\n\t\t\t\t\tif(rank[rootX] > rank[rootY]){\n\t\t\t\t\t\troot[rootY] = rootX;\n\t\t\t\t\t}else if(rank[rootX] < rank[rootY]){\n\t\t\t\t\t\troot[rootX] = rootY;\n\t\t\t\t\t}else{ // if size of both are equal\n\t\t\t\t\t\troot[rootY] = rootX;\n\t\t\t\t\t\trank[rootX] += 1;\n\t\t\t\t\t}\n\t\t\t\t}\n\n\t\t\t\tbool connected(int x,int y){\n\t\t\t\t\treturn find(x)==find(y);\n\t\t\t\t}\n\t\t};\n\t\tint findCircleNum(vector<vector<int>>& isConnected) {\n\t\t\tint n = isConnected.size();\n\t\t\tvector<int> LeaderVisit(n,false);\n\t\t\tUnionFind uf(n);\n\t\t\tint connect = 0;\n\t\t\tfor(int i = 0; i<n;i++){\n\t\t\t\tfor(int j = 0;j<n;j++){\n\t\t\t\t\tif(i!=j and isConnected[i][j]==1){\n\t\t\t\t\t\tint p1 = uf.find(i);\n\t\t\t\t\t\tint p2 = uf.find(j);\n\n\t\t\t\t\t\tif(p1!=p2){\n\t\t\t\t\t\t\tconnect++;\n\t\t\t\t\t\t\tuf.Union(i,j);\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\n\t\t\treturn n - connect;\n\t\t}
| 6 | 0 |
['Depth-First Search', 'Breadth-First Search', 'C++']
| 0 |
number-of-provinces
|
Python - DFS Connected Components
|
python-dfs-connected-components-by-sgall-pcnb
|
\nclass Solution(object):\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n circles = 0
|
sgallen
|
NORMAL
|
2019-10-04T17:59:54.688964+00:00
|
2019-10-04T18:01:55.518944+00:00
| 1,066 | false |
```\nclass Solution(object):\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n circles = 0\n length = len(M)\n visited = [False] * length\n\n def dfs(person):\n if visited[person]: return\n visited[person] = True\n for friend, is_friend in enumerate(M[person]):\n if is_friend and not visited[friend]:\n dfs(friend)\n\n for person in xrange(length):\n if visited[person]: continue\n circles += 1\n dfs(person)\n \n return circles\n```
| 6 | 0 |
['Depth-First Search', 'Python']
| 0 |
number-of-provinces
|
C# Solution
|
c-solution-by-csharp-4ocq
|
```\npublic int FindCircleNum(int[,] M) {\n int result = 0;\n bool[] visited = new bool[M.GetLength(0)];\n \n for (int i = 0; i <= M
|
csharp
|
NORMAL
|
2017-06-08T12:52:22.017000+00:00
|
2017-06-08T12:52:22.017000+00:00
| 979 | false |
```\npublic int FindCircleNum(int[,] M) {\n int result = 0;\n bool[] visited = new bool[M.GetLength(0)];\n \n for (int i = 0; i <= M.GetLength(0) - 1; i++)\n if(!visited[i])\n {\n DFS(i, M, visited);\n result++;\n }\n \n return result;\n }\n \n private void DFS(int startNode, int[,] graph, bool[] visited)\n {\n visited[startNode] = true;\n \n for (int i = 0; i <= graph.GetLength(1) - 1; i++)\n {\n if (startNode == i)\n continue;\n \n if (graph[startNode, i] == 1 && !visited[i])\n DFS(i, graph, visited);\n }\n }
| 6 | 1 |
[]
| 1 |
number-of-provinces
|
Number of Provinces (Two Recursive STACK BFS Approach in Java)
|
number-of-provinces-recursive-bfs-approa-z7bs
|
IntuitionThe problem requires us to find the number of provinces (connected components) in a given adjacency matrix.
Each city is a node, and a connection betwe
|
Kushagra_95
|
NORMAL
|
2025-02-22T15:38:22.960771+00:00
|
2025-02-22T15:52:02.325857+00:00
| 1,272 | false |
# Intuition
The problem requires us to find the number of provinces (connected components) in a given adjacency matrix.
- Each city is a node, and a connection between cities represents an edge.
- If a city is connected to another directly or indirectly, they belong to the same province.
- The problem can be visualized as a graph traversal problem where we count the number of connected components.
# Approach
1. **Use BFS to traverse the graph recursively:**
- We maintain a visited array to track visited cities.
Iterate through each city:
- If it's not visited, it means we found a new province.
- Start a BFS traversal using a recursive approach with two functions (bfs1 and bfs2).
- The BFS will visit all connected cities, marking them as visited.
After BFS completes, we increment the province count.
2. **Recursive BFS Implementation:**
- bfs1: Picks a city from the queue, marks its unvisited neighbors, and passes them to bfs2.
- bfs2: Moves the nextQueue into queue and calls bfs1 again.
# Complexity
- **Time complexity:**
- We traverse each city once O(n).
- For each city, we check all its neighbors in O(n).
- Total complexity: O(n²) (since we traverse the adjacency matrix).
- **Space Complexity:**
- O(n) for the visited array.
- O(n) for the recursion call stack in the worst case.
Total: O(n).
# Code
```java []
class Solution {
public static int findCircleNum(int[][] isConnected) {
int n = isConnected.length;
boolean[] visited = new boolean[n];
int provinceCount = 0;
for (int i = 0; i < n; i++) {
if (!visited[i]) {
List<Integer> queue = new ArrayList<>();
queue.add(i);
visited[i] = true;
bfs1(isConnected, queue, visited);
provinceCount++;
}
}
return provinceCount;
}
private static void bfs1(int[][] isConnected, List<Integer> queue, boolean[] visited) {
if (queue.isEmpty()) return;
int city = queue.remove(0);
List<Integer> nextQueue = new ArrayList<>();
for (int neighbor = 0; neighbor < isConnected.length; neighbor++) {
if (isConnected[city][neighbor] == 1 && !visited[neighbor]) {
visited[neighbor] = true;
nextQueue.add(neighbor);
}
}
bfs2(isConnected, queue, nextQueue, visited);
}
private static void bfs2(int[][] isConnected, List<Integer> queue, List<Integer> nextQueue, boolean[] visited) {
if (!nextQueue.isEmpty()) {
queue.addAll(nextQueue);
}
bfs1(isConnected, queue, visited);
}
}
```
```cpp []
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
int n = isConnected.size();
vector<bool> visited(n, false);
int provinceCount = 0;
for (int i = 0; i < n; i++) {
if (!visited[i]) {
vector<int> queue;
queue.push_back(i);
visited[i] = true;
bfs1(isConnected, queue, visited);
provinceCount++;
}
}
return provinceCount;
}
private:
void bfs1(vector<vector<int>>& isConnected, vector<int>& queue, vector<bool>& visited) {
if (queue.empty()) return;
int city = queue.front();
queue.erase(queue.begin());
vector<int> nextQueue;
for (int neighbor = 0; neighbor < isConnected.size(); neighbor++) {
if (isConnected[city][neighbor] == 1 && !visited[neighbor]) {
visited[neighbor] = true;
nextQueue.push_back(neighbor);
}
}
bfs2(isConnected, queue, nextQueue, visited);
}
void bfs2(vector<vector<int>>& isConnected, vector<int>& queue, vector<int>& nextQueue, vector<bool>& visited) {
if (!nextQueue.empty()) {
queue.insert(queue.end(), nextQueue.begin(), nextQueue.end());
}
bfs1(isConnected, queue, visited);
}
};
```
```python []
class Solution:
def findCircleNum(self, isConnected: List[List[int]]) -> int:
n = len(isConnected)
visited = [False] * n
province_count = 0
for i in range(n):
if not visited[i]:
queue = [i]
visited[i] = True
self.bfs1(isConnected, queue, visited)
province_count += 1
return province_count
def bfs1(self, isConnected: List[List[int]], queue: List[int], visited: List[bool]):
if not queue:
return
city = queue.pop(0)
next_queue = []
for neighbor in range(len(isConnected)):
if isConnected[city][neighbor] == 1 and not visited[neighbor]:
visited[neighbor] = True
next_queue.append(neighbor)
self.bfs2(isConnected, queue, next_queue, visited)
def bfs2(self, isConnected: List[List[int]], queue: List[int], next_queue: List[int], visited: List[bool]):
if next_queue:
queue.extend(next_queue)
self.bfs1(isConnected, queue, visited)
```
| 5 | 0 |
['Breadth-First Search', 'C++', 'Java', 'Python3']
| 0 |
number-of-provinces
|
💢☠💫Easiest👾Faster✅💯 Lesser🧠 🎯 C++✅Python3🐍✅Java✅C✅Python🐍✅C#✅💥🔥💫Explained☠💥🔥 Beats 100
|
easiestfaster-lesser-cpython3javacpython-hhor
|
\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n\n Describe your first thoughts on how to solve this problem. \n- J
|
Edwards310
|
NORMAL
|
2024-12-04T06:29:57.354362+00:00
|
2024-12-04T06:29:57.354386+00:00
| 2,117 | false |
\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n- ***JavaScript Code -->*** https://leetcode.com/problems/number-of-provinces/submissions/1469892799\n- ***C++ Code -->*** https://leetcode.com/problems/number-of-provinces/submissions/1469820297\n- ***Python3 Code -->*** https://leetcode.com/problems/number-of-provinces/submissions/1469859399\n- ***Java Code -->*** https://leetcode.com/problems/number-of-provinces/submissions/1469848647\n- ***C Code -->*** https://leetcode.com/problems/number-of-provinces/submissions/1469886584\n- ***Python Code -->*** https://leetcode.com/problems/number-of-provinces/submissions/1469859072\n- ***C# Code -->*** https://leetcode.com/problems/number-of-provinces/submissions/1469890861\n- ***Go Code -->*** https://leetcode.com/problems/number-of-provinces/submissions/1469900329\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N^2)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n# Code\n\n
| 5 | 0 |
['Depth-First Search', 'C', 'Python', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'C#']
| 0 |
number-of-provinces
|
✅ C++ || easy solution || Step By Step Explanation
|
c-easy-solution-step-by-step-explanation-2hxd
|
Approach\n### Understanding the Problem:\n\n- We need to determine the number of provinces (connected components) in a graph where cities are represented as nod
|
NightCat_
|
NORMAL
|
2024-10-02T18:41:25.913594+00:00
|
2024-10-02T18:42:57.157888+00:00
| 455 | false |
# Approach\n### Understanding the Problem:\n\n- We need to determine the number of provinces (connected components) in a graph where cities are represented as nodes and direct connections between cities are represented as edges.\n\n- The graph is represented as an `n x n` matrix isConnected, where `isConnected[i][j]` = 1 indicates that city `i` is directly connected to city `j`.\n\n### Graph Traversal:\n\n- To find all connected components (provinces), we can use Depth-First Search (DFS) or Breadth-First Search (BFS). Here, we\'ll use DFS.\n\n- Each time we initiate a DFS from an unvisited city, we identify a new province.\n\n### Algorithm Steps:\n\n- **Initialization**: Start by initializing a counter (answer) to keep track of the number of provinces. Create a `vector<bool>` called alreadyChecked to track which cities have been visited.\n\n- **Iterate Through Cities**: Loop through each city:\nIf the city has not been visited (`alreadyChecked[i] == false`), initiate a DFS from that city, which means we have found a new province. Increment the answer counter.\n\n- **DFS Implementation**: In the DFS function:\n - If the current city (`cI`) has already been checked, return false (this indicates that we\u2019ve reached a city we\u2019ve already processed).\n - Mark the current city as visited by setting `alreadyChecked[cI]` = true.\n - Loop through all cities to find direct connections:\n If there is a direct connection (`isConnected[cI][i] == 1`), recursively call DFS for city `i`.\n\n- **Return Result**: After iterating through all cities and performing DFS for each unvisited city, return the value of answer as the total number of provinces.\n\n\n# Complexity\n- Time complexity:\nThe time complexity of the algorithm is $$O(n^2)$$ where n is the number of cities. This is because we may need to traverse the entire adjacency matrix to check for direct connections for each city.\n\n- Space complexity:\nThe space complexity is $$O(n)$$ due to the additional space used by the alreadyChecked vector to keep track of visited cities. The recursion stack in the DFS function can also contribute to the space complexity in the worst case, leading to a total space complexity of $$O(n)$$.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int findCircleNum(vector<vector<int>>& isConnected) {\n int answer = 0;\n vector<bool> alreadyChecked(isConnected.size(), false);\n for (int i = 0;i < isConnected.size();i++) {\n if (dfs(isConnected, i, alreadyChecked)) {\n answer++;\n }\n }\n return answer;\n }\n bool dfs(vector<vector<int>>& isConnected,int cI, vector<bool>& alreadyChecked) {\n if (alreadyChecked[cI]) {\n return false;\n }\n alreadyChecked[cI] = true;\n for (int i = 0;i < isConnected.size();i++) {\n if(isConnected[cI][i] == 1) {\n dfs(isConnected, i, alreadyChecked);\n }\n }\n return true;\n }\n};\n```\n\n\n
| 5 | 0 |
['C++']
| 0 |
number-of-provinces
|
Efficient DFS Solution for Provinces 🚀🗺️| Beats 90% in Speed
|
efficient-dfs-solution-for-provinces-bea-bgpw
|
Intuition\nThe problem involves identifying groups of interconnected cities, which can be visualized as finding connected components in an undirected graph. Ini
|
rshikharev
|
NORMAL
|
2024-08-07T11:21:17.262443+00:00
|
2024-08-07T11:21:17.262476+00:00
| 1,688 | false |
# Intuition\nThe problem involves identifying groups of interconnected cities, which can be visualized as finding connected components in an undirected graph. Initially, the thought process involves recognizing that each city and its direct or indirect connections form a distinct group, or province. DFS is an efficient way to traverse these connections and group cities into provinces.\n# Approach\nTo solve the problem, we use Depth-First Search (DFS). Here\'s the step-by-step approach:\n\n1. Initialize a set `visited` to keep track of cities that have already been explored.\n2. Iterate over each city in the matrix. For each unvisited city, initiate a DFS to explore all cities that are connected to it, marking them as visited.\n3. Each DFS initiation from an unvisited city represents the discovery of a new province, so increment the province count accordingly.\n\nThe DFS function will recursively visit each city that is directly connected to the current city, and mark all reachable cities as visited. This ensures that all cities within the same province are identified and marked in a single DFS traversal.\n\n\n\n# Complexity\n- Time complexity: $$O(n^2)$$ because we potentially check every connection between the cities in the `isConnected` matrix. Each city is visited once, and for each visit, we could traverse its connections, leading to a quadratic time complexity.\n\n- Space complexity:\n$$O(n)$$. This is due to the space required for the `visited` set, which stores up to `n` cities, and the recursion stack used by DFS, which, in the worst case, can grow up to the size of `n` if the cities form a single large connected component.\n\n# Code\n```\nclass Solution:\n def findCircleNum(self, isConnected: List[List[int]]) -> int:\n def dfs(city):\n for neighbor, connected in enumerate(isConnected[city]):\n if connected == 1 and neighbor not in visited:\n visited.add(neighbor)\n dfs(neighbor)\n\n n_provinces = 0\n visited = set()\n for city in range(len(isConnected)):\n if city not in visited:\n visited.add(city)\n dfs(city)\n n_provinces += 1\n\n return n_provinces\n```
| 5 | 1 |
['Depth-First Search', 'Breadth-First Search', 'Union Find', 'Graph', 'Python3']
| 1 |
number-of-provinces
|
Simple Union Find
|
simple-union-find-by-kshitij_pandey-cdag
|
Code\n\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n int n = isConnected.length;\n int[] parent = new int[n+1];\n
|
Kshitij_Pandey
|
NORMAL
|
2023-06-01T02:30:19.578487+00:00
|
2023-06-01T02:30:19.578538+00:00
| 29 | false |
# Code\n```\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n int n = isConnected.length;\n int[] parent = new int[n+1];\n int[] size = new int[n+1];\n\n for(int i=0; i<= n; i++){\n parent[i] = i;\n size[i] = 1;\n }\n\n for(int i= 0; i< n; i++){\n for(int j =0; j< n; j++){\n if(isConnected[i][j] == 1){\n int u = find(parent, i+1);\n int v = find(parent, j+1);\n\n if(u != v){\n union(parent, size, u, v);\n }\n }\n }\n }\n int provinces =0;\n for(int i=1; i<= n; i++){\n if(parent[i] == i) provinces++;\n }\n return provinces;\n }\n private int find(int[] parent, int i){\n if(parent[i] != i){\n parent[i] = find(parent, parent[i]);\n }\n return parent[i];\n }\n private void union(int[] parent, int[] size, int u, int v){\n if(u < v){\n parent[u] =v;\n size[v] += size[u];\n }\n else{\n parent[v] =u;\n size[u] += size[v];\n }\n }\n}\n```
| 5 | 0 |
['Java']
| 1 |
number-of-provinces
|
Easy & Clear Solution Python3
|
easy-clear-solution-python3-by-moazmar-ld6m
|
Approach:\n\n1. Initialize a variable res to 0, which will keep track of the total number of provinces.\n2. Get the size of the input matrix isConnected and sto
|
moazmar
|
NORMAL
|
2023-03-30T01:13:49.936743+00:00
|
2023-06-04T00:04:41.993798+00:00
| 928 | false |
# Approach:\n\n1. Initialize a variable res to 0, which will keep track of the total number of provinces.\n2. Get the size of the input matrix isConnected and store it in the variable n.\n3. Define a helper function dfs(i) to perform DFS starting from city i.\n4. In the dfs function, mark city i as visited by setting cnx[i][i] to 2.\n5. Iterate through all cities j from 0 to n-1:\n- If city i and city j are directly connected (cnx[i][j] == 1) and city j is not visited (cnx[j][j] != 2), mark city j as visited by setting cnx[j][j] to 2 and recursively call dfs(j).\n6. Iterate through all cities i from 0 to n-1:\n- If city i is not visited (cnx[i][i] == 1), increment res by 1 and call dfs(i) to explore all the cities in the province.\n7. Return the final result res, which represents the total number of provinces.\n# Complexity:\n# Time complexity:\n The algorithm visits each city at most once, so the time complexity is O(n^2), where n is the number of cities.\n# Space complexity: \nThe space complexity is O(n) for the recursive calls in the DFS function.\n\n# Code\n```\nclass Solution:\n def findCircleNum(self, cnx: List[List[int]]) -> int:\n res=0\n n=len(cnx)\n def dfs(i):\n cnx[i][i]=2\n for j in range(0,n):\n if cnx[i][j]==1:\n cnx[i][j]=2\n dfs(j)\n for i in range(0,n):\n if cnx[i][i]==1:\n res+=1\n dfs(i)\n return res\n\n```
| 5 | 0 |
['Depth-First Search', 'Python3']
| 0 |
number-of-provinces
|
Best O(N) Solution
|
best-on-solution-by-kumar21ayush03-q0up
|
Approach\nUsing DFS Traversal\n\n# Complexity\n- Time complexity:\nO(N) + O(N + 2E) --> O(N)\n\n- Space complexity:\nO(N) + O(N) --> O(N)\n\n# Code\n\nclass Sol
|
kumar21ayush03
|
NORMAL
|
2023-03-11T13:26:29.931980+00:00
|
2023-03-11T13:26:29.932041+00:00
| 359 | false |
# Approach\nUsing DFS Traversal\n\n# Complexity\n- Time complexity:\n$$O(N) + O(N + 2E)$$ --> $$O(N)$$\n\n- Space complexity:\n$$O(N) + O(N)$$ --> $$O(N)$$\n\n# Code\n```\nclass Solution {\nprivate:\n void dfs(int node, vector<vector<int>>& isConnected, vector <bool>& vis) {\n vis[node] = true;\n for (int i = 0; i < vis.size(); i++) {\n if (node != i && !vis[i] && isConnected[node][i])\n dfs(i, isConnected, vis);\n }\n } \npublic:\n int findCircleNum(vector<vector<int>>& isConnected) {\n int n = isConnected.size();\n vector <bool> vis(n, false);\n int cnt = 0;\n for (int i = 0; i < vis.size(); i++) {\n if (!vis[i]) {\n cnt++;\n dfs(i, isConnected, vis);\n }\n }\n return cnt;\n }\n};\n```
| 5 | 0 |
['C++']
| 1 |
number-of-provinces
|
C++ || Using DFS || T.C : O(N^2) || S.C. : O(V)
|
c-using-dfs-tc-on2-sc-ov-by-knowgaurav-g2k0
|
\nclass Solution {\n \n /*\n Time Complexity : O(N^2)\n Space Complexity : O(V)\n */\n \nprivate:\n void dfs(int node, vector<vecto
|
knowgaurav
|
NORMAL
|
2023-01-29T02:14:00.579175+00:00
|
2023-01-29T02:14:00.579219+00:00
| 1,647 | false |
```\nclass Solution {\n \n /*\n Time Complexity : O(N^2)\n Space Complexity : O(V)\n */\n \nprivate:\n void dfs(int node, vector<vector<int>> &adj, vector<bool> &visited){\n visited[node] = true;\n \n for(int v : adj[node]){\n if(!visited[v]){\n dfs(v, adj, visited);\n }\n }\n }\npublic:\n int findCircleNum(vector<vector<int>>& isConnected) {\n int n = isConnected.size();\n vector<vector<int>> adj(n, vector<int>());\n \n for(int i=0; i<n; i++){\n for(int j=0; j<n; j++){\n if(i==j) continue;\n \n if(isConnected[i][j]){\n adj[i].push_back(j);\n }\n }\n }\n \n vector<bool> visited(n, false);\n int count = 0;\n \n for(int i=0; i<n; i++){\n if(!visited[i]){\n dfs(i, adj, visited);\n count++;\n }\n }\n \n return count;\n }\n};\n```
| 5 | 0 |
['Depth-First Search', 'Graph', 'Recursion', 'C++']
| 3 |
number-of-provinces
|
C++ || BFS & DFS approach || Easy and clean code
|
c-bfs-dfs-approach-easy-and-clean-code-b-5cfc
|
Here is my c++ code for this problem.\nBFS approach:-\n\'\'\'\n\n\tclass Solution {\n\tpublic:\n\t\tint findCircleNum(vector>& isConnected) {\n\t\t\tint V=isCon
|
mrigank_2003
|
NORMAL
|
2022-11-09T11:36:21.286065+00:00
|
2022-11-09T11:42:58.127182+00:00
| 987 | false |
Here is my c++ code for this problem.\nBFS approach:-\n\'\'\'\n\n\tclass Solution {\n\tpublic:\n\t\tint findCircleNum(vector<vector<int>>& isConnected) {\n\t\t\tint V=isConnected.size();\n\t\t\tvector<int>adjls[V];\n\t\t\tfor(int i=0; i<V; i++){\n\t\t\t\tfor(int j=0; j<V; j++){\n\t\t\t\t\tif(isConnected[i][j]==1 && i!=j){\n\t\t\t\t\t\tadjls[i].push_back(j);\n\t\t\t\t\t\tadjls[j].push_back(i);\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t\tvector<int>v(V, 0);\n\t\t\tint cnt=0;\n\t\t\tfor(int i=0; i<V; i++){\n\t\t\t\tif(v[i]==0){\n\t\t\t\t\tcnt++;\n\t\t\t\t\tqueue<int>q;\n\t\t\t\t\tq.push(i);\n\t\t\t\t\twhile(!q.empty()){\n\t\t\t\t\t\tint ft=q.front();\n\t\t\t\t\t\tq.pop();\n\t\t\t\t\t\tfor(auto it: adjls[ft]){\n\t\t\t\t\t\t\tif(!v[it]){\n\t\t\t\t\t\t\t\tv[it]=1;\n\t\t\t\t\t\t\t\tq.push(it);\n\t\t\t\t\t\t\t}\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn cnt;\n\t\t}\n\t};\n\'\'\'\nDFS approach:-\n\'\'\'\n\n\tclass Solution {\n\tpublic:\n\t\tvoid dfs(int st, vector<int>adjls[], vector<int>& v){\n\t\t v[st]=1;\n\t\t for(auto it: adjls[st]){\n\t\t\t if(!v[it]){\n\t\t\t\t v[it]=1;\n\t\t\t\t dfs(it, adjls, v);\n\t\t\t }\n\t\t }\n\t }\n\t\tint findCircleNum(vector<vector<int>>& isConnected) {\n\t\t\tint V=isConnected.size();\n\t\t\tvector<int>adjls[V];\n\t\t\tfor(int i=0; i<V; i++){\n\t\t\t\tfor(int j=0; j<V; j++){\n\t\t\t\t\tif(isConnected[i][j]==1 && i!=j){\n\t\t\t\t\t\tadjls[i].push_back(j);\n\t\t\t\t\t\tadjls[j].push_back(i);\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t\tvector<int>v(V, 0);\n\t\t\tint cnt=0;\n\t\t\tfor(int i=0; i<V; i++){\n\t\t\t\tif(v[i]==0){\n\t\t\t\t\tcnt++;\n\t\t\t\t\tint st=i;\n\t\t\t\t\tdfs(st, adjls, v);\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn cnt;\n\t\t}\n\t};\n\'\'\'
| 5 | 0 |
['Depth-First Search', 'Breadth-First Search', 'C']
| 1 |
number-of-provinces
|
Java soln using dfs [If any help needed just comment]
|
java-soln-using-dfs-if-any-help-needed-j-9e83
|
\nclass Solution {\n static class Edge{\n int src;\n int dest;\n Edge(int s,int d){\n this.src=s;\n this.dest=d;\n
|
akash0228
|
NORMAL
|
2022-11-08T14:58:28.725535+00:00
|
2022-11-08T14:58:28.725574+00:00
| 1,275 | false |
```\nclass Solution {\n static class Edge{\n int src;\n int dest;\n Edge(int s,int d){\n this.src=s;\n this.dest=d;\n }\n }\n public int findCircleNum(int[][] isConnected) {\n ArrayList<Edge> graph[]=new ArrayList[isConnected.length];\n for(int i=0;i<isConnected.length;i++){\n graph[i]=new ArrayList<>();\n }\n //graph creation\n for(int i=0;i<isConnected.length;i++){\n for(int j=0;j<isConnected[0].length;j++){\n if(isConnected[i][j]==1){\n graph[i].add(new Edge(i,j));\n } \n }\n }\n int prov=0;\n boolean vist[]=new boolean[graph.length];\n for(int i=0;i<graph.length;i++){\n if(!vist[i]){\n prov++;\n dfsUtil(graph, vist,i);\n }\n }\n return prov;\n \n }\n public static void dfsUtil(ArrayList<Edge> graph[],boolean vist[],int curr){ //O(V+E)\n //visit\n vist[curr]=true;\n //call for neighbours\n for(int i=0;i<graph[curr].size();i++){\n Edge e=graph[curr].get(i);\n if(!vist[e.dest]){\n dfsUtil(graph, vist, e.dest);\n }\n }\n }\n}\n```
| 5 | 0 |
['Depth-First Search', 'Graph', 'Java']
| 2 |
number-of-provinces
|
2 Solutions (BFS & UnionFind)
|
2-solutions-bfs-unionfind-by-zaidzack-zn45
|
\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n int cities = isConnected.length;\n int provinces = 0;\n \n
|
zaidzack
|
NORMAL
|
2022-03-12T07:46:18.442178+00:00
|
2022-07-24T04:39:18.569365+00:00
| 622 | false |
```\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n int cities = isConnected.length;\n int provinces = 0;\n \n boolean[] visited = new boolean[cities];\n Queue<Integer> q = new LinkedList();\n for(int i = 0; i < cities; i++)\n {\n if(!visited[i])\n {\n q.offer(i);\n provinces++;\n }\n while(!q.isEmpty())\n {\n int current = q.poll();\n visited[current] = true;\n for(int j = 0; j < cities; j++)\n {\n if(j != current && isConnected[current][j] == 1 && !visited[j])\n q.offer(j);\n }\n } \n }\n \n return provinces;\n }\n\n}\n```\nUnionFind Solution to perform Union between related Cities.\n\n```\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n int cities = isConnected.length;\n UnionFind uf = new UnionFind(cities);\n boolean[] visited = new boolean[cities];\n for(int i = 0; i < cities; i++)\n {\n visited[i] = true;\n for(int j = 0; j < cities; j++)\n {\n if(i != j && !visited[j] && isConnected[i][j] == 1)\n uf.Union(i, j);\n }\n }\n \n return uf.provinces();\n }\n class UnionFind{\n int components;\n int[] parent;\n \n public UnionFind(int len)\n {\n components = len;\n parent = new int[len];\n \n for(int i = 0; i < len; i++)\n parent[i] = i;\n }\n \n private int Find(int node)\n {\n if(node != parent[node]) \n parent[node] = Find(parent[node]);\n \n return parent[node];\n }\n \n private void Union(int a, int b)\n {\n int parentA = Find(a);\n int parentB = Find(b);\n \n if(parentA == parentB) return;\n \n components--;\n parent[parentA] = parentB;\n }\n \n private int provinces()\n {\n return components;\n }\n }\n}\n```
| 5 | 0 |
['Breadth-First Search', 'Union Find', 'Java']
| 0 |
number-of-provinces
|
Python DFS solution
|
python-dfs-solution-by-kaushikb258-vsul
|
Python DFS solution\n\n\t\tN = len(isConnected)\n visited = [False] * N\n \n conn = defaultdict(list)\n for i in range(N):\n
|
kaushikb258
|
NORMAL
|
2021-03-18T21:54:52.479091+00:00
|
2021-03-18T21:54:52.479135+00:00
| 1,041 | false |
Python DFS solution\n\n\t\tN = len(isConnected)\n visited = [False] * N\n \n conn = defaultdict(list)\n for i in range(N):\n for j in range(N):\n if i != j:\n if isConnected[i][j] == 1:\n conn[i].append(j)\n \n def dfs(i):\n for j in conn[i]:\n if visited[j] == False:\n visited[j] = True\n dfs(j)\n \n nprov = 0\n for i in range(N):\n if visited[i] == False:\n visited[i] = True\n nprov += 1\n dfs(i)\n \n return nprov
| 5 | 0 |
[]
| 1 |
number-of-provinces
|
JavaScript DFS beats 98.97%
|
javascript-dfs-beats-9897-by-ponyoluvsha-ywvh
|
\n\n\nvar findCircleNum = function(isConnected) {\n let visited = new Set, provs = 0;\n for(let i = 0; i < isConnected.length; i++) {\n if(!(visite
|
ponyoluvsham
|
NORMAL
|
2021-02-23T00:23:02.683865+00:00
|
2021-02-23T00:23:02.683897+00:00
| 635 | false |
\n\n```\nvar findCircleNum = function(isConnected) {\n let visited = new Set, provs = 0;\n for(let i = 0; i < isConnected.length; i++) {\n if(!(visited.has(i))) {\n provs++;\n DFS(isConnected, i, visited);\n }\n }\n return provs;\n};\n\nconst DFS = (isConnected, i, visited) => {\n visited.add(i);\n for(let j = 1; j < isConnected.length; j++) {\n if(isConnected[i][j] && !(visited.has(j))) {\n DFS(isConnected, j, visited);\n }\n }\n}\n```
| 5 | 0 |
['Depth-First Search', 'Recursion', 'Ordered Set', 'JavaScript']
| 1 |
number-of-provinces
|
C++ Union Find Solution 94.57% faster than other solutions
|
c-union-find-solution-9457-faster-than-o-c4m4
|
In this we consider making subsets of all friends group and return the value of number of such subsets.\nTo make a friends group subset initially we put\nfriend
|
koko_99
|
NORMAL
|
2020-10-07T12:04:08.709805+00:00
|
2020-10-07T12:04:08.709848+00:00
| 551 | false |
In this we consider making subsets of all friends group and return the value of number of such subsets.\nTo make a friends group subset initially we put\nfriends[i] = i (i.e everyone is a friend of itself)\nthen as we perform union find operation we connect the elements if they do not have same friends initially .\neg . points 1-3 , 2-4 , 3-5 are friends \nthen \nfriends[3] = 1 ; \nfriends[4] = 2 ;\nfriends[5] = 3 ;\nand friends[2] = 2 , friends[1] = 1;\nThen we count the number of elements with friends[i] = i because it showcases either it has no other friend or in a friends group subset one element would have this which is considered the initial point eg. points 1 and 2.\nHere is the solution ,\ni\'ve tried my best to explain it but if u guys have doubts , I\'ll be happy to answer them :)\n```\nclass Solution {\npublic:\n vector<int>friends;\n \t\n int find(int i)\n {\n return friends[i]==i?i:find(friends[i]);\n }\n int findCircleNum(vector<vector<int>>& M) {\n \n int n = M.size();\n friends.resize(n);\n for(int i = 0; i < n; i++){\n friends[i] = i;\n }\n for(int i=0;i<n;i++)\n {\n for(int j = 0;j < n;j++)\n {\n if(M[i][j]==1)\n {\n int x = find(i);\n int y = find(j);\n if(x != y)\n {\n friends[y] = x;\n }\n }\n }\n }\n int ans = 0;\n for(int i = 0;i < n ;i++)\n {\n if(friends[i]==i)\n ans++;\n }\n return ans;\n }\n};\n```\n**Please Upvote if you like it ^_^**
| 5 | 0 |
['Union Find', 'C++']
| 0 |
number-of-provinces
|
Easy to Understand (slow Python) Template for Problem: number of island and friend circle
|
easy-to-understand-slow-python-template-oomqs
|
| 1 | 0 | 0 | 1 |\n|---|---|---|---|\n| 0 | 1 | 1 | 0 |\n| 0 | 1 | 1 | 1 |\n| 1 | 0 | 1 | 1 |\nIf this example is for the problem number of isla
|
frankenstein
|
NORMAL
|
2020-07-02T15:33:43.725826+00:00
|
2020-07-02T15:33:43.725878+00:00
| 563 | false |
| 1 | 0 | 0 | 1 |\n|---|---|---|---|\n| 0 | 1 | 1 | 0 |\n| 0 | 1 | 1 | 1 |\n| 1 | 0 | 1 | 1 |\nIf this example is for the problem number of islands, the answer should be 4: (0, 0), (0, 3), (3, 0), (1, 1) four different starting nodes\n\nFor friend circle, (0, 3) or (3, 0) mean that 0-th and 3-th are friends! Take a moment and let that sink in!\nThis brings 4 isolated islands/friend circles into 1\n\nHow do we explore this kind of relationship?\n\nFor number of islands, we start with a square area in a grid marked as \'1\' then explore its close neighbors if there is. Assume that (i, j) is a grid marked as \'1\'. Then next we will explore its close neighbors: (i+1, j), (i-1, j), (i, j+1), (i, j-1)\n\nFor friend circles, starting point remains the same. The difference is how do you see its close neighbors?\nAssume that (i, j) is what we\'re inspecting now. Assume we stand on this tiny area. Look at your row direction to see if there is any one out there? If there is, he/she is your friend. Do the same for your column direction. \n\nNow, we could reason our neighbors to be explored: we still explore our close neighbors: (i+1, j), (i-1, j), (i, j+1), (i, j-1). But on top of this, we want to explore the entire row and column as well. \n\nAlright. That\'s everything we need to know. Code it up.\n\nJust a tiny change of code and we can solve number of island problem.\n\n\n\n```\nclass Solution:\n def findCircleNum(self, M: List[List[int]]) -> int:\n \n m = len(M)\n n = len(M)\n \n def dfs(i, j):\n if (i, j) in visited:\n return\n \n visited.add((i, j))\n \n # NOTE: potential exploratory places.\n\t\t\t# This is the key differnce between the two problem: number of island and friend circle.\n\t\t\t# number of island: just pick the base\n\t\t\t# friend circle: pick all three (base, tmp1, tmp2)\n\t\t\t\n base = [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]\n tmp1 = [(i, j) for i in range(m)] # column-wise lookup\n tmp2 = [(i, j) for j in range(n)] # row-wise lookup\n \n \n for nodeIndex in base + tmp1 + tmp2:\n if 0 <= nodeIndex[0] < m and 0 <= nodeIndex[1] < n:\n if nodeIndex not in visited and M[nodeIndex[0]][nodeIndex[1]] == 1:\n dfs(nodeIndex[0], nodeIndex[1]) \n \n visited = set()\n count = 0\n for i in range(m):\n for j in range(n):\n if (i, j) not in visited and M[i][j] == 1:\n dfs(i, j)\n count += 1\n \n return count\n#############################\nclass Solution:\n def numIslands(self, grid: List[List[str]]) -> int:\n M = grid\n \n m = len(M)\n count = 0\n \n if m == 0:\n return count\n n = len(M[0])\n \n def dfs(i, j):\n if (i, j) in visited:\n return\n \n \n visited.add((i, j))\n \n \n # potential exploratory places\n base = [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]\n #tmp1 = [(i, j) for i in range(m)]\n #tmp2 = [(i, j) for j in range(n)]\n \n \n for (I, J) in base:\n if 0 <= I < m and 0 <= J < n:\n if (I, J) not in visited and M[I][J] == \'1\':\n dfs(I, J)\n \n \n \n visited = set()\n for i in range(m):\n for j in range(n):\n if (i, j) not in visited and M[i][j] == \'1\':\n dfs(i, j)\n count += 1\n \n return count\n```
| 5 | 0 |
[]
| 0 |
number-of-provinces
|
C# - Simple DFS to count number of disjoint, each forming one friend circle
|
c-simple-dfs-to-count-number-of-disjoint-qh3i
|
csharp\npublic int FindCircleNum(int[][] M) \n{\n\tbool[] visited = new bool[M.Length];\n\tint groups = 0;\n\n\tfor(int i = 0; i < M.Length; i++)\n\t{\n\t\tif(!
|
christris
|
NORMAL
|
2020-05-30T11:10:56.411509+00:00
|
2020-05-30T11:10:56.411627+00:00
| 292 | false |
```csharp\npublic int FindCircleNum(int[][] M) \n{\n\tbool[] visited = new bool[M.Length];\n\tint groups = 0;\n\n\tfor(int i = 0; i < M.Length; i++)\n\t{\n\t\tif(!visited[i])\n\t\t{\n\t\t\tvisited[i] = true;\n\t\t\tdfs(M, i, visited);\n\t\t\tgroups++;\n\t\t}\n\t} \n\n\treturn groups;\n}\n\nprivate void dfs(int[][] M, int node, bool[] visited)\n{\n\tfor(int neighbour = 0; neighbour < M.Length; neighbour++)\n\t{\n\t\tif(M[node][neighbour] == 1 && !visited[neighbour])\n\t\t{\n\t\t\tvisited[neighbour] = true;\n\t\t\tdfs(M, neighbour, visited);\n\t\t}\n\t}\n}\n```
| 5 | 0 |
[]
| 0 |
number-of-provinces
|
c++ 12ms O(N^2) recursion
|
c-12ms-on2-recursion-by-jeremy41-brma
|
\nclass Solution {\npublic:\n void clear(vector<vector<int>>& M, int p) {\n M[p][p] = 0;\n for (int i = 0; i < M.size(); ++i) {\n if
|
jeremy41
|
NORMAL
|
2018-11-14T15:29:34.110774+00:00
|
2018-11-14T15:29:34.110815+00:00
| 270 | false |
```\nclass Solution {\npublic:\n void clear(vector<vector<int>>& M, int p) {\n M[p][p] = 0;\n for (int i = 0; i < M.size(); ++i) {\n if (M[i][i] == 1 && M[p][i] == 1) clear(M, i);\n }\n }\n \n int findCircleNum(vector<vector<int>>& M) {\n int cnt = 0;\n for (int i = 0; i < M.size(); ++i) {\n if (M[i][i] == 1) {\n ++cnt;\n clear(M, i);\n }\n }\n return cnt;\n }\n};\n```
| 5 | 0 |
[]
| 0 |
number-of-provinces
|
python dfs iter version
|
python-dfs-iter-version-by-zqfan-b3j7
|
recursion version is easier to understand, but the iterate version shows up in my mind firstly.\n\nclass Solution(object):\n def findCircleNum(self, M):\n
|
zqfan
|
NORMAL
|
2017-04-02T05:13:44.869000+00:00
|
2018-08-13T01:38:53.511358+00:00
| 1,336 | false |
recursion version is easier to understand, but the iterate version shows up in my mind firstly.\n```\nclass Solution(object):\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n circle = 0\n n = len(M)\n for i in xrange(n):\n if M[i][i] != 1:\n continue\n friends = [i]\n while friends:\n f = friends.pop()\n if M[f][f] == 0:\n continue\n M[f][f] = 0\n for j in xrange(n):\n if M[f][j] == 1 and M[j][j] == 1:\n friends.append(j)\n circle += 1\n return circle\n```\nother people have already posted recursion solutions, but here I still paste mine:\n```\nclass Solution(object):\n def findCircleNum(self, M):\n """\n :type M: List[List[int]]\n :rtype: int\n """\n def dfs(node):\n visited.add(node)\n for friend in xrange(len(M)):\n if M[node][friend] and friend not in visited:\n dfs(friend)\n\n circle = 0\n visited = set()\n for node in xrange(len(M)):\n if node not in visited:\n dfs(node)\n circle += 1\n return circle\n```
| 5 | 0 |
[]
| 0 |
number-of-provinces
|
Java Detailed Solution for beginners 🚀🚀🚀🚀
|
java-detailed-solution-for-beginners-by-i9itu
|
Approach\n1. Construct a Graph Representation:\nFirst, we convert the adjacency matrix into a graph representation that\'s easier to traverse. Each node (or cit
|
utkarshpriyadarshi5026
|
NORMAL
|
2024-05-07T20:21:55.867624+00:00
|
2024-05-07T20:21:55.867654+00:00
| 989 | false |
# Approach\n1. **Construct a Graph Representation:**\nFirst, we convert the adjacency matrix into a graph representation that\'s easier to traverse. Each node (or city) is connected \u27A1\uFE0F to its neighbors a based on the matrix. For each `1` in the adjacency matrix that isn\'t on the diagonal (ignoring self-loops), we add a connection.\n\n\n ```\n public Map<Integer, List<Integer>> makeGraph(int[][] connected) {\n Map<Integer, List<Integer>> graph = new HashMap<>();\n for (int i = 0; i < connected.length; i++) {\n graph.put(i, new ArrayList<>()); // Initialize a list for each node\n }\n for (int i = 0; i < connected.length; i++) {\n for (int j = 0; j < connected[i].length; j++) {\n if (connected[i][j] == 1 && i != j) { // Ensure we are adding only valid connections\n graph.get(i).add(j); // Add a connection from node i to node j\n }\n }\n }\n return graph; // Return the fully formed graph\n }\n ```\n2. **Depth First Search (DFS) to Explore Connected Components:**\nWe use a recursive DFS to explore each node\'s connections thoroughly. Once we start a DFS from a node, we mark all reachable nodes as visited, which means they all belong to the same province.\n\n ```\n public void dfs(int node, Map<Integer, List<Integer>> graph, boolean[] visited) {\n visited[node] = true; // Mark this node as visited\n List<Integer> neighbors = graph.get(node); // Get all direct connections\n\n for (int neighbor : neighbors) {\n if (!visited[neighbor]) { // If the neighbor hasn\'t been visited\n this.dfs(neighbor, graph, visited); // Recursively visit this node\n }\n }\n }\n ```\n\n3. **Count Provinces by Initiating DFS Where Necessary:**\nWe iterate through all nodes and initiate a DFS from each unvisited node. Each initiation of DFS corresponds to a new province, and thus, we increase our province count each time we start a new DFS from an unvisited node.\n ```\n public int findCircleNum(int[][] isConnected) {\n Map<Integer, List<Integer>> graph = makeGraph(isConnected);\n boolean[] visited = new boolean[isConnected.length];\n int provinces = 0;\n for (int i = 0; i < isConnected.length; i++) {\n if (!visited[i]) { // If this node has not been visited\n this.dfs(i, graph, visited); // Perform DFS from this node\n provinces++; // Increment the province count\n }\n }\n return provinces; // Return the total number of provinces found\n }\n ```\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$ - The time complexity of this solution is $$O(n^2)$$, where $$n$$ is the number of cities or nodes in the matrix `isConnected`. The complexity arises from two main operations:\n\n - The `makeGraph` method iterates through every element in the `isConnected` matrix, which is a $$n\xD7n$$ matrix, to construct the adjacency list representation of the graph.\n\n - The DFS traversal is invoked for each unvisited node to explore all its connected components. While each DFS call itself might seem \uD83E\uDD28 to explore multiple nodes more than once across different calls, each node is `visited` exactly once \uD83E\uDD17 due to the visited array check.\n\n- Space complexity:\n$$O(n)$$ - The space complexity is $$O(n)$$. The main contributors to space complexity are:\n\n - The adjacency list, which in the worst case (when every node is connected to every other node) contains $$n$$ lists, each potentially with up to $$n$$ entries. However, in practice, because *each edge (connection) is only stored once, it contributes linearly to the space.*\n\n - A `visited` array of size $$n$$ that keeps track of which nodes have been visited.\n\n# Code\n```\nclass Solution {\n public int findCircleNum(int[][] isConnected) {\n Map<Integer, List<Integer>> graph = makeGraph(isConnected);\n boolean[] visited = new boolean[isConnected.length];\n int provinces = 0;\n for (int i = 0; i < isConnected.length; i++) {\n if (visited[i]) continue;\n this.dfs(i, graph, visited);\n provinces++;\n }\n return provinces;\n\n }\n\n public void dfs(int node, Map<Integer, List<Integer>> graph, boolean[] visited) {\n visited[node] = true;\n List<Integer> nbrs = graph.get(node);\n\n for (int nbr : nbrs) {\n if (!visited[nbr])\n this.dfs(nbr, graph, visited);\n }\n }\n\n public Map<Integer, List<Integer>> makeGraph(int[][] connected) {\n Map<Integer, List<Integer>> graph = new HashMap<>();\n for (int i = 0; i < connected.length; i++) {\n graph.put(i, new ArrayList<>());\n }\n for (int i = 0; i < connected.length; i++) {\n for (int j = 0; j < connected[0].length; j++) {\n if (connected[i][j] == 1)\n graph.get(i).add(j);\n }\n }\n return graph;\n }\n}\n```
| 4 | 0 |
['Depth-First Search', 'Java']
| 0 |
number-of-provinces
|
Beginner-friendly solution using C++ || DSU || Beats 99,47% Users
|
beginner-friendly-solution-using-c-dsu-b-dea0
|
\n\n# Code\n\nclass Solution {\npublic:\n int findCircleNum(vector<vector<int>>& isConnected) {\n int n = isConnected.size();\n\n vector<int> p
|
truongtamthanh2004
|
NORMAL
|
2024-04-27T06:59:20.563898+00:00
|
2024-04-27T06:59:20.563929+00:00
| 924 | false |
\n\n# Code\n```\nclass Solution {\npublic:\n int findCircleNum(vector<vector<int>>& isConnected) {\n int n = isConnected.size();\n\n vector<int> parent(n);\n for (int i = 0; i < n; i++)\n {\n parent[i] = i;\n }\n\n int res = n;\n\n for (int i = 0; i < n; i++) \n {\n for (int j = i + 1; j < n; j++)\n {\n if (isConnected[i][j] == 1) \n {\n int x = Find(i, parent);\n int y = Find(j, parent);\n\n if (x == y) continue;\n\n res--;\n if (x > y) \n parent[x] = y;\n else\n parent[y] = x;\n }\n }\n }\n\n return res;\n }\n\nprivate:\n\n int Find(int x, vector<int>& parent)\n {\n if (x != parent[x]) \n {\n parent[x] = Find(parent[x], parent);\n }\n\n return parent[x];\n }\n};\n```
| 4 | 0 |
['C++']
| 0 |
number-of-provinces
|
[C++] Disjoint Set Union - Clean Code - "Template for most of DSU problem"
|
c-disjoint-set-union-clean-code-template-2b93
|
\n# Code\n\nclass DSU{\nprivate:\n vector<int>Parent,Size;\npublic :\n DSU(int n){\n Parent.resize(n);\n Size.resize(n);\n for(int i=
|
lshigami
|
NORMAL
|
2024-04-19T01:53:15.328219+00:00
|
2024-04-19T01:53:15.328241+00:00
| 156 | false |
\n# Code\n```\nclass DSU{\nprivate:\n vector<int>Parent,Size;\npublic :\n DSU(int n){\n Parent.resize(n);\n Size.resize(n);\n for(int i=0;i<n;i++){\n Parent[i]=i;\n Size[i]=1;\n }\n }\n int Find(int x){\n if(x==Parent[x]) return x;\n return Parent[x]=Find(Parent[x]);\n }\n bool Union(int x,int y){\n x=Find(x);\n y=Find(y);\n if(x==y) return false;\n if(Size[x]<Size[y]){\n swap(x,y);\n }\n Parent[y] = x;\n Size[x] += Size[y];\n return true;\n }\n};\nclass Solution {\npublic:\n int findCircleNum(vector<vector<int>>& isConnected) {\n int n=isConnected.size();\n DSU dsu(n);\n int ans=n;\n for(int i=0;i<n;i++){\n for(int j=i+1;j<n;j++){\n if(isConnected[i][j] && dsu.Find(i)!=dsu.Find(j) ){\n ans-=1;\n dsu.Union(i,j);\n }\n }\n }\n return ans;\n }\n};\n```
| 4 | 0 |
['C++']
| 1 |
number-of-provinces
|
Striver Sheet||🔥Easy C++ Solution Using DFS || Beats 96.47%
|
striver-sheeteasy-c-solution-using-dfs-b-by51
|
\n\n# Intuition\nA province is a group of directly or indirectly connected cities and no other cities outside of the group. Considering the above example, we ca
|
vanshwari
|
NORMAL
|
2024-03-05T11:44:34.467024+00:00
|
2024-03-13T08:26:19.070850+00:00
| 611 | false |
\n\n# Intuition\nA province is a group of directly or indirectly connected cities and no other cities outside of the group. Considering the above example, we can go from 1 to 2 as well as to 3, from every other node in a province we can go to each other. As we cannot go from 2 to 4 so it is not a province. We know about both the traversals, Breadth First Search (BFS) and Depth First Search (DFS). We can use any of the traversals to solve this problem because a traversal algorithm visits all the nodes in a graph. In any traversal technique, we have one starting node and it traverses all the nodes in the graph. Suppose there is an \u2018N\u2019 number of provinces so we need to call the traversal algorithm \u2018N\u2018 times, i.e., there will be \u2018N\u2019 starting nodes. So, we just need to figure out the number of starting nodes.\n\n# Approach\n1. We initialize a vector `visited` to keep track of visited cities. Initially, all cities are marked as not visited.\n2. We iterate through each city, and if a city is not visited, we perform DFS to traverse all directly and indirectly connected cities.\n3. During DFS, we mark each visited city as visited in the `visited` vector.\n4. We increment the province count every time we start DFS from an unvisited city.\n5. Finally, we return the total number of provinces.\nThe number of provinces signify no. of component in graph\n# Complexity\n- Time complexity: O(N) + O(V+2E), Where O(N) is for outer loop and inner loop runs in total a single DFS over entire graph, and we know DFS takes a time of O(V+2E). \n- Space complexity: O(n), where n is the number of cities. We use the `visited` vector to keep track of visited cities.\n# Code\n```\nclass Solution {\npublic:\n void dfs(int i, vector<int>&visited, std::vector<std::vector<int>>& roads) {\n visited[i] = 1;\n for (int j=0;j<roads[i].size();j++) {\n if(roads[i][j]==0)continue;\n if (visited[j]==0) {\n dfs(j, visited, roads);\n }\n }\n}\n int findCircleNum(vector<vector<int>>& roads) {\n int n=roads.size();\n vector<int>visited(n,0); \n int ans = 0;\n for (int i = 0; i < n; i++) {\n if (visited[i]==0) {\n ans++;\n dfs(i, visited, roads);\n }\n }\n return ans;\n }\n};\n```
| 4 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Union Find', 'Graph', 'C++']
| 0 |
number-of-provinces
|
easy c++
|
easy-c-by-harsh_saini_3878-3odf
|
Approach:\n\nHar node ko ek baar mark karte hain, aur uske saare connected nodes ko mark karte hain.\nJo nodes mark nahi ki gayi hain, unko dekhte hain aur unke
|
HARSH_SAINI_3878
|
NORMAL
|
2024-01-21T12:27:13.259109+00:00
|
2024-01-21T12:27:13.259142+00:00
| 7 | false |
Approach:\n\nHar node ko ek baar mark karte hain, aur uske saare connected nodes ko mark karte hain.\nJo nodes mark nahi ki gayi hain, unko dekhte hain aur unke connected nodes ko bhi mark karte hain.\nYeh process har unvisited node ke liye repeat hota hai, jisse connected components milte hain.\nTotal kitne connected components hain, woh count hota hai, aur wahi answer hai.\nTime Complexity (tc):\n\nHar node ko ek baar dekhna padta hai, aur har node ke saath connected nodes ko bhi dekhna padta hai. Isse O(V + E) time complexity aata hai, jahan V nodes hain aur E edges hain.\nSpace Complexity (sc):\n\nHar node ko mark karne ke liye ek boolean array (vis) use hoti hai. Worst case mein saare nodes mark hote hain, isliye space complexity O(V) hota hai, jahan V nodes hain.\nCode Explanation:\n\nfindCircleNum function mein har node ko dekha jata hai aur unke saath connected nodes ko DFS se mark kiya jata hai.\nHar unvisited node ke liye yeh process repeat hoti hai.\nFinal count, jo connected components ko represent karta hai, woh return kiya jata hai.\n\n# Code\n```\nclass Solution {\npublic:\nint n;\nvoid dfs(vector<vector<int>>& isConnected,int u,vector<bool>&vis){\n vis[u]=true;\n for(int v=0;v<n;v++){\n if(!vis[v] && isConnected[u][v]==1 ){\n dfs(isConnected, v,vis);\n }\n }\n}\n int findCircleNum(vector<vector<int>>& isConnected) {\n n=isConnected.size();\n vector<bool>vis(n,false);\n int count=0;\n for(int i=0;i<n;i++){\n if(!vis[i]){\n count++;\n dfs(isConnected,i,vis);\n }\n }\n return count;\n }\n};\n```
| 4 | 0 |
['Depth-First Search', 'C++']
| 0 |
number-of-provinces
|
[C++] ✅|| Using Disjoint Set 💯|| Union by Rank 🔥
|
c-using-disjoint-set-union-by-rank-by-ri-i3ze
|
\nclass DisjointSet {\npublic:\n vector<int> rank, parent;\n\n DisjointSet(int n)\n {\n rank.resize(n + 1, 0);\n parent.resize(n + 1);\n
|
RIOLOG
|
NORMAL
|
2023-11-13T15:00:01.214048+00:00
|
2023-11-13T15:00:01.214078+00:00
| 17 | false |
```\nclass DisjointSet {\npublic:\n vector<int> rank, parent;\n\n DisjointSet(int n)\n {\n rank.resize(n + 1, 0);\n parent.resize(n + 1);\n for (int i = 0; i <= n; i++) \n {\n parent[i] = i;\n }\n }\n\n int findUPar(int node)\n {\n if (node == parent[node]) return node;\n return parent[node] = findUPar(parent[node]);\n }\n\n void unionByRank(int u, int v)\n {\n int ulp_u = findUPar(u);\n int ulp_v = findUPar(v);\n\n if (ulp_u == ulp_v) return;\n if (rank[ulp_u] < rank[ulp_v]) parent[ulp_u] = ulp_v;\n else if (rank[ulp_v] < rank[ulp_u]) parent[ulp_v] = ulp_u;\n else \n {\n parent[ulp_v] = ulp_u;\n rank[ulp_u]++;\n }\n }\n};\n\nclass Solution {\npublic:\n int findCircleNum(vector<vector<int>>& isConnected) \n {\n // Using disjoint set:\n int n = isConnected.size();\n DisjointSet ds(n);\n\n for (int i = 0; i < isConnected.size(); i++)\n {\n for (int j = 0; j < isConnected[0].size(); j++) \n {\n if (isConnected[i][j] == 1)\n ds.unionByRank(i, j);\n }\n }\n\n int totalComponent = 0;\n for (int i = 0; i < n; i++)\n {\n if (ds.findUPar(i) == i) totalComponent += 1;\n }\n\n return totalComponent;\n }\n};\n```
| 4 | 0 |
['C++']
| 0 |
number-of-provinces
|
Simple C++ solution
|
simple-c-solution-by-gcsingh1629-qfqz
|
\n# BFS\n\nclass Solution {\npublic: \n int findCircleNum(vector<vector<int>> &isConnected){\n int n=isConnected.size();\n vector<int> adj[n];\
|
gcsingh1629
|
NORMAL
|
2023-08-25T02:40:54.798604+00:00
|
2023-08-25T02:40:54.798622+00:00
| 74 | false |
\n# BFS\n```\nclass Solution {\npublic: \n int findCircleNum(vector<vector<int>> &isConnected){\n int n=isConnected.size();\n vector<int> adj[n];\n for(int i=0;i<n;i++){\n for(int j=0;j<n;j++){\n if(isConnected[i][j]==1){\n adj[i].push_back(j);\n adj[j].push_back(i);\n }\n }\n }\n vector<int> visited(n,0);\n queue<int> q;\n int res=0;\n for(int i=0;i<n;i++){\n if(!visited[i]){\n visited[i]=1;\n q.push(i);\n res++;\n while(!q.empty()){\n int node=q.front();\n q.pop();\n for(auto adjNode:adj[node]){\n if(!visited[adjNode]){\n visited[adjNode]=1;\n q.push(adjNode);\n }\n }\n }\n }\n }\n return res;\n }\n};\n\n```\n# DFS\n```\nclass Solution {\npublic: \n void dfs(int node,vector<int> adj[],vector<int> &visited){\n visited[node]=1;\n for(auto it:adj[node]){\n if(!visited[it]){\n dfs(it,adj,visited);\n }\n }\n }\n int findCircleNum(vector<vector<int>>& isConnected) {\n int m=isConnected.size(),n=isConnected[0].size();\n vector<int> visited(m,0);\n vector<int> adj[m];\n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n if(isConnected[i][j]==1){\n adj[i].push_back(j);\n adj[j].push_back(i);\n }\n }\n }\n int res=0;\n for(int i=0;i<m;i++){\n if(!visited[i]){\n dfs(i,adj,visited);\n res++;\n }\n }\n return res;\n }\n};\n\n```
| 4 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Graph', 'C++']
| 0 |
number-of-provinces
|
[Python] - Simple & Clean Solution - Using DFS
|
python-simple-clean-solution-using-dfs-b-bdcu
|
Code\n\nclass Solution:\n def findCircleNum(self, g: List[List[int]]) -> int:\n v = [False] * len(g)\n\n def dfs(i):\n for j in rang
|
yash_visavadia
|
NORMAL
|
2023-07-02T11:15:11.297043+00:00
|
2023-07-02T11:15:11.297060+00:00
| 1,668 | false |
# Code\n```\nclass Solution:\n def findCircleNum(self, g: List[List[int]]) -> int:\n v = [False] * len(g)\n\n def dfs(i):\n for j in range(len(g)):\n if g[i][j] and not v[j]:\n v[j] = True\n dfs(j)\n\n ans = 0\n for i in range(len(g)):\n if not v[i]:\n dfs(i)\n ans += 1\n return ans\n```
| 4 | 0 |
['Depth-First Search', 'Graph', 'Python3']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.